The holistic pattern
|
The gematria number values of the ten Sephiroth in the four Kabbalistic Worlds are given here for reference:

(The listed numbers are written in bold wherever they appear in the text).
The inner form of the Tree of Life, the I Ching table of 64 hexagrams, the five Platonic solids, the Sri Yantra and the disdyakis triacontahedron are equivalent representations of holistic systems that express the divine paradigm. This is demonstrated in this website, firstly, by showing how the Godname numbers of the ten Sephiroth mathematically determine aspects of their structure, thereby revealing their holistic nature, and, secondly, by proving that their properties are quantified in analogous ways by the same set of parameters, which display the following divisions:
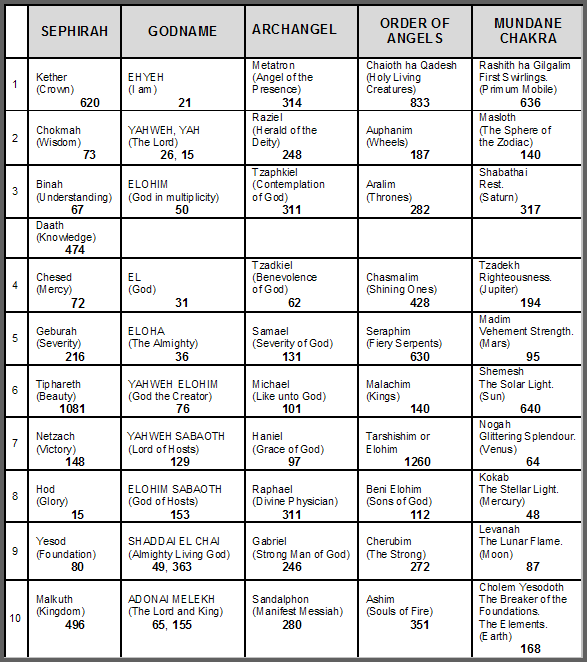
Holistic systems always exhibit these patterns of divisions (apart, perhaps, from a factor of 10). Explicitly, they are:
|
384 = |
192 + 192 |
|
= |
[24+168] + [24+168] |
|
= |
[3+21+84+84] + [3+21+84+84] |
|
= |
(3+3) + (21+21) + (84+84) + (84+84) |
|
= |
6 + 42 + (168+168) |
|
= |
48 + 336, |
where
48 = 24 + 24,
24 = 3
+ 21,
336 = 168 + 168,
168 = 84 + 84,
and
192 = 24 + 168.
Each division will now be illustrated in the context of the various sacred geometries that are discussed in this website. The author’s research articles and latest book analyze in more detail how various sacred geometries display these parameters and divisions.
384 = 192 + 192
The primary split of the holistic parameter 384 into two 192’s represents a bifurcation or — more accurately —a polarisation of the system into two complementary but polar-opposite sets of elements. For the case of sacred geometries, it divides into two halves that are either: 1. mirror images of each other, if the sacred geometry has inversion symmetry; 2. related by a 1:1 isomorphic mapping between pairs of structural elements belonging to each half; 3. related to each other as metaphysical opposites. For example:
1. 7-tree
Counting from its base, there are 384 yods up to the top of
the 7-tree mapping the Theosophical "physical plane" (the physical universe) when its triangles are tetractyses.
There are 192 yods below Chesed of the fourth Tree and 192 yods from the top of the 7-tree down to the Path
connecting Chesed and Geburah of this Tree (see here).
2. Inner Tree of Life
3. Outer & inner Tree of Life
When combined, they comprise 384 points,
lines & triangles outside the root edge. Because each is symmetric with respect to reflection in a plane
containing the central Pillar of Equilibrium, 192 such geometrical elements can be associated with the left-hand
side of the combined pair of objects and 192 geometrical elements can be associated with their right-hand side
(see here). Also, the 384 geometrical elements comprise 192 points
& triangles and 192 sides (see previous link).
4. The I Ching table of 64 hexagrams
The 384 lines & broken lines making up the 64 hexagrams of the I Ching table comprise 192 (Yang) lines and 192 (Yin) broken lines (see here & here).
5. Sri Yantra
When its 43 triangles are turned into tetractyses, 192 yods are in one half of the Sri Yantra and 192 yods are in
its other half (see here & here). However, because these halves are not mirror images of each other, the
corresponding members of each pair of yods are not reflections of each other across the horizontal plane. There
is mirror symmetry across the vertical plane, but the pairing disappears for those yods lying along the
vertical axis. What is crucial here is not the lack of mirror symmetry but the inversion symmetry through the
centre of the Sri Yantra. This means that each hexagonal yod on the sides of the central tetractys has its
counterpart in the other triangular array whose overlap forms a Star of David, so that the 384 yods really do
divide into 192 pairs.
6. Disdyakis triacontahedron
Surrounding an axis passing through two diametrically opposite A vertices are 384 geometrical elements in its faces (60 vertices, 180 edges & 120 triangles) and in the central 12-gon (12 triangular sectors & their 12 internal sides) that is perpendicular to this axis. They divide into the 192 elements making up one half of the polyhedron & 12-gon and the 192 inverted images of these elements in their other half (see here).
7. {3,7} tiling of 3-torus
When the 56 triangles of the {3,7} tiling of the 3-torus are
turned into tetractyses, 192 yods line their sides. Similarly, 192 yods line the sides of the 56 tetractyses in
the turned inside-out version of the 3-torus (see here).
8. F4 as an exceptional subgroup of E8
The dimension of the rank-8, exceptional Lie group E8 is 248. It has 8 simple roots and
240 roots. Its exceptional subgroup F4 has 48 roots. There are
(240−48=192) roots of E8 that are not roots of F4. In the case of
E8×E8, one of the two anomaly-free symmetry groups describing superstrings, it has
(192+192=384) roots that are not roots of the two similar F4 groups it contains. The 48
roots of F4 divide into two sets of 24, each defined by an 8-d root vector. Each set has (8×24=192)
coordinates in its 24 root vectors. For more details see (7) here.
In the case of the seven musical scales, the primary 192:192
division in this holistic system manifests as the 192 rising intervals between their notes and their 192 falling
counterparts, when the tonic, unit interval and the octave are included (see here).
|
|
|
Shiva and Shakti |
Holistic systems, therefore, display a fundamental two-foldness,
or duality, being composed of 192 pairs of elements that are either mirror-images or polar
opposites of each other in some sense, just as members of a biological species are divided into males and
females. In the case of the notes of the seven musical scales, rising and falling intervals are the musical
counterpart of reflected or inverted geometrical elements. The 192:192 division of the global parameter 384 is a
manifestation of a fundamental duality present in all holistic systems. In Taoism it is embodied in the cosmic
duality of Yang and Yin. In the Kabbalistic Tree of Life it is represented by the right-hand Pillar of Mercy and
the left-hand Pillar of Judgement. In Tantric Hinduism it is personified by the divine masculine power invested
in the God Shiva and the divine feminine power of the Goddess Shakti, sometimes referred to in Hinduism as “The
Great, Divine Mother.” One of the ways this cosmic polarity manifests in physics is as the basic distinction
between matter and antimatter. Another way is the difference between the positive and negative UPAs — the two
chiral forms of the basic units of physical matter that Annie Besant & C.W.
Leadbeater claimed over a century ago make up the subatomic particles that they described with
micro-psi vision (see here) and which the author has proved are the constituents of the quarks
making up protons and neutrons inside atomic nuclei (see here). The two types of UPAs carry "colour magnetic charges" of opposite
sign.
The Decad expresses the beautiful, mathematical properties of holistic systems. An example of this is that 385 yods other than the three corners of the central triangle (symbolizing the trimûrti, or Hindu trinity, of Shiva, Brahma & Vishnu) surround the central bindu point of the 3-dimensional Sri Yantra when it is constructed from tetractyses, where
|
12 |
||||
| 22 | 32 | |||
| 385 = |
42 |
52 |
62 |
|
|
72 |
82 | 92 | 102 |
see here). The Tree of Life counterpart of the 384 yods in the Sri Yantra that surround the centre of the central triangle are the 384 yods up to the top of the 7-tree that maps the Theosophical physical plane, namely, the physical universe with 25 spatial dimensions (see here). They divide into 192 yods below the Chesed-Geburah Path of the fourth Tree of Life and 192 yods down to this point. As another example of the influence of the Decad, there are 385 tetractyses below the top of the 10-tree prescribed by ADONAI, the Godname of Malkuth, that contain 1680 yods — the Tree of Life basis of the 1680 turns of each ten-dimensional whorl making up the UPA as the subquark state of the E8×E8 heterotic superstring (see here). Their counterparts in the disdyakis triacontahedron are the 385 extra yods needed to transform into Type A triangles the sectors of the seven polygons perpendicular to an axis passing through two opposite C vertices that are formed by its vertices and which lie either above or below its central plane [1]. The centres of these seven polygons correspond in the Sri Yantra to the lowest corner of the central triangle and the six hexagonal yods on its three sides.
192 = 24 +
168
Each half of a holistic system embodying the holistic parameter 192 divides into a basic set of 24 elements and a set of 168 elements that fill out the form delineated by the primary elements. For example:
Inner Tree of Life
Their counterparts in each half of the inner Tree of Life are the 24 geometrical elements surrounding the centre of the hexagon and the 168 geometrical elements surrounding the centres of the six other polygons when they are all divided into their sectors. Their counterparts in the first (6+6) enfolded polygons are the 24 corners of each set of the first six enfolded polygons outside the root edge and the 168 other yods associated with them when their sectors become tetractyses.
The I Ching table of 64 hexagrams
In each diagonal half of the I Ching table, they are the 24 Yang & Yin lines making up the eight upper or lower trigrams in its eight diagonal hexagrams and the 168 Yang & Yin lines in the 28 off-diagonal hexagrams.
Sri Yantra
There are 24 hexagonal yods either at the centres of the 21 triangles in each half of the Sri Yantra or at the corners of each overlapping triangle forming a Sign of Vishnu/Star of David within its central triangle. There are also 168 yods lying on the 63 edges of these triangles.
Disdyakis triacontahedron
24 geometrical elements make up each half of the central, 12-sided polygon perpendicular to an axis passing through two opposite A vertices; 168 geometrical elements (24 vertices, 84 edges & 60 triangles) are above or below it.
Seven musical scales
There are 21 notes above the tonic comprising second, third & fourth notes, as well as the tonic, unit interval & octave interval, totalling 24 intervals, and 168 remaining intervals between the notes of the seven musical scales (including notes below the octave that are the inversions* of these 21 notes).
Roots of E8
The 192 roots in
E8 that are not roots of F4 consist of the 168 roots that are not roots
of E6 and the 24 roots in E6 that are not roots of F4.
In this division, the number 24 denotes the primary/basic elements that determine the global nature of a holistic system and the number 168 measures those elements that build up the complete form of the system delineated in skeletal outline by these 24 building blocks.
The number 4 (tetrad) generates the division 192 = 24 + 168 in the following way: four different objects have:
Therefore, (24+72+96=24+168=192) objects make up the (12+24+24=60) permutations of 2, 3 & 4 objects, each object appearing 48 times. The 192 objects consist of the 24 objects making up the 12 permutations of 2 objects and the 168 objects that make up the 48 permutations of 3 & 4 objects. The 24:168 distinction in holistic systems has its arithmetic counterpart in the 192 objects making up the 60 permutations of 2, 3 & 4 objects, which consist of 12 permutations of 2 objects, i.e., 24 objects, and 48 permutations of 3 & 4 objects, i.e., 168 objects.
* The inversion of a note with tone ratio n is the note with tone ratio 2/n.
24 = 3 +
21
The three hexagonal yods at the corners of each triangle that form
a Star of David in the central triangle of the Sri Yantra correspond in the inner Tree of Life to the corners of
the triangle and hexagon that coincide with Sephiroth on each side pillar of the outer Tree of Life. In the I
Ching table of 64 hexagrams, they correspond to the three Yang lines of the Heaven trigram and to the
three Yin lines of the Earth trigram. In the 14 separate polygons of the inner Tree of Life, they correspond to
three corners of each hexagon that form an equilateral triangle, the remainder of the hexagon having 21
geometrical elements surrounding its centre. The 21 corners in each set of the first six enfolded
polygons that do not coincide with Sephiroth correspond to the hexagonal yods at the centres of the 21
triangles in each half of the Sri Yantra when they are regarded as tetractyses. They correspond to the 21
Yang & Yin lines of the seven upper or seven lower trigrams in the diagonal hexagrams other than the Heaven
trigram. The counterparts in the seven musical scales of the two sets of 21 elements are the 21
notes (2nd, 3rd & 4th notes of each scale) and their 21 inversions. The two sets of three hexagonal
yods in the central tetractys/triangle of the Sri Yantra, the two triads of Sephiroth in the side pillars of the
Tree of Life and the Heaven and Earth trigrams have their musical counterparts in, respectively, the tonic, the
octave & rising octave interval and the unit interval, the subharmonic octave with tone ratio ½ and the
falling octave interval of ½.
The 24 geometrical elements in each half of the central, 12-sided polygon of the disdyakis triacontahedron:
|
|
|
comprise two copies of three sets of four elements: three types of vertices (A, B, C), three types of outer edges (AB, BC, AC), three types of inner edges (AO, BO, CO) & three types of triangular sectors (TA = OAB, TB = OBC & TC = OCA). The three kinds of vertices, the outer edges & inner sides and the triangular sectors are denoted by the three rows of Yang/Yin lines of a trigram:
| A | AB | AO | TA | A' | A'B' | A'O | TA' |
| B | BC | BO | TB | B' | B'C' | B'O | TB' |
| C | CA | CO | TC | C' | C'A' | C'O | TC' |
(a prime indicates not the mirror image of its unprimed counterpart but its second version or copy, rotated
through 90° around an axis perpendicular to the plane containing the 12-gon; for clarity, the prime notation is
omitted from the diagram shown above). The polyhedral counterpart of the Heaven trigram, etc is (A, B, C); the
counterpart of the Earth trigram, etc is (TA, TB, TC). The two upper sets of
four trigrams in the eight diagonal hexagrams of the I Ching table correspond to the four types of geometrical
elements in the 12-gon, each being of three kinds, and their repetition, these making up half the 12-gon. The lower
group of eight trigrams in the diagonal hexagrams correspond to the mirror images of these geometrical elements in
the other half of the 12-gon.
Just as the three types of vertices generate 189 more geometrical elements in each half of the disdyakis triacontahedron, so the seven types of musical scales contain 189 intervals below the octave, there being 27 such intervals for each eight-note scale, and 7×27 = 189. The three types of vertices can be said to play the defining role of the tonic, octave & octave interval. The 84 edges above or below the central 12-gon form 28 sets of three edges (AB, BC, CA). The 84 vertices & triangles above or below the polygon form 28 sets of vertices & triangles: (8 A vertices, 20 triangles), (8 C vertices, 20 triangles) and (4 A, 4 B vertices, 20 triangles). Hence, above or below the 12-gon are 28 sets of three edges and 28 sets of three geometrical elements that are either vertices or triangles. They correspond in the I Ching table to the 28 pairs of trigrams either above or below the eight hexagrams in its diagonal. The eight sets of three types of geometrical elements in half the 12-gon correspond to the eight upper trigrams in the diagonal hexagrams; the eight sets of three types of elements in the other half of the 12-gon correspond to the eight lower trigrams in these hexagrams. The 84 vertices & triangles and the 84 edges in an upper or lower half of the disdyakis triacontahedron correspond to the 84 lines and 84 broken lines in the upper or lower diagonal halves of the I Ching table. In other words, the basic Yang/Yin duality of holistic systems manifests in the disdyakis triacontahedron as the distinction between the two types of geometrical elements that are, mathematically speaking, scalar in nature (points and the areas bounded by triangles) and the third type (straight line edges) that is a vector because it has direction. In a metaphysical sense, the geometrical correspondence that emerges here illustrates the Pythagorean principles of apeiron (Unlimited) and peras (Limit, or Boundary, such as that created in the polyhedra by their edges). The former is a masculine quality because it is the inchoate pre-cursor to fully developed structure, the latter is a feminine principle because it bestows form by organizing and imposing limitation). The 12 points & triangles and the 12 straight lines in each half of the 12-gon are the geometrical counterpart of the 12 Yang lines and the 12 Yin lines in the eight upper or lower trigrams making up the hexagrams in the diagonal of the I Ching table of 64 hexagrams.
An alternative way of understanding how the (192+192) elements in a holistic system manifest in the disdyakis triacontahedron (and one that is clearer because it provides a more obvious geometrical counterpart to the Yang/Yin distinction between lines and broken lines) is to regard each of the 192 polyhedral edges & internal sides of the central, 12-sided polygon as orientated lines, i.e., as arrows that can point in opposite directions. Then the 12 Yang lines and 12 Yin lines of the eight trigrams making up the upper and lower halves of the diagonal hexagrams would correspond to the 12 external edges and internal sides in each half of the 12-gon, each straight line generating two oppositely pointing arrows, whilst the 84 Yang and 84 Yin lines in the 28 hexagrams on either side of the diagonal in the I Ching table would correspond to the 84 pairs of arrows created by the 84 edges in the upper or lower halves of the polyhedron. This time, the three rows of a trigram would represent just the three types of edges or internal sides, and the eight trigrams would signify triplets of arrows of each type, the Yang or Yin polarity denoting whether the arrow pointed, respectively, towards, say, the right or left. As before, the two diagonal halves of the I Ching table would denote a half of the polyhedron and its mirror-image half. But the 192 Yang lines and the 192 Yin lines in the table would symbolize, respectively, the 192 arrows that point to the right and the 192 arrows that point to the left. Suppose in the diagram above that the centre of the polygon is labelled “O”. Then we can write the arrow pointing from B to A as –EA, the arrow pointing from C to B as –EB & the arrow pointing from A to C as –EC. Similarly, the arrow AO pointing from A to O is eA and the arrow OA pointing from O to A is –eA (and similarly for vertices B & C). Using primes to indicate the repeated set of vertices & edges, there are four triplets of arrows:
| AB = EA | AO = eA | A'B' = EA' | A'O = eA' |
| BC = EB | BO = eB | B'C' = EB' | B'O = eB' |
| CA = EC | CO = eC | C'A' = EC' | C'O = eC' |
and four triplets of their counterparts pointing in the opposite direction. The 12 positively pointing and 12 negatively pointing arrows are symbolized, respectively, by the 12 Yang and 12 Yin lines in the eight trigrams, which can be identified in terms of the following sets of arrows:
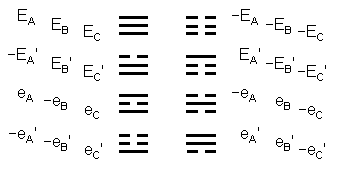
The pairing of similar trigrams in the eight diagonal hexagrams of the table of 64 hexagrams expresses the fact that every set of three arrows belonging to one half of the central polygon has its mirror counterpart in the other half. We saw a similar interpretation for the (24+24=48) geometrical elements in the pair of hexagons when we considered the I Ching table as a representation of the (192+192) geometrical elements surrounding the centres of the two sets of seven separate polygons making up the inner Tree of Life (see here).
The 84 Yang lines and the 84 Yin lines in the 28 pairs of trigrams on either side of the diagonal of the table denote the 84 positive and 84 negative arrows defined by the 84 edges of the disdyakis triacontahedron above or below the central plane containing its central 12-gon. As with the edges of the latter, they consist of three types of edges, so that there are 28 edges of each type, i.e., 28 (±EA), 28 (±EB) & 28 (±EC) arrows that form two groups of 28 sets of three arrows. Each hexagram symbolizes a pair of sets of three arrows. The inversion of trigrams in a hexagram on the other side of the diagonal corresponds to the spatially inverted counterparts of these arrows in the other half of the polyhedron. What demonstrates the holistic nature of the disdyakis triacontahedron is that it is the polyhedral representation of all 64 possible pairs of eight trigrams when Yang and Yin lines are identified as the orientated edges of its faces and sectors of its central polygon.
A musical manifestation of the holistic
pattern
The divisions:
384 = 48 + 168 + 168
and
48 = 24 + 24
embodied in the first (6+6) enfolded polygons, the I Ching table of 64 hexagrams, the Sri Yantra & the disdyakis triacontahedron have a remarkable, musical interpretation. According to Table 1, G5, the perfect fifth of the fifth octave, the tenth overtone, the 33rd note and the 11th Pythagorean harmonic, has a tone ratio of 24 and G6, the perfect fifth of the sixth octave, the 40th note and the 15th Pythagorean harmonic, has a tone ratio of 48. The Tetrad expresses both tone ratios because 10 = 1 + 2 + 3 + 4, 33 = 1 + 1×2 + 1×2×3 + 1×2×3×4, 24 = 1×2×3×4, and 40 = 4 + 8 + 12 + 16, whilst 15 is the number of combinations of four objects, taken 1, 2, 3 & 4 at a time.
Table 1. Table of tone ratios of the first 11 octaves of the Pythagorean musical scale.
(overtones are in pink cells)
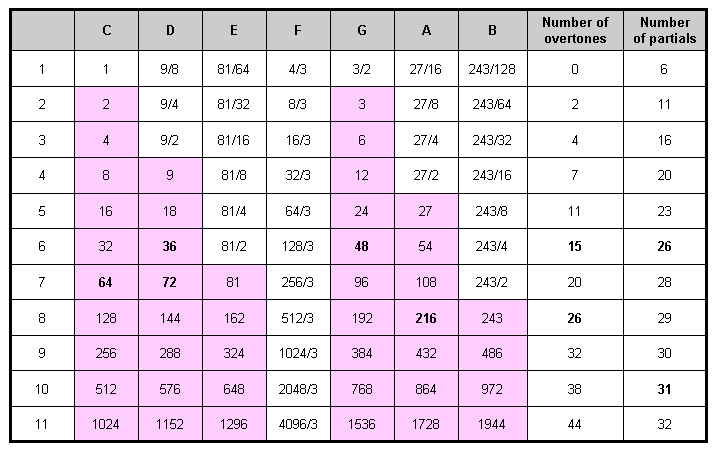
The 26th Pythagorean harmonic is A8 with tone
ratio 216 (the number value of Geburah). Therefore, the Godname YAH prescribes G6, up to which
there are 48 harmonics (15 Pythagorean) and the Godname YAHWEH prescribes A8, up to
which there are 216 harmonics, i.e., 168 extra harmonics. The note G9, the perfect
fifth of the ninth octave, has the tone ratio 384; it is the 30th overtone. The Godname EL (אל) with number
value 31 prescribes this note as the 31st Pythagorean harmonic and as the 61st
note,.png) where 61 is the 31st odd integer. The value 1 of the letter E (א) denotes the tonic
and the value 30 of L (ל) denotes the 30 overtones up to G9.
where 61 is the 31st odd integer. The value 1 of the letter E (א) denotes the tonic
and the value 30 of L (ל) denotes the 30 overtones up to G9.
As the Pythagorean measure of wholeness and perfection, the Decad determines all the 61 notes up to G9 because, constructed from tetractyses, the decagon has 61 yods (see here). The central yod denotes the tonic, the 30 internal yods surrounding it denote the 30 partials up to G9 and the 30 boundary yods denote the 30 overtones, the ten corners denoting the ten overtones up to G5. The Decad also determines the 26th musical harmonic A8 with tone ratio 216 as the 55th note, where
55 = 1 + 2 + 3 + ... + 10.
This geometrical correspondence is evidence that the 60 note intervals above the tonic up to G9 constitute a holistic set symbolized in the tetractys-constructed TOL by its 60 hexagonal yods symbolizing Sephiroth of Construction, in the dodecagon by its 60 hexagonal yods and in the disdyakis triacontahedron by the 60 vertices surrounding an axis joining two opposite vertices. The Tetrad also defines the number 384 because the 61 notes can be assigned to the 61 yods in a Type B square (see here).
The 61 notes up to G9 are the counterparts of the 61 sounds created by playing the 15 notes of the Hypatôn, Mesôn, Diezeugmenôn and Hyperbolaiôn tetrachords making up the Greater Perfect System of ancient Greek music — another holistic system, discussed here. The 31 sounds (notes, harmonic intervals & chords) that can be made by playing the eight notes of the first octave correspond to the 31 harmonics up to G9; the 30 sounds created by playing the second octave correspond to the 30 partials.
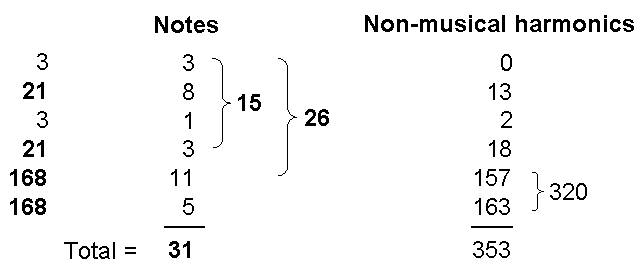
Table 2
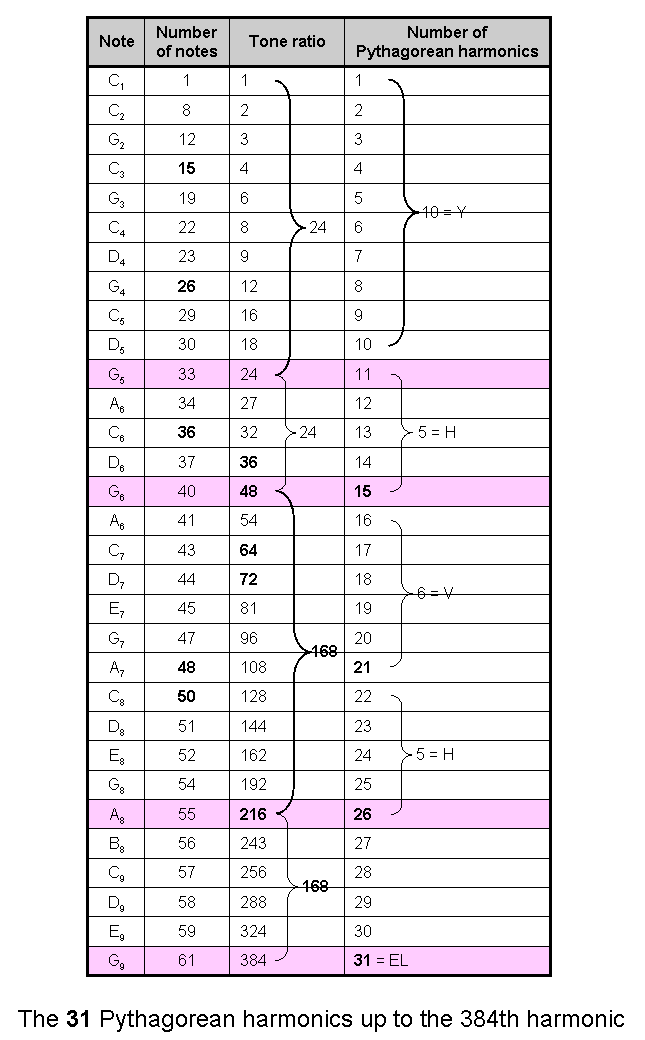
Table 2 displays the 31 harmonics of the Pythagorean scale up to G9 and their tone ratios. YAH (YH) separates the 48 harmonics up to G6 from the remaining 336 harmonics up to G9, which is prescribed by EL. The last 168 harmonics with five notes are separated by the Godname YAHWEH (YHVH). Amazingly, the number value 10 of yod (Y) and the value 5 of heh (H) divide the 48 harmonics into two sets of 24, which is characteristic of this number when it is a parameter of sacred geometries. The 48 harmonics contain 15 musical notes prescribed by YAH. The first set of 168 harmonics up to A8 contains 11 notes — the sum of the remaining values of the Hebrew letters vav (V)and heh (H) of YAHWEH — and 157 non-musical harmonics. The second set of 168 harmonics up to G9 contains five notes and 163 non-musical harmonics. Of the 336 harmonics, 16 are notes and 320 are non-musical harmonics. Of the 384 harmonics, 31 are notes and 353 are non-musical harmonics. Of the former, 22 are notes other than octaves. As 22 is the 21st odd integer after 1, EHYEH with number value 21 prescribes the overtones that are not octaves. It also prescribes G9 because this is the 21st note above G6. The 61 notes have 52 notes other than octaves. 52 is the 26th even integer, showing how YAHWEH prescribes this archetypal set of notes.
What confirms that these
48:336, 168:168 and 24:24 divisions in the Pythagorean scale have significance is that they
are prescribed by the Godnames YAH, YAHWEH and EL through their number values. This cannot, plausibly, be
attributed to chance. The 384 harmonics up to G9 consist of the fundamental frequency 1 and 383
higher harmonics. Amazingly, 383 is the 76th prime number, showing how the Godname YAHWEH ELOHIM with
number value 76 prescribes the archetypal set of the first 61 notes of the Pythagorean scale that span
384 harmonics. There are 383 hexagonal yods at the centres of the tetractyses whose yods make up the 1680 yods
below the top of the tenth Tree of Life (65th SL) that symbolize the 1680 turns of a helical whorl of the
heterotic superstring (see here). In other words, these 1680 yods comprise 383 yods of the type that
symbolize Malkuth (see here the equivalence between the Tree of Life and the tetractys). This shows
how YAHWEH ELOHIM prescribes this superstring structural parameter. ELOHIM with number value 50
prescribes the 50 notes other than the 11 musical harmonics up to G5, the perfect fifth with
tone ratio 24. The first ten overtones and the 22 partials up to G5 were shown in The seven musical scales to constitute a Tree of Life pattern because they are analogous to its
ten Sephiroth and 22 Paths (see #19).
The 11:50 division of the 61 notes corresponds in the
tetractys-constructed 1-tree to the 11 corners of its 19 triangles and to the 50 hexagonal yods lying on
their 25 sides. The number 61 creates the shape of the 1-tree as the number of yods lining the sides (Paths) of
its tetractyses. Its counterparts in the tetractys-constructed dodecagon are the 61 yods on the sides of
its sectors:
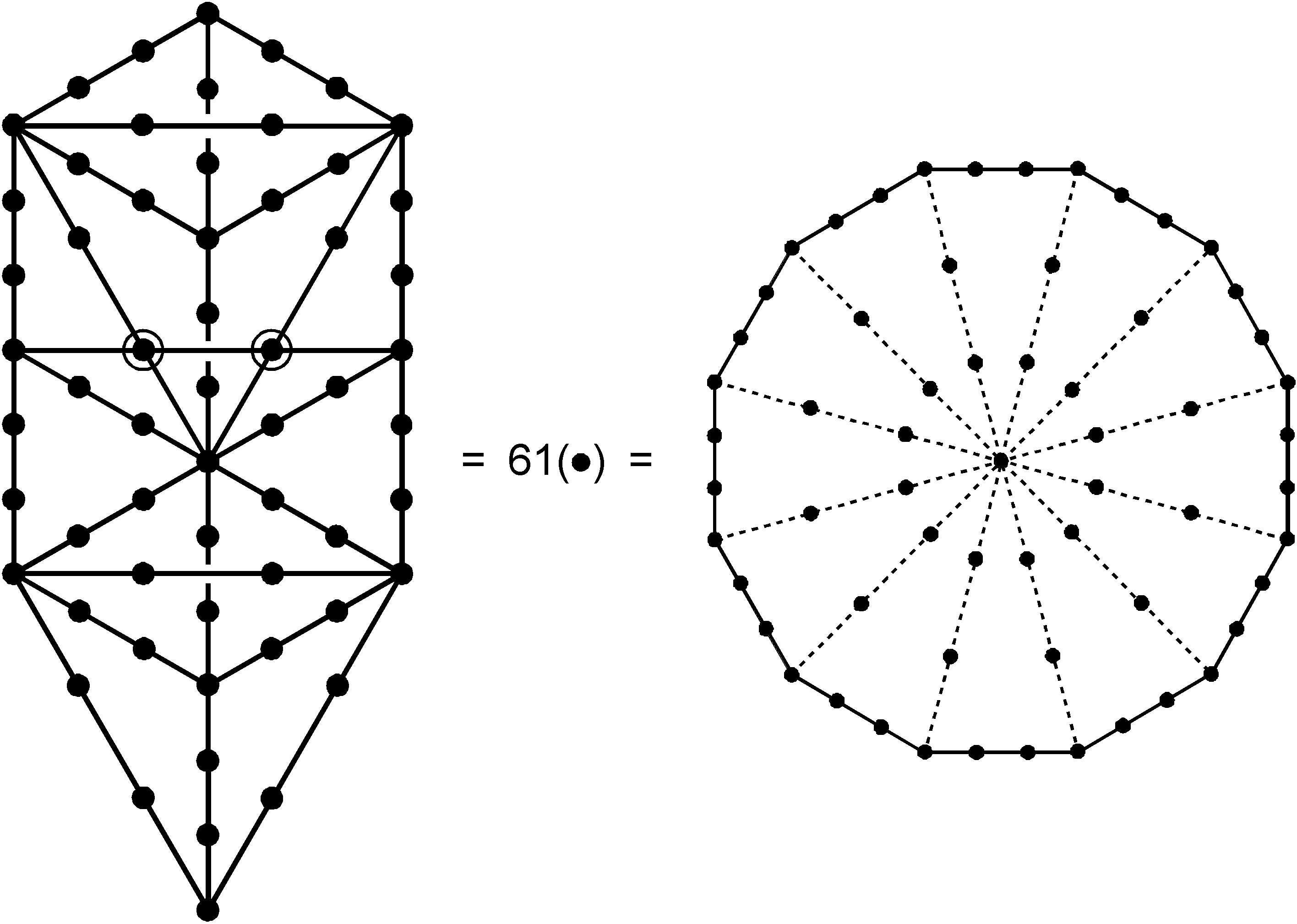
Its counterparts in the disdyakis triacontahedron are its centre,
the ten B vertices and the 50 A & C vertices that surround an axis passing through two opposite B
vertices. The 20 C vertices correspond to the 20 hexagonal yods lying on the ten sides of triangles in the trunk
of the 1-tree and the 30 A vertices correspond to the 30 hexagonal yods lying on the 15 sides of
triangles making up its branches. The musical counterparts of the 20 C vertices, the ten B vertices and the 30 A
vertices are, respectively, the 20 partials in the first four octaves, the ten remaining partials and the 30
overtones, with the centre of the polyhedron denoting the fundamental, C1. The disdyakis
triacontahedron is the geometrical representation of the 60 notes above the tonic up to G9, the 384th
harmonic and the 31st musical harmonic.
The division:
24 = 3 + 21
found in sacred geometries manifests in the Pythagorean scale, firstly, as the three harmonics (all notes) up to G2 (see Table 1) and the 21 higher harmonics (eight notes & 13 non-musical harmonics) up to G5 and, secondly, as the three harmonics (one note & two non-musical harmonics) beyond G5 up to the next note A5 and the 21 harmonics (three notes & 18 non-musical harmonics) beyond that up to G6. The (3+3=6) harmonics comprise four notes and two non-musical harmonics; the (21+21=42) harmonics comprise 11 notes and 31 non-musical harmonics. The composition of the 384 harmonics is:
Its 31 musical harmonics prescribed by the Godname EL comprise every type of note except perfect fourths.
|
|
|
|
Disdyakis triacontahedron |
Central 12-gon |
Surrounding an axis passing through any two opposite A vertices of the disdyakis triacontahedron are 24 vertices, 84 edges & 60 triangles, i.e., 168 geometrical elements, either above or below the central, 12-sided polygon perpendicular to this axis (see here). The 12-gon has 48 geometrical elements surrounding its centre made up of 12 corners, 24 sides & 12 triangles. Compare these geometrical compositions with the composition of harmonics up to G9:

Starting from G6, the 15th musical harmonic with tone ratio 48, there are 60 more harmonics up to A7, the 21st musical harmonic, then 84 more harmonics up to G8 and 24 more harmonics up to A8, the 26th musical harmonic. The composition of the 168 geometrical elements either above or below the central polygon of the disdyakis triacontahedron matches the 168 harmonics between G6 and A8, making it too unlikely that the correspondence between the geometry and the notes of the Pythagorean scale could be coincidental. As the 48 geometrical elements of the polygon correspond to the 48 harmonics up to G6, this note prescribed by YAH corresponds to the central polygon, whilst the note A8 prescribed by YAHWEH corresponds to half of the polyhedron with 216 geometrical elements. The 168 harmonics beyond A8 up to G8 correspond to the 168 geometrical elements in the other half of the polyhedron below the polygon. Each element is the geometrical counterpart of a harmonic, the 336 harmonics between G6 and G9 being the musical counterpart of the 336 geometrical elements above and below the central polygon. This is the musical manifestation of the division:
384 = 48 + 168 + 168
that is characteristic of holistic systems. It is powerful evidence of the universality of this pattern, as embodied in sacred geometries like the
first (6+6) enfolded polygons of the inner Tree of Life, its seven separate Type B polygons, the I Ching table
of 64 hexagrams, the Sri Yantra and the disdyakis triacontahedron.
The Tetrad Principle (see page 4 in Article 1) expresses the 384 harmonics (the musical manifestation of this holistic parameter) because 384 = 424!:
| 4! |
4! | 4! | 4! | ||
|
384 = |
4! |
4! | 4! | 4! |
(4! = 1×2×3×4) |
| 4! |
4! | 4! | 4! | ||
| 4! | 4! | 4! | 4! |
They include (42=16) octaves and perfect fifths. The 378 geometrical elements above and below the
48 elements of the central polygon are the geometrical counterpart of the 378 harmonics above G6.
They contain (42=16) overtones. The 48 harmonics up to G6 contain 15
Pythagorean harmonics, where 15 is the fourth triangular number after 1. The three harmonics up to
G2 and the three harmonics above G5 to A5 comprise four Pythagorean harmonics (1,
2, 3 & 27).
168 = 84 + 84
We pointed out in #19 at Superstrings as sacred geometry/Tree of Life that the first six polygons of the inner Tree of Life have 84 yods lying on their edges outside their shared root edge. Both sets have 168 yods:
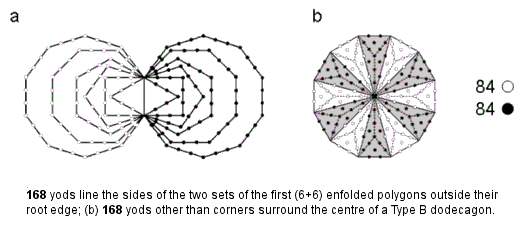
This property demonstrates par excellence the shape-defining character of the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth. The same 84:84 pattern is displayed in the 168 extra yods needed to construct the Type B dodecagon the last of the regular polygons making up the inner Tree of Life. In each case, every yod has its mirror image. The 7-tree has 168 corners & sides of its 91 triangles [2]. They comprise 84 corners & complete sides below Chesed of the fourth Tree of Life and 84 corners & sides above it.
In the I Ching table, there are 84 Yang lines and 84 Yin lines in the 28 hexagrams on either side of the diagonal. We saw in Article 18 that the eight types of trigrams symbolize the binary numbers corresponding to the integers 0–7. We showed in Article 20 that they also express the eight sets of three faces of a cube whose intersection defines its corners. This means that these integers can be assigned to the corners, with lines that join pairs of corners representing hexagrams. Numbers can be assigned to lines whose values are the sum of the integers assigned to the two corners that they join. The 12 diagonals of the six square faces of the cube are the edges of two interpenetrating tetrahedra. The integers associated with them add up to 84, as do the integers associated with the 12 edges of the cube. The 84:84 division of Yang & Yin lines therefore manifests geometrically as the two tetrahedra whose vertices form a cube.
In Article 16 we found that there are 84 rising and 84 falling Pythagorean intervals between notes of the seven musical scales that are repetitions of the basic set of 12 notes between the tonic and octave belonging to these scales. They are the musical counterpart of the 84 Yang and 84 Yin lines in the off-diagonal hexagrams. They are composed of 78 rising and falling D & E intervals and 90 rising and falling F, G & A intervals — the gematria number values of the Hebrew words "Cholem" and "Yesodoth" in the Mundane Chakra of Malkuth. These are the numbers of lines in, respectively, two and three types of off-diagonal hexagrams (see Article 20). We saw in The power of the polygons/hexagon that 168 yods are needed to transform a pair of hexagons joined at one edge into Type B hexagons, 84 per hexagon. There are also 84 Yang lines and 84 Yin lines in the 28 hexagrams that line the sides of the square array of hexagrams in the I Ching table.
The 28 triangles in the first three layers of the
three-dimensional Sri Yantra have 84 edges and 84 vertices & triangles. The four layers have 168
edges & triangles made up of 84 edges of triangles in the first three layers, 42 triangles in all four
layers and 42 edges in the fourth layer. When the triangles become tetractyses, there are 168 hexagonal
yods on the edges of the triangles in the first three layers (84 in each half). When the triangles are divided
into their sectors, the fourth layer has 84 edges and 84 vertices & triangles, that is, 168
geometrical elements.
As already mentioned when comparing it with the 64
hexagrams in the I Ching table, the disdyakis triacontahedron has 168 edges above and below the central,
12-sided polygon, 84 on each side. Its 60 vertices surrounding an axis joining two opposite A vertices are the
corners of seven polygons parallel to the central one. The polygons in the inner Tree of Life with corresponding
numbers are its last four ones. They have 168 yods outside their shared edge lying on their boundaries. The
uppermost two polygons in the polyhedron have 84 such yods, as do the next two. The shapes of the four types of
polygons making up half the polyhedron are therefore defined by the number value 168 of Cholem
Yesodoth. Moreover, they display the basic 84:84 division of this holistic parameter. It is the 206 yods
associated with the last four polygons enfolded in the inner Tree of Life with corresponding numbers of corners
that symbolize the 206 bones of the human skeleton. The 84:84 division of the boundary yods in the four types of
polygons in half the disdyakis triacontahedron therefore reflects the distinction between the axial and
appendicular skeletons. Here is a mathematical connection between the two parts of the human skeleton and the core
and outer half of the subquark superstring, each with 8400 1st-order spirillae that are manifesting the basic 84:84
division of holistic systems. They are different manifestations of the same holistic pattern.
We saw earlier in the discussion of the division 192 = 24 + 168 that 168 objects make up the 48 permutations of 3 and 4 objects selected from a set of 4 objects. Every permutation has its mirror image, so that there are 24 permutations of 3 and 4 objects and 24 mirror images of them, each set of 24 permutations comprising 84 objects. The division 168 = 84 + 84 that manifests in holistic systems has its arithmetic counterpart in the 84 objects making up the 24 permutations of 3 and 4 objects and the 84 objects that make up their 24 mirror images. Each set of 84 objects comprises the 36 objects in 12 permutations of 3 objects taken 3 at a time and the 48 objects in 12 permutations of 4 objects taken 4 at a time. This 36:48 division manifests in the 2nd-order tetractys as the 36 yods lining its sides and the 48 internal yods that surround its centre (black yod):
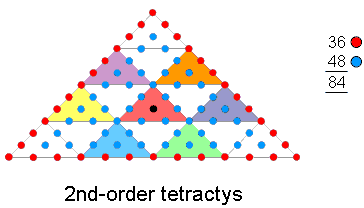
Article 64 analyses in detail the 24:24, 168:168 & 84:84 divisions in seven sacred geometries and the seven diatonic musical scales.
3360 = 1680
+ 1680 (or 336 = 168 + 168)
The ten whorls of the UPA wind five times around its spin axis, each revolution containing 3360 spirillae and each half-revolution containing 1680 spirillae. Sacred geometries embody this division in the following ways:
Outer Tree of Life
Below Binah of the 1-tree are 67 yods (see here). This is the gematria number value of Binah (see here). Below Binah of 67 overlapping Trees of Life are 3360 yods [3]. They divide into the 1680 yods making up the 33-tree, the highest Binah of which is the 67th SL on the Pillar of Judgement, and the 1680 yods above them. This is the remarkable way in which Binah, embodying the feminine principle in nature, encodes not only the superstring structural parameter 3360 but also its division into two 1680s that correspond to the 1680 1st-order spirillae in an outer or an inner half of one revolution of the ten whorls of the UPA/subquark superstring. Truly, Binah, “The great mother,” is the mother of all forms because it gives birth to the 3360 yods symbolizing the 3360 turns in one revolution of the ten whorls of the very fundamental particle that makes up the atomic nuclei of all the chemical elements.
Inner Tree of Life
As discussed here, there are 3360 yods in the seven enfolded polygons of the inner Tree of Life when their 48 sectors are each transformed into a 2nd-order tetractys:
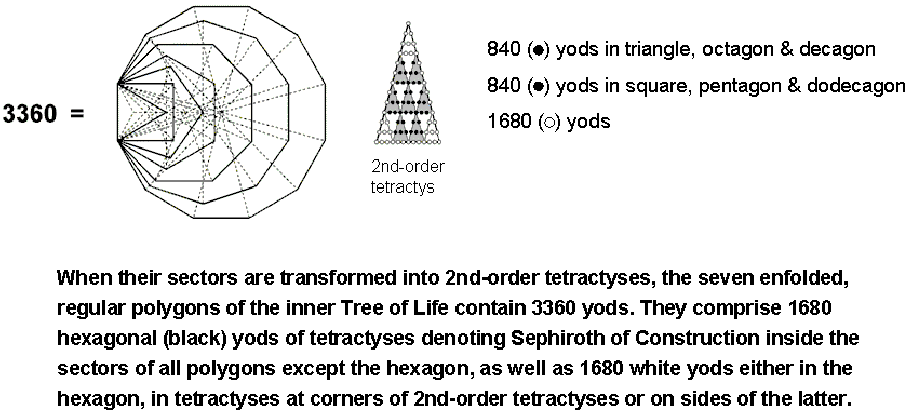
Inside the latter are 49 yods, nine of which (white yods in the diagram above) belong to the tetractyses at the corners of the 2nd-order tetractys corresponding to the Supernal Triad of Kether, Chokmah & Binah. This leaves 40 internal (black) yods (36 hexagonal yods surrounding its centre) that belong to tetractyses expressing the Sephiroth of Construction. In conformity with the pattern characteristic of holistic systems:
48 = 6 + 42 = 6 +
21 + 21,
the 48 sectors group into the six sectors of the hexagon
and the 42 sectors of the six other polygons. The latter form two unique sets, each with 21 sectors:
(triangle, octagon & decagon) and (square, pentagon & dodecagon). They contain (42×40=1680) internal
black yods, 840 in each set. There are also 1680 yods either in the hexagon, in tetractyses at corners of
2nd-order tetractyses or on their sides.
Eight hexagonal yods line each of the 42 sides of the seven
enfolded polygons, totalling 336 hexagonal yods. This property has its counterpart in the Sri Yantra when its 42
triangles are turned into tetractyses, namely, 336 yods line their sides (see here). It demonstrates the shape-determining character of the Tree of
Life parameter 336, which manifests in the subquark state of the E8×E8 heterotic
superstring as the 336 circularly-polarized waves in each revolution of a whorl around the spin axis of the
particle. Eleven yods lie on each side of the seven enfolded polygons with 36 corners. The number of yods
lining their sides = 42×11 + 36 = 498. Given that one corner of the triangle is the centre of the hexagon
and that one corner of the pentagon is the centre of the decagon, there are 496 yods that belong to
and line only the boundaries of the seven enfolded polygons, thereby shaping them. 496 is both
the gematria number value of Malkuth (see here) and the number of spin-1 particles that transmit the unified
superstring force (see here). This is a
very remarkable example of how sacred geometries embody numbers discovered by advances in theoretical
physics to have fundamental significance. We saw in #20 at Superstrings as sacred geometry/Tree of
Life that the twenty Type B dodecagons enfolded in the 10-tree have 3360 yods other than their 220
corners. In other words, 1680 new yods are associated with each set of ten dodecagons. One revolution of all ten
whorls of the UPA/superstring represents a whole in itself that manifests in all seven enfolded polygons as
their 3360 yods, when their sectors are 2nd-order tetractyses.
We also found in #20 that 1680 yods other than corners are associated with each set of the first
six types of polygons enfolded in ten overlapping Trees of Life. As the Tree of Life representation of each
whorl, each set has 168 yods other than corners that denote the 168 spirillae in a half-revolution
of the whorl, both sets representing one complete revolution of 336 spirillae. The division: 336 = 168 +
168 is characteristic of holistic systems.
Sri Yantra
When the 42 triangles surrounding the centre of the Sri Yantra are converted into tetractyses, their sides are lined by 336 yods, 168 yods in each half (see here). A yod is a potential tetractys of ten yods. If, therefore, the Decad (10) is assigned to these boundary yods shaping the Sri Yantra, its two halves generate the number 3360 as the sum of 1680 and 1680.
Disdyakis triacontahedron
The vertices of the disdyakis triacontahedron form 21
Platonic solids of the four types thought by the ancient Greeks to be the shapes of the particles of the four
Elements Fire, Air, Earth & Water (see here). When their faces are constructed from tetractyses, they
contain 1680 hexagonal yods. The polyhedral vertices also form a dodecahedron, five rhombic dodecahedra and a
rhombic triacontahedron. Constructed from tetractyses, their faces, too, contain 1680 hexagonal yods.
1680 = 840 +
840
This division appears in the micro-psi description by Besant & Leadbeater of the 1680 1st-order spirillae of each whorl of the UPA, because there are 840 spirillae in each of its 2½ outer or inner revolutions around the axis about which this spin-½ superstring spins. It is hardly unexpected, therefore, that a fundamental feature of a holistic system such as a whorl — itself a whole within another whole — should turn out to be a property of sacred geometries.
Outer Tree of Life
The lowest ten Trees of Life in CTOL are the counterpart of the lowest ten dimensions in 26-dimensional space-time. When all triangles are turned into Type A triangles, there are 1680 yods below the top of the tenth Tree, which is prescribed by the Godname ADONAI with number value 65 because it is the 65th SL (see here).
Inner Tree of Life
We saw in #20 at Superstrings as sacred geometry/Tree of
Life that, when the 700 sectors of the 120 polygons of the first six types enfolded in the lowest ten
Trees of Life of CTOL are turned into tetractyses, 1680 yods line the boundaries of these polygons other than
their shared edges, 840 yods being on either side of the Pillar of Equilibrium. They symbolize the 840 spirillae
in the inner and outer halves of each whorl. 480 of these yods are corners of polygons and 1200 are hexagonal
yods. As there are 120 yods on the boundaries of the seven enfolded polygons, which have 48 corners when
separate, the number 480 is embodied in the ten sets of seven separate polygons as the number of their corners,
whilst the number 1200 is embodied as the number of boundary yods in ten separate sets of seven enfolded
polygons.
We also pointed out in #20 that the dodecagon in the inner Tree of Life has 168 yods other than
corners of its sectors, that is, 168 extra yods. They comprise 84 yods and their 84
counterparts on the other side of its centre. The ten dodecagons enfolded in the 10-tree contain 840 extra yods
and their 840 mirror images. They symbolize the 840 1st-order spirillae in a quarter-revolution of all ten
whorls of the UPA and the 840 spirillae in the next quarter-revolution. Their counterparts in the ten dodecagons
enfolded on the other side of the Pillar of Equilibrium denote the spirillae in the other half-revolution of the
ten whorls. The 1680 yods in the ten dodecagons include 120 hexagonal yods at centres of tetractyses formally
symbolizing Malkuth, leaving 1560 yods (the yods in 156 tetractyses) surrounding these centres. 156 is the
155th integer after 1, showing how ADONAI MELEKH, the complete Godname of Malkuth with number value
155, prescribes the superstring structural parameter 1680 determined by Charles W. Leadbeater about 1908,
when he counted the spirillae in each helical coil of a whorl in the UPA (see p. 23 of Occult
Chemistry, 3rd ed.).
Sri Yantra
The intersection of the nine primary triangles in the two-dimensional version generates 42 triangles, which, when Type B triangles, possess 1680 new yods other than corners of tetractyses inside each one (see here). They divide into 840 yods belonging to the set of 21 triangles in one half of the Sri Yantra and 840 yods belonging to its other half. Unlike in the inner Tree of Life, they are not mirror images of each other because the Sri Yantra is not exactly symmetric. However, they are still counterparts that form pairs. In the three-dimensional case, there are 1680 yods other than tips of triangles and internal vertices of tetractyses (see here). Again, each set of 21 triangles has 840 such yods.
Disdyakis triacontahedron
When the polyhedron is constructed from triangles, with each internal triangle formed by its centre and an edge divided into three sectors, 1680 corners, triangles and their sides surround an axis joining any two diametrically opposite vertices, whether they are A, B or C vertices (see here & here). The 1680 geometrical elements comprise 840 elements in one half of the polyhedron and their 840 diametrically opposite mirror images, reflected through the centre of the disdyakis triacontahedron, which possesses inversion symmetry.
Pythagorean scale (the musical connection with the superstring)
Inspection of Table 1 reveals that there are 1680 harmonics
between note G6 with tone ratio 48 and note A11 with tone ratio 1728. The latter is
the 76th note. YAHWEH ELOHIM with number value 76 prescribes the very note in the Pythagorean
scale that is separated by 1680 harmonics from G6! This amazing fact demonstrates how YAHWEH ELOHIM
prescribes the musical counterpart of the superstring structural parameter 1680 as well as the structural
parameter 336. The Godname ELOHA with number value 36 prescribes A11 as the
36th note above G6, the 48th harmonic, whilst there are 151 notes and successive
intervals up to A11, where 151 is the 36th prime number. The Tetrad aptly expresses
A11 because it is the 44th musical harmonic. Moreover, there are ten (=1+2+3+4) octaves, ten perfect
fifths and 24 (=1×2×3×4) other Pythagorean harmonics up to A11. This note is the only overtone other
than A8 and G9 that is separated from G6 by an integer multiple of 168.
It is readily verified that G6 and A11 are the only notes of the Pythagorean scale whose
tone ratios differ by 1680. Clearly, A11 is unique in the context of the 1680 turns of the helical
whorl of the heterotic superstring, whose embodiment in the inner form of ten Trees of Life shows that they
consist of ten sets of 168 turns. Its connection to superstring physics is further demonstrated by the
fact that, as the 75th note above the fundamental, A11 is the 65th note other than the ten
octaves, i.e., it is prescribed by ADONAI, the Godname of Malkuth (denoting the physical universe), whose number
value is 65. A11 is the 33rd overtone other than octaves, where 33 = 1! + 2! + 3! +4!. The
33rd note and the tenth overtone is G5 with tone ratio 24. Therefore, A11 is the 33rd
non-octave overtone above the 33rd note! Given that there are 1680 yods in the 33-tree, the role played by the
number 33 in each context in determining this superstring structural parameter is remarkable. The 50th
note prescribed by ELOHIM is the seventh octave C8 with tone ratio 128. It is 80 harmonics
above G6, so that the next 26 notes prescribed by YAHWEH up to A11 span 1600
harmonics. The two words in the Godname of Tiphareth define a 80:1600 division in the number 1680 that
appears in the 33-tree as the 80 yods in the 1-tree and as the 1600 yods in the 32 Trees above it. This
section of CTOL is prescribed by ADONAI because Malkuth of the 33rd Tree of Life is the 65th SL on the
central pillar. There are 1730 yods up to the top of the 34th Tree of Life, that is, 1728 yods below its top
other than that at Daath of this Tree. Alternatively, there are 48 yods below the top of the 34th Tree of
Life other than its Daath that are outside the 33-tree. This 48:1728 division is the Tree of Life
counterpart of the 48 harmonics up to G6 and the 1728 harmonics up to A11. Each yod
denotes a harmonic. The 48 harmonics from G6 to G7 are the counterpart of the
48 yods up to Chesed of the 1-tree. The 80 harmonics from G6 to C8 are the
counterpart of the 80 yods of the 1-tree. The first of the 1680 harmonics above G6 up to
A11 is the 49th harmonic, so that it is prescribed by the Godname EL CHAI of Yesod.
None of the 14 basic types of notes in the seven musical scales:
| 1 |
256/243 |
9/8 |
32/27 |
81/64 |
4/3 |
1024/729 |
729/512 |
3/2 |
128/81 |
27/16 |
16/9 |
243/128 |
2 |
(see here) has a higher octave whose tone ratio is 1680. This number must
be understood as referring, not to a note of any scale, but to the number of harmonics between G6 and
A11. Inspection of Table 1 confirms that A11, which is the first note to have a tone ratio
larger than 1680, is also the only note differing by 1680 harmonics from a note of lower pitch! The note
A14 is the last note to differ from its predecessor by less than 1680 harmonics, whilst all
subsequent, consecutive notes differ by more than 1680 harmonics. G6 and A11 are,
therefore, the only notes in any octave of the Pythagorean scale whose tone ratios differ by 1680. The
uniqueness of this pair of notes is highly significant because it eliminates the criticism that any discussion
based upon a particular choice of pairs of notes would be ad hoc if other pairs existed that differ by
1680 harmonics.
The 1680 harmonics from G6 to A11 contain 29 overtones. 29 is the tenth prime number. The Decad, therefore, determines how many of these 1680 harmonics are overtones! Table 1 shows that they contain 24 overtones other than octaves, where 24 = 1×2×3×4 and 10 = 1 + 2 + 3 + 4. Counting from G6, we see that the 1680th harmonic is the 24th Pythagorean harmonic other than octaves. The first 168 harmonics up to A8 include nine such notes, the next 168 harmonics up to G9 include four such notes and the remaining harmonics include 11 notes that are not octaves. The 24 non-octave overtones are distributed nine to the first 168 harmonics and 15 to the remainder. This 9:15 division reminds us of the distinction in string theory between the nine transverse dimensions existing in the 11-dimensional space-time of M-theory and the 15 higher transverse dimensions belonging to bosonic strings in 26-dimensional space-time. If we take the analogy seriously, it suggests that oscillations in the 24 transverse directions generate 24 particles as 24 vibration modes that correspond to the 24 overtones, the nine overtones up to A8 corresponding to the nine particles representing Kaluza-Klein-type oscillations in each of the nine transverse dimensions and the 15 remaining overtones corresponding to the 15 vibration modes for the 15 higher dimensions. Are the 1680 helical turns of a closed whorl the manifestation of the charge sources of 24 gauge fields of E8, the ten whorls of the UPA/superstring being the manifestation of the sources of the 240 gauge fields associated with its 240 roots? The musical analogy strongly implies such an interpretation.
When G6 is regarded as the fundamental frequency, the
tone ratios of the 24 higher overtones other than octaves are shown below (new overtones are written in
red):

The overtones, starting with A6 with tone ratio 54,
span exactly five octaves, the last note A11 having the new tone ratio 36 relative to
G6. The set of 24 overtones is prescribed by ELOHA, Godname of Geburah with number value 36.
The note in the Pythagorean scale with tone ratio 36 is D6. It is the 36th note above
the tonic. It is the only note in the scale whose tone ratio is identical to its position number above
the tonic — another reason why A11 is special.
There are three overtones up to the note A8 with tone ratio 216 that remain overtones when G6 is regarded as the fundamental. The remaining 21 overtones comprise A6, the first one, five partials up to A8, followed by ten harmonics and five partials spanning the last three octaves. Amazingly, these are the letter values of EHYEH (AHIH) with number value 21, namely, A = 1, H = 5, I = 10 & H = 5! In terms of its geometrical counterpart in the disdyakis triacontahedron, A8 represents the last of the 216 geometrical elements constituting exactly half of the polyhedron. It is the reason for the thick, vertical line dividing the 24 overtones at this note. The 24 overtones display the 3:21 division characteristic of holistic systems, as illustrated earlier.
Just as the 1680 helical turns of each whorl of the UPA/heterotic superstring revolve five times around its spin axis, so the 1680 harmonics between G6 with tone ratio 54 and A11 with tone ratio 1728 contain 24 overtones other than octaves that span five complete octaves, that is, five musical cycles. In both cases, the number 1680 quantifies an underlying five-fold cycle. The relative frequencies of the 24 overtones increase by a factor of 1728/54 = 25 = 32). This is the number of components of the Dirac wave function describing spin-½ fermions in 10-dimensional space-time, e.g., the UPA. A remarkable analogy exists between the vibrating, string-like whorl and the harmonics of the Pythagorean scale because they are both holistic systems.
Table 3. The 1680 harmonics between G6 and A11.

Let us next compare the pattern of 1680 harmonics with the 1680 geometrical elements surrounding any axis of the disdyakis triacontahedron. If the former truly constitute a holistic set, their composition should correlate with the geometrical structure of this polyhedron, which many research articles posted to this website by the author have confirmed is the polyhedral form of the outer Tree of Life. When the axis passes through two diametrically opposite A vertices, the 1680 elements comprise 24 vertices above the 12-gon in the central plane of the polyhedron, 24 vertices below it, 12 vertices of this 12-gon and 180 vertices of the 540 internal triangles, i.e., 240 vertices. Their musical counterparts are the 24 harmonics up to D7 (Table 3), then 24 harmonics up to G7, 12 more harmonics to A7 (the first of the five octaves and the 21st Pythagorean harmonic) and the next 180 harmonics up to D9, which, as the perfect fourth of the third of these octaves, is the middle of the five octaves. Then, there are 180 edges, 60 internal sides ending on polyhedral vertices & 120 external triangles, i.e., 360 edges & triangles. Their Pythagorean musical counterpart is the 360 harmonics beyond D9 up to E10. Finally, there are 540 more internal edges of 540 internal triangles, i.e., 1080 internal edges & triangles. Their counterpart is the 1080 harmonics above E10 up to A11.
There is no overtone that is the 840th harmonic above G6. The only two notes that differ by 840
harmonics are G5 with tone ratio 24 and A10 with tone ratio 864, but they do not all fall
within the range of the 1680 harmonics. However, there are 840 odd harmonics from 49 to 1727 and 840 even
harmonics from 50 to 1728. The musical counterpart of the 840 helical turns
in the 2½ revolutions of an outer or inner half of a whorl in the UPA/heterotic superstring are the 840 even
and 840 odd harmonics between G6 and A11. As the former note is the 15th
Pythagorean harmonic and the 40th note, and the latter note is the 44th Pythagorean harmonic, the 76th note
and the 36th note after G6, this shows how YAH, YAHWEH ELOHIM and ELOHA prescribe these five
octaves spanned by the 1680 harmonics. Their counterparts in the disdyakis triacontahedron are the 840 geometrical
elements in one half of the polyhedron that surround an axis joining two opposite vertices and their 840 mirror
images in its other half.
The 24 overtones other than octaves in the 1680 harmonics between G6 and A11 are notes of the first five octaves of the A scale (Hypodorian mode). In terms of this scale, they comprise 12 harmonics and 12 partials with the following tone ratios:
|
A |
B |
D |
E |
G |
|
| 1st octave: |
1 |
|
4/3 |
3/2 |
16/9 |
| 2nd octave: |
2 |
|
8/3 |
3 |
32/9 |
| 3rd octave: |
4 |
9/2 |
16/3 |
6 |
64/9 |
| 4th octave: |
8 |
9 |
32/3 |
12 |
128/9 |
| 5th octave: |
16 |
18 |
64/3 |
24 |
256/9 |
| 6th octave: |
32 |
In terms of the Pythagorean scale, 22 of the 24 overtones have even tone ratios and two overtones (E7 with tone ratio 81 (3/2 in the A scale) and B8 with tone ratio 243 (9/2 in the A scale)) have odd tone ratios. Compare this with the prediction by string theory that bosonic strings exist in 26-dimensional space-time and vibrate along two transverse, large-scale dimensions of space and 22 transverse, microscopic dimensions, i.e., 24 transverse dimensions = 22 compactified dimensions + 2 large-scale dimensions. That two notes are, likewise, differentiated from the other 22 is further evidence that the 24 overtones are analogous to the 24 transverse dimensions. One of the 22 curled-up dimensions is the dimensional segment separating the two space-time sheets occupied by E8×E8′ heterotic superstrings of ordinary matter (singlet state of E8′) and shadow matter (singlet state of E8), so that the compactification of 21 dimensions is instrumental in creating each type of superstring, where 21 is the number value of EHYEH, Godname of Kether. They correspond to the 21 even overtones above A6, which, as the lowest note of the five octaves of notes shown above, corresponds to the dimensional gap between the two space-time sheets. The numbers of overtones and partials in the five octaves of the A scale are the letter values of AHIH (אהיה), the Hebrew form of EHYEH:
| A = 1: lowest octave with tone ratio 2. |
| H = 5: five octaves of partials (16/9, 32/9, 64/9, 128/9, 256/9). |
| I = 10: ten overtones (3, 4, 6, 8, 9, 12, 16, 18, 24, 32). |
| H = 5: five octaves of partials (4/3, 8/3, 16/3, 32/3, 64/3). |
Notice that the letter values Y = 10 & H = 5 of the Godname YAH (Hebrew: YH, or יה) with number value 15 denote, respectively, the ten overtones and the five octaves of perfect fourths. Notice also that the first ten overtones in the A scale are the same as the first ten overtones in the Pythagorean scale (see Table 1). These and the 22 partials up to the tenth overtone were shown in #19 at The seven musical scales to constitute a Tree of Life pattern. Seven of them (notes B, D & E) belong also to the A scale.
Given this correlation between the letter values of EHYEH and the numbers of overtones and partials spanning the first five octaves of the A scale — a pattern of such detail that it could not, plausibly, arise by chance — the following question arises: what compactified dimensions correspond to the numbers? Six of them are predicted by superstring theory and 15 are dimensions of bosonic strings. This division is indicated by the letters A and H of AHIH, whose gematria sum is 6, and by the letters I and H, which sum to 15. It means that the ten overtones up to that with relative tone ratio 32 (the 1680th harmonic after G6) and the five octaves of perfect fourths in the A scale have their counterparts in the 15 higher, bosonic dimensions. What is the string counterpart of this 10:5 distinction between overtones and partials? It is the role played by ten of the bosonic dimensions when a membrane wraps itself around each of them to generate the ten whorls of the UPA/superstring. The dimensional counterparts of the three overtones with tone ratios 3, 4 & 6 create the three major whorls corresponding to the Supernal Triad of the Tree of Life. The counterparts of the remaining seven overtones 8, 9, 12, 16, 18, 24 & 32 create the seven minor whorls corresponding to the seven Sephiroth of Construction. A11, the 1680th harmonic beyond G6 in the Pythagorean scale, is the fifth octave of the A scale with tone ratio 32. It is its 36th note, prescribed by ELOHA, the Godname of Geburah with number value 36. Relative to one another, the first three overtones are the tonic, perfect fourth and octave of the Pythagorean scale and that the last seven overtones form two successive octaves of the tonic, major second and perfect fifth, ending with the third octave. This 3:3:1 pattern is analogous in the Tree of Life to the two triads of Sephiroth of Construction (Chesed-Geburah-Tiphareth & Netzach-Hod-Yesod) and Malkuth, to which the seven minor whorls correspond.
The compound of two
600-cells
The 600-cell is the 4-dimensional counterpart of the icosahedron. It is well-known to mathematicians that the
compound of two concentric 600-cells, one of different size inside the other, is the 4-dimensional,
Coxeter plane projection of the 8-dimensional polytope called the "421 polytope" whose 240 vertices
define 240 vectors that are identical to the 240 root vectors of the Lie group E8 appearing in heterotic
superstring theory. The 600-cell has 120 vertices and 720 edges, i.e., 840 vertices & edges. The two 600-cells
have (840+840=1680) vertices & edges. This provides a connection to the 1680 turns in a helical whorl of
the UPA described by Besant & Leadbeater (and therefore irrefutable evidence that the latter is an
E8×E8′ heterotic superstring) that cannot, plausibly, be dismissed as due to chance. For
more details, see 4-d sacred geometries.
Basic parameters of holistic systems
Holistic systems are hierarchical, that is, they display different levels of differentiation, each a whole in itself. For example, starting with the Tree of Life, we can generate its inner form, then analyze the inner form of ten Trees of Life or a subset of its 14 polygons that itself constitutes a whole. Similarly, we can start with the nine primary triangles of the Sri Yantra, then analyze the properties of its two-dimensional and three-dimensional forms when constructed from tetractyses and their higher-order differentiations. What is remarkable (although not surprising from a theoretical perspective) about holistic systems is that they should display the same set of parameters. Those discussed up till now refer to higher levels of differentiation of holistic systems. Their more basic parameters and their characteristic divisions are discussed below.
70 = 10 +
60
Tree of Life
|
a |
b |
Of these, 10 blue sides (see b) are solid, straight lines making up the boundary of the "trunk" of the Tree of Life, namely, the Chokmah-Binah Path (one side), the Chesed-Geburah-Tiphareth triangle (three sides), and the Netzach-Hod-Yesod-Malkuth tetrahedron (six sides), whilst 60 red sides are either dashed sides of the 48 sectors of the 16 triangles or solid sides of the 11 triangles making up the "branches" of the Tree of Life.
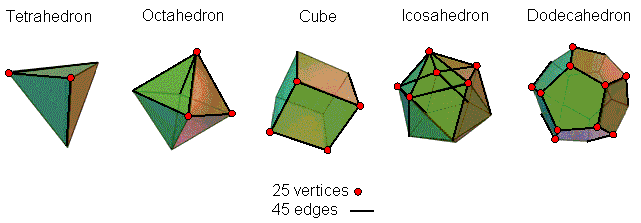
Platonic solids
Constructed from tetractyses, the tetrahedron has 70 yods surrounding its centre (see here). Ten yods are either vertices or centres of internal tetractyses. The simplest Platonic solid is a polyhedral representation of the Tree of Life that has its apotheosis in the disdyakis triacontahedron, which is the polyhedral representation of ten overlapping Trees of Life. The five Platonic solids have 50 vertices and 90 edges. (25+45=70) vertices & edges make up each set of five halves of the regular polyhedra:
2nd-order tetractys
This Pythagorean representation of holistic systems is an array of ten 1st-order tetractyses with 70 hexagonal yods (see here), ten of which are at their centres and 60 of which are at corners of hexagons.
Sri Yantra
The 43 triangles of the two-dimensional Sri Yantra have 70 vertices if we include the central bindu point formally as an isolated vertex (see here). Ten vertices lie on the central, vertical axis passing through it, so that the 70 vertices divide into sets of 10 & 60.
Disdyakis triacontahedron
There are 28 vertices and seven centres of the polygons either above or below the central, 6-sided polygon that is perpendicular to an axis passing through two opposite C vertices (see here). The (28+7+28+7=70) points that are either polyhedral vertices or corners of the 54 sectors of these 14 polygons include the centres of 10 triangles.
70 = 35 +
35
Outer Tree of Life
There are 70 yods in the Tree of Life when its 16 triangles are tetractyses. Its trunk (see here) contains 35 red yods, leaving 35 blue yods in its branches.
Inner Tree of Life
The (7+7) enfolded regular polygons of the inner Tree of Life have 70 corners. Associated with one set of seven
polygons are 35 red corners and associated with the other set are 35 blue corners. The former corresponds to the
trunk and the latter corresponds to the branches of its outer form.
2-d Sri Yantra
The 2-dimensional Sri Yantra is made up of 70 points (the bindu point at its centre & the 69 corners of its 43 triangles). Two points belong exclusively to the central triangle, its uppermost two corners coinciding with corners of the innermost violet triangles. One of the latter is associated with the upper half of the Sri Yantra and is coloured red; the other corner is coloured blue because it is associated with the lower half of the Sri Yantra. This means that the bindu and the lowest corner of the central triangle must have different colours. But which? These two points cannot correspond in the outer Tree of Life to Kether and Malkuth because both Sephirothic points belong to its trunk, whereas one has to belong to its branches, which are composed of blue yods. They correspond in the inner Tree of Life to the two endpoints of the root edge, which represent the start and end of the generation of this geometrical structure. They are the projection onto the plane containing the left-hand and right-hand pillars of the Tree of Life of, respectively, Daath, which is a blue yod because it belongs to the branches, and Tiphareth, which is a red yod, belonging to the trunk. The bindu symbolizes the source of all levels of reality and corresponds to the upper (blue) endpoint of the root edge in the inner Tree of Life because Daath projects onto this point. Hence, it must be coloured blue and the lowest corner of the central triangle must be coloured red, as it corresponds to the other endpoint. The two halves of the Sri Yantra correspond to the trunk and branches of the outer Tree of Life and to the two sets of seven enfolded polygons of its inner form.
Disdyakis triacontahedron
Sixty vertices of the disdyakis triacontahedron surround an axis that passes through two diametrically opposite C
vertices. They form the corners of 15 polygons, the central one of which is a hexagon (see
here & here). The 14 polygons in the upper & lower halves of the
polyhedron (shown red & blue) have (60−6=54) corners, so that 27 belong to each half. Including the isolated
C vertex (denoted by a red or blue dot), there are (1+27+7=35) points in the upper half of the polyhedron that
are either vertices or corners of sectors of polygons and 35 points in the lower half that are likewise. The
35:35 division that is characteristic of holistic systems manifests in the disdyakis triacontahedron as its
upper and lower halves and the internal polygons that its vertices form. The two C vertices correspond to:
1. the two endpoints of the root edge of the (7+7) enfolded polygons of the inner Tree of Life;
2. the bindu & lower corner of the central triangle of the Sri Yantra;
3. Daath and Tiphareth of the Tree of Life.
The icosahedron
When the sectors of the faces of the icosahedron are turned into tetractyses, there are (30×2=60) hexagonal yods on
its 30 edges. Ten vertices surround an axis that passes through two opposite vertices. Hence, (10+60=70) yods
surround this axis, lining its edges to create its form. This pattern is another example of the 10:60 division
discussed earlier in the case of the tetrahedron which, constructed from tetractyses, has 70 yods, 35 yods being
distributed in each half of it. 35 red yods line the 15 edges of one half of the icosahedron
and 35 blue yods line the 15 edges of its other half (for clarity, the diagram above displays
only an illustrative set of four yods of each colour).
The 35:35 pattern in sacred geometries is also discussed here.
120 &
144
Tree of Life
The outer Tree of Life consist of 10 corners and 22 sides of 16 triangles, i.e., 48 corners, sides & triangles (see here); its inner form has 48 corners (see here). When its 16 triangles are Type A, it has (3×16=48) triangles with (10+16=26) corners and (22+48=70) sides, i.e., (26+70+48=144) corners, sides & triangles. The counterparts of this in the inner Tree of Life are the 144 yods along the boundaries of the seven separate, regular polygons, 48 of which are corners. Enfolded, the seven polygons have 120 boundary yods and 144 internal yods (see here). This is how the inner Tree of Life encodes the Polyhedral Tree of Life. This is a pair of polyhedra consisting of one with 74 vertices & 144 faces and the disdyakis triacontahedron with 62 vertices & 120 faces (see here). The 48 sectors of the seven separate polygons have 144 corners & sides surrounding their centres. There are 120 hexagonal yods in the pair of Type A dodecagons, which constitute a Tree of Life structure in themselves. A single, Type B dodecagon has 144 yods surrounding its centre other than hexagonal yods at centres of its 36 tetractyses. It also has 120 geometrical elements surrounding its centre. There are 120 hexagonal yods on the 60 edges of the first (6+6) enfolded polygons outside their shared root edge, indicating that they are in themselves a holistic structure within the inner form of the Tree of Life (see Article 4 for how they are prescribed by the Godnames).
Sri Yantra
There are 240 geometrical elements in the 43 triangles of the two-dimensional Sri Yantra that surround its central bindu point (see here). 120 elements belong to each half. Unlike the 42 triangles surrounding it, the central triangle with three sides and with its lowest corner unshared with the surrounding triangles does not divide into two identical halves. However, these four elements do form two sets of two elements: (side, side) & (corner, side). This makes it possible to divide the 240 geometrical elements into two same-sized sets. There are 144 yods on the 54 sides of the 18 triangles in the first and second layers.
Disdyakis triacontahedron
The central 12-gon formed by the 12 vertices in its equatorial plane:
.png)
is perpendicular to an axis passing through two opposite A
vertices. Surrounding its centre are 12 sectors composed of 48 geometrical elements. The
polyhedron has 120 faces (60 in each half). The 84 edges on each side of the central plane containing the 12-gon
are sides of 84 internal triangles that meet at the centre of the polyhedron. (60+84=144) internal and
external triangles exist on each side of the central polygon.
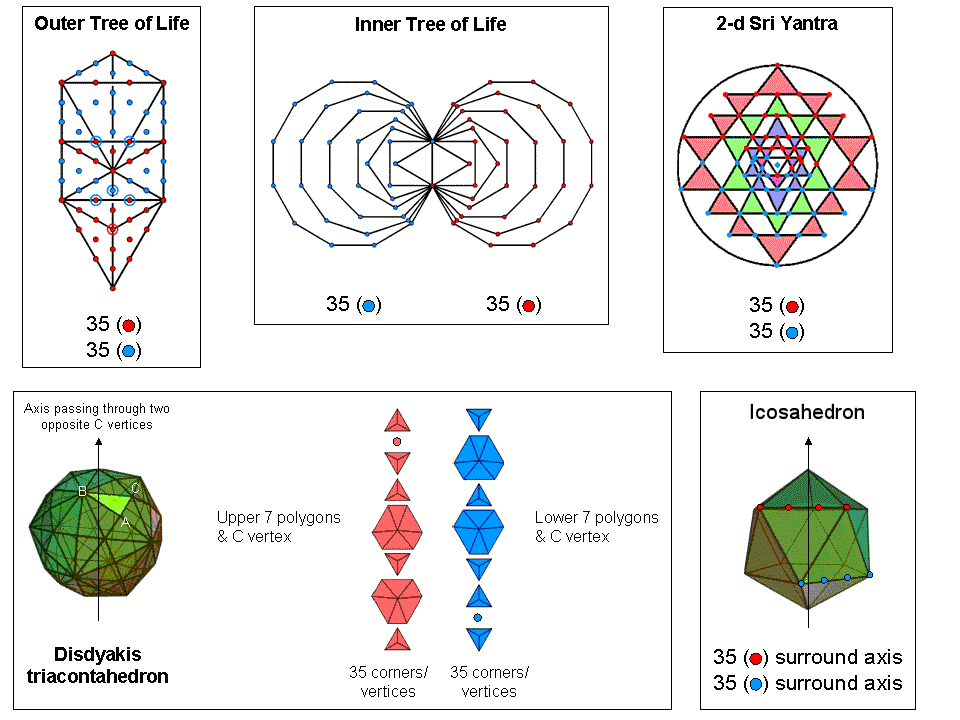
350 = 90 + 260,
where
90 = 36 + 54
Lambda Tetractys
This is the division generated by the Tetrahedral Lambda, the
arithmetic version of the universal pattern displayed by sacred geometries (see here). The sum of the ten integers in the Lambda Tetractys is 90 and the sum
of the remaining ten integers is 260. The Tetrad defines this division of numbers because, in a square whose
sectors are tetractyses, the 12 red integers 2–13 assigned to the 12 yods on its edges add up to 90, whilst the
next 13 black integers 14–26 that can be assigned to its 13 internal yods add up to 260. In other words,
the sum of the 25 integers 2–26 is 350, which is the sum of the 20 integers making up the
Tetrahedral Lambda:
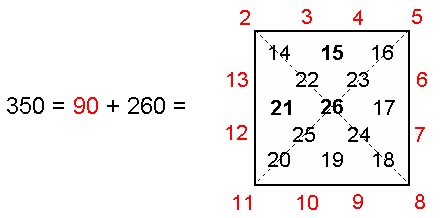
Notice that not only do the integers 2, 5, 8 & 11 at the four corners add up to 26, the number value of YHVH, but also the three smallest ones add up to 15, the number value of YH. The 11:15 division that this generates is characteristic of holistic systems. For example, the trunk of the Tree of Life consists of the geometrical sequence: point, line, triangle & tetrahedron (see here and Figure 4 here). The first three comprise 11 points, lines & triangles and the fourth consists of 15 points, lines, triangles & tetrahedra.
Tree of Life
350 corners are intrinsic to the 70 polygons enfolded in the inner form of the 10-tree (see here). Ninety corners outside their root edges belong to the first four types of polygons and 260 corners belong to the last three types. Every ten overlapping Trees consist of 350 vertices, edges, triangles & tetrahedra. Divided into their sectors, the seven enfolded polygons of the inner Tree of Life have 176 vertices, edges & triangles (see here). The topmost vertex of the hexagon coincides with the lowest vertex of the hexagon enfolded in the next higher Tree of Life, leaving 175 geometrical elements intrinsic to that set of polygons. The two separate sets of enfolded polygons have 350 intrinsic geometrical elements (90 in the first three types of polygons and 260 in the last four types). 350 hexagonal yods line the 175 edges of the 94 sectors of the (7+7) enfolded polygons (see here). Ninety of them are in the pairs of squares & octagons.
Sri Yantra
Regarded as tetractyses, the nine basic triangles generating the Sri Yantra have 90 yods. 36 yods are at their corners or centres and 54 yods are hexagonal yods (see here).
The Platonic solids
The 90 edges of the five Platonic solids consist of the 36
edges of the tetrahedron & dodecahedron and the 54 edges of the octahedron, cube & icosahedron. Table 4
shows the number of geometrical elements in their faces and interiors when internal sectors are Type A triangles
(“1” denotes the centre of a regular polyhedron):
Table 4. Numbers of corners, sides of triangles & triangles in the Platonic solids.
|
Corners |
Sides |
Triangles |
Total |
||||
|
Interior |
Exterior |
Interior |
Exterior |
Interior |
Exterior |
||
| Tetrahedron |
6 + 1 = 7 |
4 + 4 = 8 |
4 + 6×3 = 22 |
6 + 4×3 = 18 |
6×3 = 18 |
4×3 = 12 |
84 + 1 = 85 |
| Octahedron |
12 + 1 = 13 |
6 + 8 = 14 |
6 + 12×3 = 42 |
12 + 8×3 = 36 |
12×3 = 36 |
8×3 = 24 |
164 + 1 = 165 |
| Cube |
12 + 1 = 13 |
8 + 6 = 14 |
8 + 12×3 = 44 |
12 + 6×4 = 36 |
12×3 = 36 |
6×4 = 24 |
166 + 1 = 167 |
| Icosahedron |
30 + 1 = 31 |
12 + 20 = 32 |
12 + 30×3 = 102 |
30 + 20×3 = 90 |
30×3 = 90 |
20×3 = 60 |
404 + 1 = 405 |
| Subtotal = |
60 + 4 = 64 |
30 + 38 = 68 |
210 |
60 + 120 = 180 |
180 |
120 |
818 + 4 = 822 |
| Dodecahedron |
30 + 1 = 31 |
20 + 12 = 32 |
20 + 30×3 = 110 |
30 + 12×5 = 90 |
30×3 = 90 |
12×5 = 60 |
412 + 1 = 413 |
| Total = |
90 + 5 = 95 |
50 + 50 = 100 |
320 |
90 + 180 = 270 |
270 |
180 |
1230 + 5 = 1235 |
The 150 triangles in the dodecahedron have 62 corners surrounding its centre (the same number as the number of vertices surrounding the centre of the disdyakis triacontahedron). YAH prescribes the dodecahedron because 150 = 15×10. EL prescribes it because 62 is the 31st even integer, 31 being the number value of this Godname of Chesed. The fifth Platonic solid has 90 sides of triangles in its faces, 110 internal sides and 150 triangles, i.e., 260 triangles & internal sides, making a total of 350 sides & triangles. Its 90 external sides correspond to the sum of the ten integers in the Lambda Tetractys and the 260 triangles & internal sides correspond to the sum of the remaining ten integers in the Tetrahedral Lambda. The dodecahedron has 200 sides and 150 triangles. This 200:150 division corresponds to the sum (200) of the 12 integers at the corners of the six-sided polygons in each face and to the sum (150) of the eight integers at the vertices and centres of faces of the tetrahedral array of 20 integers (see Figure 3 here). These proportions do not occur in the icosahedron. Although, mathematically speaking, the dodecahedron is merely its dual, it can be said to be more perfect than the icosahedron because its geometrical composition is characterized by various parameters of the Tetrahedral Lambda. Moreover, it is the only Platonic solid that embodies these numbers. Perhaps, however, "perfect" is not quite the right word. Rather, it is more correct to say that the complete realisation of the divine archetype is most explicit in the dodecahedron.
The table shows that the five Platonic solids have 1230
geometrical elements surrounding their centres. The average number is 246, which is the number value of
Gabriel, the Archangel of Yesod. The average number of triangles is 90 (54 internal, 36 external).
This 36:54 division is displayed by the Lambda Tetractys. 550 geometrical elements make up their faces.
This is the number of SLs in CTOL. Notice that the Decad measures not only this number:
550 = 10×(1+2+3+4+5+6+7+8+9+10)
but also the 190 corners of triangles surrounding the axes of the five Platonic solids. This is because 190 = 10×19, where 19 is the tenth odd integer, there being 100 (=102) comers of triangles in their faces. Including their centres, the five solids have 95 internal vertices. This is the number value of Madim, the Mundane Chakra of Geburah. The 450 triangles in the five solids have 500 (=50×10) sides that are not polyhedral edges. The Godname ELOHIM with number value 50 prescribes not only their 50 faces but also the number of extra sides of triangles needed to construct them from the latter. The number of extra corners = 90 + 50 = 140, which is the number value of Malachim, the Order of Angels assigned to Tiphareth.
Disdyakis triacontahedron
When its internal triangles are divided into their sectors, the
polyhedron has (180+120+60=360=36×10) corners & external triangles and (180×3=540=54×10) internal
triangles that surround an axis joining two opposite vertices, i.e., 900 (=90×10) vertices & triangles. The
polygons formed by the 60 vertices that surround this axis contain 900 yods distributed around it when their
sectors are Type A triangles because such an n-gon has 15n yods surrounding its centre, so that
the yod population of the polygons with 60 corners = ∑15n = 15∑n = 15×60 = 900. They comprise
(60×6=360) yods either on their edges or at centres of tetractyses and (60×9=540) yods on internal sides of
tetractyses.
Each half of this Catalan solid has 90 edges above and below the central polygon perpendicular to an axis passing through two opposite C vertices. This is a hexagon, none of whose sides are polyhedral edges because its six corners are all A vertices (see here). They form an edge with B and C vertices both above and below the central hexagon. As there are 30 AB, 30 AC and 30 BC edges in each half, there are 24 AC edges and 30 BC edges that do not touch this hexagon and which contain a C vertex. This leaves 24 AB edges that do not touch the polygon and six AB edges and six AC edges that do touch it. The 90 edges in each half of the polyhedron divide into 54 edges (30 BC & 24 AC) containing C vertices that do not touch the polygon and 36 edges (30 AB & six AC) that either do touch it or do not contain C vertices. The 90 edges in each half of the polyhedron therefore display the 36:54 division of the Lambda Tetractys.
When internal and external triangles are Type A, the disdyakis triacontahedron is composed of 900 triangles [360 (=36×10) external, 540 (=54×10) internal] (see here).
The ten-fold sequence of generation of the disdyakis triacontahedron (point–line–triangle–tetrahedron, etc) contains 351 vertices and faces, where 351 is both the number value of Ashim, the Order of Angels assigned to Malkuth, and the 26th triangular number, where 26 is the number value of YAHWEH, the Godname of Chokmah. (By "vertices" we mean not only the polyhedral vertices but also the starting point, the two endpoints of the single, straight line & the three corners of the triangle in the sequence — that is, mathematical points). Therefore, 350 vertices & faces are needed to generate the sequence of objects, given this point (the term "faces" includes the triangle). Their composition is shown below:
|
Vertices |
Faces |
|
| line: |
2 |
0 |
| triangle: |
3 |
1 |
| tetrahedron: | 4 | 4 |
| octahedron: | 6 | 8 |
| cube: | 8 | 6 |
| icosahedron: | 12 | 20 |
| dodecahedron: | 20 | 12 |
| rhombic triacontahedron: | 32 | 30 |
| disdyakis triacontahedron: | 62 | 120 |
| Total = | 149 | 201 |
The seven polyhedra in the sequence have 200 faces. The 150 (=15×10) other geometrical elements in the sequence consist of the 50 vertices of the five Platonic solids, the triangle and 99 other vertices, i.e., 100 elements. Compare these numbers with the arithmetic properties of the Tetrahedral Lambda:
Sum of integers at centres of faces = 50.
Sum of integers at corners = 100.
Sum of remaining integers = 200.
Correspondence also exists between the 6:36:48 division in the Lambda Tetractys, which is the first face of the Tetrahedral Lambda:
|
1 |
|||
| 2 | 3 | ||
|
4 |
6 |
9 |
|
|
8 |
12 | 18 | 27 |
The integer 6 at the centre of the Lambda Tetractys denotes the triangle and the five vertices of the line &
triangle, the sum (36) of the integers 1, 8 & 27 at its corners denotes the four vertices of the
tetrahedron and the 32 vertices of the rhombic triacontahedron and the sum (48) of the six other integers
denotes the four faces of the tetrahedron (4), the 14 vertices & faces of the octahedron (2+3+9=14) and the 30
faces of the rhombic triacontahedron (12+18). This leaves the 100 vertices of the cube, icosahedron, dodecahedron
and disdyakis triacontahedron and their 160 faces, i.e., 260 vertices & faces. This is the sum of the remaining
16 integers in the Tetrahedral Lambda. We conclude that the sequence of ten geometrical objects that lead to the
disdyakis triacontahedron is archetypal because their vertices and faces conform to the 6:36:48 and
90:260 proportions of the Tetrahedral Lambda. Notice that the sequence: line→rhombic triacontahedron contains
87 vertices and 81 faces, i.e., 168 vertices & faces. 87 is
the number value of Levanah, the Mundane Chakra of Yesod, which is the penultimate Sephirah, and
168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, which is the
last Sephirah. Hence, the sequence leading to the rhombic triacontahedron comprises the number values of
the Mundane Chakras of the last two Sephiroth.
137
The number that determines the fine-structure constant (see here) is always embodied in holistic systems expressing the divine archetypes. Because matter itself is the manifestation of their designing influence, there is no mystery why this parameter of such systems plays such a central, mathematical role in determining the physics of the atomic world.
Tree of Life
Below the top of the 7-tree mapping space-time (see Article 2) are 137 vertices & triangles [4]. The 14 enfolded polygons of the inner Tree of Life whose sectors are Type A triangles contain 1370 (=137×10) yods (see here). Divided into their sectors, the last four enfolded polygons have 137 sides of 72 triangles (see here).
Tetrahedral Lambda
The sum of the integers 2, 3 & 4 and their squares & cubes on the three inclined edges of the Tetrahedral Lambda is 137 (see here):
|
21 |
31 |
41 |
|
|
137 = |
22 |
32 |
42 |
|
23 |
33 |
43 |
21 + 22 + 23 = 2(1+21+22) = 2×7,
31 + 32 + 33 = 3(1+31+32) = 3×13,
and
41 + 42 + 43 = 4(1+41+42) =
4×21,
the 10 powers of 1, 2, 3 & 4 on the inclined edges can be written as a tetractys array of the integers 1, 7, 13 & 21:
| 1 | ||||
| 7 | 7 | |||
| 138 = | 13 | 13 | 13 | |
| 21 | 21 | 21 | 21 . |
Their sum is the number of yods outside the root edge in the two Type A dodecagons present in the inner form of the Tree of Life:
|
138 = |
 |
(For the sake of clarity, the four yods on the root edge are omitted). The number 137 is the sum of the nine odd integers below the apex 1 of this tetractys array. The sum of the four integers 21 (gematria number of EHYEH, the Godname of Kether) at the base of the tetractys is 84. This number is the sum of the nine integers in the Lambda Tetractys that surround its central integer 6 (see here). It is the number of circular turns in one-quarter of a revolution of each whorl of the UPA. The number 84 is expressed by the Tetrad because
|
12 + 32 + 52 + 72 = 84 = |
|
This 4×4 array of the first four odd integers is also significant for the group mathematics underlying superstrings because, when the squares of these integers are present, it generates the dimension 496 of both E8×E8 and SO(32), which are the two possible symmetries of their unified interactions that are free of quantum anomalies (see here).
The Platonic solids
The average number of yods needed to construct the faces of the four Platonic solids representing the four Elements is 137 (see here). The average number of corners & triangles making up half a Platonic solid is 137 (see here). Including their centres, the total number of such geometrical elements needed to construct the five halves of the Platonic solids = 137×5 = 685. As the inner Tree of Life has 1370 yods when the sectors of its 14 regular polygons are Type A triangles (see here), this, remarkably, is the number of yods associated with each half of the inner Tree of Life! It demonstrates the holistic nature of the mathematically complete set of five regular polyhedra. As further confirmation of its archetypal character, the number 685 is also the number of geometrical elements present in the sequence of development in 10 steps of the disdyakis triacontahedron from a point:
|
Vertices |
Edges |
Faces |
Total |
|
| 1. Point |
1 |
0 |
0 |
1 |
| 2. Line |
2 |
1 |
0 |
3 |
| 3. Triangle |
3 |
3 |
1 |
7 |
| 4. Tetrahedron |
4 |
6 |
4 |
14 |
| 5. Octahedron |
6 |
12 |
8 |
26 |
| 6. Cube |
8 |
12 |
6 |
26 |
| 7. Icosahedron |
12 |
30 |
20 |
62 |
| 8. Dodecahedron |
20 |
30 |
12 |
62 |
| 9. Rhombic triacontahedron |
32 |
60 |
30 |
122 |
| 10. Disdyakis triacontahedron |
62 |
180 |
120 |
362 |
| Total |
150 |
334 |
201 |
685 |
The cube has 137 internal yods when it is constructed from Type A triangles (see #10 at The Platonic solids and the table in #16).
Seven diatonic musical scales
Including their tonics, or starting notes, the seven diatonic scales have 137 notes and intervals that belong to the Pythagorean scale (see table on p. 13 of Article 16).
Disdyakis triacontahedron
The Type A sectors of the 15 polygons perpendicular to an
axis joining two opposite C vertices that are formed by 60 of the 62 polyhedral vertices have
(15+60+60=135) corners. The triangles making up the polyhedron and its polygons have (2+135=137) vertices
(see here).
206 = 80 +
126
This is the embodiment by sacred geometry of the 80 bones of the human axial skeleton and the 126 bones of the human appendicular skeleton.
Outer Tree of Life
The 1-tree whose 19 triangles are Type A triangles has 80 yods in its "trunk" (see here for its definition). 126 yods are added to its branches when these triangles become Type A triangles (see Article 33).
Inner Tree of Life
There are 206 yods associated with the last four enfolded polygons, whose 35 sectors have 138 vertices, edges & triangles (see here). Associated with the hexagon and octagon are 80 yods symbolizing the 80 bones of the human axial skeleton. Outside the shared edge of the decagon and dodecagon are 126 yods that symbolize the 126 bones of the human appendicular skeleton.
Disdyakis triacontahedron
In the case of its seven layers of vertices perpendicular to an
axis passing through two opposite A vertices, layers 1 and 3 consist of 6- & 8-sided polygons, and layers 2
and 4 consist of 10- & 12-sided polygons. Their enfolded counterparts in the inner Tree of Life contain,
respectively, 80 and 126 yods.
240 = 72 +
168
This expresses the fact that 72 of the 240 roots of the superstring symmetry group E8 are roots of its exceptional subgroup E6, leaving 168 roots. See here for how five sacred geometries embody this division.
1-tree
Constructed from Type A triangles, the 1-tree contains 240 yods other than SLs (see here). Noting that the Tree of Life with 22 Paths and 16 triangles is converted to the 1-tree with 25 Paths and 19 triangles by adding one corner and three sides of three triangles, the composition of the 240 yods is:
|
Hexagonal yods on Paths |
Hexagonal yods at centres of tetractyses |
Vertices |
Hexagonal yods on internal edges |
|
| Tree of Life: |
22×2 = 44 |
16×3 = 48 |
16 |
16×3×2 = 96 |
| Addition: |
3×2 = 6 |
3×3 = 9 |
3 |
3×3×2 = 18 |
| Total: |
50 |
57 |
19 |
114 |
126 yods comprise 50 hexagonal yods on Paths and (57+19=76) yods that are either corners or centres of tetractyses:
|
126 = |
44 + 6 + 48 + 9 + 16 + 3 |
|
= |
6 + 48 + (44+9+16+3) |
|
= |
6 + 48 + 72. |
The 126 yods include 72 yods that are either the 44 hexagonal yods on the Paths of the Tree of Life, the 19 corners of tetractyses inside the triangles of the 1-tree and the nine centres of the three triangles added in the conversion of the Tree of Life to the 1-tree. The 126 yods symbolize the 126 roots of E7, the rank-7 exceptional subgroup of E8, and the 72 yods symbolize the 72 roots of E6. The remaining 114 hexagonal yods on internal sides symbolize the 114 roots of E8 that are not roots of E7. The trunk of the Tree of Life has five Type A triangles on whose 15 internal sides of their tetractyses there are 30 hexagonal yods. 84 hexagonal yods lie on the 42 sides of the other 14 triangles making up the branches of the 1-tree, i.e., 114 = 30 + 84 and
168 = 6 + 48 + 114 = 6 + 48 + 30 + 84 = (48+30) + (6+84) = 78 + 90.
There are 78 hexagonal
yods that are either centres of tetractyses in the Tree of Life or on internal sides of tetractyses in its
trunk. There are 90 yods that are either hexagonal yods on Paths added by the conversion or hexagonal yods on
internal sides of tetractyses in the branches of the 1-tree. These two numbers are the number values of,
respectively, the words Cholem and Yesodoth in the Kabbalistic name of the Mundane Chakra of
Malkuth:
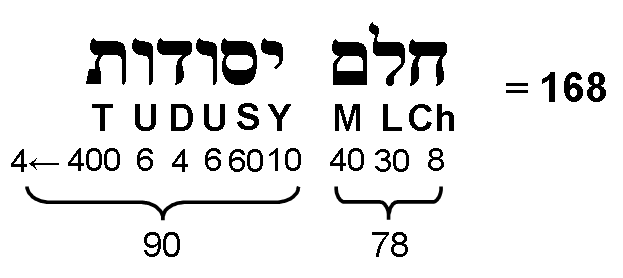
Notice also that
168 = (6+48+30) + 84 = 84 + 84.
This 84:84 division of the number 168 is characteristic of holistic systems, as we have seen previously. See also Article 64.
Inner Tree of Life
The 240 hexagonal yods of the seven separate polygons consist of
72 hexagonal yods lining the sides of the first six polygons and 168 other hexagonal yods. Of the
latter, 78 belong to the hexagon and to the dodecagon and 90 belong to the other polygons. Once again, we see
that the number values of Cholem and Yesodoth are reproduced in the inner Tree of Life as well as
in the 1-tree. As the first six polygons are a holistic system, this 240:72 division signals a
symmetry-breakdown from E8 with 240 roots to E6 with 72
roots.
Dodecagon
Surrounding the centres of two separate dodecagons with Type A sectors are 240 geometrical elements. They comprise 72 triangles and 168 corners & sides (84 in each dodecagon).
Sri Yantra
Surrounding the central bindu point of the two-dimensional Sri Yantra are 240 geometrical elements (see here). They comprise the 126 sides of the 42 triangles surrounding the central one, i.e., 168 sides & triangles (84 in each half of the Sri Yantra), as well as 69 corners and the three sides of the central triangle, i.e., 72 corners & sides.
When they are Type B triangles, the 42 triangles have 1680 yods other than their 168 internal corners and the 26 tips of the nine primary triangles that belong to them (see here). Noting that the nine tetractyses of a Type B triangle have four corners inside it, the 240 corners in the (1+42) triangles that surround the bindu are made up of the (4×42=168) corners of tetractyses making up the 42 triangles, the 68 corners of the latter and the four corners of the nine tetractyses inside the central triangle that are unshared with surrounding triangles. Therefore, the 240 corners display a 72:168 division.
Disdyakis
triacontahedron
2400 (=240×10) geometrical elements surround its axis when its faces and internal triangles are Type A triangles (see here). 1680 (=168×10) elements surround it when only internal triangles are Type A. 720 (=72×10) elements are added by the further division of its faces into their sectors.
Surrounding an axis passing through two opposite A vertices are 180 edges (12 edges of its central polygon, 168 other edges). Its 180 internal triangles have 60 internal edges surrounding the axis. Its (120+180=300) triangles have (12+60+168=72+168=240) edges surrounding the axis. 72 edges are either internal or line the middle of the polyhedron. 168 edges line its 120 faces, 84 above the middle, 84 below it.
Divided into their sectors, the seven polygons formed by the 60 vertices of the disdyakis triacontahedron that surround an axis passing through two opposite A vertices are composed of 240 geometrical elements surrounding their centres (see here). They comprise 72 elements in the two topmost polygons with 18 vertices and 168 elements in the five other polygons with 42 vertices. There are 240 geometrical elements in the faces and internal polygons in each half of the polyhedron. Of these, 168 elements are in these faces and 72 elements are in the polygons.
In the case of the 15 polygons perpendicular to an axis through two opposite C vertices that are formed by vertices of the disdyakis triacontahedron, there are 72 corners, sides & triangles in the uppermost and lowest three polygons with 18 vertices and 168 vertices, edges & triangles in the remainder of the polyhedron with 42 vertices (see here).
496 = 248 + 248
Outer Tree of Life
It was shown here that, when ten overlapping Trees of Life are interpreted as representing the ten dimensions of the space-time of superstrings, there are 496 yods up to (but not including) Chesed of the tenth Tree when their triangles are turned into tetractyses. There are 248 yods up to Chesed of the fifth Tree, each yod symbolizing one of the 248 gauge fields of E8. For E8×E8 heterotic superstrings, the division of the 496 gauge fields of the superstring symmetry group E8×E8 into two sets of 248 fields is the manifestation of the 5:5 division of Sephiroth in the Tree of Life. It results in the existence of an as yet little-understood shadow matter universe co-existing with and parallel to the familiar universe of ordinary matter. The superstrings in each universe have unified forces described by the same symmetry group E8. In terms of the four overlapping Trees of Life that represent in Kabbalah the four Worlds of Atziluth, Beriah, Yetzirah & Assiyah in which Adam Kadmon, or "Heavenly Man" exists, the Upper Face of the Assiyatic Tree is the subtle energy body comprising the matter of the etheric body, prana/chi, acupuncture meridians, etc. Called in Kabbalah the "Zelim", or image, and in Vedantic philosophy the "pranamaya kosha," it exists not in exactly the same universe as ordinary matter (in particular, the physical body, or "annamaya kosha") but in the shadow matter universe, a narrow gap that extends along the seventh of the curled-up dimensions predicted by M-theory separating the two 10-dimensional space-time sheets that contain the two universes, one visible, the other invisible.
Inner Tree of Life
The 248 roots of E8 are symbolized in the seven separate polygons of the inner Tree of Life by the endpoint of the root edge, the centres of the seven polygons and their 240 hexagonal yods (see here). The mirror symmetry of the two sets of polygons is responsible for the direct product E8×E8 of two similar Lie groups E8.
When the 70 yods of the
outer Tree of Life are projected onto the plane containing the two sets of seven enfolded polygons of the inner
Tree of Life, there are 248 yods in each set that are intrinsic to them in the sense that none of them
coincide with projections onto this plane of yods on Paths. As evidence that this is neither coincidental nor
the result of an arbitrary choice made merely in order to generate the superstring number 248, there are
78 yods associated with the first four polygons, where 78 is the dimension of E6, a subgroup of
E8. The 114 yods in the octagon and dodecagon symbolize the 114 roots of E8 that do not
belong to E7. The 56 yods in the decagon outside the root edge symbolize the two simple roots of
E8 not belonging to E6 and the 54 roots of E7 not belonging to
E6.
Sri Yantra
According to Table 8 in Article 35, when its 43 triangles are transformed into Type A triangles, the two-dimensional Sri Yantra contains 757 yods. 756 yods surround the bindu point. Of these, 16 green yods belong solely to the central triangle (its two upper corners are also corners of the innermost set of eight triangles, so that green yods are not assigned to them). According to this table, 504 hexagonal yods line the 252 sides of the 126 tetractyses in the 42 triangles surrounding the central one. The tips of some of these triangles touch twelve of their sides. From a strict, mathematical point of view, these particular sides are not single, straight lines but pairs of lines joined at the tip of another triangle. This leaves (252–12=240) true sides (i.e., single, straight lines) with 480 hexagonal yods. These yods cannot be divided into two sets of 240 that are mirror images of one another, if the mirror is horizontal, because three of the four sides excluded from the layer of ten blue triangles in Figure 1 of Article 35 (or see here) belong solely to its upper half, creating an imbalance. However, a mirror symmetry persists after excluding the 12 sides if the mirror is vertical, for, then, 240 red hexagonal yods and 240 blue hexagonal yods lie either on or, respectively, to the right and left of the vertical axis passing through the centre of the central triangle, which is surrounded by (240+240+16=496) yods on true sides:
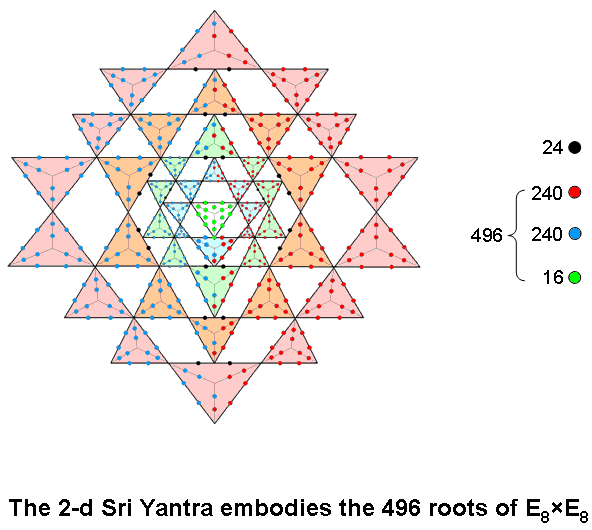
The 24 hexagonal yods lining sides that are touched by other true triangles are coloured black. The pair of hexagonal yods in the side of the triangle touched by the lowest corner of the central triangle are not black because, although it has the appearance of a triangle, the central triangle is, mathematically speaking not a true, triangular area, the bindu (a separate point) coinciding with its centre. In the 3-dimensional Sri Yantra, the central triangle really is a triangle because the bindu hovers above it instead of being embedded in its surface. If it were traversed by various lines, it would be obvious that this "triangle" could not be regarded as a pure triangle. To the mathematical novice, it is not so obvious that it loses this status when merely the bindu is embedded in its surface. But the principle remains the same even if the "triangle" is divided into its sectors. The 16 green yods in the central triangular perimeter that surround the bindu are intrinsic to this triangle because they are unshared with any of the 42 triangles around it. They symbolize the 16 simple roots of E8×E8. The (240+240=480) hexagonal yods in the 240 single lines making up the true sides of the 42 triangles denote its (240+240=480) roots. Without this axial symmetry, the 496 yods could not be divided into two similar sets of 248 yods. Instead, the Sri Yantra would embody the 496 roots of SO(32), the second Lie group with the dimension 496 that governs Type 1 open and closed superstrings and one of the two types of closed heterotic superstrings. It is as if the two possible gauge symmetry groups governing superstring forces allowed by superstring theory correspond to the two orthogonal orientations of the Sri Yantra, its traditional one (E8×E8) displaying a left/right mirror symmetry and the other one rotated by 90° (SO(32)) not doing so:
.gif)
The 72:168 division characteristic of holistic systems manifests in the 2-d Sri Yantra composed of Type A triangles as the (6×12=72) hexagonal yods in the six red triangles on either side of its central axis and as the 168 hexagonal yods in the remaining 19 triangles.
As supporting evidence that this is the correct way of seeing how the number 496 at the heart of superstring theory is embodied in the two-dimensional Sri Yantra, it was pointed out here that this sacred geometrical object is composed of 240 geometrical elements surrounding its centre when all triangles are not divided into their sectors. In other words, including this centre, there are (241–12=229) true, geometrical elements when the 12 sides touched by triangles are left out of consideration. 229 is the 50th prime number, showing how ELOHIM with number value 50 prescribes the true, geometrical composition of the two-dimensional Sri Yantra. There are 70 points and 117 true sides, i.e., 187 true points & lines, where 187 is the number value of Auphanim, the Order of Angels assigned to Chokmah. There are (70+42=112) points & triangles, where 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod.
The Platonic solids
When the vertices and
centres of faces of the five Platonic solids are connected to their centres, there are on average
496 geometrical elements other than vertices that surround their axes passing through two
vertices and their centres. 248 elements other than vertices on average surround these axes in
each half of the five Platonic solids (see here). They are the regular polyhedral counterpart of the
248 roots of the rank-8 Lie group E8. This remarkable analogy allows us to say that
the direct product nature of the symmetry group E8×E8 governing the unified interactions
between one of the two types of heterotic superstrings arises from the fact that every geometrical element
surrounding these axes that make up the five Platonic solids has a mirror-image counterpart.
Disdyakis triacontahedron
The geometrical composition of the polyhedron and the seven polygons formed by the 60 vertices surrounding an axis that passes through two diametrically opposite A vertices is analyzed here. We found that 248 vertices, sides & triangles surround the axis in each half of the polyhedron, i.e., a total of 496 geometrical elements surround this axis. The 248:248 division of this number — the polyhedral counterpart of the (248+248) roots of E8×E8 — is the result of the mirror symmetry of the disdyakis triacontahedron whereby every geometrical element or yod generated by dividing its triangles into their sectors or by turning them into tetractyses has a mirror-image counterpart.
References
1. Proof: The 15 polygons have 60 corners surrounding the axis passing through two opposite C vertices. The central polygon has six corners, so that the seven polygons above or below it have 27 corners. A Type B n-gon has (15n+1) yods when its n sectors are Type A triangles, so that, given just its n corners (vertices of the disdyakis triacontahedron), (14n+1) extra yods are needed to transform it into these sectors. Each set of seven polygons requires (14×27 + 7 = 385) more yods to turn them into Type B polygons.
2. Proof: the n-tree is composed of (12n+7) triangles with (6n+5) corners and (16n+9) sides, i.e., (22n+14) corners & sides. The 7-tree has (12×7 + 7 = 91) triangles with (22×7 + 14 = 168) corners & sides.
3. Proof: n overlapping Trees of Life have (50n+20) yods. 67 overlapping Trees have 3370 yods. Their uppermost triangle with Kether, Chokmah & Binah at its corners has ten yods when it is a tetractys. Below Binah of the 67th Tree are (3370−10=3360) yods.
4. Proof: the n-tree is composed of (12n+7) triangles with (6n+5) corners and (16n+9) sides, i.e., (18n+12) corners & triangles. The 7-tree has (18×7 + 12 = 138) corners & triangles. Below its apex are 137 corners & triangles. Compare this with the number 1 at the apex of the Tetrahedral Lambda and the numbers on its inclined edges that add up to 137 (see Fig. 3 here). The apex of the 7-tree is the 168th Sephirothic level (SL) on the central Pillar of Equilibrium from the top of CTOL.* This connects the superstring structural parameter 168 to the mysterious number 137 that determines the fine-structure constant α = e2/ħc well-known to physicists (see previous discussion of this parameter of holistic systems). Below the 168th SL on the central pillar from the top of CTOL are the 137 corners & triangles of the 7-tree. Its 91 triangles have (6×7 + 5 = 47) corners and (16×7 + 9 = 121) sides, i.e., 168 corners & sides, further demonstrating how the gematria number 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, not only marks out the commencement in CTOL of the 7-tree mapping the physical plane/universe (the plane formally corresponding to Malkuth) but also measures the number of points & lines needed to construct this map! Here is an amazing conjunction of two fundamental parameters of particle physics (one yet to be discovered) that is too implausible to be attributed to chance. Indeed, what is the likelihood that it could be mere coincidence that there are 168 corners & sides of 91 triangles below the 168th SL on the central pillar of CTOL from the top of its 91 Trees of Life?
* Proof: the number of SLs in the n-tree on its central Pillar of Equilibrium = 2n + 3. There are 17 such SLs in the 7-tree. The number of SLs on the Pillar of Equilibrium of n overlapping Trees of Life = 2n + 2. There are 184 SLs on the Pillar of Equilibrium of CTOL (n=91). Hence, there are (184−17=167) such SLs above the 7-tree, the apex of which is therefore the 168th SL on the central pillar, counting from the top of CTOL. The number 168 of the Mundane Chakra of Malkuth specifies this apex, i.e., where in CTOL Malkuth (the 7-tree), as the physical universe with 25 spatial dimensions, begins to emerge from the superphysical realms of consciousness mapped by the 84 Trees of Life beyond the 7-tree mapping the physical plane.
Two useful reference works that describe the esoteric/metaphysical, cultural, mathematical and scientific meanings of numbers are available as free PDFs from this website:
Numbers, by W. Wynne Wescott (1890) (64 pages);
Numbers 1 to 100 (419 pages).