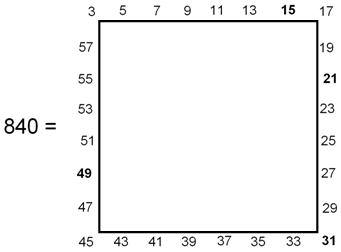
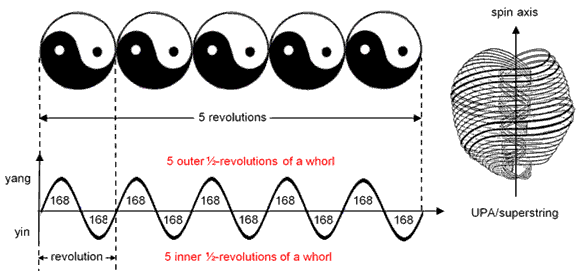
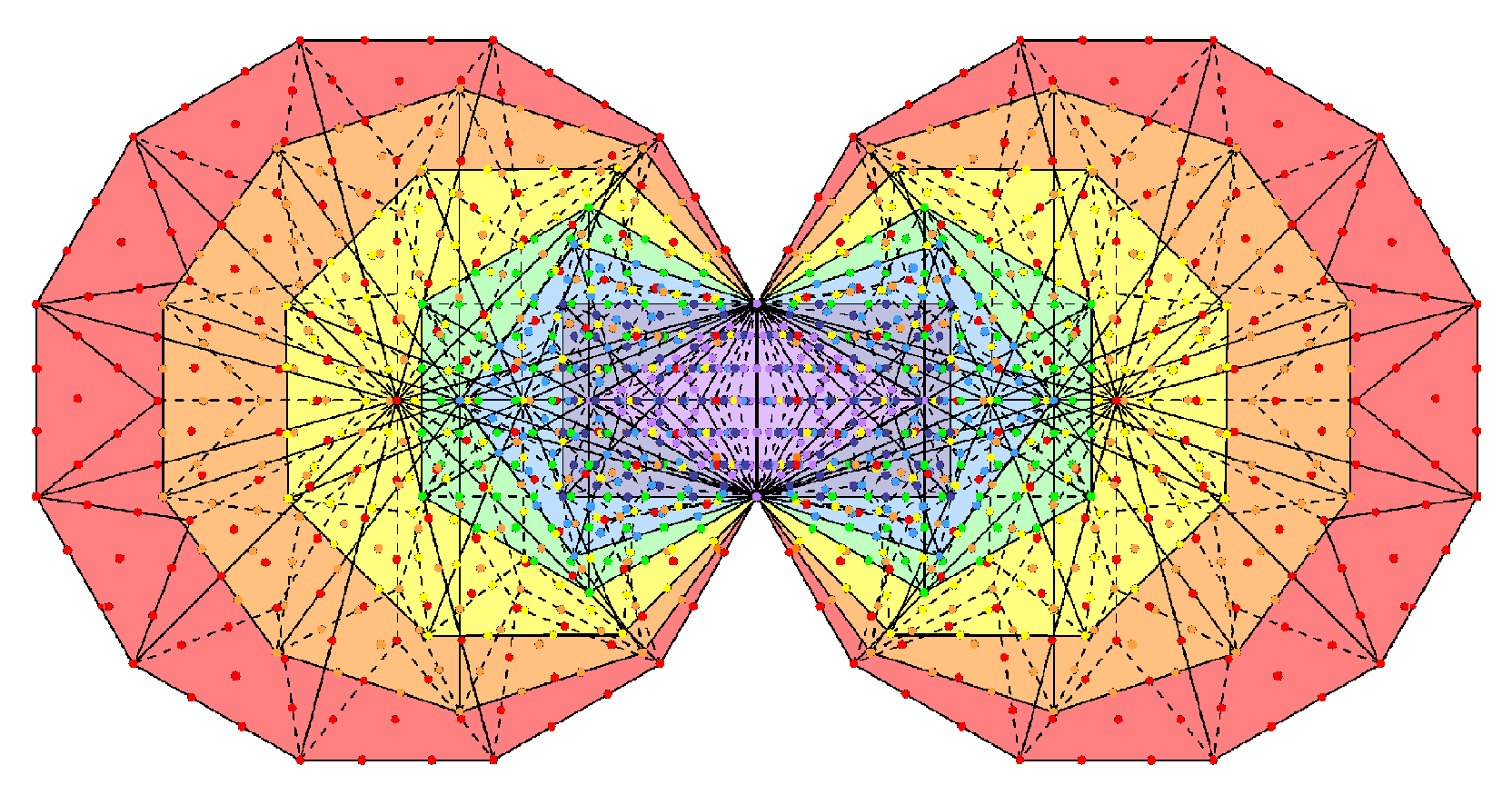
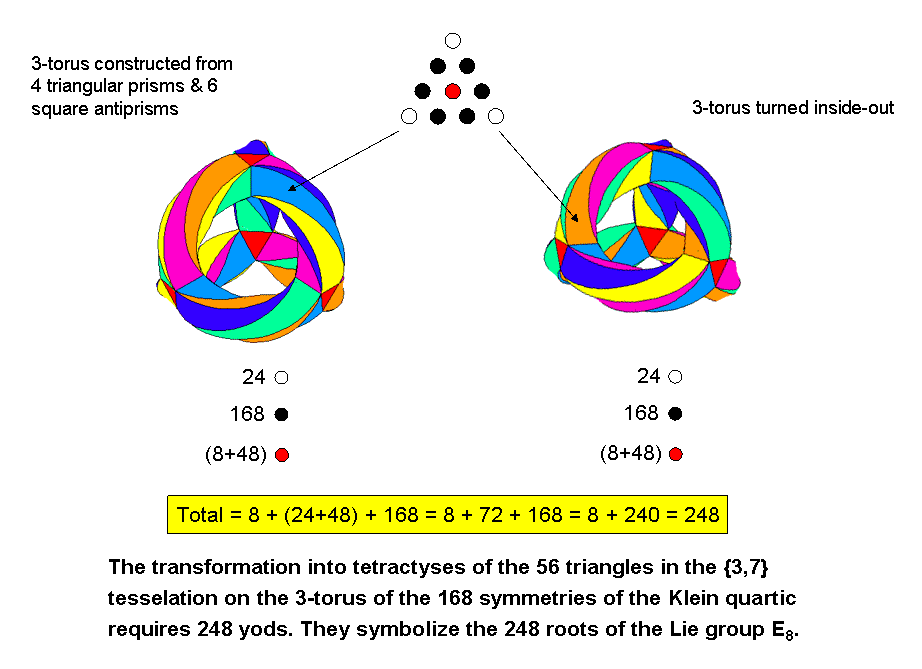
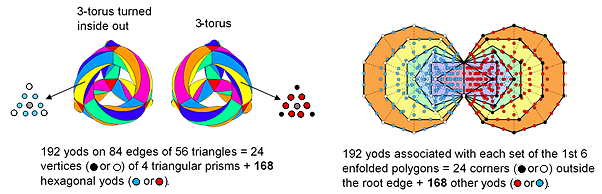
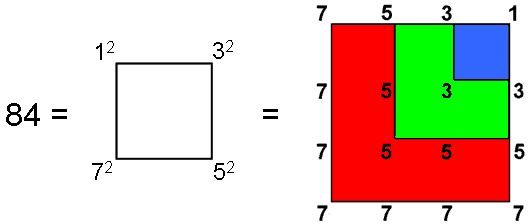
ARTICLE 64

by
Stephen M. Phillips
Flat 4, "Oakwood House," 117-119 West Hill Road. Bournemouth. BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
Previous articles have revealed in sacred geometries analogous patterns of division of shared parameters. This article will analyse those divisions that have particular relevance to the account given by Annie Besant and C.W. Leadbeater of their remote viewing of what they took to be the basic constituents of atoms. The divisions: 48 = 24 + 24, 336 = 168 + 168 and 168 = 84 + 84 in these shared numbers will be examined for the following examples of holistic systems/sacred geometries: 1. the inner form of the Tree of Life; 2. the dodecagon; 3. the Sri Yantra; 4. the 64 hexagrams known to students of the I Ching; 5. the five Platonic solids; 6. the disdyakis triacontahedron; 7. the {3,7} tessellation of the 3-torus; 8. the seven diatonic musical scales. The exact correspondences in their properties are too extensive to be attributed, plausibly, to chance. Instead, these holistic systems should be recognised as triangular, polygonal, polyhedral, topological or musical manifestations of a universal, mathematical pattern that governs such systems and which is realised in the subatomic world in the E8×E8 heterotic superstring that was paranormally described over a century ago by Besant and Leadbeater. |
1
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
SEPHIRAH
GODNAME
ARCHANGEL
ORDER OF ANGELS
MUNDANE CHAKRA
1
Kether
(Crown)
620
EHYEH
(I am)
21
Metatron
(Angel of the Presence)
314
Chaioth ha Qadesh
(Holy Living Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
636
2
Chokmah
(Wisdom)
73
YAHWEH, YAH
(The Lord)
26, 15
Raziel
(Herald of the Deity)
248
Auphanim
(Wheels)
187
Masloth
(The Sphere of
the Zodiac)
140
3
Binah
(Understanding)
67
ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317
Daath
(Knowledge)
474
4
Chesed
(Mercy)
72
EL
(God)
31
Tzadkiel
(Benevolence of God)
62
Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
194
5
Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
95
6
Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76
Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
640
7
Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97
Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
64
8
Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
48
9
Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living God)
49, 363
Gabriel
(Strong Man of God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
87
10
Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155
Sandalphon
(Manifest Messiah)
280
Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the Foundations.
The Elements.
(Earth)
168
(All numbers in this table that the article refers to are written in boldface).
The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Orders of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters. Numbers from the table are written in boldface in the article.
2
1. Introduction
Previous articles have established that sacred geometries embody in their mathematical properties a common set of patterns relating a shared set of structural parameters. Some of these numbers — like 26, 248 and 496 — have become established in the research literature of theoretical physics in the form of superstring physics, although whether they apply to the real world remains experimentally uncertain, despite the beautiful, mathematical ideas that surround them. Other parameters have not (yet) appeared, giving sceptics scope to dismiss as the product of chance all evidence of correlations between these geometries and recent discoveries in theoretical physics. This article will analyse and compare those mathematical correspondences that have particular relevance to the remote-viewing investigations of subatomic particles by Annie Besant and C.W. Leadbeater. The number relationships in question are:
336 = 168 + 168,
168 = 84 + 84 = 24 + 144.
The upward continuations of these divisions:
672 = 336 + 336
and
1344 = 672 + 672,
also appear in sacred geometries. As they have been analysed in detail and given scientific interpretation at the author’s website [1], they need not be discussed here. The purpose of this article is more than just to map out the correspondences. It is to convince the reader that they are too detailed and too
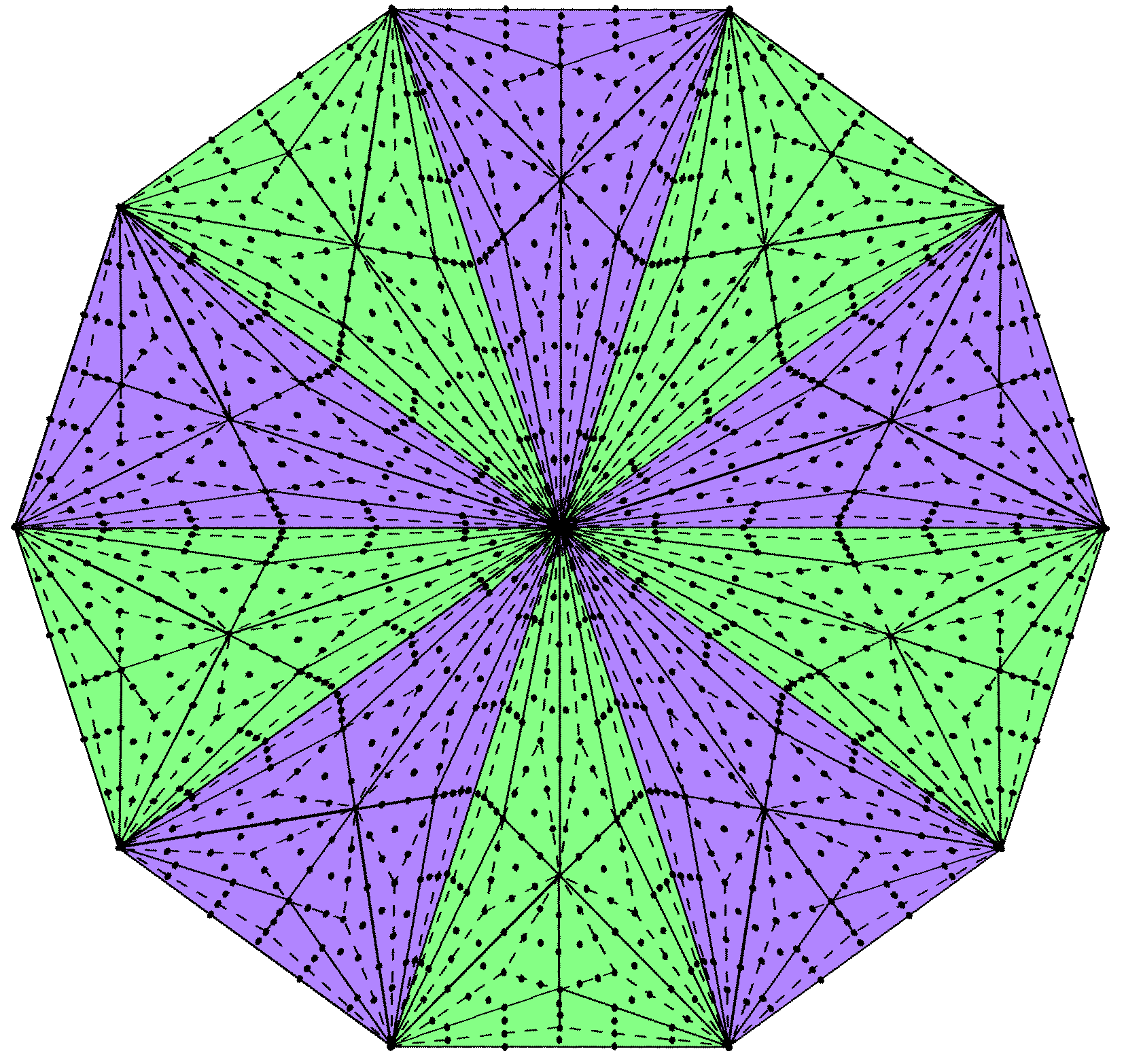
Figure 1. The inner form of the Tree of Life.
Figure 2. Each set of 7 enfolded polygons in the inner Tree of Life shares with its outer form three corners & two sides of its triangles (coloured green).
pervasive to be due to chance. The fact that this demonstration provides highly convincing support for the objective character of the paranormal observations of Besant & Leadbeater is incidental, although highly pertinent.
2. The Inner Tree of Life
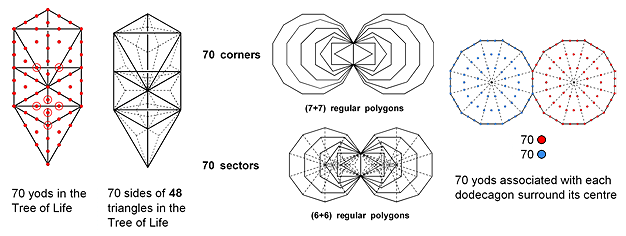
Implicate in the geometry of the outer form of the Tree of Life (Etz Hayim, עץ חיים) known to traditional Kabbalah is its inner form. It consists of two sets of seven enfolded, regular polygons:triangle, square, pentagon, hexagon, octagon, decagon, dodecagon.
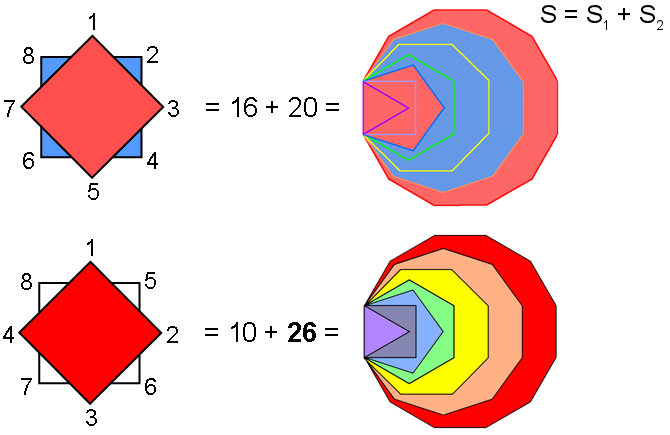
Figure 3. The 7 separate polygons with 48 corners is divided into two sets, each with 24 corners. Figure 4. The two sets of enfolded polygons: S1 & S2.
Figure 5. The two sets of enfolded polygons: S1 & S2 and their mirror images S1′ & S2′.
3
The polygons in one set are the mirror images of their counterparts in the other set (Fig. 1) and share the so-called “root edge” separating the two sets. The 14 polygons lie in the plane formed by the two side pillars of the outer Tree of Life, namely, the right-hand Pillar of Mercy and the left-hand Pillar of Judgement (Fig. 2). The top, bottom and centre of each hexagon coincides with corners of triangles belonging to the outer Tree of Life, and the two internal, vertical sides of their sectors are sides of these triangles. Hence, 10 of the geometrical elements making up the inner Tree of Life are shared with its outer form.
It has been pointed out in previous articles that these seven separate, regular polygons with 48 corners comprise two sets of polygons with 24 corners: the first set (let us call it “S1”) consists of the triangle, square, pentagon & dodecagon; the second set (call it “S2”) consists of the hexagon, octagon & decagon (Fig. 3). (remember that in situ (Fig. 4), S2 has the sector of its hexagon missing that is occupied by the violet triangle in S1 because all the polygons lie in the same plane). Similarly, Figure 5 indicates that each red polygon in S1 has its mirror-image in S1′ and that each blue polygon in S2 has its mirror image in S2′. As we shall discover later, two other sets of polygons with 24 corners exist, but — unlike S1 & S2 — they do not exactly divide in half the collective properties of the seven polygons — whether the latter are separated or enfolded.
This 24:24 division of the parameter 48 is characteristic of all holistic systems. It manifests in the 4‑dimensional projection of the 421 polytope as the 120 vertices of each of the two 600-cells whose compound is the 4-dimensional projection of this polytope in the Coxeter plane [1]. This is because the 120 hexagonal yods in the four separate polygons of S1 constructed from tetractyses symbolise the 120 vertices in one 600-cell and the 120 hexagonal yods in the three polygons of S2 symbolise the 120 vertices in the other 600-cell. If the inner form of the Tree of Life is thought of as the "DNA" encoding how its outer form replicates, then S1 and S2 are the "strands" of this DNA and have their microscopic realisation in the outer and inner halves of the 10 helical whorls of the UPA/E8×E8 heterotic superstring, the two halves being generated by the 240 vertices of the two 600-cells (or, rather, the 240 E8 gauge charges that these vertices represent). It is worthwhile, therefore, to examine the geometrical and yod compositions of S1 and S2. Later, it will be shown that these combinations are unique in the sense that no other grouping of the seven polygons into two sets with equal numbers of yods and equal numbers of geometrical elements leads to equal numbers when they become enfolded in one another as the inner form of the Tree of Life.
Geometrical composition of S1 & S2
Listed in Table 2 are the numbers of corners, sides & triangles in the seven separate, regular polygons of the inner Tree of Life when they are divided into their sectors:
Table 2. Geometrical composition of the seven separate Type A polygons.
Triangle
Square
Pentagon
Hexagon
Octagon
Decagon
Dodecagon
Total
Corners
4
5
6
7
9
11
13
55
Sides
6
8
10
12
16
20
24
96
Triangles
3
4
5
6
8
10
12
48
Total
13
17
21
25
33
41
49
199
When they are separate, S1 and S2 have — by definition — the same number of corners (24), the same number of sides (48) and the same number of triangles (24). When they are enfolded (Fig. 6), the right-hand corner of the triangle coincides with the centre of the hexagon, its two sloping sides coincide with sides of sectors of the hexagon and the right-hand corner of the pentagon coincides with the centre of the decagon. Associating the root edge with S1,
.png)
Figure 6. The 7 enfolded polygons have 47 sectors with 41 corners & 88 sides. Figure 7. S1 (red polygons) & S2 (blue polygons).
the polygons in both S1 and S2 have 18 corners and 21 sides. In terms of just their boundaries, S1 and S2 are the two halves of the right-hand half of the inner Tree of Life. The same is true for their respective mirror images S1′ and S2′ in its left-hand half. But what happens when their sectors are taken into account? Table 3 lists the geometrical compositions of the root edge and what is outside it in S1 and in S2 when their enfolded polygons are divided into their sectors (Fig. 7):
4
Table 3. Geometrical composition of S1 & S2 outside the root edge.
Root edge
S1
S2
Total
Corners
2
20
19
41
Sides
1
44
43
88
Triangles
0
24
23
47
Total
3
88
85
176
S1 and S2 cannot have the same number of corners of their sectors because the total number (41) is an odd integer, not an even one, and is, therefore, not exactly divisible by 2. However, if we associate the root edge with S2, the latter has the same number of sides (44), as well as the same number of corners & triangles (44) and the same number of corners, sides & triangles (88), as S1. Whether as combinations of just polygons or as combinations of polygons divided into their sectors, S1 and S2 can be regarded as the two halves of the set of seven enfolded polygons provided the root edge is assigned to S2.
Intrinsic geometrical elements
The right-hand corner of the triangle coincides with Chesed in the Tree of Life, whilst the two internal vertical sides of sectors of the hexagon form its side pillars. This means, referring to Table 2, that, outside the root edge, S1 has 87 geometrical elements unshared with the Tree of Life and that S2 has 81 unshared geometrical elements, so that S1 & S2 have (87+81=168) geometrical elements outside the root edge that are intrinsic to them. The number 87 is the number of Levanah, the Mundane Chakra of Yesod, which is the penultimate Sephirah. The number 168 is the number of Cholem Yesodoth, the Mundane Chakra of the last Sephirah. Amazingly, it is embodied in the inner Tree of Life in two different ways because the topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree, so that (176−1−7=168) elements intrinsic to each set of seven polygons surround their centres.
Yod populations of S1 & S2
Let us now consider the yod compositions of S1 and S2. Listed in Table 4 are the numbers of yods in the seven separate, regular polygons whose sectors are constructed from tetractyses:
Table 4. Yod populations of the seven separate, Type A polygons.
Triangle
Square
Pentagon
Hexagon
Octagon
Decagon
Dodecagon
Total
Corners
4
5
6
7
9
11
13
55
Hexagonal yods
15
20
25
30
40
50
60
240
Total
19
25
31
37
49
61
73
295
Table 5 lists the yod populations of the root edge and what is outside it in S1 and in S2:
Table 5. Yod compositions of S1 & S2 outside the root edge.
Root edge
S1
S2
Total
Corners
2
20
19
41
Hexagonal yods
2
112
109
223
Total
4
132
128
264
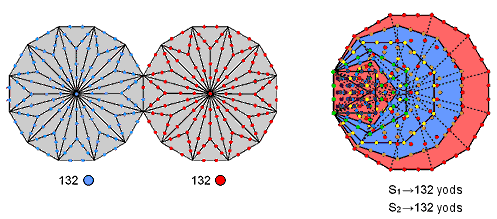
If we associate the root edge and its four yods with S2, the latter has the same number of yods (132) as S1. In other words, the yod population of the seven enfolded polygons then becomes evenly divided between S1 and S2, just as we saw earlier that their number of geometrical elements is. The split of the seven separate polygons into two sets with the same numbers of corners, sides & triangles surrounding their centres and the same numbers of yods surrounding their centres persists when they are enfolded in the form of S2 having the same number of yods as S1 has outside the root edge.
Proof of uniqueness of S1 & S2 as the two halves of the seven polygons
In terms of the numbers of corners of the seven regular polygons making up the inner Tree of Life:
3, 4, 5, 6, 8, 10, 12
four combinations of numbers add up to 24:
1. 3 + 4 + 5 + 12
2. 6 + 8 + 10
3. 3 + 5 + 6 + 10
4. 4 + 8 + 12
5
This allows two possible sets of polygons with 24 corners: either (1) & (2) or (3) & (4). The sets (1) & (2) are, respectively, S1 and S2. Let us call the sets (3) & (4), respectively, S3 & S4. The geometrical compositions of the root edge and what is outside it in S3 and in S4 are shown in Table 6:
Table 6. Geometrical compositions of S3 & S4 outside the root edge.
Root edge
S3
S4
Total
Corners
2
18
21
41
Sides
1
42
45
88
Triangles
0
23
24
47
Total 3
83
90
176
We see that the geometrical compositions of S3 and S4 (either for each type of geometrical element or in total) cannot be made equal by associating the three geometrical elements in the root edge with either S3 and S4. Listed in Table 7 are their yod populations:
Table 7. Yod populations of S3 & S4 outside the root edge.
Root edge
S3
S4
Total
Corners
2
18
21
41
Hexagonal yods
2
107
114
223
Total
4
125
135
264
We see that their various yod populations cannot be made equal by associating the four yods in the root edge with either S3 or S4. Only the 24:24 division of the seven separate polygons into S1 and S2 creates equal total numbers of geometrical elements and equal yod populations when the two combinations with 24 polygonal corners become enfolded. This remarkable fact indicates that only S1 and S2 can be regarded as true halves of the set of seven polygons and vindicates the use of only these two combinations in various analyses in previous articles of the inner Tree of Life basis of holistic parameters, such as the superstring structural parameters 1680, 336 & 168. As this has shown, they are in fact the only two sets of polygons that have equal populations of geometrical elements and yods.
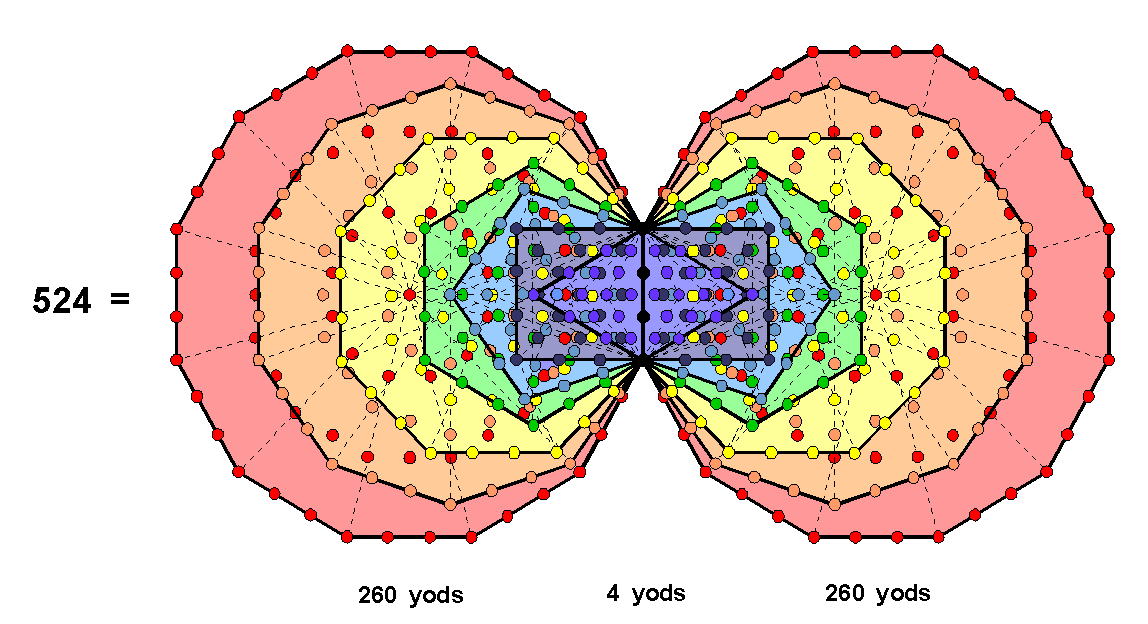
Figure 8. The root edge with 4 yods separates the two sets of 7 enfolded polygons containing 260 yods. Further evidence of the unique status of S1 and S2 vis-à-vis the inner Tree of Life is provided by the (S1+S1′) and the (S2+S2′) making up the (7+7) enfolded polygons. According to Table 5, (S1+S1′) have (2×132=264) yods outside the root edge and (S2+S2′) have (2×128=256=44) yods outside the root edge, i.e., 260 yods when the latter is included. Compare this with the fact that the seven enfolded polygons have 264 yods, of which 260 yods lie outside the root edge (Fig. 8). (S1+S1′) without the root edge have the yod population of the seven enfolded polygons, i.e., one half of the inner Tree of Life, and (S2+S2′) with the root edge have the yod population of the other set of seven enfolded polygons outside their root edge. Table 8 lists the numbers of yods lining the tetractyses in S1 and S2:
Table 8. Numbers of boundary yods in S1 & S2.
S2′
S1′
Root edge
S1
S2
Yod population
128
132
4
132
128
Number of hexagonal yods at centres of tetractyses
23
24
−
24
23
Number of boundary yods
105
108
4
108
105
6
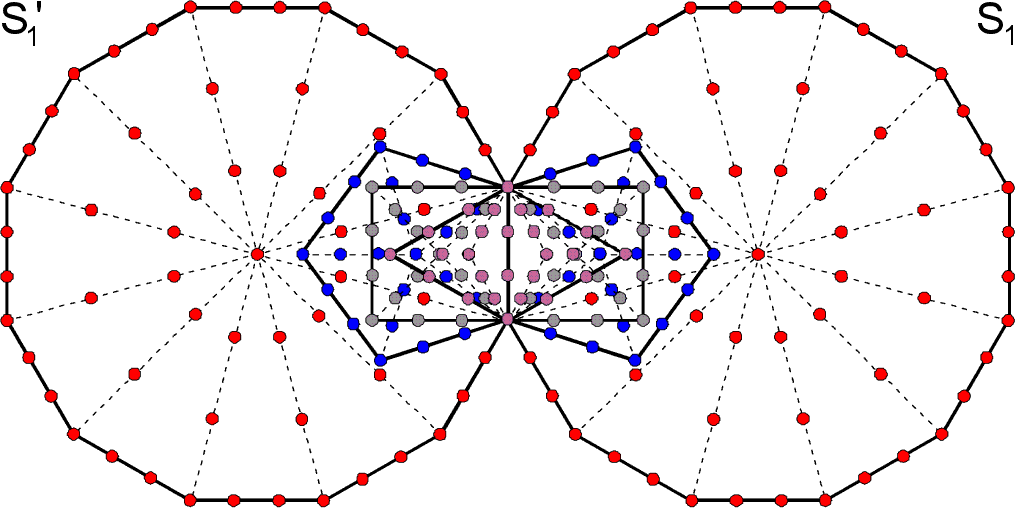
Figure 9. 216 yods intrinsic to a set of 7 enfolded polygons line their 47 tetractyses. Figure 10. 216 yods outside the root edge line the 48 tetractyses in S1 & S1′.
We see that S1 and S1′ have 216 boundary yods outside the root edge. The seven enfolded polygons have 264 yods, of which 47 are hexagonal yods at centres of tetractyses. This leaves 217 boundary yods, of which one is the top of the hexagon and coincides with the lowest corner of the hexagon enfolded in the inner form of the next higher Tree of Life. This means that 216 yods lining the sides of tetractyses are intrinsic to the inner form of each overlapping Tree (Fig. 9). This is the number of boundary yods in S1 & S1′ (Fig. 10).
According to Table 8, S2 & S2′ have 214 boundary yods when the root edge is included. This is the number of yods in the outer Tree of Life with Type A triangles (Fig. 11). S2 has 109 boundary yods when the root edge is included. As it contains the hexagon, the topmost corner of which coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life, 108 such yods are intrinsic to S2. This is also the number of boundary yods in S1 outside the root edge.
The Tree of Life contains 214 yods when its 16 triangles are Type A.
214 yods line the 46 tetractyses in S2 & S2′.
Figure 11. (S2+S2′) are lined by as many yods as the Tree of Life contains yods when its triangles are Type A.
Not only are the yod populations of S1 and S2 equal, but so, too, are the numbers of yods on the boundaries of their tetractyses when the root edge is associated with S2. The 216 boundary yods intrinsic to the seven enfolded polygons are divided equally by S1 and S2, whilst (S1+S1′) and (S2+S2′) embody the same holistic parameter. It is further evidence that S1 and S2 uniquely embody properties that are quantified by the same numbers that quantify properties of the complete form of the inner Tree of Life. The implication of this is that these two halves of the inner Tree should be regarded as holistic structures in themselves. It should, therefore, come as no surprise that S1 and S2 can be regarded as representing the two 600-cells that are the two halves of the Petrie projection onto the Coxeter plane of the 421 polytope which in turn generate the outer and inner halves of the UPA, the subquark state of the E8×E8 heterotic superstring (see the discussion under Fig. 4 here). They can further be associated with the 120 vertices & edges of the 24-cell making up each 600-cell and with its 120 faces & octahedral cells, that is, with its 0- & 1-polytopes and with its 2- & 3-polytopes, for the polytope composition of the 24-cell conforms to the archetypal pattern of the seven regular polygons in the inner Tree of Life (see beginning of #4 here). This 120:120 division exists in S1 and S2 not only when their polygons are regarded as enfolded but also when they are separate. The number of hexagonal yods in an n-gon is 5n, so that each combination of separate polygons has 5×24 = 120 yods. Assigning a different colour to each of the five hexagonal yods per sector of an n-gon, every colour appears 24 times in S1 and 24 times in S2. For the 600-cell, each hexagonal yod denotes a vertex of a 24-cell, the five
7
colours signifying the five such cells whose compound is the 600-cell (Fig. 12).
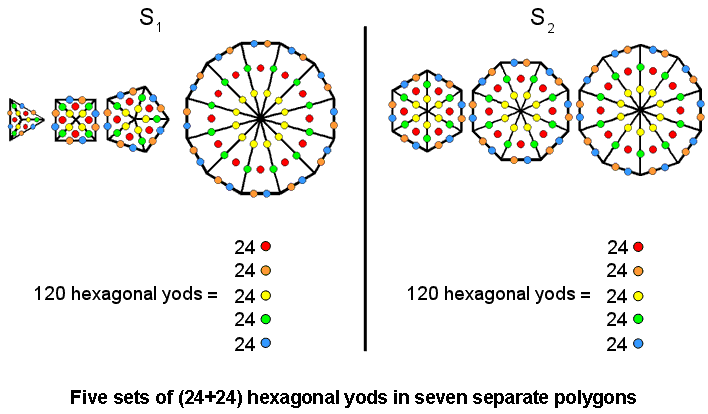
Figure 12. The five sets of 24 hexagonal yods in S1 denote the five sets of 24 vertices in the compound of five 24-cells that is the 600-cell. Similarly, for S2. (S1+S2) represents the 240 vertices of the compound of two 600-cells that is the Coxeter plane projection of the 421 polytope whose 240 vertices map the 240 roots of E8. Similarly, (S1′+S2′) represents the 240 roots of E8′. Therefore, the complete inner form of the Tree of Life represents E8×E8′. The number of corners, sides & triangles surrounding the centre of a Type B n-gon is 10n. The 10 geometrical elements per sector comprise five sides and five corners & triangles. The 240 geometrical elements in either S1 or S2 that surround centres of polygons comprise 120 sides and 120 corners & triangles (Fig. 13). So they display the 120:120 division characteristic of holistic systems in both their sides and their corners & triangles.
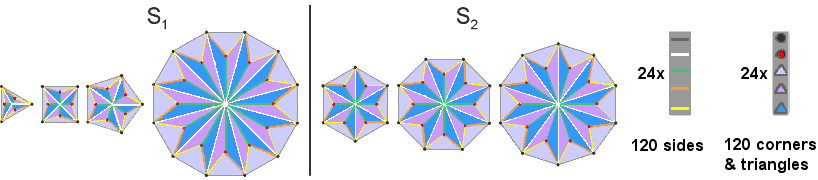
Figure 13. Containing Type B polygons, S1 and S2 each has 240 geometrical elements comprising five sets of 24 sides and five sets of 24 corners & triangles. This is the geometrical analogue of the (240+240) roots of E8×E8′. The five types of sides, repeated 24 times, correspond to the five 24-cells, each with 24 vertices, making up a 600-cell. The five types of vertices or triangles, repeated 24 times, correspond to the five 24-cells making up a second 600-cell. S1 is geometrically analogous to the compound of two 600-cells whose 240 vertices are the projections of the 240 vertices of the 421 polytope representing the 240 roots of E8. Similarly, S2 is analogous to E8′. (S1+S2) is analogous to E8×E8′. The division of the seven enfolded polygons into S1 & S2 generates, therefore, a pattern of geometrical elements that is analogous to the root composition of E8×E8′. This is the symmetry group of one of the two types of heterotic superstrings that has been shown to be free of quantum anomalies.
Whether we are speaking of hexagonal yods in Type A polygons or geometrical elements in Type B polygons, the number 240 is present. In the case of the latter, because the 10 geometrical elements per sector divide into two sets of five, S1 and S2, the two halves of the seven separate polygons, whose centres are surrounded by 480 geometrical elements, each comprise 240 such elements. As the parameter 240 always refers in sacred geometries to the 240 roots of E8, we see that the two halves signify the two identical E8 Lie groups that appear in the direct product E8×E8, one of the two symmetry groups that were discovered in 1984 to describe the interactions of superstrings that are free of quantum anomalies. We saw earlier that, even though they are, separately, only half of the whole set of polygons making up the inner Tree of Life, S1 and S2 possess properties quantified by numbers that refer to this whole set. Here, once again, is evidence that S1 and S2 can be regarded as wholes in themselves. They remind one of the division of the Tao into the polar opposites of Yin and Yang — complementary components of the Whole, yet complete in themselves.
Superstring structural parameters 84, 168 & 336 embodied in S1 & S2
According to Table 3, S1 has 88 geometrical elements outside the root edge, i.e., 84 elements surround the centres of its four polygons. S2 has 85 geometrical elements outside the root edge. Of these, one is the centre of the octagon, the centres of the hexagon and decagon being counted as belonging to S1 because the right-hand corner of the triangle coincides with the centre of the former and the right-hand corner of the pentagon coincides with the centre of the latter. Therefore, 84 geometrical elements surround the centres of its three polygons. Surrounding the centres of S1 & S2 in Figure 7 are (84+84=168) geometrical elements outside the root edge. Similarly, (84+84=168) geometrical elements outside the root edge surround the centres of their mirror images S1' & S2′. (S1+S2) and (S1′+S2') consist of (168+168=336)
8
geometrical elements outside the root edge that surround the (5+5) centres that are not also corners of polygons. They comprise four sets of 84 geometrical elements, so that 168 geometrical elements surround the centres of not only S1 and its mirror image S1′ but also S2 and its mirror image S2′ (Figs. 14 & 15).
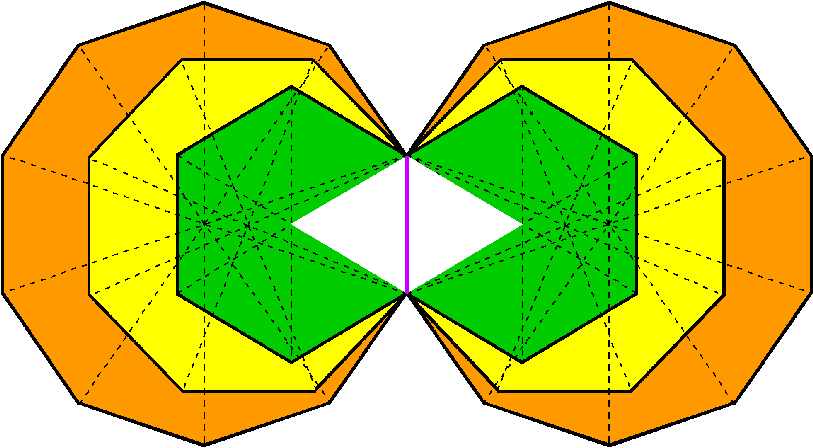
Figure 14. (84+84=168) geometrical elements surround the centres of the eight polygons in S1& S1′.
Figure 15. (84+84=168) geometrical elements surround the centres of the six polygons in S2 & S2′.
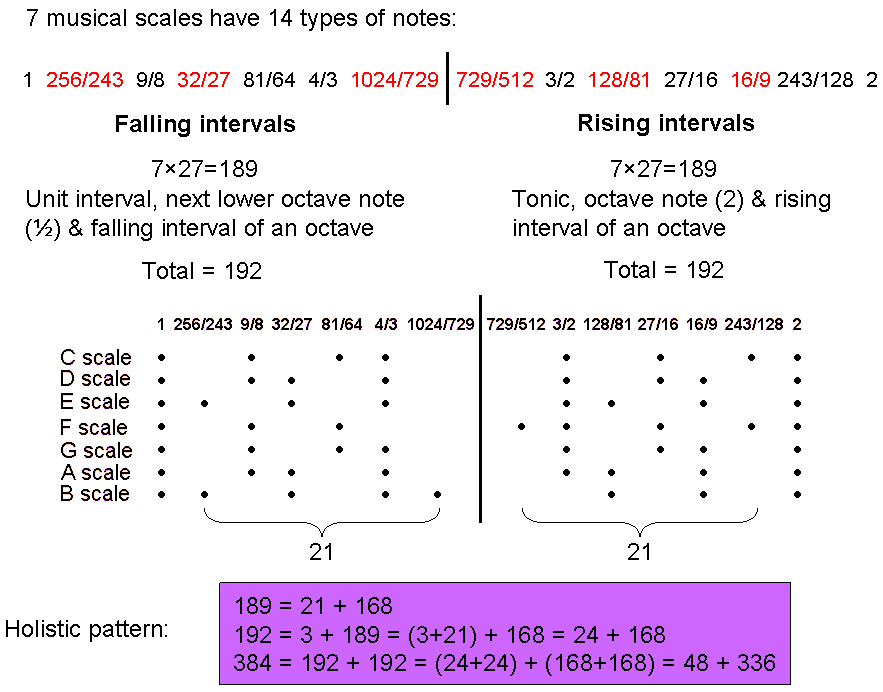
According to Table 3, the seven enfolded polygons have 176 geometrical elements, including the root edge. Therefore, (176−7=169) geometrical elements surround their centres. One of them is the topmost corner of the hexagon in S2, which coincides with the lowest corner of the hexagon enfolded in the next higher Tree. The number of geometrical elements surrounding the centres of the 7n polygons enfolded in the n-tree = 168n + 1. 168 such elements are intrinsic to each set of polygons. S2 has 85 geometrical elements outside the root edge, so that 83 elements intrinsic to it surround its centres. Including the root edge, S1 has 91 geometrical elements, so that (91–4–2=85) elements are not centres. The 168 intrinsic elements that are not centres comprise 85 elements in S1 and 83 in S2. The 84:84 division of the holistic parameter 168 exists for the generic set of seven polygons enfolded in a single Tree. It does not exist in the inner forms of successive Trees of Life. The S1:S2 division does not lead to an 840:840 division in 10 Trees of Life. But this should not be a surprise, because we know that holist systems embody the number 336, which divides into two halves, and this is not possible in this context because the number 168 includes the root edge, so that it cannot have a mirror-image set of 168 elements. The correct embodiment in the inner Tree of Life that permits generalisation to multiple Trees is the pattern of 168 geometrical elements outside the root edge in each set that are unshared with the outer Tree of Life. S1 has 88 geometrical elements outside the root edge, of which one (corner of triangle) is shared with the Tree of Life. The 168 elements intrinsic to the inner form of each Tree comprise 87 elements in S1 and 81 elements in S2. 87 is the number value of Levanah, the Mundane Chakra of Yesod, which is the Sephirah preceding Malkuth, whose Mundane Chakra has the number value 168! Here is a remarkable example of how the gematria number values of the Sephiroth, their Godnames, etc. quantify properties of whatever is a holistic system (in this case, that part of the inner Tree of Life that is intrinsic to it).Both the 84:84 division of the holistic parameter 168 and the 168:168 division of the holistic parameter 336 have been discussed in many earlier articles as characteristic of sacred geometries. Later sections of this article will review their embodiment in the Sri Yantra, disdyakis triacontahedron, the four Platonic solids, the table of 64 hexagrams used in I Ching, the seven diatonic, musical scales and the 3-torus. The 8:6 division of the 14 regular polygons making up the inner Tree of Life splits in half the 336 intrinsic geometrical elements surrounding their centres. As discussed in Section 10, we find a similar division in the 14 types of notes that make up the seven diatonic scales [2] and whose tone ratios are:
1 256/243 9/8 32/27 81/64 4/3 1024/729 │ 729/512 3/2 128/81 27/16 16/9 243/128 2
The vertical line divides the first seven notes from their inversions.[1] Eight notes with their tone ratios written in black) constitute the Pythagorean scale and six notes written in red are non-Pythagorean notes. It occurs also in the outermost group of 14 triangles of the Sri Yantra. Six of these triangles touch the circular ring of eight lotus petals that surrounds the 43 triangles and eight triangles do not touch it (see Fig. 34).
The inner Tree of Life has 336 intrinsic geometrical elements outside the root edge surrounding the centres of its 14 polygons. It is divided into two halves (S & S′), with S′ the mirror image of S. Each half has 168 such geometrical elements and is further split into two halves: S1 & S2. Each "quarter" of the inner Tree of Life has 84 geometrical elements surrounding centres of polygons. Compare this with the following structural properties of the UPA: each helical whorl with 1680 turns twists five times around the axis of spin. It makes five half-revolutions, each of 168 helical turns, in the larger spiral of its outer half and five half-revolutions, each of 168 turns, in the narrower spiral of its inner half. Each turn is a circularly polarised oscillation consisting of two perpendicular plane waves vibrating 90° out of phase, so that a half-revolution
[1] The inversion of a musical note with tone ratio m is a note with tone ratio 2/m.
9
comprises 336 plane wave oscillations grouped into 168 pairs. A factor of 2 manifests in a half-revolution of a whorl, firstly, as its two quarter-halves and, secondly, as the two perpendicular oscillations generating each turn. Two schemes of correspondence between the inner Tree of Life and a half-revolution of a whorl are possible:
Case A
Case B
168 oscillations
→ 168 geometrical elements in S
168 geometrical elements in S1 & S1′
168 oscillations with 90° phase difference
→ 168 geometrical elements in S′
168 geometrical elements in S2 & S2′
84 oscillations in first ¼-revolution
→ 84 geometrical elements in S1
84 geometrical elements in S1
84 oscillations in first ¼-revolution with 90° phase difference
→ 84 geometrical elements in S1′
84 geometrical elements in S2
84 oscillations in second ¼-revolution
→ 84 geometrical elements in S2 84 geometrical elements in S1′
84 oscillations in second ¼-revolution with 90° phase difference
→ 84 geometrical elements in S2′
84 geometrical elements in S2′
Intuitively speaking, case A seems the correct correspondence, with S1 and S2 denoting the two quarter-revolutions and the two halves of the inner Tree corresponding to the two plane wave oscillations that are 90° out of phase. This is because each half of the inner form of the Tree of Life constitutes a whole in itself and is a more fitting representation of each set of 168 orthogonal plane waves that makes up the half-revolution of a whorl. This is consistent with the Tree of Life nature of a whorl because the latter makes 10 half-revolutions around the spin axis of the UPA, each being analogous to one of the 10 Sephiroth, so that a whorl is represented by 10 Trees of Life, each corresponding to a Sephirah, and its 10 half-revolutions are also represented by 10 overlapping Trees. Figure 16 summarises the analogy between the geometries of the inner Tree of Life and the UPA. Figure 17 shows the inner form of 10 overlapping Trees of
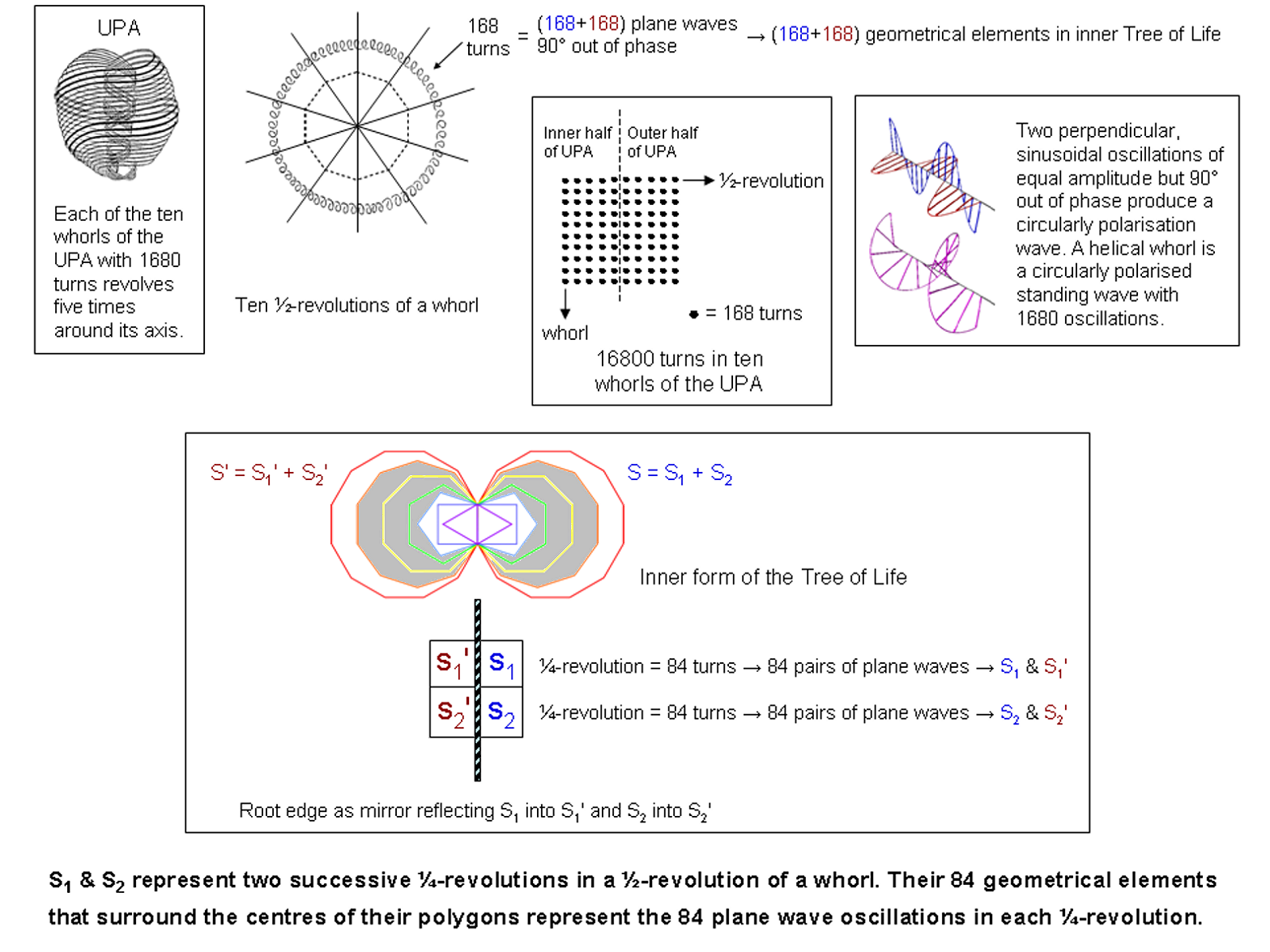
Figure 16. The (7+7) enfolded polygons of the inner Tree of Life represent a half-revolution of the 10 whorls of the UPA/subquark state of the E8×E8 heterotic superstring.
Life divided into the sets of polygons S1, S2, S1′ & S2′. Each of the 3360 intrinsic geometrical elements in the (79+70=140) polygons that make up this inner form corresponds to a plane wave component of the 1680 circularly polarised oscillations present in a half-revolution of the 10 whorls of the UPA. That there are four components of the inner Tree of Life and that each half of it results from pairing of these components only in one way:
S1 → S2 and S1′ → S2′
10
11
not:
S1 → S2′ or S2 → S1′
reminds us of the four types of nitrogen bases in the DNA molecule: A, T, G & C, and how base A always pairs with base T through two hydrogen bonds and base C with base G through three hydrogen bonds when they form a rung of base pairs in the helical DNA ladder. It is as though the complementary pairs of bases (A, T) and (C, G) are analogous, respectively, to (S1, S2) and (S1′, S2′), so that the two helical halves of the DNA molecule are analogous to the two sets of sinusoidal waves in each helical whorl of the E8×E8 heterotic superstring that generate its 1680 circularly polarised waves because the waves in one set are 90° out of phase with those in the other set. A turn in a whorl would then correspond to a rung of base pairs, whilst the complementary nitrogen bases at each end of a rung would correspond to the two sinusoidal oscillations of the same amplitude but 90° out of phase that constitute a turn. The pairing of complementary bases in the molecule of life is an expression of the Taoist principle that the yang aspect of nature is always balanced by its yin aspect. The supposition of two orthogonal, sinusoidal oscillations in every turn of a whorl is another manifestation of this cosmic balance. In the inner form of the Tree of Life, it is expressed by its two halves, one associated with the right-hand Pillar of Mercy, which embodies the male principle (Siva, or Yang), and the other associated with the left-hand Pillar of Judgement, which embodies the female principle (Shakti, or Yin). These principles, of course, are entirely metaphysical.
S2 & S2′ embody the dimension 248 of E8
According to Table 4, S1 has 132 yods outside the root edge, where 132 = 4×(1!+2!+3!+4!). S2 has 128 yods outside the root edge. This is the sum of the Godnames of the first four Sephiroth:
21 + 26 + 50 + 31 = 128.
S2 & S2′ have 256 yods outside the root edge, where 256 = 44. These properties demonstrate the role of the Tetrad in determining the yod population of the inner Tree of Life. Of the 128 yods in S2, six yods lie on the two vertical sides of tetractyses inside the hexagon that are shared with triangles in the outer Tree of Life because they form its Pillar of Mercy and Pillar of Judgement. (128−6=122) yods outside the root edge are intrinsic to S2. Including the root edge,
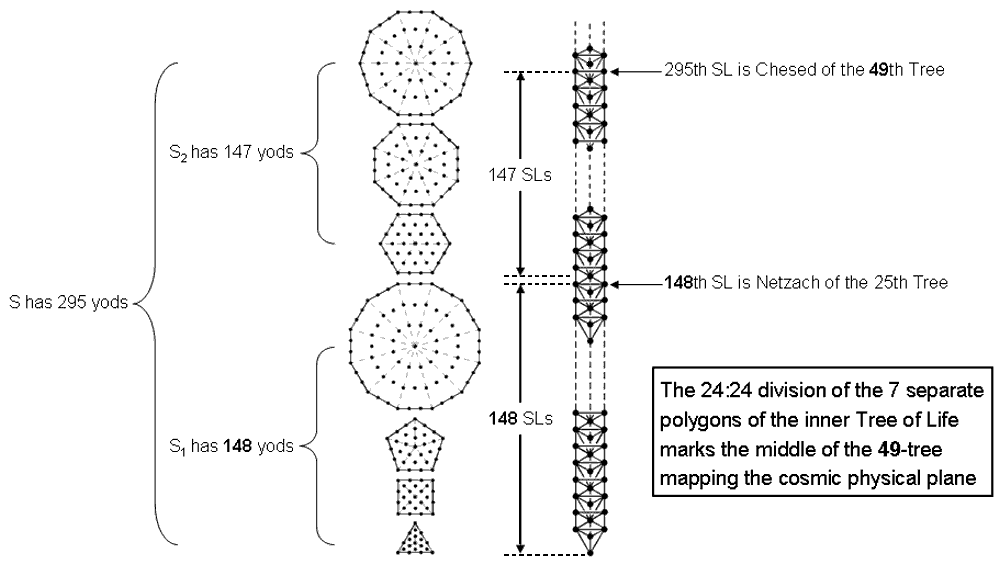
Figure 18. The 295 yods in the seven polygons denote the 295 SLs up to Chesed of the 49th Tree. The S1:S2division corresponds to the middle of the 49-tree and is marked by the 148th SL. This is Netzach of the 25th Tree. It is the SL most characteristic of this Sephirah, whose gematria number value is 148. the number of yods intrinsic to S2+S2′ in the inner form of the Tree of Life = 4 + 2×122 = 248. This is the dimension of E8, the Lie group associated with the E8×E8 heterotic superstring. Of the 132 yods in S1, one yod (right-hand corner of the triangle) is shared with the outer Tree because it is located at the Sephirah Chesed; this leaves 131 intrinsic yods. 131 is the number value of Samael, the Archangel of Geburah, whose number 216 was found earlier to be the number of yods lining the 48 tetractyses in the two S1, 48 being the number of Kokab, the Mundane Chakra of Hod.
The significance of the S1:S2 division for CTOL
According to Table 4, the seven separate Type A polygons have 295 yods. 288 yods surround their centres, where
12
288 = 1!×2!×3!×4!.
There are 295 SLs up to Chesed of the 49th Tree (Fig. 18). In order of emanation in the Tree of Life, Chesed is the first of the seven Sephiroth of Construction. The 49th Tree is the first of the 49 Trees mapping the 49 subplanes of the seven planes of consciousness. As each Tree expresses the essence of one of these Sephiroth of Construction, the 49th Tree expresses Chesed. So the 295th SL expresses par excellence the quality of this Sephirah. Each yod in a polygon denotes one of the 295 SLs up to the starting point for the emanation of the 49-tree representing the cosmic physical plane. According to Table 3, the four separate polygons in S1 contain 148 yods and S2 has 147 yods. The S1:S2 division therefore splits in half the yod population of the seven separate polygons of the inner Tree of Life. The number 148 is the gematria number value of Netzach. The 148th SL is Netzach of the 25th Tree, which is the middle of the lowest 49 Trees. The 25th Tree maps the fourth subplane of the fourth plane of consciousness, both the subplane and the plane corresponding to Netzach because it is the fourth Sephirah of Construction. So the number 148 — the halfway point in the emanation of the 295 SLs —locates the very SL in the 49-tree that most expresses this Sephirah, just as the number 295 locates the SL most expressive of the Sephirah Chesed! This remarkable property cannot be a mere coincidence. Instead, because of the correspondence between yods and SLs, the 24:24 division of the corners of the seven polygons, which splits the 168 intrinsic geometrical elements surrounding their centres into two sets of 84 elements, also divides in half the SLs that their yods symbolise and which belong to the 49 Trees mapping the cosmic physical plane. The following correspondences between yods and SLs exist:
Here is remarkable confirmation of this conclusion: the numbers of corners, sides, triangles & tetrahedra making up the n-tree are shown below:
Number of corners = 6n + 5;
Number of sides = 16n + 9;
Number of triangles = 12n + 7;
Number of tetrahedra = n +1.Total number of points, lines, triangles & tetrahedra in the n-tree = 35n + 22.
Every 48 overlapping Trees of Life contain (48×35=1680) geometrical elements and every 24 Trees contain 840 elements. Dividing any section of 48 Trees into two sets of 24 Trees generates two sets of 840 geometrical elements. Apart from the Pythagorean factor of 10, here is the 84:84 division
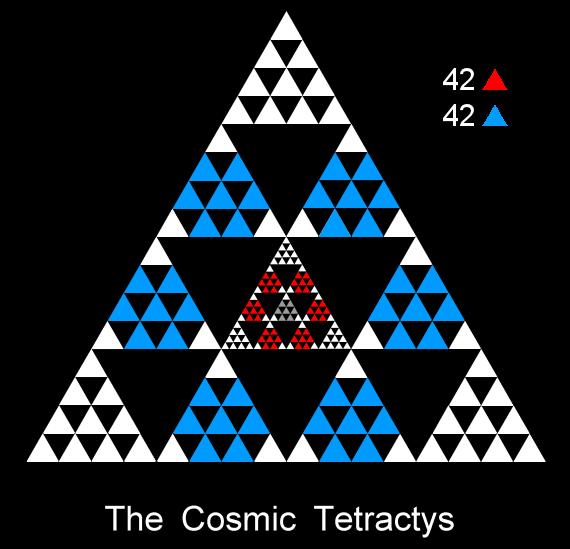
Figure 19. The 42 blue “yods” in the Cosmic Tetractys symbolise the 42 subplanes above the cosmic physical plane; the 42 red yods denote the 42 subplanes above the physical plane, whose 7 subplanes are symbolised by the 7 grey yods in the central tetractys. Figure 20. 84 yods in the 2nd-order tetractys surround the central black yod denoting Malkuth, or the physical universe.
13
of geometrical elements found earlier for the division of the seven polygons with 48 corners into S1 and S2, each with 24 corners. In fact, in the encoding of CTOL in the 12 separate polygons other than one square and one triangle, their corners mark out Trees of Life, so that S1 with 24 corners is associated with 24 Trees and S2 with 24 corners is associated with the next higher 24 Trees. The same 840:840 division exists in the inner form of 48 Trees. This is because the number of corners of the 7n polygons enfolded in the n-tree = 35n + 1, so that the 336 polygons enfolded in 48 Trees have (48×35=1680) corners and the 168 polygons enfolded in 24 Trees have 840 such corners. Their counterparts in the UPA are the 840 turns in either an outer or an inner half of a single whorl or in a quarter-revolution of all 10 whorls. This mathematical analogy between the subquark superstring and the cosmic physical plane is a powerful and beautiful illustration of the hermetic principle: "As above, so below." The 70 enfolded polygons making up the inner form of 10 Trees of Life consist of 10 S1, with 840 intrinsic geometrical elements surrounding the centres of 40 polygons, and 10 S2, with 840 intrinsic geometrical elements surrounding the centres of 30 polygons.
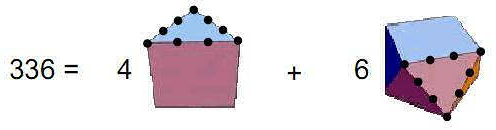
336 = 
Figure 21. The Tetrad expresses the holistic parameter 84. Figure 22. The Tetrad expresses the 4-fold pattern within the holistic parameter 336.
Returning to CTOL, the number of SLs on the central Pillar of Equilibrium of the n-tree = 2n + 3. For n overlapping Trees, the number = 2n + 2. Seventeen SLs span the central pillar of the 7-tree mapping the physical plane and 184 SLs span the 91 Trees of CTOL. 167 SLs span the 84 Trees above the 7-tree, that is, the apex of the 7-tree is the 168th SL on the central pillar, counting from the top of CTOL. The apex of the 49‑tree mapping the cosmic physical plane is the 101st SL on the central pillar, that is, the 84th SL, counting from the top of CTOL. Fittingly, the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, locates the Malkuth level of CTOL. The 84:84 division created by the geometrical composition of S1 and S2 in the inner Tree of Life appears in CTOL as the 84 SLs on the central pillar down to the top of the 49-tree and the next 84 SLs down to the top of the 7-tree. Each set of 84 SLs belongs to 42 Trees (Fig. 19).
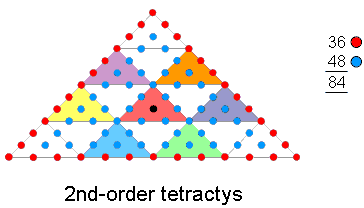
As the next higher order tetractys above the well-known tetractys, or 1st-order tetractys, the 2nd-order tetractys (Fig. 20) is a representation of holistic systems. Its 10 tetractyses contain 85 yods, where
85 = 40 + 41 + 42 + 43.
84 yods surround its central yod, where
84 = 12 + 32 + 52 + 72.
(Fig. 21). The pattern of four groups of 84 structural units will always be found in a holistic system. It is represented by a cross pattée whose four arms are 2nd-order tetractyses (Fig. 22) with 84 yods outside their shared apex. The diagram aptly illustrates how the Tetrad expresses parameters characterising holistic systems and their four-fold division.
Compare this with the result obtained earlier that the centres of the four polygons in S1 are surround by 84 geometrical elements, as are the centres of the three polygons in S2. The two halves of the set of seven enfolded polygons are themselves holistic because they require 84 bits of information in the form of points, lines & triangles to create them, starting in each case from a mathematical point. This is what the 2nd-order tetractys signifies: 84 bits of information (whatever their meaning) symbolised by the 84 yods surrounding its centre are required to generate a holistic system, the outer, material form of which is symbolised by this central yod, signifying Malkuth. In the case of CTOL, they are the 84 Trees/subplanes whose final manifestation at the level of Malkuth is the 7-tree that maps the physical plane, or physical universe. In the case of the UPA, they are the 84 turns in an outer or inner half-revolution of each whorl. The factor of 4 results from each turn being a circularly polarised oscillation with two plane wave components and two half-revolutions forming a complete, 360° revolution of a single whorl: 4 = 2×2.
14
3. The 24:24 division in the 1st (6+6) polygons
Article 4 analysed how the gematria number values of the Godnames of the 10 Sephiroth prescribe the properties not only of the (7+7) enfolded polygons making up the inner Tree of Life but the first six polygons and their mirror image counterparts on the other side of the root edge. The first six separate polygons have 36 sectors with 42 corners, so that the first (6+6) separate polygons have 72 sectors with 84 corners. Whether they are separate or enfolded, let us call them “H.” Their embodiment of the holistic parameter 84 expressed by the 2nd-order tetractys in Fig. 20 indicates that this subset of the 14 polygons constitutes a holistic system in itself. The 42:42 division of its corners is analogous to the same division of Trees in CTOL above the 7-tree shown in Fig. 19 that is created by the six cosmic superphysical planes with 42 subplanes and by the six superphysical planes with 42 subplanes. Their holistic character is confirmed by their enfoldment to produce a geometrical structure with 50 corners, where 50 is the number value of ELOHIM, the Godname of Binah. YAHWEH, the Godname of Chokmah on the other side of the Tree of Life with number value 26, prescribes the first six enfolded polygons because they have 26 corners. Each set has 24 corners outside the root edge, so that both sets have (24+24=48) external corners (Fig. 23). The 24:24 division that splits in half the seven separate polygons with 48 corners re-appears by dividing H in half. As the topmost corner of each hexagon coincides with the lowest corner of its counterpart enfolded in the next higher Tree of Life, the H enfolded in each Tree has 48 unshared corners (24 associated with each set of six). Unlike that displayed in Fig. 23, this 24:24 division gets repeated in every Tree, which means that, as the correct way of dividing the 48 corners, the two endpoints of the root edge must be included, one with each set of 24 corners.The 168:168 division in the 1st (6+6) polygons
When its (35+35=70) sectors are turned into tetractyses, H has 386 yods [3]. The topmost corners of the two hexagons coincide with the lowest corners of the two hexagons enfolded in the next higher Tree, leaving 384 yods intrinsic to the H in each Tree. This is another indication of its holistic nature, for previous articles have revealed how this number appears as a global parameter of well-known sacred geometries, as well as objects for which considerable evidence has been accumulated in the author’s articles and website to indicate that they possess a similar status. Surrounding the hexagonal yods at the centres of the 70 tetractyses are (384–70=314) yods intrinsic to H. Outside the four yods in the root edge are 310 (=31×10) intrinsic yods lining these tetractyses. This shows how EL, the Godname of Chesed with number value 31, prescribes H. 155 yods outside the root edge lie on the boundaries of the 35 tetractyses in each set of six polygons. This shows how ADONAI MELEKH, the complete Godname of Malkuth with number value 155, prescribes the form of H.
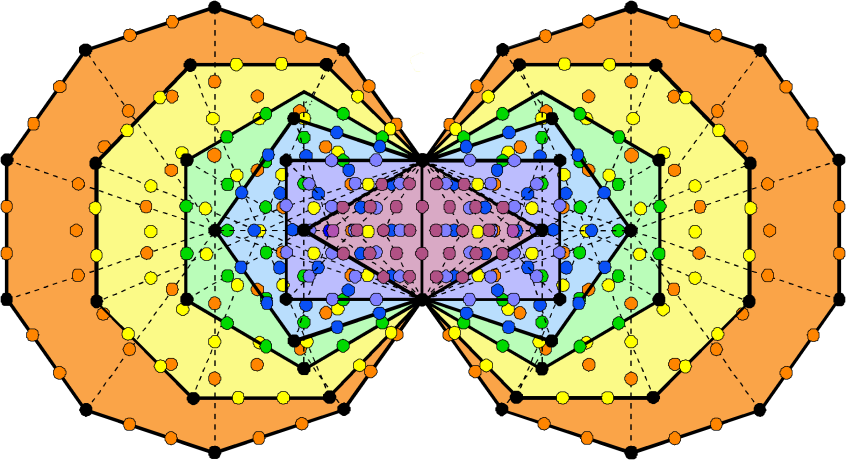
Figure 24. 24 intrinsic corners & 168 yods are associated with the first 6 polygons enfolded in each Tree.
The 384 yods intrinsic to H comprise 48 corners of its 12 polygons and 336 other yods, where
336 = 4×84 = 22 + 62 + 102 + 142.
Associated with each half of H are 24 corners and 168 other yods (Fig. 24). The division:
48 = 24 + 24
15
in the polygonal corners intrinsic to H automatically generates the division:
336 = 168 + 168
in its yod population. Each set of 168 yods consist of 78 yods in the triangle, square & octagon and 90 yods in the square, hexagon & decagon (Fig. 25).
Figure 25. The yod populations of subsets of polygons are the gematria number values of Cholem & Yesodoth appearing in the Kabbalistic name of the Mundane Chakra of Malkuth These numbers are the gematria number values of, respectively, Cholem and Yesodoth, which are the two words making up the Kabbalistic name of the Mundane Chakra of Malkuth.
The 84:84 division in the 1st (6+6) enfolded polygons
Just as the 24:24 division of the corners of the seven separate polygons generates an 84:84 division of the yods in S1 & S2, so, too, the 24:24 division of the corners of H corresponds to a 84:84 division in the yods lining the sides of its polygons, as now shown. The first six separate polygons have 36 sides. Enfolded, they have 31 sides, showing how ELOHA, the Godname of Geburah with number value 36 and EL, the Godname of Chesed opposite it with number value 31, prescribe this holistic set of polygons. Two hexagonal yods lie on each side, totalling 62, where 62 is the number value of Tzadkiel, the Archangel of Chesed.
Figure 26. (84+84=168) yods outside the root edge line the sides of the 1st (6+6) enfolded polygons. They include (24+24) corners.
Notice that, as H contains 384 intrinsic yods, 192 yods are associated with each half of it, so that the first six enfolded polygons contain (192+2=194) yods that are intrinsic to them, where 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Both sets of six separate polygons have 72 corners, where 72 is the number value of Chesed. Here is a remarkable conjunction of four gematria numbers referring to the same Sephirah! The 12 polygons in H have 61 sides lined by (61×2=122) hexagonal yods and 50 corners, i.e., 172 yods. Hence, 168 yods outside the root edge lie on the sides of these polygons (Fig. 26). Each set of six polygons has 84 such yods (coloured red or blue in the diagram). (172–2=170)
Figure 27. Examples of the number 70 as a holistic parameter.
16
boundary yods are intrinsic to H, and 87 such yods line the sides of each set of six enfolded polygons. 87 is the number value of Levanah, the Mundane Chakra of Yesod.
The 84 yods lining the sides of each set of six enfolded polygons divide into 42 yods on the sides of the triangle, pentagon & decagon and 42 yods lining the square, hexagon & octagon. These are the only possible combinations of polygons showing this division. The sequence of divisions:
336→168→84→42
Is always displayed by holistic systems. The way other sacred geometries exhibit it will be discussed in the remaining sections. Their higher-order transformations reveal that the sequence proceeds in the opposite direction as well. The most remarkable example of this is the Gosset polytope, whose 672 edges divide into the 336 edges in each half and which has (2×672=1344) hexagonal yods lining its edges when its faces are turned into tetractyses. Its Tree of Life basis is analysed in Article 62 (see ref. 1).
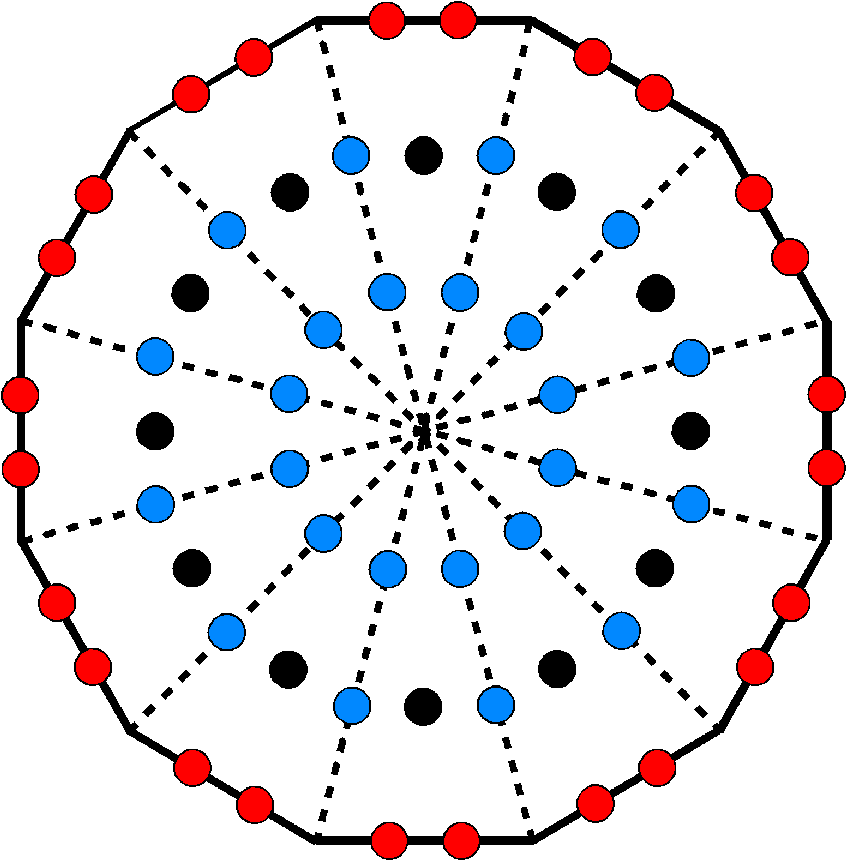
4. The dodecagon
As the tenth type of regular polygon and the last of the seven polygons making up the inner Tree of Life, the dodecagon is unique in that it is the single, polygonal representation of holistic systems. One of the parameters that define such systems is the number 70. It is embodied in the outer Tree as its 70 yods when its 16 triangles are tetractyses and as the 70 sides of the sectors of these triangles when they are Type A (Fig. 27). It is embodied in the inner Tree of Life as the 70 corners of its polygons, in the first (6+6) enfolded polygons as their 70 sectors and in the dodecagon as the 70 yods associated with each of the two joined dodecagons that surround its centre. The number 48 of Kokab, the Mundane Chakra of Hod, is embodied in these sacred geometries because 1. the outer Tree of Life is composed of 48 geometrical elements (10 corners of 16 triangles with 22 sides), 2. its 16 triangles have 48 sectors, 3. the seven separate polygons have 48 corners, 4. the first (6+6) enfolded polygons have 48 corners that are intrinsic to them, and 5. 48 geometrical elements
Figure 28. 24 red hexagonal yods & 24 blue hexagonal yods surround the black centres of the 12 tetractys sectors of the dodecagon.
surround the centre of a Type B dodecagon. It is also embodied in the Type A dodecagon, as it contains 73 yods, of which one is its centre, 12 are corners and 60 are hexagonal yods, 48 of which surround those at the centres of its 12 tetractyses (Fig. 28). The dodecagon conforms to the division:
48 = 24 + 24
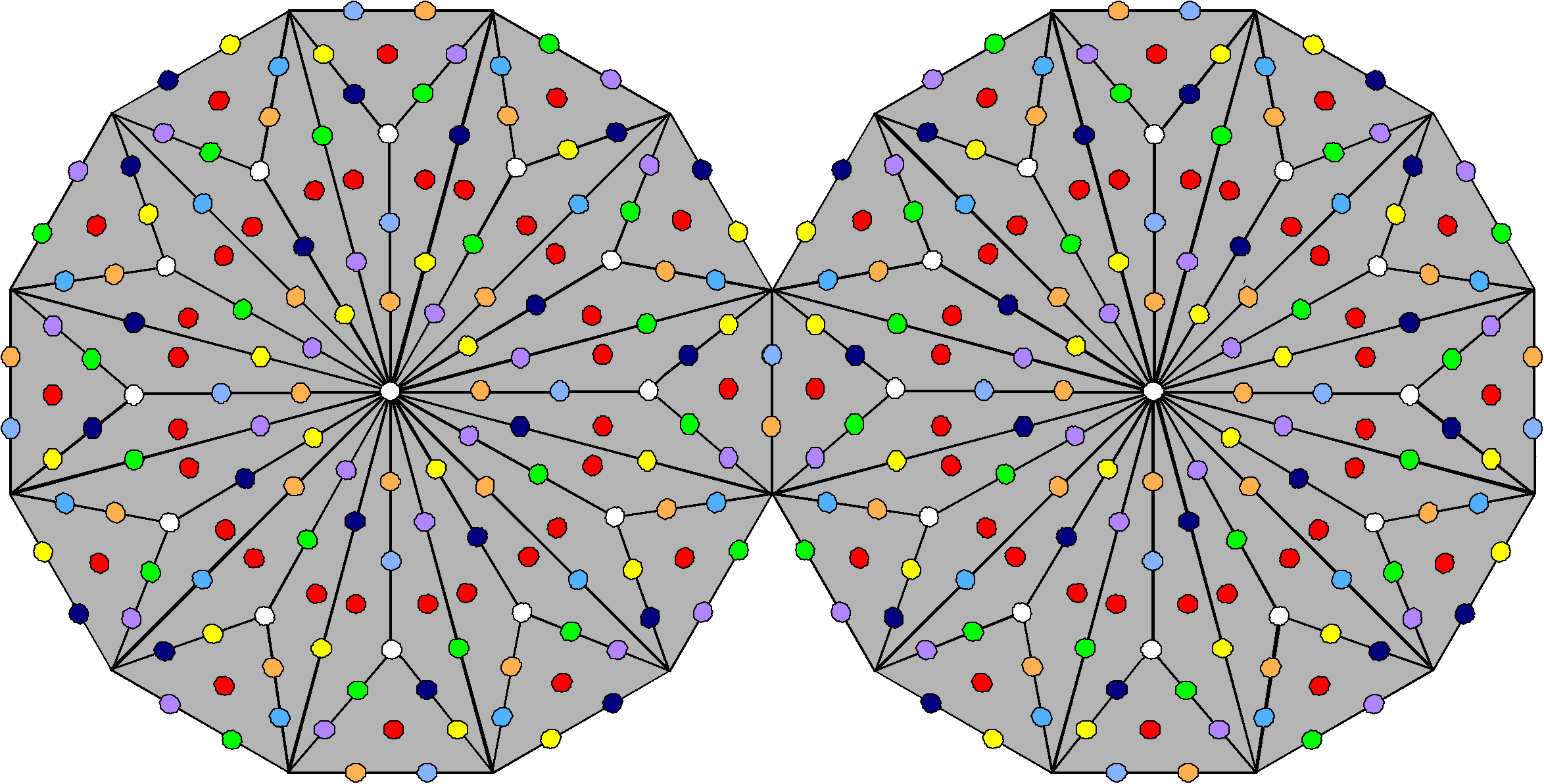
that is characteristic of holistic systems because 24 hexagon yods line its sides, inside of which are 24 hexagonal yods surrounding centres of tetractyses. This 24:24 division was shown in Section 2 to divide equally the 264 yods of the seven enfolded polygons into S1, whose four polygons have 24 corners when they are separate and 132 yods when they are enfolded, and S2, whose three separate polygons have 24 corners and 132 yods when enfolded. This same division appears in the two joined Type B dodecagons, as now explained. Each dodecagon has 181 yods, so that the two joined dodecagons have 358 yods. Of these, 22 are their corners and 72 are hexagonal yods at the centres of their tetractyses. This means that (358–22–72=264) yods line the sides of these tetractyses, 132 boundary yods being associated with each dodecagon (Fig. 29). The two joined dodecagons display the 24:24 division characteristic of
Figure 29. The (132+132=264) yods other than corners lining sides of tetractyses in two joined Type B dodecagons correspond to the (132+132=264) yods in S1 & S2.
17
holistic systems because their 24 sectors have 24 corners and their tetractyses have 24 more corners. There are 131 yods outside the root edge in each dodecagon. This is the number value of Samael, the Archangel of Geburah, whose Godname ELOHA has the number value 36, which is the number of yods lining the sides of the dodecagon. 130 yods outside the root edge surround the centre of each dodecagon. This is the 65th even integer and the 129th integer after 1, showing how ADONAI, the Godname of Malkuth with number value 65, and YAHWEH SABAOTH, the Godname of Netzach with the number value 129,
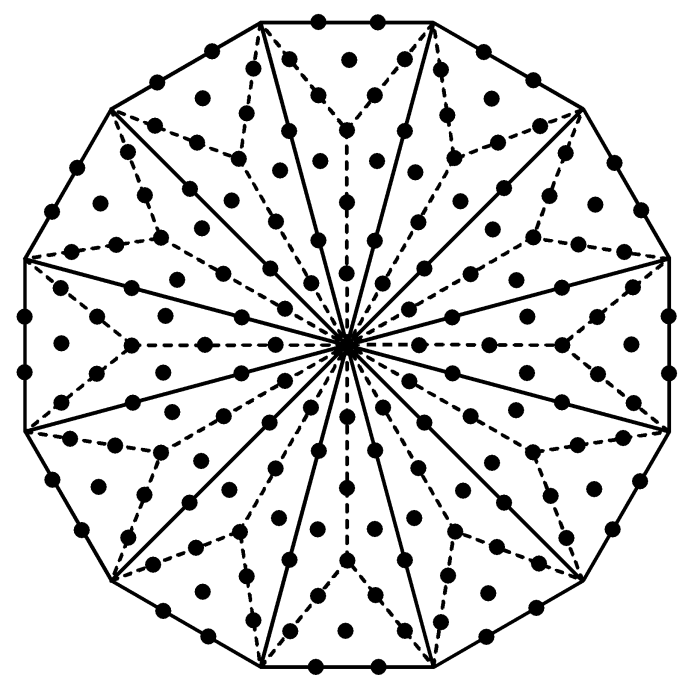
Figure 30. 168 yods are needed to transform the 12 sectors of a dodecagon into Type A triangles.
Figure 31. The two joined Type B dodecagons have (168+168=336) yods other than their 22 corners.
prescribes the Type B dodecagon. These are examples of how the Godnames mathematically prescribe the properties of holistic systems.
The 168:168 division
A Type B dodecagon with 181 yods requires 168 more yods to transform its 12 sectors into Type A triangles (Fig. 30). Joined together, two such dodecagons contain 358 yods — 336 yods in addition to its 22 corners (Fig. 31). 168 such yods are associated with each dodecagon. Their 24 sectors have 24 corners and their 72 tetractyses have another 24 corners. This is how the 24:24 division generates the 168:168 division in the outermost polygons of the inner Tree of Life. There are (358–48=310=31×10) hexagonal yods, showing how EL with number value 31 prescribes the pair of dodecagons. 155 hexagonal yods are associated with each dodecagon, where 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth. 154 such yods are outside each dodecagon, where 154 is the 153rd integer after 1. The number 153 is the number value of ELOHIM SABAOTH, the Godname of Hod.
The 84:84 division
There are 15 yods per sector of the Type B dodecagon (14 other than a corner of the polygons). Seven blue yods line internal sides of the three tetractyses in each sector and seven red yods are either hexagonal yods at their centres or yods lining the sector (Fig. 32). The 168 yods that are not corners of sectors comprise (12×7=84) red yods and 84 blue yods. When two dodecagons become joined, one of their 168 yods becomes associated with the other dodecagon.
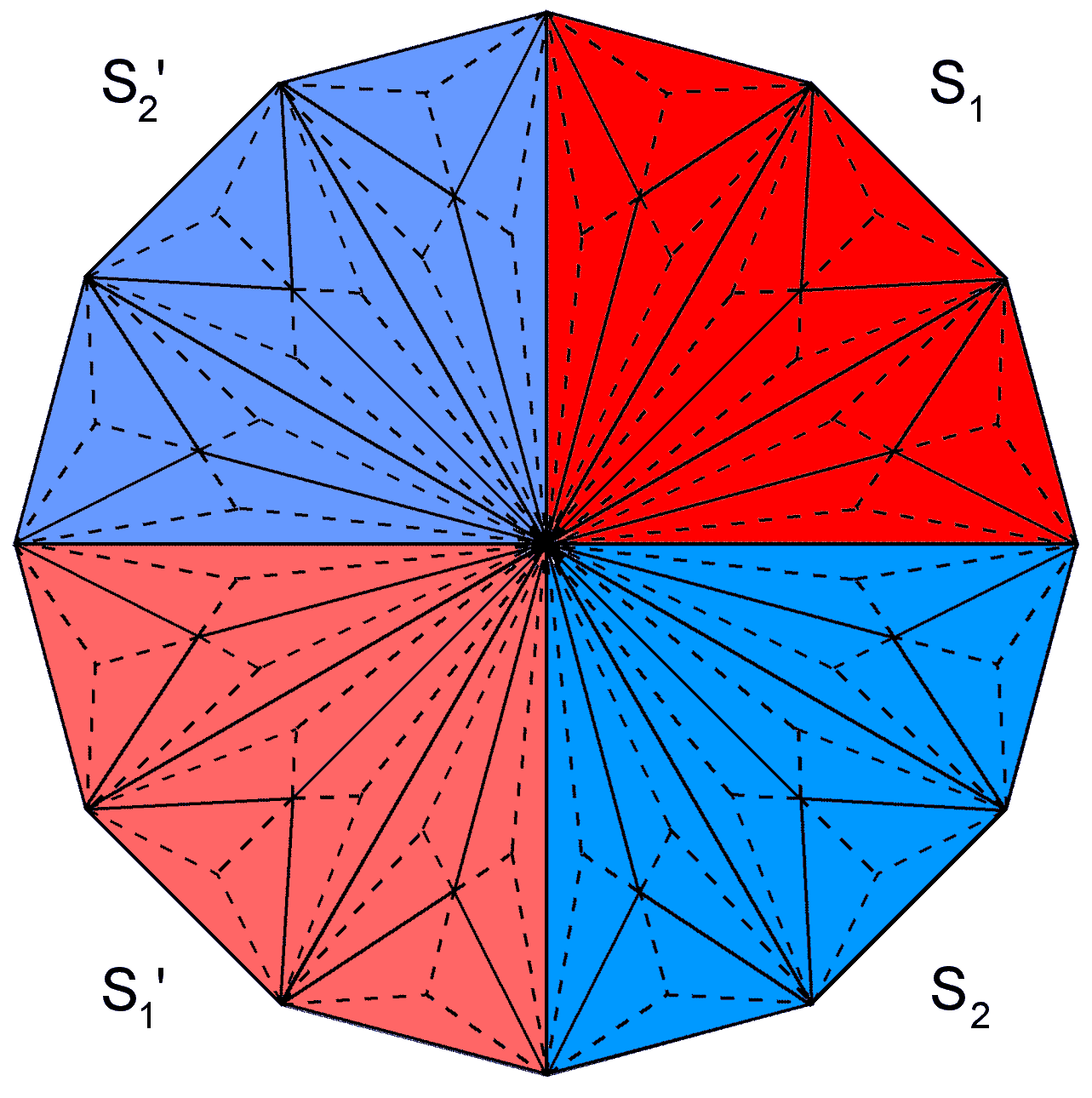
Figure 32. The two sets of 84 yods in each Type B dodecagon.
Figure 33. The 84 geometrical elements in each quadrant of a Type C dodecagon correspond to the 84 intrinsic geometrical elements surrounding the centres of S1, S2, S1′ & S2′ — the quarters of the (7+7) enfolded polygons of the inner Tree of Life. The quadrant corresponding to S1′ is diametrically opposite that for S1; similarly, for S2′ and S2.To compensate for this, the centre of the dodecagon must be included to maintain the set of 168 yods in each dodecagon. Each set is a pair of 84 yods. They correspond to the two sets of geometrical elements that surround the centres of the polygons
18
in S1 & S2 and in S1′ & S2′ (see Figs. 14 & 15). Which set corresponds to S1 and which corresponds to S2 is an issue that need not be resolved here. It is sufficient to have demonstrated that the pair of dodecagons constitute a holistic system, embodying the parameter 336 as four sets of 84 yods. However, the 84 red yods include one on the root edge, so that they “need” the root edge to make up the set, just as, according to Table 5, S2 needs it to complete the 132 yods in half of the seven enfolded polygons. This provides a reason for arguing that S1 in the right-hand dodecagon corresponds to the 84 blue yods and S2 corresponds to the 84 red yods and that S1′ corresponds to the 84 light blue yods in the left-hand dodecagon and S2′ corresponds to the 84 light red yods.
The 168:168 & 84:84 divisions manifest in the geometrical composition of a single dodecagon, namely, the Type C dodecagon. The number of corners, sides & triangles in a Type C n-gon = 28 +1. Hence, (12×28=336) geometrical elements surround the centre of a Type C dodecagon (Fig. 33). 168 elements exist in each half of the polygon and 84 elements exist in each quarter. Here is further, striking evidence for the dodecagon being the polygonal version of the inner Tree of Life, for the geometrical composition of each half is the same as that outside the root edge and surrounding the centres of the seven enfolded polygons. Each quarter corresponds to S1, S2, S1′ & S2′.
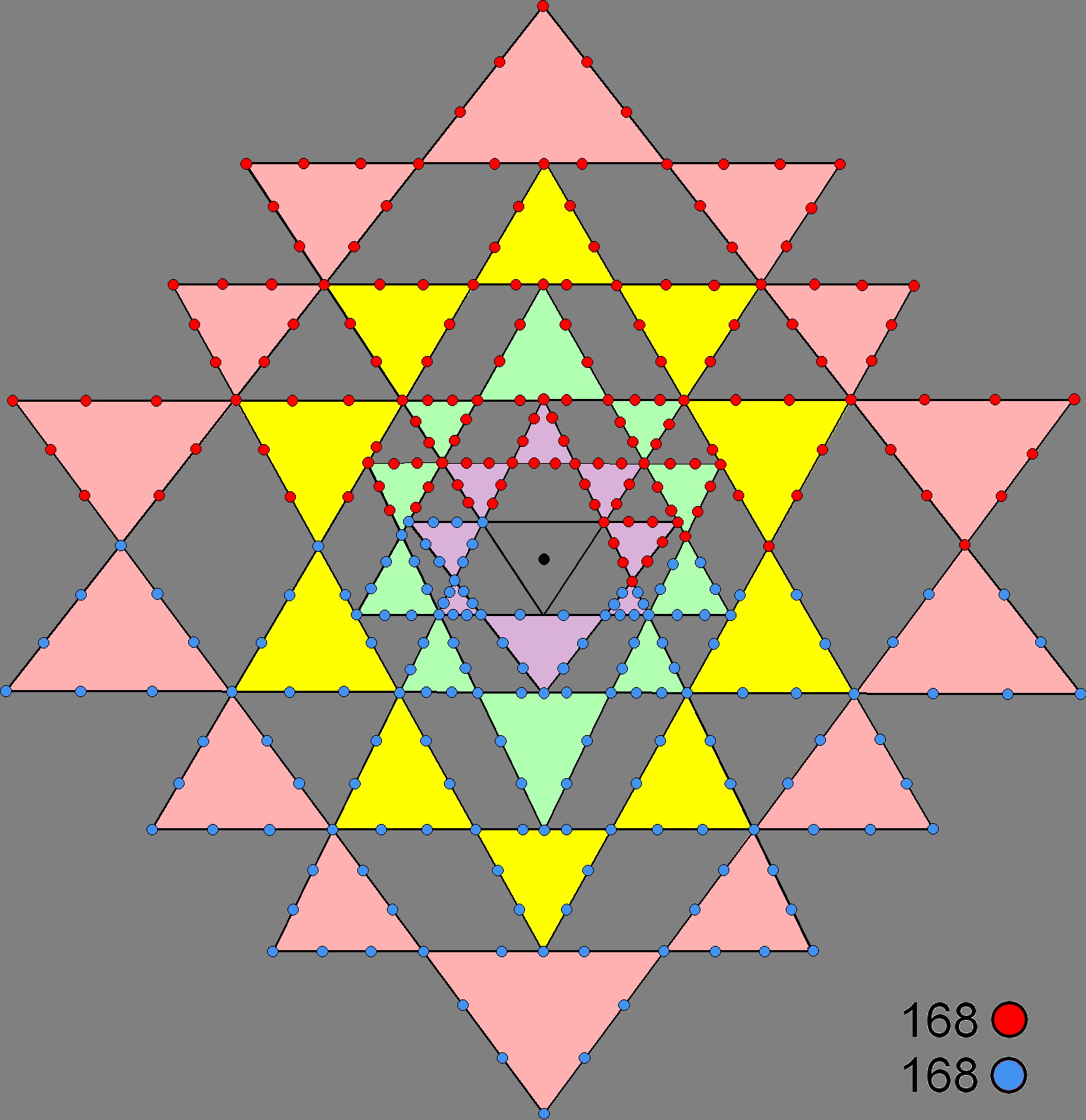
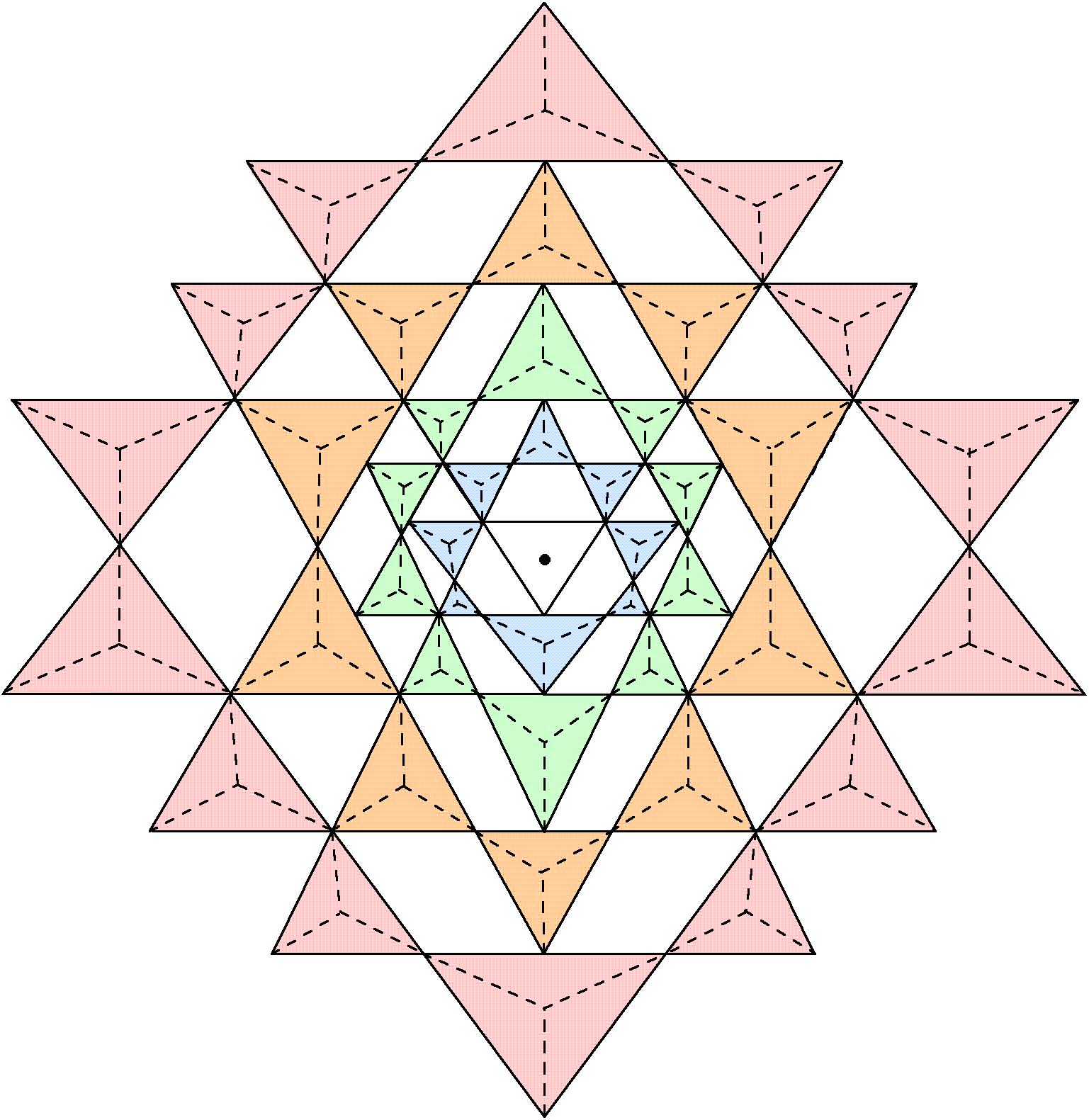
5. The Sri Yantra
The Sri Yantra (Fig. 34) is revered by Hindus as the most powerful and sacred of the yantras (images used for meditation). Five downward pointing triangles symbolizing the feminine, creative energy, or Shakti, intersect four upward pointing triangles symbolizing the masculine, creative energy, or Siva. This generates 42 triangles arranged in four layers of eight, 10, 10 and 14 triangles. They surround a down-ward-pointing triangle whose corners denote the triple
Figure 34. The Sri Yantra,
Figure 35. 336 yods line the sides of the 42 triangles of the 3-d Sri Yantra when they are tetractyses. They form four sets of 84 yods. For clarity, hexagonal yods at the centres of tetractyses are omitted.Godhead of Siva, Brahma and Vishnu. At its centre is a point, or bindu, representing the Absolute. It is the source of all levels of existence. As such, it ‘exists’ outside them, although this is hardly the right word to express such an exalted level.
Let us consider the 3-dimensional Sri Yantra, in which the parallel sheets of triangles are stacked on top of one another so that none of their outward points touch triangles in a different layer. Let us regard the 42 triangles as tetractyses. There are nine yods intrinsic to each tetractys because it shares two corners with adjacent tetractyses in the same layer. Eight of these line its sides. Therefore, (42×8=336) yods line the (42×3=126) sides of the 42 triangles. 168 boundary yods lie in the 21 tetractyses in the upper half of the Sri Yantra and 168 yods line the 21 tetractyses in its lower half (Fig. 35).[1]
Although it does not amount to exact mirror symmetry in the horizontal plane, there is an isomorphism in
[1] As long as its central triangle is excluded, the 3-d Sri Yantra can be divided in an upper half and a lower half with the same number of triangles, although — unlike the inner Tree of Life — they are not exact mirror images of each other.
19
Figure 36. (168+168=336) yods line the sides of the 42 triangles in the 3-d Sri Yantra. Those in one set of 168 yods are the inverted images of their counterparts in the other set. (The hexagonal yod at the centre of each tetractys is omitted for the sake of clarity).
Figure 37. The 336 boundary yods in the Sri Yantra comprise 4 sets of 84 yods. The 4 pairs per triangle comprise a pair of corners and 3 pairs of hexagonal yods. The 16 circles denote corners of triangles directly above corners of triangles in the next layer below them. (The hexagonal yod at the centre of each tetractys is omitted for the sake of clarity).
20
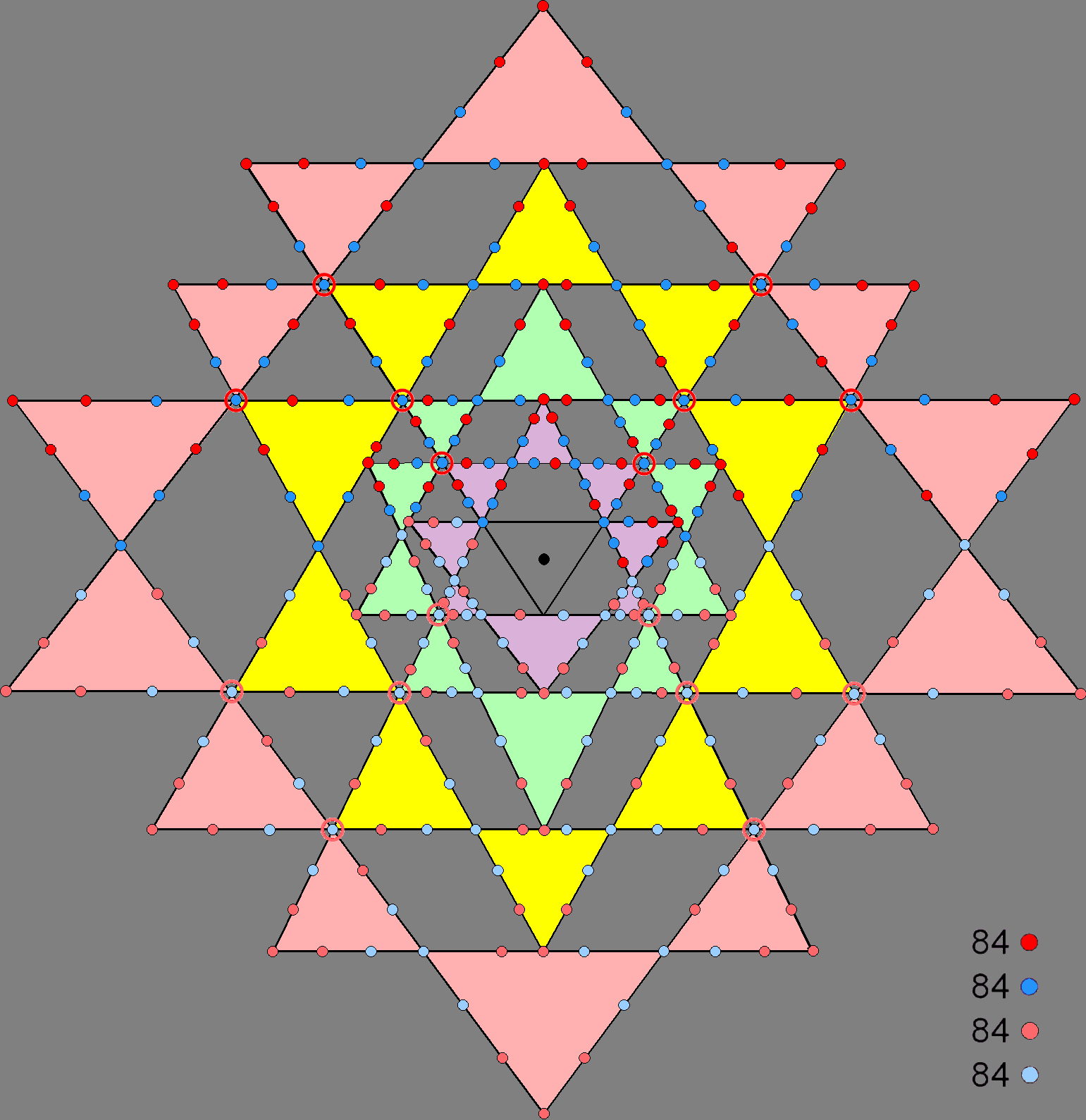
the distribution of yods in the 42 triangles to the extent that for every yod in one half of the Sri Yantra there exists a counterpart in its other half that is its inverted image, reflected not through a horizontal or vertical mirror but through its centre. There are 168 pairs of such yods (Fig. 36). Noting that two black corners are associated with each tetractys, which has three pairs of hexagonal yods on its sides (two red, two green & two blue), four pairs of yods per tetractys lie on its boundary. Each set of 21 tetractyses contains (4×21=84) pairs of yods. The 336 boundary yods consist of 168 pairs in two ways.
Comparing this property with the 168 intrinsic geometrical elements surrounding centres of polygons in S1 & S2, the following correspondences naturally emerge:
3-d Sri Yantra
Inner Tree of Life
336 yods line (21+21) tetractyses; →
336 geometrical elements surround centres of (S1+S2) and (S1′+S2′); 168 yods line 21 tetractyses in each half; →
168 geometrical elements surround polygonal centres in each half; 168 yods in each half comprise 84 pairs, or two sets of 84 yods; →
84 geometrical elements surround centres in S1 (S1′); 84 geometrical elements surround centres in S2 (S2′); The distinction between pairs of hexagonal yods or corners is what corresponds to the difference between S1 and S2 as the two halves of the set of seven enfolded polygons of the inner Tree of Life. It cannot arise from the 21 triangles themselves in each half of the Sri Yantra because, being an odd integer, the number 21 cannot be divided into two integer halves. The possibility of dividing the four pairs of yods per tetractys into two sets of two pairs is less natural because there does not seem to be any reason why one pair should join any other pair to generate a group of 84 yods. The fact that the eight yods are already forming four pairs (one pair of corners, three pairs of hexagonal yods) argues against this alternative. Fig. 37 shows the 84 pairs of yods (now coloured red & blue) in the upper half of the Sri Yantra and the 84 pairs of yods (light red & light blue) in its lower half. They correspond to, respectively, the 84 geometrical elements surrounding centres of polygons in S1 and in S2 and their mirror images in S1′ and in S2′. Each pair of yods in one half of the Sri Yantra corresponds to a geometrical element in S1 and a geometrical element in S2. Each pair of yods in the other half corresponds to a geometrical element in S1′ and a geometrical element in S2′. Unlike in the case of the inner Tree of Life, where each element has a chiral counterpart in the other set of seven enfolded polygons generated by reflection in the mirror plane containing the root edge that is perpendicular to the plane containing all the polygons, the 336 yods consist of 168 yods and their 168 point reflections, although some are not true inversions, as the 2-dimensional Sri Yantra is not centrally symmetric. Despite the lack of exact mirror symmetry in this yantra, it is symmetric enough for the counterparts of its yods and geometrical elements to be identifiable in an unambiguous way.
Geometrical composition of the Sri Yantra
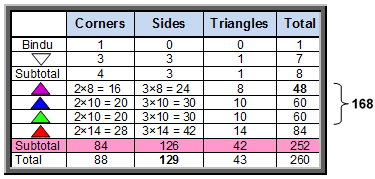
Table 9 shows the numbers of corners, sides & triangles in the 3-dimensional Sri Yantra:
Table 9. Geometrical composition of the Sri Yantra.
(The bindu is a point, like the corners of the triangles, and may be included in the count of corners because what is really being counted here are points, lines & triangles). The 42 triangles in the four levels have 84 corners and 126 sides. The Godname EHYEH with number value 21 (see Table 1) prescribes the number of triangles because 42 is the 21st even integer. It prescribes the number of sides because 126 is the sum of the values of all the possible combinations of the three letters A, H & I in AHIH:
A = 1, H = 5, I = 10
21
1. A + H + I = 16
2. AH + HI + AI + HH = 42
3. AHI + HIH + AHH = 47
4. AHIH = 21
Total
= 126
The number of geometrical elements is 252, which is the 126th even integer. The first three levels have 84 sides, 56 corners and 28 triangles, that is, 84 corners & triangles, totalling 168 geometrical elements. This 84:84 division of the number 168 was encountered in Section 2 (p. 9) as the 84 geometrical elements surrounding the centres of S1 and of S2. The fourth layer has 84 geometrical elements, whilst all four levels have 84 corners and 168 sides & triangles (84 in each half of the Sri Yantra). We do not yet see in its geometry the appearance of the holistic parameter 336 as four sets of 84 (that must await the division of the triangles into their sectors — to be discussed next). That there are, according to Table 9, 260 geometrical elements in all 43 triangles when the bindu is included is a clue to the more appropriate comparison, namely, with the yod composition of S1 & S2 outside the root edge. We see from Table 5 that S1 has 132 yods and that S2 has 128 yods outside the root edge. The centre of the triangle in S1 coincides with a hexagonal yod on the line joining Chesed and Geburah in the outer Tree of Life, whilst seven yods (four hexagonal yods & three corners) on the internal vertical sides of tetractyses in the hexagon in S2 are shared with it. Therefore, 252 yods are intrinsic to S1 & S2 and (1+7=8) yods are shared. Compare this with the 252 geometrical elements in the 42 triangles of the Sri Yantra and the eight geometrical elements (one triangle, four points & three lines) that make up the central triangle & bindu (see Table 9). All these correspondences cannot be accidental. It is clear that the geometry of the Sri Yantra manifests in a one-to-one way information abstractly symbolised by the yods in the inner Tree of Life because it is a different representation of the same archetypal blueprint.
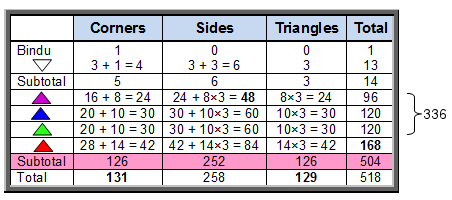
Table 10 shows the geometrical composition of the 3-d Sri Yantra when its triangles are Type A:
Table 10. Geometrical composition of the 3-d Sri Yantra with Type A triangles.
Whereas before, the first three layers had 168 geometrical elements, they now have 336 elements, whilst the fourth now has 168 geometrical elements instead of 84. The 336 elements comprise 168 sides, 84 corners and 84 triangles, i.e., 168 corners & triangles, reproducing the holistic division: 336 = 168 + 168, whilst the 168 elements in the fourth layer comprise 84 sides and 84 corners & triangles, reproducing the holistic division: 168 = 84 + 84. The division 48 = 24 + 24, which appeared in the separate polygons of S1 and S2 as their 24 corners, re-appears in the first layer of triangles as the 24 sides of the four triangles in each half, or, alternatively, as the 24 corners & triangles in each half of the Sri Yantra.
According to Table 10, the 3-d Sri is composed of 518 geometrical elements. It has 131 corners, where 131 is the number value of Samael, the Archangel of Geburah. The 43 triangles have 130 corners, 258 sides and 129 sectors, where 130 is the 129th integer after 1, 258 is the 129th even integer and 129 is the number value of YAHWEH SABAOTH, the Godname of Netzach. This number appears in the 43 triangles because 129 = 3×43. The (7+7) enfolded polygons of the inner Tree of Life contain 524 yods, of which four make up the root edge and two are the topmost corners of the two hexagons that coincide with the lowest corners of the hexagons enfolded in the next higher Tree. Hence, (524–4–2=518) yods outside the root edge belong exclusively to the set of 14 polygons enfolded in each Tree (Fig. 38). Each of these yods corresponds to a geometrical element making up the Sri Yantra with Type A triangles. Surrounding the centres of the 14 polygons are (518–14=504) such yods. They symbolise the 504 geometrical
22
a
b
Figure 38. The 518 geometrical elements composing the 3-d Sri Yantra correspond to the 518 yods in the (7+7) enfolded polygons outside their root edge that are unshared with polygons enfolded in the next higher Tree. The 504 geometrical elements in the four layers of triangles correspond to either (a) the 504 intrinsic yods that surround the centres of the 14 polygons, or (b) the 504 intrinsic yods unshared with the outer Tree of Life.
elements in the four layers of triangles. Six yods in S1, which has 132 yods outside the root edge, are centres of polygons and one yod in S2, which has 128 yods, is a centre. Hence, 126 yods in S1 are not centres and 127 yods in S2 are not centres. One of the latter yods is the topmost corner of the hexagon that is shared with the hexagon enfolded in the next higher Tree. Therefore, S2 has 126 intrinsic yods that are not centres. Compare this with the 126 corners, 126 triangles & 252 triangles in the 3-dimensional Sri Yantra, that is, with the 126 corners & triangles and the 126 sides in each half of it. Just as four sets of 126 yods in S1, S2, S1′ & S2′ surround the (7+7) centres in the polygons of the inner Tree of Life, so, too, four sets of 126 geometrical elements make up each half of the Sri Yantra. The 14 centres correspond to the 14 geometrical elements making up the central triangle and the bindu. An alternative possibility needs to be considered. The 518 yods include six yods in each hexagon that are shared with the outer Tree because they lie on its side pillars and the centre of each triangle that coincides with a hexagonal yod belonging to the outer Tree because it lies on the side of the triangle connecting Chesed to Geburah. Hence, 14 yods in the set of 518 yods are shared with the outer Tree, leaving 504 yods outside the root edge that are unshared. Each set of seven enfolded polygons contains 252 such yods. S1, then, has two shared yods (centre & corner of triangle), so that it has (132–2=130) unshared yods, whilst S2 has six shared yods, so that it has (128–6=122) unshared yods. Comparing these two numbers with the 126 corners & triangles and 126 sides in each half of the Sri Yantra, we conclude that, although the total number of yods is the same as the number of geometrical elements, S1 and S2 do not have the same
23
numbers of unshared yods. The alternative view in which the 14 yods contributed by the bindu and central triangle correspond to the 14 shared yods is, therefore, incorrect. These 14 yods correspond only to the centres of the 14 polygons making up the inner Tree of Life.
Comparison with the Type C dodecagon
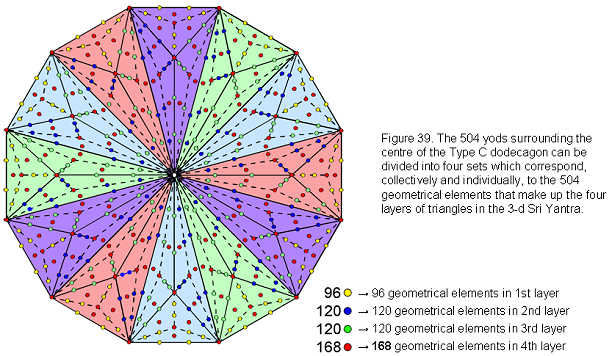
The number of yods in a Type C n-gon = 42n + 1, where “1” denotes its centre. A Type C dodecagon (n=12) has (12×42=504) yods surrounding its centre. It was pointed out in Section 4 that this regular polygon is the single, polygonal representation of the Tree of Life (see Fig. 27). The Type A version has 60 hexagonal yods, which is the number of hexagonal yods in the outer of Life, 264 yods line the 72 tetractyses in two joined Type B dodecagons and this is the number of yods in the seven enfolded polygons, whilst the 504 yods surrounding the centre of the Type C dodecagon is the number of yods intrinsic to the
(7+7) enfolded polygons that are outside the root edge. As 168 = 12×14 and 42 = 3×14, these 504 yods consist of three sets of 168 yods, the 42 yods per sector consisting of three sets of 14 yods. One set comprises 14 red yods that are either corners & centres of tetractyses (Fig. 39). The 168 such yods in the Type C dodecagon correspond to the 168 geometrical elements in the fourth layer of 14 red triangles in the 3-dimensional Sri Yantra. The 28 yods remaining in each sector comprise 10 green, hexagonal yods, 10 blue, hexagonal yods and 8 violet, hexagonal yods — the same numbers as the number of triangles in the first three layers. The 120 green yods, the 120 blue yods and the 96 violet yods in the dodecagon symbolise the geometrical elements in respectively, the third, second and first layers of the Sri Yantra with Type A triangles. In other words, the Type C dodecagon is an exact representation of the geometrical composition of the Sri Yantra. This is because they are both equivalent representations of the divine paradigm.
Figure 40. The 64 hexagrams.
This isomorphism between two sacred geometries and its embodiment of the holistic parameters 84, 168 & 336 are unmistakable, strong indications of the objective nature of the century-old, micro-psi observations of the UPA by Annie Besant and C.W. Leadbeater. Had they been otherwise, these numbers would not manifest so frequently in the geometrical and yod compositions of these and other sacred geometries to be discussed later in this article. Nor, indeed, would the gematria number values of the 10 Sephiroth and their Godnames, etc. This is not — as a sceptic might suggest — because their appearance has been contrived by some kind of cherry-picking of properties. The parameters with a paranormal provenance have entirely
24
natural meanings in the context of these sacred geometries that cannot result from random chance or deliberate selection. To suggest the latter is to beg the question that it is always possible to reproduce all the levels of correlation between two geometries as soon as some global choice of yods or geometrical properties has been made. It clearly is not possible do this deliberately. The fact that these levels exist at all can only be sensibly understood as due neither to chance, which is highly implausible, nor to cherry-picking, because the correspondence runs too deep to make that possible. Instead, it can be due only to an inherent, mathematical design that is revealing a transcendental intelligence within it.
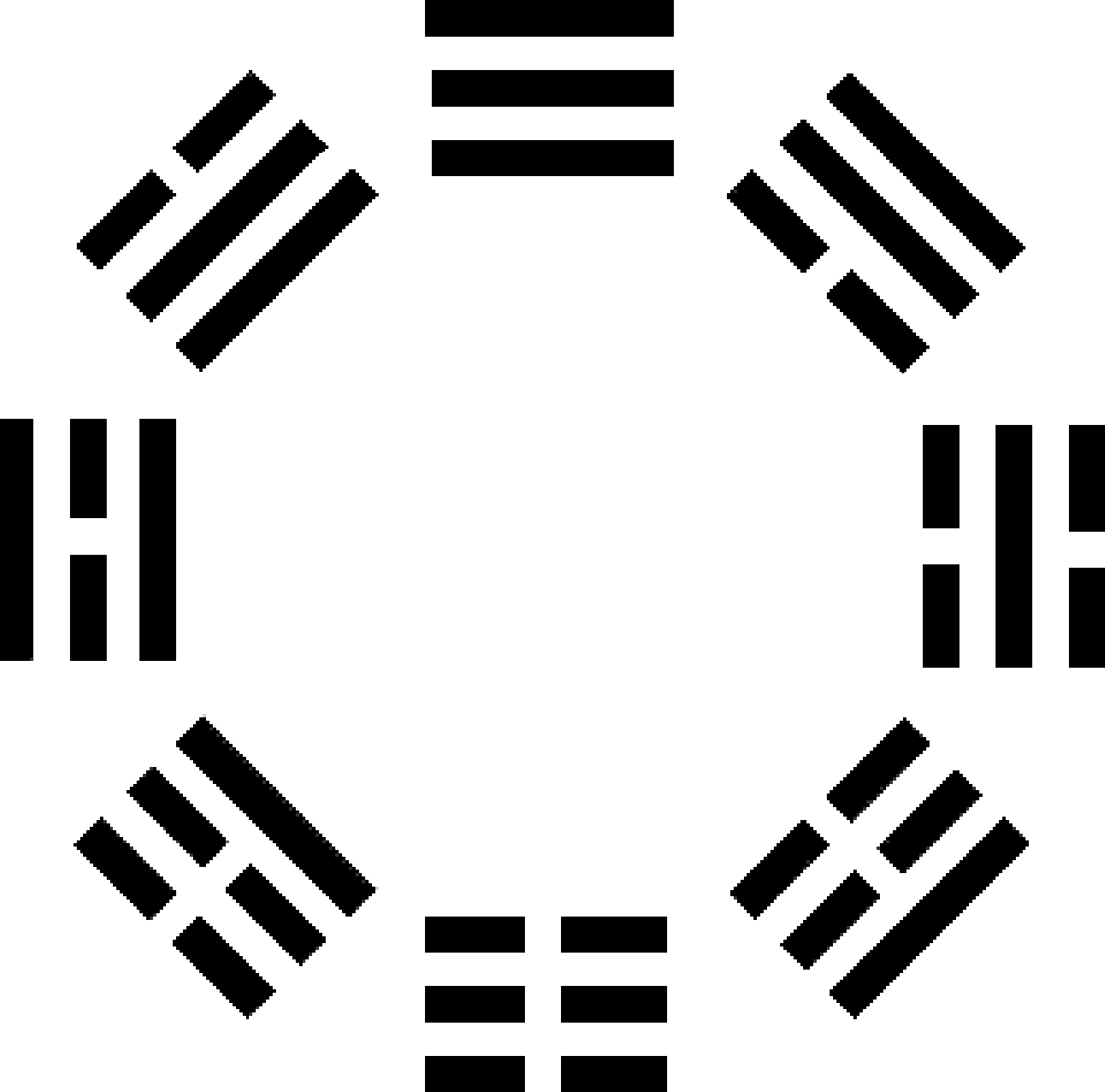
6. I Ching table of hexagrams
Used in China for thousands of years as a form of fortune telling, the system of 64 hexagrams (Fig. 40), upon which the commentaries in the famous I Ching (“Book of Changes”) are based, consists of an 8×8 square array of the (82=64) possible pairings of eight trigrams. Each trigram (Fig. 41) is a combination of
Figure 41. The eight trigrams. three lines. A line can be either ‘yin,’ the female power, or gentleness: − − , or ‘yang,’ the male power, or strength: —. Fig. 41 shows the eight combinations (2×2×2=8) of yin and yang in the three lines of a trigram. They will be called ‘lines’ if they denote yang and ‘broken lines’ if they denote yin. Each pairing of trigrams is called a ‘hexagram.’ More details can be found in Article 18 [4].
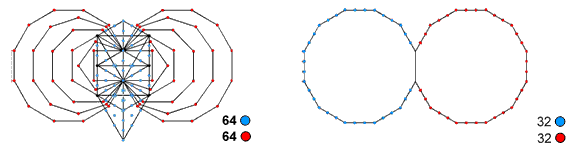
That there are (26=64) hexagrams is a direct consequence of the Taoist belief in a fundamental duality in Nature, where active (yang) and reactive, or passive (yin) forces create a balance, or harmony. This cosmic polarity is represented in the Pillar of Mercy and the Pillar of Judgement of the Tree of Life, the middle Pillar of Equilibrium representing the homeostasis resulting from the dynamic interplay of these two complementary, cosmic principles. The number 64 is the gematria number value of Nogah, the Mundane Chakra of Netzach. The number value 148 of this Sephirah is the number of yods in the four separate polygons in S1 (see Fig. 18), so that it determines the division in half of the seven types of polygons with 48 corners that make up the inner form of the Tree of Life, this number being the number value of Kokab, the Mundane Chakra of Hod, which follows Netzach in the Tree of Life.
Figure 42. The 14 enfolded polygons of the inner Tree of Life with 70 corners share six corners (black yods) with the outer Tree, which has 70 yods. 64 yods or corners are intrinsic to the outer and inner Trees. They correspond to the 64 yods outside the root edge on the boundaries of the two dodecagons whose sectors are tetractyses. The holistic parameter 64 is revealed by superimposing the outer form of the Tree onto the plane of its inner form (Fig. 42). When the 16 triangles in the former are tetractyses, three of their corners located at the positions of Sephiroth (the black yods in Fig. 42) lie on each side pillar and are shared with each hexagon as corners of its sectors. Of the 70 yods in the outer Tree of Life, (70−6=64) yods are not corners of triangles in the inner Tree. Similarly, 64 of the 70 corners in the inner Tree are intrinsic to it. None of the four yods in the root edge are shared because they lie in the plane formed by the two side pillars and this does not contain any yods belonging to triangles in the outer Tree of Life. The 94 sectors of the (7+7) enfolded polygons have 80 corners, (80−6=74) of which are unshared with the outer Tree, so that the (94+16=110) triangles in the combined Trees of Life have (10+74=84) corners. This embodiment of the holistic parameter 84 demonstrates par excellence their holistic character. Their counterpart in the Sri Yantra are the 84 corners of the 42 triangles surrounding the central one. The pair of dodecagons also display the holistic parameter 64 because 32 yods outside the root edge line each one, so that 64 yods line both.
According to Table 10, the 42 Type A triangles in the 3-dimensional Sri Yantra have 126 corners & 252 sides. The corners of the central triangle symbolise the Hindu trinity, or trimȗrti, of Siva, Vishnu & Brahma. If we regard it as an ordinary triangle without sectors, so that it has three corners and three sides, 129 corners and 255 sides surround the centre of the Sri Yantra, that is, 384 corners & sides. This is the
25
counterpart of the polygonal geometry of the inner Tree of Life because 384 corners, sides & triangles surround the centres of the 14 polygons, each half of the Sri Yantra having 192 corners & sides and each of the inner Tree of Life having 192 corners, sides & triangles. The 384 corners & sides include the 24 corners & 24 sides of the eight triangles in the first layer. This corresponds to the 24 corners, sides & triangles surrounding the centre of each hexagon.
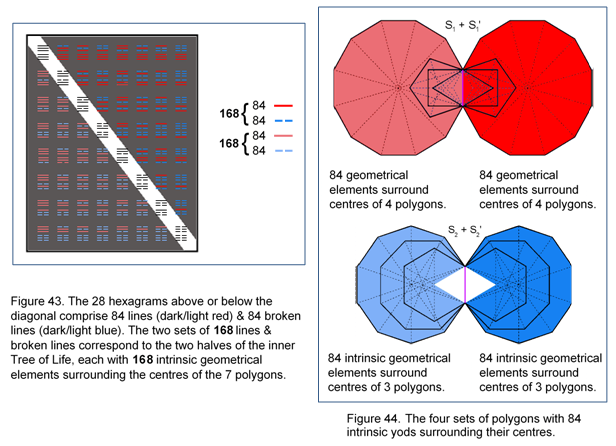
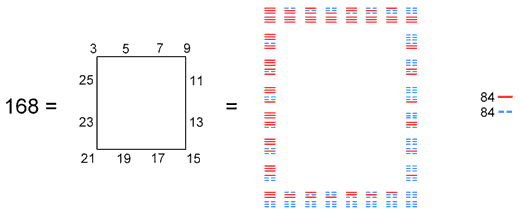
Surrounding the centres of the six other polygons in each half of the inner Tree of Life are 168 geometrical elements. Similarly, the Sri Yantra has 336 geometrical elements (168 elements in each half) other than the 48 corners & external sides of the eight Type A triangles. The counterparts of these in the table of hexagrams are the 48 lines & broken lines in the eight diagonal hexagrams and the 168 lines & broken lines in the 28 off-diagonal hexagrams in the upper and lower halves of the 8×8 square array of 64 hexagrams (Fig. 43). It is no coincidence that the first layer in the Sri Yantra has eight triangles. They correspond to the eight diagonal hexagrams, each trigram corresponding to either three corners (two external, one internal) of each Type A triangle or its three external sides.
Figure 45. 168 is the sum of the 12 odd integers after 1 forming the edges of a square. It is the number of lines and broken lines in the 28 hexagrams on the four sides of the 8×8 square array.
26
The 84:84 division
The 168 lines & broken line in the 28 hexagrams on either side of the diagonal of the 8× 8 array consist of 84 lines and 84 broken lines. The yang lines are coloured dark or light red and the yin lines are dark or light blue. This colour scheme is applied in order to correspond to that used earlier to distinguish the two halves of the inner Tree and the two halves of each half (Fig. 44). As both yang and yin lines exist in each diagonal half of the square array, the two halves
Figure 46. The sum of the first 28 odd integers arranged eight to a side of a square is 840. This is the number of circularly polarised oscillations in the inner or outer half of a whorl of the UPA. It is also the number of such oscillations in a half-revolution of all 10 whorls. The Tetrad symbolised by the square determines holistic parameters like this structural parameter of the E8×E8 heterotic superstring.
of the inner Tree should not be seen as the manifestation of the cosmic polarisation or duality of yang and yin. Rather, as each half is a whole in itself, it has a yang sector and a yin sector that correspond to, respectively, S1 & S2 (and to S1′ & S2′). What is remarkable that each sector should embody the same
Figure 47. Two sets of 84 yods surround the centre of a Type C square. The (4×84=336) yods in two separate Type C squares are the counterpart of the 336 geometrical elements in the pair of two sets of polygons [(S1, S2) & (S1′, S2′)] that make up the inner Tree of Life. parameter 84 as both the Sri Yantra and the square array of 64 hexagrams — extraordinary, certainly, but not surprising, in view of the fact that they are all isomorphic representations of the same archetypal pattern.
The boundary of the 8×8 array of hexagrams contains 28 hexagrams with 168 lines & broken lines made up of 84 lines and 84 broken lines (Fig. 45). Arithmetically, this can be expressed as the sum of the first 12 odd integers after 1 lining the sides of a square, four to each side, because:
132 – 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 = 168.
As
292 – 1 = 3 + 5 + 7 +… + 57 = 840,
the number 840 is the sum of the first 28 odd integers after 1 that can be assigned to the sides of a square, eight to each side (Fig. 46). That the square, either four units long or eight units wide, where 8 is the fourth, even integer, should determine both the superstring parameters 168 and 840 is a remarkable illustration of the Tetrad Principle at work [5]. The square even embodies the number 168 as the number of yods surrounding the centre of a Type C square (Fig. 47).
The archetypal divisions:
384 = 192 + 192,
84 = 48 + 336,
48 = 24 + 24,
336 = 168 + 168,
etc,
displayed by holistic systems are hidden within them when they are sacred geometries. They are most
27
explicit in the 8×8 array of hexagrams because they can be recognised by simple counting. Moreover, the yin/yang nature of its lines and broken lines is explicit. But this duality does not correspond to the chiral nature of the geometrical elements in the two mirror-symmetric halves of sacred geometries (or almost so, in the case of the Sri Yantra). The 192 lines & broken lines in each diagonal half of the square array of hexagrams consist of 96 lines and 96 broken lines that form eight copies of the basic set of eight trigrams. The 168 lines & broken lines in each set of 28 off-diagonal hexagrams are seven copies of the 12 lines & 12 broken lines making up the basic set of eight trigrams. The two sets of 28 hexagrams are not mere mirror images of each other, reflected across the diagonal. Nor is the “reflection” of each hexagram the result of replacing each line by a broken line and vice versa. Rather, its reflection inverts the order of its pair of trigrams. This is like what happens in the intervals between the eight notes in a musical scale. The rising interval between two notes with tone ratios m & n (m>n) is m/n. The falling interval between them is n/m. It is as though the array of 56 off-diagonal hexagrams is representing the 28 rising intervals between the eight notes in an octave (represented by the eight trigrams) and their 28 falling intervals, whilst the eight diagonal hexagrams represent the unit interval between a note and itself. In fact, it is doing so, as the eight-note diatonic scale is a holistic system, the 36 possible intervals being symbolised by the 36 corners of the seven enfolded polygons of the inner Tree of Life. But a more fundamental level of interpretation exists for the trigrams, lines & broken lines: the 64 hexagrams also express the intervallic composition of the seven types of diatonic scales [6]. As explained in Article 39 [7], the 192 lines & broken lines in the upper diagonal half of the square array denote the 192 rising intervals between the notes in the seven types of diatonic musical scales, whilst the 192 lines & broken lines in the lower half denote their falling counterparts with reciprocal tone ratios. How the rising and falling intervals and the types of intervals correspond to the 84 geometrical elements in S1 and the 84 geometrical elements in S2 will be discussed in Section 10. The following correspondences exist between the 64 hexagrams and inner form of the Tree of Life:
28 upper, off-diagonal hexagrams
84 yang lines → 84 geometrical elements surrounding centres of polygons in S1.
84 yin lines → 84 geometrical elements surrounding centres of polygons in S2.
eight diagonal hexagrams → root edge.
28 lower, off-diagonal hexagrams
84 yang lines → 84 geometrical elements surrounding centres of polygons in S1′.
84 yin lines → 84 geometrical elements surrounding centres of polygons in S2′.
The connection to the UPA
Each whorl of the UPA makes 168 circularly polarised oscillations in every half-revolution around its axis. The five inner half-revolutions and the five outer half-revolutions of each whorl correspond in the Tree of Life to, respectively, the five Sephiroth belonging to its Upper Face and the five Sephiroth spanning
Figure 48. Each half-revolution of a whorl of the UPA/superstring comprises 168 circularly polarised oscillations. Each oscillation has a positive phase (yang) and a negative phase (yin). The 168 positive phases correspond to a yang line in the 56 off-diagonal hexagrams. The 168 negative phases correspond to a yin line. They are split into 84 oscillations belonging to an outer ¼ revolution and 84 oscillations belonging to an inner ¼-revolution. The two sets of 28 off-diagonal hexagrams, each with 84 yang lines & 84 yin lines, represent these two sets of 84 oscillations, each having a positive and a negative phase.
28
its Lower Face. This ten-fold nature of a whorl is, simply, the manifestation of its Tree of Life nature, each one corresponding to a Sephirah because the UPA with 10 whorls is a microscopic manifestation of the Tree of Life blueprint. As a Tree of Life structure in its own right, a half-revolution may be divided into an “Upper Face,” namely, a quarter-revolution comprising 84 oscillations that belong to the inner half of the UPA, and a “Lower Face”, a quarter-revolution with 84 oscillations that belongs to its outer half. Being a whole, it is represented by a 2nd-order tetractys, the 84 yods surrounding its centre symbolising these oscillations.
A sinusoidal oscillation has a positive phase and a negative phase. The upper diagonal half of the 8×8 array with 28 off-diagonal hexagrams composed of 84 yang lines and 84 yin lines represents the 84 positive and 84 negative phases of 84 oscillations making up the outer half of the UPA (Fig. 48); the lower diagonal half with 28 off-diagonal composed of 84 yang lines and 84 yin lines represents the 84 positive and 84 negative phases of 84 oscillations making up its inner half.
Notice that in all cases of sacred geometries considered so far (including the 64 hexagrams), a one-to-one correspondence exists between certain subsets and their elements in each one. There is not necessarily the same number of elements in all cases, only the same numbers of corresponding elements in certain subsets of structural elements. The differences between these cases arises from the different forms taken by source. It may be a mathematical point, as in the case of the dodecagon, the root edge in the case of the inner Tree of Life, the central triangle and bindu in the case of the Sri Yantra and the generic set of eight trigrams whose pairing with themselves forms the eight hexagrams in the diagonal of the square array of 64 hexagrams. They all display a
Figure 49. The five Platonic solids with Type A polygons as their faces.
symmetry (point reflection symmetry in the inner Tree of Life, imperfect mirror symmetry of the Sri Yantra, inversion symmetry for the dodecagon and symmetry between yang and yin lines in the table of hexagrams). This symmetry exists in them because they are different, but equivalent, representations of the Whole, which, by definition, is mathematically complete.
7. The five Platonic solids
Let us consider the construction of the five regular polyhedra from the tetractys. The simplest case is when their regular faces are Type A polygons (Fig. 49). To be consistent, the internal triangles generated by joining their centres to their vertices must be Type A as well. The yod populations of individual Platonic solids need not be discussed here. Details may be found in Article 3 [8]. For the present purpose, only the classes of yods and their numbers needed to construct the mathematically complete set of five Platonic solids need be considered here. Table 11 lists the numbers of yods & hexagonal yods in the faces and interior of each polyhedron.Table 11. Yod populations of the five Platonic solids.
(V = number of vertices; E = number of edges; F = number of faces; m = number of sectors of a face).
Polyhedron
Face
V
E
F
m
Surface
Interior
Total
Number
of yodsNumber of hexagonal
yodsNumber
of yodsNumber of hexagonal
yodsNumber of yods
Number of hexagonal yods
Tetrahedron
Triangle
4
6
4
3
56
48
68 + 1
62
124 + 1
110
Octahedron
Triangle
6
12
8
3
110
96
132 + 1
120
242 + 1
216
Cube
Square
8
12
6
4
110
96
136 + 1
124
246 + 1
220
Icosahedron
Triangle
12
30
20
3
272
240
324 + 1
294
596 + 1
534
Dodecahedron
Pentagon
20
30
12
5
272
240
340 + 1
310
612 + 1
550
Total
50
90
50
–
820
720
1000 + 5
910
1820 + 5
1630
(“1” denotes the centre of the polyhedron).
1820 yods surround the centres of the five regular polyhedra. Of these, 50 yods are centres of faces and 90 yods are centres of internal triangles. Hence, (1820−50−90=1680) yods surround these (90+50=140) centres. 140 is the number value of Malachim, the Order of Angels assigned to Tiphareth. As we shall see, these centres, which are the starting points for the construction of faces and internal triangles, play
29
the same role as the centres of the (7+7=14) regular polygons of the inner Tree of Life, surrounding which are (168+168=336) yods that are intrinsic to them. In a remarkable, analogous way, (1680/5=336) yods on average surround the centres of faces and internal triangles in the five Platonic solids, 168 yods in each half. These famous polyhedra are the 3-dimensional representation of the 1680 turns of each helical whorl of the UPA, there being 168 turns in each half of one revolution of a whorl. It is unequivocal evidence for C.W. Leadbeater’s paranormally derived number 1680 being embodied in the five Platonic solids constructed from tetractyses. The average yod population 336 is the number of turns in one revolution of a whorl. The 840 yods in each half of all five Platonic solids correspond to the 840 turns in each half of a whorl. There are, of course, not 168 yods in the half of every Platonic solid. That number represents only an average, made possible by the fact that the number of Platonic solids is the same as the number of revolutions of each whorl, so that the 10 halves of the former correspond to the 10 half-revolutions of the latter.
Let us now examine the classes of yods making up the tetractyses in the faces and interiors of the Platonic solids, as well as the numbers of each type. There are seven types, excluding the centres of faces and internal triangles:
Faces
1. vertices (V);
2. hexagonal yods on edges (2E);
3. hexagonal yods on sides of sectors (2mF);
4. hexagonal yods at centres of sectors (mF);
Interior
5. hexagonal yods on sides joining centre of polyhedron to vertex (2V);
6. hexagonal yods on sides of sectors of internal triangles (6E);
7. hexagonal yods at centres of sectors of internal triangles (3E).
Total number of yods = 3V + 11E + 3mF = 6 + 14E + 3(m−1)F,
where Euler’s polyhedral formula for a convex polyhedron:
V – E + F = 2
has been used. The number “6” measure the number of yods on the two semi-axes passing through two opposite vertices and the centre of a polyhedron. Excluding their centres, 30 yods line the 10 semi-axes of the five Platonic solids, so we see from Table 11 that 1790 yods surround these axes. On average, a Platonic solid has 384 yods (192 in each half), of which six yods line its two semi-axes and 378 yods surround them (189 in each half). These divisions define all sacred geometries. For example, the 3-dimensional Sri Yantra has six hexagonal yods on the sides of its central triangle/tetractys and 336 yods line the 126 sides of its surrounding 42 tetractyses (Fig. 36), at the centres of which are 42 hexagonal yods, so that it has 384 yods. On average, it takes as many yods to build a Platonic solid as it does to construct the 3-dimensional Sri Yantra from tetractyses. This, of course, is not a coincidence, for they are both expressions of a universal, archetypal pattern. The number that shapes the 42 triangles is 336, and this is the average number of yods in a Platonic solid that surround the centres of its faces and interior triangles. The question to be answered now is whether the 168 yods in an average half of a Platonic solid divide evenly into two sets of 84 yods, just as we have seen for the 168 yods or geometrical elements in other sacred geometries.
Table 12 displays the yod populations of half a Platonic solid for the seven classes of yods other than centres of faces and internal triangles:
Table 12. Yod populations in half a Platonic solid for the seven classes of yods.
Faces
Interior
Total
Vertices
Hexagonal yods on edges
Hexagonal yods on sides
Hexagonal yods at centres
Hexagonal yods on sides
Hexagonal yods on sides of sectors
Hexagonal yods at centres
Tetrahedron
2
6
12
6
4
18
9
57
Octahedron
3
12
24
12
6
36
18
111
Cube
4
12
24
12
8
36
18
114
Icosahedron
6
30
60
30
12
90
45
273
Dodecahedron
10
30
60
30
20
90
45
285
Total
25
90
180
90
50
270
135
840
En passant, it is worth noting that each half of the tetrahedron — the building block of solid geometry —
30
has 26 yods in its faces of each half and 31 yods in its interior, showing how YAHWEH, the Godname of Chokmah with number value 26, and EL, the Godname of Chesed below it with number value 31, prescribe this Platonic solid. Also, the 12 faces of the complete dodecahedron contain 260 (=26×10) yods, showing how it is prescribed by YAHWEH. Of its 285 yods in each half, three yods lie on the semi-axis, leaving 282 yods, where 282 is the number value of Aralim, the Order of Angels assigned to Binah.
The following analysis applies to either half of a Platonic solid: according to Table 12, there are (30+45=75) hexagonal yods at the centres of the 75 tetractyses in the dodecahedron, leaving (285−75=210) yods lining their sides. The corresponding numbers for the first four Platonic solids are tabulated below:
Table 13. Boundary & central hexagonal yods in the first four half-Platonic solids.
Platonic solid
Central hexagon yods
Boundary yods
Tetrahedron
6 + 9 = 15
57 – 15 = 42
Octahedron
12 + 18 = 30
111 – 30 = 81
Cube
12 + 18 = 30
114 – 30 = 84
Icosahedron
30 + 45 = 75
273 – 75 = 198
Total
150
405
The number of yods in the tetrahedron and on the sides of tetractyses in the octahedron, cube & icosahedron = 405 + 15 = 420. This leaves (150−15=135) central hexagonal yods in these three solids. The octahedron, cube, icosahedron & dodecahedron have (135+75=210) central hexagonal yods. The number of yods either at centres of tetractyses in these four solids or lining the sides of tetractyses in the dodecahedron = 210 + 210 = 420.
We find that the 840 yods in each half of the five Platonic solids comprise two sets of 420 yods. On average, the 168 yods in half a Platonic solid consist of two sets of (420/5=84) yods. On average, there are 336 yods in a complete Platonic solid that comprise four sets of 84 yods surrounding the centres of their faces or internal triangles. This is the polyhedral counterpart of the 84:84:84:84 division of the holistic parameter 336 found in previous sections for the inner Tree of Life, the dodecagon and the Sri Yantra.
According to Table 12, the number of yods in the faces of the five half-solids is 385. This the sum of the squares of the first 10 integers:
It is a beautiful illustration of how the Decad expresses properties of holistic systems. The dodecahedron has 285 yods in each half surrounding centres of faces and internal triangles, so the first four Platonic solids have (840−285=555) such yods in each half, i.e., 1110 altogether, where
1110 = 101 + 102 + 103.
If we imagine them as concentric and orientated so that none of their yods coincide, the total number of yods, including their shared centre = 1111, where
1111 = 100 + 101 + 102 + 103.
This is the sum of the first four powers of the fourth triangular number. It demonstrates in a remarkable way how the Tetrad expresses the properties of holistic systems.
Table 14. Yod and geometrical composition of the five complete Platonic solids.
Polyhedron
Vertices
Hexagonal yods on sides
Central hexagonal yods
Total number of yods
Sides
Triangles
Total number of geometrical elements
Tetrahedron
4
80
30
114
40
30
74
Octahedron
6
156
60
222
78
60
144
Cube
8
160
60
228
80
60
148
Icosahedron
12
384
150
546
192
150
354
Dodecahedron
20
400
150
570
200
150
370
Total
50
1180
450
1680
590
450
1090
31
It is instructive and revealing to calculate the average yod and geometrical composition of a Platonic solid. Table 14 shows how many yods & geometrical elements surround the centres of faces and internal triangles of each whole Platonic solid (the centres of the solids are excluded for the moment).
Comments
1. (1180+50=1230) yods line the 450 tetractyses. Including the 140 corners that are centres of faces or internal triangles, 1370 yods lines their sides. This property is stunning, for it is the number of yods in the inner form of the Tree of Life with Type B polygons (Fig. 50)! It means that the number of yods that shape all the tetractyses needed to construct the five Platonic solids is precisely the number of yods in the inner Tree of Life. Moreover, it means that, on
Figure 50. The (7+7) enfolded Type B polygons of the inner Tree of Life contain 1370 yods. This is the number of yods that line the 450 tetractyses needed to build the five Platonic solids.
average, 137 yods line the 45 tetractyses in a half-Platonic solid, showing how the Platonic solids embody the mysterious number 137 at the heart of atomic and particle physics whose reciprocal is the approximate value of the fine-structure number 137.
2. The number of vertices & sides is 640. This is the number value of Shemesh, the Mundane Chakra of Tiphareth, whose Order of Angels is Malachim, with number value 140! If the 140 centres of faces and internal triangles are included, it is also the number of corners & central hexagonal yods.
3. The 25 vertices of the five half-Platonic solids are joined by 25 sides of 225 tetractyses, where 225 = 152 and 15 is the number value of YAH, the shorter form of the Godname assigned to Chokmah. Each side has two hexagonal yods, and therefore the number of yods (including centres of solids) that line these sides in the five half-solids = 2×25 + 25 + 5 = 80. This is the number value of Yesod. The number of yods lining the sides joining centres to the 50 vertices of the Platonic solids = 2×50 + 50 + 5 = 155. This is the number value of ADONAI MELEKH, the complete Godname of Malkuth.
4. According to Table 12, the number of hexagonal yods lining tetractyses in the faces of the five half-Platonic solids = 90 + 180 = 270. Their number of sides = 135. The 50 faces of the five Platonic solids have 270 sides of 180 triangles with 50 vertices and 50 more corners that are the centres of faces. The total number of geometrical elements in the faces = 550, that is, 50 vertices and (50×10) more geometrical elements. This demonstrates how ELOHIM, the Godname of Binah with number value 50, prescribes the shapes of the Platonic solids. It is determined by the Decad because 550 = 10×55 and 55 is the tenth triangular number:
55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10.
5. Including the 140 centres of faces & internal triangles, the total number of geometrical elements = 1090 + 140 = 1230. This is also the number of boundary yods (excluding the 140 corners) in the 450 tetractyses. The average number is 246. This is the number value of Gabriel, the Archangel of Yesod. There are, on average, 123 geometrical elements per half-Platonic solid. 123 is the tenth Lucas number in the Lucas series:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, ...
32
named after French mathematician, François Édouard Anatole Lucas (1842-1891), who gave the name of “Fibonacci numbers” to the closely related type of number. The number of yods in a Type D n-gon = 123n + 1. Therefore, the Type D decagon has 1230 yods surrounding its centre (Fig. 51).
Figure 51. 1230 yods surround the centre of the Type D decagon. This is the number of geometrical elements in the 5 Platonic solids whose faces & internal triangles are Type A. The 123 yods per sector denote the 123 geometrical elements on average in each half-Platonic solid.
Once again, the Decad determines the geometrical composition of the five Platonic solids. It is a remarkable example of the Tetrad Principle at work in determining holistic parameters, for the decagon has 10 corners, where 10 is the fourth triangular number, and the Type D decagon is the fourth in the series of types of division of the decagon:
Type A decagon → Type B decagon → Type C decagon → Type D decagon.
6. The five Platonic solids have 90 edges and 500 (=50×10) more sides of 450 triangles.
The average Platonic solid has:
1. (50/5=10) vertices, (90/5=18) edges, (1180/5=236) hexagonal yods lining the (590/5=118) sides of (450/5=90) tetractyses. There are (450/5=90) hexagonal yods at their centres. The average number of boundary yods excluding vertices (236) is the same as the number of yods that line the sides of the (7+7) enfolded polygons of the inner Tree of Life (Fig. 52).
Figure 52. 236 yods line the sides of the (7+7) enfolded polygons of the inner Tree of Life.
2. 55 geometrical elements in its faces, where 55 is the tenth triangular number.
3. (10+236+90=336) yods and (1090/5=218) geometrical elements surrounding centres of faces and internal triangles. Including, on average, the 28 centres of faces & internal triangles per solid, (336+28=364) yods and (218+28=246) geometrical elements surround the centre of the solid, whilst (236+28=264) yods other than vertices line the 90 tetractyses. This is the number of yods in the seven enfolded polygons of the inner Tree of Life (Fig. 8). Including vertices, (10+264=274) yods on average line the 90 tetractyses, 137 in each half of a Platonic solid, which also contains 168 yods other than the 14 centres of faces & internal triangles. As a check, according to Table 11, the five Platonic solids have 1820 yods, so that the average number of yods per half-solid = 182 = 137 + 45, where 45 is the average number of hexagonal yods at the centres of the 45 tetractyses in half a Platonic solid, all five complete Platonic solids having 450 tetractyses.
33
8. Disdyakis triacontahedron
There are only five Platonic solids, each having regular polygons, that can exist in 3-dimensional space. If a polyhedron has two or more faces that are different polygons, then 13 so-called “Archimedean solids” exist (15, including two chiral varieties). Their duals are called the Catalan solids (Fig. 53). The Catalan solid with the most faces is the disdyakis triacontahedron. It has 62 vertices (31 in each half), where 62 is the number value of Tzadkiel, the Archangel of
Figure 53. The disdyakis triacontahedron has the most faces of all the Catalan solids.
Figure 54. 360 (=36×10) geometrical elements surround the axis of the disdyakis triacontahedron.
Chesed, and 31 is the number value of EL, the Godname of this Sephirah. It has 180 edges and 120 faces that are scalene triangles. The disdyakis triacontahedron is formed by sticking rhombic pyramids on the 30 faces of the rhombic triacontahedron (another Catalan solid that is the compound of the icosahedron and the dodecahedron). Figure 54 shows the three types of vertices: 30 A vertices (peaks of the pyramids), 12 B vertices (vertices of the icosahedron) and 20 C vertices (vertices of the dodecahedron). There is the same number (60) of the three types of edges.
Many previous articles by the author have accumulated evidence that the disdyakis triacontahedron is the single, polyhedral form of the inner Tree of Life (or, more generally, the universal blueprint governing holistic systems). The five Platonic solids, too, are its polyhedral form, but only collectively, not in any individual sense. The disdyakis triacontahedron should be seen as their apotheosis, containing all those types of information that exist separately in individual members of the mathematically complete set of regular polyhedra. In confirmation of this conclusion about its status as sacred geometry, further evidence will now be presented proving that the holistic divisions:
336 = 168 + 168
and
168 = 84 + 84
found in earlier sections to be present in the inner Tree of Life, the dodecagon, the Sri Yantra & the 64 hexagrams are embodied as well in the disdyakis triacontahedron.
Let us, firstly, consider the case where all faces and internal triangles formed by joining vertices to the centre of the polyhedron are simple triangles; later, we shall consider them divided into their sectors. Table 15 shows the geometrical composition of the faces and interior of the disdyakis triacontahedron.
Table 15. Geometrical composition of the disdyakis triacontahedron.
Corners
Sides
Triangles
Total
Faces
2 + 60
180
120
2 + 360
Interior
1
2 + 60
180
3 + 240
Total
3 + 60
2 + 240
300
5 + 600
600 geometrical elements surround the axis, which comprises five elements (three vertices, two sides).
34
Including the centre, there are 363 corners & triangles, where 363 is the number value of SHADDAI EL CHAI, the complete Godname of Yesod. There are 150 (=15×10) corners & sides surrounding the semi-axis in each half of the polyhedron, where 15 is the number value of YAH. Including this semi-axis, each half has (150+3=153) corners & sides, where 153 is the number value of ELOHIM SABAOTH, the Godname of Hod. Including both semi-axes, there are (150+5=155) corners & sides in the axis and faces of half the polyhedron. This is the number value of ADONAI MELEKH, the complete Godname of Malkuth. They comprise one centre, (2+30=32) vertices, 90 edges and 32 internal sides, i.e., 90 edges and 65 corners & sides. 90 is the number value of MELEKH and 65 is the number value of ADONAI.
Surrounding the axis are 24 vertices, 84 edges & 60 triangular faces either above or below the central 12-gon. They comprise (24+60=84) corners & triangles and 84 sides. These 168 geometrical elements consist of two sets of 84 elements, so that the 336 geometrical elements surrounding the axis in both halves of the polyhedron comprise four sets of 84 elements. This is the polyhedral counterpart of the four sets of 84 structural elements found in previous sections for the inner Tree of Life, the dodecagon, the 64 hexagrams and the Platonic solids. This pattern is part of the larger holistic pattern:
384 = 48 + 336 = (24 + 168) + (24 + 168),
which is revealed particularly clearly in the 64 hexagrams as the 48 lines & broken lines in the eight diagonal hexagrams and as the 336 lines & broken lines in the 56 off-diagonal hexagrams (168 in each half). The counterpart in the disdyakis triacontahedron of the central set of 48 lines & broken lines (24 lines, 24 broken lines) are the 24 corners & triangular sectors of the central 12-gon and their 24 sides.
Next, consider each face and internal triangle as a Type A triangle. Table 16 lists the geometrical composition of the disdyakis triacontahedron:
Table 16. Geometrical composition of the disdyakis triacontahedron with Type A triangles.
Corners
Sides
Triangles
Total
Faces
2 + 60 + 120 = 2 + 180
180 + 3×120 = 540
3×120 = 360
2 + 1080
Interior
1 + 180
2 + 60 + 3×180 = 2 + 600
3×180 = 540
3 + 1320
Total
2 + 360
2 + 1140
900
5 + 2400
2400 geometrical elements surround the five geometrical elements making up the axis. The 900 (=90×10) triangles comprise 360 (=36×10) triangles in the faces and 540 (=54×10) internal triangles. This simple 36:54 division of the holistic parameter is characteristic of holistic systems, being embodied in Plato’s Lambda Tetractys [9] as the difference between the sum (36) of the integers at its corners and the sum (54) of the seven remaining integers at the centre and corners of a hexagon (Fig. 55). Comparing Tables 14 & 15, the intermediate stage of transformation of the disdyakis triacontahedron in which only internal triangles are Type A adds 1320 internal geometrical elements (180 corners, 600 sides, 540 triangles) to the 360 elements (60 corners, 180 sides, 120 triangles) that surround the axis The 1680 geometrical elements surrounding the axis comprise 840 in each half. This should be compared with the 1680 turns
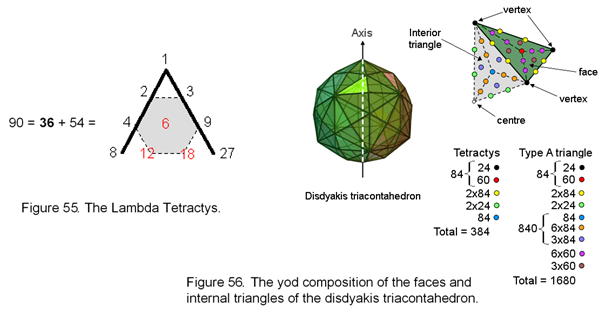
35
in each whorl of the UPA described paranormally by C.W. Leadbeater, its outer or inner half having 840 turns. It is additional evidence for the disdyakis triacontahedron being the polyhedral version of the universal blueprint that governs the form of the basic constituent of matter that he claimed to remote-view. Notice that the upper or lower half of the polyhedron is now composed of (600+180=780=78×10) sides and (180+540+60+120=900=90×10) corners & triangles. As well as embodying the number value 168 of Cholem Yesodoth, its geometry also embodies the gematria number value 78 of Cholem and the number 90 of Yesodoth! Evidence that this particle really was (and is) a superstring is the fact that 720 geometrical elements are added by dividing the 120 faces of the disdyakis triacontahedron into their 360 sectors, so that:
2400 = 720 + 1680.
Compare this with the mathematical fact that the rank-8 exceptional Lie group E8 in E8×E8 heterotic superstring theory has 240 roots, whilst E6, its rank-6 exceptional subgroup, has 72 roots, leaving 168 other roots. We see that there is a correlation between the geometrical composition of the disdyakis triacontahedron and the root composition of E8 and its subgroups (it is analysed in detail on the author’s website (10)). This would not exist unless:
1. the UPA is a state of the E8×E8 heterotic superstring, making its “observed” structural parameter 168 assume group-theoretical significance;
2. the disdyakis triacontahedron is the polyhedral representation of holistic systems in which the group E8 plays a fundamental role.
The central plane of the disdyakis triacontahedron is a 12-gon whose corners are three A vertices, three B vertices & three C vertices. As the number of geometrical elements surrounding the centre of a Type A n-gon = 10n, the centre of the 12-gon is surrounded by 120 geometrical elements. (2400−120=2280=228×10) geometrical elements above and below the central plane surround the axis. 228 is the 227th integer after 1, where 227 is the 49th prime number. This shows how EL CHAI, the Godname of Yesod with number value 49, prescribes the disdyakis triacontahedron.
Figure 56 depicts the types of yods in a face and an internal triangle when both are either tetractyses or Type A triangles. In the former case, in each half of the disdyakis triacontahedron (24+60+84=168) corners or centres of tetractyses, (2×84=168) hexagonal yods on edges and (2×24=48) hexagonal yods on internal sides surround the axis. In other words, the holistic parameter 384 manifests in each half of the disdyakis triacontahedron. It embodies the characteristic pattern:
384 = 48 + 336 = 48 + 168 + 168
that we find in the 64 hexagrams and sacred geometries [11]. As the 24 vertices consist of 12 A vertices, four B vertices & eight C vertices, i.e., all even numbers, and all the other sets of yods are exactly divisible by 2, the 384 yods divide naturally into two sets of 192 yods that display the characteristic pattern:
192 = 24 + 168.
The number of yods surrounding the axis above or below the 12-gon that line faces = 24 + 2×84 = 192. The same pattern therefore appears in just the yods that line the 120 tetractyses in the disdyakis triacontahedron. The division:
384 = 192 + 192
divides the polyhedron into two equal halves above or below the central 12-gon, each half being composed of 60 tetractyses bounded by 192 yods.
Let us now regard as a tetractys every sector of the 300 triangles making up the disdyakis triacontahedron. For simplicity, the yods on the axis will be excluded from the calculation. Table 17 shows the number of yods in the faces and interior that surround an axis perpendicular to the 12-gon passing through two diametrically opposite A vertices. Figure 56 depicts the different types of yods.
Table 17. Yod composition of the disdyakis triacontahedron with Type A triangles.
Faces
Interior
Total
Corners
Hexagonal yods
Corners
Hexagonal yods
Sides
Central
Sides
Central
Above
24 + 60 = 84
2×84 + 2×3×60 = 528
3×60 = 180
84
2×24 + 2×3×84 = 552
3×84 = 252
1680
12-gon
12
2×12 = 24
–
12
2×4×12 = 96
3×12 = 36
180
Below
24 + 60 = 84
2×84 + 2×3×60 = 528
3×60 = 180
84
2×24 + 2×3×84 + 552
3×84 = 252
1680
Total
180
1080
360
180
1200
540
3540
36
Above or below the central plane are 1680 yods surrounding the axis that include 24 vertices. The 24:24 division of the 48 vertices surrounding the axis above and below the central plane defines the division:
3360 = 1680 + 1680,
which (apart from the tetractys/Tree of Life factor of 10) was proved in earlier sections to exist in certain sacred geometries. The question is whether each yod population 1680 has the natural division:
1680 = 840 + 840
which (apart, again, from the factor of 10) was found for these sacred geometries. Figure 56 shows that 10 yods are inside an internal Type A triangle having an edge of the polyhedron as its base. But there are 84 such edges above the central plane containing the 12-gon and 84 edges below it. Hence, the 1680 yods in each half contain (10×84=840) yods inside 84 internal triangles, leaving 840 yods either in the faces or on sides of internal triangles. The 3360 yods outside the 12-gon that surround the axis divide into four sets of 840 yods. This conforms to the pattern:
336 = 4×84
found for sacred geometries discussed in previous sections.
By exchanging the 84 blue yods at the centres of internal Type A triangles with 24 black vertices, one set of 840 yods decreases by 60, becoming 780 (=78×10) yods, and the other set increases by 60, becoming 900 (=90×10) yods (see Fig. 56). With its yods regrouped this way, the disdyakis triacontahedron is seen to embody in a natural way the gematria number values 78 and 90 of, respectively, the words Cholem and Yesodoth making up the Kabbalistic name of the Mundane Chakra of Malkuth.
Including the central 12-gon, 3540 yods surround the axis of the disdyakis triacontahedron, of which 360 yods are yods at the centres of tetractyses in faces and 540 yods are at centres of tetractyses in the interior. The number of yods lining the 900 tetractyses = 3540 – 360 – 540 = 2640 = 264×10. The number of yods in the seven enfolded polygons of the inner Tree of Life is 264 (Fig. 8). Assigning the Decad to all their yods generates the number of yods on the sides of the tetractyses in the disdyakis triacontahedron. Including just its centre, the polyhedron has 3541 yods. Amazingly, this is the 496th prime number, where 496 is the number of Malkuth and the dimension of the two symmetry groups SO(32) and E8×E8 providing superstring interactions that are free of quantum anomalies! [12]. Alternatively, including the seven yods spaced evenly along its axis, the disdyakis triacontahedron constructed from Type A triangles contains 3547 yods in total, where 3547 is the 496th prime number after 2. There must be a profound connection between the prime numbers and the structural parameters of holistic systems, for it is too improbable for these two properties to be due to chance.
9. 3-torus
The German mathematician Felix Klein (1849-1925) is well-known to mathematicians for his work in group theory, complex analysis, non-Euclidean geometry and on the connections between geometry and group theory. In 1878 he discovered that the quartic equationu3v + v3w + w3u = 0
(henceforth called the “Klein quartic” [13]) relating three complex variables u, v, w that are the homogenous coordinates of a point on its Riemann surface has the 336 symmetries of the group SL(2,7). Klein showed that it is mapped onto itself by 168 analytic transformations, or orientation-preserving “automorphisms.” The remaining 168 antiautomorphisms” reverse orientation, causing reflection. Hurwitz [14] showed that a compact Riemann surface of genus g≥2 has at most 84(g−1) automorphisms and the same number of antiautomorphisms. A Riemann surface with the maximum number of automorphisms for a given g is called a “Hurwitz curve” of genus g (g≥3). A Hurwitz curve of genus 3 has 168 automorphisms, so that the Klein curve is the Hurwitz curve with the smallest genus g = 3. In plain English: it has the most symmetries of any surface that is topologically equivalent to a sphere

Figure 57. The 3-torus.
with three holes, and there is no sphere with fewer holes that has the most symmetries for that number of holes. Macbeath [15] showed that there is an infinite number of Hurwitz curves. But none other than the Klein curve with g = 3 and one with genus 7 have equations currently known to mathematicians [16]. Because the Klein Quartic is a Riemann surface of genus 3, it can be realised as a regular map in an orientated 2-manifold of genus 3, i.e., the 3-torus (Fig. 57).
SL(2,7) is the double cover of the Klein quartic symmetry group PSL(2,7). Its order 336 is the number of
37
Figure 58. The {7,3} & {3,7} tiling on the Poincaré disk of the 168 symmetries of the Klein quartic.
automorphisms and antiautomorphisms of the Klein quartic. The 168 elements of PSL(2,7) are represented either by the {7,3} tiling [17] of the Poincaré disc with 24 heptagons having 168 vertices, three heptagons meeting at each of the 56 vertices, or by its {3,7} tiling with 56 triangles having 168 vertices, seven triangles meeting at each of the 24 vertices (Fig. 58). The Riemann surface of the Klein quartic is a 168-sheeted covering of the sphere, branched over the following three points of the sphere:
The author’s website and articles has provided illustrations of not only how the numbers 336 & 168 are characteristic parameters of sacred geometries but also how they naturally display the factorisations:
336 = 2×168
168 = 84×2 = 56×3 = 24×7.
If we dismiss as implausible that these properties appear merely by coincidence, it implies that the geometry underlying the Klein quartic conforms to the archetypal patterns of sacred geometries. This was explored in earlier articles ([18], [19]). To avoid repetition, we shall focus here on showing how the {3,7} tessellation of the 3-torus by triangles that are either tetractyses or Type A triangles displays the 168:168
Figure 59. The 3-torus constructed from 4 triangular prisms and 6 square antiprisms.
Figure 60. The triangular prism and the square antiprism constructed from tetractyses.
38
division of 336 and the 84:84 division of 168, thereby providing more evidence that the geometry underlying the Klein quartic conforms to the patterns characteristic of sacred geometries.
Figure 59 shows the {3,7} tessellation onto the 3-torus of the 56 orbits of order 3 that correspond to the 56 bitangents of the Klein quartic. The 3-torus is topologically equivalent to six square antiprisms (Fig. 60) with their 12 square faces stuck to the 12 square faces of four triangular prisms in a tetrahedral formation, each antiprism being given a twist. This leaves 56 triangular faces. Each triangular prism has six vertices, nine edges & two triangular faces; each square antiprism has eight vertices, 16 edges, of which eight edges coincide with edges of the former when they are stuck together, and eight triangular faces. This leaves 24 vertices and (4×9 + 6×8 = 84) edges. Compare this with the 24 vertices and 84 edges of 60 triangles that surround the axis of the disdyakis triacontahedron in its upper or lower halves (Fig. 61). In fact, just as it has 144 edges & faces, so the six square antiprisms have 144 edges & triangular faces. Of itself, this does not prove some kind of isomorphism exists between the polyhedron and the 3-torus constructed from prisms and antiprisms, because it is illegitimate to compare an intact system with the separate components of another — whether holistic or not! However, the division:
168 = 24 + 144
is characteristic of such systems because it is part of the tetractys representation of the holistic parameter 240:
For example, the 168 yods needed to transform the sectors of a dodecagon into Type A triangles comprise 24 hexagonal yods on its sides and 144 yods inside it (Fig. 62), whilst the 168 corners & sides in two separate Type B dodecagons consist of their 24 corners and 144 sides & other corners (Fig. 63). This
Figure 62. The 168 yods needed to turn the sectors of a dodecagon into Type A triangles consist of 24 red hexagonal yods lining its sides and 144 black yods. Figure 63. 240 geometrical elements surround the centres of the two Type B dodecagons. They comprise 72 blue triangles and their 168 corners & sides. The latter comprise 24 red corners of the dodecagons and 144 black corners & sides.
division reflects the fundamental Kabbalistic distinction between Malkuth and the six Sephiroth of Construction preceding it:
7 = 1 + 6
168 = 24×7 = 24×1 + 24×6 = 24 + 144.
39
The 24 vertices surrounding the axis above or below the equator of the disdyakis triacontahedron minimally mark out the skeletal shape of each half of the polyhedron, as expressed by its 144 edges & faces (see Fig. 61); similarly, the 24 vertices of the four triangular prisms minimally define the prismatic construction of the 3-torus, the 48 vertices of the six square antiprisms not adding to its shape because they coincide with these vertices when the 12 square faces of the triangular prisms are stuck to the 12 square faces of the square antiprisms.
To investigate other analogous properties, we will analyse the geometrical and yod composition of the prisms and antiprisms when separate and when assembled. Table 18 shows the populations of geometrical elements and yods in the separate polyhedra when their faces are simple triangles/tetractyses and when they are Type A triangles.
Table 18. Geometrical/yod composition of the four triangular prisms & the six square antiprisms.
Tetractys
Type A triangle
Triangular
Prism
Square
Antiprism
Total
Triangular
Prism
Square
Antiprism
Total
Number of vertices
4×6 = 24
6×8 = 48
72
24 + 4×2 = 32
48 + 48×1 = 96
128
Number of edges
4×9 = 36
6×16 = 96
132
36 + 8×3 = 60
96 + 48×3 = 240
300
Number of triangles
4×2 = 8
6×8 = 48
56
8×3 = 24
48×3 = 144
168
Number of geometrical elements
68
192
260
116
480
596
Number of hexagonal yods on sides of tetractyses
2×36 = 72
2×96 = 192
264
2×60 = 120
2×240 = 480
600
Number of hexagonal yods
8 + 72 = 80
48 + 192 = 240
320
24 + 120 = 144
144 + 480 = 624
768
Number of yods on sides of
tetractyses24 + 72 = 96
48 + 192 = 240
336
32 + 120 = 152
96 + 480 = 576
728
Number of yods
8 + 96 = 104
48 + 240 = 288
392
24 + 152 = 176
144 + 576 = 720
896
Comments
1. The 10 separate prisms & antiprisms have 72 vertices. This is the 36th even integer, showing how ELOHA, the Godname of Geburah with number value 36, prescribes the geometry of the 3-torus in a minimal way. They have 132 edges, where 132 is the 65th even integer after 2. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the form of the 10 prisms & antiprisms through their edges. The two types of structural units have 14 vertices, 25 edges & 10 triangular faces, i.e., 49 geometrical elements, showing how they are prescribed by EL CHAI, the Godname of Yesod with number value 49.
2. There are 260 (=26×10) geometrical elements in the 10 separate prisms & antiprisms. This is strong evidence for the holistic nature of the 3-torus prescribed by the Godname YAHWEH with number value 26 because there are 260 yods outside the root edge of the seven enfolded polygons, whilst 260 geometrical elements make up the 3-dimensional Sri Yantra (Fig. 64).
Figure 64. The Godname YAHWEH with number value 26 prescribes the yod population of the inner Tree of Life and the number of geometrical elements in both the 3-d Sri Yantra & the 10 separate prisms & antiprisms that form the 3-torus.
3. 264 hexagonal yods line the 132 edges of the 10 prisms & antiprisms. This is the number of yods in the seven enfolded polygons of the inner Tree of Life when their 47 sectors are tetractyses. The 132 hexagonal yods in half the complete set of prisms & antiprisms have their counterparts in the 132 yods
40
making up S1 and the 132 yods in S2 — the two halves of the set of seven polygons. This correlation indicates that the 3-torus is the counterpart of one set of seven enfolded polygons. The counterpart of the set in the mirror-image half of the inner Tree of Life will be discussed shortly.
4. 336 yods line the 132 sides of the 56 tetractyses (Fig. 65). The number 336 is the order of SL(2,7), the group describing the 336 automorphisms and antiautomorphisms of the Klein quartic whose Riemann surface is topologically equivalent to a 3-torus. It is remarkable that this parameter of holistic
Figure 65. 336 yods line the edges of the 10 separate prisms and antiprisms
systems should be embodied in the separate building blocks needed for the {3,7} tessellation of the 3-torus. Not that it is unique, for 336 yods are needed to turn the separate polygons in either S1 or S2 with 24 sectors into Type B polygons, whilst the seven separate Type B polygons have 336 corners & sides of 144 triangles [20]. Furthermore, compare this property with the fact that 336 yods line the sides of the 42 triangles in the Sri Yantra (see Fig. 35), whilst 336 yods other than corners surround the centres of two joined, Type B dodecagons (see Fig. 31). This number appears in the building blocks of the {3,7} tessellation of the 3-torus not by accident but because the geometry underlying the Klein quartic conforms to the universal patterns of sacred geometry.
5. The 168 sectors of the 56 Type A triangles contain 896 yods, of which 56 are their centres, leaving 840 yods that surround these centres. When the triangles are tetractyses, there are 336 yods surrounding these same centres. Here is the meaning of these two numbers in the context of the structure of the UPA: one revolution of each helical whorl with 1680 turns contain 336 turns and the 2½ revolutions constituting an outer or inner half of a whorl contain 840 turns. It is remarkable that the ten prisms & antiprisms embody three structural parameters (168, 336 & 840) of the basic unit of matter paranormally described over a century ago by Annie Besant & C.W. Leadbeater. Far from being coincidental, it points towards the Klein quartic and its connection to the octonions playing a leading role in the still-sought unification of superstrings and supergravity by M-theory.
Let us now consider the prisms and antiprisms joined together at their square faces to form the {3,7} tessellation of the 3-torus. Table 19 lists their geometrical and yod composition.
Table 19. Geometrical/yod composition of the 3-torus constructed from tetractyses & Type A triangles.
Tetractys
Type A triangle
Triangular
Prism
Square
Antiprism
Total
Triangular
Prism
Square
Antiprism
Total
Number of vertices
4×6 = 24
–
24
24 + 4×2 = 32
48×1 = 48
80
Number of edges
4×9 = 36
6×8 = 48
84
36 + 8×3 = 60
48 + 48×3 = 192
252
Number of triangles
4×2 = 8
6×8 = 48
56
8×3 = 24
48×3 = 144
168
Number of geometrical elements
68
96
164
116
384
500
Number of hexagonal yods on sides of tetractyses
2×36 = 72
2×48 = 96
168
2×60 = 120
2×192 = 384
504
Number of hexagonal yods
8 + 72 = 80
48 + 96 = 144
224
24 + 120 = 144
144 + 384 = 528
672
Number of yods on sides of
tetractyses24 + 72 = 96
96
192
32 + 120 = 152
48 + 384 = 432
584
Number of yods
8 + 96 = 104
48 + 96 = 144
248
24 + 152 = 176
144 + 432 = 576
752
Comments
1. When each face is a tetractys, the 56 tetractyses contain 248 yods. Given the connection to UPAs as superstrings indicated by the presence of three of their structural parameters, it is very remarkable that the dimension 248 of the very Lie group E8 that describes the unified force of one of the two types of heterotic superstrings should manifest as the number of yods needed to construct the prisms and antiprisms from tetractyses. Once again, it is highly implausible to be due to chance. Rather, the presence of the holistic parameter 248 is yet again an indication of the sacred geometrical nature of the {3,7} tessellation of the 3-torus whose 56 triangles represent the 168 automorphisms of the Klein quartic. But it is more than this, for, if each yod corresponds to one of the roots of E8, then we should expect to see the geometry of the prisms and antiprisms dividing this group up into certain subgroups. Indeed, we do. The 248 yods comprise eight yods at the centres of the faces of the four triangular prisms, leaving 240 yods that are made up of their 24 vertices, 48 hexagonal yods at the centres of the faces of the six
41
antiprisms, i.e., 72 yods, and 168 hexagonal yods on the 84 sides of the 56 tetractyses. The division:
248 = 8 + 240
corresponds to the eight simple roots of E8 and its 240 roots. The division:
240 = 72 + 168
corresponds to the 72 roots of E6, an exceptional subgroup of E8, and to the 168 remaining roots of E8. We see that the tetractys construction of the tessellated 3-torus reveals some of the root structure of E8 (this will not be explored further here).
The division:
168 = 2×84
that was shown in previous sections to appear in sacred geometries manifests trivially in the pair of hexagonal yods lying on each of the 84 sides of the tetractyses in the six square antiprisms. It denotes the 84 sextactic points where the 168 sheets of the Riemann surface of the Klein quartic join in 84 pairs. It corresponds in the 64 hexagrams as the 84 solid lines (yang) and the 84 broken lines (yin) that make up the 56 trigrams in the upper or lower set of 28 off-diagonal hexagrams. The division:
336 = 2×168
that previous sections showed resulted from the mirror symmetry of the sacred geometry (or near mirror symmetry, in the case of the Sri Yantra) expresses the fact that the number of antiautomorphisms of the Klein quartic is equal to the number of its automorphisms. The former can be represented by a version of the 3-torus which is turned inside out, reversing the orientations of all triangles (Fig. 66). Their counterparts in the inner Tree of Life are the 168 geometrical
Figure 66. The 496 yods in the (56+56) tetractyses tiling the 3‑torus and its turned-out version symbolise the 496 roots of E8×E8.
elements outside the root edge that are intrinsic to one set of seven enfolded polygons and their 168 chiral counterparts in the other set of seven enfolded polygons. The pair of 3-tori contains 336 hexagonal yods on sides of the two sets of 56 Type A triangles, there being (248+248=496) yods altogether. The number 496 is the crucial dimension of any gauge symmetry group that describes superstring forces free of quantum anomalies [12]. The conjunction of
Figure 67. Correspondence between the 1st (6+6) enfolded polygons of the inner Tree of Life and the {3,7} tessellation of the 3-torus & its version turned inside out.structural parameters of a particle claimed to have been remote-viewed over a century ago and this theoretical requirement for a certain type of superstring is undeniable. These numbers have not been concocted by cherry-picking. Instead, they quantify natural, mathematical features of the tessellated 3-torus. It is evidence that UPAs are E8×E8 heterotic superstrings.
2. The number of yods on the 84 sides of the 56 tetractyses is the sum of the 24 vertices of the four triangular prisms and the 168 (=84×2) hexagonal yods on these sides:
42
24 + 168 = 192.
This is a characteristic division of holistic systems. For example, Figure 67 shows that, associated with each set of the first six enfolded polygons of the inner Tree of Life, are 24 corners and 168 other yods. The pair of chiral 3-tori exhibit the complete division displayed by holistic systems:
384 = 192 + 192 = 48 + 336,
where
48 = 24 + 24
is the number of vertices of their eight triangular prisms and
336 = 168 + 168.
is the number of hexagonal yods on the sides of their 112 tetractyses. The number 48 is the number value of Kokab, the Mundane Chakra of Hod, and 112 is the number value of Beni Elohim, the Order of Angels assigned to this Sephirah. Figure 31 in Article 43 compares how the holistic parameter 384 is embodied in various sacred geometries, including the {3,7} tessellation of the 3-torus.
3. The 10 prisms & antiprisms constructed from Type A triangles form a 3-torus with 500 (=50×10) geometrical elements. This shows how ELOHIM, the Godname of Binah with number value 50, prescribes the form-determining geometrical composition of the 3-torus constructed from Type A triangles. It is a clear demonstration of the archetypal power of Godnames in their prescription of holistic systems. It is the counterpart of the 500 geometrical elements needed, starting from their 50 vertices, to shape the faces of the five Platonic solids (see comment 4, p. 33).
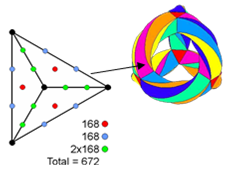
Figure 68. The 672 hexagonal yods in the 168 tetractyses of the 56 Type A triangles of the 3-torus comprise two sets of 336 yods (336 red or blue yods; 336 green yods). 4. The 168 triangles making up the 3-torus when the triangular faces of the prisms &antiprisms are Type A consist of the 24 triangles in the former and the 144 triangles in the latter. This is another example of the pattern displayed by holistic systems that was discussed on p. 39. The 56 sets of three triangles and their counterparts in the 3-torus turned inside out are the geometrical analogue of the 56 trigrams in the 28 off-diagonal hexagrams that make up the upper and lower diagonal halves of the 8×8 square array of hexagrams.
5. The 168 tetractyses in the 3-torus tessellated with 56 Type A triangles contain 168 hexagonal yods on the 84 edges of the prisms & antiprisms, 168 hexagonal yods at the centres of these tetractyses and 168 pairs of hexagonal yods on sides inside the Type A triangles (Fig. 68). The 672 hexagonal yods comprise two sets of 336 yods. This division conforms to the patterns of sacred geometry. For example, the first four Platonic solids contain 672 yods (336 yods in each half) when they are constructed from tetractyses [22], whilst each set of seven separate Type B polygons in the inner form of the Tree of Life has 336 corners & sides surrounding their centres [23]. The 3-torus and its version turned inside out have (672+672=1344) hexagonal yods. This is the number of yods surrounding the centres of the 14 enfolded Type B polygons of the inner Tree of Life that are unshared with the outer Tree of Life [24]. This demonstrates that the 3-torus with Type A triangles is the counterpart of one half of the inner Tree of Life and that its turned inside-out version is the counterpart of its other half. The turning inside out of the 3-torus, which reverses the orientation of all triangles, is analogous to the reflection of all geometrical elements/yods in the seven enfolded polygons across the root edge that joins them to their chiral images.
For further analysis of the remarkable correspondences between the 3-torus and sacred geometries, see reference 19.
10. The seven diatonic musical scales
Two divisions characteristic of holistic systems:336 = 168 + 168
and
168 = 84 + 84
are embodied not only in sacred geometries but also in the seven ancient, diatonic musical scales that
43
were known to the ancient Greeks as “harmoniae” and which entered the plainsong of the Roman Catholic Church. That these patterns exist in music will be demonstrated in this section in two ways.
The Pythagorean musical scale consists of five tone intervals of 9/8 (T) and two leimmas of 256/243 (L):
By starting with successive notes to generate scales of eight notes and then normalising the tone ratios so that the tonic in each scale has a tone ratio of 1, the pattern of intervals is repeated at the eighth sequence, thereby generating seven distinct, octave species:
8. T L T T T L T Hypomixolydian (Mode 8, D' scale) 7. T T L T T T L Hypolydian (Mode 6, C scale) 6. L T T L T T T Hypophrygian (Mode 4, B scale) 5. T L T T L T T Hypodorian (Mode 2, A scale) 4. T T L T T L T Mixolydian (Mode 7, G scale) 3. T T T L T T L Lydian (Mode 5, F scale) 2. L T T T L T T Phrygian (Mode 3, E scale) 1. T L T T T L T Dorian (Mode 1, D scale) These are the musical modes used for hundreds of years in the plainsong of the Roman Catholic Church. Mode 8 (Hypomixolydian) is the D scale with different ‘dominant’ and ‘finalis’ notes. Table 20 displays the values of the tone ratios of their notes with Pythagorean tuning.
Table 20. Tone ratios of the seven diatonic scales.
Musical scale
Tone ratio
B scale
1
256/243
32/27
4/3
1024/729
128/81
16/9
2
A scale
1
9/8
32/27
4/3
3/2
128/81
16/9
2
G scale
1
9/8
81/64
4/3
3/2
27/16
16/9
2
F scale
1
9/8
81/64
729/512
3/2
27/16
243/128
2
E scale
1
256/243
32/27
4/3
3/2
128/81
16//9
2
D scale
1
9/8
32/27
4/3
3/2
27/16
16/9
2
C scale
1
9/8
81/64
4/3
3/2
27/16
243/128
2
Tone ratios of notes belonging to the Pythagorean scale are written in black and non-Pythagorean tone ratios are written in red. The 42 notes between the tonic and the octave comprise 26 notes with Pythagorean tone ratios belonging to the Hypolydian mode (C scale) and 16 with non-Pythagorean values. Table 1 indicates that 26 is the gematria number value of YAHWEH, the Godname of Chokmah. As 42 is the 21st even integer, EHYEH, the Godname of Kether with number value 21, prescribes the seven musical scales. We shall see shortly that it does so in a more direct way.
The seven diatonic scales comprise 14 different notes. In order of increasing tone ratios, they are:
1 256/243 9/8 32/27 81/64 4/3 1024/729 │ 729/512 3/2 128/81 27/16 16/9 243/128 2
There are six Pythagorean notes and six notes that belong to the six other diatonic scales. Let us define the inversion of a note with tone ratio n as a note with tone ratio m, where nm = 2. The inversion of a note has a tone ratio that is equal to the interval between that and the octave. It does not necessarily belong to the same scale as the note. But, if not, it will be a note of another diatonic scale, as can be seen from a comparison of Table 20 with the 14 notes arranged as seven pairs of notes and their inversions:
1. 1
2
1×2
= 2
2. 256/243
243/128
256/243×243/128
= 2
3. 9/8
16/9
9/8×16/9
= 2
4. 32/27
27/16
32/27×27/16
= 2
5. 81/64
128/81
81/64×128/81
= 2
6. 4/3
3/2
4/3×3/2
= 2
7. 1024/729
729/512
1024/729×729/512
= 2
The rising interval between two notes with tone ratios n and m (m>n) is the ratio m/n. The falling interval is n/m. Just as eight objects can be paired in 28 ways, so there are 28 rising intervals between the eight notes forming one octave of a diatonic scale. One of these is the octave itself, so that in each diatonic scale, there are 27 intervals below this last note. They comprise six notes above the starting note, or tonic, and 21 intervals, including 15 intervals between these six notes. The Godnames EHYEH with number value 21 and YAH, the shorter Godname of Chokmah with number value 15, prescribe these intervals.
44
Figure 69. The intervals between the notes in the seven diatonic scales/Church modes.
45
There are (7×27=189) intervals below the octave between the notes on the seven diatonic scales. They comprise 21 notes up to the note with tone ratio 1024/729 and 168 more intervals made up of the remaining 21 notes that are the inversions of the first set of 21 notes and 147 intervals. Figure 69 displays their values. They are all instances of the basic set of 13 types of notes above the tonic that make up the seven diatonic scales. All cases where these intervals first appear are given dark blue cells. Cells enclosing Pythagorean repetitions of the basic set are coloured dark red, whilst yellow cells refer to repetitions of non-Pythagorean intervals. The corresponding cells for falling intervals are coloured light blue, light red and light yellow. Counting the numbers of Pythagorean repetitions in each Church mode (i.e., dark red cells), we find that the 168 intervals, including inversions with tone ratios larger than 1024/729, contain 84 repetitions that have the intervals of notes belonging to the Pythagorean scale (Hypolydian mode). These are actually among the 147 non-note intervals because they are repetitions of notes. In terms of Pythagorean notes, five different intervals make up the composition of the 84 Pythagorean intervals:
D E F G A 28 11 23 17 5
The interval 243/128 for note B is absent because it is the only note amongst the first seven notes that never appears more than once in a church mode (Phrygian, Lydian, Hypophrygian & Hypolydian) and so it has no repetitions.
We discover that the divisions:
336 = 168 + 168
168 = 84 + 84
found in previous sections to be characteristic of holistic systems manifest in the seven diatonic scales as:
1. the 168 rising intervals (and their 168 falling counterparts) other than the ‘core’ set of 21 notes up to that with tone ratio 1024/729;
2. the 84 repetitions (red cells) of the six Pythagorean notes among the basic set of 12 notes and the 84 intervals that are either members of this set (blue cells) or repetitions of their non-Pythagorean members (yellow cells).
Figure 70. 36 yods line the sides of the 2nd-order tetractys, leaving 48 yods that surround its centre.
Figure 71. The patterns of division amongst the 384 rising and falling intervals between the notes of the 7 diatonic scales.Notice that the four Authentic Modes (Dorian, Phrygian, Lydian & Mixolydian) have 48 repetitions among the 84 that are Pythagorean, whilst the three Plagal Modes (Hypolydian, Hypophrygian & Hypodorian) have 36 such repetitions. This 36:48 division of the holistic parameter 84 corresponds in the 2nd-order tetractys (Fig. 70) to the 36 red yods that line its boundary and to the 48 blue yods inside it that surround its central, black yod. In the case of the 3-torus, it corresponds to the 36 edges of the four triangular prisms and to the 48 unshared edges of the six square antiprisms (see Fig. 60).
These holistic divisions are a part of the more-inclusive division found in sacred geometries:
46
384 = 192 + 192,
where
192 = 24 + 168
and
24 = 3 + 21,
so that
192 = 3 + 189 = 3 + 21 + 168.
The three extra intervals are the tonic (1), the octave (2) as a note and the interval of 2 between corresponding notes in successive octaves. The 168 falling intervals are the counterparts of:
1. the 168 anti-automorphisms of the Klein quartic mapped by the {3,7} tessellation onto the inside-out version of the 3-torus;
2. the 168 solid lines & broken lines of the 28 off-diagonal hexagrams in the lower diagonal half of the 8×8 array;
3. the 168 intrinsic geometrical elements making up the reflected half of the inner Tree of Life;
4. the 168 yods other than corners associated with the second dodecagon that is the mirror image of the first one;
5. the 168 yods lining the 21 triangles in the second half of the 3-dimensional Sri Yantra.
We will now consider the second way in which the number 168 appears in the intervallic composition of the seven diatonic scales. Each of the seven scales has 27 intervals below the octave. The (7×27=189) intervals include the 42 notes between the tonic and octave. Inspection of Fig. 71 shows that there are 21 notes that pair with their 21 inversions. The Godname EHYEH with number value 21 prescribes each set because its letter values denote subsets of notes and their inversions:
AHIH = 21
A = 1 → 1×(1024/729)
→
1×(729/512)
H = 5 → 5×(9/8)
→
5×(16/9)
I = 10 → 4×(32/27) + 6×(4/3)
→
4×(27/16) + 6×(3/2)
H = 5 → 2×(256/243) + 3×(81/64)
→
2×(243/128) + 3×(128/81)
Just as a note is at least mathematically paired with its inversion (even though it may not appear in the same diatonic scale), so any interval can be paired with its inversion. However, unlike notes, there is not the same number of intervals and their inversions. Figure 72 below:

Figure 72. The 168 notes & intervals in the 7 diatonic scales other than the 21 notes of the first 6 types consist of 42 pairs of intervals and their inversions and (21+62+1=84) inversions or unpaired intervals.
lists the numbers of notes, intervals and their inversions that can be paired, as well as the numbers of unpaired intervals and their inversions (black tone ratios are those of the Pythagorean scale, red tone ratios are those of notes in the other diatonic scales). There are 125 intervals of the first six kinds (21 notes) but they have only 64 inversions (21 notes). As the inversion 729/512 appears once more often than the interval 1024/729, whilst each of all the other types of inversions appears less often than their counterparts, there are 63 notes & intervals47
that can be paired with their inversions, leaving (125–63+1=63) other intervals that cannot be paired (see the last "Total" row in Fig. 72). Hence, the 189 intervals below the octave split naturally into three sets of 63: 1. 63 notes & intervals; 2. their 63 inversions, and 3. 63 intervals without their accompanying inversions. Notice that they consist of 21 notes of the first six types and 168 inversions & intervals (see the bottom of the table). As discussed earlier, the 21:168 split shown by the number 189 is characteristic of sacred geometries and non-geometrical holistic systems, such as the seven musical scales. As confirmation that chance is not involved here, notice that the 168 inversions & intervals consist of 42 pairs of intervals & their inversions, i.e., 84 intervals, and 84 inversions & unpaired intervals that comprise the 21 inversions paired with the 21 notes of the first six types, 62 unpaired intervals of the first six types & one unpaired inversion. This is another way in which the holistic division:
168 = 84 + 84
manifests in the seven diatonic scales. The two sets of 84 intervals are the musical counterpart of the two sets of polygons in the inner Tree of Life, each with 84 geometrical elements surrounding their centres.
11. Conclusion
Table 21 summarises the primary analogous divisions of the holistic parameters 336 and 168 in nine holistic systems:Table 21. Comparison of two divisions in various holistic systems.
Sacred geometry or holistic system
336 = 168 + 168
168 = 84 + 84
Inner Tree of Life
The set of 7 enfolded polygons in each half of the inner Tree of Life has 168 intrinsic, geometrical elements outside the root edge.
84 intrinsic geometrical elements in the triangle, square, pentagon & dodecagon; 84 elements in the hexagon, octagon & decagon.
1st (6+6) enfolded polygons
168 yods other than corners of polygons in each set of 6 enfolded polygons.
84 yods line each set of 6 enfolded polygons outside the root edge.
Dodecagon
168 yods other than corners associated with each joined, Type B dodecagon.
84 hexagonal yods at the centres of 36 tetractyses or on the 24 sides of the 12 sectors; 84 hexagonal yods or corners on 36 internal sides of tetractyses.
Sri Yantra
168 yods line the 21 triangles/tetractyses in each half of the 3-d Sri Yantra.
84 pairs of yods line the 21 triangles/tetractyses in each half.
64 hexagrams
168 solid lines & broken lines in the 28 off-diagonal hexagrams in each half of the 8×8 array of 64 hexagrams.
28 off-diagonal hexagrams comprise 84 solid lines & 84 broken lines.
5 Platonic solids
168 yods on average in each half of a Platonic solid surround the centres of faces & internal triangles.
These 168 yods comprise: 84 yods in the tetrahedron and on sides of tetractyses in the octahedron, cube & icosahedron; 84 yods either at centres of tetractyses in these solids or lining sides of tetractyses in the dodecahedron.
Disdyakis triacontahedron
168 hexagonal yods on edges above/below the central 12-gon perpendicular to an axis passing through two opposite A vertices.
1680 (=168×10) yods above/below the central 12‑gon for Type A triangles.
These 168 hexagonal yods comprise 84 pairs of hexagonal yods.
840 (=84×10) yods inside 84 internal Type A triangles and 840 yods either lining their sides or in faces in the upper/lower half of the polyhedron.
3-torus with {3,7} tiling
168 automorphisms & 168 anti-automorphisms of the Klein quartic form the group SL(2,7) with order 336.
168 hexagonal yods on sides of the 56 tetractyses in the 4 prisms & 6 antiprisms of the 3‑torus; 168 hexagonal yods on sides of the 56 tetractyses in the 3-torus turned inside-out.
84 sextactic points on the Riemann surface of the Klein quartic where 168 sheets join in pairs.
84 pairs of hexagonal yods on 84 sides of the 56 tetractyses in the {3,7} tessellation of the 3-torus.
7 diatonic musical scales
168 rising intervals & 168 falling intervals other than the 21 notes of the first 6 types belonging to the basic set of 12 notes.
1. These 168 intervals comprise 84 repetitions of Pythagorean notes & 84 intervals that either belong to the basic set of 12 notes or are repetitions of non-Pythagorean notes.
2. 168 intervals comprise 42 pairs of intervals & their inversions and 84 inversions or unpaired intervals.
48
The holistic parameters 336, 168 & 84 manifest in the UPA described by Annie Besant & C.W. Leadbeater because what they remote-viewed were E8×E8 heterotic superstrings whose 3-dimensional structure conforms to the very same universal pattern that this article has shown is embodied in sacred geometries and the seven diatonic scales.
References
1. Article 62; see also Polychorons & Gosset polytope, Page 2.2. Article 42. “Comparison of the eight Church musical modes and the human skeleton as holistic systems.”
3. Proof: the seven enfolded polygons with their 47 sectors turned into tetractyses have 264 yods. The dodecagon constructed from tetractyses has 73 yods, that is, 69 yods outside the four yods in the root edge. The number of yods in the first six enfolded polygons = 264 – 69 = 195 (i.e., 191 outside the root edge). The number of yods in H = 4 + 2×191 = 386.
4. Article 18: “Encoding of planetary distances and superstring structural parameters in the I Ching table.”
5. Article 1: “The Pythagorean nature of superstring and bosonic string theories,” p. 5.
6. Article 14: "Why the ancient Greek musical modes are sacred.”
7. Article 39: ”The correspondence between the inner Tree of Life, the Sri Yantra & the I Ching diagram and their realization in the seven musical scales.”
8. Article 3: “The sacred geometry of the Platonic solids.”
9. Article 11: “Plato’s Lambda — its meaning, generalisation and connection to the Tree of Life.”
10. Disdyakis triacontahedron, Page 14.
11. The holistic pattern.
12. https://en.wikipedia.org/wiki/Anomaly_%28physics%29.
13. https://en.wikipedia.org/wiki/Klein_quartic; and:
http://gregegan.customer.netspace.net.au/SCIENCE/KleinQuartic/KleinQuarticEq.html
14. Hurwitz, A. “Über algebraische Gebilde mit eindeutigen Transformationen in sich,” Math. Ann. 41 (1893), 403-442.
15. Murray Macbeath, A. “On a theorem of Hurwitz.” Proc. Glasgow Math. Assoc. 5 (1961). 90-96.
16. Murray Macbeath, A. “Hurwitz groups and surfaces.” The Eightfold Way. MSRI Publications, vol. 35, 1998, 11.
17. The Schläfli symbol {n,k} denotes the tessellation of a surface by polygons with n vertices, k polygons meeting at each vertex.
18. Article 15: “The mathematical connection between superstrings and their micro-psi description: a pointer towards M-theory.”
19. Article 43: “The Tree of Life nature of the {3,7} tessellation of the 168 automorphisms of the Klein quartic on the 3-torus.”
20. Proof: the number of yods in a Type B n-gon = 15n + 1. Given the (n+1) corners of its n sectors, 14n more yods are needed to create a Type B n-gon. Transformation of the 24 sectors of the four polygons in S1 or the three polygons in S2 requires (24×14=336) more yods. A Type B n-gon has 7n corners & sides surrounding its centre. Surrounding the centres of the seven separate Type B polygons are (7×48=336) corners & sides.
21. Ref. 12.
22. Polychorons & Gosset polytope Page 15.
23. Polychorons & Gosset polytope Page 10.
24 Polychorons & Gosset polytope Page 12.
Addendum
The two halves of the seven enfolded, regular polygons that constitute half of the inner Tree of Life were identified in Section 2 as the set S1, whose members are the triangle, the square, the pentagon & the dodecagon, and the set S2, whose members are the hexagon (with one sector missing because it is occupied by the triangle), the octagon and the decagon. S1 and S2 have 36 corners, where
36 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8.
This number is determined by the Tetrad (4) in two ways. Firstly, 36 = 62, where 6 is the fourth polygonal number of order 1. Secondly, 36 is the sum of the first four odd integers and the first four even integers:
36 = (1+3+5+7) + (2+4+6+8) = 16 + 20.
16 (= 42) is the number of yods in a 4×4 square array of yods, whilst a tetrahedron — the regular polyhedron with four vertices — has 20 yods in its faces when they are tetractyses. S1 has 16 corners outside the root
49
edge and S2 has 20 corners (Fig. 73). The odd and even integers making up the number 36 therefore divides the seven enfolded polygons, respectively, into the two halves S1 and S2. Picturing the eight corners of an octagon as those of two squares rotated through 45°, we see that one square (red) with the first four odd integers assigned to its four corners corresponds to S1 with 16 corners, whilst the second square (blue) with the first four even integers assigned to its corners corresponds to S2 with 20 corners.
Figure 73. The odd/even division of the first 8 integers divides the 7 enfolded polygons (S) of the inner Tree of Life into its two halves S1 (red) & S2 (blue). The ordering of these integers into the Pythagorean subset (1, 2, 3 & 4) and the subset (5, 6, 7 & 8) divides S into the dodecagon and the first 6 enfolded polygons, both of which are holistic systems.
If, instead, the first four integers 1, 2, 3 & 4 symbolising the four rows of dots in the Pythagorean tetractys are assigned to the corners of one square and the remaining integers 5-8 are assigned to the corners of the second square, this generates the division:
36 = 10 + 26,
where
10 = 1 + 2 + 3 + 4
and
26 = 5 + 6 + 7 + 8
correspond, respectively, to the 10 corners of the dodecagon outside the root edge and to the 26 corners of the first six enfolded polygons. This ordering of integers divides the seven polygons into two parts, both of which are holistic in character (see Sections 3 & 4).
These two orderings of the integers 1-8 illustrate the beautiful, natural harmony between number and sacred geometry.
50
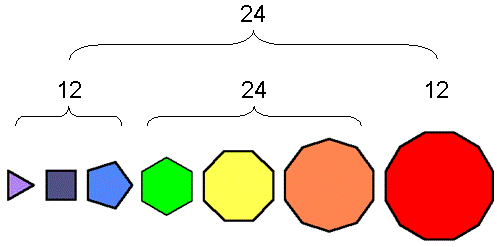
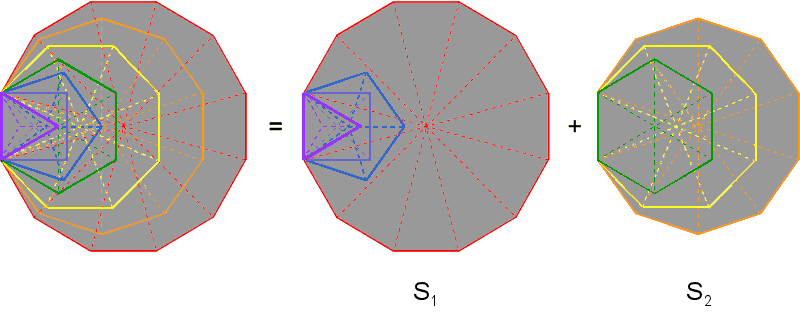
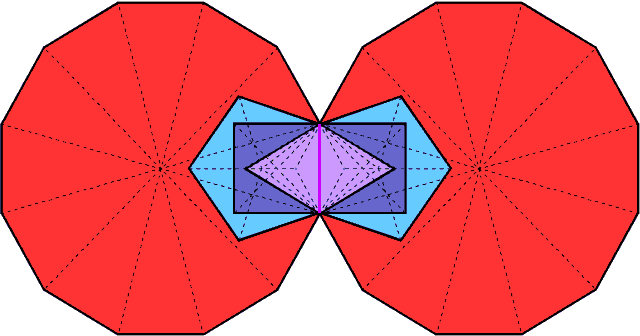

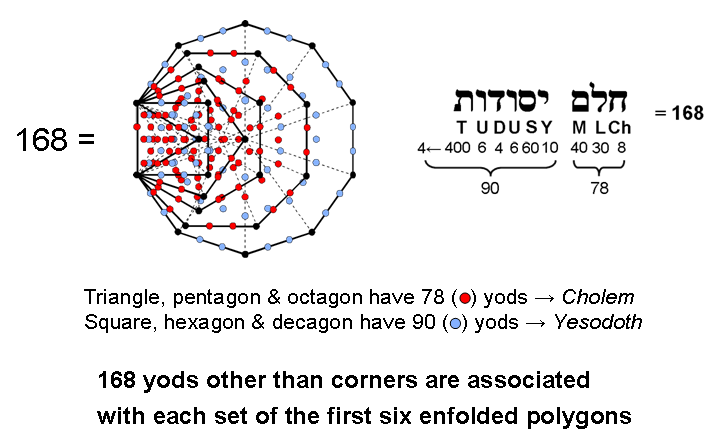
.png)