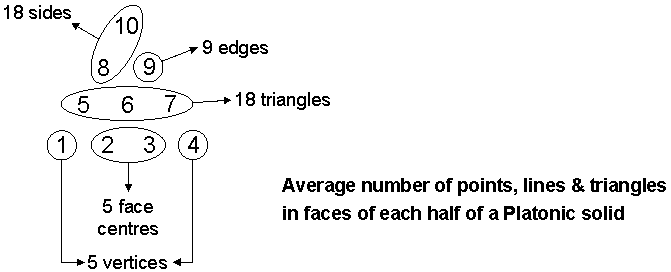
| << Previous 1... 17 18 [19] 20 21 ...56 Next >> |
#19 Embodiment of the 496 roots of E8×E8 in the five Platonic solids
In the discussion in #22 of Wonders of Sacred geometry/Wonders of correspondences, it was found that 1230 geometrical elements surround the centres of the five Platonic solids with Type A interior triangles formed by joining their centres to their vertices and then dividing each triangle into its three sectors. Internal triangles can also be created by joining the centres of Platonic solids to the centres of their faces so that sides of sectors become sides of internal triangles as well. For a regular polyhedron with m n-gons as its faces, this adds mn internal triangles with mn new corners and (3mn+m) new sides of 3mn triangles. ∑mn = 180 and ∑m = 50, where '∑' signifies summation over all Platonic solids.
Tabulated below are the geometrical compositions of the faces, interiors and new interiors created by joining the centres of the regular polyhedra to the centres of their faces ("+ 5" denotes the centres of the five Platonic solids):
|
Corners |
Sides |
Triangles |
Total |
|
| Faces: | 50 + 50 = 100 |
90 + 180 = 270 |
180 |
550 |
| Interiors: | 90 + 5 | 50 + 3×90 = 320 | 3×90 = 270 | 680 + 5 |
| Subtotal = | 190 + 5 | 590 | 450 | 1230 + 5 |
| Addition to interiors: | 180 | 3×180 + 50 = 590 | 3×180 = 540 | 1310 |
| New interiors: | 270 + 5 | 910 | 810 | 1990 + 5 |
| Total = | 370 + 5 | 1180 | 990 | 2540 + 5 |
The table indicates that the faces of the five Platonic solids have 550 geometrical elements. On average, there are 55 elements in half a Platonic solid, where
| 10 | ||||
| 8 | 9 | |||
| 55 = | 5 | 6 | 7 | |
| 1 | 2 | 3 | 4 . |
They comprise five vertices, five centres of faces, nine edges, 18 sides of sectors & 18 triangular sectors. These numbers are generated by various combinations of the integers making up the tetractys of the first 10 integers:
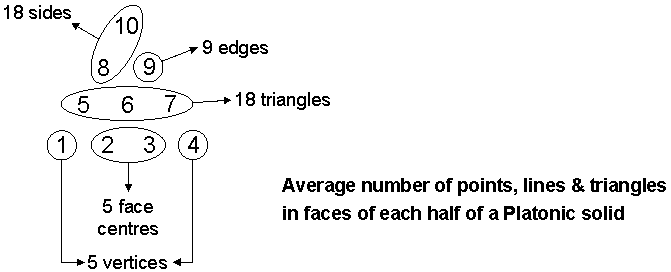
According to the table, 2540 corners, sides & triangles surround the centres of the five Platonic solids. 1270 (=127×10) geometrical elements are in each half of them. 127 is the 31st prime number, showing how EL, the Godname of Chesed with number value 31, prescribes the complete, geometrical composition of the five regular polyhedra constructed from triangles. They now have 990 triangles with 370 corners surrounding their centres. The axis of each Platonic solid passes through its centre and two vertices, so that (370 – 5×2 = 360 = 36×10) corners surround the axes. This is how ELOHA, the Godname of Geburah with number value 36, prescribes their geometrical composition. There are [370+1180=1550 (=155×10)] corners & sides surrounding their centres, showing how ADONAI MELEKH, the complete Godname of Malkuth with number value 155, prescribes the five Platonic solids. There are (910+810=2170) sides & triangles, of which (2170 – 5×2 = 2160 = 216×10) sides & triangles surround the five axes, where 216 is the number of Geburah. The number of corners & triangles surrounding the five centres = 370 + 990 = 1360, of which (1360 – 50 = 1310 = 131×10) triangles & corners other than vertices surround the axes, where 131, the number value of Samael, the Archangel of Geburah, is the 65th odd integer after 1, showing how ADONAI with number value 65 prescribes the five Platonic solids. The 450 triangles in their faces and in their interiors with edges as some of their sides have 190 corners surrounding their centres, i.e., 95 corners in each set of five halves. 95 is the number value of Madim, the Mundane Chakra of Geburah.
The number of geometrical elements surrounding the five axes other than polyhedral vertices = 2540 – 50 – 5×2 = 2480 = 248×10. This is the number of yods in the 49-tree that maps the cosmic physical plane (see here). According to superstring theory, the unbroken E8 symmetry of superstring forces is mediated by 248 spin-1 messenger particles in 10-dimensional space-time. Each particle is described by a gauge field with 10 space-time components, so that the 248 fields that transmit their forces have 2480 such components. This number manifests in the five Platonic solids as the number of extra geometrical elements that are needed to construct them from triangles, i.e., elements other than those defining their axes and the 50 points in 3-dimensional space where their vertices are located.
The average number of geometrical elements other than vertices surrounding an axis = 2480/5 = 496. This is the number value of Malkuth, the last Sephirah of the Tree of Life, denoting the outer, physical form of whatever conforms to this universal blueprint. On average, each half of a Platonic solid has 248 geometrical elements other than vertices surrounding its axis. This is truly amazing and beautiful, for the counterparts of this property in E8×E8 heterotic superstring theory are the 248 roots of each Lie group E8. The average geometrical composition of the five Platonic solids is analogous to the root composition of one of the two symmetry groups describing superstring forces, the two halves of each one corresponding to the two similar groups! The 2480 geometrical elements comprise:
The 248 geometrical elements surrounding an axis in an average half-Platonic solid consist of 32 corners (five in faces, 27 internal), 117 sides (27 in faces, 90 internal) and 99 triangles (18 in faces, 81 internal). In other words, the faces in each half of a Platonic solid on average have (5+27+18= 50) geometrical elements other than vertices, whilst their interiors on average have (27+90+81=198) geometrical elements surrounding their axes. This shows how ELOHIM, the Godname of Binah with number value 50, determines the average outer form of the Platonic solids, as well as the 50 vertices & 50 faces of all five solids. It also determines their 50 faces because they are composed of 500 (=50×10) geometrical elements other than their 50 vertices. As they have 90 edges and 50 face-centres, their faces are composed of (500−50−90=360=36×10) triangles and sides other than edges and vertices, where 36 is the number value of ELOHA, the Godname of Geburah, which is the Sephirah below Binah on the Pillar of Judgement of the Tree of Life. The number of corners of the 990 triangles in the five Platonic solids other than their 50 vertices = 375 – 50 = 325. On average, therefore, a Platonic solid is composed of 198 triangles with 65 corners in addition to its 10 vertices, showing how ADONAI, the Godname of Malkuth with number value 65, determines the average number of extra points in space that create their forms from triangles.
The composition of the 248 geometrical elements other than vertices in the five half-Platonic solids that surround their axes is tabulated below:
|
Corners |
Sides |
Triangles |
Total |
|
| Faces | 5 | 27 | 18 | 50 |
| Interior | 27 | 90 | 81 | 198 |
| Total | 32 | 117 | 99 | 248 |
The half-axis associated with a half-Platonic solid consists of the centre of the solid, one side of internal triangles and a vertex. On average, the number of geometrical elements in a half-Platonic solid = 248 + 3 = 251. This is both the number of yods in the 1-tree (see here) and the sum of the four yods in the root edge and the 247 yods on the 96 sides of the 48 tetractyses making up the seven separate polygons of the inner Tree of Life (see #6). This analogous pattern demonstrates the Tree of Life basis of the five Platonic solids. On average, there are 496 geometrical elements other than the eight vertices surrounding the axis of the full Platonic solid, i.e., 504 geometrical elements in total surround it.
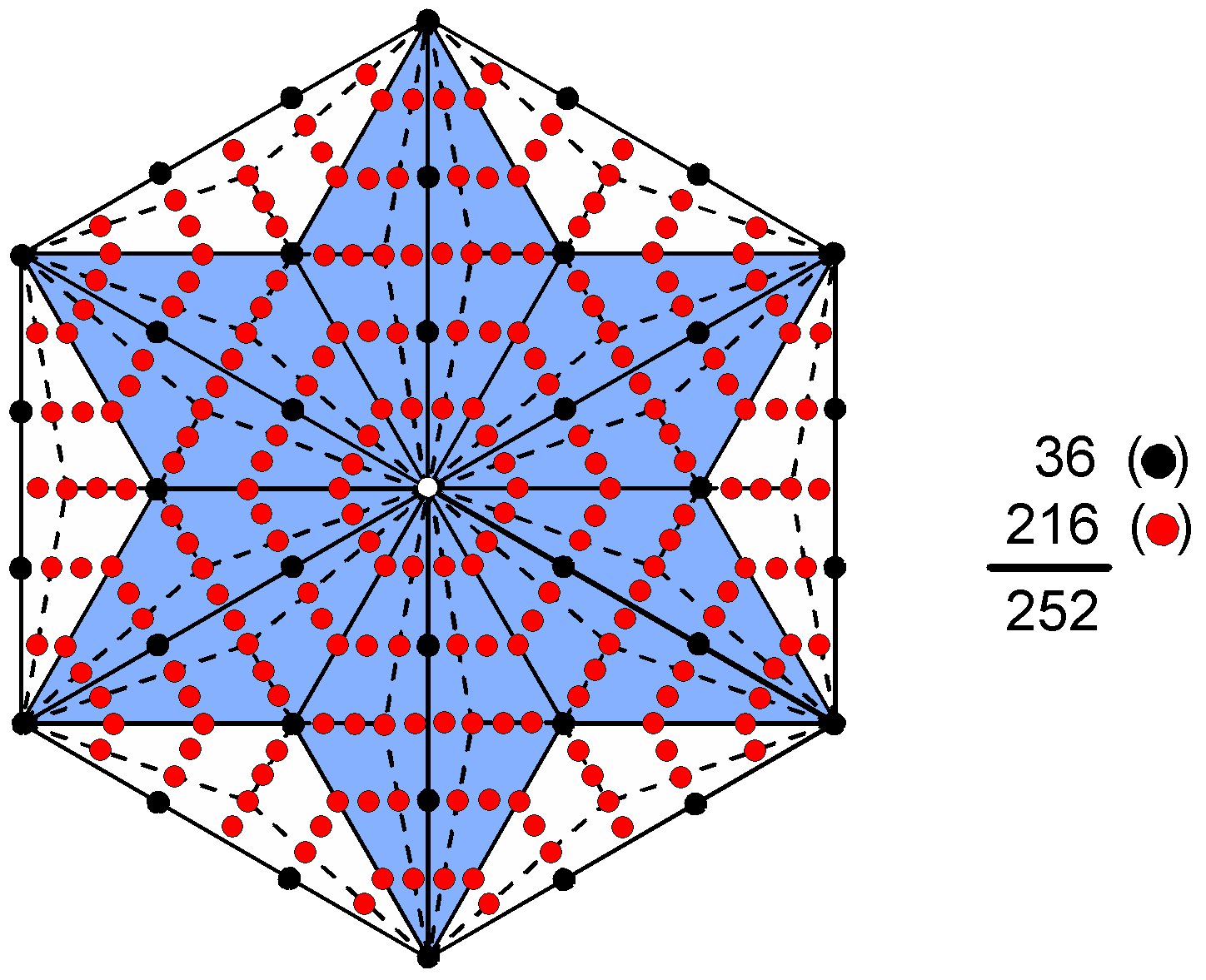 Including vertices, 2520 corners, sides & triangles surround the axes of the five Platonic
solids. On average, 252 geometrical elements in each half of a solid surround the axes. They comprise
36 corners, 117 sides and 99 triangles, i.e., 153 corners &
sides and 216 sides & triangles. ELOHIM SABAOTH, the Godname of Hod with number
value 153, prescribes each average half of a Platonic solid. 252 yods surround the centre of
a Type C hexagon. They comprise 36 black yods of the Type A hexagon and
216 red yods added by converting it to a Type C hexagon. It provides a remarkable,
polygonal representation of the average geometrical composition of a Platonic solid, and it demonstrates the
amazing way in which geometrical information about sacred geometries is embodied in the various tetractys
constructions of the polygons. As pointed out in #16 for the embodiment in the Type C hexagon of the dimension
248 of the Lie group E8, this is the fourth member of an infinite
series of hexagons:
Including vertices, 2520 corners, sides & triangles surround the axes of the five Platonic
solids. On average, 252 geometrical elements in each half of a solid surround the axes. They comprise
36 corners, 117 sides and 99 triangles, i.e., 153 corners &
sides and 216 sides & triangles. ELOHIM SABAOTH, the Godname of Hod with number
value 153, prescribes each average half of a Platonic solid. 252 yods surround the centre of
a Type C hexagon. They comprise 36 black yods of the Type A hexagon and
216 red yods added by converting it to a Type C hexagon. It provides a remarkable,
polygonal representation of the average geometrical composition of a Platonic solid, and it demonstrates the
amazing way in which geometrical information about sacred geometries is embodied in the various tetractys
constructions of the polygons. As pointed out in #16 for the embodiment in the Type C hexagon of the dimension
248 of the Lie group E8, this is the fourth member of an infinite
series of hexagons:
hexagon → Type A → Type B → Type C .....
It is an illustration of the Tetrad Principle formulated in Article 1, whereby the fourth member of a class of mathematical object always embodies a number that characterizes holistic systems.
Including vertices, 504 geometrical elements on average surround the axes of the Platonic solids (252 elements in each half of them). This has significance from the perspective of the Cosmic Tree of Life with 550 SLs because there are 504 SLs down to the top of the 7-tree, which maps the physical plane (the space-time continuum). Moreover, there are 252 SLs down to the top of the 49-tree mapping the cosmic physical plane and 252 more SLs down to the top of the 7-tree mapping the physical plane — an analogous section of CTOL. This is remarkable, for it means that every geometrical element surrounding the axis of the purely hypothetical, "average" Platonic solid has its counterpart in an SL of the 84 Trees of Life mapping superphysical regions of CTOL. The 252 elements in one half of each Platonic solid on average surrounding their axes correspond to the 252 SLs in the 42 highest Trees that map the 42 subplanes in the six cosmic superphysical planes. The 252 elements on average in their inverted halves that surround their axes correspond to the 252 SLs in the next 42 lower Trees that map the 42 subplanes in the six planes above the physical plane. The 7-tree is represented by the axis of the average Platonic solid. The counterpart of this 252:252 division in the Sri Yantra is the set of 252 hexagonal yods on sides of tetractyses inside its 42 triangles when they are Type A triangles and the set of 252 hexagonal yods that lie on their boundaries (see here). How other sacred geometries embody the number 252 is discussed here.
| << Previous 1... 17 18 [19] 20 21 ...56 Next >> |