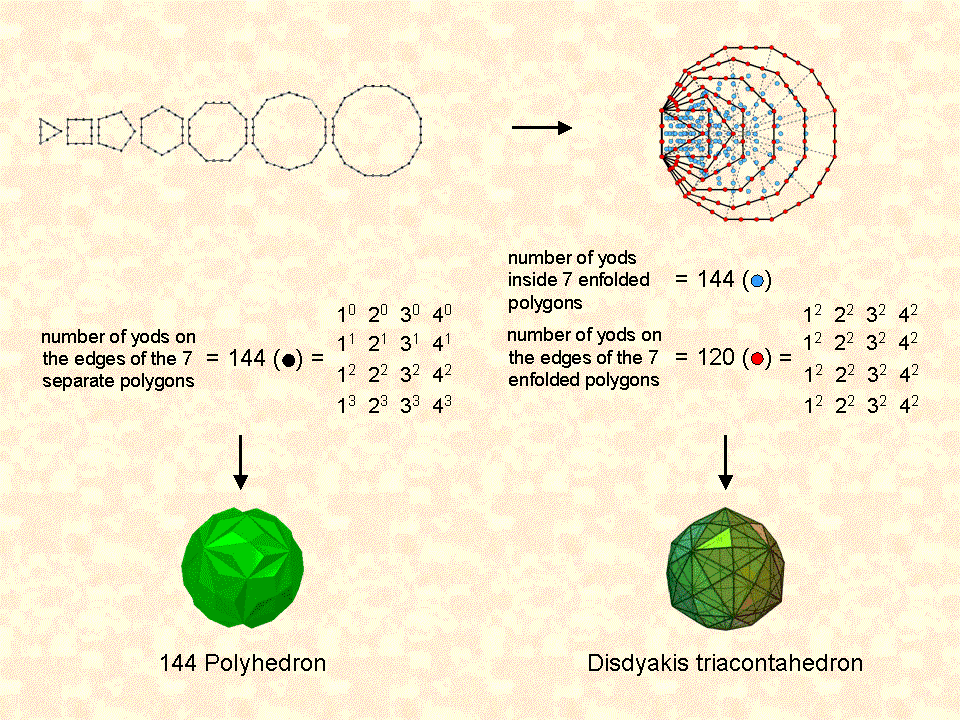
The 144 black yods that line the 48 sides of the seven separate, regular polygons making up the inner form of the Tree of Life become the 120 red yods on the 42 sides of these enfolded polygons, the 24 yods on the left-hand, vertical edges of six polygons disappearing in the enfoldment. The 151 yods that are inside the seven separate polygons become the 144 blue yods inside the enfolded polygons that do not coincide with any corners of a polygon to which they do not belong. The two numbers 120 & 144 are parameters of holistic systems (see The holistic pattern). They are expressed by 4×4 arrays of, respectively, the squares of the integers 1, 2, 3 & 4 and the first four powers of these integers. This is an example of the Tetrad Principle propounded in Article 1 (WEB, PDF) whereby numbers that quantify holistic systems are always simple functions of the integers 1, 2, 3 & 4 symbolized by the four rows of dots in the Pythagorean tetractys.

The boundary of the seven enfolded polygons is the shape, or outer form, of the inner Tree of Life. In the language of Taoism, it is its Yin aspect, whilst the interiors of the polygons are its Yang aspect. The question arises: is this exterior/interior distinction realized in a polyhedral counterpart of the polygonal, inner form of the Tree of Life? If so, how? These questions are answered in the next two pages.

For more details about the remarkable properties of the polyhedral version of the Tree of Life, see Article 23 (WEB, PDF).

<< Previous    1  [2]  3  4  5  ...15    Next >>

Home