| << Previous 1... 18 19 [20] 21 22 ...56 Next >> |
#20 How the first four Platonic solids embody the superstring structural parameter 1680
Consider a Platonic solid with V vertices, E edges & F faces that are regular n-gons. Dividing their faces into their nF sectors generates F corners, so that the Platonic solid has (V+F) corners & (E+nF) sides of nF triangles in its faces. Joining its V vertices to its centre creates V sides of E internal triangles. When the latter are Type A, there are also E corners & 3E sides of 3E sectors of these internal triangles. Joining the F centres of faces to the centre of the solid generates nF internal triangles & F internal sides. When these triangles are Type A, nF corners & 3nF sides of 3nF sectors are added. The numbers of geometrical elements surrounding its centre are:
Corners Sides Triangles Total Faces: V + F E + nF nF 2 + 2E + 2nF Interior: E + nF V + F + 3E + 3nF 3E + 3nF 2 + 8E + 7nF Total: 2 + 2E + nF 2 + 5E + 4nF 3E + 4nF 4 + 10E + 9nF
(Euler's polyhedral formula for a simply-connected polyhedron:
V – E + F = 2
has been used to simply the expressions). The number "2" in the expression for the total geometrical composition of the faces can be interpreted as the two vertices lying on an axis that passes through the centre of the polyhedron. The number "2" in the expression for the composition of the interior denotes the two sides shared by some internal triangles that form this axis. The number "4" in the expression for the total number of geometrical elements denotes the two internal sides that form the axis and the two vertices at their ends. The number of corners, sides & triangles surrounding the axis of the Platonic solid = 10E + 9nF. For the first four Platonic solids with 60 edges & 38 faces with 120 sectors, the number of geometrical elements that surround their axes = 10×60 + 9×120 = 1680. The dodecahedron with 30 edges & 12 faces with 60 sectors has (10×30 + 9×60 = 840) elements surrounding its axis. This is very remarkable, for the number 1680 is the number of 1st-order spirillae in each whorl of the UPA, whilst the number 840 is the number of 1st-order spirillae in an outer or inner half of a whorl (see here)! Embodied, therefore, in what the ancient Greeks believed are the shapes of the particles of the Elements Fire, Air, Water & Earth is the very structural parameter 1680 of the subquark state of the E8×E8 heterotic superstring remote-viewed over a century ago by Annie Besant & C.W. Leadbeater. The 840 geometrical elements in each half of the first four Platonic solids that surround their axes correspond to the 840 circular turns in either an outer or an inner half of these regular polyhedra. This is one of the most important discoveries discussed on this website that relate sacred geometries to superstring physics. It compares with the 1680 geometrical elements that surround an axis of the disdyakis triacontahedron — the outer form of the polyhedral Tree of Life (see here & here) — when its internal triangles are not divided into their sectors and centres of faces are not joined to its centre. When they are joined (noting that E = 180, F = 120, n = 3 and nF = 360), the number of geometrical elements surrounding the axis of the disdyakis triacontahedron = 10×180 + 9×360 = 5040. This fact is just as remarkable, for the number 5040 (=3×1680) is the number of 1st-order spirillae in the three major whorls of the UPA/heterotic superstring! So the basic construction of this polyhedron from triangles creates 1680 geometrical elements around its axis, whilst addition of internal triangles, some of whose sides divide its faces into their sectors, requires 2×1680 elements; each element corresponds to a 1st-order spirilla in the three major whorls of the UPA.
The numerical counterpart of this 1680:2×1680 division in the Tree of Life was discussed in #15. It arises from the distinction between the region outside the Lower Face of the Tree of Life and the latter when the first 70 odd integers after 1 are assigned to the 70 yods of its 16 tetractyses. Whereas the first four Platonic solids embody only the superstring structural parameter 1680, the disdyakis triacontahedron embodies the superstring structural parameter 5040 as well. This is because the subquark state of the E8×E8 heterotic superstring is the physical realisation of the cosmic blueprint which, whilst expressed in the Platonic solids collectively, has its single, polyhedral representation in the disdyakis triacontahedron.
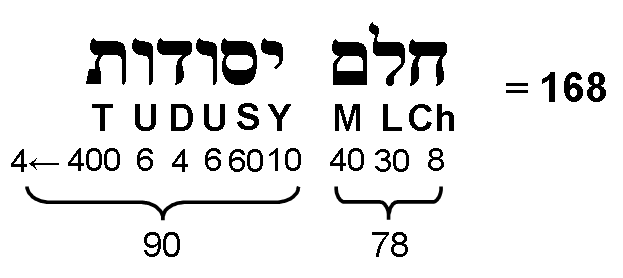
The number of sides surrounding the axis of a Platonic solid = 5E + 4nF. The number of sides surrounding the axes of the first four Platonic solids with 60 edges & 120 sectors of 38 faces = 5×60 + 4×120 = 780 = 78×10. The number of corners & triangles = 1680 – 780 = 900 = 90×10. This is remarkable confirmation of the result obtained above because 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, the number value of Cholem is 78 and the number value of Yesodoth is 90:

It is highly implausible that subsets of geometrical elements would make up the first four Platonic solids that, by mere chance, are the number values of these two Hebrew words. The same division appears in the inner Tree of Life as the 78 yods associated with the triangle, pentagon & octagon other than corners and as the 90 yods in the square, hexagon & decagon other than corners (see here). This gematria-based division manifests in the simplest Platonic solid — the tetrahedron, as shown in the table below listing the numbers of geometrical elements surrounding the axes of the five Platonic solids:
| Platonic solid | Parameters | Corners | Sides | Triangles | Total |
| Tetrahedron | E = 6, n = 3, F = 4 | 24 | 78 | 66 | 168 |
| Octahedron | E = 12, n = 3, F = 8 | 48 | 156 | 132 | 336 |
| Cube | E = 12, n = 4, F = 6 | 48 | 156 | 132 | 336 |
| Icosahedron | E = 30, n = 3, F = 20 | 120 | 390 | 330 | 840 |
| Subtotal = | 240 | 780 | 660 | 1680 | |
| Dodecahedron | E = 30, n = 5, F = 12 | 120 | 390 | 330 | 840 |
| Total = | 360 | 1170 | 990 | 2520 |
78 sides & (24+66=90) corners & triangles surround its axis. It demonstrates in an unambiguous way how the
simplest regular polyhedron embodies not only the number value 168 of the Mundane Chakra of
Malkuth but also the number values of the two words that compose it. What better evidence could one have that this
is, indeed, the correct Kabbalistic name of the Mundane Chakra of Malkuth? The geometrical compositions of the
octahedron and its dual — the cube — are the same, with 336 geometrical elements surrounding each axis
(168 elements in each half). Surrounding the axes of the tetrahedron, octahedron & cube
are 840 geometrical elements — the same as for the icosahedron. The 840:840 division in the outer 2½ and inner 2½
revolutions of each whorl of the UPA/heterotic superstring corresponds to the distinction between the first three
Platonic solids and the fourth one. Alternatively, it corresponds to the 840 geometrical elements in the upper
halves of the four Platonic solids and to the 840 elements in their lower halves. The dodecahedron has the same
geometrical composition as the icosahedron. Indeed, they have the same numbers of corners, sides & triangles.
The 840:840 division of geometrical elements for this pair reflects the fact that each is the dual of the other, so
that they have the same value 30 of E (edges) and the same value 60 of nF (face sectors) appearing in the formulae
listed above.
The table indicates that the entries in each column for the subtotal row for the first four Platonic solids are ten times those for the tetrahedron, whilst the entries for the total row are 15 times the corresponding ones for the tetrahedron. They depend on the value of E (number of edges) and nF (number of sectors in all faces). Taking the values E = 6 & nF = 12 for the tetrahedron as the base values, their values for the five Platonic solids increase according to ×1, ×2, ×2, ×5 and ×5. We see that, in terms of these base values, the sums of the values for E and nF for the first four Platonic solids (and therefore for their numbers of corners, sides & triangles) = 1 + 2 + 2 + 5 = 10, whilst the sums for all five solids = 10 + 5 = 15. This reflects the Godname YAH (Hebrew: YH = 10 + 5 = 15). The factor of 10 appears only in the first four Platonic solids. For historical reasons, the dodecahedron is regarded as the fifth Platonic solid, being associated with the fifth Element, Aether. As it is dual to the icosahedron, it has the same number of edges and the same number of face sectors as the icosahedron. This means that these two Platonic solids are composed of the same numbers of corners, sides & triangles. Moreover, the first three solids have the same total numbers as the icosahedron or dodecahedron because they have the same number of edges and the same number of sectors. Arithmetically speaking, it makes no difference whether the superstring structural parameter 1680 is regarded as compounded from the icosahedron and the dodecahedron, from the first three solids and the fourth solid or from the first three solids and the fifth one. However, although the modern mathematician or physicist may regard as arbitrary which choice is correct, the fact that the dodecahedron displays the Golden Ratio in its pentagonal faces — a proportion that has been believed for 2500 years to embody the divine ideal of beauty — distinguishes it from the other Platonic solids. It is, therefore, fitting that the dodecahedron should be viewed as the last in the mathematical sequence of regular polyhedra, quite apart from being the one with the most vertices. The Tetrad Principle formulated in Article 1 states that numbers of universal significance like 1680 are always determined by either the fourth member, or the first four members, of a class of numbers or mathematical objects. The principle indicates that, of the three combinations of solids with 1680 geometrical elements surrounding their axes, the embodiment of this number by the first four Platonic solids is the correct one. It is a remarkable confirmation of how this principle yields numbers of universal significance — both to Earthlings and to ETs, in this case the number of circularly polarized waves that run around each of the 10 closed curves of the E8×E8 heterotic superstring constituents of the up and down quarks in the protons and neutrons of atomic nuclei.
The 1680 geometrical elements surrounding the axes of the first four Platonic solids consist of 240 corners and 1440 sides & triangles (720 sides & triangles in the first three solids & 720 sides & triangles in the fourth solid, or, alternatively, 720 sides & triangles in each half of the four solids). This 240:720:720 pattern manifests in the outer & inner forms of the Tree of Life as the 240 yods other than Sephiroth in the 1-tree and the 720 yods that surround the centres of each set of seven separate, Type B polygons:
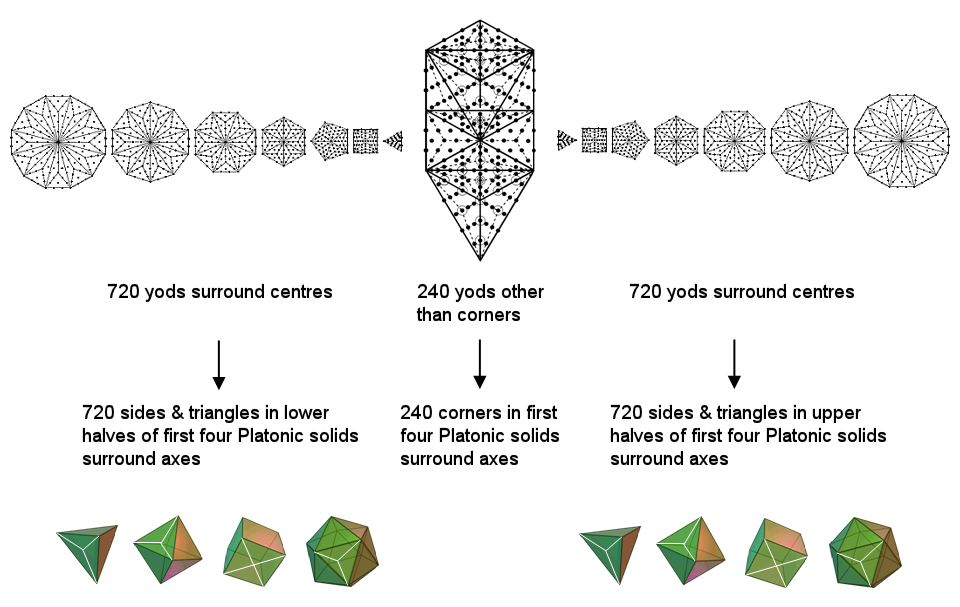
The tetrahedron & octahedron have 72 corners and the cube & icosahedron have 168 corners. This 72:168 division is characteristic of holistic systems. In terms of the root structure of the superstring gauge symmetry group E8, its 240 roots consist of the 72 roots of its exceptional subgroup E6 and the 168 roots of E8 that are not roots of E6. That this is not a coincidence is indicated by the fact that the 240 corners of the first four Platonic solids surround the eight endpoints of their axes, which correspond to the eight simple roots of E8. Amazingly , these Platonic solids embody not only the superstring structural parameter 1680 but also the superstring dynamical parameter 248 as the dimension of E8!
The number of corners surrounding the axes of the five Platonic solids = 360 = 36×10. This is also the number of geometrical elements in the faces of the first four Platonic solids that surround their axes. The Divine Name ELOHA of Geburah with number value 36 prescribes both all five Platonic solids and the first four solids. The number of sides & triangles surrounding the axes of the five solids = 2160 = 216×10, where 216 is the number value of Geburah. Here is an example of the conjunction of two or more number values referring to the same Sephirah. The average number of corners surrounding the axes of the five Platonic solids is 72. This is the number value of Chesed, the Sephirah preceding Geburah in the Tree of Life. Including the centres, there are 375 corners, that is, (375 – 50 = 325) corners other than the 50 polyhedral vertices, making an average of 65 extra corners. This demonstrates how ADONAI, the Godname of Malkuth, prescribes the average additional number of points in space needed to construct the five Platonic solids out of triangles.
The number of corners & sides surrounding the axes of the five Platonic solids = 1530 = 153×10. This shows how ELOHIM SABAOTH, the Godname of Hod with number value 153, prescribes the geometry of the five Platonic solids. Including the 20 corners & sides making up the five axes that surround their centres, (1530 + 20 = 1550 = 155×10) geometrical elements surround their centres. ADONAI MELEKH, the complete Godname of Malkuth, prescribes the complete geometrical composition of the five Platonic solids. As 1550 = 31×10×5, the average number of geometrical elements surrounding their centres = 31×10, showing how EL, the Godname of Chesed with number value 31, prescribes the five Platonic solids. (310/2 = 155) geometrical elements on average in each half of a Platonic solid surround its centre, again showing how ADONAI MELEKH prescribes the regular polyhedra.
The number of sides & triangles surrounding the axes of the five Platonic solids = 2160 = 216×10, where 216 is the number value of Geburah. Each half of a Platonic solid on average has 216 such elements.
Fine-structure number 137
The number of corners & triangles surrounding the axes
of the five Platonic solids = 1350. Including the 10 endpoints of their axes, the number of corners & triangles
surrounding the centres of the five Platonic solids = 1360
| 10 | 20 | 30 | 40 | |
| 50 | 60 | 70 | 80 | |
| = | ||||
| 90 | 100 | 110 | 120 | |
| 130 | 140 | 150 | 160 . |
This is the sum of the gematria number values of Malkuth, its Godname ADONAI, its Archangel Sandalphon, its Order of Angels Ashim, and its Mundane Chakra Cholem Yesodoth:
496 + 65 + 280 + 351 + 168 = 1360.
The sceptic will, no doubt, attribute this to chance. But it would mean that it is also just chance that the number 155 of the complete Godname of Malkuth is the average number of corners & sides in half a Platonic solid that surround its centre. It is, surely, stretching common sense too far to believe that the same Sephirah could appear twice by accident in this context?! The average number of corners & triangles surrounding the centres of the five Platonic solids = 1360/5 = 272. This is the number value of Cherubim, the Order of Angels assigned to Yesod. The average number of corners & triangles in each half of a Platonic solid that surround its centre = 136. Therefore, including the centre, 137 corners & triangles (38 corners, 99 triangles) are needed on average to create half a Platonic solid. This show how the scientifically mysterious number 137, which determines the approximate value of the fine-structure constant α = e2/ħc ≅1/137 at the heart of atomic physics, measures the geometry of the five Platonic solids (see also #16 in Sacred geometry/Platonic solids). Its geometrical basis indicates that it divides into (1+136). It is predicted that any theoretical derivation of the fine-structure constant will replicate in some analogous way this geometrical distinction between the centre of a Platonic solid and the 136 corners & triangles needed on average to shape half of it.
Dimensions 248 of E8 & 496 of
E8×E8
The table above indicates that 2520 corners, sides & triangles surround the
axes of the five Platonic solids. Of these, 40 are vertices. Hence, (2520−40=2480) geometrical elements other than
vertices surround their axes. On average, (2480/5 = 496) geometrical elements other than vertices
are needed to construct a Platonic solid around its axis, 248 elements in each half.
Remarkably, the five Platonic solids embody both the dimension 496 of the heterotic
superstring symmetry group E8×E8 and the dimension 248 of
E8! This is another one of the most astounding properties of sacred geometries to
be revealed in this website. It was discussed in the previous page but is repeated here to
emphasize how the Platonic solids embody both the structural and dynamical parameters of the
E8×E8 heterotic superstring. As a 10-dimensional gauge field is
associated with each of the 248 roots of E8, the number 2480 is the number
of space-time components of all the gauge fields transmitting the forces between superstrings of ordinary
matter. It was shown here in Superstrings as sacred geometry/Tree of
Life that the 49-tree mapping the cosmic physical plane has 2480 yods when
its 595 triangles are turned into tetractyses. This is no coincidence. Instead, we are encountering the amazing
way in which the same number appears in different holistic systems as a parameter quantifying
analogous aspects of them. The superstring physics of matter is embodied in the
49-tree mapping the cosmic physical plane — the cosmic counterpart of the space-time
continuum.
The axis of each Platonic solid consists of its two endpoints, its middle & two straight lines, i.e., five geometrical elements. Therefore, (5+496=501) geometrical elements other than the 8 vertices surrounding the axis are needed on average to build a Platonic solid, that is, 500 (=50×10) elements, starting with its centre. This demonstrates another way in which the Godname ELOHIM with number value 50 prescribes the five Platonic solids with 50 vertices & 50 faces. Indeed, as was seen in #9 of this section, 50 overlapping Trees of Life comprise 2520 yods when their 604 triangles are tetractyses and this is, precisely, the number of corners, sides & triangles that surround the axes of the five Platonic solids! Here is the way in which the Tree of Life encodes parameters of analogous, holistic systems such as the five Platonic solids. The 40 yods in the 50th Tree next above the 49-tree with 2480 yods correspond to the 40 vertices of the five Platonic solids that surround their axes.
| << Previous 1... 18 19 [20] 21 22 ...56 Next >> |