ARTICLE 4

     The Godnames Prescribe the Inner Tree of Life    

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com

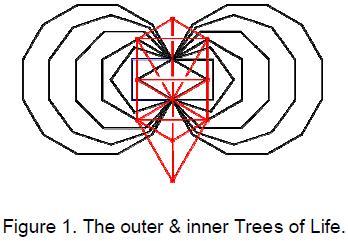
It was stated in Article 3 that a geometrical object or pattern constitutes sacred geometry if the ten Godname numbers shown in Table 1 prescribe its properties. It was also said that the historically known, outer Tree of Life has an inner form (Fig. 1) which, as my book The Mathematical Connection between Religion and Science (1) proves, encodes the group parameters of E₈ and  E₈×E₈, the  gauge  symmetry group associated with  the  so-called ‘heterotic superstring,’ as well as its structural parameters 168, 336, 840, 1680 & 3360. It consists of two similar sets of seven regular polygons: triangle, square, pentagon, hexagon, octagon, decagon and dodecagon. The fourteen polygons share a common side, which I have called their ‘root edge,’ so-called because they should be  
 
                                                                                              Table 1

considered like a tree that grows out of its root, each polygon being analogous to a branch. The seven members of each set are enfolded in one another, those in one set being the mirror image of their counterparts in the other set. The four corners of the two joined triangles are shared with the Tree of Life because the endpoints of the root edge coincide with Daath and Tiphareth and because their other corners coincide with Chesed and Geburah — or, rather, the projections of their locations onto the plane containing the polygons, as it must always be kept in mind that the outer Tree of Life, although traditionally depicted in books on Kabbalah as 2-dimensional, is really a 3-dimensional object. This is why some of the Paths connecting two Sephiroth that appear to intersect another one are shown as broken lines in order to indicate to the eye of the reader that they are really behind it.

As the cosmic blueprint of the subatomic world, evidence for which is presented in my book, the inner, polygonal form of the Tree of Life possesses sacred geometry par excellence. Hence, the Godnames must define its properties. The manner of this prescription is indicated below, the two sets of polygons being considered both separately and enfolded in one another:

1

HOW GODNAMES PRESCRIBE (7+7) POLYGONS

(all Godname numbers are written in boldface type)

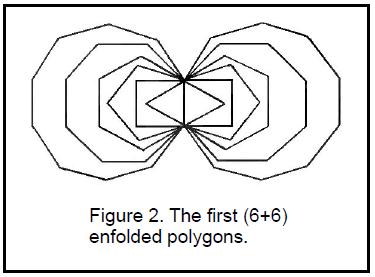
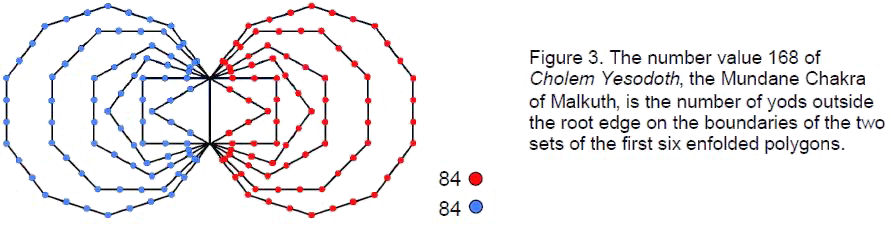
The ten Godnames of the Sephiroth of the Tree of Life also prescribe various subsets of the seven (and fourteen) polygons, which encode different types of cosmic parameters. Amazingly, each subset is a holistic object in itself because it, too, is prescribed by the Godnames and therefore embodies the same information that larger sets do. One such subset is the two sets of the first six regular polygons (Fig. 2), which, as my book proves, encode a structural parameter of E₈×E₈ heterotic superstrings, namely, the number 1680 (see earlier articles and Fig. 3). Some of their properties are worked out and listed below.

PROPERTIES OF THE 1ST (6+6) POLYGONS

Separate

1. 1st 6 regular polygons comprise 36 polygonal corners, 36 polygonal sides and 36 triangles with 42 corners and (36+36=72) sides;

2. Number of geometrical elements in the 1st 6 polygons = 42 + 72 + 36 = 150 (15×10);

3. Number of geometrical elements outside root edge of the 1st 6 polygons = 150 – 6×3 = 132;

2

4. Number of geometrical elements outside root edge of the 1st 6 polygons other than their centres = 132 – 6 = 126;

5. Number of geometrical elements in root edge and in the 1st 6 polygons outside root edge other than their centres = 126 + 3 = 129;

6. Number of geometrical elements in root edge and in the 1st 6 polygons = 3 + 150 = 153;

7. Number of yods in the 1st 6 polygons = 6×36 + 6 = 222. Of these, 6 are centres. Number of yods other than centres = 222 – 6 = 216. Of these, 36 are polygonal corners;

8. Number of hexagonal yods = 216 – 36 = 180. Of these, 36 are tetractys centres. Number of boundary hexagonal yods = 180 – 36 = 144;

9. Number of yods on sides of the 36 tetractyses = 144 + 42 = 186;

10. Number of yods on sides of the 1st 6 polygons = 2×36 + 36 = 108;

11. Number of yods in root edge and on sides of the 1st 6 polygons = 4 + 108 = 112.

12. 1st (6+6) polygons comprise 72 polygonal corners, 72 polygonal sides and 72 triangles with (72+12=84) corners and (2×72=144) sides;

13. Number of geometrical elements in the 1st (6+6) polygons = 2×150 = 300 (303, including root edge);

14. Number of yods in the 1st (6+6) polygons = 2×222 = 444;

15. Of these 12 are centres. Number of yods surrounding centres = 444 – 12 = 432;

16. Of these, 72 are polygonal corners. Number of hexagonal yods = 432 – 72 = 360 (36×10);

17. Of these, 72 are tetractys centres. Number of boundary hexagonal yods = 360 – 72 = 288;

18. Number of yods on sides of the 72 tetractyses = 288 + 84 = 372;

19. Number of yods on sides of the 1st (6+6) polygons = 2×72 + 72 = 216;

20. Number of yods in the root edge and on sides of the 1st (6+6) polygons = 216 + 4 = 220.

Enfolded

1. 1st 6 polygons have 26 corners, 31 sides & 35 sectors with 30 corners (28 outside the root edge) and 65 sides (64 outside the root edge);

2.   Of the 26 corners, 5 are either shared with the outer Tree of Life or on the root edge, leaving 21 unshared corners outside the root edge;

3. Number of corners and sides of 35 sectors in the 1st 6 polygons = 30 + 65 = 95;

4. Number of geometrical elements = 95 + 35 = 130 (127 outside root edge; 127 = 31st prime number);

5. Number of yods in the 1st 6 polygons = 30 + 65×2 + 35 = 195 (386 in the 1st (6+6) polygons). Number of yods in the 1st (6+6) polygons other than the 2 endpoints of root edge, 12 centres & 12 yods shared with Tree of Life = 360 (=36×10) unshared yods;

6. Of the 195 yods, 35 are hexagonal yods at centres of tetractyses, leaving 160 yods on sides of tetractyses (156 outside the root edge). They include the top of the hexagon, which coincides with the bottom of the hexagon enfolded in the next higher Tree. There are 155 intrinsic boundary yods outside the root edge;

7. Number of yods on sides of the 1st 6 polygons = 31×2 + 26 = 88 (84 outside root edge);

8. Number of hexagonal yods on sides of the 1st 6 polygons = 31×2 = 62 (122 in the 1st (6+6) polygons).

9. 1st (6+6) polygons comprise 50 corners (48 outside root edge), 61 sides and 70 triangles with 58 corners (56 outside root edge) and 129 sides;

10. Number of corners & sides of the 70 triangles in the 1st (6+6) polygons = 58 + 129 = 187;

11. Number of geometrical elements = 187 + 70 = 257 (55th prime number). Number of geometrical elements outside root edge = 254 (242 surrounding the 12 centres of polygons), of which two are shared with polygons in adjacent Tree of Life, leaving 240 intrinsic elements surrounding these centres;

12. Number of yods = 191×2 + 4 = 386. Of these, 58 are corners of tetractyses. Number of hexagonal yods = 386 – 58 = 328. Of these yods, 70 are at centres of tetractyses, leaving 258 hexagonal yods that line

3

their sides (256 outside the root edge, where 256 = 4⁴). 8 hexagonal yods are shared with the Tree of Life, so that 248 hexagonal yods lining the 70 tetractyses are intrinsic to the 1st (6+6) polygons.

13. Number of yods on boundaries of the 1st (6+6) polygons = 122 + 50 = 172 (168 outside root edge).

These properties of the first 6 and the 1st (6+6) polygons are prescribed by the ten Godnames as follows:

HOW GODNAMES PRESCRIBE THE 1ST 6 & THE 1ST (6+6) POLYGONS

The (6+6) enfolded polygons have 168 yods along their boundaries outside their root edge (Fig. 3). In other words, 168 yods create their shape (84 in each set of 6). This is remarkable, because 168 is the number value of Cholem Yesodoth (‘breaker of the foundations’), the Mundane Chakra of Malkuth (Mundane Chakras are the astrological bodies traditionally associated in Kabbalah with each Sephirah; the Mundane Chakra of Malkuth is the planet Earth). Moreover, as discussed in previous articles, the Theosophist C.W. Leadbeater used ‘anima,’ one of the yogic siddhis, or psychic faculties, to magnify the basic units of matter. His ‘ultimate physical atom’ (UPA) consists of ten helical coils, each with 1680 turns (Fig. 4). My book ESP of Quarks & Superstrings (2) has shown the ten-fold UPA to be the subquark state of a superstring — the microscopic manifestation of the Tree of Life, each helix corresponding to one of the ten Sephiroth. As a Sephirah is itself ten-fold, being represented by a Tree of Life, the number 168 is a structural parameter

4

of this hadronic state of the superstring. Moreover, each coil winds 2½ times around the outer surface of the UPA and 2½ times in a narrower spiral around its central axis. Each half of a coil comprises 840 turns of a helix, so that the number 84 is also a structural parameter of this state of a superstring, being the number of coils in one quarter of a complete revolution of a whorl, whilst the number 168 is the number of coils in half a revolution. The inner and outer halves of a helical whorl — or, rather, an outer and inner half-revolution — correspond in the inner Tree of Life to the
 

two similar sets of the first six regular polygons, whose shapes are delineated by 84 yods along their sides outside their shared root edge.

Earlier articles pointed out that the seven cosmic planes of consciousness are represented by the Cosmic Tree of Life (CTOL). It consists of 91 overlapping Trees of Life with 550 SLs. CTOL is encoded in a unique subset of the (7+7) polygons constituting the inner form of the Tree of Life. The root edge and a set of seven separate polygons have a yod population that is equal to the number of SLs in the 49-tree representing the cosmic physical plane. The five separate polygons with most corners have as many yods as there are SLs in the 42 Trees of Life in CTOL above the 49-tree

that map the six cosmic superphysical planes. Together with the root edge, these separate (7+5) polygons (Fig. 5) constitute sacred geometry because they are the polygonal representation of CTOL.

Listed below are ways whereby the ten Godname numbers listed in Table 1 (shown in boldface type) prescribe properties of this holistic set of (7+5) polygons. Also displayed are the ways in which these properties are expressed by the Pythagorean Tetrad (the number 4), the Pythagorean Decad (the number 10) and the integers 1, 2, 3 & 4 symbolising the four rows of dots in the Pythagorean tetractys.

PROPERTIES OF (7+5) POLYGONS

Separate

1. (7+5) polygons comprise 89 polygonal corners (89 = 44th odd integer after 1 = (24=4!)th prime number), 89 polygonal sides and 89 tetractyses with 101 corners (101 = 26th prime number = 50th odd integer after 1) and 178 sides;

5

2. Including the root edge, number of yods = 550, number of polygonal corners = 91, number of polygonal sides = 90, number of tetractys corners = 103, number of tetractys sides = 179 = 41st prime number (41 = 21st odd integer = 15 + 26) and number of geometrical elements = 103 + 179 + 89 = 371 = 7×53, where 7 = 4th prime number and 53 = (16=4²)th prime number;

3. 65 polygonal corners outside root edge.

Enfolded

1. (7+5) polygons comprise 67 polygonal corners (67 = 19th prime number, 19 = 10th odd integer), of which 65 are outside root edge, and 61 unshared with Tree (61 = 31st odd integer). 78 polygonal sides and 88 tetractyses (88 = 44th even integer) with 76 corners (74 outside root edge) and 165 sides (165 = 1² + 3² + 5² + 7² + 9² = 3×55 = 3(1²+2²+3²+4²+5²) = sum of 15 squares). Of these, 10 are shared with 1-tree (apart from root edge), leaving 155 unshared sides;

2. Number of corners and sides = 67 + 78 = 145. Of these, 3 corners are centres of polygons and 12 corners and sides are shared with 1-tree. Number of corners and sides which are not centres of polygons or shared with 1-tree = 145 – 3 – 12 = 130 = 129th integer after 1. 21 geometrical elements shared with 1-tree (1-tree has 36 unshared elements);

3. Number of yods = 494

4. Number of yods outside root edge = 494 – 4 = 490 = 49×10;

5. Number of tetractys corners not centres of polygons = 76 – 12 = 64 = 4³;

6. Number of tetractys corners not both polygonal corners and centres = 76 – 2 – 1 = 73. Of these, 6 are Sephirothic points of Tree of Life. Number of tetractys corners unshared with Tree and not both centres and corners of polygons = 73 – 6 = 67;

7. Number of hexagonal yods = 494 – 76 = 418. Of these, 88 are centres of 88 tetractyses;

8. Number of hexagonal yods on edges of 88 tetractyses = 418 – 88 = 330, of which 17 are shared with Tree, leaving 313 unshared hexagonal yods on edges of tetractyses (313 = 65th prime number) and of which 22 are shared with 1-tree, leaving 308 hexagonal yods on edges of tetractyses unshared with 1-tree. 328 hexagonal are yods outside root edge on sides of tetractyses (328 = sum of first 15 prime numbers).

Some of these properties of the (7+5) polygons are prescribed by the Godnames as follows:

HOW GODNAMES PRESCRIBE (7+5) POLYGONS

6

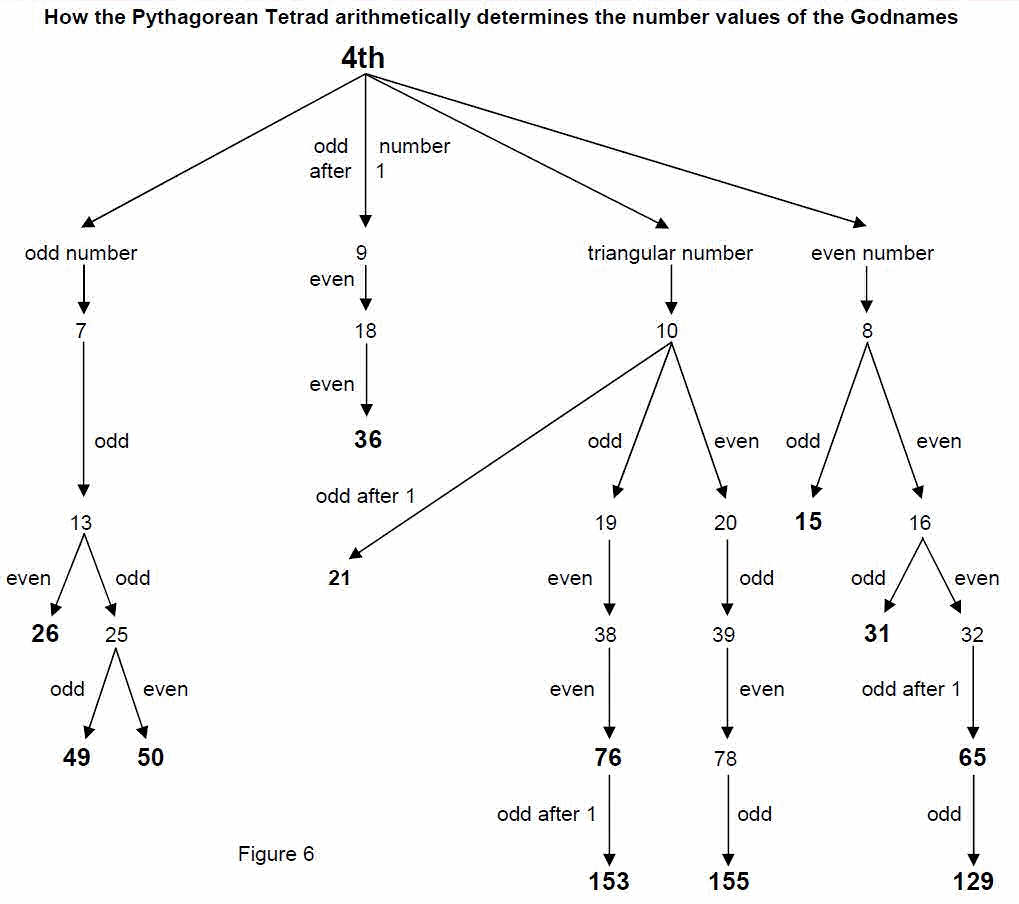
In general, those different sections of the 7 and (7+7) polygons whose properties are defined by the set of Godname numbers constitute sacred geometry and therefore encode cosmic parameters such as numbers associated with bosonic and superstring theories.

Article 1 proposed a new mathematical principle called the Tetrad Principle that governs the Tree of Life description of nature. Evidence for this principle was discussed in the form of the remarkable way the number 4 (Tetrad) and the numbers 1, 2, 3 and 4 symbolised by the Pythagorean tetractys define and express parameters of the theories of superstrings and bosonic strings. My book The Mathematical Connection between Religion and Science shows how Godname numbers prescribe these parameters. In fact, the Godname numbers (“even” or “odd” denote the type of arrowed number defined by the previous one in the sequence, e.g., 13 is the 7th odd integer and 25 is the 13th odd integer).

themselves are determined arithmetically by the Tetrad (Fig. 6). It illustrates one of the profound properties of the Pythagorean Tetrad as the root source of Godname numbers and hence of superstring parameters like 248 and 496 — the numbers of states of the particle that transmits the unified force between, respectively, superstrings of either ordinary or shadow matter and superstrings of both these kinds of matter.

References

1) “The Mathematical Connection between Religion and Science,” Stephen M. Phillips (Antony Rowe Publishers, England, 2009).

2) “ESP of Quarks & Superstrings,” Stephen M. Phillips (New Age International, New Delhi, India, 1999).

7