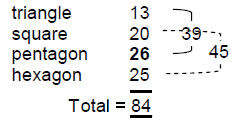Greeks believed that each of their keys, which they identified by the tribal names Dorian, Phrygian, etc., possessed a strongly marked ethical character.”¹ This opening statement in her treatise on the history of the psychological attributes of musical keys may state what is now commonly accepted by many (but not all) scholars but it still begs the question. If the ethos of ancient Greek music was really a matter of higher and lower pitch, one has, like Donald Grout, one of the giants of American musicology, to ask: “... how could a mere transposition by one tone up or down account for the difference in ethos which Plato postulates between the Dorian and the Phrygian modes?” … Its “only audible effect would be a redistribution of the tones and semitones within one and the same octave range...”² It is quite possible that the different ethical attributes of the ancient modes had more to do with the nature of the songs and melodies of the different races from whom the ancient Greeks descended. No one, however, knows how the music of ancient Greece sounded. In the absence of reliable, surviving evidence like musical score sheets or playable musical instruments, one can argue either case, citing various authorities to support one’s position, whilst at the same time ignoring past and present writers of equal prestige who take the contrary view. As Donald Jay Grout remarked: “…we do not know, and in all probability we shall never know, exactly what were the modes about which Plato and Aristotle wrote, or how these may have been different from the modes as understood by later writers. …Each of the various hypotheses about the modes has claims to credibility, and each is warmly defended by its champions. No field of musicology has produced a richer crop of disputation from a thinner soil of fact.”³ This position of neutrality seems a more honest attitude to take than that of Steblin, whose partisanship deceives her readers into thinking that the argument was long won, whereas controversy persists amongst scholars on this issue.

The problem hinges on the question of whether the Greek musical terms harmonia and tonos meant different things or the same thing. Some scholars, who believe that the ancient Greeks knew only keys argue for the latter, whilst others propose that the Greek modes had a double meaning. For the latter, the use of the word harmonia indicated a “mode” and signified the order in which the intervals followed one another, i.e., the species of the octave scale, whilst tonos signified a fixed pattern of intervals that could be transposed in pitch, i.e., a key. Unless one is wedded to the implausible view that all the modes — however dissimilar in ethos — were the same diatonic scale, differing only by pitch, it is hard to believe that two different musical terms meaning the same would have been in use in the Greek musical lexicon. They are, surely, evidence that the ancient Greeks did know of both keys and octave species. The historical evidence cannot decide whether the ethos of their modes was due to the former or to the latter. Why, however, should it be a case of one or the other? It is possible that both played a role in defining the distinctions between modes and that this ambiguity led to the disagreements between writers as to the correct ethos to be attached to a particular mode. They may have been all correct, because the modality ascribed to the same pieces of music might not over time have always been determined by the same criterion! This possibility seems to have been ignored in the longstanding, polarised debate.

Another argument used against the octave species interpretation of Greek modes is that the church modes had Byzantine origins, their four authentic and four plagal modes arising from the Byzantine octoechoi, which, too, were grouped into four pairs and which were not scales but collections of melodic motives expressing more or less the same quality of feeling. However, the fact that early, Western musical theorists deduced the scales from which these groups of motives were formed and then incorporated (wrongly, as it turned out) ancient Greek names of modes into their labelling of these scales does not imply that the original Greek modes differed by key. This is a non sequitur, although a convenient one for advocates of the key interpretation of modes to make. Yet it is implicit in the arguments used by Steblin against the interpretation of the Greek modes as octave species. In her discussion of the origins of Christian church music, she is satisfied to stop at the Byzantine era, not bothering to ask whether its music was influenced by that of Greece, Egypt, Syria and other regions where Christians settled. As Grout

2

points out, the early Christians were Jews and would have borrowed their music from the chants of the Hebrew synagogues, which had melodies based upon modes.⁴ Far from being, as she supposes, a false attribution to the ancient Greeks by early Christian musical theorists, modes as octave species may have been known to the Greek cognoscenti and may have influenced the creation of the church modes indirectly through the largely unknown impact of Greek music on the Byzantine system. In other words, although the church modes were not derived from the Greek musical modes, they could still have amounted to their rediscovery! This possibility is not considered by Steblin in her defence of the orthodox position in the debate over the meaning of the Greek modes.

The weakness of the scholastic approach to this problem is that it does not discover the truth of the matter but merely recirculates opinions that, however learned, must remain speculative for the obvious reason that these authorities were not contemporaneous with the culture of ancient Greece but, instead, were separated from it by many centuries. No scholar can have read all that was written later about music in that era. Quotations will inevitably be selective and self-serving, excluding whatever contradicts firmly held beliefs. Pressure in the academic world to conform to orthodox opinion can never be overestimated.

.

2. Ancient evidence for modes being octave species

There are only seven octave species because they are generated by taking successive notes of the seven-note Pythagorean scale as their tonic (it makes no difference to this fact whether musical scales are regarded as ascending or descending):

(T is the Pythagorean whole tone interval of 9/8, which is slightly sharper than its equal-tempered counterpart, and L is the Pythagorean leimma, an interval of 256/243, which is somewhat flatter than the semitone). It must be emphasized that the modal labels shown here are those of the church. It is now recognised that the early church musical theorists assigned the Greek labels Dorian, Phrygian, Lydian, etc to successive octaves of the ascending musical scale, not realising that in ancient Greece it was always regarded as descending. This caused mislabelling, so that the ethos that the church associated with the modes sometimes disagreed with ancient opinion owing to their misnaming. It was also confusing to number the four Authentic Modes by odd integers and the four Plagal (Hypo) Modes by even integers because this destroyed all sense of their order of generation from successive notes of the diatonic scale, as is shown above by the modal numbers being out of sequence. Perhaps the motivation for this was to make Plato’s ideal mode — the Dorian — the first in the list.

Given that the ancient Egyptians had an 8-note scale and that Pythagoras spent many years studying mathematics, music and astronomy with the Egyptian priesthood, it is very likely that he did not discover the mathematics of the musical scale, as popular textbooks on the history of science still inform us, but that he learnt it from his Egyptian teachers. It is therefore not hard to believe that he would have passed on his acquired knowledge to his brotherhood of disciples in Croton, Italy, some of whom then imparted it to their students in ancient Greece itself. Indeed, we know that Plato obtained some of the mathematical secrets of the early Pythagoreans by purchasing a book called Fragments from the parents of its author, Philolaus of Tarentum (ca. 480–unknown B.C.E.). Philolaus was educated by Lysis, one of the two disciples of Pythagoras

3

who escaped the massacre of the Pythagorean community at Croton and who subsequently became the first to write down his master’s teachings in his Fragments.⁵ A tradition is recorded by Strabo⁶ that Plato spent thirteen years of study at Heliopolis, making it highly plausible that he learnt there the mathematics of music. In his The History of Music, W. Chappell went as far as to say that the “entire Greek system was mainly derived from Egypt, Phoenicia, Babylon, or other countries of more ancient civilisation than Greece.”⁷ He pointed out that:

“Diodorus Siculus says that the musicians and poets of Greece visited Egypt for the purpose of improvement, and that the Egyptian priests had records of their visits in their books. The first two names so recorded were those of Orpheus and Musæus, and Homer followed. So, at least, the Egyptians claimed to have taught music and poetry to the Greeks at a very early period. The later names in Diodorus’s list, such as those of Solon, Plato, and others, are admittedly authentic.”⁸

Furthermore, he said:

“Nichomachus, quoting Pythagoras and Plato, tells us that the Egyptians ascribed twenty-eight sounds to the universe, calling it “twenty-eight sounding.” So the Egyptians must have had twenty-eight sounds, i.e., twenty-eight notes, in their scales. That is the precise total number of Greek notes, in their greater and lesser perfect systems combined, and including all their scales — Diatonic, Chromatic, and Enharmonic. Neither in Egypt nor in Greece was there an actual limit to twenty-eight sounds, because all scales were transposable, but only twenty-eight notes could be defined, starting from any given pitch. Euclid, Nicomachus, Aristides Quintilianus, and others, enumerate the Greek scales and their notes, and all authors are agreed as to the number being precisely twenty-eight. This most remarkable coincidence between Egypt and Greece seems nevertheless to have escaped the observation of historians of music. If it stood alone, it would almost suffice to prove the origin of Greek music. The number is too peculiar to have been arrived at by accident, within a compass of only two Octaves.”⁹

A simple calculation reveals the significance of this number. Table 1 below shows the tone ratios for each mode, derived from the patterns of intervals that were listed above:

Table 1. Tone ratios of the seven Church modes.

Lydian	1	9/8	81/64	729/512	3/2	27/16	243/128	2
Phrygian	1	256/243	32/27	4/3	3/2	128/81	16//9	2
Dorian	1	9/8	32/27	4/3	3/2	27/16	16/9	2
Hypolydian	1	9/8	81/64	4/3	3/2	27/16	243/128	2
Hypophrygian	1	256/243	32/27	4/3	1024/729	128/81	16/9	2
Hypodorian	1	9/8	32/27	4/3	3/2	128/81	16/9	2
Mixolydian	1	9/8	81/64	4/3	3/2	27/16	16/9	2

Blue cells contain Pythagorean tone ratios and white cells contain tone ratios not belonging to any octave of the Pythagorean scale. There are 16 such ‘non-Pythagorean’ notes. The (7×7=49^†) notes below the octaves of the seven modes comprise (49–16=33) Pythagorean tone ratios, of which seven are 1’s, leaving (33–7=26) Pythagorean tone ratios other than 1. Including the tonic and octave, the seven modes have 28 notes belonging to the Pythagorean scale. This confirms the quotation above. It proves that the ancient Egyptians must have known about seven different octave
_______________________________
^†Numbers appearing throughout the text in bold type are the number values of the Hebrew Godnames of the ten Sephiroth of the Tree of Life (see previous articles for their tabulated values).

4

species, for Pythagoras (556 B.C.E.–unknown) and Plato (428–347 B.C.E.) certainly knew that the Egyptians had knowledge of 28 musical sounds. As both studied with the Egyptian priesthood, it is reasonable to infer that they knew about the seven octave species with 28 Pythagorean notes. This means that the existence of seven musical scales, if not common knowledge, was at least known to musicians who had visited Egypt, to Pythagoras, Plato and to mathematicians that came after him, like Euclid (4th–3rd C B.C.E.), and the Pythagorean, Nicomachus of Geras (about 60–about 120 C.E.). This does not necessarily imply that the musical modes were octave species. However, given that the evidence presented here proves that some learned, ancient Greeks were, indeed, acquainted with seven scales and that musicians visited Egypt to improve

their art, it makes the possibility very likely, if not certain. Scholars who deny this identity are ignoring the fact that music has never recognised borders. It has always been influenced and enriched by styles and talent imported from other countries. It would explain why two ancient Greek musical terms — harmonia and tonos — were in use, which advocates of the ‘key’ interpretation of modes have, implausibly, to assume to have been synonymous. It seems that the agreement between ancient Egyptians and Greeks as to the number of musical notes and its implication that both knew about the existence of seven octave species have escaped the attention of modern musical scholars as much now as it did when Chappell wrote his book in 1874! Otherwise, they would not keep dogmatically denying that musicians of ancient Greece were unacquainted with them. It does not make sense that they knew about different scales yet played only one of them in different keys!

The possibility of seven octave species would have been in accord with Pythagorean principles for the following reason: the Pythagorean tetractys* symbolises the three archetypal and seven formative principles inherent in all holistic systems. The former — the noumenal aspect of a holistic system, are symbolised by the three points or yods at its corners, which give the tetractys its bare shape as a triangle; the latter — its phenomenal nature — are symbolised by the seven yods arranged at the centre and corners of a hexagon (so-called “hexagonal yods”). Just as the first seven notes of an 8-note musical scale are symbolised by the seven hexagonal yods (shown in Figure 1 as coloured dots, so the 49 notes below the octaves of the seven octave species are symbolised by the analogous 49 hexagonal yods of the next higher-order tetractys — the 2nd-order tetractys (Fig. 2). The seven octaves species represent a more differentiated version of the whole system of musical notes. They constitute another whole.
______________________________
^* The author calls this the ‘1st-order tetractys,’ the point symbolising the Pythagorean Monad being the 0th-order tetractys. In general, the nth-order tetractys has 7ⁿ hexagonal yods.

5

 

6

The yods at the corners of the 1st-order tetractys mark out the shape of this template, from which the other seven yods emerge as independent, phenomenal qualities of the holistic system. In the same way, the number 1 denoting the tonic, the number 2 denoting the octave and the number 3/2 denoting the perfect fifth should be assigned to these three yods because 1 and 2 define the pitch range of the musical scale, whilst their arithmetic mean: (1+2)/2 = 3/2 is the pitch of the perfect fifth G from which the other notes of the scale can be generated by jumps of intervals of a perfect fifth or a perfect fourth — the interval between G and the octave C' (Fig. 3).

As the Pythagorean scale has eight notes, they form ⁸C₂ = 28* pairs or intervals. There are as many intervals in the Pythagorean scale as there are notes in the seven octave species that belong to the Pythagorean scale. Representing the eight notes of the scale by the corners of an octagon, these intervals correspond to the straight lines that join pairs of corners (Fig. 4). An octagon is formed by the corners of two squares rotated relative to each other by 45°. By joining corners of each square and grouping analogous connections, the 28 lines group naturally into four sets of seven. Column 1 indicates consecutive edges of one square (shown by solid lines); column 2 shows consecutive edges of the second square (shown by dotted lines); column 3 shows opposite diagonals of each square; column 4 shows corners of one square joined along an edge of the octagon to a corner of the other square; column 5 indicates corners of the second square joined along an edge of the octagon to a corner of the first square; column 6 exhibits corners of the first square joined internally to corners of the other square; column 7 shows corners of the second square joined internally to corners of the first square. The corresponding intervals are indicated inside each octagon. The 20 Pythagorean intervals include five tone intervals of 9/8. The eight non-Pythagorean intervals include two leimmas of 256/243. There are five seconds, three thirds, four perfect fourths, four perfect fifths, two sixths, one seventh and one octave. No one row contains all the seven Pythagorean one ratios. If we do not join corners in a clockwise sequence in each column, at least one row (the top) can contain all seven diatonic notes. It is unimportant which column or row is treated as the first, although it seems appropriate to start (as shown in Figure 4) with the interval from C to D. All that matters in any rearrangement is that similar types of lines remain in the same column.

The following passage from Chappell’s book seems to give significance to this 4×7 pattern of intervals:

“The Greeks copied the Egyptians in associating musical sounds with the heavenly bodies; but, as they made their computations of time by the lunar month, they connected the twenty-eight notes of the scales with the twenty-eight days of the moon; and the fifteen notes of the Diatonic scale were the fifteen

______________________
* The number of combinations of r objects from a set of n objects is ⁿC_r = n!/(r!(n-r)!, where n! = 1×2×3×… n.

7

days of the moon’s increase.¹⁰ The Egyptians subdivided the lunar month into weeks through dedicating the first hour of each of the seven days to the seven planets, as the seven deities, who were supposed to watch over them. This association seems to have originated in Babylon. The seven planets and the seven days coincided with the seven notes of the Octave.”¹¹

Quintilianus’s reference to the 15 notes of the diatonic scale must be an error because the seven octave species have (including the tonic) 14 different notes, of which eight are Pythagorean, whilst, although the first two octaves of the Pythagorean scale have 15 notes, eight of them belong to the Pythagorean scale on the next higher octave and so the seven notes above the first octave do not belong to the 28 notes making up the seven scales, which all belong to the first octave. The numbers of notes of each type are: 1 (×1), 9/8 (×5), 81/64 (×3), 4/3 (×6), 3/2 (×6), 27/16 (×4), 243/128 (×2) & 2 (×1). Suppose that Quintilianus was confusing the 28 notes of the seven octave species with the 28 intervals of the Pythagorean scale, among which are the eight notes and their seven intervals, totalling 15, the number that he mentions. Figure 4 shows that, by interchanging columns 1 and 2 and then rows 3 and 4, the first octave with tone ratio 2 will go into the 15th member of the set of 28 intervals. However, this will not work because, among the 15 notes and intervals of the Pythagorean scale, is the non-Pythagorean interval 256/243, a number which is absent from the 28 Pythagorean tone ratios. Given this, does the set of 28 notes in the seven scales still have a subset made up of 15 notes defined in some way? Fortunately, the list of numbers of notes given above provides a natural solution because the number of notes in the list up the perfect fourth is 15! Intuitively, this seems right because, just as the 15th note is the midpoint of the sequence of 28 notes, so the perfect fourth with tone ratio 4/3 is the middle note of the scale:

                                                                                           1                                 243/12
                                                                                              9/8                      27/16
                                                                                                    81/64       3/2
                                                                                                              4/3

As a week corresponds to a row and as there are as many as six notes of the same type, at least one week must have two days with the same note. This is to be expected because, whether they are intervals of one scale or notes of seven scales, the set of 28 musical elements are not all different. However, the quotation above definitely refers to the “twenty-eight notes of the scales,” that is, the ancient Egyptians associated the 28 notes of the seven octave species, not the 28 intervals of the Pythagorean scale, with the 28 days of the lunar month. It is the subset of 28 numbers in the turquoise cells of Table 1 that needs to be grouped into four sets of seven.

Table 2. Pythagorean notes corresponding to the 28 Days of the Egyptian Lunar Month.

Week 1 Week 2 Week 3 Week 4

1 9/8 81/64 4/3 3/2 27/16 2 9/8 4/3 3/2 4/3 9/8 81/64 4/3 3/2  27/16 243/128 9/8 4/3 3/2 27/16 4/3 3/2 9/8 81/64 3/2 27/16 243/128

Quintilianus was right about the Egyptians associating lunar days with notes but erred in thinking that the first 15 days were associated with the notes of the first two octaves, some of which do not belong to the notes of the seven scales and so cannot be included with them. Some criterion must determine the ordering of notes into subsets of 15 and 13, as the former can be neither the 15 notes of two octaves nor the 15 notes and intervals of one scale. It seems reasonable to assume that the progression of the days of the lunar month follows the order of the notes in the natural mathematical sequence of the seven modes as they are generated from

8

successive notes of the Pythagorean scale. There are two possibilities: Mixolydian–Lydian, if the notes are ascending, and Lydian–Mixolydian, if they are descending. Considering the former first, the fourth note of the fourth mode (the Hypolydian), when it is part of the modal sequence of 28 notes, is a perfect fifth, 3/2 (see Table 1), and it is the 15th note, which make it fitting that the turning point of the lunar cycle as the full moon begins to wane should coincide with the very musical centre of gravity of the seven scales, namely, the fourth note of the fourth scale in the unfolding series of seven octave species. This is shown in Table 2 as the white cell. Considering the second possibility, according to Table 1, the 15th note in the set of 28 Pythagorean notes is E, the third note of the fourth mode, the Hypolydian, with tone ratio 81/64. This is not the middle of the Hypolydian mode. If the days of the lunar month start with the notes of the Lydian mode, its turning point is not the middle of the middle scale. As symmetry in the modal spectrum should have its counterpart in the lunar cycle, with the two halves of the cycle having their counterparts in the seven scales, the correct sequence of modes is Mixolydian–Lydian. This is indicated in Table 2 by the tone ratios being written in the seven colours of the spectrum. As both the perfect fourth and the perfect fifth occur six times, it is inevitable that some notes appear more than once in a week, however they are assigned to the days.

3. Intervallic structure of the seven modes

The pattern of notes and intervals for each mode are displayed below, together with their numbers of Pythagorean and non-Pythagorean intervals and their minimum numbers of different intervals.

Table 3. Hypolydian mode.

C D E F G A B C C 1 9/8 81/64 4/3 3/2 27/16 243/128 2 D 8/9 1 9/8 32/27 4/3 3/2 27/16 16/9 E 64/81 8/9 1 256/243 32/27 4/3 3/2 128/81 F 3/4 27/32 243/256 1 9/8 81/64 729/512 3/2 G 2/3 3/4 27/32 8/9 1 9/8 81/64 4/3 A 16/27 2/3 3/4 64/81 8/9 1 9/8 32/27 B 128/243 16/27 2/3 512/729 64/81 8/9 1 256/243 C 1/2 9/16 81/128 2/3 3/4 27/32 243/256 1

Blue cells contain rising intervals belonging to the basic set of 13 intervals/notes. Violet cells contain their falling intervals. White cells contain repeated intervals.

Number of intervals = 28 (Pythagorean) + 8 (non-Pythagorean) = 36.
Minimum number of different intervals = 7 (Pythagorean) + 5 (non-Pythagorean) = 12.

Table 4. Mixolydian mode.

	C	D	E	F	G	A	B	C
C	1	9/8	81/64	4/3	3/2	27/16	16/9	2
D	8/9	1	9/8	32/27	4/3	3/2	128/81	16/9
E	64/81	8/9	1	256/243	32/27	4/3	1024/729	128/81
F	3/4	27/32	243/256	1	9/8	81/64	4/3	3/2
G	2/3	3/4	27/32	8/9	1	9/8	32/27	4/3
A	16/27	2/3	3/4	64/81	8/9	1	256/243	32/27
B	9/16	81/128	729/1024	3/4	27/32	243/256	1	9/8
C	1/2	9/16	81/128	2/3	3/4	27/32	8/9	1

9

Number of intervals = 25 (Pythagorean) + 11 (non-Pythagorean) = 36.
Minimum number of different intervals = 6 (Pythagorean) + 5 (non-Pythagorean) = 11.

Table 5. Lydian mode.

	C	D	E	F	G	A	B	C
C	1	9/8	81/64	729/512	3/2	27/16	243/128	2
D	8/9	1	9/8	81/64	4/3	3/2	27/16	16/9
E	64/81	8/9	1	9/8	32/27	4/3	3/2	128/81
F	512/729	64/81	8/9	1	256/243	32/27	4/3	1024/729
G	2/3	3/4	27/32	243/256	1	9/8	81/64	4/3
A	16/27	2/3	3/4	27/32	8/9	1	9/8	32/27
B	128/243	16/27	2/3	3/4	64/81	8/9	1	256/243
C	1/2	9/16	81/128	729/1024	3/4	27/32	243/256	1

Number of intervals = 27 (Pythagorean) + 9 (non-Pythagorean) = 36.
Minimum number of different intervals = 7 (Pythagorean) + 6 (non-Pythagorean) = 13.

Table 6. Dorian mode.

	C	D	E	F	G	A	B	C
C	1	9/8	32/27	4/3	3/2	27/16	16/9	2
D	8/9	1	256/243	32/27	4/3	3/2	128/81	16/9
E	27/32	243/256	1	9/8	81/64	729/512	3/2	27/16
F	3/4	27/32	8/9	1	9/8	81/64	4/3	3/2
G	2/3	3/4	64/81	8/9	1	9/8	32/27	4/3
A	16/27	2/3	512/729	64/81	8/9	1	256/243	32/27
B	9/16	81/128	2/3	3/4	27/32	243/256	1	9/8
C	1/2	9/16	16/27	2/3	3/4	27/32	8/9	1

Number of intervals = 26 (Pythagorean) + 10 (non-Pythagorean) = 36.
Minimum number of different intervals = 6 (Pythagorean) + 5 (non-Pythagorean) = 11.

Table 7. Hypodorian mode.

	C	D	E	F	G	A	B	C
C	1	9/8	32/27	4/3	3/2	27/16	16/9	2
D	8/9	1	256/243	32/27	4/3	3/2	128/81	16/9
E	27/32	243/256	1	9/8	81/64	4/3	3/2	27/16
F	3/4	27/32	8/9	1	9/8	32/27	4/3	3/2
G	2/3	3/4	64/81	8/9	1	256/243	32/27	4/3
A	81/128	729/1024	3/4	27/32	243/256	1	9/8	81/64
B	9/16	81/128	2/3	3/4	27/32	8/9	1	9/8
C	1/2	9/16	16/27	2/3	3/4	64/81	8/9	1

10

Number of intervals = 25 (Pythagorean) +11 (non-Pythagorean) = 36.
Minimum number of different intervals = 6 (Pythagorean) + 5 (non-Pythagorean) = 11.

Table 8. Phrygian mode.

	C	D	E	F	G	A	B	C
C	1	256/243	32/27	4/3	3/2	128/81	16/9	2
D	243/256	1	9/8	81/64	729/512	3/2	27/16	243/128
E	27/32	8/9	1	9/8	81/64	4/3	3/2	27/16
F	3/4	64/81	8/9	1	9/8	32/27	4/3	3/2
G	2/3	512/729	64/81	8/9	1	256/243	32/27	4/3
A	81/128	2/3	3/4	27/32	243/256	1	9/8	81/64
B	9/16	16/27	2/3	3/4	27/32	8/9	1	9/8
C	1/2	128/243	16/27	2/3	3/4	64/81	8/9	1

Number of intervals = 28 (Pythagorean) + 8 (non-Pythagorean) = 36.
Minimum number of different intervals = 7 (Pythagorean) + 5 (non-Pythagorean) = 12.

Table 9. Hypophrygian mode.

	C	D	E	F	G	A	B	C
C	1	256/243	32/27	4/3	1024/729	128/81	16/9	2
D	243/256	1	9/8	81/64	4/3	3/2	27/16	243/128
E	27/32	8/9	1	9/8	32/27	4/3	3/2	27/16
F	3/4	64/81	8/9	1	256/243	32/27	4/3	3/2
G	729/1024	3/4	27/32	243/256	1	9/8	81/64	729/512
A	81/128	2/3	3/4	27/32	8/9	1	9/8	81/64
B	9/16	16/27	2/3	3/4	64/81	8/9	1	9/8
C	1/2	128/243	16/27	2/3	512/729	64/81	8/9	1

Number of intervals = 27 (Pythagorean) + 9 (non-Pythagorean) = 36.
Minimum number of different intervals = 7 (Pythagorean) + 6 (non-Pythagorean) = 13.

INTERVALLIC COMPOSITION OF SEVEN MODES
Total number of intervals = 7×36 = 252.
Total number of intervals other than 1 = 252 – 7×8 = 196.
Total number of inverse intervals = 7×28 = 196.
Total number of intervals and their inverses = 252 + 196 = 448.
Total number of intervals and their inverses other than 1 = 2×196 = 392.
Total number of Pythagorean intervals = 186 (186 – 56 = 130 Pythagorean intervals other than 1). Total number of Pythagorean intervals and their inverses = 2×130 + 7×8 = 316.
Total number of Pythagorean intervals and their inverses other than 1 = 2×130 = 260.
Total, minimum number of different intervals = 46 (Pythagorean) + 37 (non-Pythagorean) = 83

All the pitches of these intervals are pitches of tones of the seven Church modes. Including the seven tonics, the total, minimum number of Pythagorean intervals = 7 + 46 = 53. Total, minimum

11

number of different intervals (including that between each note and itself) = 53 (Pythagorean) + 37 (non-Pythagorean) = 90.

Table 10. Tone ratios of the notes of the seven Church musical modes.

Lydian	1	9/8	81/64	729/512	3/2	27/16	243/128	2
Phrygian	1	256/243	32/27	4/3	3/2	128/81	16/9	2
Dorian	1	9/8	32/27	4/3	3/2	27/16	16/9	2
Hypolydian	1	9/8	81/64	4/3	3/2	27/16	243/128	2
Hypophrygian	1	256/243	32/27	4/3	1024/729	128/81	16/9	2
Hypodorian	1	9/8	32/27	4/3	3/2	128/81	16/9	2
Mixolydian	1	9/8	81/64	4/3	3/2	27/16	16/9	2

Table 10 shows the tone ratios of the notes of the seven octave species. White cells indicate non-Pythagorean tone ratios. The modes have notes with thirteen different tone ratios other than 1 (the “basic set”), as well as their thirteen inverses, totalling 26 (27, including 1):*

256/243    9/8    32/27    81/64     4/3    1024/729     729/512    3/2    128/81     27/16    16/9     243/128     2
243/256    8/9    27/32    64/81     3/4     729/1024    512/729    2/3     81/128    16/27    9/16    128/243     1/2

The number value 26 of Yahweh ('הוה), the Godname of Chokmah, is the number of different rising and falling tone intervals in the seven modes. The Godname prescribes their tonal range. This is consistent with the location of Chokmah in the Tree of Life at the head of the Pillar of Mercy, for this Sephirah denotes the creative power of God, and Yahweh lays down the fullness or scope of the archetypal ideas of the Divine Mind as abstract possibility. The number 26 is also the number of Pythagorean tone ratios other than 1 in the seven modes:

The letter values of YHVH denote the numbers found in individual modes: Y = 10 denotes the number of Pythagorean notes other than 1 in the Dorian, Hypodorian, Phrygian and Hypophrygian modes, H = 5 denotes the number of such Pythagorean notes in the Mixolydian mode and in the Lydian mode and V = 6 denotes the number of such Pythagorean notes in the Hypolydian mode.

The Godname Yah ('ה) with number value 15 prescribes the eight notes of each mode and their seven intervals. This is consistent with its Sephirah Chokmah for the same reason as that given above for Yahweh, the later, full version of this Godname. The Godname Eloha with number value 36 prescribes the 36 notes and intervals of an 8-note musical scale. The Godname Ehyeh with number value 21 prescribes the seven notes below the octave because they have 21 intervals. Of the 56 separate notes in the seven modes, 14 are different notes, leaving (56–14=42) repetitions, where 42 is the 21st even integer. Ehyeh therefore also prescribes those notes that are repeated. Six of them are the tonic 1, leaving (42–6=36) repeated notes above the tonic. Eloha prescribes those notes of the seven modes above the tonic that are repeated. The numbers of intervals of each type in the seven octave species are:

The numbers of intervals of each type in the seven octave species are:
____________________________
* The rising intervals are listed in ascending order of pitch.

12

 

There are 130 Pythagorean intervals other than 1 and 130 of their inverses, totalling 260 (=26×10). Yahweh with number value 26 prescribes the number of Pythagorean intervals and their inverses. This intervallic composition is encoded in the inner form of the Tree of Life as the 260 yods in the seven enfolded polygons outside their shared root edge (Fig. 2). It demonstrates the fact that the seven musical modes constitute an archetypal musical whole. The 36 intervals of each mode are symbolised by the 36 corners of these polygons (Fig. 3).

130 is the 129th integer after 1. The number value 129 of Yahweh Sabaoth, Godname of Netzach, is the number of rising, Pythagorean intervals other than 1 in the seven octave species.

Including the intervals 1, the total number of Pythagorean intervals and their inverses = 260 + 56 = 316. The number of Pythagorean intervals and their inverses other than ½, 1 and 2 = 316 – 7(8+1+1) = 316 – 70 = 246. This is the number value of Gabriel, Archangel of Yesod. It is the number of true intervals and their inverses in the seven modes other than whole octaves.

There are 66 non-Pythagorean intervals and 66 of their inverses, totalling 132. 66 is the 65th integer after 1, where 65 is the number value of Adonai, Godname of Malkuth. This also

13

prescribes the number of Pythagorean intervals other than 1 because 130 is the 65th even integer. The number of intervals other than 1 = 130 + 66 = 196.

The number of intervals (including 1) = 56 + 196 = 252. The number of intervals (including 1) and their inverses = 56 + 2×196 = 448. As a check, this is 7×8×8, the number of entries in the seven 8×8 arrays of intervals.

Table 11 indicates that the Pythagorean scale has 13 repetitions of Pythagorean notes and three repetitions of non-Pythagorean intervals shown in white cells, totalling 16 (purple cells). This is the 15th integer after 1.

Table 11

	C	D	E	F	G	A	B	C
C	1	9/8	81/64	4/3	3/2	27/16	243/128	2
D		1	9/8	32/27	4/3	3/2	27/16	16/9
E			1	256/243	32/27	4/3	3/2	128/81
F				1	9/8	81/64	729/512	3/2
G					1	9/8	81/64	4/3
A						1	9/8	32/27
B							1	256/243
C								1

It shows how the Godname Yah with number value 15 prescribes this pattern of intervals of the Pythagorean scale. It more fundamentally prescribes the 8×8 array of intervals (including 1) and their inverses in terms of the 15 entries forming two adjacent sides of this square array:

The number value 36 of Eloha, Godname of Geburah, is the number of intervals between the eight notes of any scale, counting the intervals 1 between the notes themselves:

14

The number value 49 of the Godname El Chai is the number of intervals between successive notes of the seven octave species:

The number of different intervals between the 56 notes of the seven modes is 90. Remarkably, this is the sum of the integers in the tetractys formed by Plato’s Lambda:

                                                                                                                     1
                                                                                                                   2  3
                                                                                                                4   6   9
                                                                                                              8 12 18 27.

27, the largest integer in the Lambda, is the number of different tone intervals and their inverses between the notes of the seven modes. The sum of the integers 1, 8 and 27 at the corners of the tetractys is 36, which is the number of intervals in each mode.

The four simplest polygons in the inner form of the Tree of Life have 90 yods outside their shared root edge (Fig. 4). This is a remarkable illustration of the Tetrad Principle defining a set of geometrical objects that embody a number of universal significance — in this case the total minimum

number of different intervals between the notes of the seven musical modes. As confirmation that this is not just coincidence, the numbers of yods in the triangle, square, pentagon and hexagon outside their root edge are, respectively, 15, 21, 27 and 27, which are the sums of the integers along diagonal rows of the Lambda tetractys:

This beautiful parallel between the inner geometry of the Tree of Life and the arithmetic properties of the Lambda serves to demonstrate their archetypal character.

15

The minimal set of 90 different intervals in the seven modes includes ones where an interval occurs once in a mode, e.g. the interval 1024/729 in the Lydian mode. The basic set has 14 different ones, so (90–14=76) intervals are repeated. The number value 76 of Yahweh Elohim, Godname of Tiphareth, is the minimum number of these repeated intervals.

Inspection of the tables of intervals reveals that, of the 66 non-Pythagorean intervals, 16 (=4²) are between the tonic C and other notes. There are (66–16=50) non-Pythagorean intervals between notes other than C. This shows how the Godname Elohim with number value 50 prescribes non-Pythagorean intervals between notes other than the tonic. The number of non-Pythagorean intervals and their inverses between the notes and the tonic C or octave C' is 32, which is the 31st integer after 1. This shows how the Godname El assigned to Chesed with number value 31 prescribes the non-Pythagorean intervals between notes and opposite ends of each mode.

Similarly, the tables show that, of the 130 Pythagorean intervals, 33 (= 1! + 2! + 3! + 4!) intervals are between C and other notes, leaving (130–33=97) Pythagorean intervals between notes other than the tonic. 97 is the 49th odd integer, showing how the Godname El Chai assigned to Yesod with number value 49 prescribes this number. 97 is also the number value of Haniel, the Archangel of Netzach. Including the unit intervals between the 56 notes themselves, the number of Pythagorean intervals between notes other than the tonic = 97 + 56 = 153. This is the number value of Elohim Sabaoth, the Godname assigned to Hod. The number of Pythagorean and non-Pythagorean intervals between C and other notes = 33 + 16 = 49. Therefore, El Chai prescribes the intervals in the seven modes between the tonic and other notes, as well as the Pythagorean intervals between notes above the tonic.

Below is a summary of how the Godnames prescribe properties of the seven octave species.

Kether: 21.	21 intervals between 7 notes below the octave; 42 repetitions of basic set of 14 notes forming the 7 modes, where 42 = 21st even integer.
Chokmah: 15.                  26.	8 notes in each mode separated by 7 intervals, totalling 15 notes & intervals. number of different intervals other than 1 and their inverses; number of harmonics in 7 cycles of 7 modes. 260 (=26×10) Pythagorean intervals and their inverses.
Binah: 50.	number of non-Pythagorean intervals between notes above the tonic.
Chesed: 31.	number of non-Pythagorean intervals and their inverses between notes and the tonic or octave = 32, which is the 31st integer after 1.
Geburah: 36.	number of repetitions of basic set of 14 notes above the tonics of the 7 modes; each mode has 8 notes and 28 intervals, totalling 36 notes and intervals.
Tiphareth: 76.	minimum number of repeated intervals.
Netzach: 129.	130 Pythagorean intervals, where 130 = 129th integer after 1.
Hod: 153.	number of Pythagorean intervals (including those between the notes themselves) between notes above the tonic.
Yesod: 49.	number of intervals between successive notes of 7 modes; number of Pythagorean and non-Pythagorean intervals between the tonic and other notes; 97 Pythagorean intervals between notes other than the tonic, where 97 = 49th odd integer.
Malkuth: 65.	number of non-Pythagorean intervals = 66, where 66 = 65th integer after 1; 130 Pythagorean intervals, where 130 = 65th even integer.

16

4. The Lambda Tetrahedron

The number of Pythagorean and non-Pythagorean intervals between notes other than the tonic = 97 + 50 = 147. Similarly, these have 147 inverse intervals on the opposite sides of the diagonals of Tables 3–9. Therefore, there are (147+147=294) Pythagorean and non-Pythagorean

intervals between notes other than C together with their inverses. Including the 56 intervals 1 on the diagonals, there are (56+294=350) such intervals. They comprise 50 non-Pythagorean intervals and their 50 inverses, that is, 100 non-Pythagorean intervals, leaving (350–100=250) diagonal intervals, Pythagorean intervals between notes other than the tonic and their inverses (check: 250 = 56 + 97 + 97). The division:

350 = 100 + 250

between the 100 non-Pythagorean intervals and their inverses and the 250 Pythagorean ones and their inverses has its parallel in the tetrahedral version of the Lambda tetractys discussed in Article11.¹² The 20 integers arranged in tetractyses on the four faces of the tetrahedron add up

to 350 (Fig. 5), the sum of the cubes of 1, 2, 3 & 4 at its four corners is 100 and the sum of the 16 other integers is 250. The tetrahedron embodies the interval composition of the seven modes.

5. Pattern of modal intervals in superstring oscillations

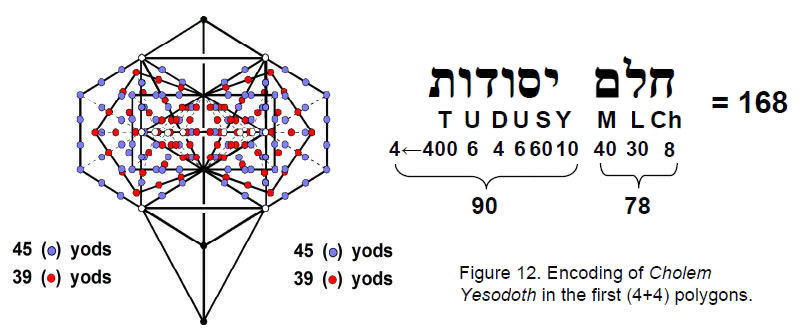
The seven modes have 130 rising, Pythagorean intervals other than 1, of which 46 comprise the minimum number of different Pythagorean intervals, these varying from mode to mode. There are (130–46=84) such Pythagorean intervals that are repetitions of the basic set. Similarly, there are 84 falling, Pythagorean intervals with reciprocal tone ratios that are repetitions. There are (84+84=168) repetitions of the Pythagorean intervals and their inverses. The number value 168 of Cholem Yesodoth, Mundane Chakra of Malkuth, is the number of Pythagorean intervals and their inverses

17

that are repetitions of any of the seven basic Pythagorean intervals other than 1 and their inverses. This 84:84 division is embodied in the inner Tree of Life as the 168 yods lying on the sides of the first (6+6) enfolded polygons, 84 on either side of the root edge (Fig. 6).

The 2nd-order tetractys has 84 yods surrounding its centre (Fig. 7), where 84 = 1² + 3² + 5² + 7² . This means that any aspect of physical reality that embodies cosmic wholeness symbolised by the tetractys is expressed by 84 degrees of freedom in this reality, which is symbolised by the central yod of the central 1st-order tetractys of the 2nd-order tetractys. This number accords with the Tetrad Principle because 1, 3, 5 & 7 are the first four odd integers.

The 84:84 division corresponds in the subquark superstring to the inner and outer halves of the UPA, each of which comprises 2½ revolutions of ten whorls with 840 1st-order spirillae in each one (Fig. 8). Every ten spirillae can be said to correspond to a diatonic interval between the notes of the seven Greek modes, the outer and inner halves corresponding to the intervals and their inverses. It is as if the circularly polarised oscillations of each whorl reproduce all the diatonic intervals between different notes of the seven musical modes.

6. Comparison of modal intervals with the octonions

This conclusion in the context of superstring structure returns us full circle to the discussion in Article 15 of the similarity between the 8-note scale and the eight unit octonions, as now explained. The octonions, or Cayley numbers, form the fourth class of division algebras. There are one real unit octonion, 1, and seven imaginary unit octonions e_i (i = 1–7) with the property e_i² = -1 (i = 1–7). Their multiplication is anti-commutative:

e_ie_j = -e_je_i

(i ≠ j)

18

Table 12 is the multiplication table for the 8-tuple of unit octonions: (1, e₁, e₂, e₃, e₄, e₅, e₆, e₇).

There are 28 octonions in the violet triangle and 28 octonions in the blue triangle. The 21 octonions formed by multiplication of pairs of e₁, e₂ … e₇ in the dashed triangle on one side of the diagonal of the square array are the negatives (that is, reciprocals, because e_i² = -1, so that -e_i = 1/e_i) of their 21 counterparts in the dashed triangle on the other side of the diagonal. There are 21 octonions with positive signs and 21 with negative signs. The Godname El Chai with number value 49 prescribes the number of products of imaginary octonions, the Godname Ehyeh with number value 21 prescribing how many of them have positive signs and how many have negative signs, that is, how many are the reciprocals of them.

Compare this with the intervals between the notes of the Pythagorean scale shown below in Table 13.

The pitch decreases of the 28 falling intervals (D-C, etc) in the violet triangle are the reciprocals of the pitch increases of the 28 corresponding rising intervals (C-D, etc) in the blue triangle. The eight diagonal entries 1 denote the zero pitch difference between each note and itself.

19

In both tables, the diagonal set of entries is like a mirror that reflects each entry into its image. Each entry in a triangle in Table 12 corresponds to an interval, a negative octonion being the counterpart of a falling interval because it is the reciprocal of an octonion, just as the decrease in pitch of a falling interval is the reciprocal of the increase in pitch of the same rising interval.

Multiplication of two imaginary octonions: e_i×e_j (j>i) corresponds to the interval between two rising notes i and j. Multiplication in the reverse order corresponds to the interval between the notes j and i in order of descending pitch. Non-commutativity of octonion multiplication: e_ie_j = - e_je_i corresponds to the pitch decrease of a falling interval being the reciprocal of that of the same rising interval.

The seven imaginary octonions form seven 3-tuples:

1. (e₁, e₂, e₄)
2. (e₂, e₃, e₅)
3. (e₃, e₄, e₆)
4. (e₄, e₅, e₇)
5. (e₅, e₆, e₁)
6. (e₆, e₇, e₂)
7. (e₇, e₁, e₃)

It was proposed in Article 15¹³ that these 3-tuples are the octonion equivalent of the seven Greek octave species because they each form seven combinations of one, two and three octonions in analogy to the seven notes of each species. Furthermore, it was shown that the seven 3-tuples have 84 permutations of pairs and triplets and that the seven 3-tuples of negative octonions (inverses of octonions) have 84 permutations of their pairs and triplets, a total of 168 permutations. Each 3-tuple corresponds to an octave species. Each mode has on average 12

repetitions of its diatonic intervals (see below) and each of these intervals correspond to a permutation.

The same pattern is displayed in the Klein Configuration (Fig. 9) of the 168 elements of the group of transformations of the Klein Quartic Equation, which is well known to mathematician.¹⁴ Each of the 14 slices shown numbered has 12 coloured triangles. The slices are of two types, each type containing 12 triangles arranged in the whole configuration as 24 heptagons. The seven slices of one type correspond to the repeated, rising intervals of the seven octave species and the seven slices of the other type correspond to their repeated, falling intervals, the 12 coloured triangles in a slice corresponding to the average number of 12 repetitions of diatonic intervals or their inverses.

Such precise parallelism between the seven musical modes and an object that is regarded in

20

the mathematical world as possessing great beauty is evidence of the archetypal Ideas of the Divine Mind being realised in two contexts that appear superficially to have nothing in common, namely, music and the M-theory underlying superstring physics, which physicists are currently seeking in order to unify their understanding of the forces of nature in a single theory. However, sound is a vibration of the air and, just as a plucked string creates musical notes of different frequencies, so superstrings vibrate in a variety of ways to create all the subatomic particles of which they are components. The form of a superstring is therefore generated by a process analogous to playing the intervals — both rising and falling — between (as shown below) the notes D, E, F, G & A of the seven musical modes.

By inspecting the table of intervals for each mode, counting its number of Pythagorean intervals and subtracting the number of different Pythagorean intervals indicated under each table, the numbers of repetitions of these intervals for individual modes are found to be:

Hypolydian	Mixolydian	Lydian	Dorian	Hypodorian	Phrygian	Hypophrygian
13	11	12	12	11	13	12

Total = 84.
Average = 84/7 = 12.

In terms of notes, the composition of the 84 Pythagorean intervals is:

D	E	F	G	A
28	11	23	17	5

The interval 243/128 for note B and the interval 2 for note C' are absent because they are the only ones that never appear more than once in a mode (Phrygian, Lydian, Hypophrygian and Hypolydian) and so have no repetitions. Five different intervals comprise the set of 84. This 5:1 division has the following analogy with the Tree of Life: the lowest five Sephiroth of Construction:

Malkuth, Yesod, Hod, Netzach & Tiphareth (Fig. 10) constitute what in Kabbalah is called its ‘Lower Face,’ or ‘Microposopus.’ They formally correspond to the five types of intervals that are repeated 84 times. The octave and note B, which are not repeated, formally correspond, respectively, to Chesed and Geburah, which are unshared with adjacent members of a set of overlapping Trees of Life, that is, they are intrinsic to their own trees.

This 5:2 division is reflected also in the five tone intervals (T) and two leimmas (L) of each mode:

21

T L T T T L T   L T T T L T T   T T T L T T L   T T L T T L T   T L T T L T T   L T T L T T T   T T L T T T L

Dorian Phrygian Lydian Mixolydian Hypodorian Hypophrygian Hypolydian

It is also manifested by the seven modes themselves because, regarding the 14 notes that they span as a cycle that starts again on the second octave, five successive cycles generates 15 harmonics and seven cycles creates 26 harmonics, where 15 is the number value of the Godname Yah, the older version of the Godname Yahweh, whose number value is 26.

In Kabbalistic traditions of esoteric knowledge, the lowest five Sephiroth of Construction have the following correspondence with the five Elements:

Tiphareth	↔	Aether
Netzach	↔	Fire
Hod	↔	Air
Yesod	↔	Water
Malkuth	↔	Earth

The very diatonic intervals that correspond to the five Elements are therefore those whose repetitions and their inverses number 168, the number value of Cholem Yesodoth, Mundane Chakra of Malkuth, the lowest Sephirah.

The 168 automorphisms of the Klein Quartic are represented by the 168 coloured, hyperbolic triangles of the Klein Configuration:

168 = 7×24 = 7×[(1 + 2) + (4 + 3) + (4 + 3) + (4 + 3)]         = 7(4 + 4 + 4) + 7[(3 + 3 + 2) + (3 + 1)]         = (28 + 28 + 28) + (56 + 28)         = 84 + 84.

Seven slices of one type have 84 triangles made up of 28 red, 28 yellow and 28 green triangles and the seven slices of the other type have 84 triangles made up of 21 yellow, 21 green, 21 red and 21 blue triangles. Compare the former with the fact that the 84 Pythagorean intervals between notes D, E, F, G & A comprise 28 seconds, 11 thirds, 23 perfect fourths, 17 perfect fifths and 5 sixths, that is, 28 seconds, 28 thirds and fifths and 28 perfect fourths and sixths. For the

22

84 coloured triangles belonging to seven slices of one type, the same pattern of three groups of 28 exists in both cases, although which sets of 28 coloured triangles correspond to which groups of 28 intervals cannot be ascertained at this stage. The four important features to notice are:

1. the Klein Configuration naturally divides the number 168 into two sets of 84 as its two types of slices have a total of 84 hyperbolic triangles;
2. the 168 Pythagorean intervals between notes D, E, F, G & A of the seven modes divide into 84 ascending and 84 descending intervals (the 84 entries on one side of the diagonal of their tables of intervals and 84 entries on the other side;
3. the seven 3-tuples of octonions have 84 permutations of two and three octonions and 84 permutations of two and three of their inverses;
4. the 168 1st-order spirillae in each half-revolution of a whorl of the UPA comprise 84 in its outer half and 84 in its inner half.

They indicate the following correspondences:

rising/falling Pythagorean intervals in seven modes

permutations of two and three octonions/inverse octonions in seven 3-tuples

coloured triangles in seven slices of Klein Configuration

1st-order spirillae in inner or outer half of UPA making a half-revolution

The division of the Klein Configuration into two types of slices corresponds to the distinction between rising and falling intervals and to the difference between octonions and their inverses. The profound consequences of this analogy will be explored in a future article.

It was found earlier that the first four polygons of the inner form of the Tree of Life have 90 yods outside their root edge that correspond to the different intervals (including 1) of the seven Greek musical modes. Four of these yods are their centres and two (the top and bottom corner of the hexagon) coincide with Chokmah and Netzach (Fig. 11).
 

There are (90–4–2=84)other yods in these polygons outside their root edge, both sets of four polygons having (84+84=168) such yods. The yods in one set of polygons correspond to the coloured triangles in the seven similar slices of the Klein Configuration, repeated, rising Pythagorean intervals between the notes D, E, F, G, & B in the seven modes, permutations of two and three octonions in the seven 3-tuples and 1st-order spirillae in one-half of a revolution of the inner or outer half of the UPA. The yods in the other, mirror image set of polygons correspond to the coloured triangles in the other set of

23

similar slices of the Klein Configuration, repeated, descending Pythagorean intervals, permutations of two and three inverse octonions in their seven 3-tuples and 1st-order spirillae in a half of a revolution of the outer or inner half of the UPA. The musical counterpart of the two identical halves of the inner form of the Tree of Life is the musical distinction between rising and falling intervals. Its octonion counterpart is the difference between the imaginary octonions and their inverses. Its counterpart in the Klein Configuration is the difference between its two types of slices (their mathematical difference is too technical to discuss here).

Remarkable confirmation that it is not coincidental that the first (4+4) polygons should have 168 yods other than their centres and those coinciding with the positions of Sephiroth comes from the way in which the number values of the Hebrew words ‘Cholem’ and ‘Yesodoth’ summing to 168 are themselves embodied in the yod populations of these polygons (Fig. 12). The numbers of yods in the triangle, square, pentagon and hexagon that are outside the root edge and which are not centres of polygons or coincident with the positions of Sephiroth of the Tree of Life when the latter is projected onto the plane containing the polygons are listed below:

The triangle and pentagon have 39 yods and the square and hexagon have 45 yods. Hence, both sets of triangles and pentagons have 78 yods and both sets of squares and hexagons have 90 yods. The number value of Cholem is 78 and the number value of Yesodoth is 90. The very numerical values of the Hebrew words of the Mundane Chakra of Malkuth are encoded geometrically in the first (4+4) polygons! This is an example of the Tetrad Principle,¹⁵ wherein the fourth member or the first four members of a sequence of mathematical objects always embody a number that has cosmic significance, such as the number of space-time dimensions, the number of particles transmitting superstring forces or the oscillatory form of a superstring.

Set out below are the ways in which properties of the first four polygons and the first (4+4) polygons are prescribed by the number values of the Godnames of the ten Sephiroth:

Kether: 21	21 geometrical elements in the first (4+4) polygons are shared with the 1-tree;*
Chokmah: 15                                  26	the first 4 enfolded polygons have 15 sides and 15 corners of their 17 tetractyses. The number of yods on the boundaries of the 34 tetractyses of the first (4+4) polygons = 150 = 15×10. The first (4+4) polygons share 15 corners and sides with the Tree of Life; the first (4+4) enfolded polygons have 26 corners outside their root edge. Every first 4 polygons enfolded in successive Trees of Life have 26 corners & sides. The first (4+4) enfolded polygons share 26 corners & sides with the Tree of Life;
Binah: 50	number of corners & sides of the first (4+4) enfolded polygons = 51 = 50th integer after 1. The first (4+4) enfolded polygons have 50 sides unshared with the 1-tree;
Chesed: 31	number of sides of 17 tetractyses in the first 4 enfolded polygons = 31. Tree of Life has 31 geometrical elements unshared with the first (4+4) enfolded polygons;
Geburah: 36	the first 4 separate polygons have 36 corners and sides and 36 sides of their 18 tetractyses. The polygons have 36 hexagonal yods on their boundaries. The first (4+4) separate polygons have 36 corners and 36 sides;
Tiphareth: 76	the first 4 separate polygons have 76 geometrical elements. The first (4+4) enfolded polygons have 76 yods outside their root edge on their boundaries and 152 yods unshared

____________________________________________
*The 1-tree is the lowest Tree in a set of overlapping Trees of Life.

24

	with the 1-tree, where 152 = 76th even integer;
Netzach: 129	the first (4+4) enfolded polygons have 130 yods on their boundaries other than corners outside their root edge, where 130 = 129th integer after 1;
Hod: 153	the first (4+4) enfolded polygons have 154 hexagonal yods outside their root edge, where 154 = 153rd integer after 1;
Yesod: 49	every first (4+4) polygons enfolded in successive Trees have 49 corners and sides;
Malkuth: 65	66 hexagonal yods in the first 4 enfolded polygons are unshared with the 1-tree, where 66 = 65th integer after 1;
155	the first (4+4) enfolded polygons have 156 yods outside their root edge unshared with the Tree of Life, where 156 = 155th integer after 1.

The Godnames define that section of the inner form of the Tree of Life blueprint that encodes the structural parameter 168 of superstrings. Actually, they prescribe other sections as well that embody the same number (e.g., the first (6+6) polygons).¹⁶ This is because of the fractal-like quality of the inner form of the Tree of Life, in which the same information about the physical manifestation of the blueprint is encoded in different but equivalent sections of it.

Conclusion

In coming to the consensus (or almost so) that the ancient Greek musical modes were likely to have been different keys of a single scale, scholars have either ignored or been oblivious of ancient writers who told of how Pythagoras, Plato and Greek musicians learned from the ancient Egyptians, who, according to Nichomachus, ascribed 28 sounds to the universe. This meant that the latter — and almost certainly also the former — knew about the seven octave species with 28 notes. This makes it highly likely, if not certain, that the Greek modes were different scales and that their patterns of intervals were known to those with musical learning, for why would ancient Greeks have played all their music in different keys of one scale if some of them knew of seven such scales? The fact that early Christian musical theorists appropriated Greek modal labels in their derivation of the church modes from the Byzantine octoechoi does not have the implication that the ancient Greeks did not understand their modes as scales. All it means is that the church modes were not directly inherited from Greek octave species. To conclude from this fact that the Greek modes were not different musical scales, as musical scholars like Rita Steblin do, is simply a non sequitur.

The ten Godnames prescribe different sets of intervals between the notes of the seven scales. The reason for this is that the seven octave species constitute a whole — both mathematically and spiritually. The tetractys version of Plato’s Lambda has ten numbers that sum to 90. This is the number of different intervals between the notes of the seven scales. Just as four numbers — 1, 2, 4/3 & 3/2 — generate the Pythagorean scale and therefore all seven scales with a minimum number of 90 different intervals, so four yods lie on the shared base of the first four polygons of the inner form of the Tree of Life, having 90 yods outside it. The fact that the four inclined rows of the Lambda tetractys add up to the yod population of each polygon confirms that this remarkable correspondence is not coincidental. The tetrahedral generalisation of the Lambda tetractys has 20 numbers that sum to the number of intervals between notes above the tonic of each scale. There are 84 copies of the rising, Pythagorean intervals in the seven scales and similarly for the falling, Pythagorean intervals. This 84:84 pattern is present in the first (4+4) polygons as their (84+84) yods that are neither centres of polygons nor coincident with the positions of Sephiroth of the Tree of Life. Confirmation that this is not coincidental is the fact that the number values of the two words making up the Hebrew name of the Mundane Chakra of Malkuth with number value 168 are the yod populations of pairs of polygons in the set of four and their counterparts on the other side of their shared edge. The ten Godnames prescribe the first (4+4) polygons as a Tree of Life pattern encoding the superstring structural parameter 168.

The eight unit octonions are the counterpart in number theory of the eight notes of the musical scale. The real unit octonion corresponds to the octave and the seven imaginary unit octonions

25

correspond to the seven notes below it. Multiplication of pairs of octonions is equivalent to the rising interval between two notes. Division is equivalent to their falling interval, that is, to the interval between them in reverse order. Anticommutivity of their multiplication corresponds to the pitch difference of two notes being the reciprocal of that of the two notes in reverse order. The counterpart in the Klein Configuration of the 168 copies in the seven musical scales of the basic set of rising and falling Pythagorean intervals is its 168 triangles denoting the automorphisms of the Klein Quartic. Its seven slices of one type with 84 triangles correspond to the set of 84 rising, Pythagorean intervals in the seven scales and the seven slices of the other type with 84 triangles correspond to their set of 84 falling, Pythagorean intervals. The triangles denote the 168 elements of PSL(2,7). As every element of a group has its inverse, the rising and falling Pythagorean intervals correspond to group elements of PSL(2,7) and their inverses. The 84 permutations of two and three octonions in the seven 3-tuples and the 84 similar permutations of their inverses are the octonion counterparts of the 84 copies of rising intervals and the 84 copies of falling intervals that are Pythagorean.

The seven notes above the tonic of the Pythagorean scale and the seven unit imaginary octonions in the fourth division algebra are analogous in ways beyond coincidence because they are examples of the seven-fold nature of the phenomenal aspect of God manifested in the world, as abstractly symbolised by the seven hexagonal yods of the tetractys and as expressed in the Tree of Life by its seven Sephiroth of Construction. Music is patterns of sound frequencies, or real numbers (the first division algebra), ordered in time, i.e., pairs of numbers (frequency, time coordinate) that are analogous to the complex numbers (the second division algebra). Sound is a vibration of a three-dimensional medium taking place in time, i.e., sets of four numbers define its displacement, analogous to the four-dimensional quaternions (the third division algebra). The eight-dimensional octonions associated with vibrating superstrings are the fourth and last division algebra. In conformity with the title “holding the key of nature” assigned by the Pythagoreans to the Tetrad, the vibrations of the macrocosm and the microcosm are connected by four classes of number.

References

¹ A History of Key Characteristics, Rita Steblin (University of Rochester Press, 2003), p. 13.

² A History of Western Music (3rd ed.), Donald Jay Grout (J.M. Dent & Sons Ltd, 1980), p. 32.

³ Ibid, p. 34.

⁴ Ibid, pp. 14-15.

⁵ The Pythagorean Sourcebook and Library, Kenneth Sylvan Guthrie (Phanes Press, 1987), p. 167.

⁶ Strabo, lib. xvii, p. 29.

⁷ The History of Music, vol. 1, W. Chappell (London, 1874), p. 1.

⁸ Ibid, p. 60.

⁹ Ibid, pp. 50-51.

¹⁰ Aristides Quintilianus, lib. iii, p. 136.

¹¹ Ibid, p. 52.

¹² Phillips, Stephen M: Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF), pp. 7-16.

¹³ Phillips, Stephen M: Article 15: "The Mathematical Connection between Superstrings and

26

 

their Micro-psi Description: a Pointer Towards M-theory,” (WEB, PDF), pp. 28-30.

¹⁴ Ibid, pp. 24-27.

¹⁵ Phillips, Stephen M: Article 1: “The Pythagorean Nature of Superstring & Bosonic String Theories,” (WEB, PDF), p. 5.

¹⁶ Phillips, Stephen M. Article 4: “Godnames prescribe inner Tree of Life,” (WEB, PDF), p. 4.

27