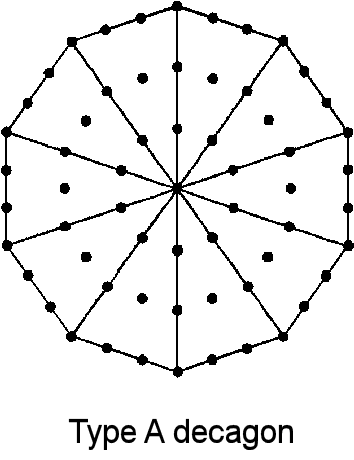
 (1) The decagon contains 61 yods, where
(1) The decagon contains 61 yods, whereThe decagon
TYPE A DECAGON
 (1) The decagon contains 61 yods, where
(1) The decagon contains 61 yods, where
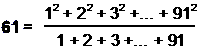
is the 31st odd integer and the gematria number of AIN ("Light"), the Absolute, the first of the three "Veils of Negative Existence" that precede Kether, the first Sephirah of the Kabbalistic Tree of Life. The decagon has 50 hexagonal yods. The decagonal representation of the Godname number of Malkuth was discussed in #17 in Superstrings as sacred geometry/Tree of Life. The decagon has 31 internal yods. The 61 yods correspond to the 61 yods that line the sides of the 19 tetractyses making up the 1-tree, there being 50 hexagonal yods on its 25 Paths:
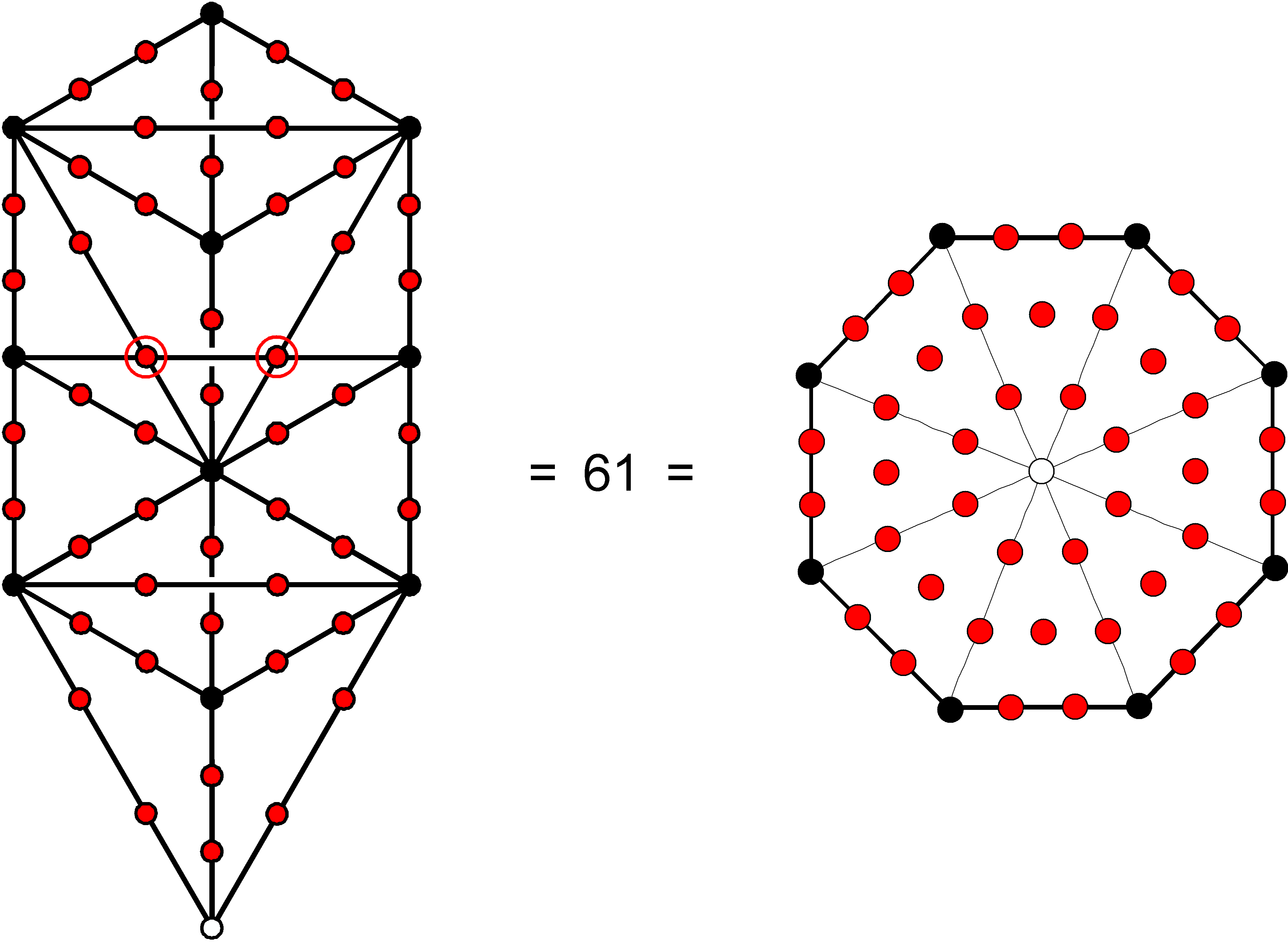
The values of the Hebrew letters making up AIN are: A =1,
I = 10 & N = 50. They are represented by, respectively, the white yod at the centre of
the decagon, its 10 black corners and its 50 red hexagonal yods.
(2) Two enfolded decagons have 118 yods. Of these, 49 hexagonal yods are associated
with each one.
(3) The yod population of the (6+6) separate polygons up to the decagon is 444 [1].
Remarkably, this is the number of hexagonal yods in (7+7) enfolded polygons (see here). The first six separate polygons have 36 corners, the same
number as seven enfolded polygons. This is how the Godname ELOHA of Geburah prescribes a subset of the separate
polygons whose yod population (444) is a Tree of Life parameter. The first six enfolded polygons have 26
corners, whilst the (6+6) enfolded polygons have 50 corners. This set, which is prescribed by YAHWEH
and ELOHIM, as well as by the other Godnames, constitutes a holistic system that embodies the gauge
symmetry group E8 and 3-dimensional structure (see here & here) of the subquark state of superstrings, as described by Annie Besant and
C.W. Leadbeater in their book Occult Chemistry.
(4) The number of hexagonal yods in an n-gon = 5n. The number of hexagonal yods in
the (6+6) separate polygons up to the decagon = 2×5(3+4+5+6+8+10) =2×5×36 = 360, where
|
36 |
34 |
|||||||
| 36 | 36 | 35 | 35 | |||||
| 360 = |
36 |
36 |
36 |
= |
36 |
36 |
36 |
|
| 36 | 36 | 36 | 36 | 37 | 37 | 37 | 37 . |
The number of corners and centres in this set of 12 polygons =
12 + 36 + 36 = 84, where
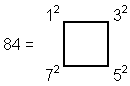
i.e., the number of yods
surrounding the centre of a 2nd-order tetractys (see here).
(5) The
sum of the first 61 integers is 1891 = 61×31, where 31 is the number of EL (“God”).
Assigning these integers to the yods in the decagon, the sum of the first 31 integers inside the decagon
is 496, i.e., the decagon encodes the number of Malkuth. As the tetractys-divided decagon is a
representation of the 10-tree up to the first Sephirah of Construction (Chesed) of the 10th tree (the
counterpart of the first of the 10 dimensions of superstring space-time), we see that the prediction by
superstring theory that 10-dimensional superstrings interact through 496 gauge fields is actually
encoded arithmetically in the decagon, the symbol of the Decad sacred to the Pythagoreans. Alternatively, assigning the
first 31 odd integers to the interior yods and the first 30 even integers to the yods on the boundary,
the sum of the former is 961 = 312 and the sum of the latter is 930 = 30×31, i.e.,
31 is the arithmetic mean of both the internal odd integers and the even integers on the
boundary.
(6) Sum of squares of first 61 integers = 77531 = 61×31×41, where 41 = 15 + 26.
Sum of squares of 31 internal integers = 39711 = 61×31×21.
Sum of squares of 30 boundary integers = 37820 = 61×620, where 620 is the number of Kether.
(7) The decagon defines the ratio
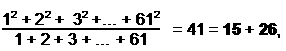
which is the 21st odd integer and the sum of the numbers of YAH and YAHWEH. This number determines the 3-dimensional form of each whorl of the subquark superstring described with micro-psi vision by Besant & Leadbeater because 412 − 1 = 1680.
TYPE B DECAGON
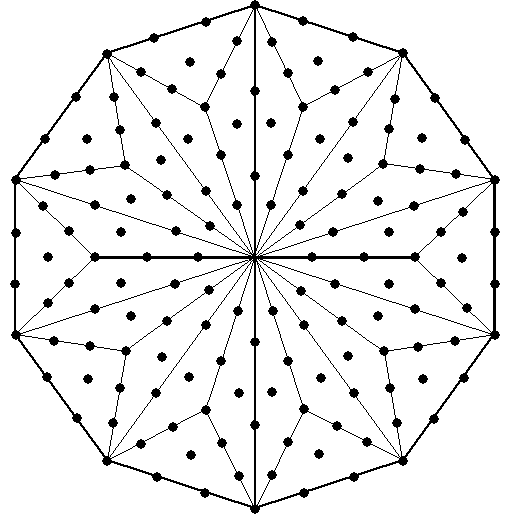 (1) The decagon contains 151 yods (76th odd integer). It
therefore encodes a parameter of CTOL, the 49-tree having 151 tree levels [2]. The decagon
has
(1) The decagon contains 151 yods (76th odd integer). It
therefore encodes a parameter of CTOL, the 49-tree having 151 tree levels [2]. The decagon
has
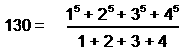
hexagonal yods and 21 yods at the corners of its 30 (=
12 + 22 + 32 + 42) tetractyses.
(2) The decagon has 30 boundary yods and 120 (= 22 + 42 + 62
+ 82) internal yods surrounding its centre. Two separate decagons have 240 internal yods surrounding
their centres and 260 hexagonal yods. The Type B decagon encodes the population of hexagonal yods in seven
separate Type A polygons and the population of yods in seven enfolded Type A polygons (see here). Two enfolded decagons have 256 (= 44) hexagonal yods
outside their shared root edge, illustrating the powerful influence of the Tetrad in defining the properties of
the various polygons generated by the Tree of Life.
(3) The ratio:
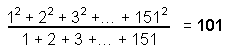
is the 26th prime
number and the number value of Michael, the Archangel of Tiphareth. It is a parameter of CTOL, being the
number of SLs on the central pillar of the 49-tree that maps the seven planes of the cosmic physical plane
(see here).
(4) The
sum of the first 151 integers = 11476 = 151×76, i.e., the same as the sum of the number of YAHWEH ELOHIM
assigned to each yod in the decagon. The Godname of Tiphareth is embodied arithmetically in the decagon as
the arithmetic mean of these integers. Assigning them to the yods, the sum of the 121 internal integers is 7381
= 121×61, i.e., the same as the sum of the number of AIN assigned to each internal yod. The sum of the
boundary integers is 4095 = 45×91. This is the sum of the 45 integers forming the boundary of the
tetractys array shown below with the number
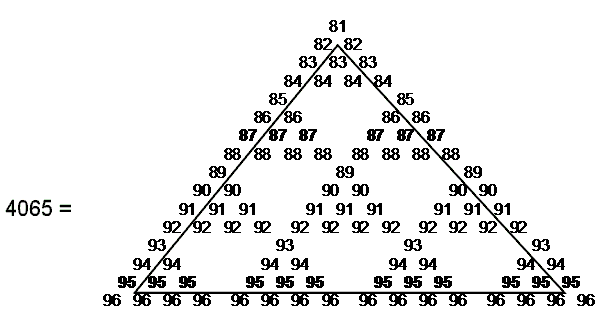
91 at its centre, demonstrating a remarkable analogy between the tetractys and the decagon. Notice that 55 integers are inside its boundary, where 55 is the tenth triangular number.
(5) The sum of the squares of the first 151 integers is 1159076 = 151×76×101, where 76 is the number of the Godname of Tiphareth and 101 is the number value of Michael, its Archangel.
TYPE A + TYPE B DECAGONS
(1) Two
separate decagons contain 212 yods, i.e., there are
|
21 |
||||
| 21 | 21 | |||
| 210 = |
21 |
21 |
21 |
|
| 21 | 21 | 21 | 21 |
yods surrounding their centres, which, together with the other independent centres, are prescribed by the Godname EHYEH with number value 21. Of these yods, 180 are hexagonal yods and 30 are corners. There are
|
15 |
||||
| 15 | 15 | |||
| 150 = |
15 |
15 |
15 |
|
| 15 | 15 | 15 | 15 |
internal yods surrounding their centres, where 15 is the number of YAH, the Godname of Chokmah.
(2) Number of hexagonal yods in the first six separate (Type A+Type B) polygons up to the decagon = 648
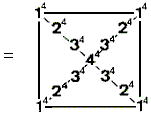
This illustrates in a remarkable way the connection between the
Tetrad and this set of polygons, which, having 50 corners when enfolded, is prescribed by the number of
ELOHIM as a new variant of the holistic geometry of the inner Tree of Life.
DECAGON WITH 2ND-ORDER TETRACTYSES AS SECTORS
As discussed in #5 at Wonders of sacred
geometry/Miscellaneous, a decagon with 2nd-order tetractyses as its sectors has
620 hexagonal yods (the red & blue yods in the diagram below). Appropriately, the 10-sided
polygon embodies the number value 620 of Kether, the first Sephirah and the seed source of
the ten-fold Tree of Life. The number of yods surrounding its centre is 720. This is the number of yods
surrounding the centres of the seven regular Type B polygons making up each half of the inner form of the
Tree of Life:

The 360 yods in the five-fold array of red or blue sectors correspond to the 360 yods surrounding the centres of either these combinations of polygons with 24 corners:
(triangle, square, pentagon, dodecagon) and (hexagon, octagon, decagon)
or these combinations:
(triangle, pentagon, hexagon, decagon) and (square, octagon, dodecagon).
The 5:5 division of sectors in the decagon corresponds to the 24:24 division of the holistic parameter 48 displayed by holistic systems (see The holistic pattern). This is how the Decad, symbolized by a decagon, determines the yod population of the seven separate, regular polygons that make up the inner form of the Tree of Life. Both ELOHA, the Godname of Geburah with number value 36, and EL, the Godname of Chesed with number value 31, prescribe this 5:5 division because each set of five sectors has 360 (=36×10) yods and 310 (=31×10) hexagonal yods surrounding the centre of the decagon.
Notes
1. Proof: The number of yods in an n-gon = 6n + 1. The number of yods in the first six separate n-gons of the inner
Tree of Life = 6∑n + 6 = 6(3+4+5+6+8+10) +
6 = 6×36 + 6 = 222. The number of yods in the two sets of the first six separate n-gons =
2×222 = 444.
2. Proof: a tree level:
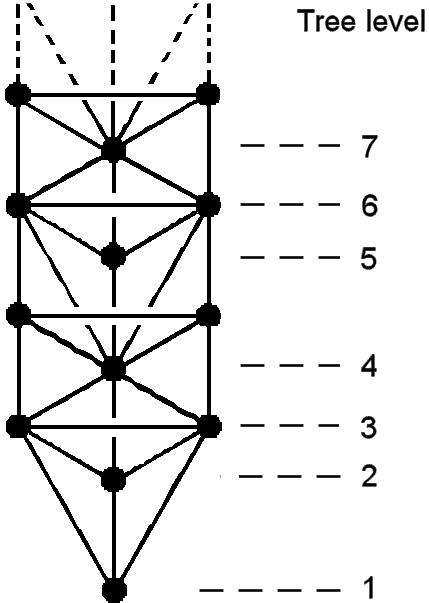
is a horizontal level in any set of overlapping Trees that is marked by either one or two Sephiroth shared with neighbouring Trees. Daath is included here in the definition because, being Yesod of the next higher Tree, it is shared with that Tree, whilst the Path connecting Chesed and Geburah does not count as a tree level because these two Sephiroth are unshared with adjacent Trees. The n-tree has (3n+4) tree levels, so that the number of tree levels in the 49-tree = 3×49 + 4 = 151. As this number is the 76th odd integer, the Godname YAHWEH ELOHIM with number value 76 prescribes the 49-tree mapping the cosmic physical plane.