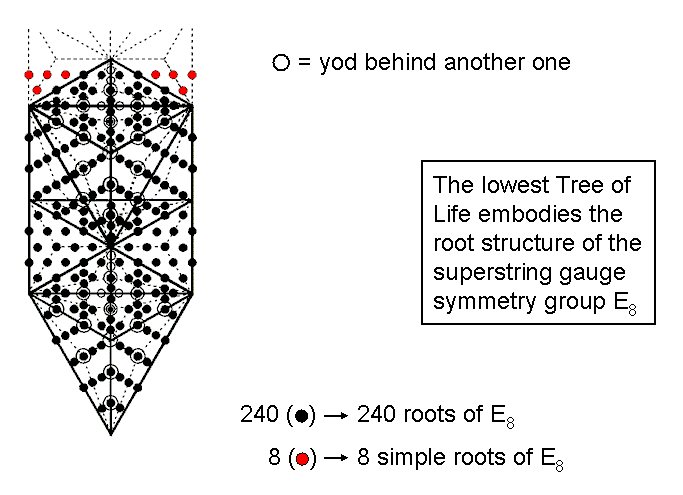
When its 19 triangles are divided into their 57 sectors and the latter then turned into tetractyses, the lowest of any set of overlapping Trees of Life have 251 yods.* Eleven of these are SLs, leaving 240 black yods. There are four red yods below its top outside this Tree on either side of the central Pillar of Equilibrium. The eight red yods symbolize the eight simple roots of E₈ and the 240 black yods denote its 240 roots. 248 yods are needed to construct the lowest Tree of Life (the most Malkuth level of the Cosmic Tree of Life), starting from its apex. This demonstrates par excellence the holistic nature of this number.

The roots of the E₈ algebra can be described in terms of eight orthonormal unit vectors {u_i}. Eight zero roots correspond to points at the centre of the root diagram and 240 non-zero roots all have length √2. They are given by

* Proof: the lowest Tree ("1-tree") consists of 19 triangles with (19×3=57) sectors. When each sector is a tetractys, there are 57 hexagonal yods at the centres of the tetractyses. The 19 triangles have 11 corners and 25 sides with (25×2=50) hexagonal yods lining them. Their sectors have 19 internal corners and 57 internal sides lined by (57×2=114) hexagonal yods. Total number of yods in 1-tree = 11 + 19 + 50 + 114 + 57 = 251.

 

<< Previous    1...   11  12  [13]  14  15  ...50    Next >>

Home