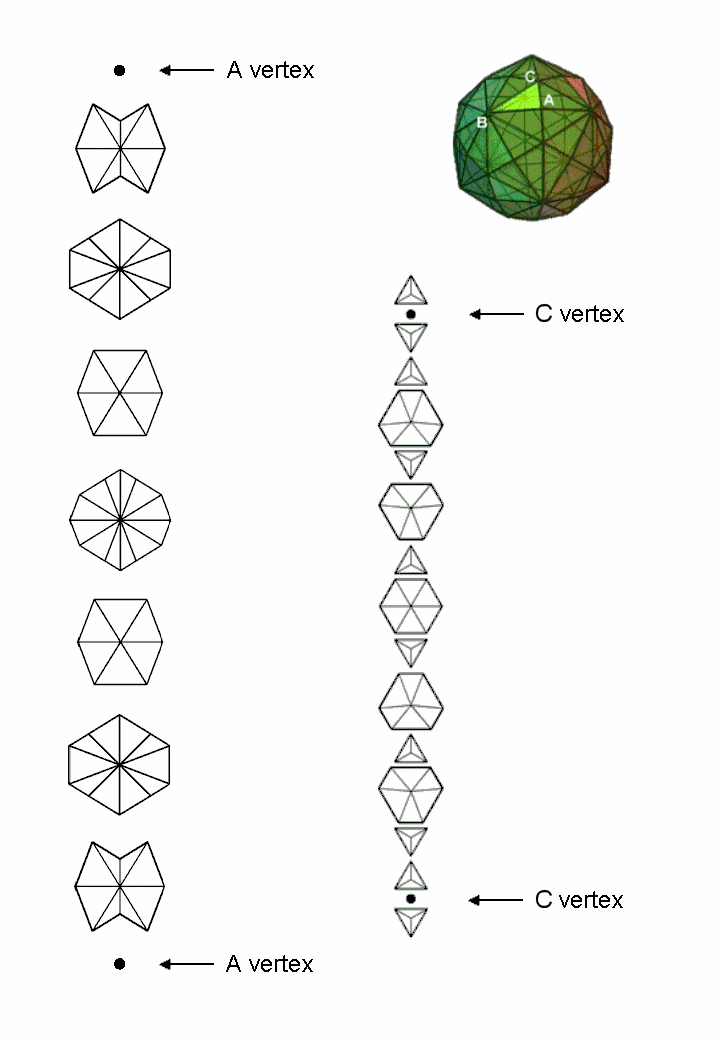
With A vertices as its "poles," the 60 other vertices of the disdyakis triacontahedron are corners of seven polygons. With C vertices as poles, the 60 vertices are corners of 15 polygons. They are shown here divided into their sectors. The sides of the seven polygons are edges of the polyhedron apart from the six sides of the 6-sided polygon and the two vertical sides of the 10-sided polygon. None of the sides of the 15 polygons are polyhedral edges because the corners in a given polygon are all the same type of vertex (A, B or C). The significance of these facts will emerge in the discussion in Superstrings as sacred geometry/Disdyakis triacontahedron of how the sets of seven and 15 polygons encode the three-dimensional structure and group dynamics of the E₈×E₈ heterotic superstring.

 

<< Previous    1...   10  11  [12]  13  14  ...15    Next >>

Home