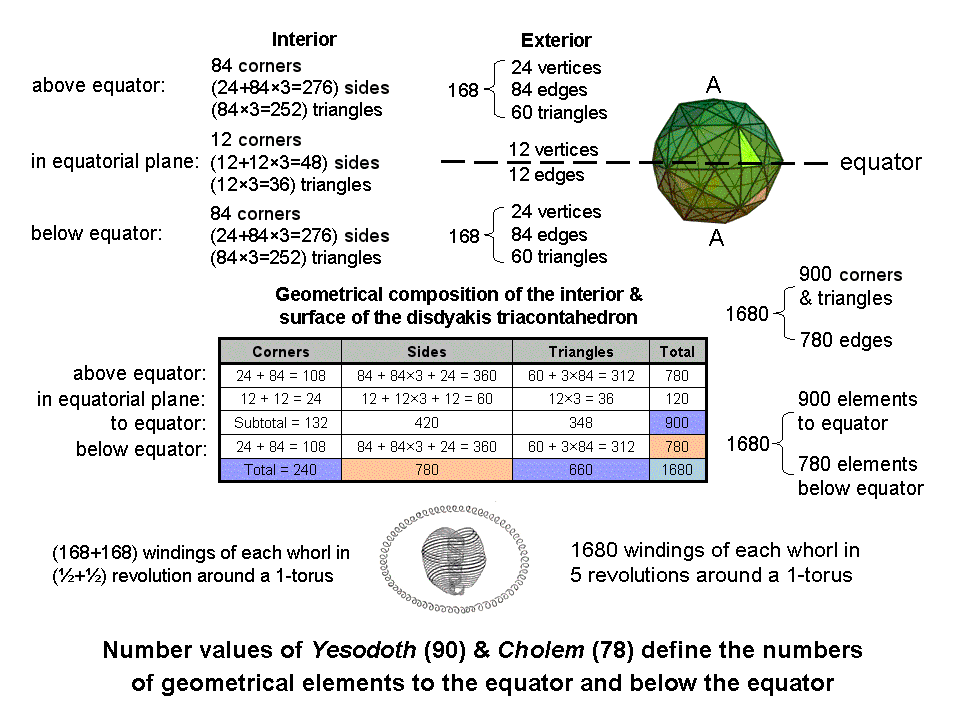
The geometry of the disdyakis triacontahedron naturally embodies the gematria number value of Cholem Yesodoth in the following, amazing ways: the 60 vertices surrounding an axis passing through two diametrically opposite A vertices are the corners of seven polygons arranged in seven layers perpendicular to this axis. The central polygon is 12-sided. Therefore, as the polyhedron has 180 edges, 168 edges lie above and below the central polygons, 84 to each half, which also have 24 vertices of 60 triangular faces surrounding the axis. The 84 edges in each half form internal triangles with the centre of the polyhedron as a shared corner. When the triangles are Type A, they have (84×3=252) sectors with 84 corners and (3×84 + 24 = 276) sides. The central 12-gon with Type A sectors has 12 centres of its sectors, (12×3=36) triangles and (12 + 12×3 = 48) sides. The table shows that there are 900 (=90×10) corners, sides & triangles in one half of the polyhedron, including its central polygon, and 780 (=78×10) geometrical elements in the remainder of the polyhedron. 90 is the value of Yesodoth and 78 is the number of Cholem! Not only this, there are 900 corners & triangles and 780 sides surrounding the axis of the disdyakis triacontahedron! The geometrical composition of the polyhedron embodies in two different ways the number values of the two Hebrew words composing the Mundane Chakra of Malkuth. This cannot, plausibly, be coincidence.

Here is yet more powerful evidence that the Kabbalistic names assigned to the Sephiroth in the four Worlds are not arbitrary, human inventions, as a rationalist might naively argue. Instead, they have an objective, sacred-geometrical basis, expressing all mathematical aspects of the divine archetypes that sacred geometries embody. These names express numbers, and it is the latter that are more important, for they quantify properties of these geometries.

<< Previous    1...   10  11  [12]  13  14  ...18    Next >>

Home