
| << Previous 1... 3 4 [5] 6 7 ...13 Next >> |
The nature of MPAs can be understood only if their basic constituents — UPAs — are correctly identified. As might be expected, hydrogen, the first element in the periodic table, provides the clue to their nature because its MPA is the simplest one. But, before the UPA can be recognized for what it is, it is first necessary to review both some pertinent discoveries about the structure of matter and current research efforts to develop a unified theory of particles and their forces.
 |
|
 |
Quark model
The proliferation of subatomic particles discovered in high-energy physics laboratories in the early 1960s made
physicists realise that those that interacted strongly with one another (so-called "hadrons") were of two types,
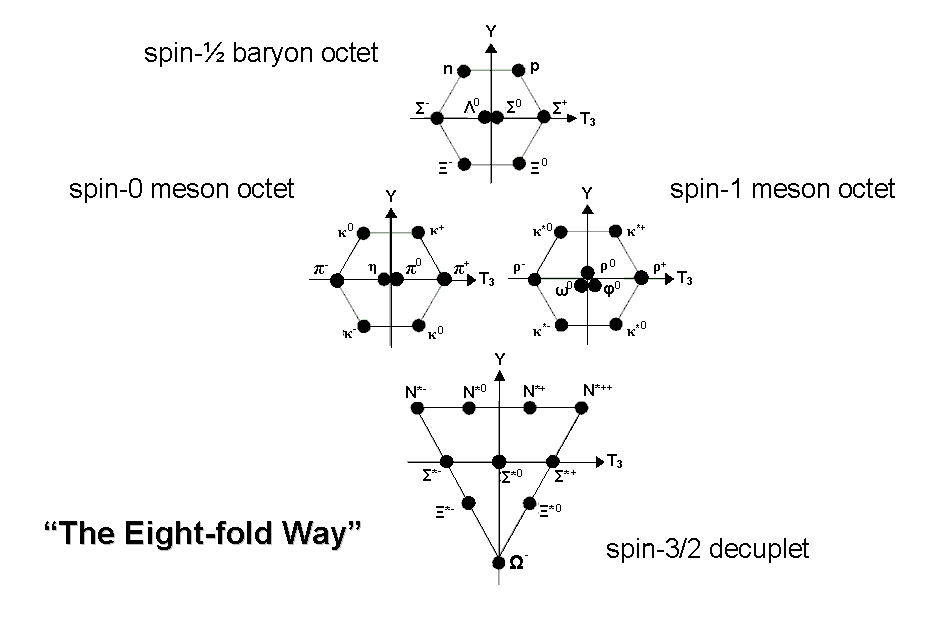
according to how they decayed. They found that these "baryons" and "mesons" formed families according to their spin
and properties like electric charge and hypercharge. The classification scheme was called the "Eight-fold way"
(after what Buddhism calls the "Eight-fold Noble Path") when it was found that baryons and mesons could be grouped
into sets of eight, or octets. This pattern was explained by the American theoretical physicist Murray Gell-Mann
and by the Israeli physicist Yuval Ne'eman, who postulated in 1964 the
existence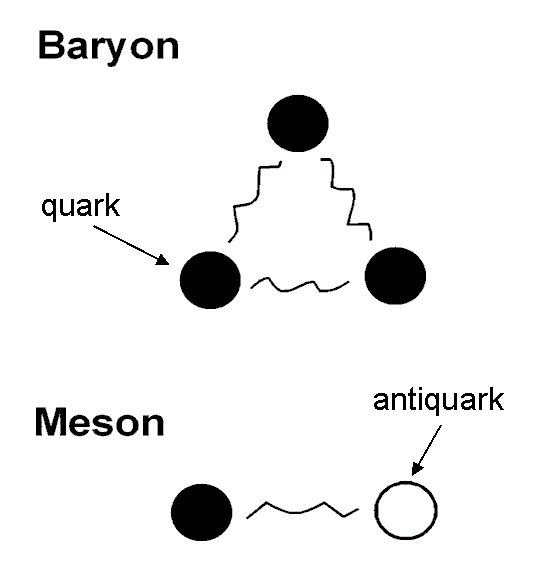 of three types of fundamental particles called
"up," "down" & "strange" quarks. They interact with one another to form bound states of either three
quarks (baryon) or a quark and an antiquark (meson), the latter being the antimatter counterpart of a
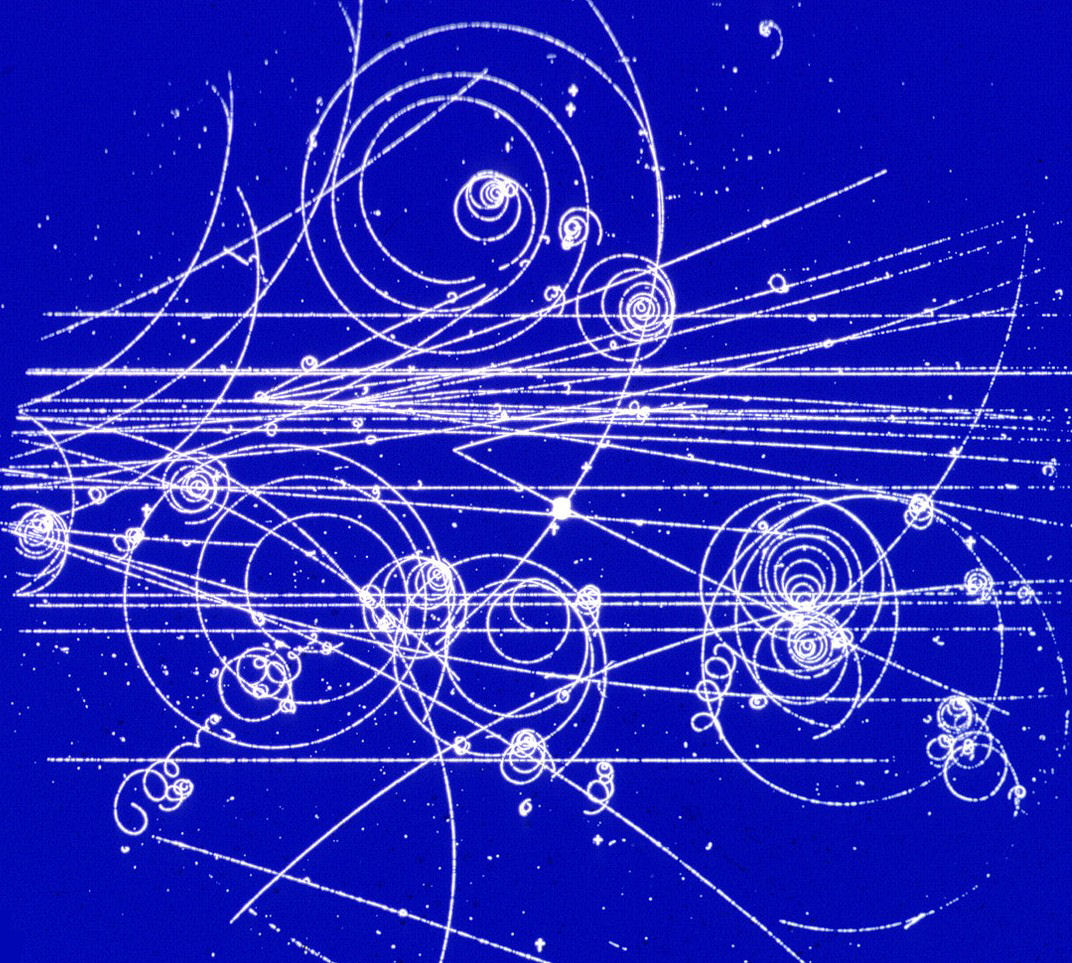
quark. The detection of the predicted omega-minus (Ω−) shown in the diagram above as a member of
the spin-3/2 decuplet of baryons, was one of the initial successes of the quark model. However, it led to
the problem that baryons like the omega-minus had to consist of three quarks in identical states and this is
forbidden by a basic rule of quantum mechanics called the "Exclusion Principle," which states that no
two spin-½ particles, such as quarks, can be in the same quantum state. The problem was solved
by attributing to a quark a new state called its "colour state," labelled red, blue & green. This led
to the formulation of the theory of quantum chromodynamics (QCD), which proposed that a 'colour force'
operates between the three colour states of a quark, binding quarks together by their exchanging eight spin-1
particles called "gluons." Because each state possesses one of three types of colour charge, the sum of which
is zero, baryons with three quarks in different colour states have zero colour charge. The colour charges of
antiquarks are opposite in sign to those of quarks and their colour states are complementary to red, blue
& green. As quark-antiquark bound states. mesons have no net colour charge. Both baryons and mesons are
said to be "colourless," in analogy to the three primary colours red, blue & green making up white light.
According to QCD, only colourless combinations of quarks and antiquarks can exist. Whilst this
explains why free, coloured quarks have not been detected, it does not rule out the possibility of
particles composed of certain combinations of quarks and antiquarks.
of three types of fundamental particles called
"up," "down" & "strange" quarks. They interact with one another to form bound states of either three
quarks (baryon) or a quark and an antiquark (meson), the latter being the antimatter counterpart of a
quark. The detection of the predicted omega-minus (Ω−) shown in the diagram above as a member of
the spin-3/2 decuplet of baryons, was one of the initial successes of the quark model. However, it led to
the problem that baryons like the omega-minus had to consist of three quarks in identical states and this is
forbidden by a basic rule of quantum mechanics called the "Exclusion Principle," which states that no
two spin-½ particles, such as quarks, can be in the same quantum state. The problem was solved
by attributing to a quark a new state called its "colour state," labelled red, blue & green. This led
to the formulation of the theory of quantum chromodynamics (QCD), which proposed that a 'colour force'
operates between the three colour states of a quark, binding quarks together by their exchanging eight spin-1
particles called "gluons." Because each state possesses one of three types of colour charge, the sum of which
is zero, baryons with three quarks in different colour states have zero colour charge. The colour charges of
antiquarks are opposite in sign to those of quarks and their colour states are complementary to red, blue
& green. As quark-antiquark bound states. mesons have no net colour charge. Both baryons and mesons are
said to be "colourless," in analogy to the three primary colours red, blue & green making up white light.
According to QCD, only colourless combinations of quarks and antiquarks can exist. Whilst this
explains why free, coloured quarks have not been detected, it does not rule out the possibility of
particles composed of certain combinations of quarks and antiquarks.
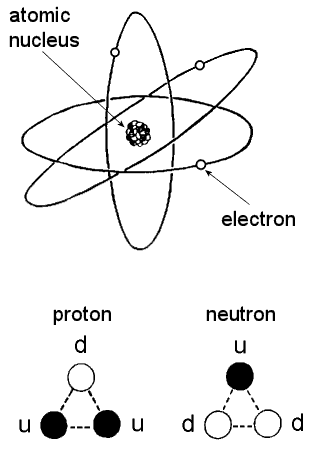
Atomic nuclei consist of positively charged protons and electrically neutral neutrons. In terms of up (u) quarks with electric charge (2/3)e and down (d) quarks with electric charge (−1/3)e, where e is the magnitude of the electric charge of an electron, protons and neutrons have the following quark composition:
proton = u-u-d, neutron = d-d-u,
Discovery of the long-lived 'J/psi meson' in 1974 made physicists realise that a fourth, so-called 'charm' quark (c) exists with the same electric charge as the up quark. Physicists then realized that quark species formed a sequence of two pairs or generations that mirrored the two known pairs of leptons: the electron (e–) and the muon (μ–) and their associated neutrinos (νe and νμ, respectively). This pattern was required by the electroweak theory, which had been proposed several years earlier by A. Salam, S. Weinberg and S. Glashow as a unification of electromagnetic and weak forces. This theory joined the photon — the transmitter of the former force — to three other particles: W+, W– and Z0, which transmit the latter force and which were later discovered in 1983 at CERN, the European Particle Physics Laboratory in Geneva, Switzerland. With the subsequent discovery in 1975 of the tau lepton (τ–) and its associated neutrino (ντ), as well as the discovery in 1977 of the upsilon meson, which is made up of the so-called" bottom" quark (b) and its antiparticle, a third generation of quarks was suspected to exist. Physicists reported in 1995 their discovery of the top quark (t), the other member of this generation of quarks:
1st generation 2nd generation 3rd generation
quarks: u c t
d
s
b
leptons:
νe
νμ
ντ
e−
μ−
τ−
One of the most important issues of particle physics has been how many quark generations can exist. In August, 1989, the Stanford Linear Collider at SLAC, University of California at Stanford was able to put a limit on the number of generations at 3.0 ± 0.9, which excludes four families of quarks with a confidence level of about 70%. By September, the Large Electron-Positron Collider (LEP) at CERN established a better limit of 2.7 ± 0.7, excluding four generations with a confidence level of 96%. The pattern of pairs of quarks having a pair of lepton counterparts was required by the electro-weak theory, which had been proposed several years earlier by A. Salam, S. Weinberg and S. Glashow as a unification of electromagnetic and weak forces. This theory joined the photon — the transmitter of the former force — to three other particles: W+, W– & Z0, which transmit the latter force and which were later discovered in 1983 at CERN, the European Particle Physics Laboratory in Geneva, Switzerland.
Videos
The electroweak theory also requires a heavy, spin-0 boson called the "Higgs
particle" to exist in order to be mathematically consistent. This particle is currently being sought at the
Large Hadron Collider at CERN. The importance to physics of its detection cannot be
overestimated, for its coupling to fundamental particles is predicted to generate their masses and, without it,
physicists have few, alternative ways of explaining their origin. The three generations of quarks and leptons,
the photon, the eight gluons, the W, Z and Higgs boson constitute what is known as the "Standard Model" of
particle physics. It is recognized by most physicists to be only a piece of the complete picture that will
eventually emerge. Some (including the author) have constructed composite models of quarks and leptons
(so-called "preon models"), hoping to derive the Standard Model and to reduce the number of free
parameters (over twenty) that it needs. If quarks are not fundamental but are composed of three spin-½ preons or
"subquarks," then protons and neutrons (and baryons in general) would consist of nine subquarks. The
significance of this implication will become apparent later.
Strings &
superstrings
The notion that basic subatomic particles
could be extended, 1-dimensional objects, or "strings," rather than the mathematical points that quantum field
theories assumed them to be arose from a theory of the strong force that had rivalled QCD at first, before falling
into disfavour for some years. The string model of the confinement of quarks inside baryons and mesons will be
discussed later. Physicists abandoned it because:
|
Supersymmetry Mechanically speaking, a rotating body has an angular momentum, which is a
measure of both its speed of rotation and the distribution of its mass in space. Classical
mechanics allows the angular momentum of a body to assume any value from a continuous range.
However, quantum mechanics permits the intrinsic angular momentum, or so-called spin, of particles
to take values that are only integer multiples of ½ħ, where ħ is Planck's Constant h divided by 2π.
Fermions are particles whose spin is an odd integer multiple of ½ħ, i.e. ħ/2, 3ħ/2, 5ħ/2 etc;
bosons are particles whose spin is an even integer multiple of ½ħ, i.e. 0, ħ, 2ħ, 3ħ, etc. For ease
of expression, it is conventional to drop the unit ħ, so that one then speaks of a particle with
spin ½ħ as having ‘spin-½,' a particle with spin ħ as having ‘spin-1,' etc. Examples of fermions
are quarks and leptons, which have spin-½; examples of bosons are the particles transmitting the
electroweak force, viz. the photon, W+, W– and Z0, which have spin-1, and the graviton, which has
spin-2. As mentioned earlier, fermions are subject to the Pauli Exclusion Principle, which states
that no identical fermions can occupy the same quantum state. Bosons, however, are not subject to
this restriction. Physicists believed for a long time that the distinction between these two types
of particles was absolute. At the fundamental level of matter, fermions were quarks and leptons,
and bosons were the particles mediating the four forces of nature. Then, in the early 1970s,
theorists discovered a new kind of geometrical symmetry conceptually different from the known
symmetries of these forces. Known as supersymmetry, its operation takes place in superspace, a
mathematical space consisting of the four dimensions of ordinary space-time and another four
‘fermionic’ dimensions that are not space or time dimensions, as we know them. In a supersymmetric
universe, fermions and bosons are different spin states of a single, fundamental, supersymmetric
entity. This means that each ordinary fermion should have a superpartner that is a boson and each
ordinary boson should have a superpartner that is a fermion. As long as supersymmetry is an exact
symmetry, the strengths of the interactions between the proposed superpartners should be identical
to the strengths of the forces between the various normal partners. In reality, of course, the
great disparity between the masses of bosons and fermions means that supersymmetry is badly
broken. |
A few physicists, however, did not abandon string theory, hoping that a mathematical symmetry called "supersymmetry" might solve some of these problems. This is a symmetry that treats bosons and fermions as different spin states of a single, fundamental, supersymmetric object (see box). It means that each ordinary fermion should have a superpartner that is a boson and that each ordinary boson should have a partner that is a fermion. In 1976, F. Gliozzi, J. Scherk and D.A. Olive showed that tachyons could be eliminated in the ten-dimensional spinning string of fermions developed in 1971 by P. Ramond, A. Neveu & J.H. Schwarz, and they speculated that the new model might be supersymmetric, serving as a model for both fermions and bosons. But it was not until 1980 that J. Schwarz and M. Green began to investigate the properties of strings that incorporate supersymmetry — so-called "superstrings." In 1984, they made the surprising and remarkable discovery that a theory of superstrings formulated in ten-dimensional space-time is free of "quantum anomalies" (a technical problem that had plagued point-field theories) provided that the unified superstring force is transmitted by 496 spin-1 bosons. Moreover, the infinities that plague calculations based upon point-field theories disappear, at least to the first level of approximation. These virtues of superstrings led to much renewed interest in string theories.
Prof. Michael Green on superstring theory
Because they are inherently supersymmetric, superstrings can be either bosons or fermions. Different harmonics or normal modes of their vibrations correspond to different particles. Its tension, about 1039 tonnes, sets the mass scale. If its size is the so-called "Planck length" of 10−33 cm (the distance from a gravitating object at which the quantum nature of its gravitational field becomes important enough to render invalid the meaning of distance and time), all excited modes of vibration have masses of
about 1019 times that of the proton, or larger. Such a huge mass scale greatly
exceeds the energy output that the Large Hadron Collider or any future particle accelerator will achieve, so
that these massive modes of vibration will never be created and detected in the high-energy physics
laboratory. It means that all observed (and observable!) subatomic particles must contain superstrings in
their lowest state of vibrational energy. Higher modes of vibration of superstrings could have been excited
only during a period up to about 10−43 seconds after the Big Bang, when the temperature of the
universe was about 1032 degrees Celsius. Superstrings with this size would behave effectively as
massless point particles at all energies ever likely to be achieved by any particle accelerator. But the
question is: are they larger than the Planck length?
1019 times that of the proton, or larger. Such a huge mass scale greatly
exceeds the energy output that the Large Hadron Collider or any future particle accelerator will achieve, so
that these massive modes of vibration will never be created and detected in the high-energy physics
laboratory. It means that all observed (and observable!) subatomic particles must contain superstrings in
their lowest state of vibrational energy. Higher modes of vibration of superstrings could have been excited
only during a period up to about 10−43 seconds after the Big Bang, when the temperature of the
universe was about 1032 degrees Celsius. Superstrings with this size would behave effectively as
massless point particles at all energies ever likely to be achieved by any particle accelerator. But the
question is: are they larger than the Planck length?
There are two types of superstrings:
It was thought for some time that type 2 superstrings could not be realistic models of fundamental particles because they interact only gravitationally, having no endpoints carrying charges like electric and colour charges. But in 1985, D.J. Gross, J.A. Harvey, E. Martinec and K. Rohm formulated the theory of a new kind of closed superstring called the "heterotic superstring," in which the charge sources of the non-gravitational forces predicted by superstring theory are regarded as being smeared out over the entire length of the closed string. In the same year, P.G.O. Freund had suggested that a 10-dimensional superstring might result from shrinkage to infinitesimally small scales of sixteen of the 26-dimensional string originally predicted by quantum mechanics for bosonic strings. Waves can travel around any closed string in two directions. But, according to Gross and his colleagues, the waves that travel in a clockwise direction in a closed, heterotic string are waves in 10-dimensional space-time, whereas the waves travelling anticlockwise are waves of the 26-dimensional bosonic string theory. Instead of having no quantum numbers to be associated with particles because it has no endpoints, as was originally thought to be the case for closed strings, the heterotic superstring has its possible quantum numbers and charges circulating around its length.
Compactification
Superstring theory predicts
that space-time is 10-dimensional. It requires that six of the nine spatial dimensions of space-time extend over an
infinitesimally small scale, leaving the three large-scale dimensions of the universe familiar to everyone. Because
it has not yet been formulated in a fundamental way, the theory cannot specify the geometry and topology of this
extremely small, 6-dimensional, "compactified space." It cannot even explain why this space has to be
6-dimensional. Such properties determine how, as a result of the compactification, or curling up, of these six
dimensions, the original symmetry of the superstring force in 10-dimensional space-time broke down into the
known symmetries of the electroweak and strong forces in 4-dimensional space-time. Because the unified
symmetry is so large compared with the latter, there exist many ways in which it can break down. As a consequence,
many kinds of compactified space may be consistent with the Standard Model of particle physics. However, progress
was made in demonstrating that, if the six extra dimensions form what is known as a "Calabi-Yan" space, the theory
associated with this is consistent with the Standard Model. But a large number of such spaces are possible and
further theoretical restraints have to be investigated. Another model space that string theorists have investigated
is the 6-dimensional torus. This is the 6-dimensional generalisation of a torus in which each of the six dimensions
is a circle. The superstring is pictured in this model as winding in turn around each circular dimension, all of
which are perpendicular to one another and which may or may not have the same radius. The number of times it wraps
itself around a given circular dimension is called its "winding number." The 6-dimensional torus has been
generalized to what are called "orbifolds." These are highly curved spaces with holes and singular points, which
can trap strings winding through them by preventing them from unlooping. Such topologically trapped strings can
manifest the properties of fractionally charged particles, e.g., quarks, or of magnetic monopoles — the magnetic
counterparts of point-like electric charges. Their topology can lead to a number of generations of particles.
The presence of holes or singularities in an orbifold space has the effect of destroying its basic symmetry, so
that the full symmetry of the unified superstring force operating in flat, 10-dimensional space-time can be broken
by the process of compactification into a particle described by the Standard Model.
Superstring gauge symmetry
group
The symmetries displayed by the forces of nature are
expressed by physicists in the language of a branch of mathematics called ‘group theory.’ The mathematical
fields that represent the particles mediating a given type of force are said to be the gauge fields of the gauge
symmetry group expressing the symmetry of this force. The mathematical transformations belonging to a gauge
group are defined by its set of generators. The dimension N of a symmetry group is the number of independent
generators defining its transformations. Each generator is associated with its own gauge field. N gauge fields
are therefore associated with a gauge symmetry group of dimension N. The complete set of N generators of a group
obeys the rules of an abstract algebra called Lie algebra. This gives rise to a certain algebraic equation,
solutions of which are specified by a set of N points in an m-dimensional Euclidean space, where m is the rank
of the group. Each point defines a root of the group. m of the N roots are said to be zero roots because they
denote points at the centre of the diagram representing these roots, and (N-m) roots are said to be non-zero
roots because they denote points a non-zero distance from this centre.
Gary Schwarz and Michael Green made the important discovery in 1984 that the gauge symmetry group describing the symmetries of the forces other than gravity that act between ten-dimensional superstrings had to have the dimension N = 496 in order that the theory be free of so-called “quantum anomalies” — a mathematical problem that had plagued quantum field theories until then. They pointed out that two groups: E8×E8 and SO(32) have this dimension. The former is the one that first became favoured by string theorists. The group E8 is called the exceptional Lie group of rank 8. It is the largest of the five exceptional Lie groups, having dimension 248 (half of 496). Its 248 roots consist of eight ‘zero roots’ (also called ‘simple roots’) and 240 non-zero roots. The 496 roots of E8×E8 consist of (8+8=16) simple roots and (240+240=480) non-zero roots. The eight simple roots of E8 comprise a zero root of one kind (which need not be specified here) and seven of another kind. Similarly, the 240 roots of E8 consist of 128 non-zero roots of one kind and 112 of another kind. The root composition of E8×E8 is laid out below:
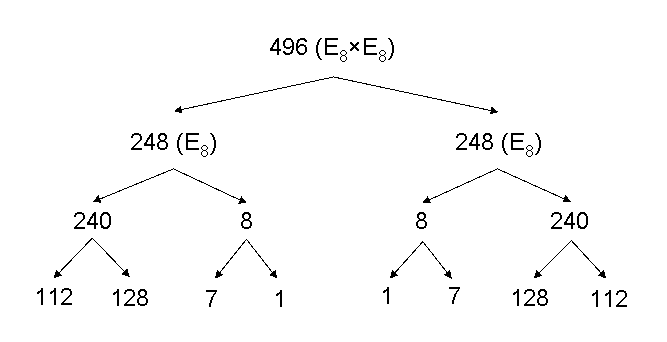 According to superstring theory, non-gravitational forces are transmitted by 496 gauge fields
whose quanta are spin-1 particles. Just as a point in three-dimensional space is specified by three Cartesian
coordinates X, Y and Z defined relative to three mutually perpendicular coordinate axes, so each gauge field
in ten-dimensional space-time has ten components measured relative to coordinate axes pointing in the
directions of the ten mutually perpendicular dimensions of superstring space-time. The total number of
components of the 248 gauge fields associated with E8 = 248×10 = 2480. The total number of
components of the 496 gauge fields associated with the complete superstring symmetry group
E8×E8 = 2480 + 2480 = 4960. The number of components of the 240 (480) gauge fields
associated with the non-zero roots of E8 (E8×E8) is 2400 (4800). In
other sections of this website, all these numbers will be shown to be embodied in various sacred geometries in
ways that cannot be attributed to chance.
According to superstring theory, non-gravitational forces are transmitted by 496 gauge fields
whose quanta are spin-1 particles. Just as a point in three-dimensional space is specified by three Cartesian
coordinates X, Y and Z defined relative to three mutually perpendicular coordinate axes, so each gauge field
in ten-dimensional space-time has ten components measured relative to coordinate axes pointing in the
directions of the ten mutually perpendicular dimensions of superstring space-time. The total number of
components of the 248 gauge fields associated with E8 = 248×10 = 2480. The total number of
components of the 496 gauge fields associated with the complete superstring symmetry group
E8×E8 = 2480 + 2480 = 4960. The number of components of the 240 (480) gauge fields
associated with the non-zero roots of E8 (E8×E8) is 2400 (4800). In
other sections of this website, all these numbers will be shown to be embodied in various sacred geometries in
ways that cannot be attributed to chance.
Two other important numbers to note are the respective dimensions 133 and 78 of E7 and
E6, which are two exceptional subgroups of E8 with, respectively, seven simple roots
and 126 roots and six simple roots and 72 roots. These groups play a prominent role in current investigations by
physicists of what superstring forces emerged at energies far below the Planck energy scale of
1019 GeV, where non-gravitational forces are expected to become as weak as gravity itself. One
of the questions to which superstring theory does not yet seem capable of giving a unique answer is how the
E8-symmetric, unified force operating between 10−43 seconds and
10−38 seconds after the Big Bang split up into the much less symmetric strong and electroweak
forces. The dimension 248 of the group E8 is so large that it permits many symmetry-breaking
schemes leading to the Standard Model and involving intermediate gauge groups of smaller dimensions.

There are five types of superstrings: Type I is an open string consisting of a segment with SO(32) symmetry, Types IIA and IIB are distinct types of closed string theories that do not have the gauge type particles that are present in Type I string theory as carriers of force and so their strings do not carry gauge charges, and two types of heterotic string theory, based upon either SO(32) or E8×E8. The latter two arise from the fact that consistency of the resulting string theory allows only two possible choices for the 16-dimensional torus around which the left-moving waves of the heterotic superstring wind anticlockwise. The E8×E8 theory was favoured initially by theorists because attempts to compactify the SO(32) strings (heterotic and Type I) appeared to destroy their parity-violating nature in ten dimensions, so that they could not account for why parity was violated in the four-dimensional universe. Type IIB theory also had this fault, whilst Type IIA theory was already parity-conserving in ten dimensions and so could not lead to parity violation in four dimensions.
E8 symmetry has been recently discovered in an ultra-cold ferromagnet (see here). This, of course, does not prove that superstring theory is correct. But it does demonstrate, contrary to what some sceptics of superstring theory may like to think, that large symmetry groups like E8 do play a role in determining the physics of materials.
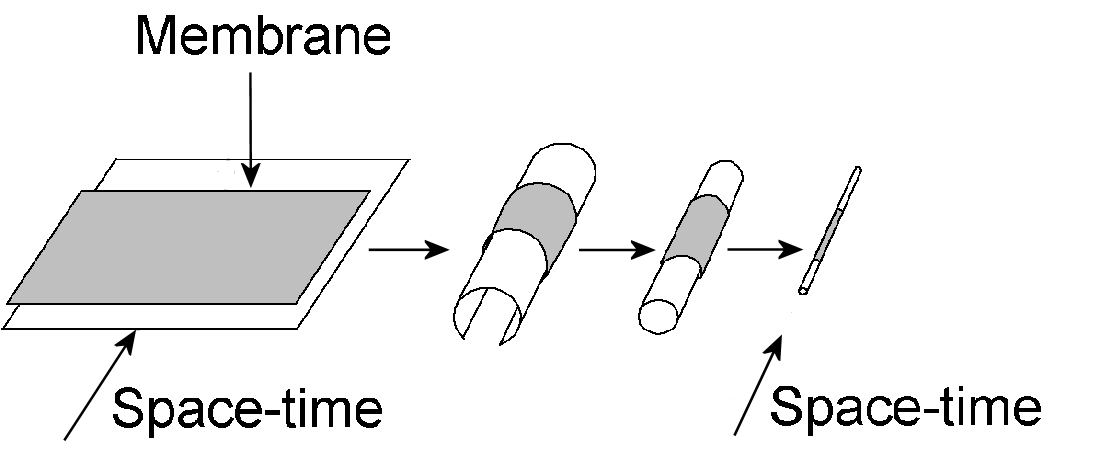
Just as physicists Green and Schwarz persisted in studying string theory when interest in it began to wane due to problems such as those discussed earlier, so a few physicists continued to investigate supergravity theories after what seemed insuperable difficulties appeared in them (e.g., they did not predict the Standard Model). Some researchers considered the possibility that strings might be the result of a two-dimensional sheet, or membrane, wrapping tightly around a tenth, circular dimension so small that the resulting cylinder was, effectively, one-dimensional, like a line (see diagram). It would then behave as a string. In 1987, Michael J. Duff, Paul S. Howe, Takeo Inami and Kellogg Stelle derived the type IIA superstring in ten dimensions from a membrane in 11 dimensions. However, no one took notice of this result and another nine years would have to elapse before Edward Witten and Petr Hořava derived E8×E8 heterotic string theory by considering the tenth dimension as a segment separating two space-time sheets. By this time, various developments had occurred, the most important of which was the generalisation of the concept of ‘duality,’ as now explained. As any physics undergraduate should know, Maxwell’s equations for the electromagnetic field due to electric charges are unchanged when the electric and magnetic fields E and B are interchanged according to:
E → B,
B → −E.
This duality symmetry still holds in the presence of both electric (Q) and magnetic charges (g) and currents. The famous British physicist Paul Dirac (6), who first derived the equation for an electron, showed that the existence of magnetic charges would explain why subatomic particles always have an electric charge that is an integer multiple of e, the charge of an electron. The strength of the coupling of electric charges to the electromagnetic field is given by the fine-structure constant α = e2/ħc ≈ 1/137,
where ħ is Planck’s constant and c is the velocity of light in the vacuum. Its magnetic counterpart is g2/ħc = 1/α, which means that the weak coupling situation for electric charges (α small) is the strong coupling limit for the dual version of Maxwell’s equations for the electromagnetic field of magnetic charges, and vice versa. Following an early conjecture in 1977 by Claus Montonen and David. I. Olive that a theory on which they were working might be symmetric to electric and magnetic charge, physicists wondered whether duality is also a property of quantum field theories of the strong force. However, this was impossible to test because their knowledge of these theories was limited to the weak coupling limit, where calculation becomes possible. In 1990, several theorists generalised the idea of Montonen-Olive duality to four-dimensional superstrings — so-called ‘S duality.’ It is now recognised that the various superstring theories are related by S duality. When one theory breaks down when a coupling constant becomes large, another theory takes its place. For example, the strong-coupling limit of the type I superstring is the weakly coupled SO(32) heterotic superstring, the strong-coupling limit of the Type IIA superstring is related to 11-dimensional supergravity and the strong-coupling limit of the E8×E8 heterotic superstring involves 11-dimensional supergravity.
It was pointed out earlier that, when the extra dimension of 11-dimensional supergravity space-time shrinks to a line segment, E8×E8 heterotic strings result. When, instead, the dimension curls into a circle, the Type IIA superstring is formed. When a string winds around a compact dimension, it can oscillate around the loop, modes of vibrations with different wavelengths and frequencies creating particles analogous to those predicted in the Kaluza-Klein theory proposed in the 1920s, in which the electromagnetic field was explained by supposing that a circular, fifth dimension exists around which a standing wave representing its electrically charged source travels. The smaller the radius of the circle becomes, the more massive these particles would become as the wavelengths of the waves would be smaller and their frequencies would be higher. Such modes are called ‘vibration modes.’ A string can also wind many times around the circle (the number of times being called the ‘winding number’). Its energy becomes higher the larger the circle and the more times it wraps around it because both stretch the string more, requiring more energy. The energies of the states corresponding to different winding numbers are called ‘winding modes.’ The differences in mass between particles will be large for winding modes on large circles and vibration modes on small circles and small for winding modes on small circles and vibration modes on large circles:
|
Mode |
Large circle |
Small circle |
|
Vibration |
Small |
Large |
|
Winding |
Large |
Small |
So-called ‘T-duality’ states that the winding mode particles predicted by one string theory compactified on a circle of radius R are the same as the vibration modes predicted by its T-dual version compactified on a circle of radius L2/R, where L is a constant with the dimensions of length. SO(32) and E8×E8 heterotic superstring theories are T-dual to each other, as are Type IIA and IIB superstrings.
It is now recognised that supergravity and the five superstring theories are related by S-duality and T-duality, being all low-energy limits of a single theory called ’M-theory,’ where ‘M’ means "magic," "mystery" or "membrane," depending upon to which physicist one speaks. The corners of the hexagon shown in the diagram represent particular values of the coupling constant and compactification radius defining different vacua. Points within the boundary of the hexagon denote M theory. How well one of
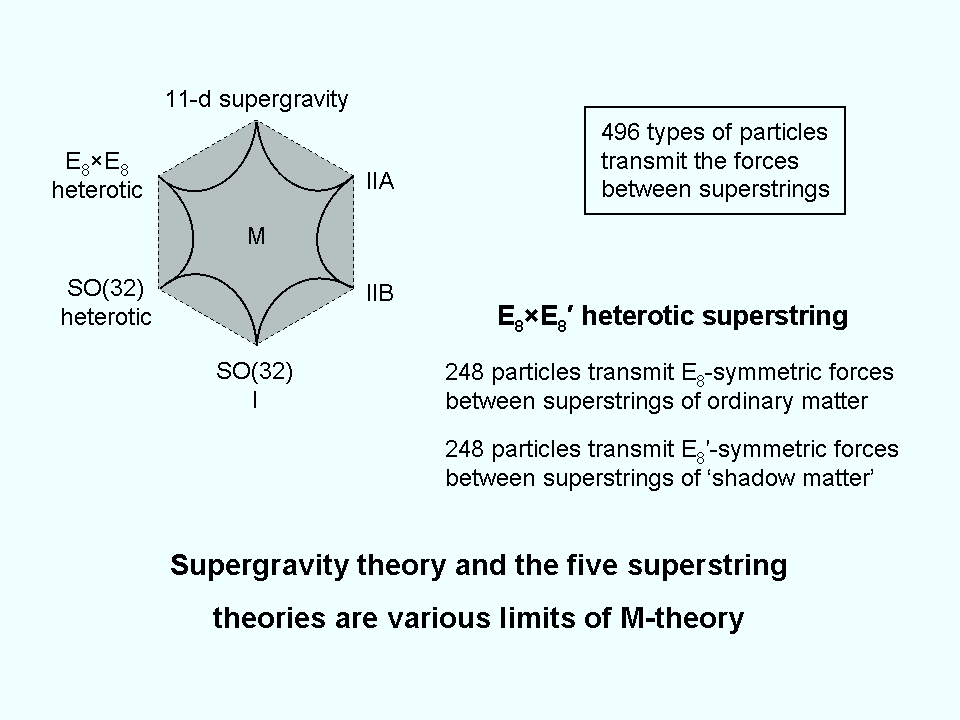
the theories approximates to it depends upon how far this point is from the corner of the hexagon corresponding to this theory. The diagram also indicates which theories are related by S- and T-duality. It is unknown as yet which superstring theory applies to the universe as it exists now, that is, what theory is compatible with the vacuum in which we find ourselves, although many physicists favour E8×E8 heterotic superstring theory. The next section will present evidence that the superstring constituents of the protons and neutrons making up the nuclei of atoms are chiral bundles of ten closed curves, which means, as parity is known to be violated, that they are either SO(32) or E8×E8 heterotic superstrings. The sacred geometries described in later sections will be proved to embody the group-theoretical dynamics of the latter type of superstring, as well as their space-time structure, as described by C.W. Leadbeater, when he used the yogic siddhi called "anima" to remote-view subatomic particles (see #2).
| << Previous 1... 3 4 [5] 6 7 ...13 Next >> |