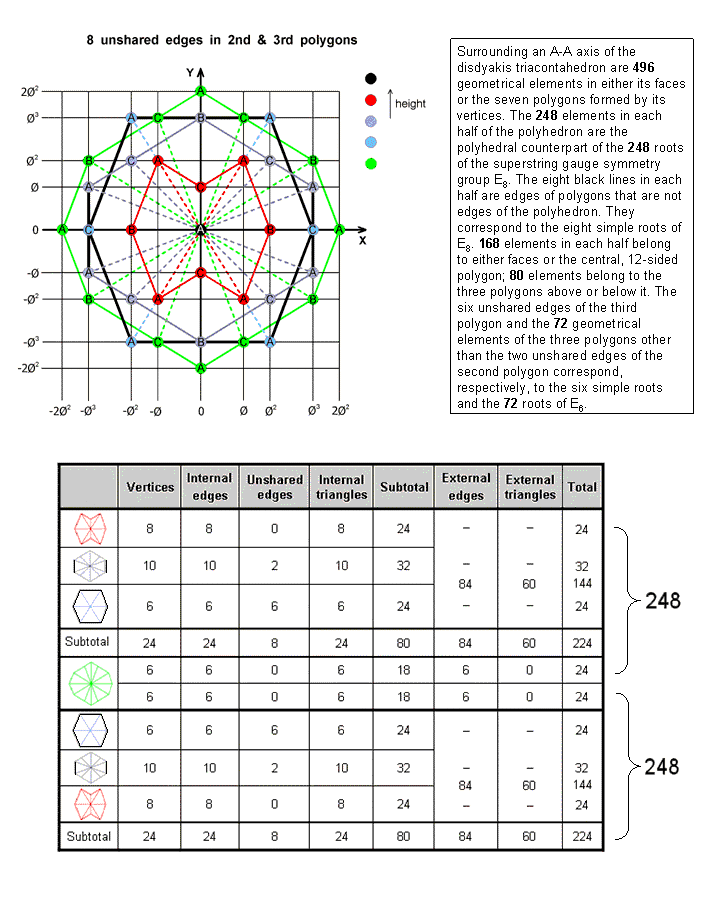
The graph displays the vertices of the disdyakis triacontahedron projected onto the central XY plane when the Z axis passes through two diametrically opposite A vertices. The vertices are corners of seven polygons stacked one above the other. The graph shows the four polygons in the upper half of the polyhedron. The only sides of the polygons that are not polyhedral edges are the six black sides of the hexagon with A & C vertices at its corners and two black sides parallel to the Y-axis of an indigo 10-gon that join two pairs of its A vertices. The table indicates that there are eight geometrical elements unshared with the polyhedron and 240 elements which belong either to its faces or to the internal sectors of the seven polygons. 80 elements belong to the three polygons above the central, green 12-gon and 168 elements belong to either faces in the upper half of the polyhedron or to half of the central 12-gon. Similarly, 80 elements belong to the three polygons below the 12-gon and 168 elements belong to either faces in the lower half of the polyhedron or to the other half of the 12-gon. Each half of the disdyakis triacontahedron has 248 geometrical elements. They are the counterpart of the 248 gauge bosons of E₈ and E₈′ that transmit the unified forces between E₈×E₈′ heterotic superstrings.

The disdyakis triacontahedron embodies the number 496 of Malkuth and the dimension of E₈×E₈′ as the number of geometrical elements in its faces and seven internal polygons formed by the 60 vertices that surround an axis joining two opposite A vertices. They include 16 unshared elements that correspond to the 16 simple roots of E₈×E₈′ and 480 elements that correspond to the 480 roots of E₈ and E₈′. They exclude the seven centres of polygons and the two A vertices.

The total number of geometrical elements that surround the centre of the disdyakis triacontahedron is 496 + 6 + 2 = 504. This number was encountered in the discussion of the Polyhedral Tree of Life as:

1. the number of yods lining the edges of the 144 Polyhedron that surround an axis passing through two opposite vertices;
2. the number of yods surrounding the centre of a Type C dodecagon;
3. the number of yods surrounding the centre of a heptagon with 2nd-order tetractyses as its seven sectors.

It was also described in Maps of reality/Sri Yantra as the 504 hexagonal yods that lie on sides of tetractyses in the Sri Yantra with Type A triangles and as the 504 SLs in CTOL down to the top of the 7-tree that represents the physical plane (physical universe). Just as it was found in these contexts that the number 504 displays a 168:168:168 division, so it does in the disdyakis triacontahedron, for there are 168 polyhedral edges above and below the central 12-gon, 168 geometrical elements that are either external triangles (120) or elements of the 12-gon (48) and (80+80+6+2=168) elements that comprise the two A vertices and the elements, including their centres, that make up the six polygons either above or below the 12-gon. The 84:84 division of 168 is characteristic of holistic systems. Here, it appears as the 84 polyhedral edges in each half of the disdyakis triacontahedron above or below the 12-gon, as the 84 elements that are either external triangles (60) in each half or elements in half the 12-gon (24) and as the 84 elements in each half that are either the A vertex, the centres of the three polygons or the 80 corners, internal edges, unshared sides & triangles.

The six unshared edges in either half of the polyhedron correspond to the six simple roots of E₆, an exceptional subgroup of E₈, and the 72 corners, internal sides & triangles of the three polygons in its upper or lower halves correspond to the 72 roots of E₆. The 24:24 division of the 48 geometrical elements in the central 12-gon is characteristic of holistic systems. For example, it was encountered in the 24 lines & broken lines making up each of the two sets of eight trigrams in the eight diagonal hexagrams in the I Ching table of 64 hexagrams.

In conclusion, the disdyakis triacontahedron embodies the structural parameters 840 & 1680 of the subquark state of the E₈×E₈′ heterotic superstring and the root composition of the gauge symmetry group of its unified force. This is one of the reasons why the basic unit of matter described by Besant & Leadbeater must be identified as this particular type of superstring. All sacred geometries exhibit a bifurcation into two similar, mirror-image (or in some sense, opposite but complementary) halves, each half encoding the dimension 248 of E₈ and embodying the 840 helical turns in the outer or inner halves of this particle. This duality or split into two sets of geometrical elements that are opposite to one another is a manifestation of the Taoist principle of the Tao, or the Cosmic Whole, being a perpetual, cyclic rhythm of the polar opposite, but complementary, phases of Yang and Yin.

<< Previous    1...   12  13  [14]  15  16  ...18    Next >>

Home