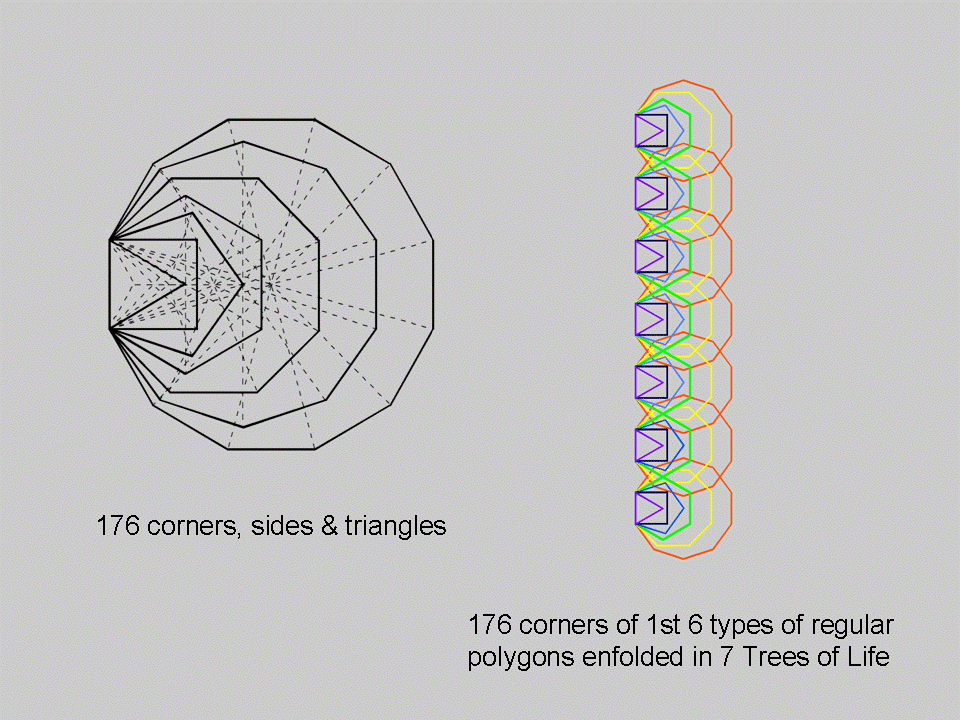
| << Previous 1... 23 24 [25] 26 27 ...50 Next >> |
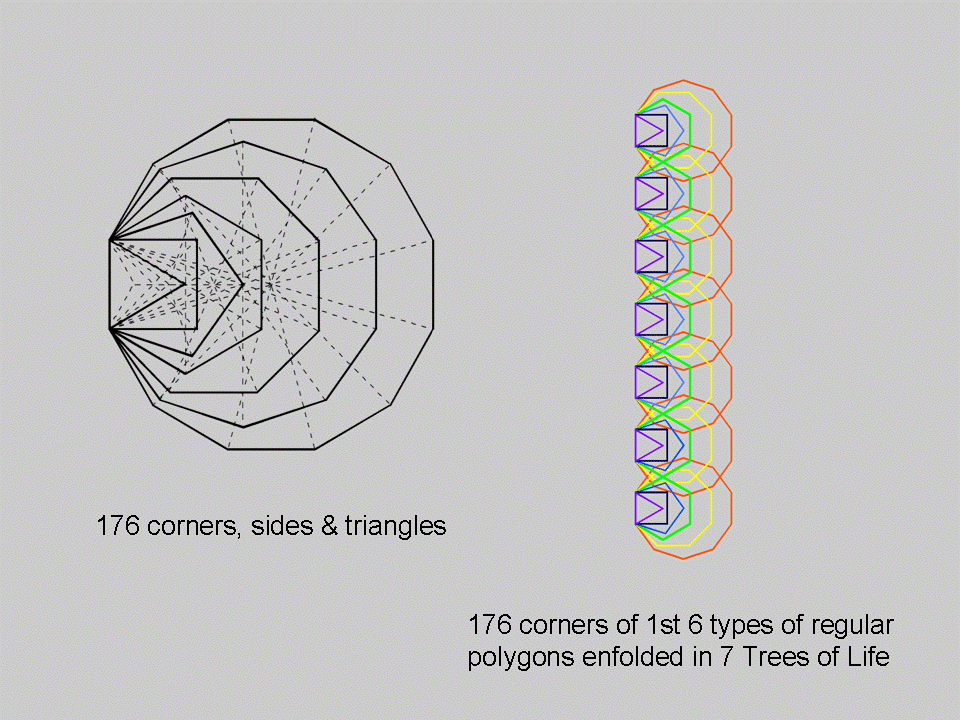
The seven-fold expansion of each spirilla proceeds uniformly through all orders making up the minor whorls. In the case, however, of the three major whorls, every 25 spirilla of a given order is, according to Besant & Leadbeater, compounded of 176, not 175, spirillae of the next higher order. An extra spirilla is inserted in the 175 spirillae composing every consecutive set of 25 spirillae of the next lower order.* Their additional spirillae is what made the major whorls look thicker when Besant & Leadbeater examined a UPA.
This 175/176 distinction between major and minor whorls appears in the very geometry of the inner Tree of Life. The seven enfolded polygons have 47 sectors with 176 corners, sides & triangles. The topmost corner of the hexagon is the only one of these geometrical elements that is shared with the seven polygons enfolded in the next higher Tree of Life because it coincides with the lowest corner of the hexagon that belongs to them. This means that 175 elements are intrinsic to each set of seven polygons so that the number of elements making up the 7n polygons enfolded in a set of n overlapping Trees of Life is 175n + 1. Every set of polygons enfolded in Tree of Life has 175 intrinsic elements, apart from the last set enfolded in the nth and last Tree of Life belonging to the set, which has 176 intrinsic elements because this time the topmost corner of its hexagon is not shared with another hexagon.
How the factor of 25 arises in the spirilla structure of the UPA/superstring can be readily seen by examining the first six enfolded polygons, which constitute a holistic system as well. Each set has 26 corners. As the topmost corner of the hexagon coincides with the lowest corner of the hexagon in the next higher Tree of Life, 25 corners are intrinsic to each successive set of polygons, except the last, which has one more corner. The 42 polygons enfolded in seven Trees of Life have (7×25 + 1 = 176) corners. Each order of spirillae corresponds to a Sephirah of Construction, which can be represented by a whole Tree of Life whose first six enfolded polygons have 25 intrinsic corners. Their counterparts in the superstring are the successive sets of 25 spirillae of any given order. Their seven-fold composition is represented by the lowest seven successive Trees of Life of a higher number of Trees, which means that 25 spirillae are compounded from 175 spirillae of the next higher order corresponding to the 175 intrinsic corners of the 42 polygons of the first six types that are enfolded in these Trees, unless they belong to a major whorl, in which case the representation is by seven, stand-alone Trees of Life, whose 42 polygons have 176 corners. The distinction between the 7-tree and seven overlapping Trees of Life is what creates the structural difference between major and minor whorls. The former is part of a more extended Tree of Life structure, whereas the latter is a complete representation of the seven Sephiroth of Construction. In this sense, the number 176 is the measure of a complete system, whereas the number 175 expresses incompleteness.
The 35 sectors of the first six enfolded polygons consist of 143 corners, sides & triangles. The root edge has two corners and one side. There are 140 geometrical elements outside it. The two sets of the first six enfolded polygons have 280 geometrical elements outside the root edge, where 280 is the number value of Sandalphon, the Archangel of Malkuth. This demonstrates how a structural (i.e., Malkuth-like) feature of the microscopic Tree of Life is quantified by one of the gematria number values of this Sephirah in the four Kabbalistic Worlds.
* The number 1680 is, of course not exactly divisible by 25. Therefore, the augmentation must apply only to the 67 complete sets of 25 1st-order spirillae (notice that this is the number value of Binah!), leaving five 1st-order spirillae in each major whorl that must consist of 175, not 176, 2nd-order spirillae.