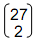|
by Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://www.smphillips.mysite.com
Abstract
1 1. Binary number interpretation of trigrams Any positive integer N can be expressed as a linear combination of integer powers of 2:
N = c020 + c121 + c222 + … cn2n,
where cn = 0 or 1. Its binary number representation is cncn-1…c1c0. The binary forms of the integers 0, 1, 2, … 7 are:
Making the identification
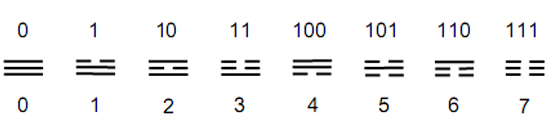
and following the convention that the line at the top of a trigram corresponds to the binary digit to the extreme right of its binary number representation, the eight trigrams of I Ching symbolise binary numbers for the Arabic numerals shown in Fig. 1. Figure 1. Binary number values of the eight trigrams.
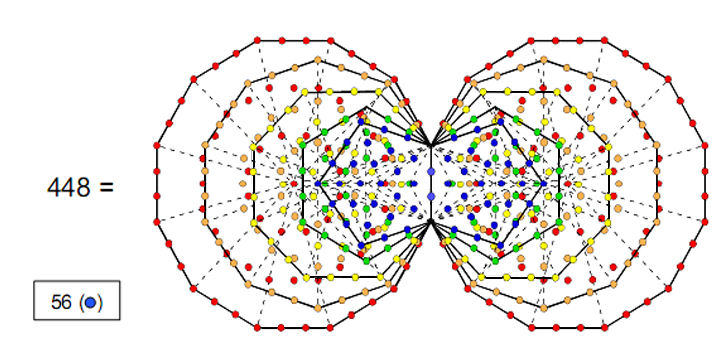
Fig. 2 depicts the values of the 64 hexagrams of the I Ching. Their sum is 448. The sum of the eight diagonal hexagrams is 56. The sum of the 56 off-diagonal hexagrams is (448–56=392). Each set of 28 off-diagonal hexagrams sums to 196. As shown in Article 17,1 this is the average distance (in units of 1/10 AU) of the planet Uranus from the Sun predicted by the logarithmic spiral basis of the Titius-Bode Law (the measured distance is 191.9). The eightfold I Ching table encodes the Bode distance of the planet completing an octet of planets analogous to the musical octave, the eight Gregorian musical modes, the eight groups of the chemical Periodic Table, the eight gluons transmitting the colour force between quarks, the eight simple roots of the superstring gauge symmetry group E8 and the eight unit octonions forming the largest division algebra. This eight-fold pattern pervading nature was discussed in Article 19.
Furthermore, the sum of the values of the first row of off-diagonal hexagrams is 28, which is the distance of the Asteroid Belt from the Sun predicted by the Titius-Bode Law. The predicted distance of Uranus from the Asteroid Belt is (196–28=168), which is the sum of the values of the 21 remaining off-diagonal hexagrams. The significance of this number as the superstring structural parameter was discussed in Article 18.2
Confirmation that this apparent encoding of the Bode numbers of planets in the I Ching table is not coincidental but fundamental comes from comparing the inner form of the Tree of Life with the table. As Fig. 20 in Article 18 depicts, an exact isomorphism exists between the pattern of yods in the two sets of the first six polygons and the pattern of
2
Figure 2. The sum of the number values of the 64 hexagrams is 448. The sum of the number values (shown in red) of the eight diagonal hexagrams is 56.
3 yin/yang lines in the table. The counterpart of this isomorphism vis-à-vis the number values of the hexagrams shown in Fig. 2 is the two sets of the last five polygons, which have 64 corners — the same as the number of hexagrams. The two sets of triangles and squares have 76 yods and there are 524 yods in both sets of seven polygons. The last (5+5) polygons therefore have (524–76=448) yods outside their shared edge, making 450 yods in total apart from the endpoints of the shared edge. Overlapping Trees of Life have a similar set of enfolded polygons. As the top corners of the two hexagons coincide with the bottom corners of hexagons enfolded in the next higher tree, there are (450–2=448) yods other than the endpoints of the shared edge that are intrinsic to both sets of the last five polygons enfolded in each tree. 448 is the sum of the number values of the 64 hexagrams, which therefore expresses the number of intrinsic degrees of freedom embodied in the last (5+5) polygons. The pair of pentagons has 56 yods other than endpoints of their shared edge. This is the sum of the number values of the eight diagonal hexagrams. The pair of five polygons corresponds to the two diagonal halves of the I Ching table, with the pair of pentagons — the first member of the quintet of polygons — corresponding to its diagonal and the last four polygons corresponding to the 28 hexagrams in each half of the table outside its diagonal.
2. Algebraic interpretation of the I Ching table
Let the yang and yin lines be symbolised by, respectively, the letters a and b:
The four Emblematic Symbols, or Hsiang, are the terms in the expansion of (a + b)2:
The four possible pairings of yang and yin
lines correspond to all the products of multiplication of a and b. a2 signifies the pair of yang lines and b2 symbolises the pair of yin lines. The correspondence is not precise
because multiplication of symbols in ordinary algebra is commutative: ab = ba, whereas the
order of arrangement of the yang and yin lines in the I Ching table does matter:
The eight trigrams (Kwa) are the eight
possible groups of three lines, each of which is either a yang or a yin line:
That their traditional ordering is correct can be confirmed by comparing it with the order of the terms in the expansion of (a+b)3, remembering that the letter to the far left of a term denotes the line at the bottom of a trigram, the left-right ordering of letters corresponds to the upward ordering of lines and the power of a letter denotes the number of lines corresponding to that letter:
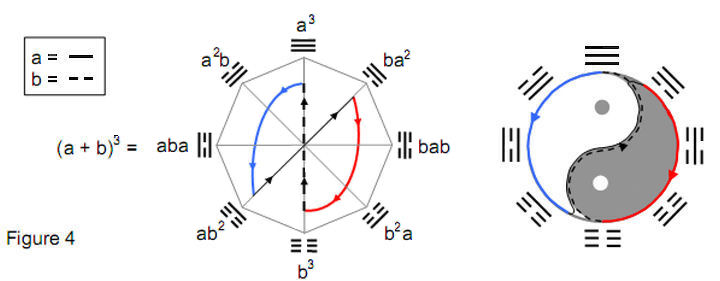
The algebraic basis of the trigrams explains why the ancient Tai Chi Tu diagram (Fig. 4) divides them into two sets of four, with the trigram at one corner of the octagon being generated from that diametrically opposite it by replacing yang lines by yin lines and yin
4 lines by yang lines. The crossover after the fourth trigram expresses the switch in the equation above from the multiplication of (a+b)2 by a to its multiplication by b. Diametrically opposite trigrams denote pairs of algebraic terms that are related in an analogous way by interchange of the symbols a and b. The pairing of trigrams to form a hexagram corresponds to multiplying (a + b)3 by itself:
Each of the (26=64) terms in this expansion is of degree 6 and denotes a hexagram
with six yang/yin lines. The first term a6 represents
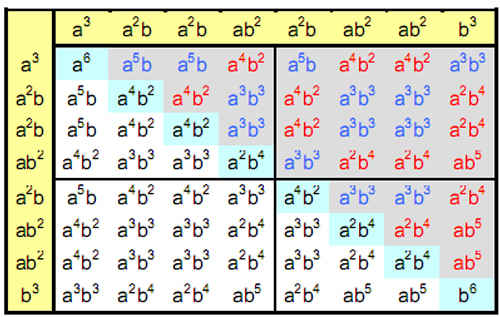
There are one hexagram with six yin lines, six hexagrams with five yang lines and one yin line, 15 hexagrams with four yang lines and two yin lines, 20 hexagrams with three yang lines and three yin lines, 15 hexagrams with two yang lines and four yin lines, six hexagrams with one yang line and five yin lines and one hexagram with six yin lines. The algebraic composition of the I Ching table can be explored further by ignoring the arrangement of the yang and yin lines in the trigrams, so that terms of the form a2b represent trigrams with two yang lines and one yin line and terms of the form ab2 represent trigrams with one yang line and two yin lines. In order of their generation, the eight trigrams have the form:
a3, a2b, a2b, ab2, a2b, ab2, ab2, b3.
(Note that there are four different cubic terms). The pairing of trigrams to form a hexagram corresponds to the mutual multiplication of these terms. Let us ignore the
5 actual order of its lines in order to focus
on the algebraic composition of the hexagrams in the I Ching table. Shown below is the
multiplication table expressing the composition of the hexagrams in terms of the algebraic
symbols a and b for a yang and a yin line:
3a5b, 6a4b2, 10a3b3, 6a2b4, 3ab5.
As this set of terms is symmetric with respect to interchange of a and b, there are 28 off-diagonal hexagrams (white cells) of the same form but with yang and yin lines interchanged.
The eight diagonal hexagrams (turquoise cells) have the compositions: a6 (×1), a4b2 (×3), a2b4 (×3) and b6 (×1). These are the terms in the expansion of (a2 + b2)3:
(a2 + b2)3 = a6 + 3a4b2 + 3a2b4 + b6.
The numbers of yin/yang lines in the five types of off-diagonal hexagrams are:
6
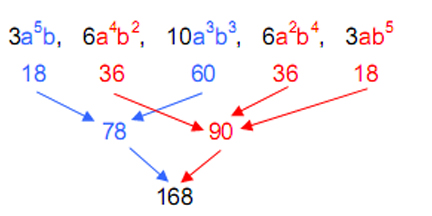
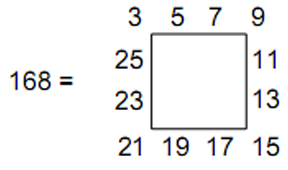
There are 168 such lines (84 yang lines and 84 yin lines), where
84 = 12 + 32 + 52 + 72.
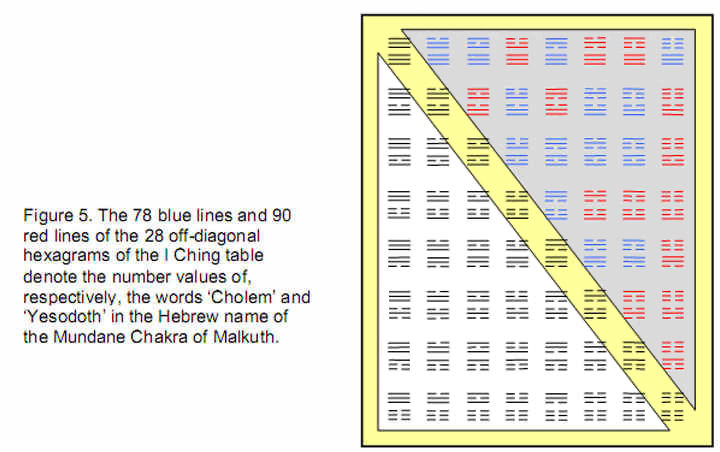
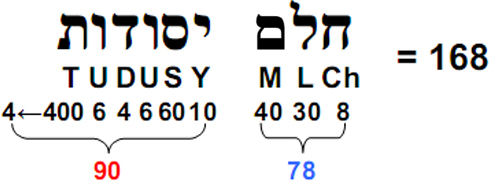
There are 78 yin/yang lines in the 13 off-diagonal hexagrams with either three yang lines and three yin lines or five yang lines and one yin line (or one yang line and five yin lines) (Fig. 5). There are 90 yin/yang lines in the 15 off-diagonal hexagrams with either four yang lines and two yin lines, two yang lines and four yin lines or one yang line and five yin lines (or five yang lines and one yin line). As discussed in Article 18, 168 is the number value of Cholem Yesodoth (“Breaker of the Foundations”), the Mundane Chakra of Malkuth, 78 being the number value of Cholem and 90 being the number value of Yesodoth:
That the various populations of lines in the five types of off-diagonal hexagrams should coincide with the number values of these two Hebrew words and their sum cannot, plausibly, be dismissed as coincidental. Instead, it indicates the profound connection between Kabbalah and I Ching, as one would expect from two mystically revealed, ancient systems of knowledge about reality. Mystical traditions may speak in different languages, but they express only one Truth.
3. Geometrical interpretation of the I Ching table
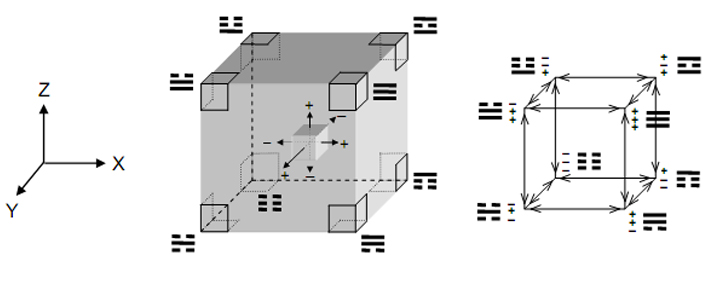
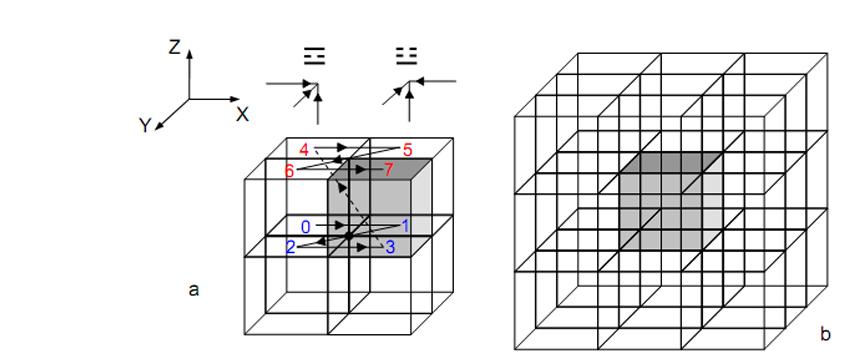
Suppose that we call the right, front and top faces of a cube ‘positive’ faces and the left, rear and bottom faces ‘negative’ faces. Let us also suppose that there is a Cartesian system of rectangular coordinates (x,y,z) with its origin at the centre of the cube and the positive X-axis pointing towards the right face, the positive Y-axis pointing towards the front face and the positive Z-axis pointing towards the top face. Let us employ the convention that:
This convention follows the order of the labelling of the Cartesian system of coordinates in which the point at (x,y,z) has the position vector:
7 the x-coordinate being at the top, the y-coordinate in the middle and the z-coordinate at the bottom. For each row, suppose that the yang line corresponds to the (+) face and that the yin line corresponds to the (–) face. The right, front and top faces are (+) faces. Their intersection defines the Heaven (Chien) trigram with three yang (positive) lines (Fig. 6).
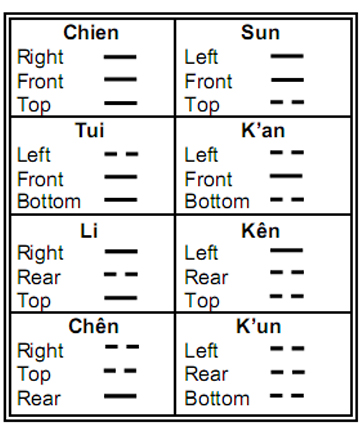
The left, back and bottom faces are (–) faces. Their intersection defines the Earth (K’un) trigram with three yin (negative) lines. Triple combinations of (+) and (–) faces define the remaining six corners of the cube. The arrows along the edges of the cube in Fig. 6 indicate the positivity or negativity of a face. It is a (+) face if the arrow points along the positive X-, Y- or Z-axes and a (–) face if it points along the negative axes. The table below interprets the trigrams in terms of the faces of the cube:
As in the case of their binary number representations, in which the integers 0 and 1 in each binary number signify the values of the Cartesian coordinates of the corners of a cube, the first four trigrams define corners of one face and the last four trigrams define corners of the face parallel to it (Fig. 7). The difference here is that the two sets of four trigrams correspond to the top and bottom faces instead of to the left and right faces.
8
The Heaven trigram corresponds to the corner with coordinates (1,1,1) formed from the three (+) faces and the Earth trigram corresponds to the corner with coordinates (0,0,0) formed from the three (–) faces, whereas these trigrams correspond as binary numbers to, respectively, (0,0,0) and (1,1,1). The cubic array of trigrams generated by the faces is identical to that generated by their binary number representations but differs by a 90° anticlockwise rotation about the positive y-axis followed by a 180° anticlockwise rotation about the positive Z-axis.
If the convention were followed that the lowest row of a trigram corresponds to the pair of (+) and (–) faces orthogonal to the X-axis, the middle row corresponds to the two faces orthogonal to the Y-axis and the top row corresponds to the two faces orthogonal to the Z-axis, the resulting cubic array of trigrams would then be generated by rotating the cube based upon binary numbers through an angle of 180° about the positive Z-axis followed by a reflection in a mirror parallel to the xy plane. In other words, it would not be superposable on this cube because it is its reflection in a mirror. This is undesirable because we want the two arrays of trigrams to be identical. For consistency, therefore, the top row of a trigram must be associated with the faces perpendicular to the X-axis.
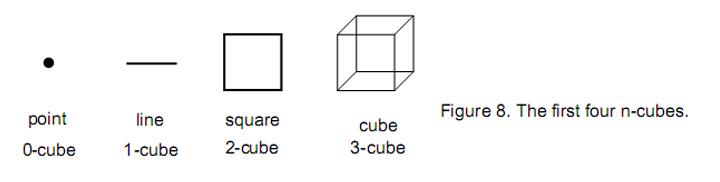
The cube can be generalised to an
n-dimensional cube, which mathematicians call the “n-cube.” Fig. 8 shows the first four
members of this family.
9
20 + 21 + 22 + 23 = 15.
Yahweh, which has number value 26, defines the 3-cube as the last member of this set because it consists of eight corners (0-cubes), 12 edges (1-cubes) and six squares (2-cubes), a total of 26 0-, 1-, & 2-cubes. The Godname Eloha with number value 36 prescribes the cube because its eight corners can be joined by 28 lines, totalling 36 corners and lines. There are 35 1-cubes joining the 15 0-cubes in the sequence, a total of 50 0- & 1-cubes. This shows how the Godname Elohim, אלהימ, withnumber value 50 prescribes the sequence from the point to the 3-dimensional cube.
The total number of 0-, 1-, 2- & 3-cubes in the set is 40, where
This is an example of how the Tetrad Principle3 prescribes a sequence of mathematical objects terminating in one that has great relevance to natural phenomena. The ancient Pythagoreans believed that particles of the solid Element Earth had the shape of a cube. As we shall now show, the cube really does define the form of superstrings.
4. Superstring structural parameter 168 encoded in cube
The eight trigrams symbolise binary representations of the integers 0–7. However, we found in Section 3 that they also define the eight corners of a cube. This means that to each corner can be assigned the Arabic numeral that is expressed by the binary number symbolised by its associated trigram.
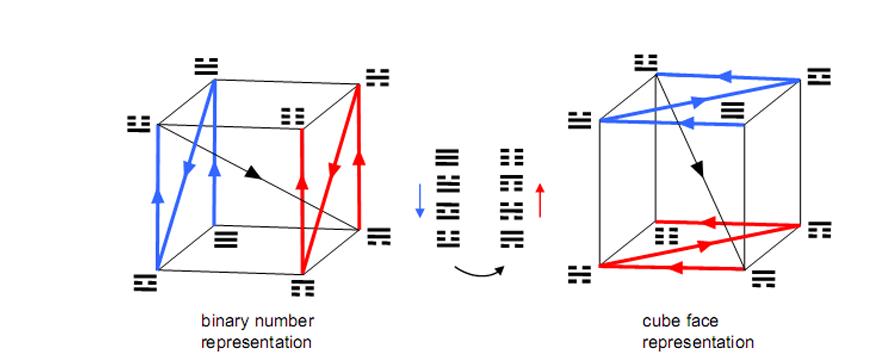
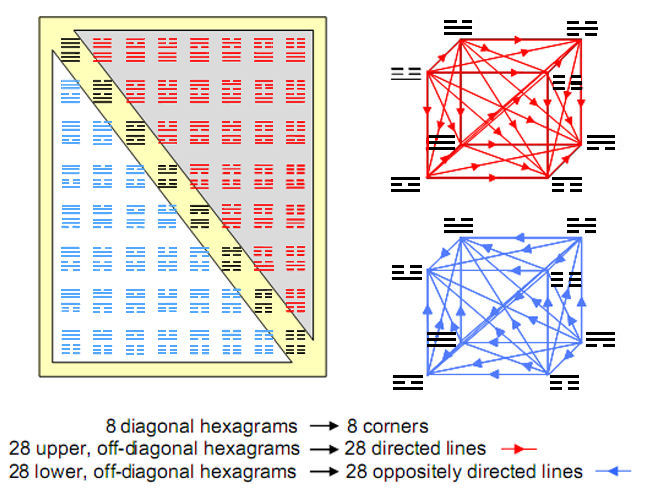
10 Each combination of two trigrams is also the pairing of two corners, and so a hexagram signifies the line joining them. The hexagrams spread along the diagonal of the I Ching table consist of pairs of identical trigrams that signify just the corners themselves, whilst the 28 hexagrams formed from pairs of different trigrams denote the 28 lines that join the eight corners (Fig. 9). The two possible orderings of a pair of trigrams correspond to the two possible directions of arrow joining two corners. This is illustrated in Fig. 9 by joining the corners of a cube by 28 arrows pointing in arbitrary directions. The red cube has 28 arrows corresponding to the 28 hexagrams above the diagonal of the table and the blue cube has 28 arrows pointing in reverse directions and corresponding to the 28 hexagrams below the diagonal, each of which is in reverse order to its counterpart above the diagonal.
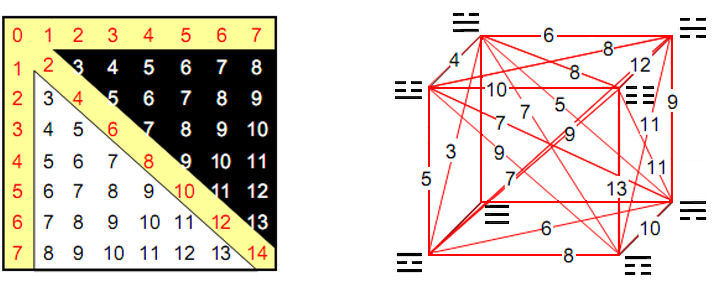
Fig. 10 shows the number values of the 64 hexagrams. The 21 numbers in the black or white triangle are the sums of the number values of pairs of trigrams located at all corners other than that defined by the Heaven trigram.
Figure 10. The number values of the hexagrams. Each set of 28 off-diagonal numbers can be assigned to the 28 lines joining the eight corners of a cube.
They can be assigned to the arrows joining these pairs of trigrams. Their sum is 168, the number value of Cholem
11 Yesodoth. Its significance as the structural parameter of superstrings has been discussed in many previous articles (in particular, see Article 18).
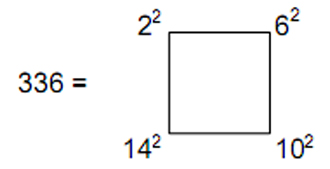
The number of yin/yang lines in the 28 hexagrams above or below the diagonal is also 168. The 56 off-diagonal hexagrams have 336 lines (168 yang lines, 168 yin lines), where
and
This again illustrates the action of the Tetrad Principle, for 336 is the number of circularly polarised oscillations that a whorl in the UPA/superstring makes during one revolution about its axis of spin,4 and this number is the sum of the squares of four integers, spaced four units apart, starting with 2, the first even integer, whilst 168, the number of oscillations made in half a revolution, is the sum of the first 12 odd integers after 1 that can be assigned to the sides of a four-sided square, four to each side.
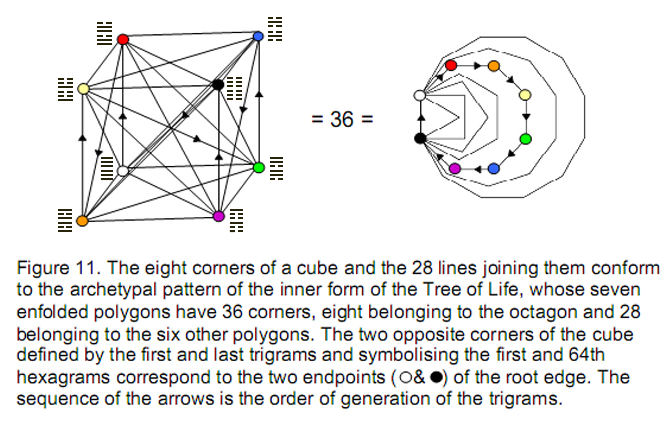
That the I Ching table is truly archetypal in nature is confirmed by its isomorphism with the inner form of the Tree of Life. The seven enfolded polygons have 36 corners, eight of which belong to the octagon (Fig. 11). The latter symbolise the eight diagonal hexagrams, the topmost pair of
Heaven trigrams corresponding to the top endpoint of the root edge shared by the polygons and the lowest pair of Earth trigrams corresponding to its bottom endpoint. The 28 other corners of the polygons denote the 28 off-diagonal hexagrams, which correspond to the 28 lines joining the corners of the cube symbolising the eight diagonal hexagrams.
12 The 12 diagonals of the six square faces of a cube are the sides of two interpenetrating tetrahedra (Fig. 12). The integers associated with these sides add up to 84, whilst those associated with the 12 sides of the cube also add up to 84. This is the arithmetic counterpart to the 84 yang lines and 84 yin lines making up the 28 hexagrams on either side of the diagonal of the I Ching table. The 24 sides of the cube and the two tetrahedra create the shapes of these two Platonic solids. So it is fitting that their associated integers — the values of their corresponding hexagrams
— add up to 168, which is the number that defines the shape of the superstring, according to Annie Besant & C.W. Leadbeater and the author's interpretation of their UPA.
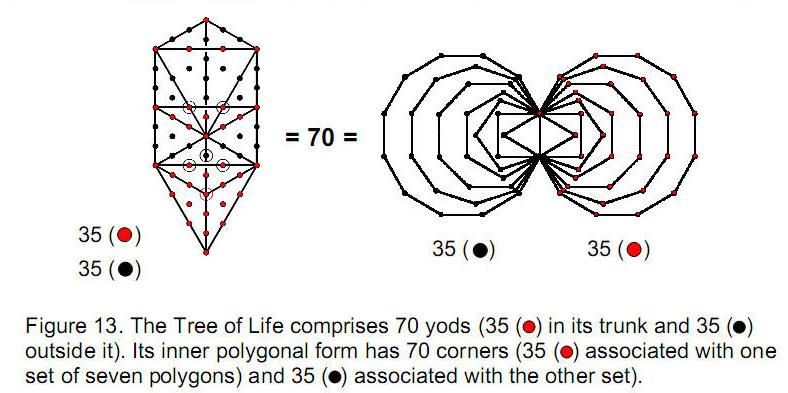
5. Superstring structural parameter 1680
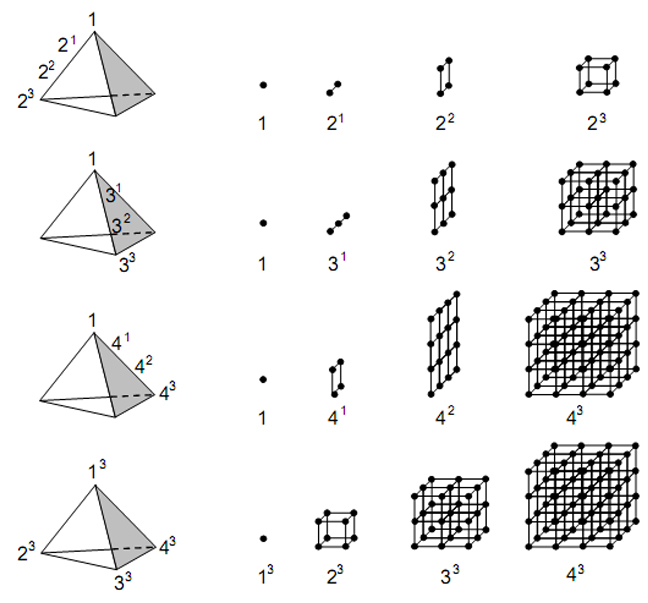
The Tree of Life is made up of 16 triangles with ten corners and 22 sides. When they are turned into tetractyses, each with ten yods, these triangles are found to contain 70 yods (Fig. 13). The ‘trunk’ of the Tree of Life is the descending sequence:
It comprises 35 yods (coloured red in Fig. 13). Outside the trunk are another 35 yods (coloured black) belonging to what may be called its ‘branches.’ The inner form of the Tree of Life consists of two sets of seven regular polygons with 70 corners, 35 corners being associated with each set. This analogous division between the two mirror-image sets of 35 corners in the inner Tree of Life and the trunk and branches of its outer form has its exact counterpart in the cube. There are
ways of choosing four corners from the cube’s eight corners. If we choose the corner (0,0,0), which we found in Section 3 (see Fig. 6) to be defined by the Earth trigram , there are
ways of choosing three other corners from the remaining seven to join to it. There are
13
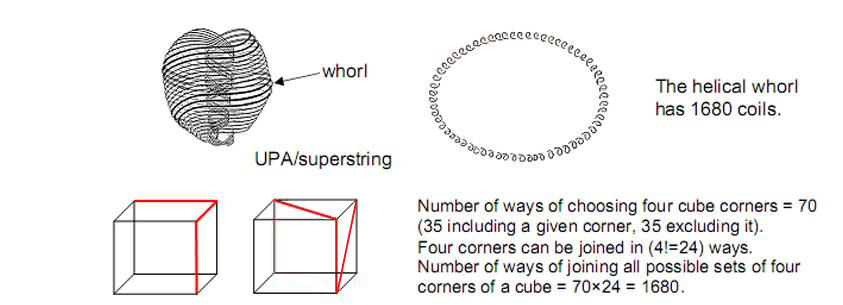
ways of choosing four corners in the cube other than (0,0,0). Four corners can be connected in (4!=24) ways. There are therefore (70×24=1680) ways of joining four corners. There are (35×24=840) paths joining (0,0,0) to three other corners and 840 paths connecting four corners other than (0,0,0).
These properties have striking parallels with the description of the UPA by Besant & Leadbeater.5 This basic building block of matter consist of ten closed curves, or ‘whorls’ (Fig. 14) that wind side by side 2½ times around the surface of an ovoid and then return to their starting points at
Figure 14. The number of ways of joining all possible sets of four corners of a cube is 1680. This is the number of circularly polarised oscillations of each whorl in the UPA/superstring.
the top by twisting 2½ times in a tighter helix, the curves separating into strands of three and seven at the pointed end of the UPA and regrouping at its top. Each whorl is essentially a helical coil with 1680 turns. A whorl represents a circularly polarised standing wave — itself the 3-dimensional projection of a vibrating, higher-dimensional membrane. The whorl winds 840 times in an outer spiral and 840 times in the narrower helix. This outer and inner winding corresponds to the two sets of 840 opposite paths connecting four corners of the cube.
The significance of the four corners is that movement through 3-dimensional space from any given starting point is tantamount to moving to a point along the X-axis, then to a point along the Y-axis and, finally, to a point along the Z-axis, that is, a path in 3-dimensional space requires a minimum of four points. Of course, not all the 35 sets of four corners lead to motion in 3-dimensional space. The point (0,0,0) is the corner of six squares or rectangles that join four corners, creating a 2-dimensional path, so that this point is connected to three other corners by (35–6=29) 3-dimensional paths, whilst the 35 sets of four corners excluding (0,0,0) include six sets that are corners of squares or rectangles, so that there are 12 2-dimensional paths and (29+9=58) 3-dimensional ones that connect four corners of a cube.
The eight trigrams of the I Ching therefore define the eight corners of a cube, their three rows of yang and yin lines defining the sets of three cube faces (positive or negative) whose intersection creates a corner. The pairing of dissimilar trigrams into 28 hexagrams defines the 28 paths joining the corners of the cube. These paths are
14 orientable. Reversing the order of trigrams is tantamount to reversing the direction of the paths. As pairs of similar trigrams, the diagonal hexagrams signify the corners themselves. There are 1680 differently directed paths joining four corners. They group into two sets of 840 paths, each path in one set having a counterpart in the other set that is oppositely directed. The two sets of 840 paths, each the opposite of the other, correspond to the outer and inner halves of the UPA/superstring, each with 840 oscillations in a whorl. In this way, the I Ching table encodes the circularly polarised oscillations of each whorl of the superstring.
That this table represents a holistic
pattern in the Kabbalistic sense is demonstrated in Figure 15. The ten Sephiroth of
the Tree of Life can each be represented by a Tree of Life, which means that 64 Sephirothic emanations
are needed to create ten overlapping Trees of Life.
15
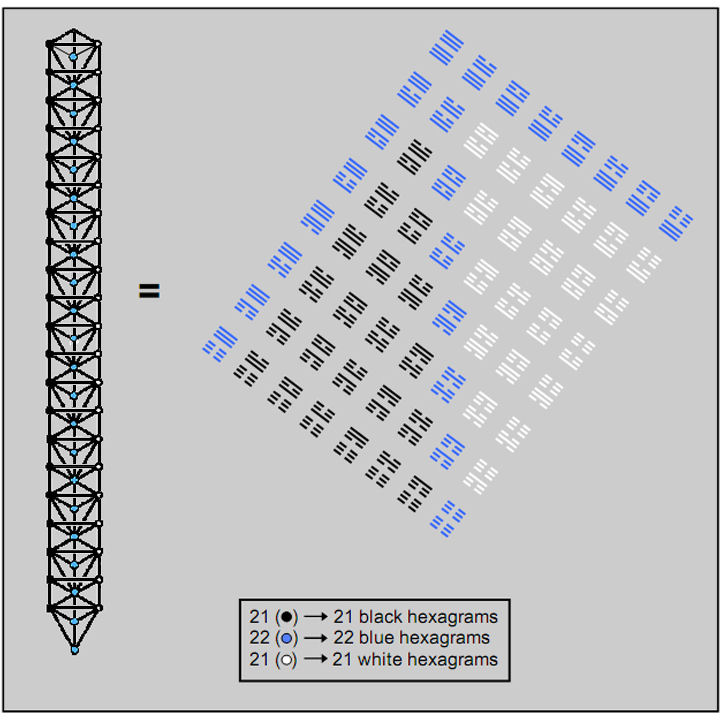
16 The lowest ten trees of a more extended set of trees have 65 emanations, where 65 is the number value of Adonai, the Godname of Malkuth, the lowest Sephirah. This is how the Divine Name prescribes the next higher-level differentiation of the Tree of Life. The number of emanations on the central Pillar of Equilibrium is 22. This is the number of hexagrams forming two adjacent sides and the diagonal of the table. The number of emanations on each side pillar is 21, which is the number of remaining hexagrams on either side of the diagonal. The yang-yin polarity represented by these two halves is realised in the Tree of Life through the Pillars of Mercy and Severity, which embody, respectively, the active, generative principle and the receptive, formative principles working in unison to perpetuate and sustain all manifestations of the Divine Life. 21 is the number value of the Godname Ehyeh (“I am”) assigned to Kether. All the Divine Names prescribe the ten overlapping Trees of Life. Another example will be given shortly.
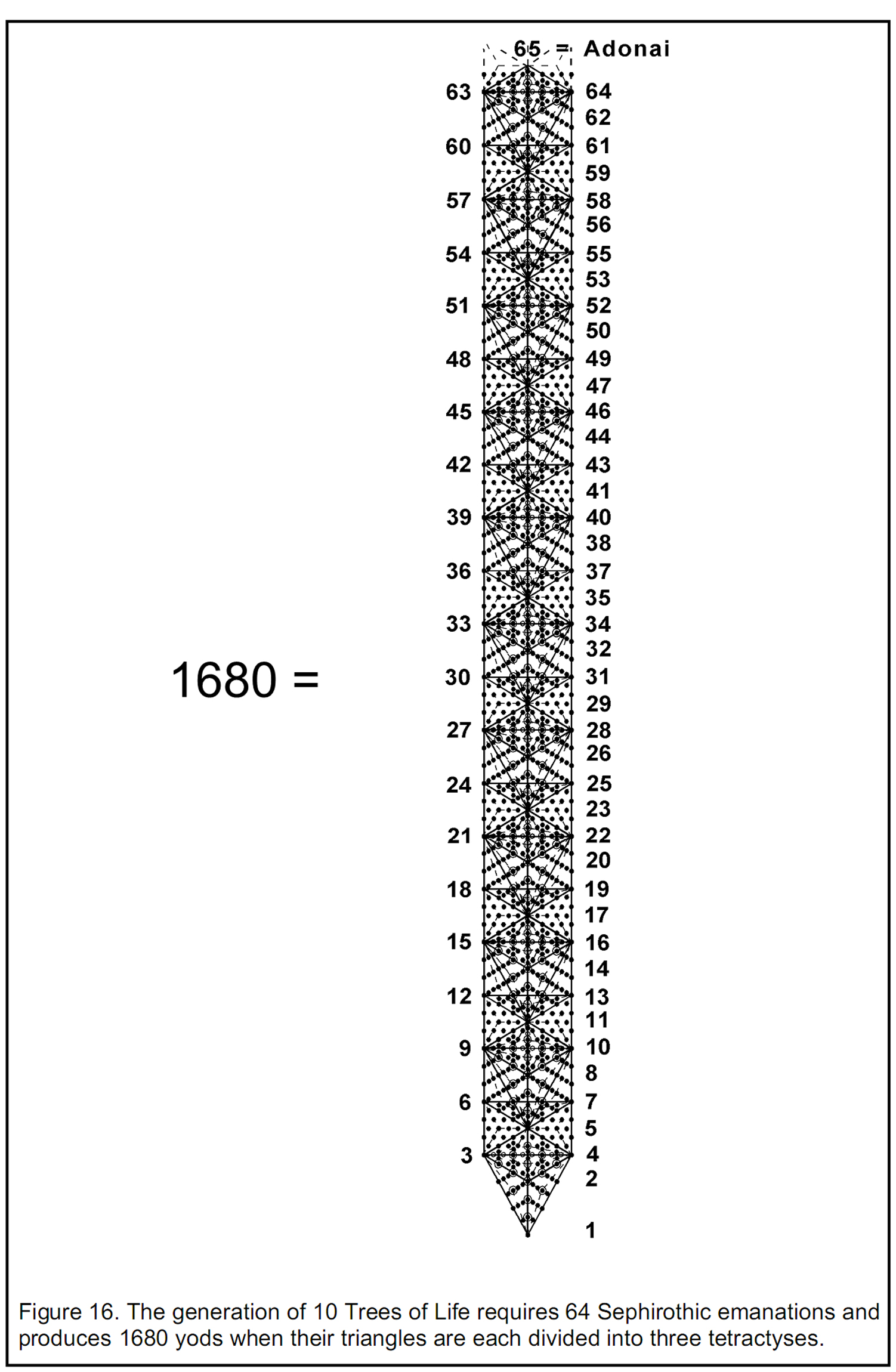
It can be shown6 that, when the triangles making up these trees are divided into three triangles that are then converted into tetractyses, the number of yods below the top of the nth tree is
N(n) = 158n + 100.
The number of yods below the top of the tenth, overlapping Tree of Life is therefore
N(10) = 1680
(Fig. 16). Eight of these yods are in four triangles outside the tenth tree. The remarkable result emerges that, just as the 64 hexagrams of the I Ching table symbolise the eight corners of a cube (diagonal hexagrams) and the 56 arrows joining them (56 off-diagonal hexagrams) and just as there are 1680 directed paths joining all sets of four corners, so 64 Sephirothic emanations complete the formation of ten Trees of Life out of tetractyses containing 1680 yods. This is further confirmation of the holistic quality of the I Ching table, which is not merely isomorphic to the complete set of ten trees but also, as a representation of the cube, encodes the superstring structural parameter 1680.
We saw earlier that the Godname Adonai with number value 65 defines the ten lowest, overlapping Trees of Life. It prescribes also the superstring structural parameter 1680 as the number of yods below the 65th emanation marking the apex of the tenth tree.
The number of triangles in the lowest n Trees of Life can be shown7 to be
T(n) = 12n + 7.
Therefore, the lowest ten trees contain
T(10) = 127
triangles. 127 is the 31st prime number, where 31 is the number value of El (“God”), אל. This is another example of how the Hebrew Godnames prescribe the ten Trees of Life. Conversion of each triangle into three tetractyses generates 127×3 = 381 tetractyses. As, according to Fig. 16, the eight yods outside the tenth tree belong to four tetractyses, the 1680 yods belong to (381+4=385) triangles, where
This demonstrates the beautiful, mathematical properties of the Tree of Life encoding of
17 the number of circularly polarized oscillations made in 3-dimensional space by each whorl of the UPA/superstring.
There are 127 centres of triangles (each the corner of a tetractys) in the ten trees and 65 corners of these triangles. Inspection of Fig. 16 reveals that there is one corner of a tetractys on each side of the central pillar at the level of the apex of the tenth tree. There are (127+65+1+1=194) corners of tetractyses up to this point. 194 is the number value of Tzadekh (“righteousness”), the Mundane Chakra of Chesed.
One of the predictions made by the logarithmic spiral theory of planetary formation developed in Article 178 is that the average distance (in units of 1/10 AU) between Mercury and Pluto is 385. This compares well with the actual value of 390.9, a discrepancy of only 1.5%. The average distance of Pluto from the centre of the logarithmic spiral-shaped planetary nebula that spawned the planets is predicted to be 384, which is the number of yin and yang lines in the I Ching table. Rather than being just coincidental, this is powerful evidence (further revealed in Article 17) that the I Ching encodes the distances of the planets in the Solar System and harmonises in a profound way with the other cosmic blueprint — the Tree of Life, as shown by their embodying the numbers 64, 168 and 1680. The marvel of it is that the same number, namely, 385, with such
Pythagorean character should appear in the context of two ten-fold systems, namely, the 10-planet Solar System and the 10-tree representation of the 10-dimensional superstring. As the mythical, Egyptian teacher of mystical wisdom, Hermes Trismegistus, wrote at the beginning of his great work The Emerald Tablet, “As above, so below.” The universe is the same as God, God is the same as man, man is the same as the cell, the cell is the same as the atom, the atom is the same as the superstring ... and so on.
6. The connection between Plato’s Lambda and the I Ching table
A cube with 26 corners, sides and faces is surrounded by 26 contiguous cubes (Fig. 17). Of their 144 sides, 12 sides are shared with the cube, leaving 132 unshared 18 sides. 132 is the 65th even integer after 2. They have 36 square faces perpendicular to each coordinate axis. The cube is surrounded by 102 square faces, where 102 is the 50th even integer after 2. This shows how the Godnames Adonai (Malkuth) with number value 65, Yahweh (Chokmah) with number value 26, Elohim (Binah) with number value 50 and Eloha (Geburah) with number value 36 prescribe the cube and its cubic lattice environment.
This configuration is symbolised by the I Ching table for the following reason: as we have seen, the yang and yin lines of a trigram denote the set of three faces (positive or negative) that intersect at a corner of a cube. The point at each corner is also the corner of three cubes at the same
Figure 18. Plato’s Lambda and its tetrahedral generalisation.
height as the cube and the corner of four cubes below it (see Fig. 17). The seven corners are each defined by three faces whose positivity or negativity corresponds to the yang or yin lines in the seven other trigrams. Associated with each corner of the grey cube defined by a trigram are seven other trigrams symbolising the sets of three faces of the seven cubes that share the same corner. The pairing of this hexagram with these trigrams generates a row of eight hexagrams in the I Ching table. The 64 hexagrams in the eight rows therefore express the 3×3×3 cubic array. The diagonal set of hexagrams made up of pairs of identical trigrams symbolise the eight corners of the cube at the centre of the array.
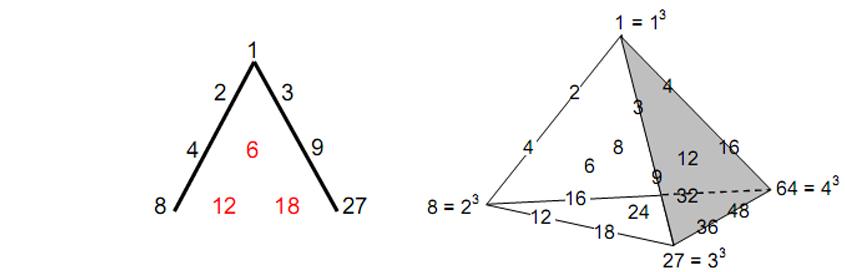
According to Timaeus, Plato’s treatise on Pythagorean cosmology, the Demiurge took a strip of the substance of the World-Soul and divided its length into portions measured by the first four terms of the two geometric series:
1, 2, 4, 8, … and 1, 3, 9, 27, … .
which have, respectively, 2 and 3 as geometrical ratios. This became known as Plato’s Lambda (Fig. 18) because of its resemblance to Λ, the Greek letter lambda. The seven integers can be regarded as belonging to a tetractys of ten integers with the interpolated inclusion of the integers 6, 12 and 18 that follow the same rules of multiplication by 2 and 3. This pattern was extended by the Pythagorean mathematician Nichomachus of Gerasa (c. 100 B.C.E.) to generate the tone ratios of the notes of the Pythagorean musical scale and its higher octaves. In Articles 11 and 12, the realisation that the Lambda tetractys is but one face of a tetrahedral array of 20 integers was shown to restore the symmetry of distribution of octaves, perfect fourths and perfect
19 fifths in the hexagonal array of integers whose ratios are the tone ratios or frequencies of all the musical notes. The integers at the corners of the tetrahedron are 1 (=13), 8 (=23), 27 (=33) and 64 (=43), showing how the integers 1, 2, 3 and 4 symbolised by the tetractys express this archetypal pattern of numbers.
Let us now compare these properties of the tetrahedral Lambda with the following aspects of the 26 cubes surrounding the central cube. The 27 (=33) cubes have 64 (=43) corners, of which eight (=23) are outermost corners of the 3×3×3 array. The cubes of the integers 1, 2, 3 and 4 at the corners of the tetrahedron, which add up to 100, where
and 20
denote the generic cube (13=1), the 2×2×2 group of eight cubes (23) defined by the eight trigrams, the 3×3×3 group of 27 cubes (33) symbolised by the 64 hexagrams of the I Ching table and the (4×4×4=64) (43) corners of these cubes. This remarkable correlation between the table and the tetrahedral Lambda tetractys exists because each is a mathematically complete (that is, holistic), archetypal pattern. This was not the case for the Lambda tetractys because, as the symbol of Divine Wholeness and its manifestation in holistic systems, the tetractys represents the integers 1, 2, 3 & 4, only the first three of which appear in the Lambda as terms of the two geometric series given above.
The integers 1, 2, 4 and 8 lying on one side of the tetrahedral Lambda tetractys denote
21 the numbers of 0-cubes in the sequence: point
The integers 1, 3, 9 & 27 lying on another side denote a corner of the 2×2×2 cubic array shown in Fig. 17a, the three points along one of its sides, the nine points on a face of the array and the 27 points of the array. The integers 1, 4, 16 & 64 lying on the third side of the tetrahedral array denote a corner of the 3×3×3 array in Fig. 17b, the four points along one side of it, the 16 points on one of its faces and the 64 points of the array. The cubes 13, 23, 33 & 43 at the corners of the tetrahedron are simply the numbers of 0-cubes (points) in the sequence:
0-cube (Fig. 19). The 3×3×3 array of 27
cubes consists of 64 corners and 108 sides of 108 squares, that is, 280 0-, 1- &
2-cubes. 280 is the
and 168 is the number value of the Mundane Chakra of Malkuth. The seven polygons making up the inner form of the Tree of Life are enfolded in each overlapping tree. Enfolded in n trees are 7n polygons with (35n+1) corners.9 The 70 polygons enfolded on one side of the central pillar of ten trees have 351 corners, where
351 = 1 + 2 + 3 + … + 26,
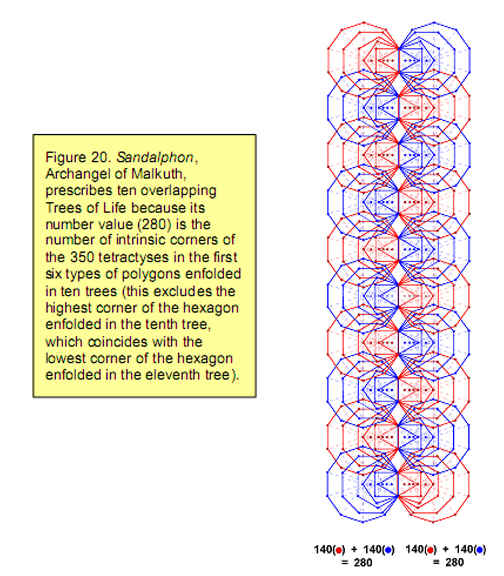
showing how the Divine Name Yahweh with number value 26 prescribes the ten trees. Sandalphon also prescribes ten trees because the number of corners of the 350 tetractyses making up the first six polygons enfolded in ten trees is 280 (Fig. 20). Both sets of these polygons have 1680 yods10 forming their boundaries (Fig. 21). 840 yods lie along edges of polygons on one side of the central pillar and 840 yods border the edges of the polygons on the other side. This is the Tree of Life counterpart to the 840 directed paths and their 840 opposite paths joining four corners of a cube (see p. 15). As we have seen, the 840:840 division is realised in the E8×E8 heterotic superstring as the 840 circularly polarised oscillations of the inner and outer halves of each of its ten whorls.
As the cube at the centre of the 3×3×3 array shown in Fig. 17b has 26 0-, 1- &
22 2-cubes, the 26 cubes surrounding it have (280–26=254) 0-, 1- & 2-cubes. 254 is the 127th even integer, where 127 is the 31st prime number. This shows how the Godname El (אל) with number value 31 prescribes the number of corners, sides and faces of the 26 cubes that surround the central one. If one can travel in space only along the edges of a cubic lattice, one can, starting from any given lattice point, move to 26 corners in passing through the space of one cube. Yahweh determines the number of nearest neighbour corners.
Consider the 3×3×3 array of cubes shown in Fig. 17b. Each corner of the central cube is the centre of four cubes above it and (including itself) four cubes below them. The three faces intersecting at this corner are in contact with seven other triplets of faces (four in the cubes above the central cube and three in the same plane as it). So (7×3=21) faces other than the faces of a cube intersect at any given one of its eight corners, that is, (8×21=168) faces (84 positive, 84 negative) of the 26 surrounding cubes intersect to define the eight corners of the central cube. This demonstrates the form-generating character of the superstring structural parameter 168. A cube is defined by its six faces and by eight triplets of positive or negative signs characterising the faces that meet at its corners, that is, by the eight trigrams. Translating the cube by one cube length along the X-, Y- and Z-axes to generate the 3×3×3 array of cubes requires 168 more positive and negative faces, all of which are distinct. This is the geometrical meaning of the grey or white triangular arrays of 28 hexagrams with 168 yang/yin lines on either side of the diagonal of the I Ching table shown in Fig. 9. The number value of the Mundane Chakra of Malkuth defines the number of two-valued bits of information needed to describe the motion of a cube in 3-dimensional space. (8×3=24) bits of information define the eight corners of the cube itself. These correspond to the eight upper trigrams in the diagonal row of hexagrams. The total number of bits of information defining the cube and its translation = 168 + 24 = 192, which is the number of yin/yang lines in each half of the I Ching table. As shown in Article 18, it is also the Bode number for the planet Uranus, which is predicted by the author’s theory of planetary distances to be the average distance from the asymptotic centre of a logarithmic spiral of the eighth and last member of the first octet of planets making up the Solar System. The average distance of the Asteroid Belt from the asymptotic centre is 24. This is represented in the table by the 24 lines of the upper
23
trigrams of the eight diagonal hexagrams, the 168 lines of the 28 hexagrams above the diagonal denoting the average distance of the Asteroid Belt from Uranus.
7. Conclusion
Because each row of a trigram has two possibilities — a yang or yin line — its eight possible forms correspond to the binary number representations of the integers 0–7. The pairing of trigrams as hexagrams expresses the addition of pairs of these integers. The 21 pairs of different integers chosen from 1–7 add up to 168, the number value of the Mundane Chakra of Malkuth. This is the number of circularly polarised oscillations in half a revolution of a whorl of the E8×E8 heterotic superstring. The 21 hexagrams on each side of the diagonal of the I Ching table that contain the trigrams expressing the integers 1–7 therefore determine the two half-cycles (yang and yin) of a complete circuit of a whorl. The sum of the values of the 64 hexagrams is the number of yods outside their shared side in the pair of the last five of the seven polygons constituting the inner form of the Tree of Life, the sum of the values of the eight diagonal hexagrams being the number of yods in the pair of pentagons — the first of these polygons. Trigrams are a symbolic representation of the eight algebraic terms in the binomial expansion of (a+b)3. Hexagrams are the 64 terms in the binomial expansion of (a+b)6. The 28 hexagrams on each side of the diagonal of the I Ching table have five algebraic forms that naturally generate the number values of the Hebrew words Cholem and Yesodoth making up the name of the Mundane Chakra of Malkuth.
Defining positive and negative orientations for each face of a cube allows trigrams to be interpreted as triple combinations of positive (yang) and negative (yin) faces. Their intersections define the eight corners of a cube. Hexagrams symbolise arrows joining pairs of corners, the ordering of their trigrams determining the direction of the arrow. There are 1680 directed paths connecting the 70 sets of four corners of a cube. To each path is one in the opposite direction. The two sets of 840 paths correspond to the 840 circularly polarised oscillations in an outer and an inner half of a whorl of the E8×E8 heterotic superstring. The superstring structural parameter 1680 is embodied in ten Trees of Life, whose pattern of 64 emanations correlates with the 64 hexagrams.
Plato’s Lambda has its mathematical completion in the tetrahedral array of numbers whose ratios are the tone ratios of the notes of the Pythagorean musical scale. The first four terms in the geometric series with 2, 3 and 4 as ratio form edges of the array and denote the number of corners of cubes in the sequence of generation of, respectively, the cube, 2×2×2 array of cubes and 3×3×3 array of cubes. The significance of the 2×2×2 array is that the triplets of faces of the eight cubes meeting at its centre correspond to the eight trigrams. The significance of the 3×3×3 array for the I Ching table is that a corner of a cube is the corner of eight such cubes where triplets of their positive or negative faces meet. The pairing of any given trigram with all eight trigrams to form a row of hexagrams therefore signifies the eight triplets of faces intersecting at the corner defined by that trigram. This means that the 64 hexagrams of the I Ching table symbolise the 3×3×3 array of cubes. The diagonal hexagrams symbolise the conjunction with itself of a triplet of faces defining a corner, the off-diagonal hexagrams in a row of the table representing the conjunction of a given triplet of faces (trigram) with the triplets of contiguous faces (trigrams) of the neighbouring seven cubes. There are 168 positive and negative faces defining the corners of the 56 cubes that are contiguous with the eight corners, seven per corner. These are symbolised by the 168 yin/yang lines of the 28 hexagrams above the diagonal of the I Ching table. The 24 faces defining the eight corners of the cube at the centre of the 3×3×3 array correspond in the Solar System to the average distance of 24 (in 1/10 A.U.) between the asymptotic
24 centre of the logarithmic spiral and the Asteroid Belt, whilst the 168 faces of the cubes surrounding it correspond to the average distance of 168 between the Asteroid Belt and Uranus, which is the last member of the first of the octets into which planets are predicted to group, according to the author’s theory presented in Article 17. As the superstring structural parameter, the number 168 is the number of binary bits of information required to define the unit translation of a cube (symbolised by the eight diagonal hexagrams) in 3-dimensional space.
The further mathematical significance of the system of 27 cubes for particle physics will be discussed in a future article.
References
25 |
||||||||||||||||||||||


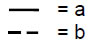
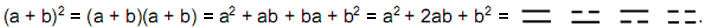
 is not the same as
is not the same as  . This is of no concern provided discussion is limited to the
algebraic structure of the table. The power of a or b in each expansion term of
(a+b)2 is the number, respectively, of yang or yin lines
in the Emblematic Symbol (pair of yin/yang lines) corresponding to that term, whilst the
integer coefficient in each term, such as 1 and 2 in the case above, is the number of
Symbols made up of those numbers of yang and yin lines.
. This is of no concern provided discussion is limited to the
algebraic structure of the table. The power of a or b in each expansion term of
(a+b)2 is the number, respectively, of yang or yin lines
in the Emblematic Symbol (pair of yin/yang lines) corresponding to that term, whilst the
integer coefficient in each term, such as 1 and 2 in the case above, is the number of
Symbols made up of those numbers of yang and yin lines.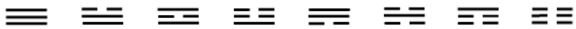
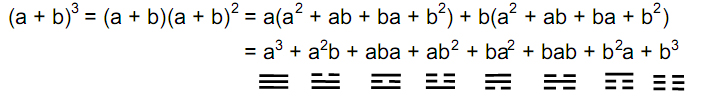
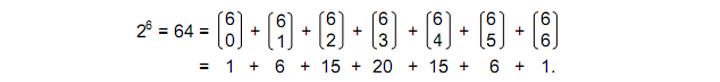
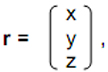
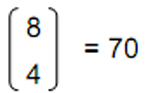
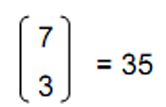
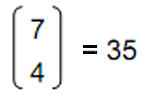
 line
line 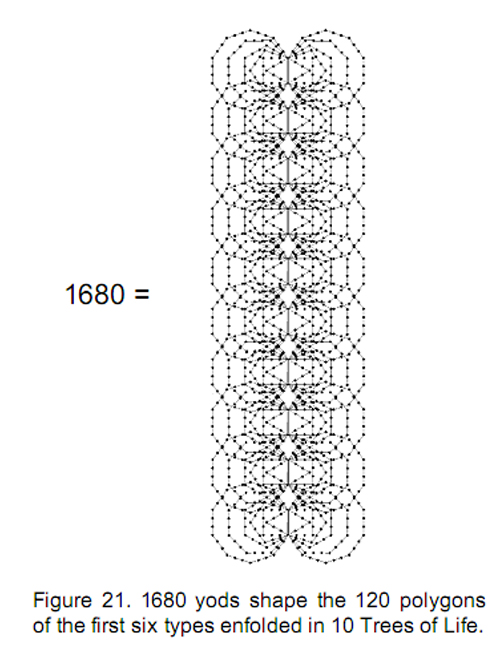 number value of
number value of