ARTICLE 1

The Pythagorean Nature of Superstring
and Bosonic String Theories

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com 

Abstract

1. Pythagorean mathematical principles

Pythagoras founded* a school of philosophy in Croton in southern Italy that was renowned throughout the ancient Mediterranean world. As much a religious brotherhood as a scholastic academy teaching music, astronomy, ethics, arithmetic and geometry, its students were taught mathematics not — as it was considered by Plato — as a preparation for an otherworldly contemplation of divine principles but in order to contemplate the divine immanent in nature. The mathematical doctrines of Pythagoras cannot be properly understood without recognising that the modern dichotomy of science and religion did not exist for the Pythagoreans, who believed that man can realise his divine nature by knowing the universal principle which governs the cosmos (a word coined by Pythagoras himself, meaning “world-order,” a world ordered in a state of mathematical harmony). This principle is Number, which is “the principle, the source and the root of all things” (1). For the Pythagoreans, the spiritual and scientific dimensions of number were complementary and could not be separated.

Pythagoras was not only the first to call himself a philosopher but also a priest -initiate of a mystery religion influenced heavily by Orphism, which taught that the essence of the gods is defined by number. Numbers, indeed, expressed the essence of all created things. According to the Pythagorean Philolaus: “All things which can be known have numbers, for it is not possible that without number anything can either be conceived or known” (2). The Pythagoreans were the first to assert that natural phenomena conformed to mathematical principles and so could be understood by means of mathematics. In this sense, they may be considered the first physicists. But their doctrine gradually became distorted into the proposition that not only does number express the essence of things but also that, ultimately, all things are numbers. Unconvinced by the peculiar emphasis Pythagoreans gave to numbers because he was not privy to the secrets of their teachings, Aristotle said of them: “These thinkers seem to consider that number is the principle both as matter for things and as constituting their attributes and permanent state” (3). The Pythagoreans thought that numbers had metaphysical characters, which expressed the nature of the

__________________________________________

* Pythagoras’ early biographers provide an unreliable, inconsistent chronology. But, as they agree that he left his home Samos for Italy during the rule of its dictator Polycrates (528–522 BCE) and was deported from Egypt after its invasion by Cambyses in 525 BCE, he must have started his school at Croton between 525 BCE and 522 BCE.

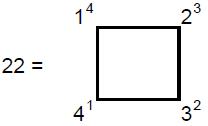
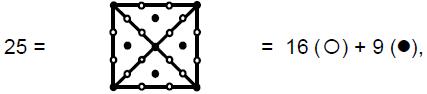
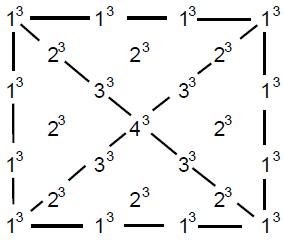
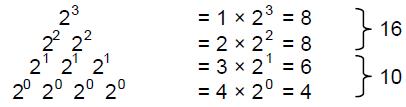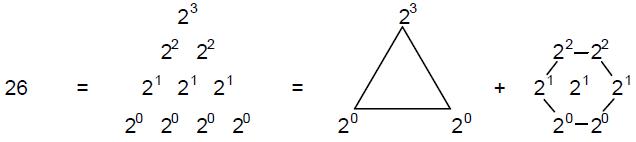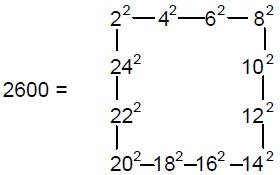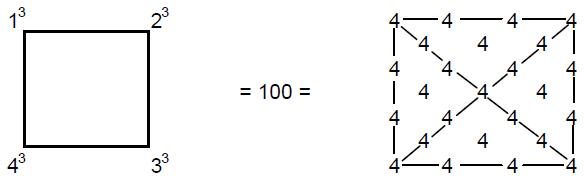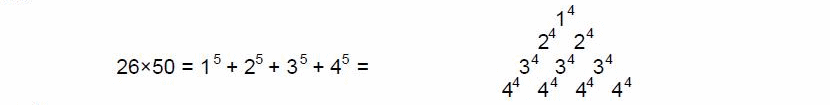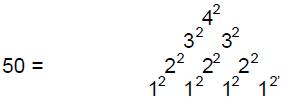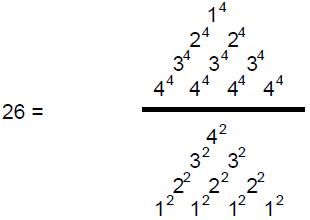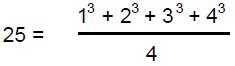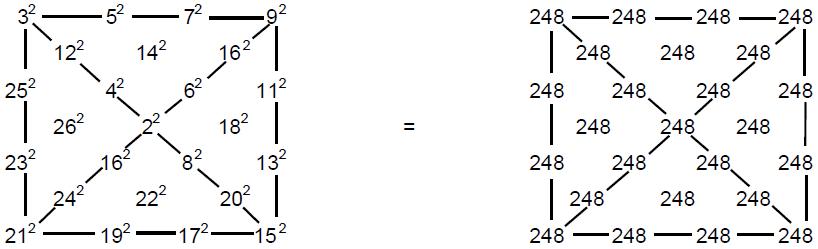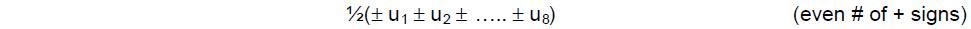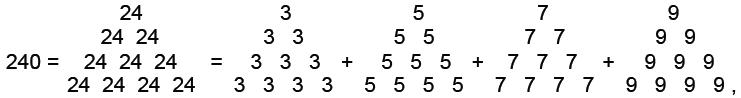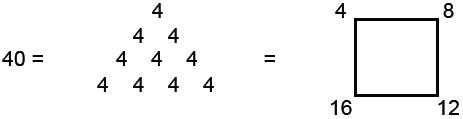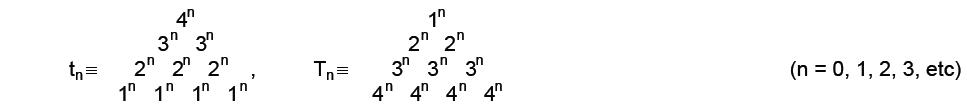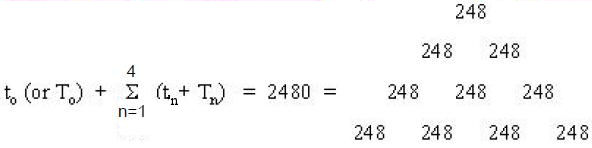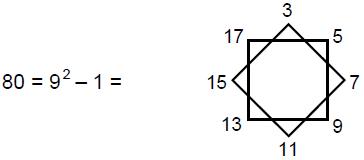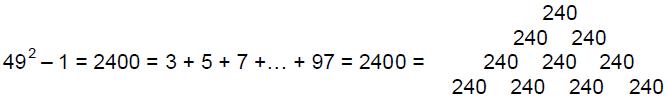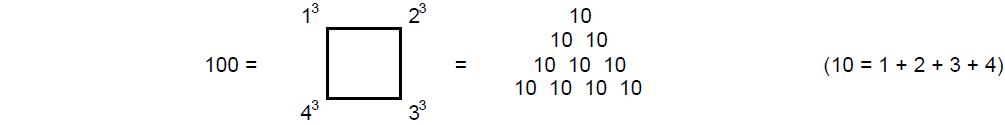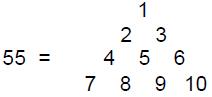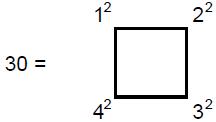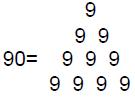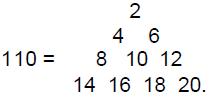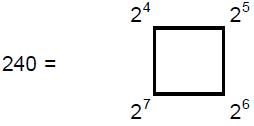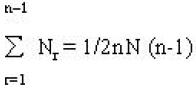gods. The number one (the Monad) represented the principle of unity — the undifferentiated source of all created things. The Pythagoreans did not even regard it as a number because for them it was the ultimate principle underlying all numbers. The number 2 (Dyad) represented duality — the beginning of multiplicity, but not yet the possibility of logos, the principle relating one thing to another. The number 3 (Triad) was called “harmony” because it created a relation or harmonia (“joining together”) between the polar extremes of the undifferentiated Monad and the unlimited differentiation of Dyad.

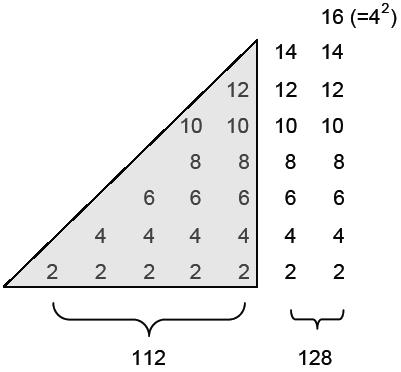
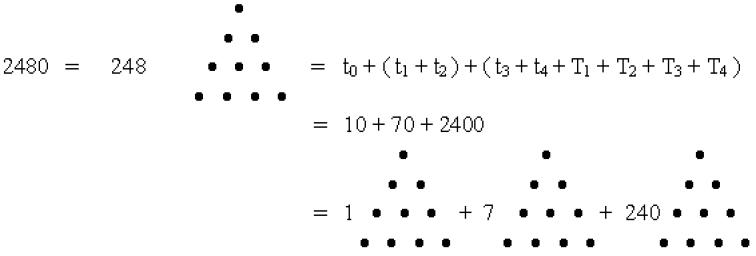
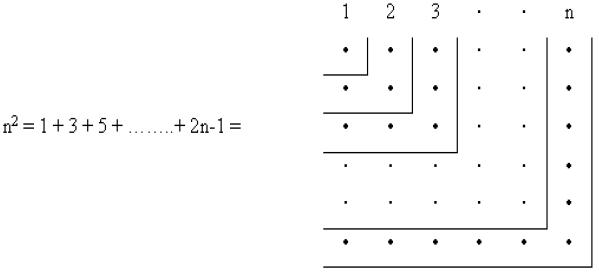
Pythagoras (Fig. 1) was the first to use geometrical diagrams as models of cosmic wholeness and the celestial order. Numbers themselves were represented by geometrical shapes: triangles,  squares, pentagons, etc. For example, a ‘triangular number’ is any number that is equal to the number of dots forming a triangular array and a ‘square number’ is one that can be represented by a square array of dots (Fig. 2). The Greeks generalised

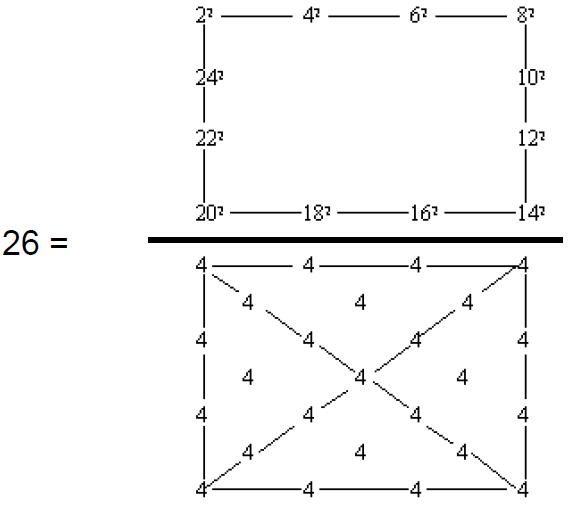
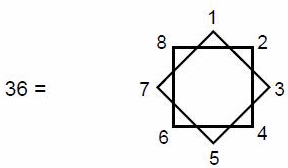
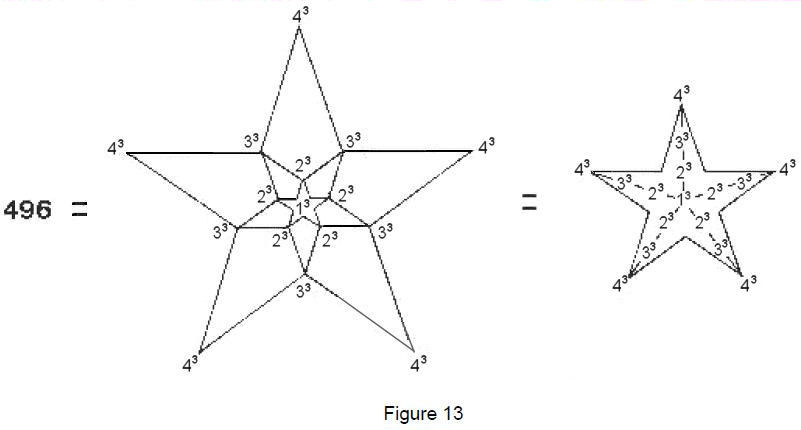
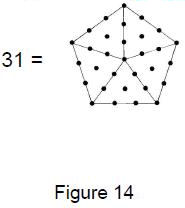
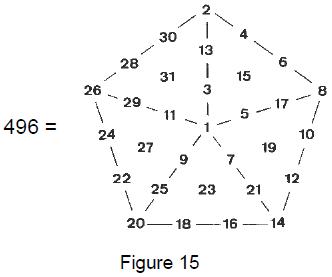
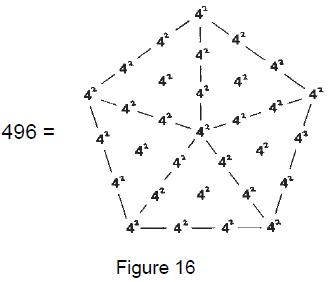
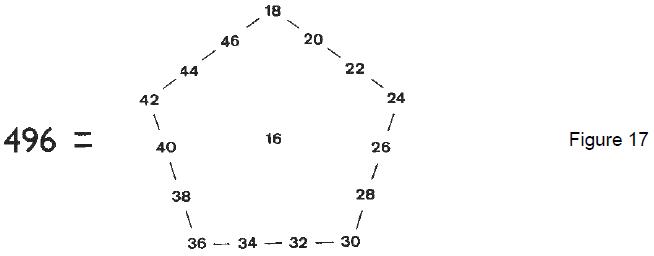
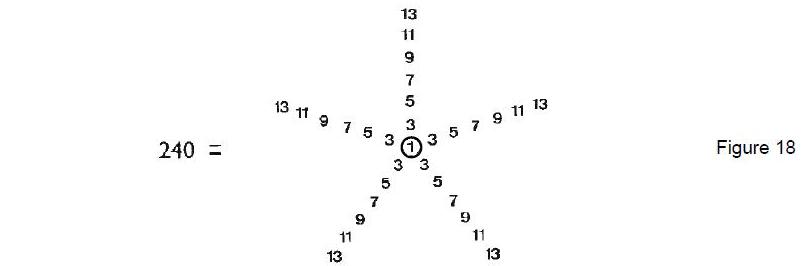
such ‘figurative numbers’ by considering nests of n regular polygons nested inside one another so that they share two adjacent sides  (Fig. 3). Dots denoting the number 1 are spaced at regular intervals along the edges of the polygons, the edge of each polygon having one more dot than the edge of its smaller predecessor. The total number P^Nn of dots in a set of n nested regular polygons with N sides is called a “polygonal number.” The 

number 1 is the first polygonal number, i.e., P^N1 = 1. The second polygonal number, which is simply the number of corners of an N-sided, regular polygons, is P^N2 = N, the third is P^N3, etc. P^Nn is given by:

P^Nn = ½n[(N–2)n – (N–4)]

Table I lists for future reference formulae expressing the first ten types of polygonal numbers of order n:

Table I

The best-known polygonal number is the famous Pythagorean Triangle or “tetractys” which, as the 4th triangular number, is an equilateral triangular array of ten dots (Fig. 4a). We shall call these dots “yods” after the dot-shaped, tenth letter yod of the Hebrew alphabet. The yod (•) at the centre of the tetractys in Fig. 4b is the centre of a hexagon whose corners are six other (•) yods. These seven yods will be called “hexagonal yods.” The four rows of yods forming the tetractys represent the first four integers 1, 2, 3 & 4. The tetractys denotes the number 10, the Decad.

For the Pythagoreans, it was the perfect number, symbolising wholeness and unity.

The importance of the tetractys to them is illustrated by their oath of fellowship:

                                                                                           “I swear by the discoverer* of the Tetractys,
                                                                                            Which is the spring of all our wisdom, 
                                                                                            The perennial fount and root of Nature (4).”

Why was this? Surely not merely because the tetractys was a representation of the perfect Decad?! Scholars know that it came to signify for the Pythagoreans an all-embracing paradigm for whole systems. They believed that a four-fold pattern permeated the natural world, examples of which are the four seasons, the point, line, surface and solid and the four elements Earth, Water, Air and Fire. However, this alone does not explain why they valued the tetractys so much. This article will reveal deeper meanings of the Pythagorean doctrine concerning the tetractys, which link it to current research into the theories of superstrings and bosonic strings. It will explain why the Pythagoreans called the Tetrad, or number 4, “the greatest miracle.” For, indeed, this is what it is, because it prescribes the mathematical description of the

subatomic world.

The mathematical counterpart of the Pythagorean metaphysical doctrine of the Tetrad will be called the “Tetrad Principle.” This states:

The most obvious example from superstring theory of this principle is its prediction that space-time has 10 dimensions, where 10 is the fourth triangular number:

10 = 1 + 2 + 3 + 4.

Many more will be encountered later. No claim is made for the converse of this principal, e.g., the fourth (or 16th) member or the first four members of any class of mathematical objects always quantify a parameter governing fundamental processes. The Tetrad Principle is a necessary, but not sufficient, condition for a number to be of significance to the subatomic world. This means that a number which is predicted by a theory as having fundamental significance in the subatomic world and which is consistent with the Tetrad Principle is not necessarily an actual parameter of the physics of this world. The fact that examples to be discussed in Section 2 can be found which show how this principle prescribes parameters of the theories of superstrings and bosonic strings does not in itself indicate that these string theories are true. Taken individually, such examples merely demonstrate that they satisfy a necessary criterion for being valid. What, however, turns this criterion into a potent principle is the large degree to which these two theories support it. As Section 2 reveals, their degree of consistency with the Tetrad Principle so exceeds what chance would lead one to expect that such detailed conformity cannot plausibly be discounted as purely coincidental. Instead, it is indicative of a powerful, hitherto unrecognised principle at work prescribing the mathematics of fundamental phenomena — one which the Pythagoreans appear to have intuited in their emphasis on the importance of the number 4 to the study of nature.

The tetractys is but one member of an infinite series of tetractyses in which the nth member T_n is generated by replacing each yod in the (n–1)th member by a tetractys, two adjacent yods being substituted by two tetractyses that share a corner (Fig. 5). The Pythagorean Monad — the geometrical point — is the first member T₀ of this series (the 0th-order tetractys), the Pythagorean Triangle (1st-order tetractys) is the second member T₁, the 2nd-order tetractys T₂ is the third, and so on. The Tetrad Principle prescribes

properties of higher-order tetractyses as well as T₁ because they, too, are paradigms of whole systems, albeit more differentiated. Because of its importance to our discussion in Section 3, we illustrate below how the Tetrad Principle prescribes properties of T₂:

1) number of yods = 85 = 4⁰ + 4¹ + 4² + 4³;

2) number of yods surrounding its centre = 84 = 1² + 3² + 5² + 7²;

3) number of corners (O) of 1st-order tetractyses = 15 = fourth Mersenne number = fourth triangular number after 1;

4) number of sides of 1st-order tetractyses = 30 = 1² + 2² + 3² + 4²;

5) number of hexagonal yods (•) = 70 = fourth, 4-dimensional, tetrahedral number after 1.

2. Tetrad Principle in string theories

In this section we shall illustrate the powerful role of the Pythagorean Tetrad Principle in prescribing the mathematical character of superstring and bosonic string theories by making explicit the arithmetic and geometric connections between the tetractys, the number 4 (as well as the integers 1, 2, 3 & 4) and group-theoretical parameters of the superstring gauge symmetry groups E₈×E₈, E₈ and its exceptional subgroups. Examples of how the Tetrad Principle defines parameters of these two string theories are listed below:

1) Dimensionality of superstring space-time = 10 = 1 + 2 + 3 + 4, whilst large-scale space-time is 4-dimensional. As the 4th triangular number, 10 is symbolised by the Pythagorean tetractys (Fig. 6). But this representation of the perfect Decad central to the number philosophy of Pythagoras is not merely a way of expressing the integers 1, 2, 3 & 4, as scholars have traditionally believed. It is the paradigm for superstring space-time itself, as its following physical interpretation demonstrates:

the three yods at the corners of the tetractys not only define the shape of the simplest geometrical figure — the triangle — but also symbolise the dimensions of large-scale space in which the fundamental particles — superstrings — move. The six hexagonal yods at the corners of the hexagon symbolise the six higher, compactified dimensions predicted by superstring theory, whilst the yod at the centre of the tetractys denotes the dimension of time. Just as the nine yods on the boundary of the tetractys delineate its shape, so they denote the nine form-creating spatial dimensions of superstrings. The differentiation:

10 = 1 + 3 + 6

between uncompactified and compactified dimensions of the 10-dimensional space-time predicted by superstring theory thus finds its geometrical counterpart in the tetractys. A modern-day Pythagorean would account for this analogy by declaring that the identity of number and form implies that the dimensionality of space-time — the precursor of form — must conform to the 10-fold nature of Unity, the Monad which, being the source of number, is also the origin of material form.

2) According to the Pythagoreans, the integers 1, 2, 3 & 4 symbolised by the four rows of yods in the tetractys define, respectively, the dimensionless point, the 1-dimensional line with its two endpoints, the 2-dimensional triangle with its three corners (hence, in general, surface) and the 3-dimensional tetrahedron with its four corners (hence, in general, volume) (Fig. 7). The four stages of generation from a point of the simplest polyhedron are an illustration of the Pythagorean doctrine of a four-fold sequence in the

generation of form. They comprise 26 points, lines, triangles and tetrahedra. In other words, 26 geometrical elements are required to create the simplest solid in four steps. Compare this with the fact that the critical dimension of space-time for free bosonic strings to have no negative-probability ghost states (5) and for the theory to be Lorentz-invariant (6) is 26. This is not a coincidence but an example of the Tetrad Principle generating identical numbers in contexts that, although ostensibly unrelated, are

analogous in the sense that both the tetrahedron and bosonic string are basic forms, the former in the large-scale world and the latter in the subatomic world.

More generally, 26 is the number of combinations of 10 different objects selected from the four rows of a tetractys without mixing between rows (Fig. 8). As 2ⁿ – 1 is the total number of different combinations of n objects and M_n = 2ⁿ – 1 is, by definition, the nth Mersenne number, 26 is the sum of the first four Mersenne numbers 1, 3, 7 and 15, indicating how the Tetrad Principle determines the dimensionality of space-time predicted by bosonic string theory.

The number 26 can be represented as a tetractys array of the first four powers of 2:

This array has one other orientation:

The sum of the four powers 2⁰ at its base is 4, the dimension of macroscopic space-time, the sum of the three powers 2¹ is 6, the number of compactified dimensions of superstrings, and the sum of the remaining powers of 2 is 16, the number of spatial dimensions of bosonic strings whose compactification was suggested originally by Freund (7) to generate E₈×E₈-invariant superstrings. The bifurcation: 26 = 10 + 16 is reproduced in this powers-of-2 representation in an intuitively more fundamental way:

i.e., the number (10) of superstring dimensions is the sum of the three powers of 2 at the form-defining corners of the tetractys and the number (16) of compactified, purely bosonic dimensions is the sum of the seven powers of 2 located at the hexagonal yods of the tetractys.

3) The square — the geometrical symbol of the Tetrad — arithmetically defines the number 26 in the following ways:

A). As

and

(a square divided into tetractyses contains 25 yods and 100 = 25×4), 26 is the ratio:

B). 26 is the arithmetic mean of the first 25 even integers up to 50:

26 = (2 + 4 + 6 + ... + 50)/25

As

and

26 has the following representation in terms of 1, 2, 3 & 4:

4) Number of dimensions of macroscopic space-time = 4, the fourth positive integer;

number of dimensions of superstring space-time = 10 = fourth triangular number;

number of bosonic string dimensions whose compactification generates superstrings = 16 = fourth square number;

number of compactified bosonic string dimensions = 22 = fourth pentagonal number = sum of 1, 2, 3 & 4 raised, respectively, to the powers 4, 3, 2 & 1:

5) As the geometrical symbol of the Tetrad, a square divided into four tetractyses generates the number of spatial dimensions of bosonic strings and differentiates between superstring and purely bosonic string dimensions:

where 16 (fourth square number) is the number of bosonic string dimensions whose compactification generates superstrings with nine remaining spatial dimensions (9 = fourth odd integer after 1). The central yod (•) symbolises the longitudinal dimension of a string, the surrounding 24 (= 1×2×3×4 = 4!) yods represent the 24 transverse dimensions of a bosonic string and the surrounding eight yods (•) denote the eight transverse, purely superstring dimensions (8 = fourth even integer). 25 is the arithmetic mean of the cubes of the first four integers:

6) The rank 8 of the unified gauge symmetry group E₈ is the fourth even number. The rank 16 of E₈×E₈ is the fourth square number.

7) A tetractys-divided square expresses the dimension 248 of E₈ in terms of 1, 2, 3 & 4:

8) Using the identity:

6200 = 248×25 = 2² + 3² + 4² + ... + 26²,

where the first term, 2² = 4, is the Tetrad and the last term, 262, is the square of the sum of the first four Mersenne numbers, the square displays the following remarkable property of the number 248:

Starting with the Tetrad 2² = 4 at the centre of the square and assigning the 24 (=4!) squares 3², 4², ... 26² to the surrounding 24 yods of the four tetractyses, with squares of even integers inside the square and squares of odd integers on its boundary, the sum of these 25 squares is that resulting from assigning the number 248 to each yod in the square.

9) Starting with the fourth triangular number T₄ = 10, the sum of the first (4+4=8) polygonal numbers of the fourth order is 248, which is the dimension of the superstring gauge symmetry group E₈:

The sum:

of the first four polygonal numbers represented by regular polygons with odd numbers of corners is the number of non-zero roots of E₈ of length squared 2 of the kind:

where the u_i are eight orthonormal unit vectors. The Tetrad also expresses this number as

where 7 is both the fourth odd number and the fourth prime number. 112 is the 7th heptagonal number (note that the heptagon is 7-sided). The Tetrad also defines the number (128) of non-zero roots of E₈ of the kind:

because 128 = 2⁷ = 4^7/2 = √(4^{4th prime number}). The total number of non-zero roots of E₈ is

This number has also the representation:

It contains 36 even integers ending in the fourth square number 16, where 36 is the sum of the first four even integers and the first four odd integers (it is also 4×9, where 9 is the fourth odd integer after 1). The sum of the shaded triangular array of 15 integers is 112, and the sum of the remaining 21 integers is 128 (15 = eighth odd integer, where 8 = fourth even integer, and 21 = 10th odd integer after 1, where 10 = fourth triangular number). The sum of the 15 integers inside the boundary of the array of 36 integers is 100, which is the (1+2+3+4=10)th square number, and the sum of the 21 integers on the boundary is

140 = 1² + 2² + 3² + 4² + 5² + 6² + 7²,

namely, the seventh square pyramidal number (7 = fourth prime/odd number). The Tetrad thus differentiates between the two types of non-zero roots of E₈. It also determines the eight zero roots of E₈ because eight is the fourth even integer.

As 24 = 5² – 1 = 3 + 5 + 7 + 9,

i.e., 240 is the sum of

odd integers arranged as 4 tetractys arrays of the first 4 odd integers after 1. E₈×E₈ has 480 non-zero roots. Since 480 = 16×30 = 4²×(1² + 2² + 3² + 4²)

this group parameter is the sum of four square numbers spaced four units apart, starting with the fourth square. The number of zero roots of E₈×E₈ is 16, the fourth square number. These examples illustrate how the Tetrad Principle defines group-theoretical parameters of the heterotic superstring gauge symmetry group E₈×E₈.

10) Defining the two possible tetractys arrays of the nth powers of 1, 2, 3 & 4:

as T_o = t_o = 10 and T_n ≠ t_n forn = 1, 2, 3, 4, there are nine different numbers generated by the values n = 0, 1, 2, 3, 4 (9 = 4th odd integer after 1). Remarkably, their sum is

2480 is the number of space-time components of the 248 ten-dimensional gauge fields of E₈. The Tetrad and the tetractys thus define this physical parameter of superstring theory. The sum above may be written:

The nine different tetractys arrays of powers of 0, 1, 2, 3 & 4 not only sum to 2480 but also differentiate between the (1+7) zero roots of E₈ and its 240 non-zero roots!

11) Using the identity

1240 = 1² + 2² + 3² + 4² + ... + 15²,

where

is the fourth Mersenne number, the cross pattée array of integers 1–15 shown in Figure 9 sums to 4960. This is the number of the components of the 496 10-dimensional gauge fields of E₈×E₈. There are 480 integers in the representation, where 480 is the number of non-zero roots of E₈×E₈, of which

integers form the boundary of the cross pattée. The 240 integers comprising a pair of arms of the cross sum to 2480, the number of space-time components of the 248 gauge fields of E₈. Of these integers,

integers form the boundary of a pair of arms. This ancient religious emblem, whose four arms symbolise the Tetrad, thus defines the number of space-time components of all the gauge fields mediating the E₈-invariant superstring force.

12) According to Aristotle, the Pythagoreans gained mathematical insights through their use of the gnomon, or carpenter's square (8). For example, by sandwiching gnomons inside one another with marked out points, they found that this generates a square array of points whose number is the sum of the (odd) numbers of points in successive gnomons, i.e.,

This made them realise that the square of any integer n is the sum of the first n odd integers. In particular, four gnomons generates the fourth square 16 as a 4×4 square array of points whose number is the sum of the first four odd integers— the numbers of points in successive gnomons:

16 = 4² = 1 + 3 + 5 + 7.

We pointed out in Section 1 that

84 = 1² + 3² + 5² + 7²

is the number of yods surrounding the centre of a 2nd-order tetractys. The sum of these four squares assigned to points along four successive gnomons is

The sum of the cubes of the first four odd integers is the crucial dimension 496 of the non-abelian

gauge symmetry group governing superstring interactions that physicists Michael Green and Gary Schwarz found to be free of quantum anomalies (9). This illustrates par excellence the prescriptive power of the Tetrad Principle and substantiates the title: “Holding the Key of Nature” that the Pythagoreans assigned to the number 4 (10).

Just as four gnomons generate the dimension 496 of E₈×E₈ from the squares of the first four odd integers, so 10 (=1+2+3+4) gnomons generate the dimension 133 of E₇, the largest exceptional subgroup of E₈, from the first 10 odd integers:

100 (= 1³+2³+3³+4³) odd integers make up the 10 gnomons. 1330 is also the sum of the 10th set of the first seven types of polygonal numbers (7 = fourth prime/odd number):

T₁₀ + S₁₀ + P₁₀ + H₁₀ + h₁₀ + O₁₀ + N₁₀ = 1330.

13) The hexagon is the fourth regular polygon. If the first 16 (=4²) hexagonal numbers are assigned to successive dots in a 4×4 square array of dots, the last and largest hexagonal number is

H₁₆ = 496,

which is the dimension of E₈×E₈. Using the identity:

H_n = 4T_n-1 + n

(Appendix B), then

H₁₆ = 4T₁₅ + 16 = 480 + 16.

This compares with the fact that the 496 roots of E₈×E₈ consist of 480 non-zero roots and 16 zero roots.

14) The number of hexagonal yods in an n-sided regular polygon whose sectors are divided into three tetractyses is

H(n) = 13n

(Appendix C). A square (n=4) has 13×4 = 52 hexagonal yods and a hexagon (n=6) has 13×6 = 78 hexagonal yods (Fig. 10). The four-sided

square thus defines the dimension 52 of the rank-4 exceptional group F₄, whilst the fourth regular polygon (the six-sided hexagon) defines the dimension 78 of the rank-6 exceptional group E₆, both groups being subgroups of E₈.

The first 12 integers evenly spaced along the sides of a square, four integers to a side, add up to 78:

15) A square whose sectors are turned into 2nd-order tetractyses (Fig. 11) has 288 yods surrounding its centre, where

288 = 1¹ + 2² + 3³ + 4⁴ = 1!×2!×3!×4!

showing how these integers 1, 2, 3 & 4 express this number. Of these yods,

are corners of 1st-order tetractyses, leaving 248 hexagonal yods (shown by (•) yods in Fig. 11). The square — the geometrical symbol of the Pythagorean Tetrad — thus generates the dimension of E₈ as well as its rank-4 exceptional subgroup F₄. Indeed, the latter number is also present in this representation as the number of hexagonal yods (•) in tetractyses at the corners of the 2nd-order tetractyses that do not also belong to adjacent tetractyses.

Appendix D shows in general that an n-sided regular polygon divided into 2nd-order tetractyses has 72n yods surrounding its centre (72 = 36th even integer, where 36 is sum of the first four even integers and the first four odd integers). Of these, 10n yods are corners of 10n 1st-order tetractyses, leaving 62n hexagonal yods. The number of yods surrounding the centre of an octagon = 72×8 = 576 = (4!)²

where

Of these 576 yods, (10×8=80) yods are corners of 40 1st-order tetractyses, where

leaving (576–80=496) hexagonal yods (notice that both 36 and 80 can be represented by octagonal arrays of integers, the former consisting of the first eight integers and the latter consisting of the first eight odd integers after 1). The octagon thus defines the dimension 496 of E₈×E₈, the direct product nature of the unified gauge symmetry group of superstrings reflecting the fact that an octagon is generated from two identical squares by rotating one relative to the other through an angle of 45º.

16) 496 as a perfect number

The ancient Greeks classified numbers not only as even or odd, prime or composite, but also as excessive, defective or perfect. In excessive (or superabundant) numbers the sum of the divisors is larger than the number. In defective (or deficient) numbers, the sum is smaller than the number. Perfect numbers are equal to the sum of their divisors. The last of the 36 propositions in Book IX of Euclid's Geometry asserts that, if (2ⁿ–1) is prime, then 2^n-1(2ⁿ–1) is a perfect number. This means that all perfect numbers of this form are even. In a work published posthumously in 1849, the mathematician Léonard Euler proved the converse of this proposition that all even perfect numbers are of the form given by Euclid. If the nth Mersenne number M_n = 2ⁿ – 1 is prime, then 2^n-1M_n is perfect (M₁ = 1 is not regarded as a prime number). The first four perfect numbers:

were known to the ancient Greeks, the neo-Pythagorean Nichomachus being known to have spent considerable time hunting for 496 and 8128.* 496 is therefore the third perfect number.

The first Mersenne number M₁ = 1 does not define 1 as a perfect number because of the convention that 1 is not regarded as a prime number. It is amusing that 496 would be the fourth perfect number if this convention were not adopted, in agreement with the Tetrad Principle that the Pythagorean Tetrad defines members of classes of numbers or mathematical objects which have significance to the physics of nature.

However, this principle is still upheld because 496 is defined by n = 5, i.e., the fourth of the integers after 1, which the ancient Pythagoreans regarded not as a number but as the source (Monad) of all numbers.

As the sum of its factors, 496 is

496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248.

Using the theorem (12) that the product of the factors, including itself, of the perfect number P = 2^n-1M_n is Pⁿ, we see that, of all the perfect numbers, 496 (n = 5) is uniquely connected to the Tetrad, 4, through its remarkable property:

496⁴ = (1+2+4+8+16+31+62+124+248)⁴ = 1×2×4×8×16×31×62×124×248.

Also, since every perfect number except 6 is (13) a partial sum of the series:

1³ + 3³ + 5³ + 7³ + ....,

then 496 (= 1³ + 3³ + 5³ + 7³) is defined by the Tetrad because it is the sum of the first four terms in this series.

The ancient religious symbol of the pentagram provides a representation of the dimensions of E₈ and E₈×E₈ (Figure 12). Notice in (b) that the first number is 2⁴ = 4² and that the last number is 2⁸ = 4⁴. The square also provides a representation of the E₈ group parameter 240:

__________________________________________

* Pythagoras’ biographer Iamblichus may have known the fifth perfect number 33,550,336, although he does not give it. See reference 11, footnote, p. 74.

This again illustrates the Tetrad Principle because 240 is the sum of four successive powers of 2, starting with 2⁴ = 4², the fourth square number. Notice that 2⁴ + 2⁵ + 2⁶ = 112, and that 2⁷ = 128, the numbers of the two different types of non-zero roots of E₈.

17) A pentagram array of the cubes of the integers 1, 2, 3 & 4 represents the number 496 (Fig. 13). Notice that the representation contains 16 (=4²) cubes.

18) A pentagon divided into tetractyses contains 31 yods, where 31 is the fourth Mersenne number above 1 (Fig. 14). 496 is the 31st triangular number:

496 = 1 + 2 + 3 + 4 + ... + 31.

If we assign the 15 even integers 2, 4, ... 30 to the 15 yods on the boundary of the pentagon and the 16 odd integers 1, 3, 5, ... 31 to the 16 internal yods, the sum of these 31 integers is 496, the sum of the interior integers is 256 (=4⁴) and the sum of the integers on the boundary is 240 (=4!×(1+2+3+4)) (Fig. 15). As 496 = 31×16 = 31×4², assigning the fourth square number to each of the 31 yods in the pentagon generates the number 496 (Fig. 16). The sum of the 15 squares on the boundary is 240, the same as the sum of the 15 internal squares surrounding the central integer 4² = 16.

So, allocating the fourth square number to each of the 31 yods of a tetractys-divided pentagon not only generates the number of roots of E₈×E₈ but also differentiates between the number (16) of its zero roots and the

number (240+240=480) of its non-zero roots. Alternatively, if the fourth square 16 is assigned to the centre of a tetractys-divided pentagon and the 15 successive even integers 18, 20, … 46 are assigned to the 15 yods on its boundary, the sum of the (4²=16) even integers that start with 16 is 496 (Fig. 17).

As

240 = 5×48 = 5(7²–1) = 5(3 + 5 + 7 + 9 + 11 + 13),

this number is the sum of the 30 odd integers surrounding the central integer 1 in a five-pointed array of consecutive odd integers (30 = fourth square pyramidal number) (Fig. 18). As the sum of the odd integers 3, 5, ... 13 in each point, the number 48 is the seventh highly composite

number (7 = fourth prime/odd number). It is the smallest integer to have 10 factors, including unity and itself (14). It is thus defined by the Decad, called by the Pythagoreans “All Perfect.” 48 is further related to the number 240 because

is the sum of the first 48 odd integers after 1.

These examples demonstrate the Pythagorean nature of superstring theory in the sense that they show that the group-theoretical parameters of E₈×E₈, and E₈ are prescribed by the Tetrad Principle and find natural representation or expression in terms of the tetractys, the Tetrad and the integers 1, 2, 3 & 4.

4. The Platonic solids

It is well known that five — and only five — polyhedra with equi-distant corners can exist in 3-dimensional space. They are the tetrahedron, cube, octahedron, icosahedron and dodecahedron (Fig. 19). The five regular polyhedra are known as the five Platonic solids, not because they were discovered by the ancient Greek philosopher Plato but because of the special emphasis he placed upon them in expounding Pythagorean cosmology in his book Timaeus, where they were first described in print. The early Pythagoreans knew

of all five polyhedra, for in the Fragments of Philolaus, regarded by scholars as the earliest surviving (and therefore most reliable) Pythagorean text, Philolaus, a student of Lysis, one of the two Pythagoreans who escaped the persecution of the Pythagorean school at Croton in southern Italy, wrote that “there are five bodies in the sphere: fire, water, earth, air and the circle of the sphere

Table 2. Geometrical properties of the 5 Platonic solids.

Number of triangles in polyhedral face = I (I = 3 for tetrahedron, octahedron & icosahedron, = 4 for cube, = 5 or dodecahedron).

which makes the fifth” (15). The ancients believed that the tetrahedron, cube, octahedron and icosahedron were the shapes of the atoms of, respectively, the elements Fire, Earth, Air and Water, whilst the cosmic sphere containing the stars was made out of the dodecahedron because the latter most resembled the perfect shape of the sphere.

Table 3. Geometrical properties of the 5 Platonic solids constructed from triangles.

Suppose that each triangular face of the tetrahedron, octahedron and icosahedron is divided into three triangular sectors, the square faces of the cube are divided into four triangles and the pentagonal faces of the dodecahedron are divided into five triangular sectors (Fig. 20). Table 2 shows the number of corners, edges and faces in each solid. Table 3 shows the numbers of corners, sides and triangles in their faces.

The five Platonic solids contain

corners of triangles and

triangles and their corners and sides, where

is the 10th triangular number (10 = fourth triangular number). The Tetrad and Decad therefore define these geometrical parameters of the faces of the Platonic solids.

According to Table 3, the tetrahedron — the simplest regular polyhedron — contains 26 corners and sides, of which four are polyhedral corners, six are polyhedral edges and 16 are corners and sides created by the division of its faces into triangles. Compare this with the requirement in bosonic string theory that the 26 dimensions of space-time consist of the four dimensions of Einstein’s space-time, the six higher compactified dimensions of superstrings and the 16 higher purely bosonic string dimensions. We see that the faces of the tetrahedron embody numbers defining the dimensional bifurcation of the string. This is an example of how the Tetrad Principle defines a physical parameter of nature, for the tetrahedron has four corners and four faces. Table 3 shows that 248 points and lines are needed to construct out of 120 triangles (120 = sum of squares of the first four even integers) the 38 faces of the four Platonic solids symbolising Earth, Air, Fire and Water (38 = 19th even number, 19 = 10th odd integer, 10 = fourth triangular number). The number of gauge bosons mediating superstring forces is thus the minimal number of geometrical elements required to define the triangle-divided surfaces of the first four regular polyhedra. Notice that the number of their polyhedral corners is:

the number of polyhedral corners and edges delineating their faces is

where 9 is the fourth odd integer after 1, and that the number of their corners, edges and faces is

128 = 2⁷ = √(4^{4th prime number}).

Now consider each triangle in the faces of the Platonic solids to be a Pythagorean Triangle or tetractys, so that four yods lie along each polyhedral edge (Fig. 20). Table 4 shows the various yod populations of the regular polyhedra. The tetrahedron has 56 yods, where 56 = 7×8 (7 = fourth prime/odd integer, 8 = fourth even integer), of which 8 yods are corners of tetractyses, 16 yods lie on its edges (16 = fourth square number) and 48 yods are hexagonal yods (48 = 7th highly composite number, 7 = fourth prime/odd number). Once again, the Tetrad defines these properties.

Table 4

The cube and octahedron each has 110 yods, where

The icosahedron and dodecahedron each has 272 yods, where

The first four Platonic solids have

yods, where 137 (the average number of yods in the first four polyhedra) is the 33rd prime number (33 = 1! + 2! + 3! + 4!). Of these,

yods are corners of tetractyses, where 17 (the average number of corners) is the 7th prime number (7= 4th prime/odd number), and

yods are hexagonal. As the fourth regular polyhedron — the icosahedron — has

such yods in its 60 tetractyses, we find that the first four regular polyhedra have 480 hexagonal yods in their 120 tetractyses (120=2²+4²+6²+8²), the fourth one having 240 such yods. The superstring gauge group E₈×E₈ has 480 non-zero roots and E₈ has 240 such roots. A remarkable correspondence thus exists between these roots and the degrees of freedom symbolised by the hexagonal yods generated by the construction of the faces of the first four Platonic solids from tetractyses.

6. Conclusion

The symbol of the Pythagorean paradigm of wholeness — the tetractys — has manifested in particle physics as the 10-dimensional space-time predicted by superstring theory. However, this representation of the Pythagorean Decad is but the most rudimentary example of a powerful Tetrad Principle governing the form of the mathematical description of subatomic reality. Many examples have been given in the context of superstring theory and bosonic string theory of how the number 4 plays a pivotal role in defining classes (and members of classes) of mathematical objects that parameterise the physics of these fundamental (and as yet hypothetical) particles. Whilst coincidence might account for a few of these, the weight of evidence for the principle accumulated in this article renders such an explanation highly implausible. This is particularly so as the Tetrad Principle has been shown to define superstring and bosonic string parameters not only for a narrow range of numbers but also for mathematical objects that at first sight would seem most unlikely to have relevance to superstring theory, namely, the regular polyhedra, for the first four of which the dimension of E₈ is embodied purely geometrically in their faces when divided into their sectors, whilst group parameters of E₈ and E₈×E₈ appear in the yod population of their faces when their sectors are tetractyses. Such evidence of beautiful harmony between number and geometry points towards the existence of a conceptual scheme in which the Pythagorean paradigm of the tetractys has a central place. From the perspective of this more general theory, the theories of superstrings and bosonic strings would then be seen to be examples of how the Tetrad Principle determines the mathematics of the microphysical version of this universal theory of whole systems. This true ‘Theory of Everything’ is the mathematics underlying all sacred geometries, such as the Tree of Life and the Sri Yantra. Its relevance to particle physics is explored

comprehensively in other research articles on this website.

References

1. Theon of Smyrna, in Mathematics Useful for Understanding Plato, R. & D. Lawlor, tr. (Wizards Bookshelf, San Diego, 1979).

2. Stobaeus, Eclog. Physic., i. 21, 7b.

3. Aristotle, Metaphysics, A5, 986a16.

4. Kenneth Sylvan Guthrie, The Pythagorean Sourcebook and Library (Phanes Press, Michigan, 1987), p. 28.

5. R.C. Brower, Phys. Rev. D6, 1655 (1972); P. Goddard & C.B. Thorn, Phys. Lett. 40B, 235 (1972).

6. P. Goddard, J. Goldstone, C. Rabbi & C.B. Thorn, Nucl. Phys. B56, 109 (1973).

7. P.G. O. Freund, Phys. Lett. 151B, 387 (1985).

8. Aristotle, Physics 203 a 10.

9. M.B. Green & J.H. Schwarz, Phys. Lett. 149B, 117 (1984).

10. Kenneth Sylvan Guthrie, The Pythagorean Sourcebook and Library (Phanes Press, Michigan, 1987), p. 322.

11. Thomas Heath, A History of Greek Mathematics (Oxford, 1921), vol. 1, footnote, p. 74.

12. David Wells, The Penguin Dictionary of Curious and Interesting Numbers (Penguin Books, London, 1986), p. 108.

13. Ibid.

14. Ibid., Table 8.

15. Iamblichus, The Life of Pythagoras, in The Pythagorean Sourcebook and Library, Kenneth Sylvan Guthrie (Phanes Press, Michigan, 1987), p. 174.

APPENDIX A

Proof of P^N_n = ½[(N–2)n – (N–4)]

The representation of P^N_n consists of the superimposition of (n–1) regular polygons with 2, 3, 4, ... n dots along each of their N edges. The rth polygon has r dots per edge. The total number of dots in (n–1) separate polygons is

Of these, there are

2 + 3 + 4 + ... + (n–1) = ½n(n+1) – 1

dots along one set of edges and

1 + 2 + 3 + ... + (n–1) = ½n(n–1)

dots along the set of adjacent edges. The total number of shared dots when the polygons are superimposed is

½n(n+1) – 1 + ½n(n–1) = n² – 1.

The total number of unshared yods is

½nN(n–1) – (n²–1) = ½n[(N–2)n – N] + 1.

Superimposed, the (n–1) polygons have n dots along one shared edge and (n–1) dots along the adjacent shared edge. Hence the total number of dots in the representation is

P^N_n = (n–1) + n + ½n[(N–2)n – N] + 1

= ½n[(N–2)n – (N–4)]

APPENDIX B

The nth hexagonal number is

H_n = ½n(4n–2) = 2n² – n.

The nth triangular number is

T_n = ½n(n+1).

Therefore,

T_n-1 = ½n(n–1).

4T_n-1 = 2n(n–1) = 2n² – 2n = H_n – n.

Therefore,

H_n = 4T_n-1 + n.

APPENDIX C

When divided into three tetractyses, each sector of an n-sided regular polygon contains 19 yods, of which 15 are hexagonal (Fig. 21). Two hexagonal yods on each of two sides of the sector are shared with adjacent sectors. Each of the n sectors therefore contributes 13 hexagonal yods. Number of hexagonal yods in polygon ≡ H(n) = 13n.

APPENDIX D

There are 85 yods in each sector of an n-sided regular polygon divided into n 2nd-order tetractyses. Of these, 13 yods on each of two sides are shared with adjacent sectors. Number of yods per sector surrounding centre of polygon = 85 – 13 = 72. Number of yods surrounding centre of n-sided polygon = 72n. Each sector has 15 corners of 1st-order tetractyses, of which five corners on each of two sides are shared with adjacent sectors. Number of tetractys corners per sector surrounding centre of polygon = 15 – 5 = 10. Number of tetractys corners surrounding centre of n-sided polygon = 10n.