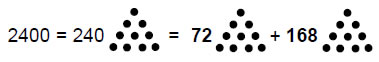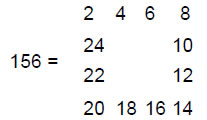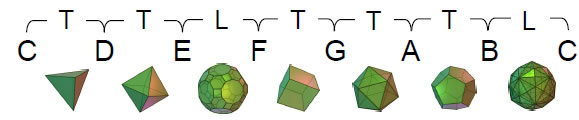ARTICLE 26

by

Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

1

Table 1. Table of gematria number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations The Elements (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

2

 

1. Geometrical composition of the disdyakis triacontahedron
The Tree of Life at the heart of Kabbalah represents Adam Kadmon, or ‘Heavenly Man.’ What this means is that the Divine archetypes determining the nature of the manifestation in space-time of holistic systems, including humans, find symbolic expression in the sacred geometry of the Tree of Life. Works on Kabbalah traditionally depict the Tree of Life in two dimensions as a set of 16 triangles with their 10 vertices connected by 22 straight lines, with only brief mention that it is actually 3-dimensional. However, this is only the outer form of the Tree of Life. It has an inner form as well (Fig. 1), consisting of two similar sets of seven regular polygons enfolded in one another: triangle, square, pentagon, hexagon, octagon, decagon and dodecagon. One set is the mirror image of the other, the mirror lying along the central Pillar of Equilibrium at right angles to the plane containing the 14 polygons. Projected onto the latter, the three Sephiroth on either side of the central pillar coincide with the uppermost and lowest corners of the hexagons and the outer corners of the triangles (indicated by the red dots in Fig. 1). The two endpoints of the ‘root edge’ shared by both sets of polygons coincide with Daath and Tiphareth. This means that eight of the 70 corners of the polygons are shared with the Tree of Life, leaving 62 unshared corners that represent geometric degrees of freedom that are intrinsic to its inner form alone. 62 is the number value of Tzadkiel, the Archangel of Chesed (see Table 1; numbers from this table will be written throughout the article in boldface).

It was pointed out in Article 25 that these 62 degrees of freedom correspond to the 62 vertices of the disdyakis triacontahedron — the most visible sign that it is the 3-dimensional realisation of the inner Tree of Life. The two endpoints of the root edge correspond to any pair of diametrically opposite vertices and the 30 unshared corners associated with each half of the inner Tree of Life correspond to the 30 additional vertices forming each half of the polyhedron. The mirror symmetry displayed by the two identical halves of the inner Tree of Life corresponds to the mirror symmetry of the positions of all the vertices. The polyhedron has 62 vertices, 180 edges and 120 triangular faces — a total of 362 geometrical elements. Between any two opposite vertices are 360 elements, where 360 = 36×10, showing how the Godname ELOHA assigned to Geburah with number value 36 prescribes this polyhedron. Because of the symmetry of this polyhedron with respect to inversion though its centre, every one of its geometrical elements has

its inverted counterpart. It is therefore meaningful to

3

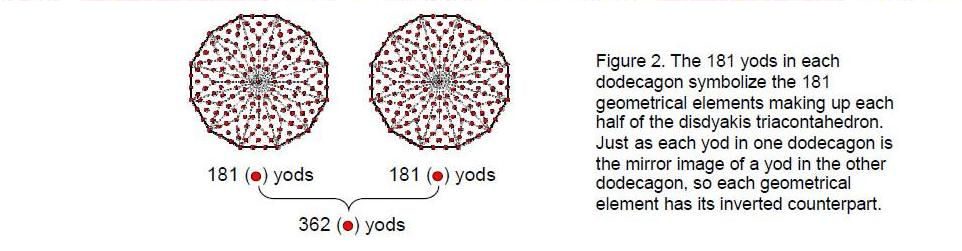
associate 31 vertices, 90 edges and 60 faces with one ‘half’ and their inverted mirror images with the other half, i.e., 181 geometric elements constitute each half. This composition is expressed in the pair of dodecagons — the last of the polygons forming the inner Tree of Life — as the 181 yods needed to construct each dodecagon when its sectors are regarded as three tetractyses (Fig. 2). The 60 yods along the sides of the 12 sectors in each dodecagon — that is, the yods defining their shapes — symbolize the 60 faces that shape each half of the disdyakis triacontahedron. The 120 yods inside the 12 sectors of each dodecagon denote the 120 vertices and edges making up each half of the polyhedron. The yods at the centres of the two dodecagons denote any two diametrically opposite vertices.

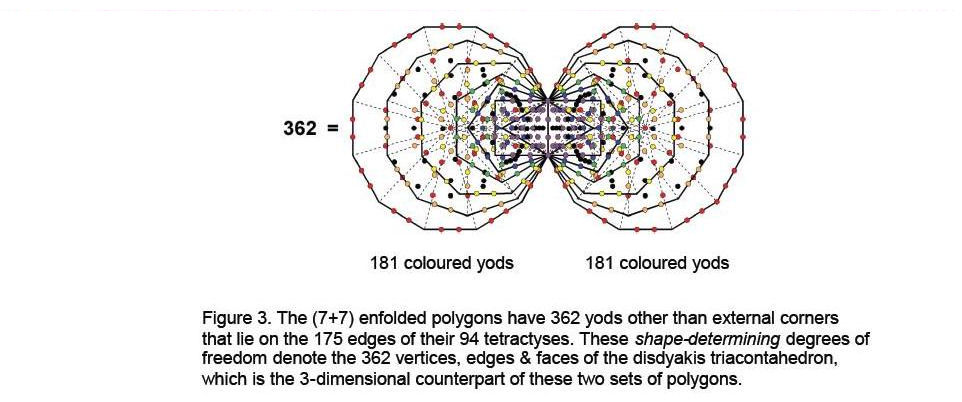
As the disdyakis triacontahedron is the 3-dimensional counterpart of the inner Tree of Life, we should expect to see the number 362 embodied in the latter. Indeed,  this is so. Starting with the two pairs of seven enfolded polygons, the number of yods lying on the 175 edges of their 94

tetractyses is 362 (Fig. 3). The two endpoints of the root edge correspond to any two diametrically opposite vertices of the polyhedron and the 180 yods lining the tetractyses that are associated with each set of polygons correspond to the 180 vertices, edges and triangles forming each half of the polyhedron. Each set of polygons has 47 tetractyses with 87 sides outside the root edge. 87 is the number value of Levanah (“The Lunar Flame”), the Mundane Chakra of Yesod.

The 94 tetractyses have 80 corners, where 80 is the number value of Yesod.

4

2. The seven musical scales
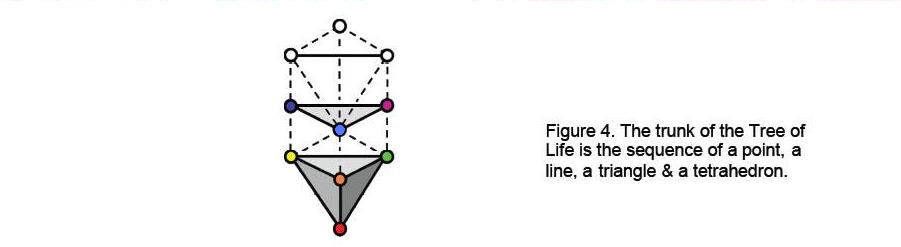
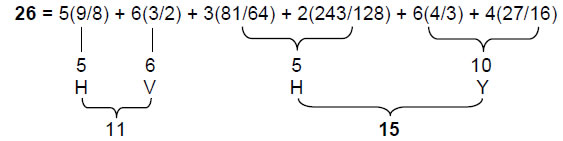
The ten Sephiroth of the Tree of Life are traditionally depicted as spheres (circles in its 2-dimensional representation). Geometrically speaking, they are the 10 vertices of 16 triangles with 22 sides (Fig. 4). Just as the tetractys symbolizes the four-fold sequence of point, line (its two endpoints), triangle (its three vertices) and tetrahedron (its four vertices), so the ten Sephiroth mark the same sequence in 3-dimensional space. This is the ‘trunk’ of the Tree of Life. It comprises 10 vertices, 10 lines, 5 triangles and one tetrahedron (Fig. 5), totalling 26 geometric elements. This illustrates the archetypal quality of the Divine Name YAHWEH with number value 26: YHVH = 10 + 5 + 6 + 5 = 26. YAH (YH), its older version with number value 15, prescribes the tetrahedron — the simplest Platonic solid — because it is composed of 15 geometrical elements. Inspection of Fig. 4 shows that there are 12 lines and 11 triangles outside the trunk, i.e., there are (26+12+11=49) geometrical elements in the Tree of Life.

 This shows how the Godname EL CHAI assigned to Yesod with number value 49 determines the geometrical composition of the Tree of Life — both trunk and branches.

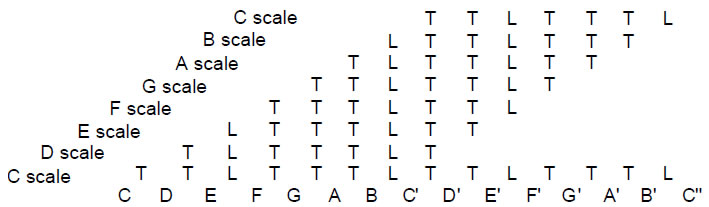
The Pythagorean scale consists of five tone intervals T of 9/8 and two leimmas L of 256/243 (corresponding to, but not identical with, the modern semitone):

T T L T T T L.

By starting successive sequences of intervals on the circumference of the circle displayed in Fig. 6, it is seen that there can be only seven different octave species:

5

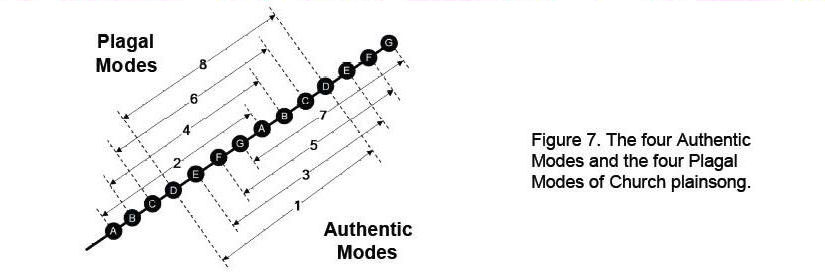
The eighth sequence of intervals is the same as mode 1. These are the eight Church musical modes. The three ‘hypo’ versions of the Dorian, Phrygian and Lydian modes are separated from the latter by a perfect fourth (Fig. 7). The early Catholic Church added an extra mode called the

"Hypomixolydian" (mode 8) to be the counterpart of the Mixolydian. It is the same octave species as the Dorian but has a distinct ethos because its finalis (ending note) and dominant (reciting note) are different.

 

Figure 8 shows the four Authentic Modes and the four Plagal Modes (the modern notation S for the semitone is used here instead of the leimma L). The double-headed arrows link an Authentic Mode and a Plagal Mode whose patterns of intervals are mirror images of each other. The pattern of intervals of the Dorian mode:

T L T T T L T

6

---

is its own mirror image and so the addition of the Hypomixolydian mode is needed to restore the left-right mirror symmetry between the three Authentic Modes and the three Plagal Modes even though it is not distinct from the Dorian mode in terms of its pattern of tone intervals, differing in the positions of the finalis and the dominant.

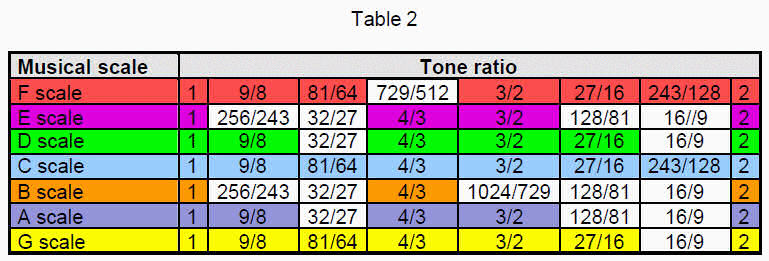
Table 2 displays the tone ratios of the seven types of musical scale. Cells containing tone ratios that belong to the Pythagorean scale (C scale):

	C	D	E	F	G	A	B	C'
Tone ratio =	1	9/8	(9/8)2	4/3	3/2	27/16	243/128	2

are coloured; white cells contain tone ratios that have non-Pythagorean values. The C scale is unique in having only Pythagorean notes (no white cells).

(Coloured cells indicate Pythagorean notes and white cells indicate non-Pythagorean notes.)

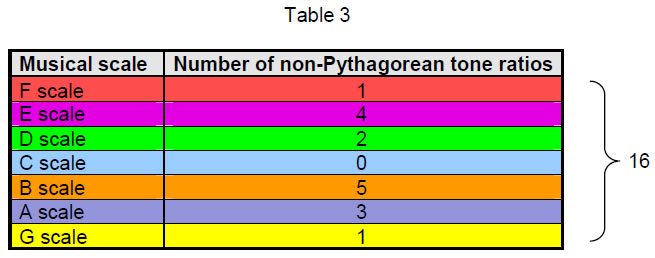
Table 3 shows the number of non-Pythagorean notes in each scale.

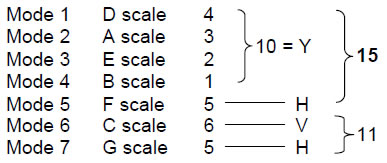
Excluding the tonic with tone ratio 1 and the octave with tone ratio 2, the seven musical scales have 26 Pythagorean tone ratios (coloured cells). Their tonal spectrum is therefore prescribed by YAHWEH (YHVH), the values of the letters of the Godname denoting the numbers of tone intervals of one or two types:

This prescription can be viewed in an alternative way. Table 2 indicates that the

7

distribution of Pythagorean tone ratios other than 1 in the seven scales is:

Remarkably, the traditional Church numbering of the seven distinct musical modes generates not only the correct letters values of the Hebrew letters of YHVH but also the order in which they are pronounced and written! It is, indeed, the Dorian scale (mode 1) — the only scale whose pattern of tone intervals is its own mirror image — that can be considered the source of all the musical scales. This was confirmed in Article 19 by comparing the eight church modes with the eight trigrams of the Chinese I Ching and by proving that there is only one scheme of correspondence between them that permits mirror symmetry in both.¹ This is where the first trigram — the Heaven trigram — corresponds to the Dorian mode and the eighth trigram — the Earth trigram — corresponds to the Hypomixolydian mode — the eighth mode. Fittingly, in view of its mathematical perfection, the seventh and last distinct scale generated from the Dorian scale is the Pythagorean scale, or Hypolydian mode (see the bottom of p. 5).

The 49 notes of the seven musical scales below the octave consist of 33 notes with tone ratios of the Pythagorean musical scale (coloured cells) and 16 notes with non-Pythagorean ratios (white cells):

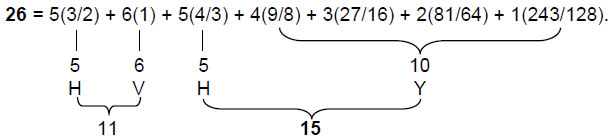
33 = 7(1) + 26 = 7 + 11 + 15,

where 7 = 7(1), 11 = 5(9/8) + 6(3/2) and 15 = 3(81/64) + 2(243/128) + 6(4/3) + 4(27/16). Alternatively, the 33 Pythagorean tone ratios may be thought of as made up of the seven tone ratios of the Pythagorean scale (C scale) and their 26 repetitions in the six other scales:

As before, the letter values of YHVH denote numbers of different notes in various sets.

Comparing the geometrical composition of the Tree of Life discussed earlier with the composition of notes in the seven musical scales, we find the following correspondence:

8

The 26 notes of the seven scales other than their tonics (or, alternatively, the 26 repetitions of the notes of the Pythagorean scale) correspond to the 26 geometrical elements composing the trunk of the Tree of Life. The 23 tonics or non-Pythagorean notes (or, alternatively, the seven notes of the Pythagorean scale and the 16 non-Pythagorean notes) correspond to the 23 geometrical elements making up the branches of the Tree of Life. This parallelism demonstrates the way in which the seven musical scales conform to the archetypal pattern of the Tree of Life.²

Because of this, music based upon these scales is intrinsically sacred. As the Pythagoreans declared, “music is geometry.”

3. The 33 sheets of vertices of the disdyakis triacontahedron

The 62 vertices of the disdyakis triacontahedron are made up of the 32 vertices of a rhombic triacontahedron, whose 30 faces are Golden Rhombi,

9

 

and 30 raised centres of the latter. The long diagonals of each golden rhombus are the edges of an icosahedron and its short diagonals are the edges of a dodecahedron. Labelling the vertices of the 120 triangular faces A, B & C (Fig. 9), there are 30 A vertices. 12 B vertices (corners of the icosahedron) & 20 C vertices (corners of the dodecahedron) arranged in seven sheets sandwiched between diametrically opposite A vertices, in 11 sheets perpendicular to a B-B axis and in 15 sheets perpendicular to a C-C axis. The disdyakis triacontahedron has therefore (7+11+15=33) generic sheets of vertices. There are more sheets than this because each pair of opposite vertices defines its own set of sheets.

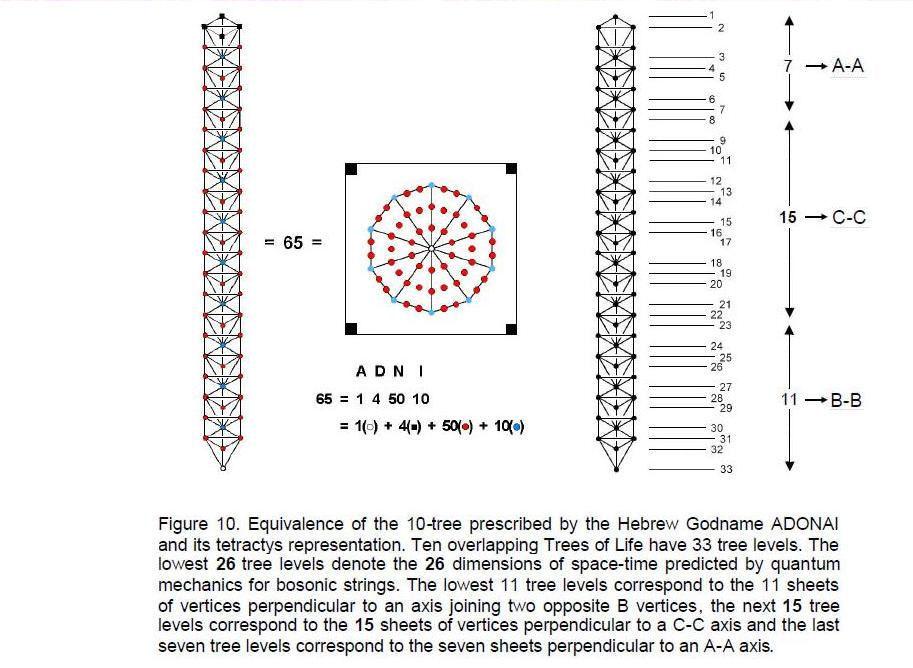
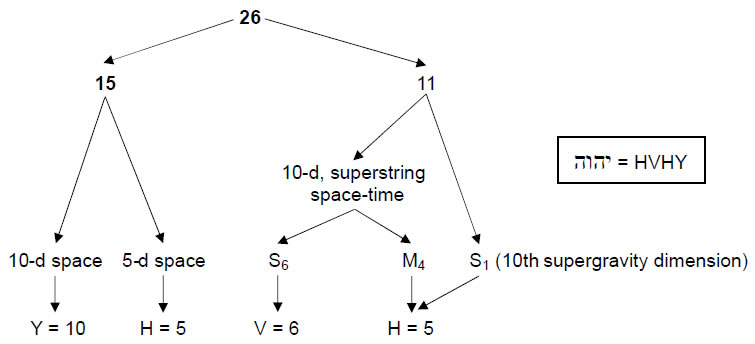
In Articles 22-24,³ evidence was presented to indicate that the disdyakis triacontahedron is the 3-dimensional realisation of the inner form of the Tree of Life. The 33-tree levels of 10 overlapping Trees of Life correspond to the 33 sheets of vertices (Fig. 10). The 62 vertices of the disdyakis triacontahedron correspond to the 62 of their 65 Sephirothic emanations whose projections onto the plane containing the 14 polygons enfolded in each tree coincide with corners of these polygons, that is, points shared between the inner and outer forms of each tree. The lowest 26 tree levels, which are spanned by 50 Sephirothic emanations, may be physically interpreted⁴ as the 26 dimensions of space-time predicted for spinless strings by quantum mechanics (this demonstrates how ELOHIM, the Godname of Binah with number value 50, prescribes the dimensionality of space-time). They correspond to the 26 sheets of vertices perpendicular to either a B-B or a C-C axis. The highest seven tree levels of ten overlapping Trees of Life correspond to the seven sheets of vertices perpendicular to an A-A axis. The lowest 11 tree levels denote the 11 dimensions of space-time predicted by supergravity theory; they correspond to the 11 sheets of vertices. The next 15 tree levels signify the 15 higher dimensions whose compactification generates superstrings and their unified forces described by SO(32) and E₈×E₈; they correspond to the 15 sheets of vertices. The compactification of 11-dimensional space-time into S₁×S₆×M₄, where S₁ is a 1-dimensional space (line segment or circle), S₆ is the 6-dimensional, compactified space predicted by superstring theory and M₄ is Einsteinian, 4-dimensional space-time, conforms to the letter values of V and H in the well-known Godname, YHVH:

4. The Archimedean & Catalan solids
Let us now compare the 33 generic sheets of vertices in the disdyakis triacontahedron with the 33 notes of the seven musical scales (seven tonics and 26 notes below the octave) that have Pythagorean tone ratios. The following correspondences exist:

10

A-A sheet of vertices tonic with tone ratio of 1;
B-B sheet of vertices major 2nd (9/8) or perfect 5th (3/2);
C-C sheet of vertices major 3rd (81/64), perfect 4th (4/3), major 6th (27/16) or major7th (243/128).

If, as discussed earlier, the 26 notes are the repetitions of the Pythagorean notes in the six other scales, an alternative set of correspondences is:

A-A sheet of vertices Pythagorean note;
B-B sheet of vertices tonic/perfect 5th;
C-C sheet of vertices major 2nd/major 3rd/major 6th/major 7th.

If we follow the previously discussed scheme based upon the natural ordering of successive sequences of intervals, starting with the Dorian, the correspondences are:

A-A sheet of vertices tonic with tone ratio of 1;
B-B sheet of vertices note of modes 6 and 7;

Whatever the scheme of correspondence, we see that the disdyakis triacontahedron is the geometrical counterpart of the seven octave species. This polyhedron is the spatial realisation of the Tree of Life and the seven species of octaves are its musical manifestation.

Article 14⁵ showed that the seven types of musical scale conform to the archetypal pattern of the Tree of Life blueprint. The fact that their notes group in the same 11:15 pattern that both the geometrical elements of the trunk of the Tree of Life and the B-B and C-C sheets of vertices do is further, strong evidence that the disdyakis triacontahedron is the 3-dimensional counterpart of the Tree of Life. 26-dimensional space-time mapped by the lowest 26 tree levels of the map of Reality called the ‘Cosmic Tree of Life,⁶ which consists of 91 overlapping Trees of Life.

The seven octave species that originate with the Dorian mode (D scale) and realise their perfection in the Hypolydian mode (the Pythagorean, or C scale) are the musical counterpart of seven polyhedra (five regular, two semi-regular) that, starting from the tetrahedron, and ordered according to increasing number of corners, completes their perfection with the disdyakis triacontahedron:

tetrahedron is dual to tetrahedron		Dorian mode is reverse of Hypomixolydian mode
octahedron is dual to cube		Mixolydian mode is reverse of Hypodorian mode
icosahedron is dual to dodecahedron		Lydian mode is reverse of Hypophrygian mode
? is dual to ?		Phrygian mode is reverse of Hypolydian mode

Just as the tetrahedron is self-dual, so the Dorian mode has a pattern of intervals that is the mirror image of itself. It is therefore the same as the pattern of the Hypomixolydian mode, the eighth mode, which both completes and recommences the cyclic sequence of intervals that started with the Dorian. Just as the octahedron and cube are dual to each other, so the Mixolydian and Hypodorian modes possess patterns of intervals that are mirror images of each other. Just as the icosahedron and dodecahedron are dual to each other, so the Lydian and Hypophrygian modes are mirror images of each other. The Phrygian musical mode is the reverse of the Hypolydian mode. What, however, is the pair of non-Platonic polyhedra that are dual to each other and are the counterpart of this fourth pair of modes? As the 32 corners of a rhombic triacontahedron consist of the 12 corners of an icosahedron and the 20 corners of a dodecagon, it might seem natural to think that the next member of the seven-fold sequence of polyhedra after the five

11

Platonic solids is this one and that the disdyakis triacontahedron  is the seventh because it is just the rhombic triacontahedron with the centres of its faces raised. However, it is not its dual. If the analogy between polyhedral duality  and modal symmetry is to be taken seriously so that the alternation between a polyhedron and its dual persists beyond the five Platonic solids and applies  as well to the last pair of polyhedra making up the seven polyhedra,  it means that either one or both of these polyhedra cannot complete the seven-fold sequence of polyhedra that mirrors the seven musical modes.  It might be expected that the disdyakis triacontahedron should, indeed, be the seventh polyhedron because of its status as the polyhedral form of the Tree of Life. But a rigorous mathematical discussion cannot make this assumption, however, persuasively it is suggested by the evidence presented in Articles 22–25.  Instead, it must explain why,  in strictly mathematical terms, this polyhedron does possess a unique significance. After all, the icosidodecahedron is an Archimedean   solid with only 32  faces.  But it, too, acquires 120 triangular faces

Table 4 Archimedean solid Types of faces Number of triangular faces cuboctahedron 8 triangles + 6 squares 8×3 + 6×4 = 48 icosidodecahedron 20 triangles + 12 pentagons 20×3 + 12×5 = 120 truncated tetrahedron 4 triangles + 4 hexagons 4×3 + 4×6 = 36 truncated cube 8 triangles + 6 octagons 8×3 +6×8 = 72 truncated octahedron 6 squares + 8 hexagons 6×4 + 8×6 = 72 truncated dodecahedron 20 triangles +12 decagons 20×3 + 12×10 = 180 truncated icosahedron 12 pentagons + 20 hexagons 12×5 + 20×6 =180 rhombicuboctahedron 8 triangles + 18 squares 8×3 + 18×4 = 96 truncated cuboctahedron 12 squares + 8 hexagons + 6 octagons 12×4 + 8×6 + 6×8 = 144 rhombicosidodecahedron 20 triangles + 30 squares + 12 pentagons 20×3 + 30×4 + 12×5 = 240 truncated icosidodecahedron 30 squares + 20 hexagons + 12 decagons 30×4 + 20×6 + 12×10 = 360 snub cube 32 triangles + 6 squares 32×3 + 6×4 = 120 snub dodecahedron 80 triangles + 12 pentagons 80×3 + 12×5 = 300

when the centres of these faces are raised above them (Table 4). Moreover, the transformed polyhedron has 62 vertices (30 old vertices and 32 new ones), which is the same number as the disdyakis triacontahedron. It has 480 hexagonal yods⁷ — just as many as the disdyakis triacontahedron. It has (60 + 20×3 + 12×5 = 180) edges — the same number, which means that it, too, has (62+180+120=362) vertices, edges and faces, a number that, as Section 1 revealed, is embodied in both the inner Tree of Life and in the last of its regular polygons. Finally, it has (180×2 + 62 = 422) yods along its sides — the same as the disdyakis triacontahedron. It thus shares some of the amazing properties of this polyhedron and their correlations with the Tree of Life that were discussed in Articles 22–25. The only other Archimedean solid with 62 corners and 120 faces when its faces are raised is the snub cube It, too, has 480 hexagonal yods, 362 vertices, edges and triangular faces and 422 yods along its sides. The lack of uniqueness in such properties of the disdyakis triacontahedron means that they, alone, cannot be regarded as evidence that makes it stand out from all other polyhedra. What does pick it out is the following: there are 13 Archimedean solids (15, including the two solids that possess enantiomorphic

12

 

Table 5. Properties of the Archimedean & Catalan solids.

(listed in order of increasing number of vertices)		(listed in order of increasing number of faces)
F E C Archimedean solid 8 18 12 truncated tetrahedron 14 24 12 cuboctahedron 14 36 24 truncated cube 14 36 24 truncated octahedron 26 48 24 rhombicuboctahedron 38 60 24 snub cube 38 60 24 snub cube (chiral partner) 32 60 30 icosidodecahedron 26 72 48 truncated cuboctahedron 32 90 60 truncated icosahedron 32 90 60 truncated dodecahedron 62 120 60 rhombicosidodecahedron 92 150 60 snub dodecahedron 92 150 60 snub dodecahedron (chiral partner) 62 180 120 truncated icosidodecahedron		Catalan solid F E C triakis tetrahedron 12 18 8 rhombic dodecahedron 12 24 14 triakis octahedron 24 36 14 tetrakis hexahedron 24 36 14 deltoidal icositetrahedron 24 48 26 pentagonal icositetrahedron 24 60 38 pentagonal icositetrahedron (chiral partner) 24 60 38 rhombic triacontahedron 30 60 32 disdyakis dodecahedron 48 72 26 triakis icosahedron 60 90 32 pentakis dodecahedron 60 90 32 deltoidal hexacontahedron 60 120 62 pentagonal hexacontahedron 60 150 92 pentagonal hexacontahedron (chiral partner) 60 150 92 disdyakis triacontahedron 120 180 62

 

C = number of vertices E = number of edges F = number of faces

 

13

counterparts). This demonstrates how the Godname YAH of Chokmah with number value 15 prescribes the family of solids that have at least two types of regular polygons as their faces. The musical counterpart of this is the fact that the 15 notes of two octaves of the Pythagorean scale are needed to generate the eight Church modes:

The duals of the Archimedean solids are the 15 Catalan solids shown in Table 5. When listed in order of increasing number of corners, starting with the truncated tetrahedron with 12 corners and eight faces, the Archimedean solid with most corners is the truncated icosidodecahedron with 120 corners and 62 faces. When listed in order of increasing number of faces, starting with the triakis tetrahedron with 12 faces and eight corners, the Catalan solid with the most faces is the disdyakis triacontahedron with 62 corners and 120 faces. This is the disdyakis triacontahedron!

There are 13 Catalan solids apart from the enantiomorphic versions of the pentagonal icositetrahedron and the pentagonal hexacontahedron. The disdyakis triacontahedron is therefore the 26th and last of the two families of Archimedean and Catalan solids. The Divine Name YAHWEH with number value 26 prescribes these two families of solids and determines the disdyakis triacontahedron as the solid with the most faces, whilst its dual, the truncated icosidodecahedron, is the solid with the most corners. These most complex of the Archimedean and Catalan solids are the sixth and seventh members of the sevenfold sequence of polyhedra that mirror the seven musical scales:

tetrahedron is dual to tetrahedron		Dorian mode is inverse of Hypomixolydian mode
octahedron is dual to cube		Mixolydian mode is inverse of Hypodorian mode
icosahedron is dual to dodecahedron		Lydian mode is inverse of Hypophrygian mode
truncated	disdyakis                                                               Phrygian	Hypolydian
is dual to		is inverse of
icosidodecahedron	triacontahedron                                                           mode	mode

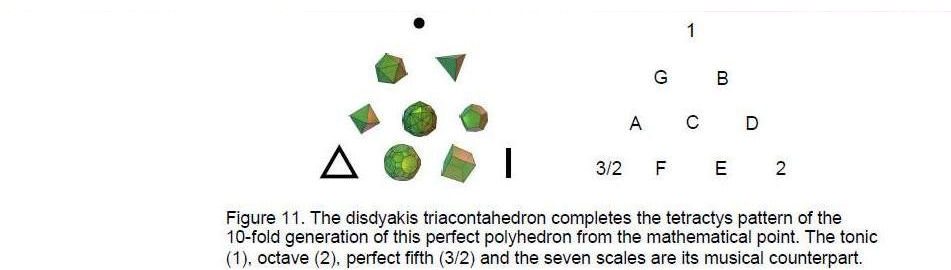
The disdyakis triacontahedron corresponds to the mathematically perfect Pythagorean scale (Hypolydian mode). It completes the tetractys pattern representing the generation from the mathematical point of the perfect solid (Fig. 11).

14

The centre and corners of a polyhedron with E edges define E internal triangles. The (6+4×3=18) tetractyses inside and on the surface of a tetrahedron have 70 yods surrounding its centre.⁸ In other words, starting from this point, 70 yods are needed to construct the tetrahedron from tetractyses. This is the meaning of the 70 yods in the Tree of Life constructed from 16 tetractyses (Fig. 12). As the simplest Platonic solid, it is the first in the archetypal sequence of seven solids leading to the 3-dimensional realisation of the Tree of Life — the disdyakis triacontahedron. As the ‘seed’ that grows into the flower of the latter, it must possess these 70 degrees of freedom. 62 of the yods are hexagonal yods (48 in the four faces, 14 internal). They symbolize in potentia the 62 faces of the fully-grown, polyhedral Tree of Life. If, instead, the internal triangles formed by the vertices and centre are divided into three tetractyses, the tetrahedron has 124 surrounding its centre.⁹ In other words, 120 yods are necessary, starting from a tetrahedron, to construct it from the 30 tetractyses. These symbolize in potentia the 120 faces of the disdyakis triacontahedron.

As we saw in Section 1, the disdyakis triacontahedron has 362 geometrical elements. Including its centre, there are 363 elements. This shows how SHADDAI EL CHAI, the complete Godname of Yesod, prescribes this polyhedron. With each internal

 triangle, a single tetractys, there are 180 internal tetractyses with 62 internal sides ending on the vertices. The number of geometrical

15

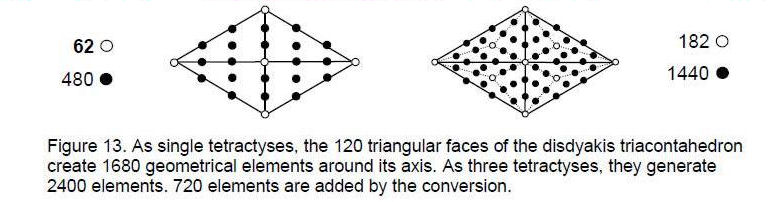
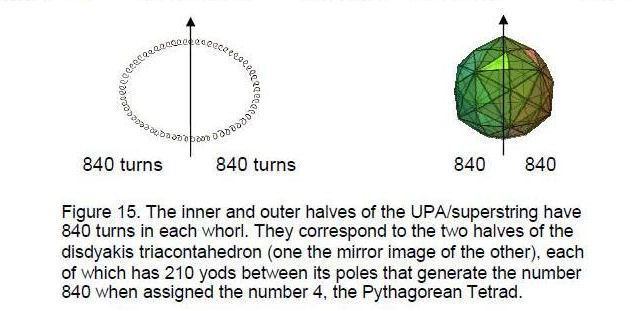
elements inside the polyhedron and on its faces = 362 + 180 + 62 + 1 = 605. Turning each internal triangle into three tetractyses generates three sides, two triangles and one vertex for each one, creating in total (605 + 180×6 = 1685) elements. Converting the triangular faces into three tetractyses adds (6×120=720) elements, totalling 2405. Constructed both internally and externally from tetractyses, the polyhedron has a central axis made up of its centre, two diametrically opposite vertices and the lines joining them to this centre, that is, five geometrical elements. The disdyakis triacontahedron therefore has 2400 (=240×10) elements surrounding its central axis, of which 1680 (=168×10) elements comprise it with single tetractyses for its 120 faces (Fig. 13). This property is truly remarkable evidence (indeed, proof) that the disdyakis triacontahedron does, indeed, represent the Tree of Life blueprint. This is because the basic unit of matter described 110 years ago by the Theosophists Annie Besant and C.W. Leadbeater, using a yogic siddhi, consists of ten closed curves, or “whorls,” each a helix with 1680 turns (Fig. 14). This fundamental superstring structural parameter is the number of geometrical elements in the disdyakis triacontahedron that surround any axis joining two diametrically opposite vertices.

The division:

was encountered in many previous articles. Its significance in the context of the superstring gauge symmetry group E₈ is as follows: The roots of the E₈ algebra can be described in terms of eight orthonormal unit vectors {ui}. Eight ‘zero roots’ correspond to points at the centre of the root diagram and 240 ‘non-zero roots’ all have length √2. They are given by

±u_i ±u_j           (i, j = 1, 2,… 8)

and

½(±u₁, ±u₂, … ±u₈)           (even number of +’s)

Their explicit forms as 8-tuples and their numbers are listed below:

The 240 non-zero roots of E₈ comprise 168 made up of four sets of 28 and one set of 56, one set of 70 and two single ones. E₆, an exceptional subgroup of E₈, has 72 nonzero roots. The 240 non-zero roots therefore comprise 168 roots that do not belong to E₆ and 72 roots that do. Each root defines its associated group generator and gauge charge that couples to a 10-dimensional gauge field. The 1680 geometrical elements of

16

 

the disdyakis triacontahedron surrounding its central axis correspond to the 1680 components of the 168 10-dimensional gauge fields of the superstring symmetry group E₈ that are not also gauge fields of its subgroup E₆.

With its faces divided into three tetractyses, the surface of the disdyakis triacontahedron is made up of (62+120=182) vertices, (180 + 120×3 = 540) edges and (120×3=360) triangles, that is, 1082 geometrical elements. Starting from a point denoting a vertex, 1081 elements are needs to create the shape of the polyhedron. 1081 is the number value of Tiphareth, the Sephirah at the centre of the Tree of Life. Tiphareth means “beauty.” The polyhedron embodies in its geometry the archetype of Divine beauty.

Inside each triangular face divided into three tetractyses are 10 yods. The number of yods other than vertices in the faces = 120×10 + 180×2 = 1560 = 156×10. The yods in 156 tetractyses are needed to construct the surface of the polyhedron. As 156 is the 155th integer after 1, this shows how ADONAI MELEKH, the complete Godname of Malkuth with number value 155, prescribes the outer form of the disdyakis triacontahedron, in keeping with the meaning of Malkuth as the outer physical form.

156 is also the sum of the number values of the four types of combinations of the letters Y, H and V in YHVH, the Godname of Chokmah:

156 is the sum of the first 12 even integers that can be arranged in a square:

The number of corners of the 360 tetractyses in the surface of the polyhedron = 62 + 120 = 182. With internal triangles divided into three tetractyses, the number of corners of the 540 internal tetractyses = 180 + 1 = 181. The (360+540=900) tetractyses needed to build the disdyakis triacontahedron have (182+181=363) corners. This is how the Godname SHADDAI EL CHAI with number value 363 prescribes its tetractys composition (see Table 1).

There are seven yods on the boundaries of the three tetractyses inside each of the 120 triangular faces. Each of the 180 sides of the polyhedron has two hexagonal yods between their 62 ends. The number of yods on the boundaries of the (120×3=360) tetractyses = 62 + 180×2 + 120×7 = 1262. There are 1260 such yods between any two diametrically opposite vertices. 1260 is the number value of Tarshishim, the Order of Angels assigned to Netzach. The number value of the name of the angelic order assigned to the seventh Sephirah is the number of yods between two diametrically opposite vertices that shape the 120 faces of the disdyakis triacontahedron, the seventh polyhedron in the sequence matching the seven musical scales.

1260 is the number of yods in 126 tetractyses. It is remarkable that the number 126 is the sum of the number values of the four types of combinations of the letters A, H and

17

in AHIH, the Godname of Kether:

A = 1, H = 5, I = 10

1. A + H + I	=	16
2. AH + HI + AI + HH	=	42
3. AHI + HIH + AHH	=	47
4. AHIH	=	21
TOTAL	=	126

This shows how EHYEH prescribes the population of yods between opposite vertices that define the shapes of the 360 tetractyses in the faces of the disdyakis triacontahedron.¹⁰

The number 126 has the remarkable property that it is the arithmetic mean of the first 26 triangular numbers, where 26 is the number value of YAHWEH:

It is an example of the profound arithmetic connections between Godname numbers. If the Pythagorean Tetrad 4 is assigned to the boundary yods of the disdyakis triacontahedron, the sum generated by the 420 yods between diametrically opposite vertices shaping the 120 faces is 1680. With the latter divided into three tetractyses, the sum generated by the 1260 yods between diametrically opposite vertices shaping the 360 tetractyses is 4×1260 = 5040 = 3×1680. Turned into tetractyses, the 120 faces of the disdyakis triacontahedron embody the number of turns of each

helical whorl of the UPA/heterotic superstring (Fig. 15). Turned into three tetractyses, they embody the number of turns of its three so-called ‘major whorls’ (the thicker whorls).

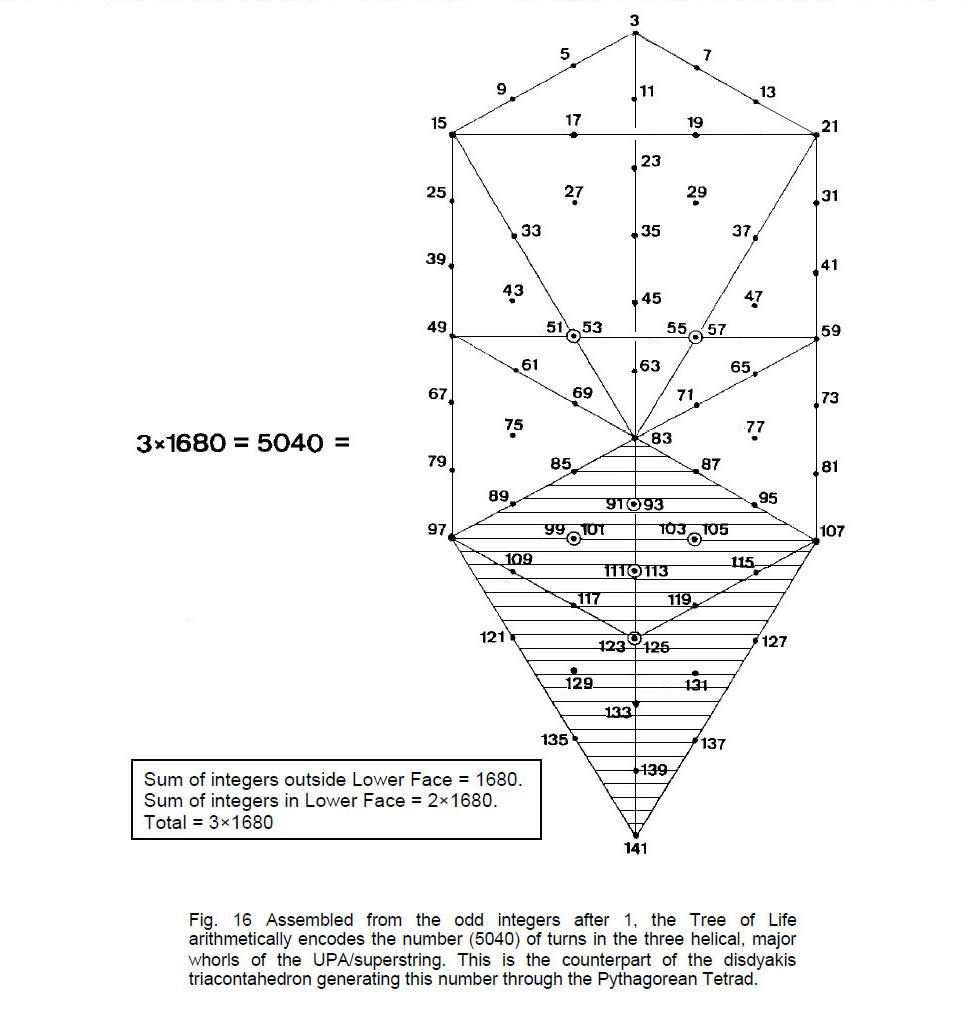
As

5040 = 71² – 1 = 3 + 5 + 7 +… + 141,

and, as the Tree of Life turned into tetractyses contains 70 yods, the number of helical turns in the three major whorls is simply the sum of the 70 odd integers after 1 that can be assigned to the yods in the Tree of Life (Fig. 16). Its Lower Face (shown shaded) has 30 yods, the rest of the Tree of Life having 40 yods. As

1680 = 41² – 1 = 3 + 5 + 7 +… + 81,

18

the sum of the first 40 odd integers up to 81 outside the Lower Face is 1680, and the sum of the next 30 odd integers composing the Lower Face is 2×1680. The Tree of Life encodes arithmetically the number of turns in the three major whorls, which are the string manifestation in 4-dimensional space-time of what Kabbalists call the ’Supernal Triad,’ Christians call the ‘Holy Trinity’ and what is familiar to Hindus as the ‘Trimûrti’ of Shiva, Vishnu and Brahma. Such is the close relationship between number and the

19

geometry of the Tree of Life that, when imagined as actually constructed from the odd integers, starting with 3, its Lower Face reproduces the distinction between the first member of the Supernal Triad and the two others in the context of their correspondence to the three major whorls in the subquark state of the E₈×E₈ heterotic superstring.

The largest odd integer, which coincides with the position of Malkuth at the base of the Tree of Life, is 141 = 76 + 65, i.e., the sum of the numbers of YAHWEH ELOHIM and ADONAI. It is the 71st odd integer, where 71 = 21 + 50, i.e., the sum of the numbers of EHYEH and ELOHIM. The integers are assigned in Fig. 16 sequentially from left to right.

Remarkably, the sum of the integers located at the positions of the 10 Sephiroth is:

 3                                          70
15 21                                     70 70
59 49 83         = 700 =         70 70 70
97 107 125 141                      70 70 70 70,

i.e., it is the sum of the number 10 (the Pythagorean Decad) assigned to each of the 70 yods in the Tree of Life! It is an example of the way in which the beautiful, mathematical properties of the Tree of Life clearly point to the designing Intelligence behind it. The following, amazing property of the

20

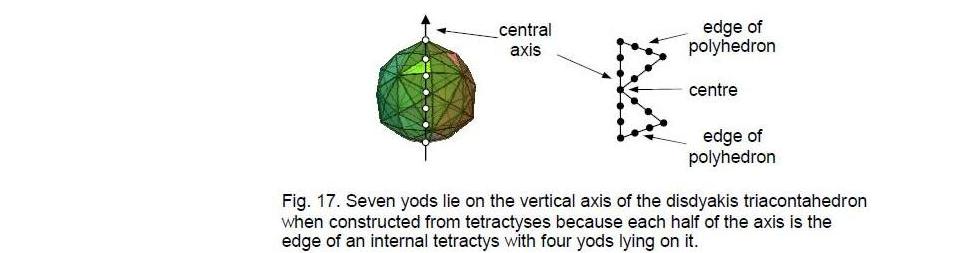
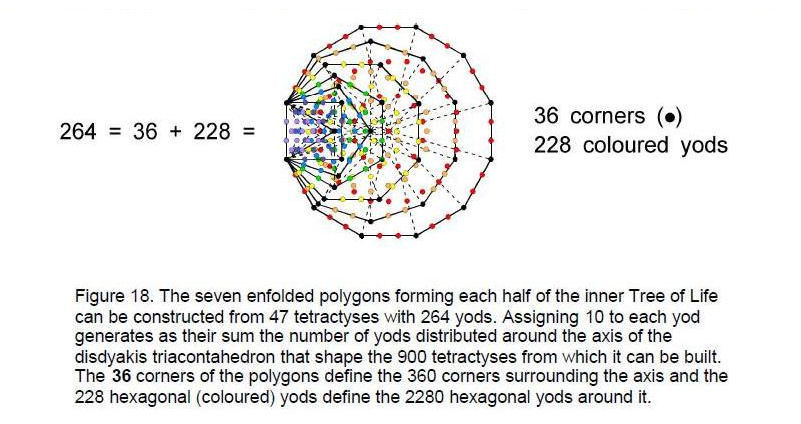
disdyakis triacontahedron provides further proof that it is the polyhedral version of the inner Tree of Life: when its 180 internal triangles are each divided into three tetractyses, there are within each triangle seven yods lying on edges of the (3×180=540) tetractyses. The line joining each polyhedral vertex to the centre of the polyhedron has two hexagonal yods in it. Therefore, the number of yods lying on edges of the internal tetractyses = 2×62 + 7×180 + 1 = 1385. We saw earlier that 1262 yods lie on the boundaries of the 360 tetractyses forming the 120 faces of the polyhedron. The total number of boundary yods inside and on the surface of the polyhedron = 1385 + 1262 = 2647. Four yods lie on the common vertical edge of the 10 tetractyses symmetrically arranged around the axis that are part of internal triangles having sides that converge on the uppermost vertex (Fig. 17). Actually, they are edges of the rhombic faces and raised halves of their longer diagonals. Similarly, four yods lie on the common vertical edge of the 10 tetractyses belonging to internal triangles whose sides converge on the lowest vertex diametrically opposite the highest one. This means that there are seven yods on the vertical axis running through the highest and lowest vertices. The number of yods lying on the boundaries of the (540+360=900) tetractyses that surround the vertical axis = 2647 – 7 = 2640 = 264×10. 264 is the number of yods in the seven enfolded polygons forming half of the inner form of the Tree of Life (Fig. 18)! Assigning 10 to each such yod therefore generates as their sum the number of yods lying on the boundaries of the 900 tetractyses that can be assembled into the disdyakis triacontahedron As seen earlier, these tetractyses have 363 corners prescribed by SHADDAI EL CHAI, Godname of Yesod. Three of the corners lie on the central axis (see Fig. 17). 360 corners surround the axis. This number is the sum of the integers 10 that can be assigned to the 36 corners of the seven enfolded polygons. There are (264–36=228) yods that are not corners. This is the number of yods on the edges of the 900 tetractyses that are not corners. A remarkable correspondence emerges between the inner Tree of Life and the disdyakis triacontahedron, whose axis is equivalent to the root edge shared by both sets of polygons. It exists because the disdyakis triacontahedron is its polyhedral form.

How do the properties of the dual of the disdyakis triacontahedron compare with it? It is readily shown that the truncated icosidodecahedron has in its 62 faces the same numbers of yods, hexagonal yods, corners and boundary yods. It also has the same number (363) of corners of tetractyses making up its faces and interior. However, the latter differs in the numbers of its hexagonal and boundary yods. The number of boundary yods inside and on the surface of the polyhedron is 2763, not the number 2647 for the disdyakis triacontahedron that proved its correspondence with the seven enfolded polygons. Its 900 tetractyses have 1563 corners and edges, a total of 2463 geometrical elements. This compares with the 2405 elements for the disdyakis triacontahedron that implied that 2400 elements surround its central axis. As expected, the properties of its dual fall short of the beautiful correlations with the properties of the seven polygons, showing that the disdyakis triacontahedron — not its dual — should be regarded as the seventh and last member of the set of seven polyhedra because it represents exact correspondence with the Tree of Life.

Of the 264 yods in the seven regular polygons forming each half of the inner Tree of Life, 73 yods belong to the dodecagon. 69 of them lie outside the root edge, leaving 195 yods in the first six polygons. Associating two yods in the shared edge with each set of six polygons, there are 193 yods associated with each set. As the uppermost corner of a hexagon coincides with the lowest corner of the hexagon enfolded in the next higher tree, there are (192n+1) yods associated with the 6n polygons enfolded in n trees. The set of polygons has 26 corners and 31 sides, each with two hexagonal yods, where 26

21

is the number value of YAHWEH and 31 is the number value of EL. Hence, there are (26 + 31×2 = 87) yods along their boundaries, where 87 is the number value of Levanah, the Mundane Chakra of Yesod. The number of boundary yods associated with each set of six polygons is 85. There are (84n+1) boundary yods associated with the 6n polygons enfolded in n trees.

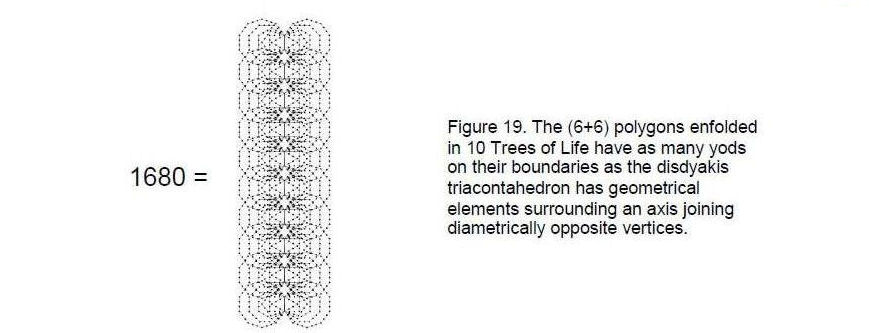
The Godname ADONAI with number value 65 prescribes the lowest 10 trees with 65 Sephiroth. There are 1921 yods associated with the 60 polygons enfolded in them. Of these, 841 yods lie on their boundaries, inside which are 1080 yods. As the uppermost corner of the top hexagon coincides with the lowest corner of the hexagon belonging to the adjacent tree, there are 840 yods intrinsic to each set of polygons, i.e., there are (2×840=1680) boundary yods intrinsic to both sets, which have (2×1080=2160) yods inside their boundaries. We find that the disdyakis

triacontahedron has as many geometrical elements surrounding its axis as there are yods forming the shapes of the two sets of the first six polygons enfolded in 10 Trees of Life. The yods symbolize bits of information — geometrical elements in the

22

disdyakis triacontahedron and circularly polarised oscillations in each whorl of the UPA/superstring. 216 is the number value of Geburah, the second Sephirah of Construction. Its Godname ELOHA prescribes the 360 tetractyses in the 120 faces of the disdyakis triacontahedron because its number value is 36.

If the number 10, which was regarded by the Pythagoreans as the perfect number, is assigned to every yod in the 360 tetractyses, the sum of the integers assigned to their 182 corners is 1820. This is the number of yods surrounding the centres of the five Platonic solids when they are constructed from tetractyses.¹¹ It is another remarkable property of the disdyakis triacontahedron that illustrates its archetypal qualities. As 1820 = 70×26, it is the sum of the number value 26 of YAHWEH assigned to each of the 70 yods that make up the Tree of Life when its 16 triangles are converted into tetractyses (see Fig. 12). It indicates that the five regular solids constitute a whole in themselves.

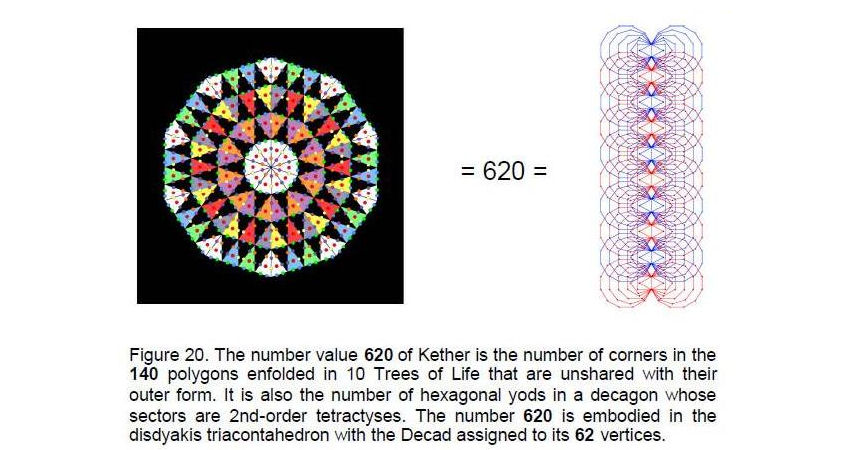
The sum of the integers 10 assigned to the 62 vertices of the polyhedron is 620. This is the number value of Kether (“crown”), the first Sephirah of the Tree of Life. It is also the number of corners intrinsic to the 70 polygons enfolded on each side of 10 Trees of Life that are unshared with their Sephiroth (Fig. 20). A symbol of the number 10, the decagon divided into 2nd-order tetractyses has 720 yods surrounding its centre. 620 of them are hexagonal yods. The 62 vertices of the disdyakis triacontahedron correspond to the 62 hexagonal yods per sector of the decagon.

As the dual of the disdyakis triacontahedron, the truncated icosidodecahedron has the same number (1440) of hexagonal yods in its 62 faces.¹² The five Platonic solids have (720=72×10) hexagonal yods in their 50 faces.¹³ The seven solids have 3600 (=36×10×10) hexagonal yods in their 232 faces, showing how the Godname ELOHA of Geburah with number value 36 prescribes the hexagonal yod population of this archetypal set of seven solids. The first six solids have (720+1440=2160) hexagonal yods, which is the number of yods in 216 tetractyses. The number value of Geburah is 216 and the number value of Chesed, the first Sephirah, is 72. It cannot be just coincidence that successive Sephirah have such significant values.

 

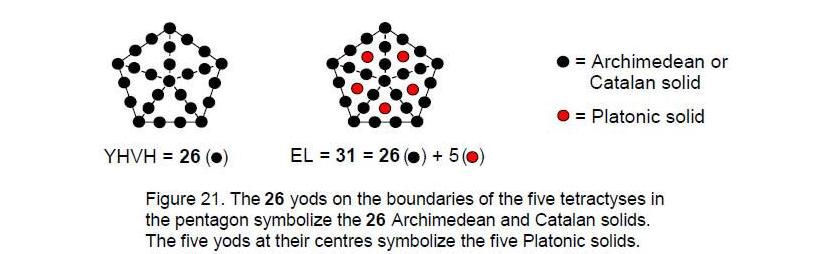
Adding the five Platonic solids to the 26 Archimedean and Catalan solids creates a new family of 31 solids. The Divine Name EL (“God”) assigned to Chesed therefore

23

prescribes how many regular and quasi-regular solids there are. Constructed from tetractyses, the pentagon has 31 yods (Fig. 21). The yods on the sides of the tetractyses symbolize the Archimedean and Catalan solids and the five yods at their centres represent the five Platonic solids.

As

168 = 13² – 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25,

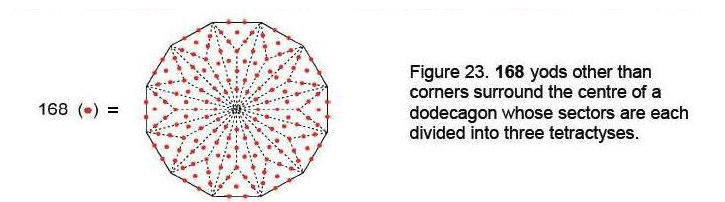
this number is the sum of the odd integers after 1 that can be assigned to the 12 corners of the dodecagon, which is the seventh type of polygon appearing in the inner Tree of Life and the tenth polygon per se (Fig. 22). The number 168 is also the number of yods generated in the dodecagon when its sectors are each divided into three tetractyses (Fig. 23). The total number of yods surrounding its centre is 180, which is the number of sides of the disdyakis triacontahedron. This is how the last polygon in the inner Tree of Life embodies information about the

properties of its polyhedral version.

168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. As the structural parameter of superstrings — the physical manifestation or Malkuth aspect of the Tree of Life in the subatomic world — this number is embodied in the disdyakis triacontahedron (apart from the Tree of Life factor of 10) as the number of geometrical elements surrounding its axis. Just as the seven solids correspond to the seven musical scales, so they correspond to the seven Sephiroth of Construction. Indeed, it is the latter that is responsible in the first place for all seven-fold

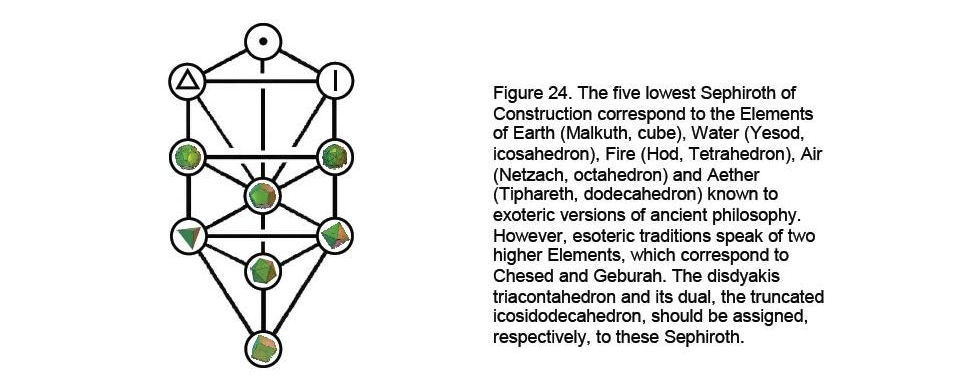
patterns in nature. Which solid is associated with which Sephirah? The solids comprise five Platonic solids and

24

two Archimedean or Catalan solids, whilst the seven Sephiroth of Construction consist of Chesed and Geburah, which are unshared by adjacent overlapping trees, and the five Sephiroth that form the Lower Face of the Tree of Life and which are shared by adjacent trees. In view of this, it is natural to make the following association:

Chesed		disdyakis triacontahedron
Geburah		truncated icosidodecahedron
Tiphareth		dodecahedron
Netzach		icosahedron
Hod		cube
Yesod		octahedron
Malkuth		tetrahedron

The ancient Greeks believed that the Platonic solids are the shapes of particles of the five elements of Earth, Water, Air, Fire and Aether. The reasons they gave for associating each element with its particular solid may now appear naïve. However, the association of the elements with the five lowest Sephiroth of Construction certainly is not so. Fig. 24 depicts the assignment of the seven solids to the Sephiroth according to the ancient association of the Platonic solids with the Elements. It shows the cube corresponding to Malkuth because it was regarded as the shape of particles of Earth, the element corresponding to Malkuth. It is inconsistent with the tetractys array of solids depicted in Fig. 11, which shows the disdyakis triacontahedron at the centre of the tetractys — the yod that symbolizes the Malkuth level or aspect of any holistic system. However, this discrepancy is not serious, because it merely reflects the fact that the association between Elements and Platonic solids made by the ancient Greeks was based upon wrong and naïve considerations, namely, the relation between the sensory experience of these polyhedra and the sensory quality of water, fire, earth, etc. They were also based upon incomplete considerations because in esoteric formulations of mystical traditions there are seven Elements, not five, the latter forming part of their exoteric versions. The order of the seven solids should be based on monotonic increase or decrease of the number of their corners or faces, i.e., with the dimension of their symmetry groups (Table 6):

Table 6

Polyhedron	Dual Polyhedron	Number of Symmetries	Symmetry Group
tetrahedron	tetrahedron	24 (12)	Td (T)
cube	octahedron	48 (24)	Oh (O)
octahedron	cube
icosahedron	dodecahedron	120 (60)	Ih (I)
dodecahedron	icosahedron
truncated icosidodecahedron	disdyakis triacontahedron	120 (60)	Ih (I)
disdyakis triacontahedron	truncated icosidodecahedron

There are three polyhedra with up to 48 symmetries and four polyhedra with 120 symmetries. This compares in the Tree of Life with the triad of Chesed, Geburah & Tiphareth and the quaternary of Netzach, Hod, Yesod & Malkuth. As the simplest regular polyhedron, the tetrahedron starts the mathematical sequence that ends with the disdyakis triacontahedron. That makes it sensible to associate the simplest solid with Chesed and the most complex solid with Malkuth. It also seems appropriate, given

25

that the number embodied in this solid is both the number value of the Mundane Chakra of Malkuth and the structural parameter of the heterotic superstring — the physical manifestation or Malkuth aspect of the Tree of Life. On the other hand, the analogy between the 2:5 pattern displayed by the Chesed-Geburah pair and the five lowest Sephiroth and the 2:5 pattern of the Catalan solid and its dual and the five Platonic solids is a strong argument for associating the disdyakis triacontahedron with Chesed rather than Malkuth. If polyhedra are to be associated with Elements at all, then this solid and its dual must be associated with, respectively, Chesed and Geburah and with their corresponding sixth and seventh Elements. This argument has to be taken seriously because the seven tone intervals in each of the seven musical scales are the musical manifestation of the universal septenary principle, and the same 5:2 pattern exists in each of them as five tone intervals and two leimmas.

The five Platonic solids correspond to the five whole tones and the Archimedean and Catalan solids correspond to the two leimmas:

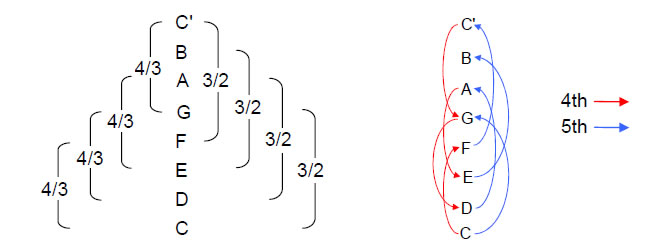
However, this association is only a formal one (although the sixth polyhedron, the dual of the disdyakis triacontahedron is third in the row above). As now explained, there is a more fundamental correspondence. The product of an interval of a perfect fourth (4/3) and an interval of a perfect fifth (3/2) is the octave: 4/3×3/2 = 2. This is the same note as the tonic but increased in pitch by a factor of 2. As intervals, the perfect fourth and perfect fifth are in a sense inverses of each other. If a note is a perfect fourth above a given note, it is also a perfect fifth below the same note in the next higher octave. Replacing corners of a polyhedron by faces and then replacing faces by corners just leaves the original polyhedron. Forming the dual of a polyhedron is like raising the pitch of a note by a perfect fourth or fifth. An interval of a perfect fourth is ‘inverse’ to an interval of a perfect fifth in a way that is analogous to how one polyhedron may be dual to another. The octave can be divided into either four perfect fourths or four perfect fifths:

In fact, all eight notes of the octave can be generated by continuous leaps of four perfects fourths and three perfect fifths, starting from the tonic C. The seven intervals creating the eight notes consist of one upward jump of a fourth (C-F), three upward jumps of a fifth (D-A, E-B, F-C') and three downward jumps of a fourth (G-D, A-E, C'-G). This 1:3:3 pattern is the same as for the seven musical scales, which consist of three pairs of scales whose intervals are in reverse order, like a reflection in a mirror, and the

26

Dorian, which is its own inverse or mirror image:¹⁴

It is also the same for the seven polyhedra, which consist of three pairs of duals and one (the tetrahedron), which is self-dual:

tetrahedron		tetrahedron
octahedron		cube
icosahedron		dodecahedron
icosidodecahedron		disdyakis triacontahedron

The pattern reflects the fact that the seven Sephiroth of Construction consist of two triads: Chesed-Geburah-Tiphareth and Netzach-Hod-Yesod, and one (Malkuth), whilst the tetractys has seven hexagonal yods, six of which are arranged in two equilateral triangles at the corners of a

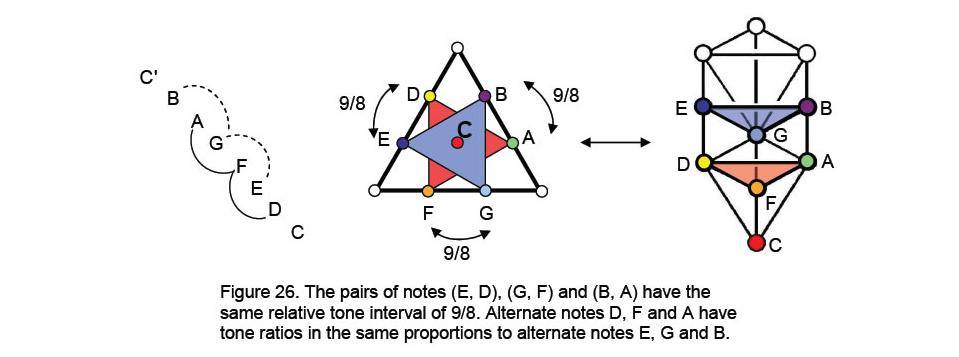
hexagon with the seventh at its centre (Fig. 25). Indeed, it was proved in Article 14¹⁵ that the six notes above the tonic form only two chords of three notes whose tone ratios are in the same relative proportions. These two natural triads of notes are DFA and EGB. Corresponding members

are separated by a tone interval of 9/8 (Fig. 26). What this means is that the eight notes form four pairs:

C     C'
D     E
F     G
A     B

27

The perfect fourth F corresponds to the icosahedron, the fourth Platonic solid, the perfect fifth G corresponds to the dodecahedron, the perfect fifth, the major sixth A corresponds to the icosidodecahedron and the major seventh B corresponds to the disdyakis triacontahedron The tonic C and the octave C' correspond to the self-dual tetrahedron.

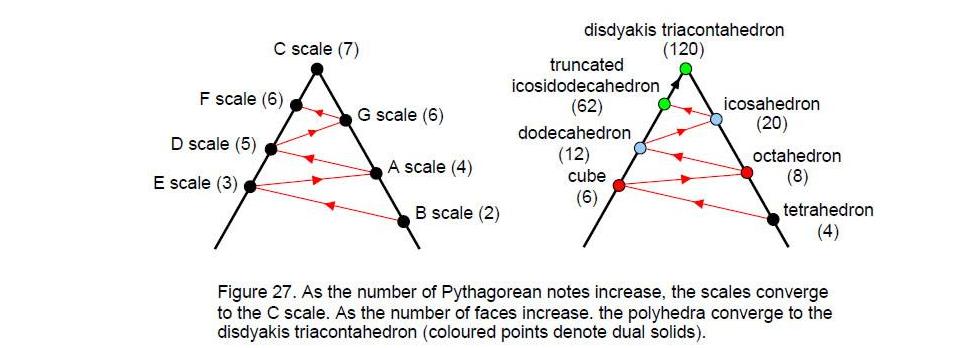
Using Table 3, the numbers of Pythagorean tone ratios in the seven scales can be represented in Fig. 27 as converging to the number 7 of the C scale. It  also depicts how the  numbers of faces in the seven solids increase to that of the disdyakis triacontahedron.

Notice that dual polyhedra (indicated by the same coloured dots) lie on opposite, sloping lines.

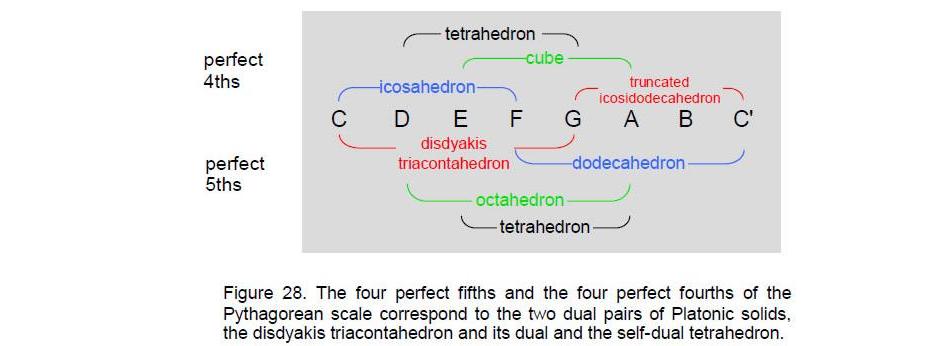
As pointed out earlier, the eight notes of the Pythagorean scale are separated by four perfect fourths and four perfect fifths. The prime division of the octave into the perfect fifth G, leaving an interval of a perfect fourth, corresponds to the disdyakis triacontahedron being dual to the

truncated icosidodecahedron. The division of the octave into a perfect fourth followed by a perfect fifth corresponds to the icosahedron being dual to the dodecahedron. The perfect fifth between note D and note A followed by a drop down by

28

a fourth corresponds to the duality of the octahedron and the cube. The perfect fourth between D and G corresponds to the tetrahedron. The two possible divisions of the complete octave — 3/2×4/3 and 4/3×3/2 — correspond to the disdyakis triacontahedron and its dual and to the dodecahedron and its dual, whilst divisions within the octave correspond to the tetrahedron, cube and octahedron (Fig. 28).

Inspection of Table 2 reveals that the seven octave species have notes with 13 different tone ratios other than 1, which, together with their 13 inversions, totals 26. In ascending and descending magnitude of pitch, the two sets of intervals are:

256/243

9/8

32/27

81/64

4/3

1024/729

729/512

3/2

128/81

27/16

16/9

243/128

2

243/256

8/9

27/32

64/81

3/4

729/1024

512/729

2/3

81/128

16/27

9/16

128/243

1/2

This shows how the Divine Name YAHWEH with number value 26 prescribes the number of different rising and falling intervals in the seven scales, i.e., their tonal range. These 13 different, rising intervals and their falling interval counterparts correspond to the 13 Archimedean solid and their duals — the Catalan solids.

The numbers of these intervals vary from scale to scale, with most repeated at least once. Let us consider the basic set of different intervals in each scale. Article 16 calculated that the seven basic sets have 53 Pythagorean intervals (including 1) and 37 non-Pythagorean intervals.16 There are therefore a minimum of 90 intervals. The significance of this number in the context of the disdyakis triacontahedron will appear shortly.

5. Plato’s Lambda & its connection to the disdyakis triacontahedron
In his Timaeus, Plato described how the Demiurge measured the World Soul, or substance of the spiritual universe as a strip divided according to the simple proportions of the first three squares of 2 and 3. This is traditionally represented by his ‘Lambda,’ so-called because of its resemblance to the Greek letter Λ (Fig. 29). These numbers line but two sides of a tetractys array of ten numbers from whose relative proportions the scientists and musicians of ancient Greece worked out the frequencies of the notes of the now defunct Pythagorean musical scale.¹⁷ The numbers missing from the Lambda are shown in red in Fig. 29. The sum of the 10 integers is 90 and the sum of the integers 1, 8 and 27 at the corners of the tetractys is 36. The seven integers at the centre and corners of the hexagon shown in Fig. 29 with dashed edges add up to 54.

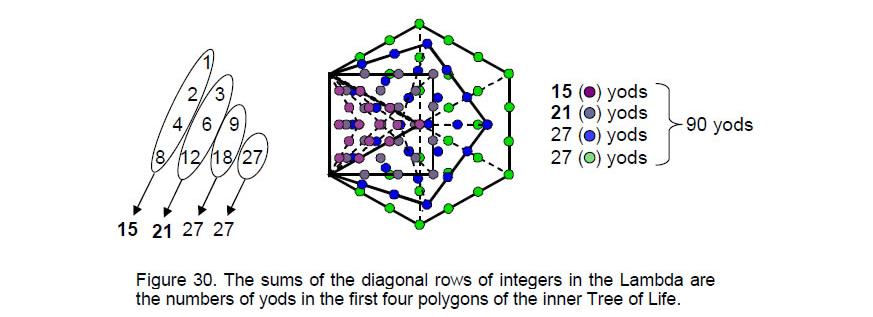
Comparing these properties of the Lambda with the number of intervals of the seven musical scales given at the end of the last section, we find that it has the remarkable property of defining not only the tone ratios of the Pythagorean scale as the ratios of its numbers but also how many of these ratios are present as a basic set in the seven types of musical scales! This is no coincidence, because the archetypal nature of the Lambda and its connection with the Tree of Life,¹⁸ the I Ching table,¹⁹ superstrings,²⁰ the musical scales²¹ and the nature of the spiritual cosmos²² has been demonstrated in previous articles. For example, in conformity with the primacy of the number 4, the first four polygons in the inner Tree of Life have 90 yods outside their shared edge (Fig. 30). This cannot be coincidence, because their individual yod populations are also the sums of diagonal rows of integers in the Lambda. It should therefore come as no surprise that the Lambda is relevant to the disdyakis triacontahedron, as now explained. Constructed

29

from tetractyses, its 120 triangular faces divide into (120×3=360) tetractyses. Each of its 180 edges is the side of an internal triangle formed by two vertices and its centre. They are constructed from (180×3=540) tetractyses. The total number of tetractyses forming the disdyakis triacontahedron = 360 + 540 = 900. The following correspondences appear:

Lambda tetractys		disdyakis triacontahedron
Sum of 10 integers = 90		number of tetractys = 900 = 90×10;
Sum of integers at corners = 36		number of tetractyses in faces = 360 = 36×10;
Sum of integers at centre & corners of hexagon = 54		number of tetractyses inside solid = 540 = 54×10.

The numbers 1³, 2³ and 3³ at the shape-defining corners of the Lambda tetractys add up to 36, which is the number of tetractyses whose yod population is the number of tetractyses creating the shape of the disdyakis triacontahedron. The seven numbers inside the Lambda tetractys add up to 54 — the number of tetractyses whose yod population is the number of tetractyses inside the disdyakis triacontahedron. Notice the similarity between the function and the character of the two sets of integers.

Moreover, the largest of the seven integers in the hexagon is 18, whilst the number of internal tetractyses creating the 180 edges is 180 = 18×10. Four arithmetic properties of the Lambda correlate with the geometry of the disdyakis triacontahedron. This cannot be coincidental.

The integers 1, 2, 3 and 4 symbolized by the four rows of dots in the tetractys express the number of tetractyses generating the disdyakis triacontahedron. As:

30 = 1² + 2² + 3² + 4²,
900 = 30² = (1²+2²+3²+4²).²

Each of the 120 faces, when divided into three triangles, has three edges meeting at a vertex inside it. The number of geometrical elements making up the insides of the faces = 120×(1+3+3) = 120×7 = 840 = 84×10, where

84 = 1² + 3² + 5² + 7².

The number of Golden Rhombic-shaped sets of four faces in the disdyakis triacontahedron = 30 = 1² + 2² + 3²+ 4².

The number of triangular faces = 120 = 4×30 = 2²(1²+2²+3²+4²)

30

= 2² + 4² + 6² + 8².

As 31 = 2⁰ + 2¹ + 2² + 2³ + 2⁴, the number of vertices = 62 = 2×31

     = 2(2⁰+2¹+2²+2³+2⁴) = 2¹ + 2² + 2³ + 2⁴ + 2⁵.

The number of vertices surrounding the axis of the polyhedron = 62 – 2 = 60

= 2² + 2³ + 2⁴ + 2⁵.

We found earlier that the number of hexagonal yods needed to construct the faces of this polyhedron = 1440 = 144×10, where

The minimum number of triangles needed to construct both the interior and exterior = 120 + 180 = 300 = (1²+2²+3²+4²)(1+2+3+4). The number of triangles = 660, so that each half of the polyhedron has 330 triangles, where 330 = (1!+2!+3!+4!)(1+2+3+4).

We also found that the number of geometrical elements surrounding the axis of this polyhedron that make up the 900 tetractyses = 2400 = (1³+2³+3³+4³)1×2×3×4. All these expressions illustrate how the Tetrad Principle²³ determines properties of archetypal objects that possess sacred geometry

31

32

6. The superstring structural parameter 1680
Surrounding the axis of the disdyakis triacontahedron are 1680 corners, edges and triangles created when its surface is formed from 180 internal triangles with the centre of the solid as corners and which are then divided into three tetractyses. This is easily seen from the table below:

	Corners		Edges		Triangles
surface:	62		180		120
interior:	180		62 + 3×180 = 602		3×180 = 540
Total =	242		782		660
minus:	–2    (two edges)		–2    (two edges)		___
Total =	240                      +		780	+	660 = 1680

There are 780 (=78×10) edges and 900 (=90×10) corners and faces. The significance of this is as follows: the ten Sephiroth of the Tree of Life each manifest as Godnames in Atziluth (the archetypal, or divine, world), Archangels in Beriah (World of Creation), Angels (Yetzirah, or Formative World) and Mundane Chakra (Physical World). According to Kabbalah, the Mundane Chakra of a Sephirah is assigned an astronomical object as its material manifestation. The planet Earth is assigned to Malkuth. It symbolizes the physical aspect of the Tree of Life. Its Mundane Chakra is Cholem Yesodoth, meaning “breaker of the foundations." Through gematria, wherein the 22 letters of the Hebrew alphabet are assigned integers, words acquire number values that

are equal to the sum of their letter values. The word ‘Cholem’ has the number value 78 and the word ‘Yesodoth’ has the value 90, giving the Hebrew name of the Mundane Chakra a value of 168 (Fig. 31). Remarkably, these numbers define (apart from the Pythagorean factor of 10), respectively, the number of edges and the number of vertices and triangles of the tetractyses needed to construct the disdyakis triacontahedron! Even if, implausibly, the total number 1680 had happened by coincidence to match the number value of the Hebrew name of the Mundane Chakra, it is improbable in the extreme that the geometrical composition of the polyhedron could be quantified by three numbers that happen to be the values of the two words in the name and their sum.

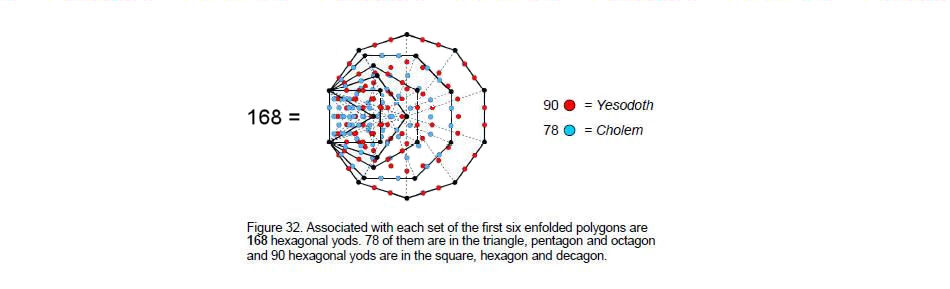
The numbers 90 and 78 appear in the first six polygons of the inner Tree of Life, which themselves constitute a whole Tree of Life pattern, being prescribed by the Godname numbers of all the Sephiroth.²⁴ Both sets of polygons have 336 hexagonal yods, so that 168 such yods are associated with each set (Fig. 32). The triangle, pentagon and octagon have 78 yods and the square, hexagon and decagon has 90 yods. Once again, it cannot, plausibly, be coincidental that some combination of polygons contains 168 hexagonal yods. Even if this were so, it would still be extremely unlikely that a subset of them would as well contain either 78 or 90 yods just by chance.

As

13² – 1 = 168

33

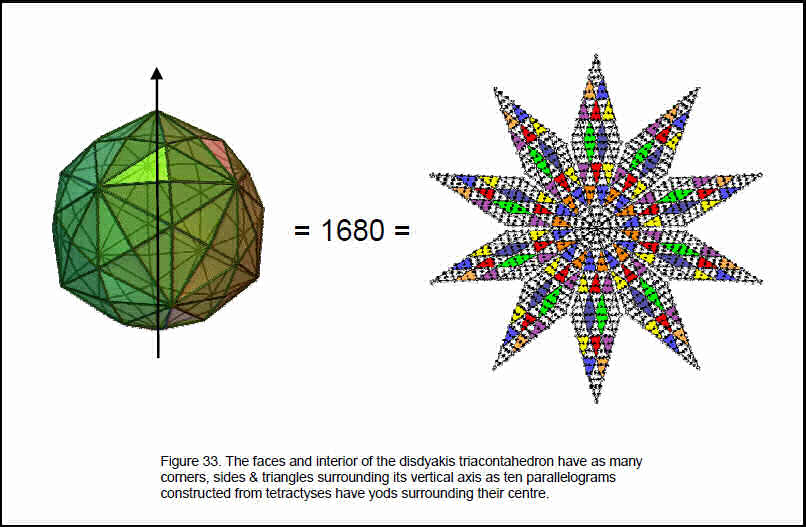
34

and, as a tetractys array of ten tetractyses has 13 yods along each edge, a parallelogram formed by two such arrays lying back-to-back has 168 yods below its apex. Ten parallelograms arranged as two pentagrams have 1680 yods surrounding their shared apices (Fig. 33). As the number of yods in a tetractys array = 1 + 2 + 3 +…+ 13 = 91, there are 90 yods below its vertex, where 90 is the number value of Yesodoth. The remainder of each arm of the ten-pointed star has (91–13=78) yods, where 78 is the number value of Cholem. Each arm is a geometrical representation of the number value of Cholem Yesodoth. The inner half of the star has 900 yods, which is the number of vertices and triangles in the interior and faces of the disdyakis triacontahedron surrounding its axis of symmetry. The outer half has 780 yods, which is the number of edges of the triangles. Each yod denotes one of the 1680 geometrical elements that surround any axis of  symmetry that joins two diametrically opposite vertices of the polyhedron. With the 120 triangular faces as single tetractyses, the number of yods in the 120 tetractyses on the surface = 62 + 2×180 + 120 = 542.

 

With the internal triangles as single tetractyses, the number of internal yods = 2×62 + 180 + 1 = 305. The total number of yods in its (120+180=300) tetractyses = 847. As there are seven yods along the axis, the number of yods surrounding the centre of the polyhedron = 840. The inner and outer halves of each whorl of the UPA/superstring each consist of 840 circularly polarised oscillations made in 2½ revolutions around its spin axis (see Fig. 14). This superstring structural parameter is therefore embodied in the disdyakis triacontahedron as the number of yods surrounding its axis of symmetry. The Tetrad Principle determines this number because a tetractys array of 10 tetractyses (Fig. 34) has 85 yods, where

85 = 4⁰ + 4¹ + 4² + 4³,

so that 84 yods surround its centre, where

84 = 1² + 3² + 5² + 7².

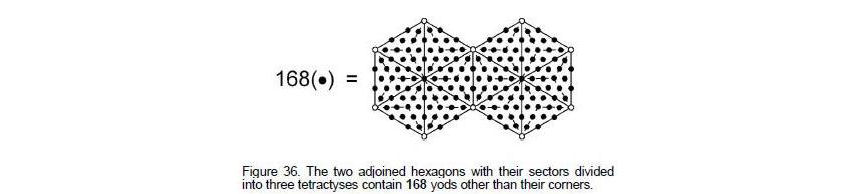
The Tetrad Principle also determines the structural parameter 168 (the number of oscillations in half a revolution of a whorl of the UPA/superstring) because, starting from a square symbolizing the Tetrad, the fourth stage of its construction from tetractyses requires 36 of them with 168 yods surrounding its centre (Fig. 35). Moreover, the fourth regular polygon is the hexagon. With its sectors constructed from three tetractyses, it contains 91 yods, i.e., 85 yods other than corners. The two joined hexagons in the inner form of the Tree of Life have 168 yods other than corners (Fig. 36). The superstring

35

36

structural parameter is the number of extra yods needed to fill up the 36 tetractyses in a pair of hexagons joined along one side. The Godname ELOHA with number value 36 prescribes the structural parameter 168. The number of hexagonal yods in two separate hexagons is 156, which is the 155th integer after 1. This shows how ADONAI MELEKH, the full Godname of Malkuth with number value 155, prescribes the number characterizing the oscillatory form of the E₈×E₈ heterotic superstring.

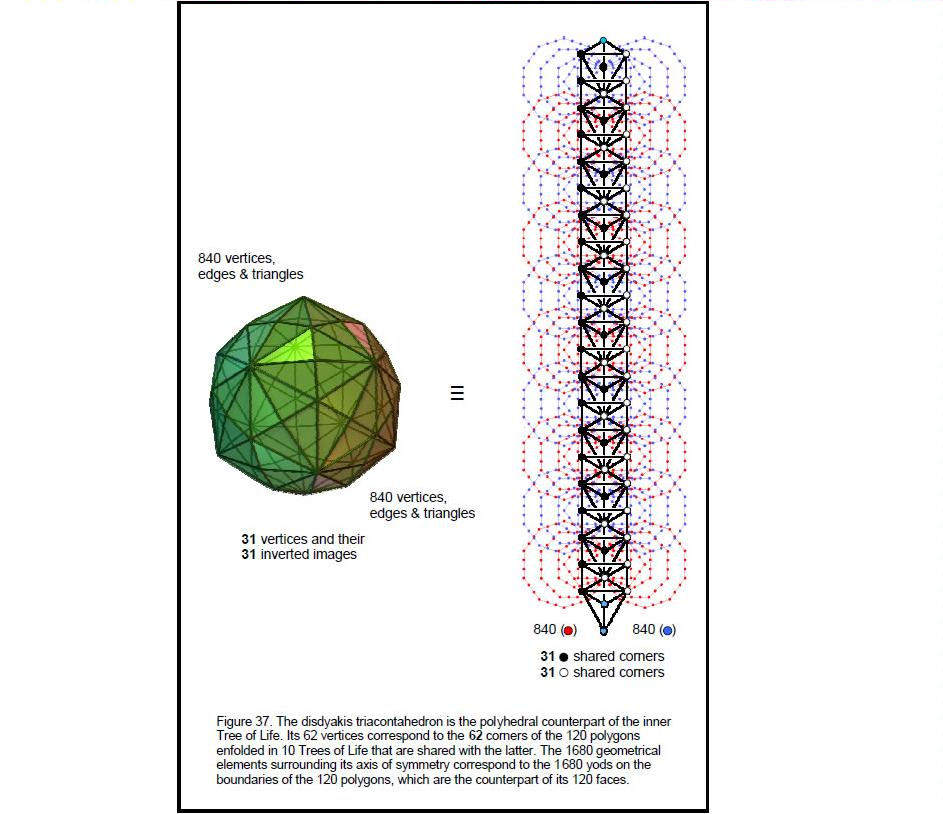
7. The disdyakis triacontahedron as the polyhedral Tree of Life
The inner Tree of Life has 70 corners, eight of which coincide with Daath and the seven Sephiroth other than Malkuth, Yesod and Kether (or, rather, the projection of them onto the plane containing the polygons). 62 corners are intrinsic to the inner Tree of Life. These degrees of freedom correspond to the 62 vertices of the disdyakis triacontahedron. 

The next level of differentiation of the outer Tree of Life is 10 Trees of Life (Fig. 37). Each tree has its own inner form consisting of 14 polygons. The 140 polygons enfolded in 10 trees have (62×10=620) corners unshared with their 62 Sephiroth. This is why the number value of Kether, the first Sephirah, has to be 620. The 62 corners that the 120 polygons enfolded in 10 trees share with the latter correspond to the 62 vertices of the disdyakis triacontahedron. There are 21 Sephiroth on each side pillar and 10 Tiphareths and 10 Yesods on the central pillar. The 62 Sephiroth therefore split into two sets of 31 associated with the active and passive pillars. They correspond to the 31 vertices and their 31 inverted images. The association of these two numbers is why the Godname EL of Chesed has the number value 31 and the number value of its Archangel

Tzadkiel is 62.

The two sets of the first six polygons have 50 corners. They are prescribed as a new Tree of Life pattern because 50 is the number value of ELOHIM, the Godname of Binah.

37

38

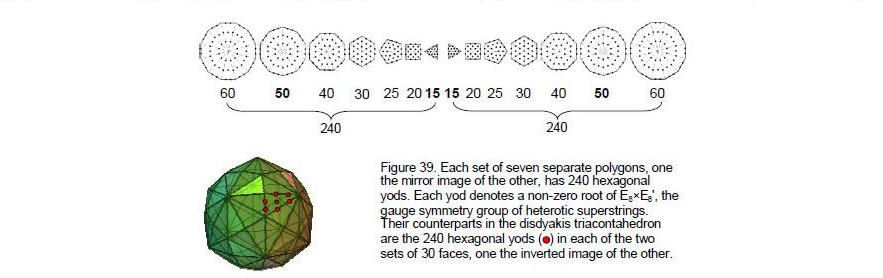
There are 12n such polygons with (48n+2) corners enfolded in n trees. The 120 polygons enfolded in 10 trees are the polygonal counterpart of the 120 faces of the disdyakis triacontahedron. They have 482 corners. Two of these — the uppermost corners of the pair of hexagons — coincide with the lowest corners of the pair of hexagons enfolded in the eleventh Tree of Life. 480 corners are intrinsic to the 120 polygons. 240 such corners lie on each side of the central pillar. Fig. 38 shows that there are 240 hexagonal yods in 60 faces of the disdyakis triacontahedron and 240 hexagonal yods in their 60 inverted images. These 480 degrees of freedom generated by turning the 120 triangles into tetractyses are the counterpart of the 480 corners of the 120 enfolded polygons. They are also the counterpart of the (240+240=480) hexagonal yods in the (7+7) separate polygons (Fig. 39) They symbolize the 480 non-zero roots of the heterotic superstring  gauge group E₈×E₈'. The distinction between the 240 hexagonal yods and their inverted images shows itself in the direct product of E₈ and E₈' and in the two sets of polygons enfolded

in the 10 trees, which are mirror images of each other. Each hexagonal yod symbolizes a non-zero root of E₈ or E₈' and therefore a gauge boson transmitting the unified superstring force. Hexagonal yods in a tetractys symbolize Sephiroth of Construction. The variety of superstring forces is linked to the differentiation between these cosmic, spiritual potencies.

840 yods lie on the 30 sides of the first six polygons on each side of the central pillar  (see Fig. 37). The 1680 boundary yods shaping the two sets of six polygons correspond to the 1680 geometrical elements surrounding the axis of symmetry of the disdyakis triacontahedron. Each yod symbolizes a bit of information needed to characterize the form of the polyhedral version of the Tree of Life, just as the 1680 circularly polarized oscillations of each whorl of the UPA/superstring create its helical shape.

Let us now examine the Tree of Life and the separate polygons. Divided into three tetractyses, the 19 triangles of the lowest tree in any set of overlapping trees acquire

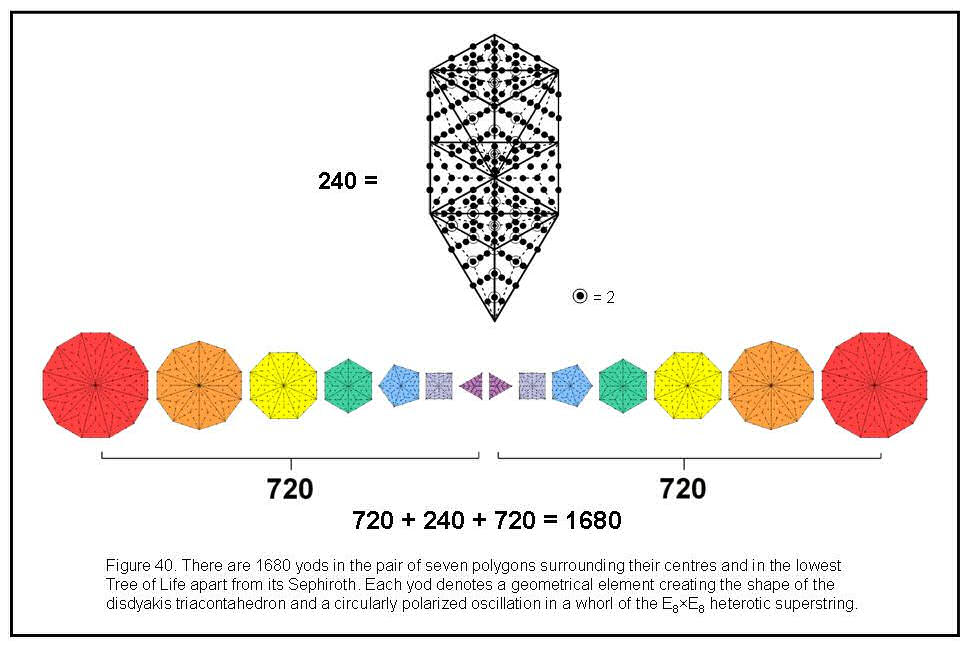
39

240 yods²⁵ (Fig. 40). These correspond to the 240 vertices of the 660 tetractyses making up the disdyakis triacontahedron that surround its axis of symmetry. The seven separate regular polygons have 48 corners. With their sectors constructed from three tetractyses, they contain 720 yods surrounding their centres.²⁶ These correspond to the 720 edges and triangles surrounding the axis that make up the 330 tetractyses in one half of the polyhedron. The similar set of seven polygons on the other side of the lowest tree also contains 720 such yods. They correspond to the 720 edges and triangles in the inverted half of the polyhedron. This exact parallelism between the disdyakis triacontahedron and the outer and inner Tree of Life is powerful evidence that the former is their polyhedral form.

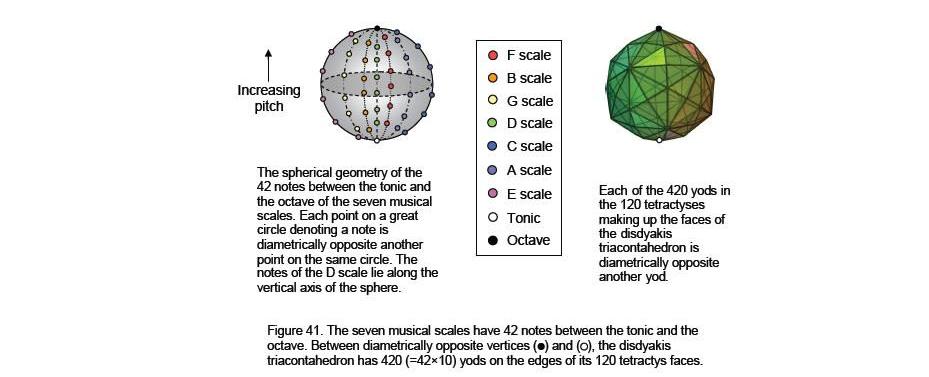
Between the tonic and the octave of a musical scale are six notes. The seven scales have (6×7=42) notes between their tonic and octave, making 44 notes in total if the latter are counted only once. They comprise 28 notes with Pythagorean tone ratios and 16 notes with non-Pythagorean tone ratios. Arranged on a half-circle according to the magnitude of their tone ratios (Fig. 41), the six notes between the tonic and octave of each scale occupy positions that are diametrically opposite notes of the scale that is its mirror image, i.e., there are 21 notes and their mirror images. The counterpart of this inversion symmetry in the disdyakis triacontahedron are the 210 (=21×10) yods in one half lying along its edges between diametrically opposite vertices that have their mirror images in the other half of the polyhedron. Actually, only the yods in 21 tetractyses are needed to create the shape of the polyhedron because the rest of it is simply their mirror reflections. This shows how the Godname EHYEH (“I am”) of Kether with number value 21 prescribes the disdyakis triacontahedron. Both the seven musical scales and this polyhedron represent holistic systems, one of sound, the other of geometry. The universal, divine archetypes find expression in many contexts, but their mathematical character is always similar, despite the differences in their cultural morphology.

The Godnames of the 10 Sephiroth prescribe the disdyakis triacontahedron in the following ways:

Kether: EHYEH = 21. There are 420 (=42×10) yods on the edges of the polyhedron between diametrically opposite vertices. 210 (=21×10) yods belong to one half of the polyhedron and 210 yods belong to its other, inverted half; EHYEH ASHER EHYEH = 543. 542 yods in faces surround the centre of the polyhedron;

Chokmah: YAH = 15. The 30 golden rhombic faces of the rhombic triacontahedron underlie the disdyakis triacontahedron. 30 = 15th even integer. Including the chiral versions of the pentagonal icositetrahedron and the pentagonal hexacontahedron, there are 15 Catalan solids, among which the disdyakis triacontahedron has the most faces; YAHWEH = 26. The disdyakis triacontahedron is the 26th and last of the two families of Archimedean and Catalan solids because it has the most faces;

Binah: ELOHIM = 50. There are 900 tetractyses when both faces and interior triangles are divided into three tetractyses. 90 = 2² + 3² + 4² + 5² + 6² = sum of five squares. 900 = 90×10 = sum of 50 squares;

Chesed: EL = 31. Of the 31 Archimedean, Catalan and Platonic solids, the disdyakis triacontahedron has the most faces. It has 62 vertices, 31 in one half and 31 in its mirror image half;

Geburah: ELOHA: = 36. Number of corners of 300 tetractyses surrounding an axis that

40

joins two diametrically opposite vertices = 360 = 36×10 = number of vertices, edges and triangles in 120 faces surrounding this axis; 37 vertices in one half of the polyhedron, where 37 is the 36th integer after 1.

Tiphareth: YAHWEH ELOHIM = 76. The 31 Platonic, Archimedean and Catalan solids can be symbolized by the 31 yods of a pentagon with its sectors turned into tetractyses. When the sectors are divided into three tetractyses, the pentagon contains 76 yods. YAHWEH ELOHIM prescribes the pentagon determining the disdyakis triacontahedron as the 31st polyhedron;

Netzach: YAHWEH SABAOTH = 129. Number of internal yods and yods on edges of the disdyakis triacontahedron = 727 = 129th prime number;

Hod: ELOHIM SABAOTH = 153. Number of internal yods = 2×62 + 180×1 + 1 = 305 = 153rd odd integer;

Yesod: SHADDAI EL CHAI = 363. With faces and internal triangles divided into three tetractyses, the number of their vertices = 62 + 120×1 + 180×1 + 1 = 363;

Malkuth: ADONAI MELEKH = 155. 1560 (=156×10) yods other than vertices in faces divided into three tetractyses. 156 = 155th integer after 1.

References

¹ Phillips, Stephen M. Article 19: “I Ching and the Eight-fold Way,” (WEB, PDF), pp. 15, 17.

² For further discussion of the Tree of Life character of the musical modes, see: Article 14: “Why the Greek Musical Modes are Sacred,” by Stephen M. Phillips, (WEB, PDF), pp. 17, 18.

³ Phillips, Stephen M. Article 22: “The Disdyakis Triacontahedron the 3-dimensional Counterpart of the Inner Tree of Life,” (WEB, PDF), Article 23: “The ‘Polyhedral Tree of Life,” (WEB, PDF) and Article 24: “More Evidence for the Disdyakis Triacontahedron As the 3-dimensional Realisation of the Inner Tree of Life and Its Manifestation in the E₈×E₈ Heterotic Superstring,” (WEB, PDF).

⁴ Phillips, Stephen M. Article 2: “The Physical Plane and Its Relation to the UPA/Superstring and Spacetime, ” (WEB, PDF).

⁵ Ref. 2.

⁶ Phillips, Stephen M. Article 5: “The Superstring as Microcosm of the Spiritual Macrocosm,” (WEB, PDF).

⁷ Divided into three tetractyses, each of the 20 triangular faces has 9 hexagonal yods inside it. Divided into five tetractyses, each of the 12 pentagonal faces has 15 internal, hexagonal yods. Total number of internal hexagonal yods = 20×9 + 12×15 = 360. Each of the 60 sides has two hexagonal yods. Total number of hexagonal yods in the icosidodecahedron = 360 + 60×2 = 480.

⁸ Proof: the tetrahedron has six edges, each with two hexagonal yods. Number of yods on edges = 4 + 6×2 = 16. It has four faces, each with 10 yods inside its edges. Number of yods on faces = 16 + 4×10 = 56. Each edge is the side of an internal tetractys. Two hexagonal yods lie on the edge joining each corner to the centre of the tetractys. One yod is at the centre of each tetractys. Number of yods inside tetrahedron = 4×2 + 1 + 6 = 15. Total number of yods = 15 + 56 = 71. 70 yods surround the centre.

⁹ Proof: dividing each internal triangle into three tetractyses instead of one tetractys adds 9 yods inside each one. Number of yods = 71 + 6×9 = 125. 120 yods other than corners surround the centre of the tetrahedron.

¹⁰ The last two members of the seven enfolded, regular polygons forming the inner Tree of Life — the decagon and dodecagon — have 126 yods outside their shared edge. As all seven polygons have 264 yods, there are 138 yods in the first five polygons. Excluding diametrically opposite vertices, there are 1260 (=126×10) yods on the boundaries of the 360 tetractyses forming the faces of the disdyakis triacontahedron. Excluding yods along the axis of symmetry joining this pair of vertices, there are 1380 (=138×10) yods on the boundaries of the 540 tetractyses inside the disdyakis triacontahedron. This 5:2

41

differentiation of polygons corresponds to the distinction between the yods on the sides of the internal and external tetractyses making up the disdyakis triacontahedron. The musical pattern of five tone intervals and two leimmas in each of the seven musical scales has its geometrical counterpart in the first five polygons generating the boundary yods inside the disdyakis triacontahedron and the last two polygons generating the boundary yods on its faces.

¹¹ Phillips, Stephen M. Article 3: “The Sacred Geometry of the Platonic Solids,” (WEB, PDF), pp. 11, 20.

¹² Proof: The truncated icosidodecahedron has 30 square faces, 20 hexagonal faces and 12 decagonal faces. The square has 12 hexagonal yods inside it, the hexagon has 18 internal hexagonal yods and the decagon has 30 internal hexagonal yods. The number of internal hexagonal yods in the polyhedron = 30×12 + 20×18 + 12×30 = 1080. The polyhedron has 180 sides, each with two hexagonal yods. The total number of hexagonal yods = 1080 + 180×2 = 1440.

¹³ Ref. 11, pp. 10, 20.

¹⁴ Suppose that each rising interval is replaced by its falling counterpart, i.e., TT^–1 and LL^–1. An ascending scale, e.g., TLTTLTT, then becomes T^–1L^–1T^–1T^–1L^–1T^–1T^–1, which is the descending version of the ascending scale TTLTTLT. Inverting each interval of a scale creates another scale whose pattern of intervals is its mirror image. Only the D scale is its mirror image: TLTTTLT = TLTTTLT.

¹⁵ Ref. 2, pp. 4, 5.

¹⁶ Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence with Octonion Algebra and Superstrings,” (WEB, PDF), p. 11.

¹⁷ Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).

¹⁸ Ibid, pp. 7, 16.

¹⁹ Phillips, Stephen M. Article 20: “Algebraic, Arithmetic and Geometric Interpretations of the I Ching Table,” (WEB, PDF), pp. 18–22.

²⁰ Ref. 17, p. 7.

²¹ Ref. 17, pp. 2–3, and Article 12, “New Pythagorean Aspects of Music and Their Connection to Superstrings,” Stephen M. Phillips, (WEB, PDF), pp. 2–4.

²² Ref. 17, pp. 3–7.

²³ Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 5.

²⁴ Phillips, Stephen M. Article 4: “The Godnames Prescribe the Inner Tree of Life,” (WEB, PDF), p. 4.

²⁵ Proof: The lowest tree has 19 triangles with 11 vertices and 25 edges. Divided into three tetractyses, each triangle has 10 internal yods. Number of yods in lowest tree = 11 +25×2 + 19×10 = 251. The 11 Sephiroth are at the vertices of the triangles. Number of yods other than Sephiroth = 251 – 11 = 240.

²⁶ Proof: Divided into three tetractyses, each sector of a regular polygon has 10 internal yods. The seven polygons have 48 sectors. Each of the 48 sides of the polygons has two hexagonal yods between its ends. Each side joining a corner to the centre of a polygon has two hexagonal yods. Number of yods in seven separate polygons = 48×10 + 48×2 + 48×2 + 48 + 7 = 727. Number of yods surrounding the centres = 727 – 7 = 720.

 

"The Universe is a thought of the Deity. Since this ideal thought-form has overflowed into actuality, and the world born thereof has realized the plan of its creator, it is the calling of all thinking beings to rediscover in this existent whole the original design."

F. Schiller, Theosophie des Julius, The World of Thinking Beings.

42