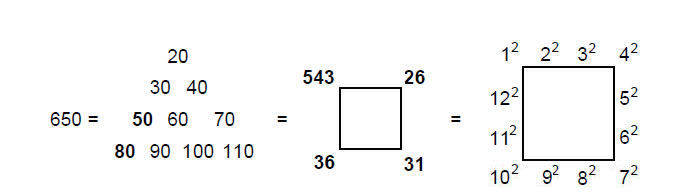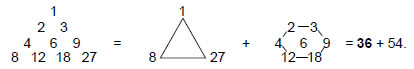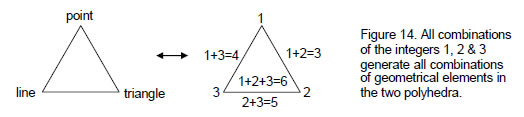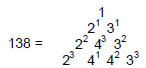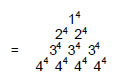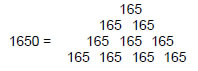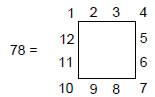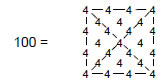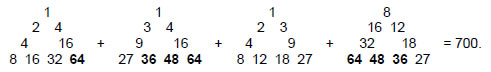ARTICLE 23
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
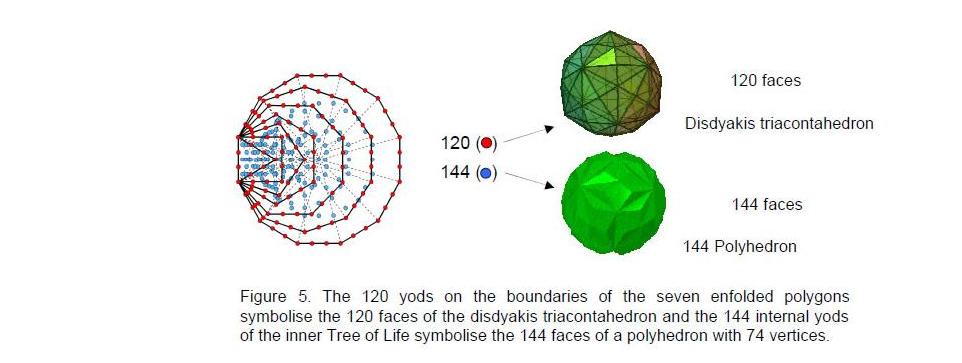
The 2-dimensional (polygonal) form of the inner Tree of Life consists of two identical sets of seven enfolded, regular polygons. Their beautiful properties expressed in terms of the integers 1, 2, 3 & 4 symbolised by the Pythagorean tetractys are prescribed by the Godnames assigned to the 10 Sephiroth of the outer Tree of Life. Constructed from 47 tetractyses, the seven enfolded polygons contain 264 yods. 120 yods are on their boundaries, inside which are 144 yods. The 120 yods shaping the inner form of the Tree of Life denote the 120 faces of the disdyakis triacontahedron, the Catalan solid with the most faces. The 144 internal yods symbolise the 144 faces of a polyhedron (‘144 Polyhedron’) formed by attaching tetrahedra to the 48 faces of the disdyakis dodecahedron, another Catalan solid. The interior and exterior of the 144 Polyhedron are made up of 720 geometrical elements that surround an axis passing through two opposite vertices. They are symbolised by the 720 yods that surround the centres of the seven separate polygons when their sectors are divided into three tetractyses. It is evidence of the Tree of Life nature of this polyhedron. Constructed from tetractyses, 650 (=65×10) yods fill up the faces of the 144 Polyhedron, showing how ADONAI, the Godname of Malkuth with number value 65, prescribes its form. The sectors of its interior and exterior triangles have 1370 edges. The number of yods in the (7+7) enfolded polygons is 1370. This is further evidence of the Tree of Life nature of the 144 Polyhedron. It also demonstrates how the polyhedron embodies the number 137 determining the fine-structure constant known to physicists. There are also 1370 hexagonal yods on the edges of the 540 tetractyses in each half of the 144 Polyhedron, as well as 1370 yods lining tetractyses in its faces. The 360:540 division of vertices & edges in each half conforms to the archetypal pattern of the Platonic Lambda Tetractys The numbers of vertices surrounding the axes of the two polyhedra, their edges and their triangles have the same proportion of 6:5. For each polyhedron, the proportion of numbers of geometrical elements in their exterior and interior is 3/2, the tone ratio of the perfect fifth in music. Their 660 triangles have 138 vertices. 138 is the sum of the powers of 1, 2, 3 & 4 on the raised edges of the tetrahedral Lambda Tetractys. The assignment of successive, odd integer multiples of 10 to the 22 Paths of the Tree of Life generates the number of geometrical elements surrounding the axes of the two polyhedra. The number of corners of the sectors of the 1400 polygons enfolded in 100 overlapping Trees of Life is the number of geometrical elements in the two polyhedra. This demonstrates that they are the polyhedral version of the Tree of Life, which can be differentiated into, firstly, 10 overlapping Trees of Life and, secondly, 100 overlapping Trees of Life. |
1
Table 5. Gematria number values of the 10 Sephiroth in the four Worlds.
SEPHIRAH GODNAME ARCHANGEL ORDER OF
ANGELSMUNDANE
CHAKRA1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living
Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
956 Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
648 Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the Foundations.
The Elements.
(Earth)
168
2
(All numbers from this table that are referred to in the article are written in boldface).
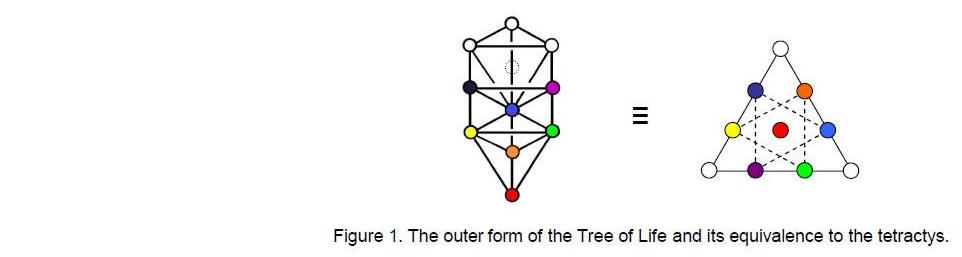
1. The outer & inner Trees of Life
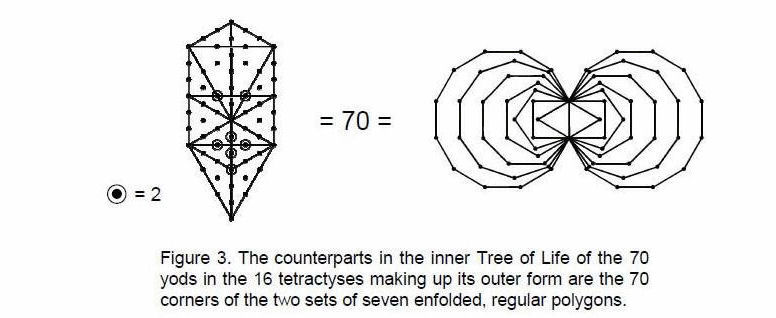
The outer form of the Tree of Life (Fig. 1) is a 3-dimensional object consisting of 16 triangles with 10 corners joined by 22 straight lines, where 10 = 1 + 2 + 3 + 4, 16 = 42 and 22 = 14 + 23 + 32 + 41. The number of vertices, sides & triangles = 48, the number value of Kokab, the Mundane Chakra of Hod (see Table 1).
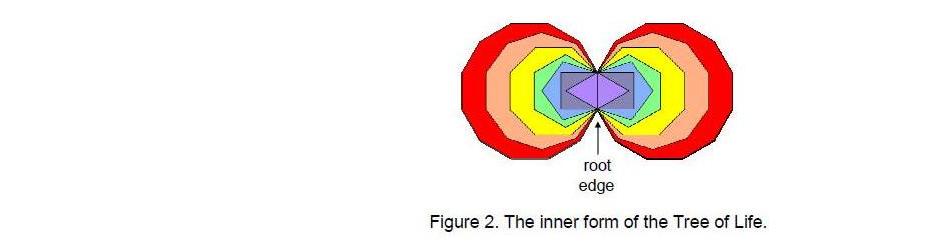
As we shall see later, this is also a basic geometrical parameter of the inner form of the Tree of Life (Fig. 2), which consists of two identical sets of
seven regular polygons — the triangle, square, pentagon, hexagon, octagon, decagon and dodecagon. They are enfolded in one another so that they share a common edge called the ‘root edge.’ When the 16 triangles of the outer Tree of Life are transformed into tetractyses, they contain 70 yods.
They denote degrees of freedom whose counterparts in the inner Tree of Life are the 70 corners of the 14 enfolded polygons (Fig. 3).
3
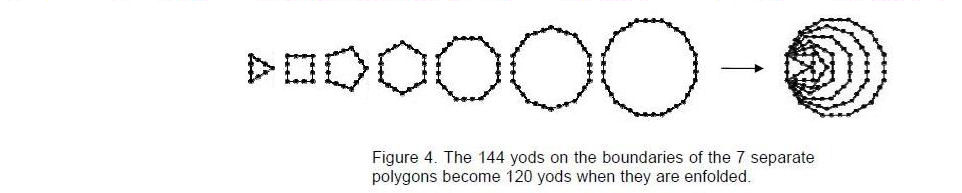
The outer and inner forms of the Tree of Life are analogous, respectively, to the human cell and its nucleus containing the DNA that encodes its replication. They both embody ‘bits’ of information of various kinds in the form of the different types of yods in the tetractyses from which they can be constructed. The
yods on the boundaries of the seven separate polygons become
yods on the boundaries of the seven enfolded polygons, i.e., 24 (=1×2×3×4) such yods disappear in the enfolding (Fig. 4). The seven centres of the separate polygons and the 144 internal yods that surround them become 144 yods inside the boundaries of the enfolded polygons, that is, seven internal yods disappear in the enfolding. (24+7=31) yods disappear in the enfolding of the seven polygons. 31 is the number value of EL (“God”), the
Godname of Chesed (Table 1), showing how it prescribes the properties of the inner Tree of Life. The 96 corners of both sets of separate polygons become the 70 corners of the 14 enfolded polygons, that is, 26 corners disappear in the enfolding. According to Table 1, 26 is the number value of YAHWEH, the Godname of Chokmah, which is the Sephirah above Chesed on the Pillar of Mercy. There are
288 = 11 + 22 + 33 + 44 = 1!×2!×3!×4!
=
3 5 7 9
11 13 15 17
19 21 23 25
27 29 31 33(33=1!+2!+3!+4!) yods inside the two sets of enfolded polygons.1 This illustrates how the properties of the inner Tree of Life are expressed in terms of the Pythagorean integers 1, 2, 3 & 4.
The number of yods in the seven enfolded polygons = 144 + 120 = 264. 260 yods are outside the root edge with four yods. This is the number of yods in 26 tetractyses. It is powerful evidence of how the creative archetype embodied in YAHWEH prescribes the yod population of the inner form of the Tree of Life (see the author’s Article 42 for how other Godnames of the Sephiroth prescribe the inner Tree of Life). The 120 boundary yods comprise 36 corners, where 36 is the number value of ELOHA, the Godname of
4
Table 2. Properties of the Archimedean & Catalan solids.
5
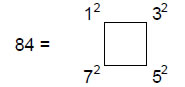
Geburah, and 84 hexagonal yods, where
36 is the sum of the first four even integers and the first four odd integers, again illustrating how the Tetrad Principle formulated in Article 13 defines properties of the Tree of Life.
We will now ascertain what these 264 yods signify by investigating a class of polyhedra called the Archimedean solids. There are 13 of these solids1. Two — the snub cube and the snub dodecahedron — exist in two chiral forms, so that, if their enantiomorphs are included, there are 15 Archimedean
solids. This how the Divine Name YAH with number value 15 (see Table 1) prescribes the number of such solids. Their duals, generated by interchanging vertices and faces, are called the Catalan solids. The 26 basic Archimedean & Catalan solids are prescribed by YAHWEH with number value 26. Table 2 lists the numbers of vertices, edges & faces in these solids. It indicates that the last Archimedean solid (truncated icosidodecahedron) has 120 vertices.
_______________________________
1 An Archimedean solid is a convex polyhedron having at least two different regular polygons as faces.
6
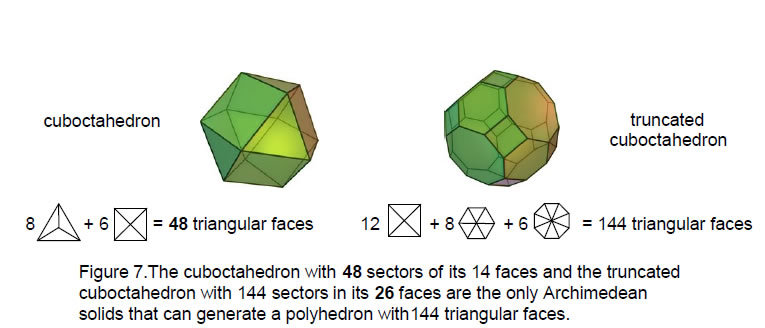
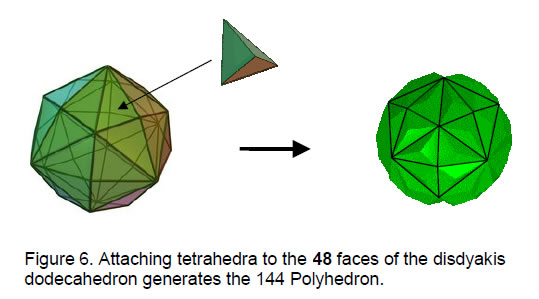
However, none of the 30 solids has 144 vertices. Moreover, if we placed pyramids on their faces, creating a new vertex for each face , none could create a polyhedron with 144 vertices because inspection of Table 2 reveals there is no Archimedean or Catalan solid with C + F = 144. This means that the yods cannot symbolise vertices. Can they symbolise faces? The only member of the family of Archimedean & Catalan solids with 120 faces is the disdyakis triacontahedron. There is no Archimedean or Catalan solid with 144 faces. However, there is one, and only one, polyhedron with F triangular faces, where 3F = 144, i.e., F = 48, namely, the disdyakis dodecahedron with 26 vertices and 72 edges. If a tetrahedron is stuck on each of its faces, a polyhedron is created that has (48+26=74) vertices, (72 + 3×48 = 216) edges and 144 faces (Fig. 6). In the case of Archimedean solids with some non-triangular faces, there are only two other possible candidates possessing 144 triangular faces when pyramids are attached to them with bases that match the shapes of their faces: the truncated cuboctahedron and the cuboctahedron (Table 3). There are 144 sectors in the 26 faces of the former that become triangular faces when pyramids are attached to them (Fig. 7). The latter has 48 sectors which become 144 faces when square pyramids and tetrahedra are attached
Table 3. Numbers of sectors in faces of the Archimedean solids.
cuboctahedron 8 triangles + 6 squares 8×3 + 6×4 = 48 icosidodecahedron 20 triangles + 12 pentagons 20×3 + 12×5 = 120 truncated tetrahedron 4 triangles + 4 hexagons 4×3 + 4×6 = 36 truncated cube 8 triangles + 6 octagons 8×3 +6×8 = 72 truncated octahedron 6 squares + 8 hexagons 6×4 + 8×6 = 72 truncated dodecahedron 20 triangles +12 decagons 20×3 + 12×10 = 180 truncated icosahedron 12 pentagons + 20 hexagons 12×5 + 20×6 =180 rhombicuboctahedron 8 triangles + 18 squares 8×3 + 18×4 = 96 truncated cuboctahedron 12 squares + 8 hexagons + 6
octagons12×4 + 8×6 + 6×8 = 144 rhombicosidodecahedron 20 triangles + 30 squares +
12 pentagons20×3 + 30×4 + 12×5 = 240 truncated
icosidodecahedron30 squares + 20 hexagons +
12 decagons30×4 + 20×6 + 12×10 = 360 snub cube 32 triangles + 6 squares 32×3 + 6×4 = 120 snub dodecahedron 80 triangles + 12 pentagons 80×3 + 12×5 = 300 7
to them. So there are two Archimedean solids and one Catalan solid which can potentially create a polyhedron with 144 triangular faces (henceforth to be referred to as the ‘144 Polyhedron’). The latter provides the simplest transformation, but one needs stronger reasons than that to regard it as the correct basis for the 144 Polyhedron. The 144 yods inside the boundaries of the seven enfolded polygons signify its faces, but their distribution provides no obvious way of differentiating between the three candidates. In order to regard the disdyakis triacontahedron as the 26th one prescribed by YAHWEH with number value 26, counting has to start with the truncated tetrahedron, the simplest Archimedean solid, whether we count down the list of each family or proceed by taking in turn each pair of solids that are dual to each other. Including the five Platonic solids makes the disdyakis triacontahedron the 31st one prescribed by EL with number value 31, whilst it is the 15th in the complete family of Catalan solids (chiral partners included) and the 26th in the family of Archimedean & Catalan solid, when chiral partners are excluded. Including the Platonic solids makes the disdyakis dodecahedron the 21st one, counting pairs of dual polyhedra at a time and the 21st one within the set of 26 Archimedean & Catalan solids, when the former are first counted. In the latter case, it becomes the 26th one when one starts counting with the Platonic solids. It is highly significant that the disdyakis dodecahedron and the disdyakis triacontahedron are picked out by three Godnames. It means that the 144 Polyhedron must be seen as generated from the disdyakis dodecahedron, not from either the cuboctahedron or the truncated cuboctahedron, even though this is geometrically possible. Its properties will now be examined.
2. The 144 Polyhedron
Formed from the disdyakis dodecahedron with 26 vertices, 72 edges & 48 faces by attaching tetrahedra to its faces, it has (26+48=74) vertices, (72 + 3×48 = 216) edges and (3×48=144) triangular faces. 72 is the number value of Chesed and 216 is the number value of Geburah, the next Sephirah after Chesed. Euler’s formula relates the C vertices, E edges & F faces of a convex polyhedron:C – E + F = 2.
As expected, the 144 Polyhedron obeys this equation because
74 – 216 + 144 = 2.
Starting with the triakis tetrahedron, the simplest Catalan solid, and counting pairs of dual polyhedra downwards in a zigzag fashion in Table 2, the disdyakis dodecahedron is the 15th, so that it is prescribed by YAH, the older Godname assigned to Chokmah with number value 15. It has (74+216+144=434) vertices, edges & triangular faces, that is, 432 geometrical elements surround its axis; these comprise 216 elements and their 216 mirror images (or, alternativel, 216 edges and 216 vertices & triangles). Surrounding the axis of the 144 Polyhedron are (216+144=360=36×10) edges & triangles, where 36 is the number value of ELOHA, the Godname of Geburah. 72 vertices and (72+144=216) vertices & triangles surround its axis, where 72 is the number value of Chesed and 216 is the number value of Geburah opposite Chesed in the Tree of Life. 288 vertices & edges surround the axis, where
288 = 11 + 22 + 33 + 44.
This shows the beautiful way in which the integers 1, 2, 3 & 4 symbolised by the four rows of the Pythagorean tetractys express properties of holistic systems.
A polyhedron with triangular faces constructed from tetractyses has (C+2E+F) yods in its faces. The 144 Polyhedron has 650 (=65×10) such yods, where
8
We see that ADONAI, the Godname of Malkuth with number value 65, appropriately prescribes the outer form of one of the two polyhedra that are the counterparts of the inner Tree of Life. The number of yods needed to create its 144 faces is the sum of the Godnames of the first four Sephiroth. It is
also the sum of the squares of the first 12 squares arranged along the edges of a square, a symbol of the Tetrad. The Decad defines the number 650 because 650 = 10×sum of first 10 integers after 1. The polyhedron has (650–74=576) yods in its faces other than vertices, where 576 = 12×22×32×42, showing again how the integers 1, 2, 3 & 4 express its properties.
There are 74 edges of 216 triangles created inside the polyhedron when all its vertices are joined to its centre. The geometrical composition of its exterior and interior is:
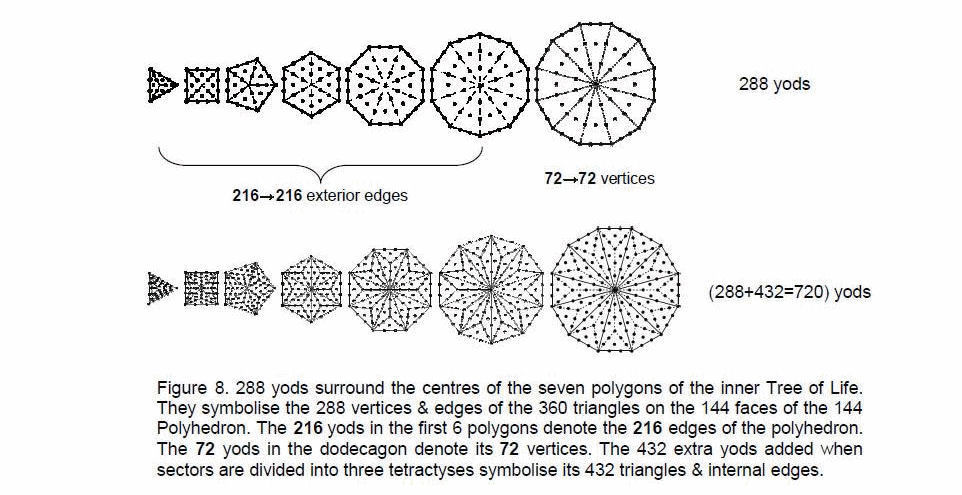
Exterior: Interior: Total = 288 edges and 288 internal edges & triangles surround its axis, which comprises three vertices and two edges, i.e., five geometrical elements. (725–5=720) geometrical elements surround the axis made up of (72+216=288) vertices & edges of faces and 432 triangles & internal edges. Compare this with the fact that 288 yods surround the centres of the seven separate polygons of the inner Tree of Life when each of their 48
9
sectors is a tetractys and 720 yods surround their centres when each sector is divided into three tetractyses, i.e., 432 yods are added (Fig. 8). The seven centres are the counterparts of the axis of the 144 Polyhedron. The 720 geometrical elements surrounding the axis have the composition:
Exterior: Interior: Total = The 72 vertices comprise the 48 peaks of the tetrahedra stuck on the faces of the disdyakis dodecahedron and the 24 of its 26 vertices that surround an axis passing through two of them. Their counterpart in the seven polygons are the 72 yods surrounding the centre of the dodecagon, which comprise 24 corners & centres of tetractyses and 48 hexagonal yods on their edges. The counterparts of the 216 edges of the 144 Polyhedron are the 216 yods
surrounding the centres of the first six polygons. They comprise 72 vertices & centres of their 36 tetractyses and 144 hexagonal yods on the 72 edges. They correspond to the 72 edges of the disdyakis dodecahedron and to the 144 edges added by attaching tetrahedra to its 48 faces. The 360 triangles consist of (48×3=144) external triangles and 216 internal ones. Their counterparts in the seven polygons with three tetractyses as each sector are the (48×3=144) hexagonal yods at centres of tetractyses and the 216 hexagonal yods on internal edges of tetractyses in the first six polygons. The 72 internal edges correspond to the 72 hexagonal yods on internal edges of tetractyses in the dodecagon.
Such detailed correlation is remarkable evidence that the polyhedron whose 144 faces correspond to the 144 yods inside the boundaries of the seven enfolded polygons embodies the archetypal pattern not of the inner Tree of Life but of its separate polygons before they become organised into the former. This is a vital point, because the disdyakis triacontahedron is the polyhedral counterpart of these polygons when they are enfolded in one another (Fig. 1). The enfoldment reduces the 295 yods of the seven separate polygons to 264 yods, i.e., the Godname EL with number value 31 prescribes the 31 yods that disappear. As four of these yods are located at Tiphareth, Chokmah,
10
Chesed & Netzach (or, rather, their projections onto the plane of the polygons), 260 (=26×10) yods are unshared. 260 yods are also outside the root edge. This is how YAHWEH with number value 26 prescribes the inner form of the
Tree of Life.
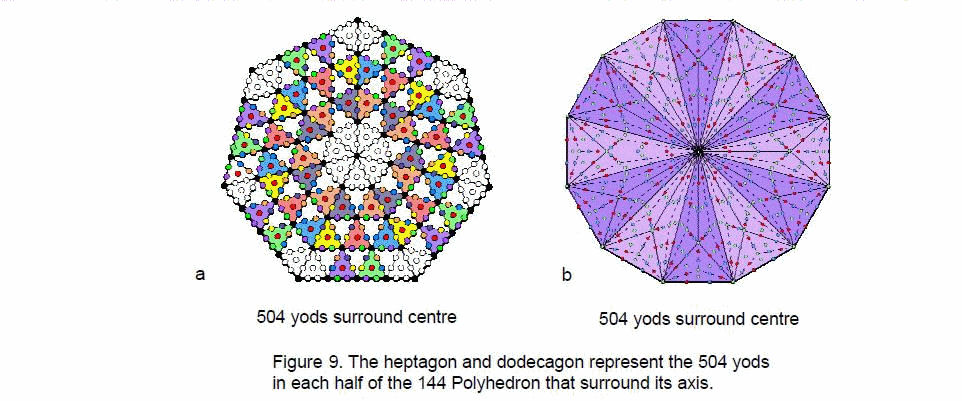
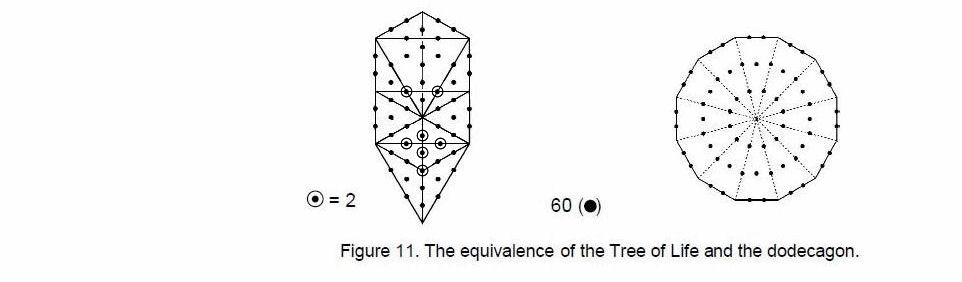
There are two hexagonal yods on each of the 74 internal edges of the 144 Polyhedron, one hexagonal yod at the centre of each internal triangle and one yod at the centre of the polyhedron. The number of internal yods = 74×2 + 216 + 1 = 365. There are 360 (=36×10) internal yods surrounding its axis. The Godname ELOHA prescribes both the 360 triangles that make up the polyhedron and the number of internal yods surrounding its axis. The total number of yods = 365 + 650 = 1015, i.e., 1008 yods surround the seven yods on its axis. Each half of the 144 Polyhedron contains 504 such yods. This is the number of yods surrounding the centre of a heptagon with 2nd-order tetractyses as sectors (Fig. 9a). It is also the number of yods surrounding the centre of a dodecagon whose sectors are constructed from nine tetractyses (Fig. 9b). The Decad determines the 720 vertices, edges & triangles surrounding the axis of the 144 Polyhedron because a decagon has 720 yods surrounding its centre when its sectors are 2nd-order tetractyses (Fig. 10). The Decad determines its yod population because the dodecagon is the tenth regular polygon. The two halves of the polyhedron are the polyhedral counterpart of the two dodecagons. The significance of this is that the dodecagon is itself equivalent to the outer Tree of Life. Both contain 60 hexagonal yods when their triangles or sectors are turned into tetractyses (Fig. 11). They symbolise the 60 vertices that surround the axis of the disdyakis triacontahedron — the minimal number of points distributed in space that create its form. As the polygonal Tree of Life, the dodecagon has the same number of yods surrounding its centre, when its sectors are each divided into three sectors and these sectors further divided into three tetractyses, as each half of the 144 Polyhedron has surrounding its axis. It demonstrates how
the polyhedron has a structure analogous to the pair of dodecagons in the inner Tree of Life. Indeed, so does the disdyakis triacontahedron, for the (60+60=120) hexagonal yods in a pair of dodecagons symbolise its (60+60) faces, one set of 60 faces being the mirror images of the other set.
11
12
These properties are powerful pieces of evidence supporting the claim made in Articles 22 that the disdyakis triacontahedron with 120 faces is the polyhedral manifestation of the exterior of the 2-dimensional, inner form of the Tree of Life, as indicated by the 120 yods on its boundaries. The 144 Polyhedron generated from the disdyakis dodecahedron is the polyhedral manifestation of its interior, the 144 internal yods of which are the counterpart of its 144 triangular faces.
3. Triangulation of the 144 Polyhedron
Instead of regarding the internal triangles and faces of the 144 Polyhedron as single triangles, let us divide them into their sectors and then turn each sector into a tetractys. In other words, we shall construct the polyhedron from triangles and then turn each one into a tetractys. The geometrical elements making up a polyhedron with C vertices, E edges and F triangular faces are:
Exterior: Interior: Total =
Using Euler’s polyhedral formula for a convex polyhedron:
C − E + F = 2,
the number (N) of geometrical elements can be written as:
N = 2C + 8E + 7F + 1 = 10E + 5F + 5 = 15E – 5C + 15 = 10C + 15F – 15.
Notice that the number value 15 of the Godname YAH is both a proportionality constant and an additive constant in the expression in terms of two geometrical elements.
Table 4 displays the numbers for the 144 Polyhedron with C = 74, E = 216 and F = 144:
Table 4. Geometrical composition of the 144 Polyhedron.
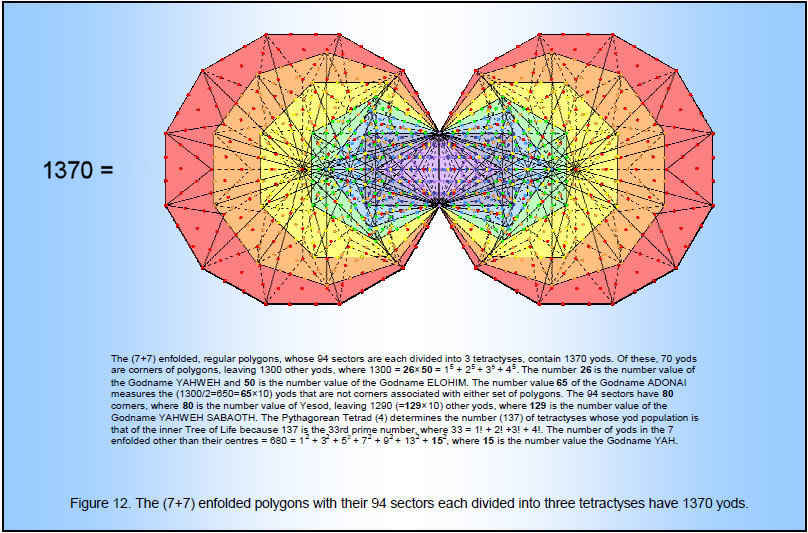
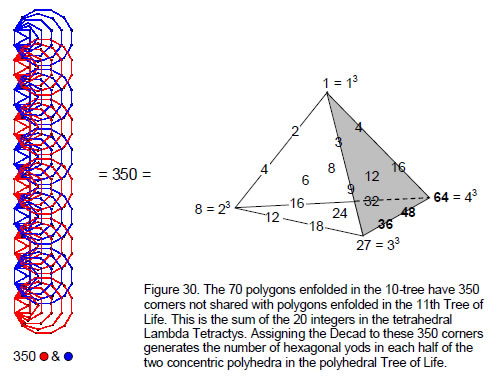
Exterior: Interior: Total = There are 216 vertices in the faces surrounding an axis and 216 internal vertices, where 216 (=63) is the number value of Geburah, the sixth Sephirah. There are also 216 triangles in the 72 faces of each half of the polyhedron. 72 is the number value of Chesed, the preceding Sephirah. 360 (=36×10) vertices are not vertices of the polyhedral, where 36 is the number value of ELOHA, the Godname of Geburah. 2880 geometrical elements surround the axis made up of five elements. It is expressed by the Tetrad because 2880 = (1+2+3+4)×(11+22+33+44). This is the number of yods surrounding the centres of the 10 sets of seven separate polygons associated with 10 overlapping Trees of Life, each a representation of a Sephirah. The 1080 tetractyses have 1370 edges. This is remarkable, because the (7+7) enfolded polygons with their 94 sectors divided into three tetractyses contain 1370 yods4 (Fig. 12). It demonstrates that the polyhedron possesses a Tree of Life structure. 1370 = (1+2+3+4)×137, where 137 is the 33rd prime number and 33 = 1! + 2! + 3! + 4!. This is how the polyhedron embodies the number 137. It is known to physicists as one of the most important numbers in Nature because its reciprocal is approximately equal to the fine structure constant e2/ħc ≈ 1/137. This sets the energy scale of atomic physics because it measures the strength of the coupling of the electron to the electromagnetic field.
1800 vertices & edges surround its axis, 900 in each half. 900 = 302 = (12+22+32+42)2.
13
The 900 vertices & edges comprise 360 internal edges and 540 vertices & external edges. This composition conforms to the 36:54 division displayed by the 10 numbers in the Lambda Tetractys5:
This is highly significant, as it shows the archetypal nature of the 144 Polyhedron paired with the disdyakis triacontahedron as, respectively, the ‘yang’ (male) and ‘yin’ (female) components of the polyhedral Tree of Life. There are 650 (=65×10) vertices & triangles in the faces, showing how ADONAI prescribes the form of the polyhedron.
Now suppose that each triangular sector is a tetractys. A polyhedron has the yod composition:
on edges
at centresExterior: C+F 2(E+3F)
3F
C+2E+10F
Interior: E+1 2(C+3E) 3E
2C+10E+1
Total = C+E+F+1 2C+8E+6F
3(E+F)
3C+12E+10F+1
Using Euler’s equation, the number (n) of yods can be written as:
n = 3C + 12E + 10F + 1 = 15E + 7F + 7 = 15C + 22F – 23 = 22E – 7C + 21.
Notice the presence of the number values of YAH (15) and EHYEH (21). The number of yods surrounding the axis, which has seven yods on it, is 15E + 7F. Table 5 lists the various yod populations for the 144 Polyhedron:
Table 5. Yod population of the 144 Polyhedron.
yods on edgesExterior: Interior: Total = There are 1370 hexagonal yods lying on the edges of the 540 tetractyses in each half of the polyhedron. There are also (218+1296–144=1370) yods on edges of tetractyses in its faces other than their centres. The number of yods on the boundaries of the 1008 tetractyses = 435 + 2740 = 3175. There are 3100 (=31×10×10) boundary yods except for the centre of the polyhedron and its 74 vertices. This is a remarkable demonstration of how EL, the Godname of Chesed with number value 31, prescribes the number of yods other than vertices needed to shape the 1370 edges of its tetractyses.
4. The polyhedral Tree of Life
The geometrical composition of the faces of the disdyakis triacontahedron and the 144 Polyhedron is:
C E F Total Disdyakis triacontahedron:
144 Polyhedron: Total = 14
The number of vertices = 136. This is the sum of a 4×4 array of the first 16 integers:
It demonstrates how the Tetrad Principle determines a parameter of both polyhedra. If one imagines the 144 Polyhedron inside the disdyakis triacontahedron and sharing the same centre, their internal and external triangles will have 137 vertices. They embody the fine-structure number 137. Including the four edges of internal triangles that define their axes, there are (796+4=800=80×10) geometrical elements (400 vertices & triangles, 400 edges) surrounding their centres. 80 is the number value of Yesod (“Foundation”), the penultimate Sephirah of the Tree of Life. It is the number of yods in the 1-tree — the lowest of any set of overlapping Trees of Life (Fig. 13). Assigning the Decad to each yod generates the number of geometrical elements in the faces and axes of the two polyhedra that surround their centres. It is more evidence of their Tree of Life nature.
The numbers of geometrical elements in the faces surrounding each axis are:
Disdyakis triacontahedron:
144 Polyhedron: Total = Notice that the numbers of vertices, edges & triangles bear the same proportion of 6/5:
72/60 = 216/180 = 144/120 = 6/5.
The integers 6 & 5 appear in the number value 65 of ADONAI, the Godname of Malkuth! Notice also that for each polyhedron (and therefore for both) the number of edges is three times the number of vertices surrounding the axis, whilst the number of triangles is twice the latter. Hence, if the numbers of
vertices that surround an axis in the disdyakis triacontahedron and 144 Polyhedron are written, respectively, as ‘X’ and ‘Y’, the seven possible combinations of geometrical elements are of magnitude nX and nY, where n =1, 2, 3, 4, 5, 6 and Y= 6X/5. If the integers 1, 2 & 3 are assigned to the corners of a triangle, not only do the latter denote the three types of geometrical elements in the two polyhedra but also all combinations of the integers generate the numbers of all combinations of these elements.
Including the interior geometrical elements, the numbers of elements surrounding each axis are:
15
Disdyakis triacontahedron exterior: interior: 0 60 180 360 Subtotal = 144 Polyhedron exterior: Subtotal = Total = Notice that, for either polyhedron, the total number of geometrical elements is 10X or 10Y, dividing as 6X:4X or 6Y:4Y, that is, as 3:2, for the relative proportion of external and internal elements. The ratio is the tone ratio of the perfect fifth in the Pythagor
ean musical scale — the note whose pitch is the arithmetic mean of those of the first and last notes.
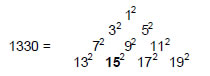
Including the 10 elements in the axes of the two polyhedra, there are 1330 geometrical elements (138 vertices, 532 edges & 660 triangles). There are 670 (=67×10) vertices & edges, showing how the number value 67 of Binah determines how many points and lines make up the two polyhedra. Below Binah in the 1-tree are 67 yods (Fig. 15). This property illustrates the meaning of Binah as the source of archetypes governing the form of holistic systems that embody the divine paradigm. The yod is the tenth letter of the Hebrew alphabet. The points of the tetractys should be called yods because they denote the number 10, not simply because the yod has the approximate appearance of a dot. Assigning the Decad to each yod below
Binah generates the number of vertices & lines needed to construct the disdyakis triacontahedron and the 144 Polyhedron. Amazingly, 67 is the 19th prime number, where 19 is the tenth odd integer and the number of yods in the triangle when its sectors are tetractyses (Fig. 16). Hence, the
16
simplest, geometrical figure determines numerically the geometrical composition of the polyhedral Tree of Life. 132 vertices surround the axes of both polyhedra, 66 in their separate halves. 66 is the 65th integer after 1, showing how the Godname ADONAI with number value 65 prescribes the pair of polyhedra. 134 vertices surround their centres, 67 in both halves. This shows again how the number value 67 of Binah determines the shapes of the two polyhedra. The number of yods below Binah in the 1-tree is the number of points in 3-dimensional space needed to construct half of each polyhedron, starting with another point. It is the minimal number because every vertex in these polyhedra has a mirror image, so that the other halves are their mirror images.
1330 is the sum of the squares of the first ten odd integers ending in 19:
The Decad therefore determines both the number 670 and the number 1330. This is a spectacular example of how the Decad defines properties of holistic systems (in this case, the polyhedral Tree of Life). ‘12’ denotes the centre of the 144 Polyhedron, the sum (530) of 132 and 192 at the two other corners of this tetractys array is the number of internal geometrical elements in both polyhedra surrounding their axes plus the two edges on the axis of the 144 Polyhedron:
132 + 192 = 530 = 240 + 288 + 2,
and the sum (799) of the seven other squares is the number of elements in their faces plus the centre and two edges on the axis of the disdyakis triacontahedron:
32 + 52 + 72 + 92 + 112 + 152 + 172 = 799 = 362 + 434 + 1 + 2.
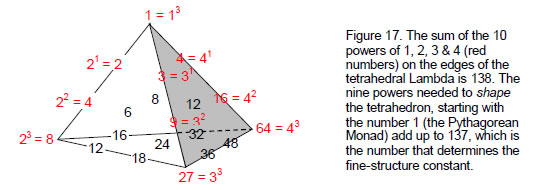
Additional evidence that the pair of polyhedra constitute an archetypal system is the fact that the sum of the ten powers of 1, 2, 3 & 4 on three edges of the tetrahedral Lambda Tetractys6 is 138 (Fig. 17):
This number is the sum of the least number of integers in the tetrahedral array of 20 integers that are needed to generate the complete set, for the 10 other integers are created by extrapolation of them, just as the Lambda Tetractys is the extrapolation of
17
the seven numbers lining Plato’s Lambda. The minimal character of the number 138 is illustrated in the 138 vertices in the 660 internal and external triangles making up the 144 Polyhedron and the disdyakis triacontahedron. The 1:137 differentiation between the integer 1 at the ‘peak’ of the tetrahedral ‘mountain’ and the integers on its slopes correspond to the centre of the 144 Polyhedron (the geometrical starting point of the generation of the polyhedral Tree of Life) and the 137 vertices that create it.
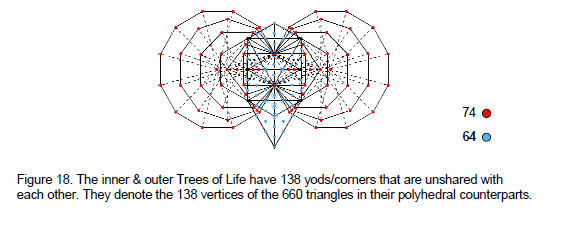
The (7+7) enfolded polygons of the inner Tree of Life have 94 sectors with 80 corners. Six of them coincide with the positions of the Sephiroth on the side pillars, leaving 74 corners (denoted by the red dots in Fig. 18) that are unshared. When the 16 triangles of the Tree of Life are turned into tetractyses, there are 70 yods, including the six shared yods. This leaves 64 unshared (blue) yods. The inner and outer Trees of Life have (74+64=138) yods or corners that are unshared with each other. These independent points are the Tree of Life basis for the 138 vertices in the two polyhedra.
5. Triangulation of the polyhedral Tree of Life
Tabulated below is the geometrical composition of the two polyhedra when their faces and internal triangles are divided into their sectors
Disdyakis triacontahedron exterior: interior: Subtotal = 144 Polyhedron exterior: interior: Subtotal =
432+3
1368+2
1080
2880+5Total =
792+6
2508+4
1980
5280+10(‘1’ denotes the centre and ‘2’ denotes either the top & bottom vertices or the two edges forming the axis).
Disdyakis triacontahedron
Surrounding the axis of the disdyakis triacontahedron are 360 (=36×10) corners of 90 triangles. This shows how the Godname ELOHA with number
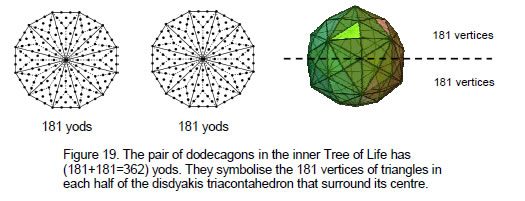
value 36 prescribes this polyhedron. Including the axis, it is made up of 363 vertices. 363 is the number value of SHADDAI EL CHAI, the complete Godname of Yesod. 181 vertices in each half of the disdyakis triacontahedron surround its centre. The counterpart of this in the inner Tree of Life is
18
the 181 yods in each dodecagon with its sectors divided into three tetractyses (Fig. 19). Their centres denote the top and bottom vertices, the 60 yods lying on the edges of the 12 sectors denote the centres of the 60 faces in each half of the polyhedron and the 120 other yods in each dodecagon denote the 30 polyhedral vertices and 90 vertices of the 270 triangles in each half. Such exact matching indicates that the disdyakis triacontahedron is the Malkuth (outer, physical) aspect of the polyhedral Tree of Life. That is why it is symbolised by the last of the enfolded polygons.
The 900 triangles in this polyhedron are divided into the 360 triangles in its faces and 540 internal triangles. This pattern is the polyhedral manifestation of the Lambda Tetractys whose 10 numbers add up to 90. The sum of the integers at its corners is 36 and the sum of the seven other integers is 54. We
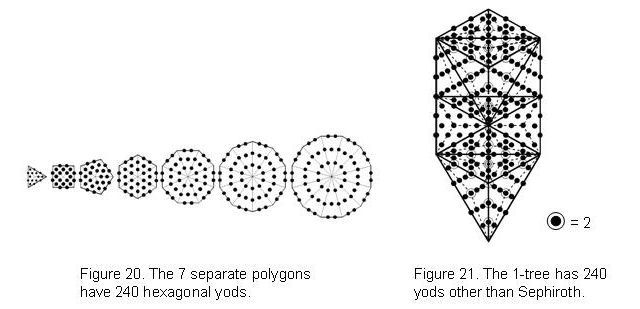
saw earlier that the 144 Polyhedron has 900 vertices & edges in each half that surround its centre that comprise 360 internal edges and 540 vertices & external edges. The archetypal pattern manifests in both polyhedra. 1500 (=15×10×10) vertices & edges surround the axis of the disdyakis triacontahedron. This shows how YAH with number value 15 prescribes it. 2400 vertices, edges & triangles surround its axis. The counterpart of this property in the inner Tree of Life is the 240 hexagonal yods in the seven separate polygons (Fig. 21). Its counterpart in the 1-tree is the 240 yods other than Sephiroth that its 19 triangles contain when their sectors are tetractyses (Fig. 20). Its significance in the context of superstring theory will be discussed in more detail in later articles. What is being encoded here is the 240 non-zero roots of E8, the largest exceptional Lie group that is part of the mathematics of superstring theory.
The number of vertices & triangles surrounding the axis is 1260. This is the number value of Tarshishim, the Order of Angels assigned to Netzach.
144 Polyhedron
We commented on its properties in Section 3. Here are some additional features. 216 vertices surround its axis in each half. 216 vertices are in its faces and 216 vertices are internal. 1296 vertices, edges & triangles surround its axis composed of three vertices and two edges. Hence, there are 1300 geometrical elements either on its faces or in its axis surrounding its centre, where1300 = 15 + 25 + 35 + 45.
19
This is a beautiful illustration of how the integers 1, 2, 3 & 4 express properties of holistic systems. 1300 = 26×50, where 26 is the number value of YAHWEH and 50 is the number value of ELOHIM, the Godnames of the Sephiroth at the top of the pillars of Mercy and Judgement. 650 (=65×10) such elements are in each half, showing how ADONAI with number value 65 prescribes the geometrical composition of each half of the 144 Polyhedron. As 650 = 262 – 26, it is the sum of the first 25 even integers up to 50. This means that the number 1300 is the sum of 50 even integers. This shows how ELOHIM prescribes the 144 Polyhedron.
144 Polyhedron & disdyakis triacontahedron
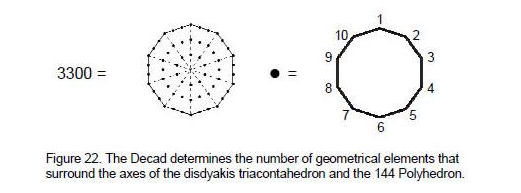
3300 vertices & edges (1500 external, 1800 internal) surround their axes. YAH with number value 15 prescribes both polyhedra because 1500 = 15×10×10. The number 33, which is the 16th odd integer after 1, where 16 = 42, is the sum of the number of permutations of 10 objects arranged in a tetractys: 33 = 1! + 2! + 3! + 4!. Hence:3300 = (1!+2!+3!+4!)(13+23+33+43).
This is another example of the expression of parameters of holistic systems by the integers 1, 2, 3 & 4. As 3300 = 60×55, where
55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10,
this number can be represented by assigning the tenth triangular number 55 to the 60 yods surrounding the centre of a decagon (Fig. 22). It
demonstrates how the Decad determines the geometrical composition of the polyhedral Tree of Life.
1650 vertices & edges in half of the two polyhedra surround their axes, where
and
165 = 12 + 32 + 52 + 72 + 92.
We see that the number 1650 is the sum of (10×5=50) squares of the first five odd integers. ELOHIM with number value 50 arithmetically prescribes the number of vertices & edges in half of the polyhedral Tree of Life. In fact, ELOHIM prescribes the
20
number of vertices & edges in both halves because 3300 = 10×330, where
330 = 62 + 72 + 82 + 92 + 102,
which means that 3300 is the sum of 50 squares.
The disdyakis triacontahedron with 120 faces has 1200 (=120×10) geometrical elements in each half surrounding its axis. The 144 Polyhedron has 1440 (=144×10) such geometrical elements. This reproduces the boundary and interior of the seven enfolded polygons with the Decad assigned to each of their 264 yods (see Fig. 5). This is an amazing property that demonstrates their Tree of Life character. We saw in Section 3 during the discussion of the triangulation of the 144 Polyhedron that the number of geometrical elements in a polyhedron with C vertices, E edges and F faces when its triangular faces and internal triangles are divided into their sectors is N = 10E + 5F + 5. There are (10E+5F) elements surrounding its axis, i.e., (5E+5F/2) elements in each half. The condition for this to be equal to 10F is E/F = 3/2. In other words, the ratio of the number of edges to the number of faces is the tone ratio of the perfect fifth. This property is found for the tetrahedron, octahedron, icosahedron and seven Catalan solids, but not for any Archimedean solids (see Table 2). The only Catalan solid that has this property and possesses 120 faces is the disdyakis dodecahedron. The Decad determines this number because
120 = 112 – 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19,
i.e., it is the sum of the first ten odd integers after 1. The Decad determines the number 144 because 144 = 122, where 12 is the number of corners of the dodecagon, the tenth regular polygon, i.e., 12 is the tenth integer that can be represented by a shape.
There are 5280 geometrical elements surrounding the axes of the disdyakis triacontahedron and the 144 Polyhedron. As 528 = 24×22 = 232 – 1 = sum of the first 22 odd integers after 1, 5280 =10×sum of the first 22 odd integers after 1. This relates the geometry of the polyhedral Tree of Life to the traditional Tree of Life with 10 Sephiroth and 22 Paths, to which the letters of the Hebrew alphabet are assigned in Kabbalah. In
21
terms of the integers, 1, 2, 3 & 4 symbolised by the four rows of the Pythagorean tetractys, 5280 = 10×24×22 = (1+2+3+4)(1×2×3×4)(14+23+32+41).
Including the 10 geometrical elements on their axes, the number of geometrical elements is 5290. This is 10×232. It is therefore determined by the 22nd integer after 1. Again, the number 22 is primary. As 288 = 172 – 1 = 3 + 5 + 7 + … + 33, 2880 is ten times the sum of the first 16 odd integers after 1. This is the number of geometrical elements surrounding the axis of the 144 Polyhedron. Therefore, the number of elements surrounding the axis of the disdyakis triacontahedron is the sum of the last six odd integers in:
5290 = 10×232 = 10[1 + (3 + 5 + 7 +…+ 33) + 35 + 37 + 39 + 41 + 43 + 45],
i.e.,
2880 = 30 + 50 + 70 + … + 330
and
2400 = 350 + 370 + 390 + 410 + 430 + 450.
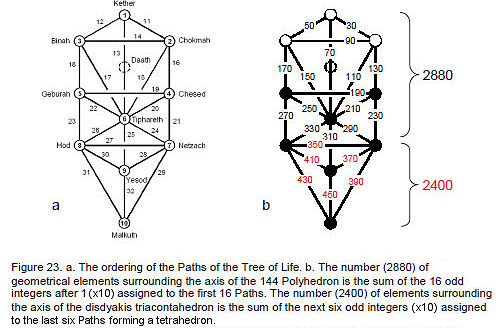
Assigning the integer 1 to each Sephirah and successive odd integer multiples of 10 to the Paths of the Tree of Life (Fig. 23), we find that the odd integers assigned to the first 16 Paths add up to 2880 and that the next six odd integers assigned to the last six Paths add up to 2400. The latter are the edges of a tetrahedron — the simplest Platonic solid and the starting point of solid geometry. The 16:6 differentiation of Paths corresponds to the difference between the geometrical compositions of the 144 Polyhedron and the disdyakis triacontahedron — or more accurately, their metaphysical meaning in representing the bipolar, divine, creative process (in Tantra, the union of Shiva and Shakti to create the phenomenal world). The former represent the polyhedral version of the upper part of the Tree of Life — its superphysical aspect — before the emergence in Malkuth of three-dimensional form. This division appears in string theory, which predicts the existence of 22 higher dimensions of space, it marks the division between the 16 dimensions whose compactification generates the superstring with a further six compactified dimensions. In view of this, it is not a coincidence that the number 2400 is the number of space-time components of the 240 10-dimensional gauge fields associated with the 240 non-zero roots of the superstring gauge symmetry group E8. The integer 1 assigned to each Sephirah denotes a geometrical element in the axes of the two polyhedra, with the following correspondences between elements and Sephirah:
Kether centre Chokmah apex Binah nadir Chesed upper edge on axis Geburah lower edge on axis Tiphareth centre Netzach apex Hod nadir Yesod upper edge on axis Malkuth lower edge on axis Tiphareth, the centre of the Tree of Life in both a geometrical and metaphysical sense, is the starting point of material creation embodied in the disdyakis triacontahedron. The distinction between the functions of the two polyhedra is that between the first five Sephirah and the last five Sephirah. We should not expect the 144 Polyhedron to
22
embody any number that relates to the structure of matter. That is the function of the disdyakis triacontahedron, as later articles will prove. Just as matter is the end product of superphysical causes, so the 144 Polyhedron and the disdyakis triacontahedron can be thought of as representing, respectively, Spirit and Matter.
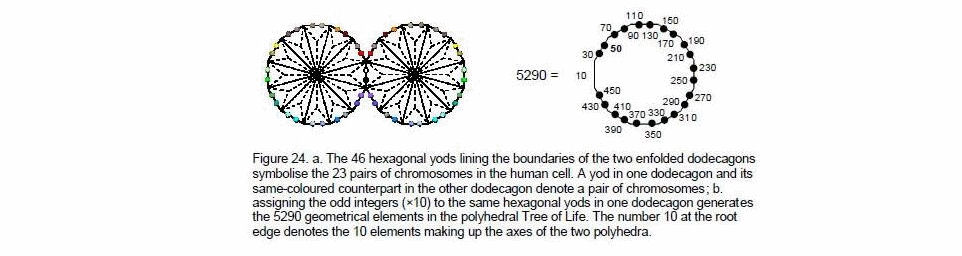
The fact that the number 23 determines the geometrical composition of the pair of polyhedra is highly significant, because it provides an analogy with the 23 pairs of chromosomes of the human cell. One pair is the X and Y sex chromosomes. The human cell displays the same 1:22 division as that which appears numerically in the polyhedra, whereby the geometrical composition of their axes is determined by the integer 1 and the composition of their shapes is determined by the next 22 odd integers! The X and Y chromosomes are analogous to the axes and the 22 other chromosomes, which determine the characteristics of the body, are analogous to the geometry of both polyhedra. This pattern appears in the pair of dodecagons of the inner
Exterior: Interior: Total =
Tree of Life (Fig. 24a). They have 22 corners and 23 edges. The X and Y chromosomes are symbolised by the pair of hexagonal yods in the root edge that generates the (7+7) polygons. A hexagonal yod in one dodecagon and its mirror image in the other one denote a pair of chromosomes (N.B. the two hexagonal yods on an edge do not denote a pair of chromosomes because there are 22 such pairs, not (11+11) pairs). Assigning the odd integers (×10) to these yods in one dodecagon generates as their sum the total number of geometrical elements in the 144 Polyhedron and the disdyakis triacontahedron. The human chromosomal pattern is analogous to the arithmetic behind the geometry of the polyhedral Tree of Life because humans are the terrestrial manifestation of the divine prototype called Adam Kadmon (“Heavenly Man”), whose geometrical representation is the Tree of Life.
6. Yod composition of the polyhedral Tree of Life
Consider, firstly, the case when triangular faces and internal triangles are tetractyses. The yod composition of a polyhedron with triangular faces is shown below:
23
Table 6 lists the yod population of the disdyakis triacontahedron and the 144 Polyhedron.
Table 6. Yod population of the polyhedral Tree of Life.
on edges
hexagonal yodsDisdyakis triacontahedron Exterior Interior Subtotal = 144 Polyhedron Exterior Interior Subtotal = Total = (‘1’ denotes the centre, ‘2’ denotes the top & bottom vertices & ‘4’ denotes the four hexagonal yods on the axis).
As we found during the analysis of its geometrical composition, the polyhedral Tree of Life has 660 tetractyses with 138 vertices. 480 hexagonal yods line the edges of the disdyakis triacontahedron, 240 in each half. They symbolise the 240 non-zero roots of E8×E8, the gauge symmetry group governing one of the five types of superstrings called the E8×E8 heterotic superstring. This property will be analysed in more detail in later articles. There are 840 yods surrounding the seven yods on its axis. They comprise 480 hexagonal yods on edges of tetractyses and 360 vertices or hexagonal yods at centres of faces. This pattern conforms to the Lambda Tetractys:
because the sum of the integers at the corners of the hexagon is 48 and the sum of the integers at the corners of the tetractys is 36. The number 840 is defined by the Tetrad because 840 = 10×84 = (1+2+3+4)×(12+32+52+72). It is the sum of the first 28 odd integers:
840 = 3 + 5 + 7 + … + 57.
where 28 is the second perfect number7 (the first perfect number is 6, the centre of the Lambda Tetractys). Together with the numbers 496 (the third perfect number and the dimension of E8×E8) and 168 (=6×28), 840 is a parameter of superstring physics, as has been discussed in previous articles.
780 hexagonal yods surround the axis of the disdyakis triacontahedron. 78 is the dimension of E6, the exceptional subgroup of E8 that physicists have investigated as a potential candidate for accommodating the current Standard Model of particle physics in superstring theory. The significance of the number 780 will become apparent when we analyse the triangulated polyhedral Tree of Life with all sectors regarded as tetractyses.
The 144 faces of the 144 Polyhedron are composed of 650 (=65×10) yods, showing how ADONAI with number value 65 prescribes its form. 360 (=36×10) internal yods
24
(216 hexagonal yods at centres of tetractyses) surround its axis, where 36 is the number value of ELOHA, the Godname of Geburah, whose number value is 216. There are 1008 yods surrounding its axis, 504 yods in each half. As we saw earlier, this number is defined by the Decad because the dodecagon has 504 yods surrounding its centre when each sector is divided into three triangles, each of which is then divided into three tetractyses. The 144 Polyhedron has 576 hexagonal yods on edges surrounding its axis, where 576 = 12×22×32×42.
Surrounding the axes of both polyhedra are 132 vertices and 1056 hexagonal yods that line the edges of 660 tetractyses, i.e., (132+1056+14=1202) yods line all edges, including axes. 1200 such yods shaping the polyhedra surround their centres. As 120 is the sum of the first 10 odd integers after 1:
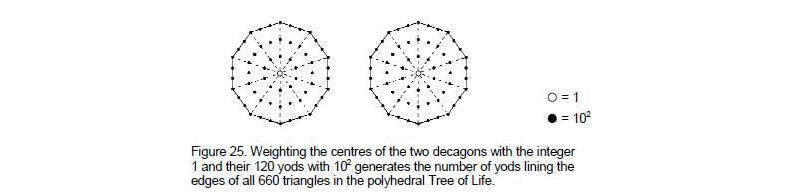
This demonstrates the beautiful way in which the Decad defines the form of the Polyhedral Tree of Life. It is demonstrated geometrically by the pair of decagons in the inner Tree of Life. With its sectors turned into tetractyses, each decagon has 60 yods surrounding its centre (Fig. 25). Assigning the
integer 1 to the two centres and 102 to each of the 120 yods in the pair of decagons generates the number 1202. Each decagon represents half of the two polyhedra and the two centres denote their centres.
1848 yods surround the 14 yods on the axes of the two polyhedra, i.e., (1848+12=1860)
Table 7. Yod populations of the polyhedral Tree of Life.
on edges
hexagonal yodsDisdyakis triacontahedron Exterior Interior Subtotal = 144 Polyhedron Exterior Interior Subtotal = Total = 25
yods surround their centres. A pentagon with its sectors turned into tetractyses has 31 yods, where 31 is the number value of EL, the Godname of Chesed. Assigning 31 to the 60 yods surrounding the centres of a pair of pentagons generates the number 1860.
Imagine the arms of a 10-pointed star as a straight line of 187 dots. The total number of dots = 1 + 10×186 = 1861. This is the number of yods in the two polyhedra when their centres coincide. 187 is the number value of Auphanim, the Order of Angels assigned to Chokmah.
Now let us consider the triangles in both polyhedra divided into their sectors and each sector then turned into a tetractys. Table 7 lists their yod populations. The disdyakis triacontahedron has 363 vertices. This is the number value of SHADDAI EL CHAI, the Godname of Yesod. Surrounding its axis are 2280 (=228×10) hexagonal yods that line edges of 900 tetractyses. 228 is the 227th integer after 1, where 227 is the 49th prime number and 49 is the number value of EL CHAI. (360+2280=2640) yods on edges of 900 tetractyses surround its axis. They are made up of 360(=36×10) vertices and 2280 (=228×10) hexagonal yods. Compare this with the 36 corners and 228 other yods in the seven enfolded polygons of the inner Tree of Life. This amazing correlation confirms the Tree of Life nature of the disdyakis triacontahedron. The 360 vertices comprise the 120 (=12×10) vertices in its faces, 60 (=6×10) polyhedral vertices & 180 (=18×10) internal vertices. This compared with the 12 corners of the dodecagon, the six corners of the first three polygons outside the root edge and the 18 corners of the next three polygons.
2740 hexagonal yods line the 1080 tetractyses of the 144 Polyhedron. 1370 hexagonal yods line the 540 tetractyses in each half. This demonstrates its Tree of Life nature, for we saw earlier that the 282 tetractyses making up the (7+7) enfolded polygons of the inner Tree of Life contain 1370 yods (see Fig. 12).
The 144 Polyhedron has 1946 yods in its 144 faces. 1946 = 36×54, where 36 is the sum of the integers at the corners of the Lambda Tetractys and 54 is the sum of its remaining integers.
The pair of polyhedra has 7788 yods surrounding their axes, i.e., (7788+12=7800) yods surround their centres. 7800 = 50×156, where 50 is the number value of ELOHIM and 156 is the 155th integer after 1, where 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth. This shows how these two Godnames
26
27
determine the number of yods needed to construct the two concentric polyhedra, starting with their shared centre. 156 is also the sum of all the different combinations of the letter value of YAHWEH.
YHVH = 26
Y = 10, H = 5, V = 6
7800 (=78×100) yods surround the centres of the two polyhedra. The number 78 is determined by the Tetrad because it is the sum of the first 12 integers that can line the edges of a square, four to each edge:
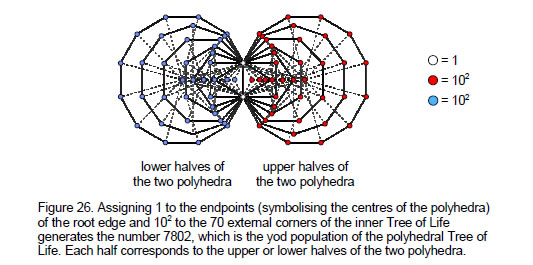
As a square contains 25 yods when its sectors are tetractyses, 100 is the sum of the Tetrad assigned to each yod:
The significance of the number 78 is that it is the number of corners of the 94 sectors of the (7+7) enfolded polygons outside their root edge. This means that if the number 1 is assigned to the endpoints (symbolising the centres of the two polyhedra) of the root edge and the square of the Decad is assigned to the 78 external corners of the 94 sectors of the 14 enfolded polygons, the sum of the 80 numbers is 7802 yods — the yod population of the two polyhedra (Fig. 26). The 3900 yods in each pair of halves that surround their centres correspond to the assignment of 102 to the 39 external yods in each half of the inner Tree of Life. Each set of seven enfolded polygons corresponds to the upper or lower halves of the two polyhedra.
As
780 = 39×20 = 1 + 2 + 3 + … + 39,
7800 = 10 + 20 + 30 + … + 390.Assigning the integer 1 to the endpoints of the root edge and the integers 10, 20, 30 etc to the 39 external corners of the seven enfolded polygons generates the number 7802 as their sum. It is a remarkable demonstration of the harmonious conjunction of number and sacred geometry in determining the properties of holistic systems. (39+2=41) integers make up this sum, where 41 is the 21st odd integer. This shows how EHYEH, the Godname of Kether with number value 21, prescribes the yod population of the polyhedral Tree of Life. ELOHA, the Godname of Geburah with number value 36, prescribes it because the seven enfolded polygons have 36 corners.
28
The number of yods in the n-tree when its triangles are tetractyses is Y(n) = 50n + 30.8 Successive Trees of Life have 50 yods, where 50 is the number value of ELOHIM, the Godname of Binah. The 15-tree has Y(15) = 780 yods. The number of triangles in the n-tree is T(n) = 12n + 7. The 15-tree has 187 triangles, where 187 is the number value of Auphanim, the Order of Angels assigned to Chokmah whose Godname is YAH with number value 15. The number of corners of triangles in the n-tree is S(n) = 6n + 5. The 15-tree has S(15) = 95 corners, where 95 is the number value of Madim, the Mundane Chakra of Geburah, and 282 corners & triangles, where 282 is the number value of Aralim, the Order of Angels assigned to Binah. If we imagine each yod in the 15-tree as the Decad, the sum of the integers is 7800. This is how YAH prescribes the yod population of the polyhedral Tree of Life.
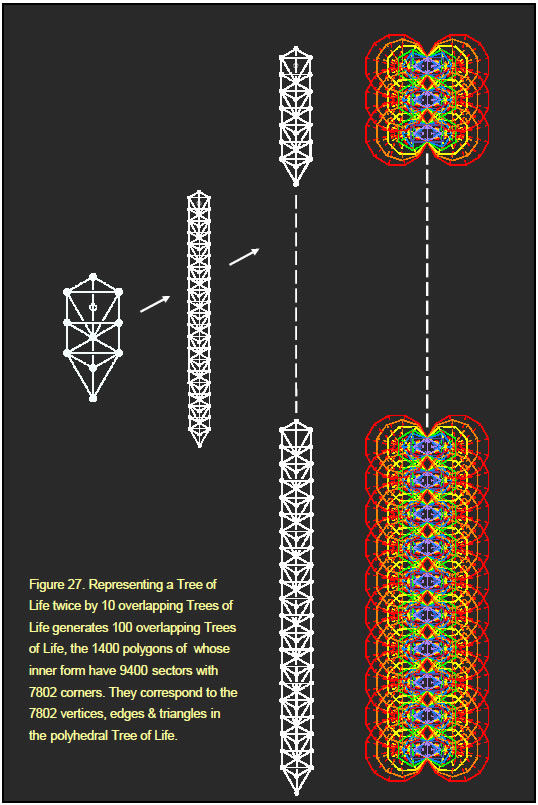
As the top corners of the two hexagons coincide with the bottom corners of the two hexagons enfolded in the next higher Tree of Life, there are 78 corners of the 94 sectors of the set of 14 polygons that are unshared. The number of corners of the 14n polygons enfolded in n overlapping Trees of Life is N(n) = 78n + 2. A Tree of Life can be represented by 10 overlapping Trees of Life because each Sephirah can be represented by a Tree of Life. This is the meaning of ADONAI, for its number value 65 is the number of Sephiroth in the lowest 10 Trees of Life. Each of the Trees of Life in the set of 10 can in turn be represented by 10 Trees of Life, so a single Tree of Life is equivalent to 10, 102, 103, etc Trees of Life. The inner form of (102=100) Trees of Life consists of 1400 polygons whose 9400 sectors have N(100) = 7802 corners (Fig. 27). Enfolded in the 50-tree are 700 polygons whose 4700 sectors have N(50) = 3902 corners, 3900 being intrinsic to them because none coincide with the corners of polygons enfolded in higher Trees of Life. This is the number of yods in one pair of halves of both polyhedra, excluding their centres. This is how the Godname ELOHIM with number value 50 prescribes the number of yods making up half of both polyhedra. As those in the other halves are merely their mirror images, this is how ELOHIM mathematically determines the structure of the polyhedral Tree of Life. The 700 polygons enfolded in the next 50 Trees of Life have 4700 sectors with 3902 corners. This is the number of yods in the other pair of halves, including their centres. The number ‘2’ in the above formula always refers to the two corners of the 14 polygons that are shared with those enfolded in the next higher Tree of Life, namely, the topmost corners of the pair of hexagons We see that the topmost pair of corners of the hexagons enfolded in the 100th Tree of Life correspond to the centres of the two polyhedra. The 50:50 division corresponds to the 5:5 division of the Sephiroth of the Tree of Life. In a fundamental sense, the halves that contain the centres are the first stage of creation of the polyhedral Tree of Life and correspond to the five Sephiroth of the Upper Face of the Tree of Life, whilst the remaining halves, which are their mirror reflections, correspond to the five Sephiroth of its Lower Face.
Table 6 indicates that the 120 faces of the disdyakis triacontahedron have 300 hexagonal yods in their centres and 480 hexagonal yods on edges surrounding its axis, that is, 780 hexagonal yods. The 940 sectors of the 140 polygons enfolded in the 10-tree have N(10) = 782 corners, 780 of them being intrinsic to them because they are not shared with polygons enfolded in the 11th Tree of Life. There are 780 corners of polygons enfolded in every 10 overlapping Trees of Life representing a Sephirah. We see that the exterior of the disdyakis triacontahedron embodies a Tree of Life pattern. Later articles will confirm that the polyhedron is the polyhedral version of 10 Trees of Life because its properties are analogous to their properties. The first (6+6) enfolded polygons constitute a Tree of Life pattern in themselves because they have 50 corners prescribed by ELOHIM and because the Godnames determine their other properties.9
29
They have 48 unshared corners. There are 30 corners that are either the 20 external corners of the two dodecagons or the 10 centres of polygons that are not also corners, The 120 polygons of the first six types enfolded in 10 Trees of Life have 480 corners intrinsic to them, leaving 300 corners that are either corners of dodecagons or centres. According to Table 6, they correspond to the 480 hexagonal yods on edges of tetractyses and to the 300 hexagonal yods at centres of tetractyses. This remarkable correlation between the inner form of 10 Trees of Life and the hexagonal yods in the disdyakis triacontahedron demonstrates its Tree of Life character. It is confirmed by the following: Table 7 indicates that 3540 (=354×10) yods surround the axis of this polyhedron. The integers 1, 2, 3 & 4 express 354 as
354 = 14 + 24 + 34 + 44.
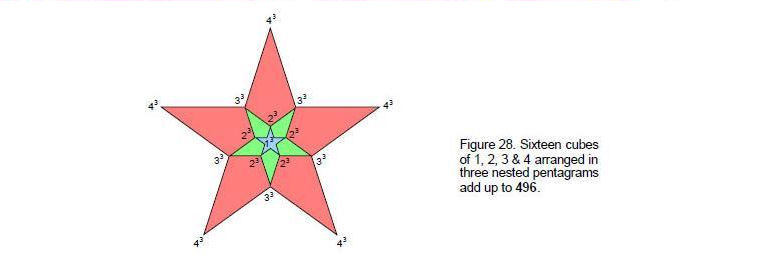
Hence, 3540 = (1+2+3+4)(14+24+34+44). This is a powerful sign of mathematical design underlying the disdyakis triacontahedron. Ten overlapping Trees of Life have 124 triangles with 64 corners and 166 edges, i.e., 354 corners, edges & triangles. The same number characterises the geometrical composition of 10 overlapping Trees of Life and the yod population of the disdyakis triacontahedron. It demonstrates that it is equivalent to 10 Trees of Life. The number of yods in the faces and at the centre of this polyhedron is 3541. This is the 496th prime number, where 496 (Fig. 28) is the number value of Malkuth and the dimension of the heterotic superstring gauge symmetry group E8×E8! Here is an astounding example of the mathematical
design of the outer form of the polyhedral Tree of Life. According to Table 6, the 360 tetractyses making up its 120 faces have 1622 yods. Starting at the apex of the disdyakis triacontahedron and counting yods, an extra 1621 yods are needed to construct its surface. 1621 is the 257th prime number, where 257 is the 55th prime number and 55 is the sum of the first 10 integers:
55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10.
This demonstrates how the Decad determines the shape of the outer form of the polyhedral Tree of Life.
The 264 faces of the two polyhedra each has 10 ten yods inside its edges. The number of yods that are needed to construct them without filling in the faces = 7802 – 264×10 = 5162. Starting from the centre of each, 5160 more such yods are needed, 2580 (=258×10) yods in either pair of halves. 256 is the 129th even number. This shows how
30
YAHWEH SABAOTH, the Godname of Netzach with number value 129, prescribes the two separate polyhedra.
Coaxial polyhedra
Suppose, finally, that the two polyhedra are concentric and share the same axis, so that their pairs of opposite vertices on the axis coincide. There are now 792 vertices surrounding the three vertices, that is, 794 vertices surrounding the shared centre. Of these, 134 are polyhedral vertices, 67 in each
pair of halves, where 67 is the number value of Binah. There are 5016 hexagonal yods on edges surrounding the four hexagonal yods on the axis, that is, 5020 hexagonal yods in total. Each pair of halves contain 2510 (=10×251) hexagonal yods. This is remarkable because there are 251 yods in the 1-tree when its 19 triangles are each divided into three tetractyses (Fig. 29).
31
If we imagine the 1-tree constructed with the Decad as building block, the resulting number that it represents is the number of hexagonal yods lying on edges of the 1980 tetractyses. There are 1980 hexagonal at the centres of tetractyses, 990 in each half. This is expressed by the Decad because 990 = 10×(102–1) = 103 – 10. The total number of hexagonal yods is 5020 + 1980 = 7000. Each pair of halves has 3500 (=10×350) hexagonal yods. The sum of the 20 integers in the tetrahedral Lambda Tetractys is 350 (Fig. 30), so this number is ten times this archetypal number. The sum of the 36 integers on the sides of the four separate tetractyses in the tetrahedral Lambda tetractys is 700, so that the number of hexagonal yods is ten times the sum of these integers:
The number of corners of the 7n polygons enfolded in the n-tree is C(n) = 35n + 1, where ‘1’ refers to the topmost corner of the hexagon in the nth Tree of Life, which coincides with the lowest corner of the hexagon enfolded in the (n+1)th Tree of Life. Hence, there are 35n corners that are intrinsic to polygons enfolded in the n-tree. The 70 polygons enfolded in the 10-tree have 350 intrinsic corners (Fig. 30). Assigning the Decad to these corners
generates the number of hexagonal yods in each pair of halves of the polyhedral Tree of Life.
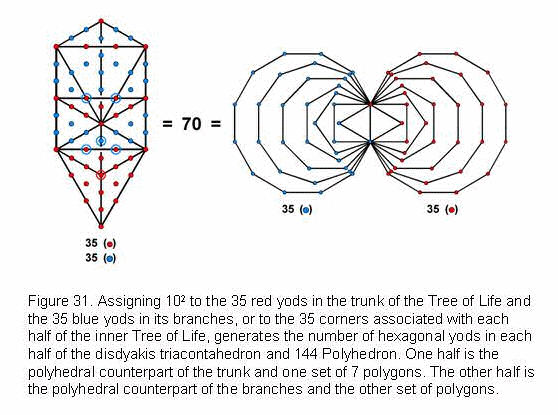
The ‘trunk’ of the outer Tree of Life is defined as the point (Kether), line (Path joining Chokmah and Binah), triangle (Chesed-Geburah-Tiphareth) and tetrahedron (Netzach-Hod-Yesod-Malkuth). It contains 35 yods, the ‘branches’ containing 35 yods as well (Fig. 31). The division of the outer Tree of Life into its trunk and branches corresponds to the two halves of the inner Tree of Life, each of which has 35 corners. This division manifests in the polyhedral Tree of Life as one half and its mirror image because assigning the square of the Decad to each yod or corner generates the number of hexagonal yods in each half. Such correlation is highly convincing evidence for the disdyakis triacontahedron and the 144 Polyhedron being the polyhedral Tree of Life.
32
Including the 794 vertices (397 in each half) that surround the centre of the two concentric polyhedra, there are (397+3500=3897) yods in each half surrounding the centre, that is, 7794 yods in total. Of these, 67 are vertices of the two polyhedra. Hence, there are (3897–67=3830) yods that are not their vertices. The polyhedral Tree of Life has (2×3830=7660) yods that are not polyhedral vertices, 3830 (=10×383) in each half. 383 is the 76th prime
number. YAHWEH ELOHIM, the Godname of Tiphareth with number value 76, prescribes the number of yods other than the 67 vertices that are needed to construct each half of the pair of concentric polyhedra from 990 tetractyses. This is an amazing property, further demonstrating how the Godname numbers define prime numbers characterising the polyhedral Tree of Life.
There are 7794 yods surrounding the centre of the coaxial pair of polyhedra. (7794– 6=7788) yods surround the axis. 7788 = 236×33. There are 236 yods on the boundary of the (7+7) enfolded polygons (Fig. 32). Assigning the number 33 to each yod generates the number of yods surrounding the axis of the polyhedral Tree of Life. Moreover, the root axis with four yods generates the number 132, which is the number of polyhedral vertices that
surround the axis shared by the two polyhedra. This reveals the importance of the number 33 (its importance in Freemasonry is well-know, but here is a more profound reason for why it is significant). In the Pythagorean context, it is the number of permutations of the 26 combinations that can be made when selecting 10 objects arranged in the four rows of a tetractys: 33 = 1! + 2! + 3! + 4!.
Referring to the geometrical composition of the two separate polyhedra detailed on page 18, they have 798 vertices, 2512 edges and 1980 triangles. When they share the same axis, centre and their opposite vertices coincide, they have (798–3=795) vertices
33
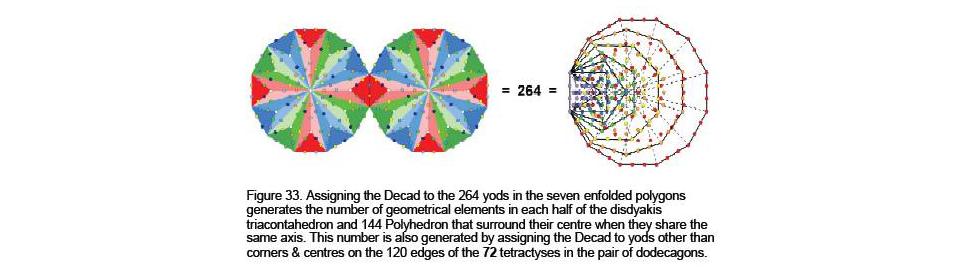
and (2512–2=2508) edges, that is, 3303 vertices & edges, 2775 vertices & triangles, 4492 edges & triangles and 5284 vertices, edges & triangles. 5280 geometrical elements surround their centre. Hence, each half of the polyhedral Tree of Life (which has 264 faces) has 2640 (=264×10) geometrical elements surrounding its centre. This number is generated by assigning the Decad to the 264 yods making up the seven enfolded polygons of the inner Tree of Life. It is remarkable proof of the Tree of Life nature of the concentric disdyakis triacontahedron and 144 Polyhedron (Fig. 33). Given two joined dodecagons divided into their 24 sectors, 264 more yods are needed to divide each sector into three tetractyses. This property illustrates how the last
polygon of the inner Tree of Life is its single polygonal counterpart. The 20 dodecagons enfolded in 10 overlapping Tree of Life need 2640 more yods to construct their sectors from three tetractyses, whilst there are 2640 yods in the 70 polygons enfolded in ten separate Trees of Life. Once again, here is proof that each half of the polyhedral Tree of Life is equivalent to 10 Trees of Life.
The coaxial polyhedral Tree of Life contains 7795 yods (see above). Of these, 1980 are hexagonal yods at centres of tetractyses. There are (7795–1980=5815) yods lining their edges. Hence, (5815–7=5808) yods line edges outside the axis, 2904 yods in each half. Including the axis, (2904+3=2907) yods in each half lie on edges. As 2907 = 19×153, this is the sum generated by assigning the number value 153 of ELOHIM SABAOTH, the Godname of Hod, to the 19 yods in a triangle divided into three tetractyses (Fig. 34). The shaping character of edges of tetractyses is reflected in the fact that Hod lies on the Pillar of Judgement. Alternatively, as 2907 = 9×17×19 = 9×(182–1) = 9(3 + 5 + 7 +… + 35), we that 2907 is the sum of (9×17=153) odd integers.
References
1 Proof: There are 120 yods on the boundary of the seven enfolded polygons, which contain 264 yods. The number of yods inside the boundary of both sets of polygons = 2×(264–120) = 2×144 = 288.2 Phillips, Stephen M. Article 4: “The Godnames Prescribe the Inner Tree of Life,” (WEB, PDF).
3 Phillips, Stephen M. Article1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 4.
4 Proof: the 7 enfolded polygons have 47 sectors with 41 corners and 88 sides. The number of yods on these sides when each sector is divided into 3 tetractyses = 41 + 88×2 = 217. There are 10 yods inside each sector. The number of yods in the (47×3=141) tetractyses = 217 + 47×10 = 687. Four yods lie on the edge shared by the polygons. The number of yods in the 7 enfolded polygons outside this edge = 687 – 4 = 683. The number of yods in the (7+7) enfolded polygons = 4 + 2×683 = 1370.
5 Phillips, Stephen M. Article 11: “Plato’s Lambda — its Meaning, Generalisation & Connection to the Tree of Life,” (WEB, PDF), p. 3.
6 Ibid, p. 8.
7 A perfect number is an integer that is the sum of its divisors.
8 Proof: the number of corners of the triangles in the n-tree is S(n) = 6n + 5. The number of edges is P(n) = 16n +9. The number of triangles is T(n) = 12n + 7. Two hexagonal yods are on each edge and one hexagonal yod is at the centre of each triangle when it becomes a tetractys. The number of yods in the
34
n-tree = S(n) + 2P(n) + T(n) = 50n + 30.
9 Ref. 2, p. 4.
35


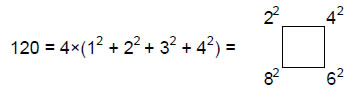
.jpg)