Home

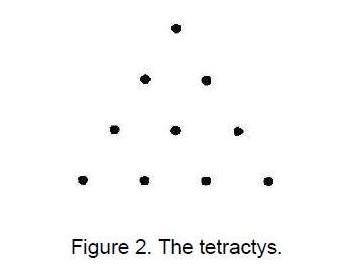
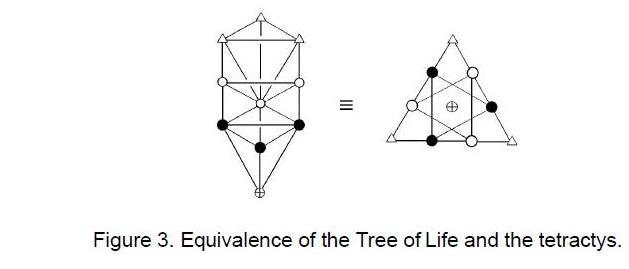
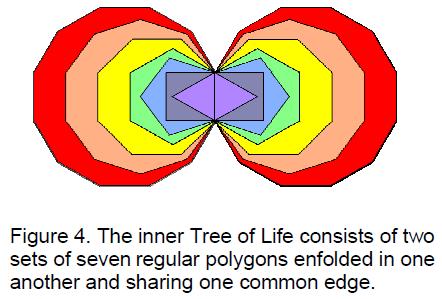
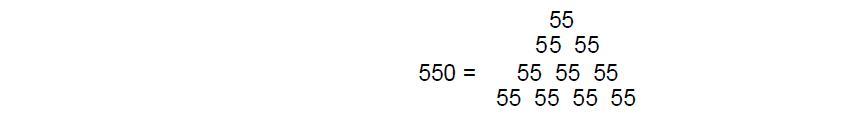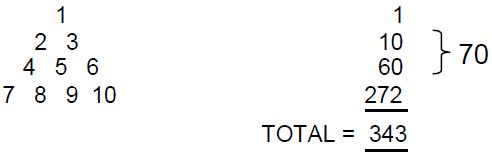ARTICLE 3

The Sacred Geometry of the Platonic Solids

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com

 

“Geometry is the knowledge of the eternally existent.”

                                                                                     Plato, Republic

 

1. Introduction

What is ‘sacred geometry’? Whether it refers to Stonehenge, the Egyptian pyramids, Gothic cathedrals or Tibetan mandalas, this notion is problematic in such contexts because whether one should regard the geometry of ancient monuments or religious artefacts as sacred depends upon one's own religious beliefs (or lack of them). Indeed, whether the word ‘sacred’ should be attributed to anything at all is contingent upon whether one has such beliefs. What is sacred to Christians or ancient Egyptians is usually not so to Jews or Hindus. However, true sacredness transcends cultural relativism and religious differences; it must exist in its own right instead of being merely an attribute projected onto some object by a particular religious frame of mind. Geometry that is sacred only in the eyes of the believer cannot be truly such. So what makes a geometrical design sacred? Indeed, does sacred geometry actually exist in this universal sense? Supposing that God exists (otherwise the word ‘sacred’ is meaningless and such geometry becomes mere religious doodles), sacred geometry would be that which embodies in a geometrical representation not just symbolic but quantitative aspects of cosmic reality (spiritual as well as physical) designed by the mind of God. It must be neither man-made symbolism, such as a cross or a six-pointed star, nor just a metaphor of universal order expressed in the doctrinal ideas of a particular religion or spiritual philosophy, which followers of another religion may not accept. Instead, sacred geometry must be a geometrical pattern or form depicting some quantitative aspect of the divine design of reality transcending all religious metaphors. It would be sacred because it encapsulates what actually exists — whether this is known or unknown — and not merely what fallible human beings speculate about in their mythologies and theologies and incorporate into the architecture of their churches. True sacred geometry does not embody human ideas about the nature of reality or God; it necessarily transcends them. But how then would we discern the divine design of reality, which this sacred geometry is supposed to express? Indeed, how would we recognise its sacredness? For those mathematicians or theoretical physicists who are Platonists, one of the signatures of mathematical truth is its beauty. However, sacred geometry has to possess more than just beautiful properties that no human mind could have artfully fabricated. Beauty may be a necessary attribute but it is not sufficient. Although what is sacred truth must be beautiful, what is beautiful may not even be true, let alone of divine origin. Sacred geometry must have such extraordinary properties (and so many of them as to discount the possibility of their being due to chance) that they can only indicate the existence of transcendental intelligence as well as artistry behind the sacred object. There must be no rational, conventional explanation for its possession of so many mathematically miraculous properties. Given this stringent requirement, how many examples of sacred geometry discussed in so-called ‘New Age’ books would meet such a criterion?!

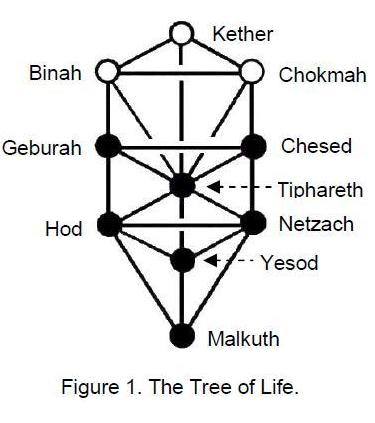
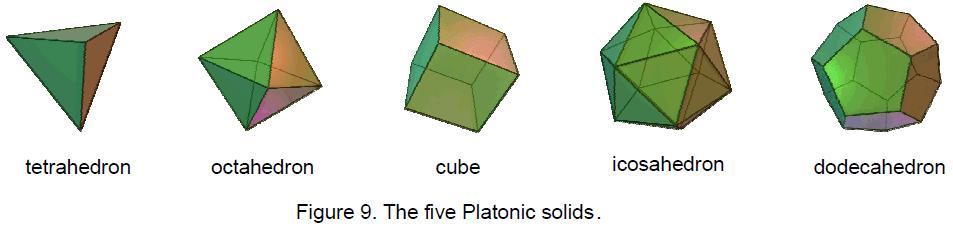
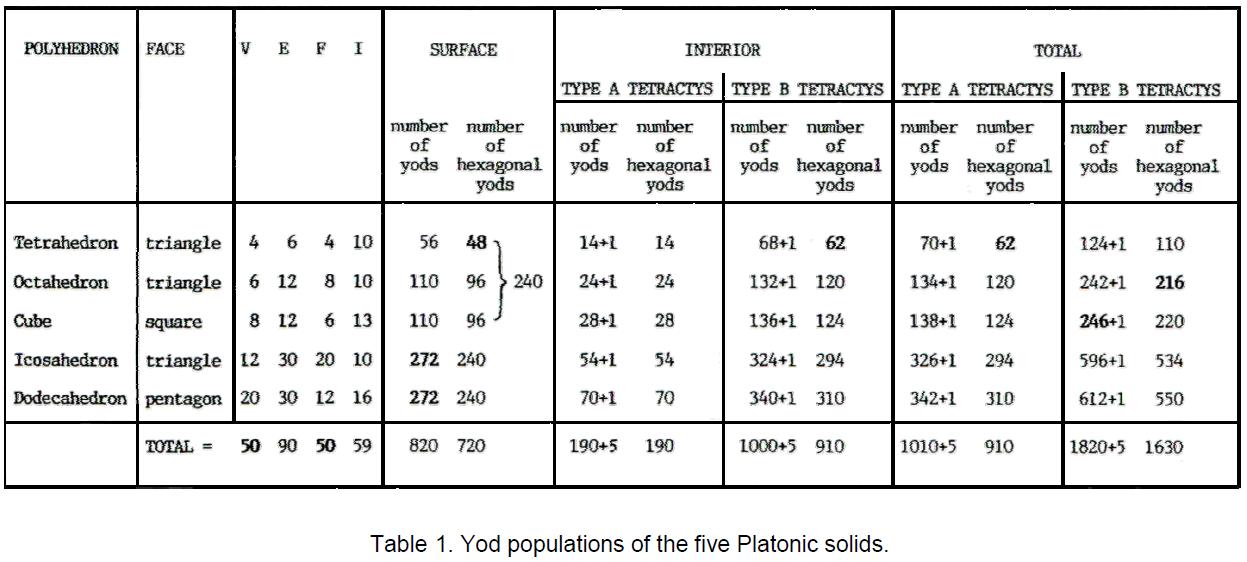
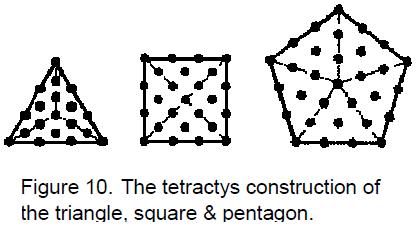
This article will prove that the five Platonic solids (called in mathematics the five ‘regular polyhedra’ because they are the only 3-dimensional shapes with equal sides) have far deeper significance than what hitherto has been known to mathematicians. It will show that their geometry is sacred in the above sense — that is, to say, not because God constructed the world out of these forms (as the ancient Greeks believed) but because they collectively embody the Divine blueprint underlying all levels of existence, including the physical universe.

1

2. The Tree of Life

The Tree of Life (Fig. 1) has claim to be sacred geometry par excellence because, according to the Jewish mystical tradition called ‘Kabbalah,’ it is God’s blueprint for Creation. It portrays the ten divine qualities, or Sephiroth (sing: Sephirah), as spheres arranged on three Pillars and connected by 22 Paths. The uppermost Supernal Triad of Kether, Chokmah and Binah signify the triple Godhead outside Creation. The seven Sephiroth of Construction, Chesed, Geburah, Netzach, Hod, Yesod and Malkuth, represent aspects of God’s immanence in Creation. The ‘Gulf’ or ‘Abyss’ of Daath separates them from the Supernal Triad, which is not a Sephirah. Malkuth, the lowest Sephirah of Construction, signifies the material manifestation of the Tree of Life, whether a subatomic particle, the human body or the whole universe. The Sephiroth manifest in four Worlds that are stages in the descent of the Divine Life into matter. They correspond to the traditional Christian divisions: Spirit, soul, psyche and body. The Godname of a Sephirah is its essence or expression in the highest World of Atziluth (the Archetypal World). Through their many elaborations by the human mind, it is mostly the Godnames that became anthropomorphized into the gods and goddesses of ancient mythologies. (Judaism and Christianity focussed on YAHWEH, the Godname of Chokmah, although other Godnames appear in the Old Testament).

In the ancient practice of gematria, numbers are assigned to the 22 letters of the Hebrew alphabet so that hidden meanings in the texts of scriptures may be extracted from phrases and sentences. Hebrew words acquire number values that are the sum of their letter numbers. Table 1 shows the number values of the Godnames of the ten Sephiroth:

Table 1

SEPHIRAH GODNAME NUMBER VALUE
Kether EHYEH 21
Chokmah YAH, YAHWEH 15, 26
Binah ELOHIM 50
Chesed EL 31
Geburah ELOHA 36
Tiphareth YAHWEH ELOHIM 26 + 50 = 76
Netzach YAHWEH SABAOTH 26 + 103 = 129
Hod ELOHIM SABAOTH 50 + 103 = 153
Yesod EL CHAI 49
Malkuth ADONAI 65

(All Godname numbers appearing in the text are written in boldface type)

In keeping with their primary nature, the Godnames prescribe — geometrically as well as arithmetically — the Tree of Life topography of all possible levels of reality, including the 4-dimensional space-time domain of physical (brain) consciousness. Godname numbers also define the dynamics and structure of the basic building blocks of matter, which is what some particle physicists call a ‘superstring’ (see Article 2). The reason for this is that the superstring is the microscopic manifestation of the Tree of Life blueprint, whose geometry is defined by Godname numbers. The Godname numbers associated with the Sephiroth are potent ‘master numbers’ quantifying the Tree of Life nature of reality, this prescription becoming ever more concrete, further down the Tree its associated Sephirah is located.

The presence of all ten Godname numbers defining properties of a geometrical pattern or set of geometrical objects such as the Platonic solids is a necessary condition for it to constitute ‘sacred geometry.’ If this criterion is upheld for a pattern or object, it will embody one or more numbers of universal significance and therefore of scientific importance because they pertain to systems that are holistic, even though science does not recognise them as such. In the case of the 3-dimensional Tree of Life, it can be shown that its projection on a plane is minimally generated from 21 points arranged in rows of 1, 2, 3, 4, 5 & 6 points, where 21 is the number value of EHYEH, the Godname of Kether. The Tree of Life consists of 10 corners of 16 triangles assembled by the joining in pairs of 34 of their 48 sides to create 22 sides or ‘Paths,’ of which 12 are the edges of two tetrahedra. 26 sides disappear in their joining, and this is the number value of YAHWEH, whilst 50 (the number of corners, edges, triangles and tetrahedra comprising the Tree, i.e., its geometrical elements) is the number value of ELOHIM, the Godname of Binah expressing the most abstract archetypes about divine form. How the remaining Godnames prescribe the geometry of the Tree requires consideration of the tetractys, which is discussed next.

2

3. The tetractys

At the heart of the Pythagorean philosophy based upon the power of numbers was the tetractys, a triangular array of ten dots, or ’yods’ (1), arranged in four rows (Fig. 2). With no insight into what Pythagoras taught other than what is provided by the few remnants of his teachings distorted by later generations of commentators, scholars of ancient Greek mathematics assume that the tetractys represents the numbers 1, 2, 3 & 4 summing to 10, which, as their sacred Decad, the Pythagoreans regarded as the perfect number. But it meant to
 

them far more than this. According to H.P. Blavatsky: “The ten Points inscribed within that ‘Pythagorean triangle’ are worth all the theogonies and angelologies ever emanated from the theological brain” (2). Partly the reason for this is that the tetractys signifies the same as the Tree of Life, namely, the ten-fold nature of God. (Fig. 3 shows this equivalence in detail). But — more important for the present discussion — the main reason for the Pythagorean reverence for the tetractys is that numbers expressing information about the nature of reality (space-time and beyond) manifest in objects possessing sacred geometry when they are re-assembled from tetractyses. In other words, the tetractys is the key that unlocks information about reality encoded in sacred geometry. This is the real reason why the followers of Pythagoras esteemed the symbol at the heart of their master’s teachings, swearing by the oath:

I swear by the discoverer of the Tetractys,
Which is the spring of all our wisdom,
The perennial fount and root of Nature (3).

The numbers generated by triangulating objects with sacred geometry and transforming the resulting triangles into tetractyses are of three types:

  1. number of yods belonging to tetractyses;
  2. number of yods at corners of tetractyses. As Figure 3 indicates, these symbolise the Supernal Triad of Kether, Chokmah and Binah;
  3. number of yods arranged at the corners and centre of a hexagon within each tetractys. Symbolising the seven Sephiroth of Construction, these will be called ‘hexagonal yods’).

The yod populations of sacred geometrical objects can also be divided into two other classes: the numbers of yods on their boundaries that delineate their shape and the numbers of yods inside them.

4. The inner form of the Tree of Life

As pointed out in Article 1, the outer Tree of Life has an inner form made up of two identical sets of seven enfolded, regular polygons (triangle, square, pentagon, hexagon, octagon, decagon and dodecagon), which share what I call the ‘root edge’ (Fig. 4). This extends between

Daath and Tiphareth, the centre of the Tree of Life in both a physical and a metaphysical sense. Remarkably, these 14 enfolded, regular polygons have 70 corners — the same number as the number of yods in the outer form of the Tree when assembled from tetractyses. This is not coincidental but the manifestation of a hidden regularity or pattern of order and design. Just as a DNA molecule encodes the development of a living organism from a single cell, so this inner Tree is found to encode in a geometrical way the self-replication of its outer form to map all possible levels or states of consciousness attainable by evolution. The complete map is called the ‘Cosmic Tree of Life’ (CTOL) (4). It consists of 91 overlapping Trees of Life, where

91 = 12 + 22 + 32 + 42 + 52 + 62.

 

3

They correspond to the 91 subplanes of the seven cosmic planes described in Theosophical literature (the cosmic physical plane comprises seven planes with 49 subplanes (49 is the number value of the Godname EL ChAI assigned to Yesod) and the six cosmic superphysical planes comprise 42 subplanes. Calling the Sephirah of each Tree a ‘Sephirothic Level’ (SL), CTOL is found to consist of 550 SLs, where

and

This is the first indication of the central role played by the Pythagorean tetractys in mathematically representing the properties of CTOL.

As these equations indicate, this map of all levels of being is a 3-dimensional, geometrical object the beauty of whose mathematical proportions reflects its divine design. As another example of its beautiful properties, this ‘Jacob’s Ladder’ consists of 3108 triangles and their corners and sides, where

3108 = 14 + 34 + 54 + 74.

There are many other examples. With their triangles turned into tetractyses, the lowest 49 Trees of CTOL mapping the cosmic physical plane have 2480 yods, which is the number of yods in 248 tetractyses. Compare this with the prediction made by superstring theory that the unified force between superstrings in ordinary matter is transmitted by 248 particles (so-called ‘gauge bosons’). Each is described by a mathematical function called a ‘gauge field’ having ten independent components because superstring theory predicts that space-time has ten dimensions (the components are measured along the directions of these dimensions). This demonstrates that the number characterising the kind of perfect, unbroken, mathematical symmetry of superstring forces described by the so-called ‘E8 group’ is encoded in the map of the cosmic physical plane, the ten yods of the equivalent 248 tetractyses denoting the ten components of each of the 248 gauge fields. Another 248 particles are predicted to mediate interactions between superstrings making up what theoretical physicists call ‘shadow matter.’ This is an as yet undetected, invisible kind of matter that may comprise some of the ‘dark matter’ believed by astronomers to make up about 90% of the mass of the universe. Its invisibility is due to the prediction that only the force of gravity acts between superstrings of ordinary matter and shadow matter. Most of these particles play no part in the physics of the cooled-down universe today because they are too massive to be created by the typical energies with which subatomic particles interact. The lighter particles of shadow matter are predicted to form a kind of parallel universe that co-exists with the one visible to human sight but which is ever beyond the ability of the five human senses to detect.

The superstring parameters 248 and (248+248=496) are also encoded in the inner form of the Tree of Life whose 49-fold replication maps the cosmic physical plane. (It is remarkable and no coincidence that 496 is the number value of Malkuth, the tenth Sephirah, signifying the physical universe). The seven separate, regular polygons of the inner Tree have 48 corners (Fig. 5). Together with the two endpoints of the root edge considered separately (which formally correspond to corners) they constitute 50 corners. This is how the Godname ELOHIM with number value 50 prescribes this pattern of sacred geometry. With their 48 triangular sectors turned into tetractyses, the seven polygons have 55 corners of tetractyses and 240 hexagonal yods, so that the two sets of polygons contain 480 hexagonal yods. But the numbers

240 and 480 are part of the group-theoretical description of the mathematical symmetry exhibited by the unified superstring force, for 240 is the number of non-zero roots of the gauge symmetry group E8 and 480 is the number of non-zero roots of the superstring symmetry group E8×E8! So we see that a parameter characterising the group-mathematics of the unified superstring force is encoded in the inner form of the Tree of Life. This is just one example among many to be discussed in later articles of how its sacred geometry incorporates the mathematical structure of superstring theory and embodies numbers of

4

significance to particle physics.

Inspection of the list of Godname numbers given above shows that 240 is the sum:

240 = 21 + 26 + 50 + 31 + 36 + 76

of the Godname numbers of the first six Sephiroth of the Tree of Life, which are located at the corners of a hexagon or, equivalently, a six-pointed star. The encoding of the number 240 in the inner form of the Tree of Life has its counterpart in the 49 trees representing the cosmic physical plane. As we have seen, they contain 2480 yods. The lowest tree in CTOL contains 80 yods. There are therefore 2400 yods above the lowest tree in this section of CTOL, i.e., the yods in 240 tetractyses. The 248 roots of E8 consist of eight zero roots and 240 non-zero roots. This is paralleled in, respectively, the eight and 240 tetractyses whose yod populations are the number of yods in the lowest tree and the 48 trees above it mapping the cosmic physical plane.

It is also remarkable that there are 67 yods below Binah of the lowest tree and 73 yods up to Chokmah (Fig. 6), for the former is the number value of the Hebrew word ‘Binah’ and the latter is the number value of the Hebrew word ‘Chokmah.’ This obviously cannot be coincidence but demonstrates a profound connection between the names of the Sephiroth (as well as their Godnames) and numbers generated in the Tree of Life when its triangles are changed into tetractyses. Correspondence between the inner and outer forms of the tree is also demonstrated by:

  

  1. the seven separate regular polygons making up the former have 48 corners, whilst, according to Fig. 6, there are 48 red yods in the lowest tree of CTOL up to Chesed, the first Sephirah of Construction;
  2. both sets of seven enfolded regular polygons have 70 corners, whilst the Tree of Life contains 70 yods (Fig. 7):

     
                                        
  3. both sets of enfolded polygons have 80 corners of their 70 tetractys-converted sectors, whilst the lowest tree in CTOL contains 80 yods (Fig. 8).

These and other remarkable correspondences are not coincidental. Instead, they indicate design.

5. The Platonic solids

Plato propounded in his Timaeus the Pythagorean doctrine that particles of the four Elements Fire, Air, Earth and Water had the shapes of, respectively, the tetrahedron, octahedron, cube and icosahedron (Fig. 9). The Pythagoreans associated the fifth regular polyhedron, the dodecahedron, with the cosmic sphere,

5

6
 

which came later to be identified with the fifth Element, Aether. But the five regular polyhedra have a more profound significance than this — one that truly justifies their geometry being called ‘sacred.’ In order to uncover it, one must regard the tetractys as the universal template out of which all sacred geometry is built, whether it be the Tree of Life, the Sri Yantra or the Platonic solids. We found in the last section how, when CTOL was considered as assembled from tetractyses, a number of significance to superstring theory appeared in a region of CTOL having ‘physical meaning’ (the word ‘physical’ is used in its widest possible sense, pertaining not only to space-time, which Article 2 indicates is mapped by the lowest seven trees of CTOL, but to its cosmic counterpart — the lowest 49 trees). Finding such a scientific parameter of cosmic relevance is evidence of the sacred geometry of the Tree of Life. But it requires reconstructing the Tree of Life from tetractyses so as to make manifest the information encoded in its geometry. Likewise, to uncover information encoded in the five Platonic solids, we must imagine their faces constructed from tetractyses. A triangular face transforms into three tetractyses, a square face is made up of four tetractyses and a pentagonal face is composed of five tetractyses (Fig. 10). Notice that 5, 4 & 3 are the sizes of the well-known, right-angled triangle illustrating Pythagoras’ Theorem. Notice also that the centre of a solid and any two of its adjacent corners form a triangle in its interior. Each polyhedron is built also from such triangles in its interior. A Platonic solid will be called ‘Type A’ if its internal triangles are turned into single tetractyses and ‘Type B’ if they are divided into three tetractyses (internal triangles divided into three tetractyses will also be called ‘Type B’ in order to distinguish them from the internal triangles of Type A solids).

Table 1 displays the numbers of corners (C) edges (E) and faces (F) of the five Platonic solids and the yod populations of their faces and interiors. The former are related by Euler’s formula for a convex polyhedron:

C – E + F = 2.

Inspection of the Godname numbers listed earlier tells us that the most obvious sign that the Platonic solids constitute sacred geometry is that they have 50 corners and 50 faces, i.e., their shapes are collectively prescribed by the number value 50 of ELOHIM, the Godname of Binah, which is the third member of the Supernal Triad in which the possibility of form — the abstract notion of spatial relationship — first arises. Indeed, there are many examples (to be discussed in later articles) of how geometrical forms or patterns of numbers expressing parameters of superstring theory or the Tree of Life are always defined arithmetically by the ten Godname numbers. Below are listed examples of how Godname numbers define the geometrical composition and yod population of each solid, together with other properties illustrating their correspondence with the outer and inner forms of the Tree of Life:

TETRAHEDRON

21 yods other than polyhedral corners on sides of 6 internal tetractyses (Type A);
26 yods in 6 internal tetractyses other than polyhedral corners surround centre (Type A);
50 internal yods on sides of 18 internal tetractyses surround centre (Type B). 55 yods on sides of 18 internal triangles;
31 yods in 6 internal tetractyses (Type A);
36 hexagonal yods in 18 sides of 12 tetractyses in 4 faces;
44 yods on sides of 12 tetractyses in faces, of which 36 are hexagonal; also 44 corners and centres of 30 tetractyses of Type B solid surrounding centre; 80 hexagonal yods on 40 sides of 30 tetractyses of Type B solid;
76 yods other than 48 hexagonal yods in faces surround centre (Type B). 50 are on edges of 18 internal tetractyses, 26 are centres of internal tetractyses and corners of tetractyses in faces: 76 = 26 + 50 = YAHWEH ELOHIM;
48 hexagonal yods in faces → 48 corners of 7 separate polygons → 48 yods up to Chesed of 1-tree. The sums of the numbers of their corners = (3+4+5) + (6+8+10) + 12 = 12 + 24 + 12 → 12 hexagonal yods on solid edges, 24 hexagonal yods on tetractys sides and 12 centres of tetractyses;
70 yods surround centre (Type A) → 70 yods of Tree of Life; 23 internal yods or tetractys corners → 23 yods above Chesed of Tree of Life.

Transformation into the Type A tetrahedron generates 67 yods (number of Binah). Transformation into Type B generates 73 yods (number of Chokmah) other than the 48 hexagonal yods in faces (also, 73 internal yods and corners of solid). 120 new yods surround centre, where 120 = 22 + 42 + 62 + 82. 95 yods are on edges of 30 tetractyses (Type B), of which 91 are generated by transformation.

7
49 corners, sides and tetractyses (Type A);
49 polyhedral corners and internal yods other than centres and corners of 18 internal tetractyses;
65 yods on faces or on sides of 6 internal tetractyses (Type A);
26 corners and sides of 12 tetractyses in 4 faces;
31 corners and sides of 18 tetractyses in Type A.

OCTAHEDRON

26 corners, edges and faces of polyhedron;
15 corners of 36 tetractyses (Type A); 26 corners of 60 tetractyses surround centre (Type B);
36 sides of 24 tetractyses in 8 faces;
50 corners and sides of 24 tetractyses in 8 faces;
129 yods other than polyhedral corners (Type A);
96
hexagonal yods in faces → 96 corners of (7+7) separate polygons;
14
corners of 24 tetractyses in faces → 14 centres of (7+7) separate polygons;
110
yods in faces → 110 corners of tetractyses in (7+7) separate polygons.

CUBE

26 corners, edges and faces of polyhedron;
36 sides of 24 tetractyses in faces;
50 corners and sides of 24 tetractyses in faces;
15 corners of 36 tetractyses (Type A); 26 corners surround centre (Type B);
96
hexagonal yods in faces;
247
yods (Type B) (7 in centres of faces and centre of cube) → 240 hexagonal yods and 7 centres of 7 polygons;
220
hexagonal yods (Type B), where 220 = 22 + 42 + 62 + 82 + 102.

ICOSAHEDRON

240
hexagonal yods in faces;
50
corners of 150 (15×10) tetractyses other than polyhedral corners surround centre (Type B);
260
(26×10) yods in 20 faces other than polyhedral corners;
597
yods (Type B) → 597 hexagonal yods outside root edge of 7 enfolded, Type B polygons.

FIRST FOUR PLATONIC SOLIDS

128 vertices, edges and faces, where 128 = 21 + 26 + 50 + 31. This is the sum of the Godname numbers of the first four Sephiroth;

Number of yods on edges of four solids = 150 = 15×10;

Average number of yods (including centres) in first four solids (Type A) = 168;

Average number of yods inside first four solids (Type A) = 31;

Average number of yods in faces of first 4 solids = 137 (1370 yods in (7+7) enfolded polygons with Type B triangular sectors). The number 137 is the nearest integer approximation to the reciprocal of the fine-structure constant α = e2/ħc ≈ 1/137;

150 (15×10) yods on polyhedral edges, of which 30 are corners and 120 are hexagonal, where 30 = 12 + 22+ 32 + 42, and 120 = 22 + 42 + 62 + 82;

DODECAHEDRON

50
corners and edges;
70
yods in interior surround centre;
Number of yods = 343 = 73 (Type A). This is the sum of the 26 combinations of the first ten integers arranged in a tetractys:

  Sum of combinations

 

Numbers 1, 70 and 272 denote, respectively, the yod at the centre, the number of internal yods surrounding centre and number of yods in faces;

Number of internal hexagonal yods (Type B) = 310 = 31×10;

Number of hexagonal yods (Type A) = 310 = 31×10;

Number of hexagonal yods (Type B) = 550;

Number of yods without faces divided into tetractyses = 91;

8

Number of yods surrounding centre other than polyhedral corners (Type B) = 592→ number of yods in two sets of 7 separate polygons + root edge other than its corners → number of yods inside Type B triangles of Tree of Life;

260 (26×10) yods in 12 faces other than their centres → 260 yods outside root edge in 7 enfolded polygons;

251 yods of internal (Type B) triangles other than centres of tetractyses → 251 yods in lowest tree of CTOL with Type B triangles → 251 yods outside root edge of 7 enfolded polygons not either Sephirothic corners of Tree of Life or centres of polygons.

COLLECTIVE PROPERTIES OF FIVE SOLIDS

50 corners and 50 faces;

720 hexagonal yods in faces → 720 yods surrounding centres of seven separate Type B polygons;

910 hexagonal yods → 91 trees of CTOL; 26-tree has 910 corners of enfolded polygons unshared with hexagon enfolded in 27th tree;

Number of yods surrounding centres (Type A) = 1010, where 101 = 26th prime number = 50th odd integer after 1;

Number of yods surrounding centres (Type B) = 1820 = 70×26;

Number of yods in five solids = 1825

where Dn is the nth decagonal number (D1 = 1);

Average number of yods on edges of solids and internal triangles = 67 = number value of Binah;

Average number of yods other than corners on edges of solids = 36;

Average number of yods on edges of internal triangles = 31;

Average number of internal yods on edges of internal triangles = 21;

Five solids have 550 corners, edges and triangles in their 50 faces;

Number of yods in 5 solids not corners of Type B tetractyses other than polyhedral corners = 1680.

NESTED SOLIDS

First four Type B solids have 1080 hexagonal yods surrounding their common centre; 1081 = number value of Tiphareth ("Beauty");

31 polyhedral corners + centre of first four solids;

Number of yods surrounding their centre on sides of internal triangles and on edges of first four solids = 210 = 21×10;

Number of corners of tetractyses in first four Type B solids = 129;

Number of corners of triangles inside five Type B solids = 91;

1820 yods surround the centre of five solids; this is the number of yods in 36 overlapping trees and in 26 separate trees;

1680 yods (including 50 polyhedral corners) surround the centres of five solids other than corners of tetractyses.

6. Discussion

It is remarkable (as well as indicative of their preternatural/archetypal design) that the four Platonic solids thought by the ancient Greeks to be the shapes of particles of the first four Elements: Earth, Water, Air and Fire are made up of 128 polyhedral vertices, edges & faces, where

128 = 21 + 26 + 50 + 31

is the sum of the Godname numbers of the first four Sephiroth. In fact, it is an example of the Tetrad Principle, proposed in Article 1, governing the mathematical properties of holistic systems.

Let us now compare the hexagonal yod populations of these solids with properties of the outer and inner forms of the Tree of Life shown in, respectively, Figure 1 and Figure 4:

1. The surface of the tetrahedron has 48 hexagonal yods. This is the number of corners of the seven separate, regular polygons (as well as the number of their tetractyses) constituting the inner form of the Tree. 48 is also the number of corners, sides and triangles in its outer form and the number of yods in the Tree of Life up to the horizontal Path connecting Geburah and Chesed, i.e., the part of the Tree spanned by the seven Sephiroth of Construction contains 48 yods. The tetrahedron embodies the minimum number of geometrical elements defining both the outer and the inner forms of the Tree;

9

 

10

2. The faces of the octahedron and cube each contain 96 hexagonal yods. This is the number of corners of the two sets of polygons;

3. The surfaces of the tetrahedron, octahedron and cube comprise 240 hexagonal yods, which compare with the 240 hexagonal yods in the 48 tetractyses of the seven polygons;

4. The surface of the icosahedron has 240 hexagonal yods, which compares with the 240 hexagonal yods of the 48 tetractyses in the second set of seven polygons.

5. The surfaces of the four Platonic solids, whose shapes the ancient Greeks thought were those of the particles of the four Elements, contain (240+240=480) hexagonal yods, which compares with the 480 hexagonal yods in both sets of seven polygons. This correspondence with the inner form of the Tree and their prescription by Godname numbers are evidence of the sacred geometry of these solids; they embody numbers of universal physical significance, namely the (240+240=480) gauge fields corresponding to the (240+240=480) non-zero roots of E8×E8 mediating the unified superstring force. The mirror symmetry of the inner form of the Tree explains why these 480 gauge fields are divided into two similar sets of 240. It confirms the basic Pythagorean insight that the tetrahedron, octahedron, cube and icosahedron defined the physics of the cosmos, if not the sense of the teaching attributed to them.

The interior of the Type A dodecahedron has 70 yods surrounding its centre. As it has 20 polyhedral corners, (1+70+20=91) yods are needed to construct its shape from tetractyses. Type B comprises 550 hexagonal yods. Symbolising for the Pythagoreans the cosmic sphere, the dodecahedron therefore embodies the number (91) of Trees in CTOL and the number (550) of its SLs, i.e., it represents the cosmic version of the Tree of Life. The Godname ELOHIM prescribes this representation because the dodecahedron has 50 corners and edges.

More evidence for the sacred geometry of the five Platonic solids comes from considering their yod populations. Remarkably, in view of the central significance of the number 10 for the Pythagoreans, who regarded it as ‘all perfect,’ the number of yods inside the five Type B solids surrounding their centres is 1000, i.e., 103. The total number of yods surrounding their centres is 1820. As 1820 = 26×70, they have as many yods as 26 separate Trees of Life, showing how the Godname YAHWEH with number value 26 prescribes their yod population. It can be proved that 1820 is the number of yods in 36 overlapping Trees with their triangles turned into tetractyses, illustrating how ELOHA, the Godname of Geburah with number value 36, also prescribes this number. 1820 is the number of yods surrounding the common centre of five Type B Platonic solids nested one inside another. Furthermore, they have the property that their 50 faces comprise 550 corners, sides and tetractys triangles, i.e., 550 geometrical elements define their shapes, whilst their interiors have 91 corners of tetractyses. This is remarkable in view of the fact that the 91 Trees of CTOL have 550 SLs. Their embodiment of the basic numbers characterising the Tree of Life map of all levels of reality is evidence of the sacred geometry of the five Platonic solids.

Perhaps the most spectacular property of the five Platonic solids with Type B internal triangles is the following: there are 180 tetractyses in their 50 faces and 270 internal tetractyses, a total of 450 tetractyses. Of the 1820 yods surrounding the centres of the solids, 450 yods are centres of tetractyses, leaving 1370 yods lining their edges. This is the number of yods in the inner form of the Tree of Life with Type A triangles as the sectors of the 14 enfolded polygons (Fig. 11))! What more convincing evidence is needed of the Tree of Life character of the five Platonic solids? The number of yods needed to create the shapes of their external and internal tetractyses is that of 137 tetractyses. This is how the five Platonic solids embody the number 137 defining the fine-structure constant. We saw in Section 4 during the discussion of the collective properties of the first four Platonic solids that they have on average 137 yods in their faces. Now we see that this number also defines the shape of all five solids.

My book Extra-sensory Perception of Quarks (5) and its sequel, ESP of Quarks and Superstrings (6), provided a wealth of evidence indicating that the Theosophists Annie Besant and C.W. Leadbeater used a form of ESP to describe quarks, the constituents of the protons and neutrons making up atomic nuclei (see Article 2). They also proved that the ‘ultimate physical atom’ (UPA), which Besant and Leadbeater claimed are the basic constituents of atoms, are fundamental particles making up the up and down quarks in nuclei. According to Leadbeater, there is a ‘positive’ and a ‘negative’ UPA (Fig. 12), one the mirror image of the other. Each comprises ten closed curves, or ‘whorls,’ which spiral 2½ times towards the base of the UPA, where three thicker whorls separate from the other seven, both strands then spiralling separately 2½ times in opposite senses around the axis of the UPA towards its top. Each whorl is a helix in which Leadbeater

11

counted 1680 circular turns. In my next book ESP of Quarks and Superstrings, I identified the UPA with the E8×E8 heterotic superstring constituents of up and down quarks. In the research articles on this website, I prove that the number 1680 — a structural parameter of the superstring — is encoded in the Tree of Life and is mathematically defined by the ten Godname numbers. Using Table 1, which shows the yod populations of the Platonic solids, it is easy to calculate that the five nested, Type B Platonic solids contain 1680 yods which, apart from those that are the 50 polyhedral corners, are not corners of tetractyses.

This astounding embodiment of a number of cosmic significance illustrates the sacred character of the geometry of the Platonic solids, for the Godname ELOHIM prescribes just that number of points whose distribution in 3-dimensional space forms five regular polyhedra, the construction of which from tetractyses requires (including these points) 1680 yods other than corners of tetractyses. The kernel 168 of this structural parameter of the superstring constituents of quarks is in fact the number value of Cholem Yesodoth (“breaker of the foundations”), the Hebrew name of the Mundane Chakra of Malkuth, which is the physical, cosmic manifestation of this Sephirah. So Kabbalah provides remarkable, independent confirmation of the number clairvoyantly determined by Leadbeater! That this might be coincidental is implausible because the number 168 refers appropriately to the very Sephirah signifying the physical manifestation of the Tree of Life. Furthermore, using the numbers listed in the table, it is straightforward to calculate that 168 is the average number of yods (including their centres) in the four Type A Platonic solids representing Earth, Air, Fire and Water. This is an amazing embodiment of the number characterising the structure in ordinary space of the subquark state of the superstring. The 120 tetractyses from which the 38 faces of the first four solids can be assembled have 248 corners and sides. In other words, 248 geometrical elements are needed to shape the surfaces of the Platonic solids corresponding to the four Elements! It was mentioned earlier that superstring theory predicts that 248 particles transmit the unified force operating between superstrings very briefly after the Big Bang, later remnants of which bound (according to my analysis of Besant’s and Leadbeater’s observations) three superstrings into quarks and then three quarks into the protons and neutrons that eventually built up through stellar nuclear synthesis the atomic nuclei of the 92 naturally occurring elements! In this sense, therefore, these four Platonic solids do determine the fundamental substance of the material world through their shapes — just as the ancient Pythagoreans claimed they did, although not, of course, as the actual form of the particles making up the four Elements. Basic parameters of superstring theory (one obtained by psychic means and awaiting confirmation by theoretical developments in particle physics) are therefore embodied in these four Platonic solids as their structural properties.

7. Conclusion

This article has demonstrated the seemingly miraculous way in which the geometry of the Platonic solids embodies numbers (240, 480 and 248) predicted by a scientific theory to describe the basic forces operating in the natural world and numbers (168 and 1680) predicted by psychic observations of superstrings to be their structural parameters. Another example of the latter is the fact that the UPA comprises 50 revolutions of its ten whorls, each one making five revolutions. This compares with the 50 corners of the five regular polyhedra. Both properties exist because both are Tree of Life structures prescribed by the mathematical archetype embodied in the Divine Name ELOHIM, whose number value is 50. The article has also demonstrated the remarkable parallels between the stages of unfolding of the inner form of the Tree of Life and the sequence of Platonic solids, reaching its culmination in the dodecahedron. This embodies two parameters of CTOL (91 and 550), showing that it is an analogous representation, just as the other solids are analogous to distinct stages of development of the inner form of the Tree of Life. For the Pythagoreans, mathematics could not be separated from theology because they taught, “the essence of the Gods is defined by Number.” Their teaching is amply illustrated by the five Platonic solids, whose beautiful, sacred geometry is prescribed by the number values of the ten divine names as the counterpart of the outer and inner forms of the Tree of Life — the universal blueprint.

ADDENDUM

THE PYRAMID

Although not a regular polyhedron, the square pyramid has remarkable properties indicating that it, too, possesses sacred geometry. These are investigated below.

Turning its four triangular faces and the four triangular sectors of its base into tetractyses, one finds (Fig. 13)

12

that there are 21 yods along its edges (five corners, two hexagonal yods inside each of the eight edges). In other words, the number value of EHYEH (“I am”), which is the Godname of Kether, the first Sephirah, is the fewest number of yods needed to create the edges of the pyramid. This illustrates the minimal nature of this Godname assigned to the first Sephirah, which signifies the embryonic source of Creation. Considering next the pyramid’s five faces (base included), there are five pyramid corners that are corners of tetractyses, one centre of the base that is the corner of four tetractyses, 12 sides of tetractyses and eight tetractyses, making a total of 26 corners, sides and tetractyses. 26 is the number value of YAHWEH, Godname of Chokmah, the second Sephirah. YAHWEH prescribes the minimum number of geometrical elements (points, lines and triangles) needed to construct the pyramid.

Now, as was done for the Platonic solids, let the triangular faces of the pyramid be constructed from three tetractyses, not one, so as to be consistent with construction of the square base from four tetractyses. As before, there are five pyramid corners and a centre of its square base, but now also four centres of its triangular faces, which are corners of tetractyses, making a total of ten corners of tetractyses. There are 24 sides of tetractyses (eight pyramid edges, four sides of tetractyses inside the perimeter of the base and three inside each triangular face), and there are 16 tetractyses (four in the square base and three in each face). The total number of corners, edges and triangles = 10 + 24 + 16 = 50, which is the number value of ELOHIM, the Godname of Binah, and the next Sephirah after Chokmah in the Tree of Life! This is appropriate in view of the fact that, according to Kabbalah, the most primitive notion of relationship and form first arises in Binah. Its Godname is here prescribing the geometrical composition of the pyramid in terms of its component corners, edges and triangles — the very geometrical elements that define its shape.

The number (80) of yods in the tetractyses forming the square-based pyramid is the
number value of Yesod ("Foundation") and the number of yods in the lowest Tree in CTOL.
                                                         

Next, consider the central, vertical line joining the apex of the pyramid to the centre of its base (Fig. 14). This is part of the assembly of the pyramid from tetractyses because it is the common edge of four internal, right-angled triangles whose eight other edges are the four sloping, pyramid sides and the four half-diagonals of the square base. So there are five geometrical elements inside the pyramid (four triangles and their shared side). A pyramid whose faces are single tetractyses has (26+5=31) geometrical elements, where 31 is the number value of EL, the Godname of Chesed, which is the next Sephirah after Binah. A pyramid with three tetractyses in each face has (50+5=55) such elements, where

The 55th SL from the bottom of CTOL is the 496th from the top of CTOL, where 496 is both the number value of the Hebrew word ‘Malkuth’ signifying (on one level of meaning) the physical universe and the number of spin-1 particles that superstring theory predicts mediates the unified force between superstrings. 496 is what mathematicians would describe as the 31st triangular number, i.e.,

496 = 1 + 2 + 3 + … + 31.

It cannot surely be coincidence that the Godname numbers of the first four Sephiroth quantify successive stages of assembly of the pyramid from tetractyses, 21 yods creating its edge, 26 (then 50) geometrical elements forming its faces, and 31 elements forming its volume? If the four internal triangles are now regarded not as single tetractyses but as three tetractyses, this adds nine yods per triangle, that is, 36 yods in all, where 36 is the number value of ELOHA, the Godname of the next Sephirah after Chesed.

Counting the yods in the 20 tetractyses assembling the pyramid, one finds that there are 80 yods (six inside, 74 on the faces and base). Of these, ten are corners of tetractyses (five pyramid corners, one centre of the base and four centres of its faces), this type of yod symbolising members of the Supernal Triad. So there are 70 yods that are not corners of tetractyses, that is, there are 70 hexagonal yods, this type of yod symbolising the Sephiroth of Construction. Compare this with the fact that the Tree of Life is made up

13

of 70 yods in its 16 tetractys-converted triangles, whilst the lowest tree in CTOL has 80 yods in its 25 tetractys-converted triangles (see Figs 7 and 8). We find that the pyramid is constructed from as many yods as there are yods in the lowest Tree of Life of CTOL. This is very remarkable. In fact, as Figure 8 shows, 80 is the number of corners of the 94 tetractyses making up the two sets of seven enfolded regular polygons constituting the inner form of the Tree of Life. Moreover, it is the number value of Yesod, the penultimate Sephirah. But the mathematical analogy extends further: the 70:10 differentiation between hexagonal yods and yods at corners of tetractyses making up the pyramid corresponds to the 70 yods of the Tree of Life and the extra ten yods that are added to it when it is turned into the lowest Tree in CTOL. It also corresponds to the 70 corners of the two sets of seven enfolded polygons and their ten extra centres, which form the 80 corners of their tetractyses. Moreover, as the surface of the pyramid has 74 yods and the base has 25 yods, there are 49 yods in its faces above its base, where 49 is the number value of EL ChAI, Godname of Yesod. The total number of yods above its base is 55, which is the number of corners of the 48 tetractyses in the seven separate regular polygons. There is therefore a significant analogy between the pyramid, the Tree of Life and its inner form.

We have found that 21 is the least number of yods needed to create the edges of a pyramid and 80 is its yod population. Suppose that we now assign either the number 21 to each yod making up the body of the pyramid or the number 80 to each yod on its edges (Fig. 15). In either case, their sum = 21×80 = 1680, which is the number of turns counted by Leadbeater in the helical whorl of the UPA. In this sense the pyramid, when seen as constructed by tetractyses, embodies the very cosmic parameter characterising the structure of the basic unit of matter, namely, the E8×E8 heterotic superstring. In fact, the meaning of the Hebrew word ‘Yesod,’ whose number value is 80, is ‘foundation,’ which is very appropriate in this context. This property connects the largest man-made object in the world to the smallest particle in the universe. The 26 geometrical elements making up the faces and base of the pyramid (and therefore determining its shape) correspond to the 26 space-time dimensions of a closed string, which I have interpreted as a whorl.

Some writers have contended that the Great Pyramid is a scale model of the Earth and claim to have found all manner of terrestrial measures in its dimensions. Whether or not any of these claims is right, one can say with certainty that the pyramid shape bears a remarkable analogy to the outer and inner forms of the Tree of Life, as well as that hidden in its construction from tetractyses can be said to be the number quantifying the structure of what ultimately constitutes the universe, namely, the superstring. Of course, as the number 1680 is not present in a patent way but requires multiplication of two numbers that are implicit in its construction from tetractyses, sceptics might dismiss this as yet more pyramidology. However, they cannot so easily ignore the remarkable parallels with the Tree of Life and the lowest tree of CTOL. Nor can they dismiss the fact that at least six Godname numbers quantify the geometrical composition of the pyramid in such a way that is consistent with the order of appearance of their corresponding Sephiroth. They may argue that I have merely looked for properties that can be quantified by Godname numbers. If these properties were more convoluted in their meaning, this might be a fair criticism. But one does not have to search hard for Godname numbers in the pyramid, as one would if there really were no underlying connection between them and its geometrical design. On the contrary, their presence in the geometry of the pyramid is so natural that it cannot plausibly be regarded as coincidental or contrived. Moreover, the mathematical properties of the pyramid are arithmetically expressed by the Pythagorean Tetrad, or number 4, which I have proved (7) expresses the geometrical properties of the outer and inner forms of the Tree of Life — indeed, any object that possesses sacred geometry because it is a mathematical counterpart to the latter, as well as numbers of cosmic significance, like group-theoretical parameters of the superstring symmetry groups E8 and E8×E8 (see Article 1). Beautiful examples of how the Tetrad defines properties of the pyramid are:

1. its surface is made up of 64 hexagonal yods, where 64 = 43;

2. it is made up of 70 hexagonal yods, where

and 7 is the fourth, odd natural integer;

3. it is made up of 80 yods, where

14

and 8 is the fourth, even natural integer;

4. its 20 tetractyses have ten corners, where 10 = 1 + 2 + 3 + 4 and 20 is the 10th even integer.

It is clear that the presence of Godname numbers in the square pyramid has not been contrived. If it had been and this shape did not possess sacred geometry, there would not be so many powerful examples of how the Tetrad expresses its properties, for this is always a signature of an object having sacred geometry when it is constructed from tetractyses. Instead, the presence of Godname numbers reflects the fact that the geometry of this pyramid is truly sacred. As a three-dimensional counterpart of the Tree of Life, its properties are necessarily prescribed by Godnames because it is an archetypal object.

References

1) Yod, the tenth letter of the Hebrew alphabet, has the approximate appearance of a dot or point.

2) The Secret Doctrine, H.P. Blavatsky (Theosophical Publishing House, London, 1950), vol. 2, p. 337.

3) The Pythagorean Sourcebook and Library, Kenneth Sylvan Guthrie (Phanes Press, 1987), p. 28.

4) Phillips, Stephen M. Article 2: “The physical plane and its relation to the UPA/superstring and spacetime,” (WEB, PDF), p. 1.

5) Extra-sensory Perception of Quarks, by Stephen M. Phillips (Theosophical Publishing House, U.S.A., 1980).

6) ESP of Quarks and Superstrings, by Stephen M. Phillips (New Age International Publishers, Mumbai, India, 1999).

7) The Mathematical Connection between Religion and Science, Stephen Phillips (Antony Rowe Publishing, England, 2009).
15

Home