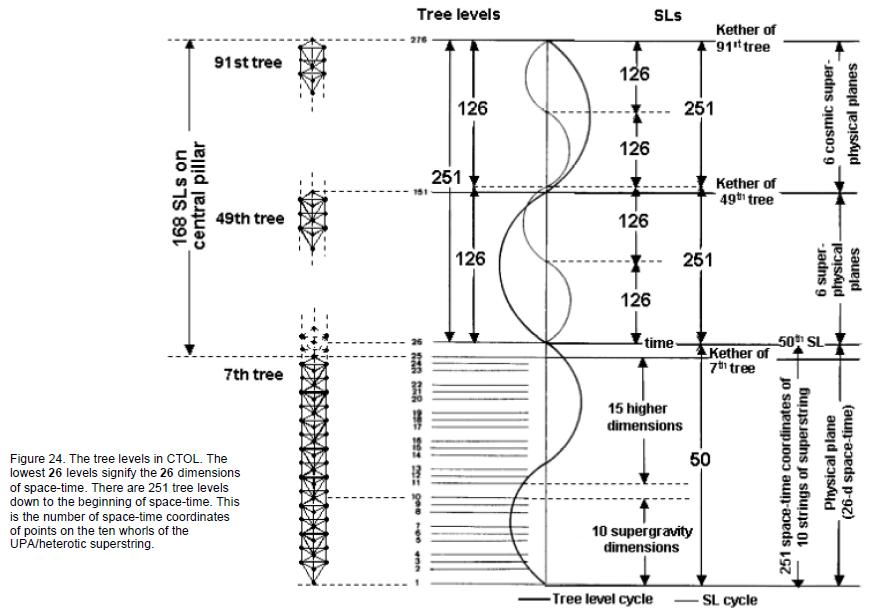
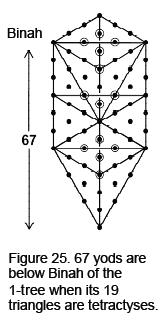
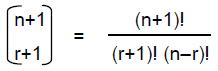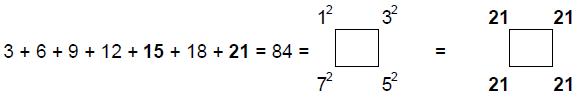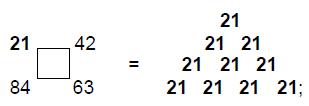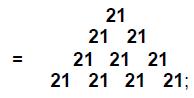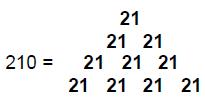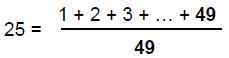ARTICLE 5
"As above, so below"
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH.
England.
Website: http://www.smphillips.mysite.com
ABSTRACT
|
Analysis by the author of the century-old description by Annie Besant and
C.W. Leadbeater of the basic units of physical matter, which they magnified
with the use of a yogic siddhi called ‘anima,’ has shown that these particles
are not only the constituents of the up and down quarks in atomic nuclei but
also E8×E8 heterotic superstrings. This paper proves
mathematically that these particles are the microscopic manifestation of
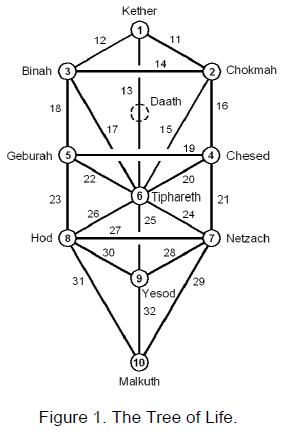
the Kabbalistic Tree of Life. Aspects of their geometrical configuration in
26-dimensional space-time, becoming superstrings as such only in ten of these
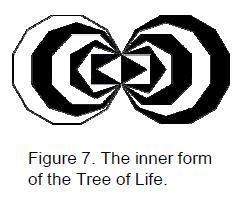
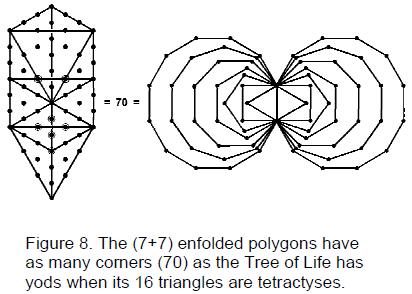
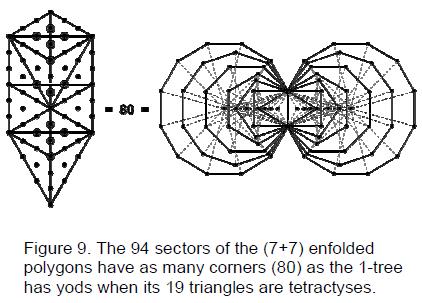
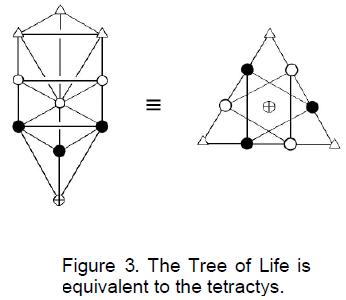
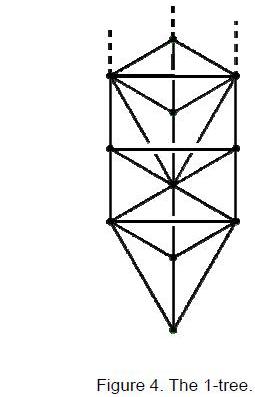
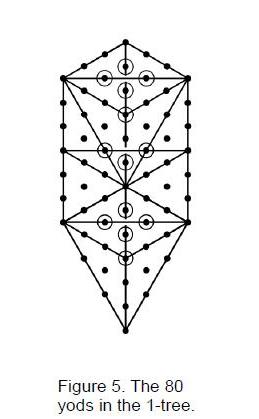
dimensions, are shown to be encoded in both the outer form of the Tree of Life
and its inner form, recently discovered by the author. The latter encodes the
Tree of Life depiction of all levels of reality, including space-time, and
confirms the Theosophical doctrine of the seven planes of consciousness. The
Tree of Life descriptions of the UPA and all domains of superphysical
consciousness are found to be analogous, indicating that the superstring is the
microcosm of the spiritual macrocosm, having a superphysical as well as a
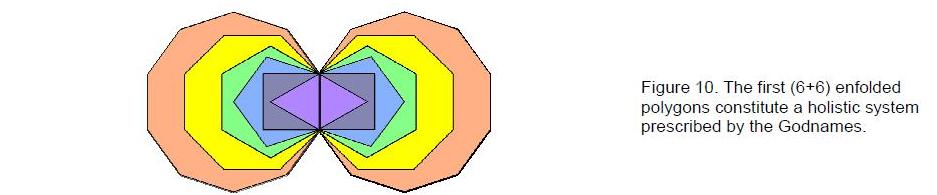
physical aspect. The archetypal Divine Names are shown to prescribe both the
psychically described structure of the subquark state of the superstring and
its unified force, as well as their encoding in the outer and inner forms of
the Tree of Life blueprint. The article discusses implications for the nature
of the ‘M-theory’ currently being sought by physicists as the basis of 11-d
supergravity theory and the five known superstring theories.
|


.png)