ARTICLE 24

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

 

Abstract

 

1. Introduction
The author has discovered that what is known to Kabbalists as the ‘Tree of Life’ is actually only the outer form of the complete, sacred geometrical system embodying the divine paradigm. It has an inner form, and Articles 22 and 23 showed that the Catalan solid called the ‘disdyakis triacontahedron’ is its polyhedral manifestation. Through the equivalence between the (6n+1) yods of an n-sided, regular polygon with its sectors turned into tetractyses and the (6n+1) Sephirothic emanations up to Chesed of the highest tree in n overlapping Trees of Life, this inner form can be shown¹ to encode the replication of its outer form to map all levels of reality, both physical space-time and

1

Table 1. Gematria number values of the 10 Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

(All numbers from this table that are referred to in the article are written in boldface).

2

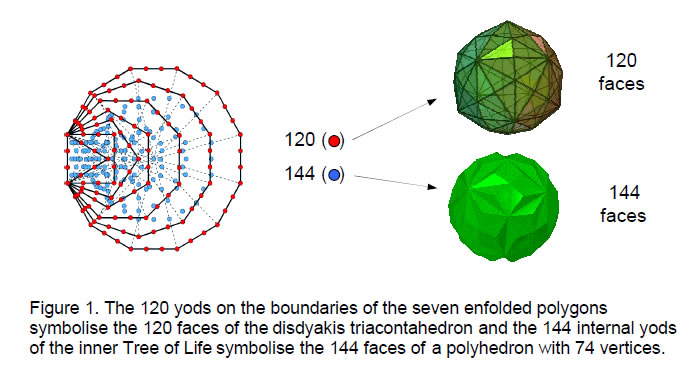
superphysical realms. The seven enfolded, regular polygons constituting one half of the inner Tree of Life map what are known in Theosophy as the 49 subplanes of the seven planes of consciousness: physical, astral, mental, buddhic, atmic, anupadaka (or Monadic) and adi (or Divine), each subplane being represented by its own Tree of Life. The 120 yods on the

boundaries of the seven polygons signify the 120 faces of the disdyakis triacontahedron and the 144 yods inside them denote the 144 faces of another polyhedron (Fig. 1). This ‘144 Polyhedron’ was identified in Article 23 as generated from the disdyakis dodecahedron (one of the 13 Catalan solids), which has 48 faces, 26 vertices & 72 edges. This is the only semi-regular polyhedron that has 48 faces, which means that it, alone, can generate a polyhedron with 144 faces when tetrahedra are stuck on its faces.

2. Polyhedral content of the disdyakis triacontahedron
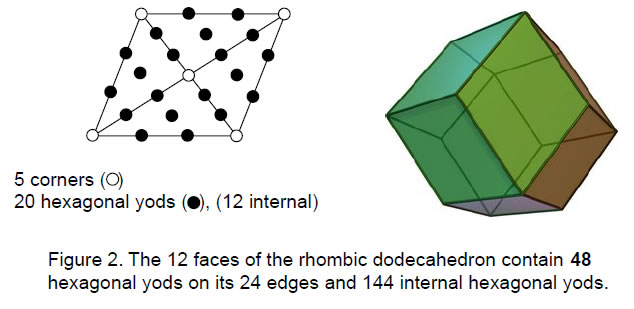
The 62 vertices of the disdyakis triacontahedron define the vertices of 28 regular and semi-regular solids: ten tetrahedra, five cubes, five octahedra, one icosahedron, one dodecahedron, five rhombic dodecahedra and one rhombic triacontahedron. A rhombic dodecahedron (Fig. 2) is an Archimedean solid with 14 vertices, 24 edges and 12 rhombic faces. Constructed from four tetractyses, each of the 12 rhombic faces has 12 internal hexagonal yods, whilst two hexagonal yods lie on each of its 24 edges. The number of hexagonal yods in the rhombic dodecahedron is therefore 2×24 + 12×12 = 192 (see Article

3

18 for the significance of this parameter of holistic systems vis-à-vis the I Ching table and the Bode numbers of the planets). When the five, separate rhombic dodecahedra group, their (5×14=70) separate vertices become the 62 vertices and raised centres of the 30 Golden Rhombic faces of the disdyakis triacontahedron, their 30 unshared vertices coinciding with the centres of these faces and their 32 shared vertices coinciding with their vertices (Fig. 3). Each rhombic dodecahedron has six unshared vertices and eight shared vertices that are vertices of these faces. Each face vertex coincides with two vertices of different

dodecahedra:

A1B1 A2C1 A3D1 A4E1 A5B2 A6C2 A7D2 A8E2

B3C3 B4D3 B5E3 B6C4 B7D4 B8E4

C5D5 C6E5 C7D6 C8E6

D7E7 D8E8

 

 

 

 

 

 
where the letters label the five dodecahedra and the numbers indicate their vertices.

Let us now construct the 28 solids from tetractyses — the template of sacred geometry — and then work out their populations of hexagonal yods. The significance of the latter is that the seven hexagonal yods of the tetractys symbolise the seven Sephiroth of Construction, the formative degrees of freedom expressing the 'objective' aspects of God). The hexagonal yod populations of the 28 polyhedra in the disdyakis triacontahedron

4

are:²

tetrahedron:	10×48 =	480
cube:	5×96 =	480
octahedron:	5×96 =	480
icosahedron:	1×240 =	240
dodecahedron:	1×240 =	240
rhombic dodecahedron:	5×192 =	960
rhombic triacontahedron:	1×480 =	480
	Total =	3360

This result is truly astounding for two complementary reasons:

1. Divine Unity symbolised by the Pythagorean Monad, or mathematical point ("0th-order tetractys"), differentiates, firstly, into the familiar tetractys ("1st-order tetractys") with 10 yods (three corners, seven hexagonal yods), secondly, into the “2nd-order tetractys” with 85 yods (15 corners, 70 hexagonal yods), and so on:

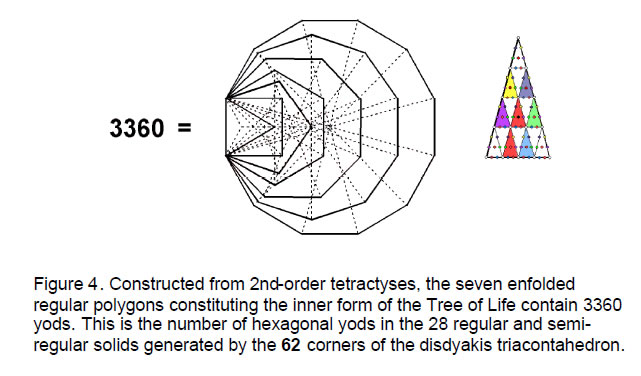
3360 is the number of yods in the seven enfolded, regular polygons constituting the inner form of the Tree of Life when their 47 sectors are each turned into the 2nd-order tetractys (Fig. 4).³ We now see that the seven types of solids terminating in the disdyakis triacontahedron contain 1680 hexagonal yods (as shown on page 14 of Article

5

22⁴ ), whilst the actual numbers for the seven types of solids in the disdyakis triacontahedron total 3360 hexagonal yods, where 3360 = 2×1680. This is the total number of yods making up the polygonal, inner form of the Tree of Life constructed from the template of the 2nd-order tetractys. The number 3360 expresses a holistic structure both in the 2-dimensional space of the polygons and in the 3-dimensional space of the disdyakis triacontahedron. This marvellous, beautiful property of the polyhedron clearly demonstrating its Tree of Life basis!

2. 3360 is the number of circularly polarised standing wave oscillations made during each of the five revolutions of the ten closed curves making up the E₈×E₈ heterotic superstring, as described by Annie Besant and C.W. Leadbeater in 1908, when they used anima to magnify subatomic particles (Fig. 5), whilst 1680 is the number of such oscillations in each curve. What this means is that, as the completion of the seven-fold sequence of regular and semi-regular polyhedra, the disdyakis triacontahedron has to be made up of the same number of formative degrees of freedom (hexagonal yods) as there are yods needed to represent its 2-dimensional counterpart, namely, the seven enfolded, regular polygons. Far from being a coincidence, the presence of the same number in two superficially different contexts reveals in an unambiguous way the beautiful, mathematical design of a transcendental, creative Intelligence. To discover this mathematical harmony, we need to understand 'sacred geometry' — not the distorted version found in many books, which lack understanding of the fundamental principles — but the only geometry worthy of being called 'sacred,’ namely, that of the Tree of Life.

Each of the 42 sides of the seven enfolded polygons has 11 yods between their ends, which number 36. The number of yods forming the boundaries of the polygons = 11×42 + 36 = 498. In other words, 496 yods form the sides of the polygons between the two endpoints of the root edge that generates them. This is the number value of the Hebrew word ‘Malkuth’ signifying the last Sephirah of the Tree of Life. It is yet another confirmation that the disdyakis triacontahedron is the outer (or Malkuth) aspect

6

of the inner Tree of Life. As discovered by physicists Michael Green and John Schwarz⁵ in 1984, 496 is the dimension of the non-abelian gauge symmetry group defining superstring interactions that are free of quantum anomalies. We therefore encounter the following amazing property of the polygonal form of the inner Tree of Life blueprint: it encodes not only the oscillatory pattern of the E₈×E₈ heterotic superstring but also the number of gauge bosons that transmit its unified force — the first as its yod population and the second as the number of yods forming its boundary between the endpoints of its generative root edge.

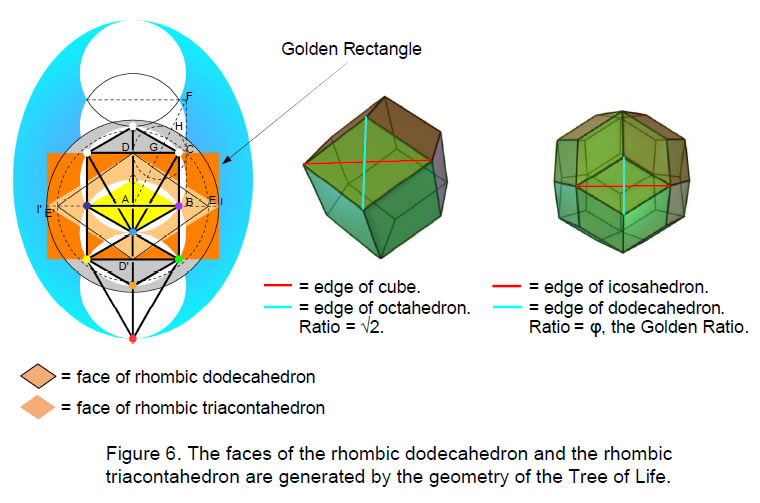
3. The rhombic dodecahedron and rhombic triacontahedron
The rhombic dodecahedron has 12 rhombic faces (Fig. 6). The longer diagonal of each face (shown as a red line in Fig. 6) is the edge of a cube and the shorter diagonal (shown as a blue line) is the edge of an octahedron. The ratio of the lengths of the longer and shorter diagonals is √2 = 1.414... . These Platonic solids are dual to each other. The two other Platonic solids that are dual to one another — the icosahedron and the dodecahedron — share an analogous property in that their edges are, respectively, the longer and shorter diagonals of the faces of the rhombic triacontahedron. Their ratio is the Golden Ratio φ = 1.618… .These rhomboids are generated in a simple way by the geometry of the Tree of Life. Fig. 6 indicates how the ten Sephiroth are the centres or points of intersection of a column of white circles. Let us take their radii as one unit. The central Pillar of Equilibrium intersects the path joining Chesed and Geburah at a point A that is one unit away from the vertical right-hand tangent BC to these circles. ABCD is a square with sides of length 1. Therefore, its diagonal AC = √(1² + 1²) = √2. With A as centre, draw a circle passing through C of radius √2 (shown as a dashed line in Fig. 6). It intersects the line drawn along AB at E. E' is the corresponding point on the other side of the central pillar. EE' = 2√2. The central pillar intersects the path joining Netzach and Geburah at D'. DD' = 2. Therefore, EE'/DD' = 2√2/2 = √2. We find that the rhombus DED'E' has the same shape as the rhombic face of the rhombic dodecahedron.

Extend the tangent at B to the point F, where BC = CF = 1. Then, BF = 2 and AF = √(2² + 1²) = √5. The line AF intersects CD at G, where AG = GF = √5/2. With G as centre, draw a circle of radius ½. It intersects AF at H, where AH = √5/2 + ½ = (√5+1)/2 = φ, the Golden Ratio. With A as centre, draw a circle of radius AH. It intersects the extension of AB at I, where AI = φ. I' is its counterpart on the other side of the central pillar. II' = 2φ. Therefore, II'/DD' = 2φ/2 = φ. The rhombus DI D'I' has the same shape as the rhombic face of the rhombic triacontahedron. What manifests finally as the fruit of the Tree of Life, namely, the disdyakis triacontahedron with golden rhombic faces, was within it as their seed shape from the very beginning!

References
¹ Phillips, Stephen M. The Mathematical Connection between Religion and Science (Antony Rowe Publishing, England, 2009).

² The hexagonal yod populations of these solids are taken from Article 22: “The disdyakis triacontahedron as the 3-dimensional counterpart of the Inner Tree of Life,” Stephen M. Phillips, (WEB, PDF), p. 6.

³ Proof: The 2nd-order tetractys has 85 yods, of which 13 yods line each of its sides. When each of the n triangular sectors of an n-sided, regular polygon are turned into a 2nd-order tetractys, there are (85–13=72) independent yods per sector of the polygon. Its yod population = 72n + 1, where “1” denotes the yod at the centre of the polygon. The polygonal form of the inner Tree of Life consists of a triangle, square, pentagon, hexagon, octagon, decagon and dodecagon. They are enfolded in one another and share the same base, or what the author has called the “root edge,” as they should be thought of as

7

growing out of this fundamental line joining Daath and Tiphareth in the Tree of Life. When the seven separate polygons are superposed on one another in their enfolded state, corresponding members of the set of 13 yods forming what becomes their shared side coincide and therefore must not be counted separately in a calculation of their yod population. Below are listed the yod populations of each polygon and (except for the triangle) their numbers of yods outside the root edge:

Polygon	n	Number of yods = 72n + 1	Number of yods outside root edge
triangle	3	217	217
square	4	289	289 – 13 =   276
pentagon	5	361	361 – 13 =   348
hexagon	6	433	433 – 13 =   420
octagon	8	577	577 – 13 =   564
decagon	10	721	721 – 13 =   708
dodecagon	12	865	865 – 13 =   852
			Total = 3385

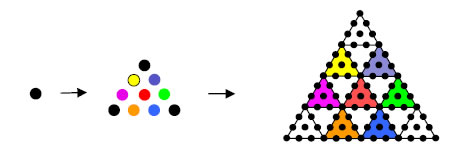
Inspection of Fig. 4 reveals that the tip of the triangle viewed with the root edge as its base is also the centre of the hexagon (the triangle is simply a triangular sector of the hexagon). Similarly, the tip of the pentagon is the centre of the decagon. With 2nd-order tetractyses as their sectors, the centroid of the triangle where corners of its three 2nd-order tetractyses meet is also the central yod of the tetractys at the centre of the 2nd-order tetractys constituting a sector of the hexagon (see diagram). The 11 yods between corners on each of the two sides of the triangle outside its shared base coincide with yods on the sides of this sector of the hexagon. There are (1 + 1 + 1 + 2×11 = 25) yods in the total population calculated above that coincide with yods belonging to other polygons (these are the only yods occupying the same positions). In determining the yod population when the separate polygons are superposed, these yods must be subtracted in order to avoid double-counting Therefore, the yod population of the seven enfolded polygons constructed from 2nd-order tetractyses = 3385 – 25 = 3360.

⁴ Ref. 2, p. 14.

⁵ Green, M.B. & Schwarz, J.H. “Anomaly cancellations in supersymmetric d = 10 gauge theory and superstring theory.” Physics Letters, B149, 117.

8