| << Previous 1... 13 14 15 16 [17] Next >> |
#17 The Holistic Nature of the 16-cell
Given that our discussion of the three polygons analogous to the Supernal Triad has revealed the 16-cell to be —
in that context —the most fundamental of the six polychorons because the 24-cell encoded in the three
polygons is a compound of three 16-cells, it is worthwhile to analyse its properties here in order to uncover
evidence of its holistic character. This will manifest by the appearance of the gematria number values of the 10
Sephiroth in the four Kabbalistic Worlds quantifying its properties and by its displaying structural parameters of
sacred geometries established elsewhere in this website. These numbers are listed in Table 3 in #2.
The 16-cell is the 4-dimensional version of the octahedron. It is composed of:
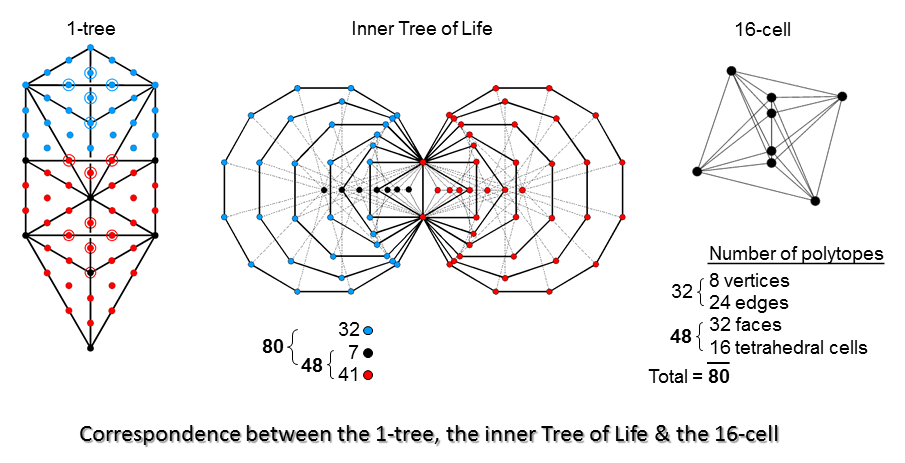
It has 80 0-, 1-, 2- & 3-polytopes, where 80 is the number value of Yesod ("Foundation"). This is the number of yods in the 1-tree constructed from tetractyses and the number of corners of the (47+47=94) sectors of the (7+7) enfolded polygons that are its inner form (see here). As evidence that the appearance of this Tree of Life parameter in the 16-cell is not coincidental but, instead, is indicative of the holistic nature of this polychoron as it belongs to the set of gematria number values of the 10 Sephiroth, observe that the distinction between the 7 Sephiroth of Construction and the rest of the 1-tree generates the division:
80 = 32 + 48
in yods (48 yods up to Chesed, the first Sephirah of Construction, and 32 blue yods above it). This division appears in the inner Tree of Life as the 48 sector corners that are either black centres of the 7 enfolded polygons in one set (see picture below) or the 41 red corners of the other set of 7 enfolded polygons and as the 32 blue corners of the former set of 7 polygons. It appears in the 16-cell as its 32 vertices & edges and its 48 faces & cells:

It would be incorrect to regard the 32 faces of the 16-cell as corresponding to the 32 yods above Chesed because one would, intuitively, expect the degree of complexity of polytopes in the 16-cell to increase with the downward descent from Kether towards Malkuth of the yods that symbolise them, but this correspondence disrupts the order by placing 2-polytopes before 1-polytopes, instead of the more natural progression: 0-polytopes→1-polytopes→2-polytopes→3-polytopes, which has been followed in the diagram above.
Suppose that the 16-cell is constructed both externally and internally from Type A triangles. The geometrical & yod compositions of the 6 polychorons are discussed here. The two compositions of the 16-cell are reproduced below:
C/C′/c = number of corners; S/S′/s = number of sides; T/T′/t = number of triangles; N/N′/n = total number of geometrical elements.
H/H′/h = number of hexagonal yods; B/B′/b = number of boundary yods; Y/Y′/y = total number of yods.
| Geometrical composition of the
16-cell |
Yod composition of the 16-cell |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(“1” denotes the centre of the 16-cell). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Comments
1) Its 32 triangular faces contain 256 geometrical elements, where 256 = 44. They
comprise:
This demonstrates very clearly how the Tetrad (4) expresses the geometrical composition of the faces of the 16-cell. It also expresses its interior, for there are 176 (=4×44) points, lines & triangles and 256 (=44) yods inside the 16-cell surrounding its centre. There are 248 geometrical elements other than the 8 vertices in its 32 faces, where 248 is the number value of Raziel, the Archangel of Chokmah. The dimension 248 of the rank-8 exceptional Lie group E8 is embodied in the facial geometry of a single 16-cell. The 248 geometrical elements comprise 128 corners & triangles and 120 sides. Its faces have (120+96=216) triangles & their sides, where 216 is the number value of Geburah. As 432 geometrical elements surround its centre, each half of the 16-cell contains 216 geometrical elements. The 16-cell has 168 triangles with 65 corners, where 65 is the number of ADONAI, the Godname of Malkuth, and 168 is the number of Cholem Yesodoth, the Mundane Chakra of this Sephirah. This conjunction of two gematria numbers associated with the same Sephirah is both remarkable and highly significant. 432 geometrical elements surround its centre ("1"), demonstrating once again the role of the integers 1, 2, 3 & 4 symbolised by the tetractys in expressing properties of the 16-cell. 264 corners & sides (64 corners, 200 sides) surround its centre, where 264 is the number of yods in the 7 enfolded Type A polygons that make up the inner Tree of Life (see Article 64, Table 5, and here). This embodiment of a primary parameter of the 7 enfolded Type A polygons of the inner Tree of Life is unmistakable evidence of the Tree of Life/holistic character of the 16-cell. It is confirmed by the fact that 24 of the 200 sides are edges of the faces of the 16-cell, leaving 176 sides of the 168 triangles that are not edges. Compare this with the fact that the 7 enfolded polygons have 176 corners, sides & triangles (see here). In both cases, the holistic structural parameter 264 divides up in the same way:
| 7 enfolded polygons: | 264 yods = 176 hexagonal yods on 88 sides + 88 corners & centres of 47 tetractyses; |
| 16-cell: |
264 corners & sides = 176 sides + (64+24=88) corners & edges. |
The 4 yods in the root edge of the 7 enfolded polygons correspond to any two opposite vertices and the
two sides of internal triangles that form an axis of the 16-cell (see (6) below). The 260
(=26×10) yods outside the root edge correspond to the 260 corners & sides outside this axis:
260 = 62 corners + 198 sides = 6 vertices + 56 corners + 24 edges + 174 sides. This is how YAHWEH
with number value 26 prescribes the 16-cell. Just as the 264 yods in the 7 enfolded polygons show
the factorisation: 264 = 3×88 as 2×88 (hexagonal yods) + 88 (corners & centres of tetractyses), so,
too, the 264 corners & sides of the 16-cell comprise the 88 sides in each half that are not edges and the
88 corners & edges of the whole polychoron. Isomorphism exists between the inner Tree
of Life and the 16-cell because the latter is the 4-dimensional manifestation of the former.
2) The 16-cell has 64 vertices, edges & faces, where 64 is the number value of Nogah, the Mundane Chakra of Netzach. It also has 64 corners of 168 triangles surrounding its centre. When its faces and interior triangles are simple triangles rather than Type A triangles, there are in its interior 24 internal triangles with one corner and 8 sides, totalling 9 corners, 32 sides & 56 triangles, i.e., 97 internal geometrical elements, where
97 = 21 + 26 + 50
is the sum of the Godname numbers of Kether, Chokmah & Binah; it is also the number value of Haniel, the Archangel of Netzach. When these triangles are tetractyses, there are (1 + 8×2 + 24 = 41) internal yods and (8 + 24×2 + 32 = 88) yods in its faces, a total of 129 yods, where 129 is the number value of YAHWEH SABAOTH, the Godname of Netzach. Nine yods are corners of 56 tetractyses, leaving 120 hexagonal yods, where
120 = 112 − 1 = 3 + 5 + 7 +... + 21
is the sum of the first ten odd integers after 1, showing how the Decad (and EHYEH with number value 21) determines the number of hexagonal yods needed to construct the 16-cell from tetractyses. 336 of the 632 yods surrounding the centre of the 16-cell with Type A triangles are hexagonal yods in its faces, leaving 296 yods (148 in each half) that are either corners or internal hexagonal yods. 148 is the number value of Netzach. Here is a conjunction of four numbers associated with the same Sephirah (Netzach). (96+16=112) points, lines, triangles & tetrahedra surround its centre, where 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod. The 16-cell has 48 faces (2-polytopes) & tetrahedral cells (3-polytopes), where 48 is the number value of Kokab, the Mundane Chakra of Hod.
3) 280 yods line the 96 tetractyses in its 32 faces. This is the number value of Sandalphon, the Archangel of Malkuth. Here is a second, remarkable, chance-defying conjunction in the same context of the gematria number values of the Godname (65), Archangel (280) & Mundane Chakra (168) of the same Sephirah (Malkuth). 140 yods line the 48 tetractyses making up the 16 faces in each half of the 16-cell, where 140 is the number value of Masloth, the Mundane Chakra of Chokmah. 376 yods make up its faces (188 in each half). 187 yods in the 16 faces in each half surround its axis, where 187 is the number value of Auphanim, the Order of Angels assigned to Chokmah. As (1) shows that the 16-cell embodies the number 248 of Raziel and the number 26 of YAHWEH and as (4) shows that it embodies the number 73 of Chokmah, here is a conjunction of all 5 numbers associated with the same Sephirah.
4) When its faces are simple triangles, they are lined by (8 + 24×2 = 56) yods; (1 + 8×2 = 17) yods line the 24 internal triangles formed by joining vertices to the centre of the 16-cell. (56+17=73) yods line its (24+32=56) triangles, 72 such yods surrounding its centre. The 16-cell embodies the number value 73 of Chokmah as the number of yods that line all its tetractyses, both externally and internally. 73 is the 21st prime number, showing how EHYEH, the Godname of Kether with number value 21, prescribes in a minimal way the form of the 16-cell. The number of yods in the 32 faces of the 16-cell = 56 + 32 = 88. There are 80 hexagonal yods, where 80 = 48 (lying on 24 edges) + 32 (at centres of 32 faces). It should be noticed that this division is the characteristic division of the 80 yods of the 1-tree and the 80 corners of the 94 sectors in its polygonal inner form that was discussed above. The double presence of this number in both the geometrical and the yod composition of the 16-cell is evidence that it acts as the polytopic "foundation." This another reason why it should be regarded as fundamental, i.e., the "hydrogen atom" of the polychorons, even though it is not the polychoron with the least number of vertices.
5) When its faces and interior triangles are simple triangles, there are (8+24=32) corners & sides of triangles in its faces and (1+8=9) internal corners & sides, a total of 41 corners & sides. This is both the 21st odd integer and the 15th prime number, showing how EHYEH, the Godname of Kether with number value 21 and YAH, the shortened Godname of Chokmah with number value 15, prescribe the minimal geometry of the 16-cell. Collecting together results discussed in (1), (3) & (4), all 6 numbers associated with the Sephirah Chokmah are now seen to be naturally embodied in the 16-cell.
6) If we consider an axis passing through two opposite vertices and its centre, it is composed of 3 corners and two sides of triangles. Therefore, (41−3−2=36) corners & sides surround it. This is the number value of ELOHA, the Godname of Geburah. 632 yods surround the centre of the 16-cell. This means that, given its centre and two "poles" (a pair of vertices at ±1 on the axis), 630 yods are needed to construct its 168 tetractyses. 630 is the number value of Seraphim, the Order of Angels assigned to Geburah. The 97 points, lines & triangles include two lines forming this axis. The 16-cell contains 95 points, lines & triangles other than these two axial lines, where 95 is the number value of Madim, the Mundane Chakra of Geburah. Surrounding the centre of the 16-cell with Type A triangles are 264 corners & sides, i.e., 262 geometrical elements other than these two lines. Each half has 131 such geometrical elements. This is the number value of Samael, the Archangel of Geburah. The 16-cell embodies all five number values associated with Geburah.
7) The 32 faces of the 16-cell contain 336 hexagonal yods (96 at centres of tetractyses, 240 lining their 120 sides). This number is discussed widely on this website as a superstring structural parameter embodied in sacred geometries, being the number of turns in one revolution of each helical whorl of a UPA (subquark state of the E8×E8 heterotic superstring) around its axis of spin. Together with the above examples of how the Godnames prescribe its properties, here is irrefutable evidence that the 16-cell is a holistic object, for it is highly improbable that a number appearing in so many sacred geometries would turn up in this context just by chance. Rather, the number 336 does so in the 16-cell because it, too, is holistic, so that this number must quantify at least one of its properties, viz., how many hexagonal yods are needed to construct its faces out of Type A triangles.
8) The symmetry group of the n-cube and its dual, the n-dimensional cross-polytope, is Bn, and is known as the hyperoctahedral group. It has order 2nn!. For n = 4, this is 384. B4 has the subgroup D4 with order 192. This is the group of rotations of the 4-cube and the 16-cell. D4 has the subgroup D3, which is the group of rotations of the cube and octahedron. The holistic parameters 384 and 192, which show the divisions:
384 = 48 + 336
and
192 = 24 + 168,
signify in the present context the 384 rotations+reflections of the 4-cube and 16-cell, the 48 rotations+reflections of their 3-dimensional counterparts — the cube and the octahedron, the 192 proper rotations* of the 4-cube and 16-cell and the 24 proper rotations of the cube and octahedron. The appearance of the holistic parameters 384 & 192 as orders of the hyperoctahedral group for 4-polytopes does not mean that all sacred geometries that embody these numbers depict only the symmetries of 4-dimensional objects. For example, the 5 Platonic solids embody them (see here), as do the 7 separate polygons making up the inner form of the Tree of Life (see here). What it does mean is that such objects, in which these numbers uniquely appear, are holistic in character, exhibiting the complete pattern of the Whole, even though they may be only components of it. The Whole is reproduced in its parts.
The rotating 16-cell.
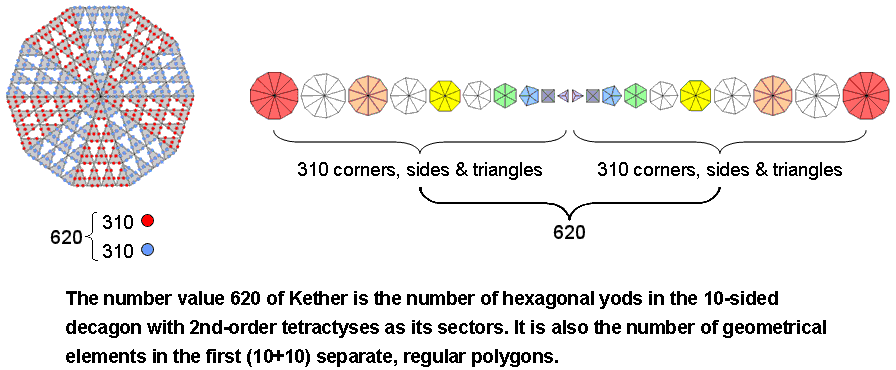
9) 632 yods surround the centre of the 16-cell constructed from Type A triangles. There are 4 hexagonal yods lining the axis. Surrounding the axis are (632−4−8=620) yods that are not vertices. In other words, 620 yods need to be added to create its shape from Type A triangles. This is the number value of Kether ("Crown"). It is:
 |
 |
|
When its 10 sectors are constructed from 2nd-order tetractyses, the decagon contains 620 hexagonal yods (310 hexagonal yods in each 5-fold array of sectors). The 1st 10 regular polygons have 75 sectors. One corner, two sides & a triangle are associated with each sector, i.e., 4 geometrical elements. Including their centres, the 1st 10 separate polygons are composed of (75×4 + 10 = 310) geometrical elements. The 1st (10+10) separate polygons comprise (310+310=620) geometrical elements. |
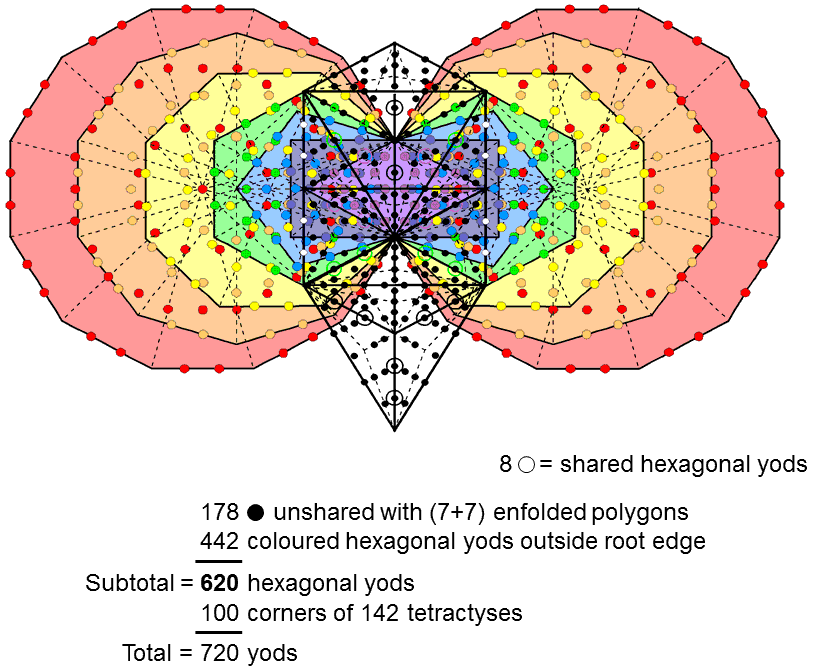
When its 16 triangles are Type A, the Tree of Life contains 214 yods. 26 yods are corners and 188 are hexagonal yods. The two hexagonal yods on the Geburah-Chesed Path coincide with the centres of the two triangles in the inner Tree of Life. 4 hexagonal yods on each side pillar are shared with it. (188−2−4−4=178) hexagonal yods are unshared with the inner Tree of Life, which has 444 hexagonal yods (442 outside the root edge, which has two hexagonal yods). The number of hexagonal yods outside the root edge in the combined Trees of Life = 178 + 442 = 620. |
These examples demonstrate how the number 620 of Kether (the first Sephirah) is a parameter of holistic systems. 310 (=31×10) such yods in each half of the 16-cell surround this axis. 31 is the number value of EL ("God"), the Godname of Chesed. 62 corners of tetractyses surround the axis. This is the number value of Tzadkiel, the Archangel of Chesed. We found in (4) that 72 yods line the 56 tetractyses in either its faces or interior when its faces and internal triangles are tetractyses. 72 is the number value of Chesed. 432 geometrical elements surround its centre. The axis is composed of two vertices, two sides and the centre. Surrounding it are (432−2−2=428) geometrical elements, where 428 is the number value of Chasmalim, the Order of Angels assigned to Chesed. Here is another remarkable conjunction of gematria number values (this time, four) associated with the same Sephirah.
10) The number of yods in the 16-cell other than the 5 internal yods on its axis = 633 − 5 = 628. Each half of the 16-cell has 314 yods other than yods inside it on its axis. The number 314 is the number value of Metatron, the Archangel of Kether. The number of yods in the 16-cell other than vertices = 633 − 8 = 625 = 54. There are 624 such yods surrounding its centre. This is the number of hexagonal yods in the 7 separate Type B polygons that make up the inner form of the Tree of Life:
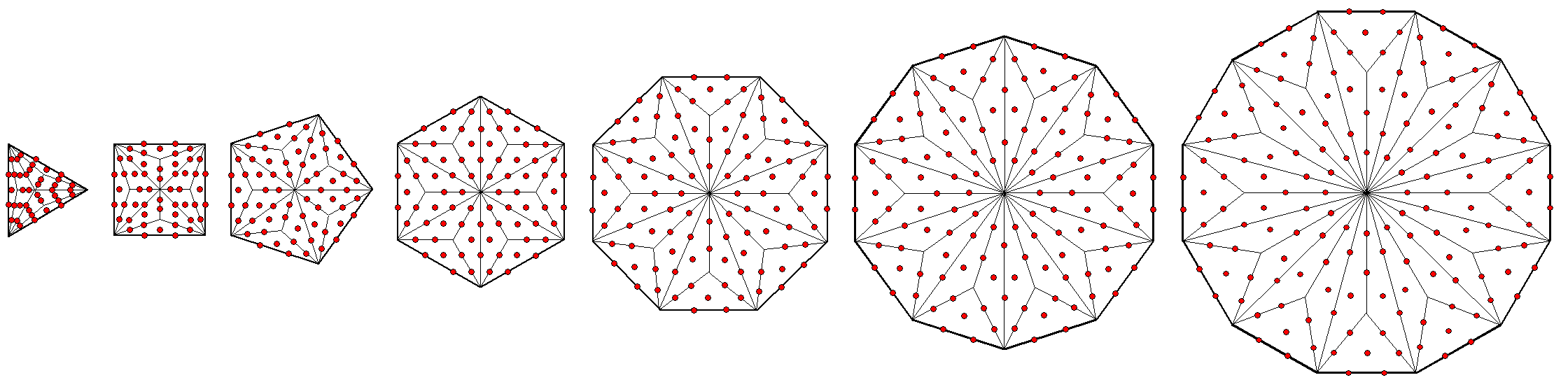 |
A Type B N-gon has (15N+1) yods that comprise (2N+1) corners & 13N hexagonal yods. The number of hexagonal yods in the 7 Type B polygons with 48 corners = ∑13N = 13×48 = 624. This is the number of yods needed to construct the 16-cell from Type A triangles, starting with its 8 vertices. |
11) The 16-cell has 568 hexagonal yods. Four of them line the axis, so that (568−4=564) hexagonal yods surround it. 282 such yods in each half of the 16-cell surround its axis. The number value of Aralim, the Order of Angels assigned to Binah, is 282. Surrounding its centre are 464 yods lining sides of 168 tetractyses. Six yods apart from the centre lie on the axis. (464−6=458) boundary yods surround the axis, 229 such yods in each half. 229 is the 50th prime number, showing how ELOHIM, the Godname of Binah with number value 50, prescribes the number of yods needed to shape the faces and interior of the 16-cell constructed from Type A triangles. 632 yods surround the centre of the 16-cell, 316 yods being in each half. Including the centre, which is shared by both halves, there are 317 yods in each half. 317 is the number value of Shabathai, the Mundane Chakra of Binah. Excluding the two hexagonal yods on each half of the axis and the 4 vertices in each half of the 16-cell, there are (317−2−4=311) yods in each half sharing the centre. 311 is the number value of Tzaphkiel, the Archangel of Binah. The axis has one corner and two sides inside the 16-cell. When they are simple triangles, the 32 faces comprise 32 corners & sides. The faces & axis comprise 9 corners, 26 sides & 32 triangles, i.e., 67 geometrical elements, where 67 is the number value of Binah. The 16-cell embodies all 5 number values associated with this Sephirah.
|
The fact just proven above that all the Kabbalistic gematria number values of the 10 Sephiroth emerge naturally from analysis of the geometrical and yod compositions of the 16-cell is powerful evidence of the holistic nature of this polychoron. Had the appearance of these numbers been manufactured artificially by adding numbers that referred to unrelated contexts, the five numbers associated with the same Sephirah would be scattered about randomly in unconnected contexts. Instead, they often appear in the same, mathematical context with a frequency that exceeds chance. This is indicative of a coherent design or conceptual order that exists because the 16-cell is a holistic object. The gematria numbers quantify 10 sets of properties of the 16-cell, each set expressing the mathematical aspect of a Sephirah functioning in the four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah & Assiyah. As we shall discover below, the 16-cell displays the same universal patterns in its structural parameters as those found in sacred geometries. |
Each half of the 16-cell has (28×3=84) sectors of 28 Type A triangles. The 16 faces in each half has (3×16=48) sectors and its 12 internal Type A triangles have (12×3=36) sectors. This 36:48 division in the 84 simple triangles making up each half of the 16-cell is characteristic of holistic systems that embody the number 84 as one of their defining parameters. For example:
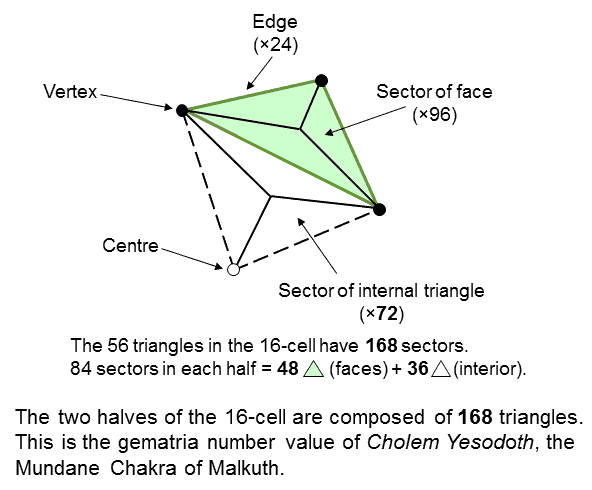 |
|
||||||||
7 Diatonic scales as the musical counterpart of the 16-cell
The
same 36:48 division of the holistic parameter 84 appears in
the 84 repetitions of Pythagorean intervals** between the notes of the 7 diatonic musical scales making up the 8
Church Modes. The 4 Authentic Modes have 48 repetitions of Pythagorean intervals between
their notes, whilst the 3 Plagal Modes have 36 repetitions of Pythagorean intervals between
their notes (for proof, see the fourth comment under the table of intervals here). One half of the 16-cell with 84 triangles is analogous to the
84 repetitions of rising, Pythagorean intervals; its opposite half with 84 triangles corresponds to the
84 repetitions of falling, Pythagorean intervals (N.B. if a rising interval has an interval of N
(N>1), its falling counterpart has an interval of 1/N). The 48 triangles making up the
16 faces in each half of the 16-cell are analogous to the 48 repetitions of Pythagorean
intervals between the notes of the 4 Authentic Modes, whilst the 36 triangles inside each
half of the 16-cell correspond to the 36 repetitions of Pythagorean intervals (rising or
falling) between the notes of the 3 Plagal Modes. The distinction between the exterior and interior of the
16-cell is what corresponds to the difference between the 4 Authentic Modes and the 3 Plagal Modes making up the
7 diatonic scales.
The 84:84 division in the UPA/superstring
The 84 sectors in each half of the 16-cell has their counterpart in the UPA/superstring. Each of its 10 whorls is a
helix with 1680 circular turns. The helix winds 5 times around its axis of spin, so that every half-revolution
comprises 168 turns (84 per quarter-revolution).
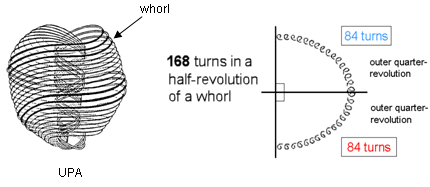 |
The rotating 16-cell. Each half has 28 triangles with 84 sectors. |
The 84:84 division in the inner Tree of Life
As evidence that the 16-cell is
a holistic object containing features analogous to those found in certain sacred geometries, consider the inner
Tree of Life when its polygons are either Type A or Type B:
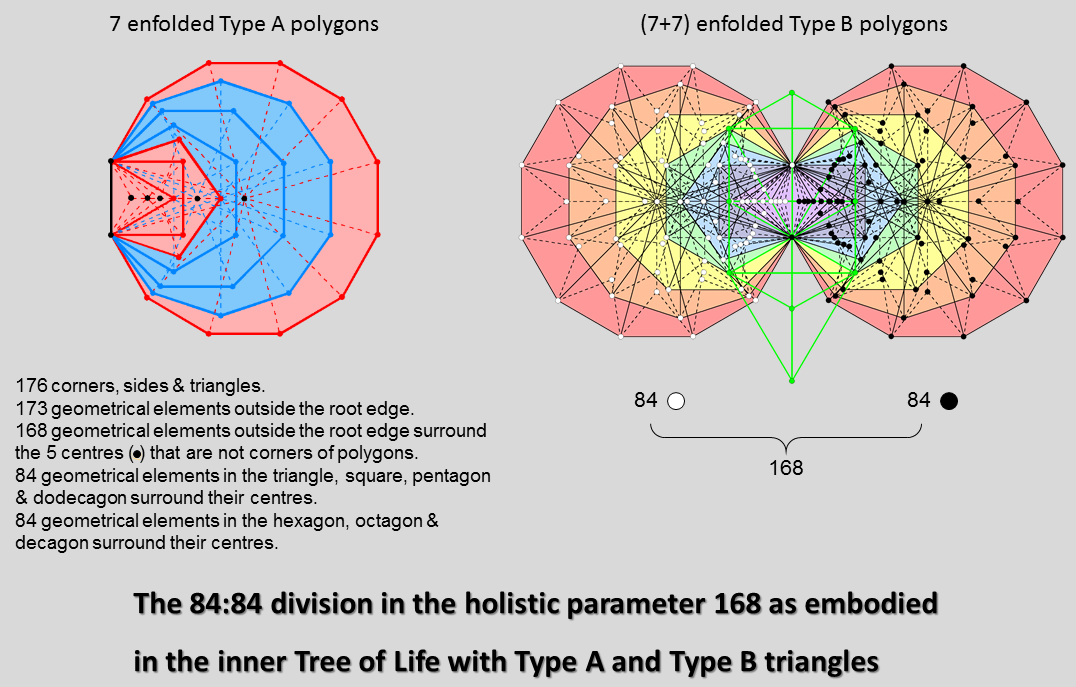 |
Type A polygons
The 7 enfolded Type A polygons have 176 corners, sides &
triangular sectors (see Table 3 here). Their shared root edge is a side with a corner at each end, i.e.,
it is composed of 3 geometrical elements, so that (176−3=173) geometrical elements are outside the root edge.
The centres of the hexagon and decagon are also corners of, respectively, the triangle and the pentagon.
Therefore, 5 centres (shown as black dots in the picture above) are not corners of polygons. They
are surrounded by (173−5=168) geometrical elements outside the root edge. The centre of a Type
A n-gon divided into its n sectors is surrounded by 4n geometrical elements. The separate Type A triangle,
square, pentagon & dodecagon with 24 corners have (4×24=96) geometrical elements surround their centres.
Enfolded, they have (96 − 3×3 = 87) such geometrical elements, i.e., (87−3=84)
geometrical elements surrounding centres of polygons are outside the root edge, where
87 is the number value of Levanah, the Mundane Chakra of Yesod. The hexagon,
octagon & decagon with 24 corners have (168−84=84) geometrical elements outside the root
edge that surround their centres.
Type B polygons
The 7 enfolded Type B polygons have 141 triangles with 88 corners. The (7+7) enfolded Type B polygons have
282 triangles with 174 corners, where 282 is the number value of
Aralim, the Order of Angels assigned to Binah. Three corners lying on the vertical axis of the hexagon
coincide with corners of triangles belonging to the outer form of the Tree of Life (coloured green in the diagram).
(174− 2×3 = 168) corners are intrinsic to the inner Tree of Life. Each endpoint of
the root edge can be associated with one set of 7 enfolded polygons. This means that 84 intrinsic corners can be
associated with each set. They are the counterpart of the (84+84) triangles in the two halves of the 16-cell. As
the set of 7 enfolded Type A polygons have 47 sectors with 41 corners, (41−2−3=36) corners outside
the root edge are intrinsic to each set. They are coloured dark blue or light blue in the diagram below:
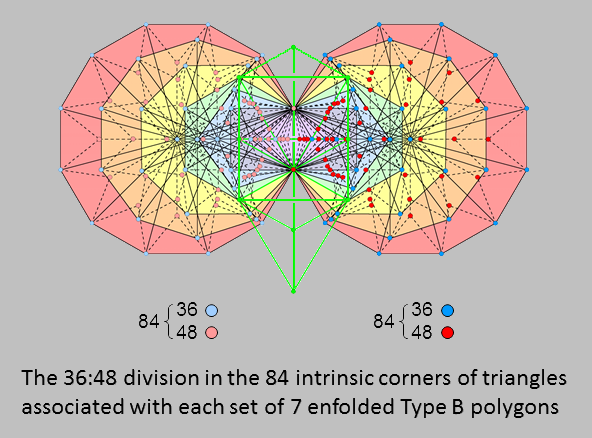
The remaining 48 corners consist of the corners at the centres of the 47 sectors and one of the two endpoints of the root edge; they are coloured either dark red or light red. The 36 light or dark blue corners correspond to the 36 triangles making up the 12 Type A triangles inside each half of the 16-cell, whilst the 48 dark red or light red corners correspond to the 48 triangles making up the 16 faces in each half when they are Type A triangles. We find that the 84 triangles making up each half of the 16-cell are the counterpart of these 84:84 divisions exhibited by the two halves of the inner Tree of Life. Furthermore, each set of 84 triangles displays the 36:48 division that is characteristic of this holistic parameter, as illustrated above for various sacred geometries, including the inner Tree of Life. It is evidence that the 16-cell is the polychoron version of the archetypal structure of a holistic system.
36:48 & 84:84 divisions in the square representation of 624
As
132 − 1 = 168 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25,
the holistic parameter 168 is the sum of the first 12 odd integers after 1. As
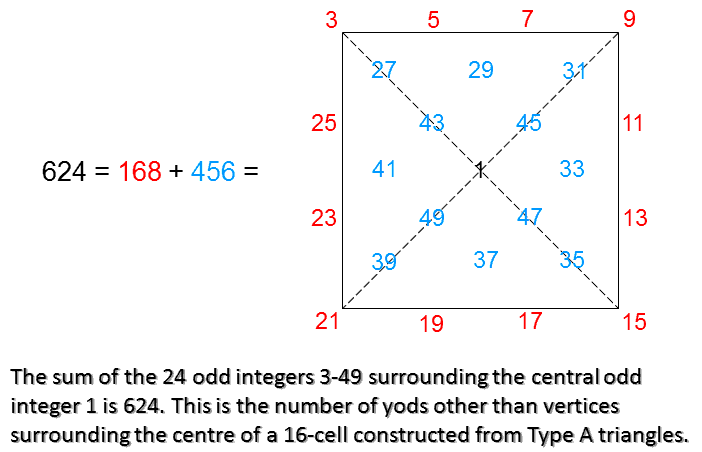
252 − 1 = 624 = 3 + 5 + 7 +... + 49 = 168 + 27 + 29 + ... + 49 = 168 + 456,
and a Type A square has 25 yods, the number of yods other than vertices (624) surrounding the centre of a 16-cell constructed from Type A triangles is the sum of the 24 odd integers 3-49 that can be assigned to the 24 yods surrounding the centre of a Type A square:
 |
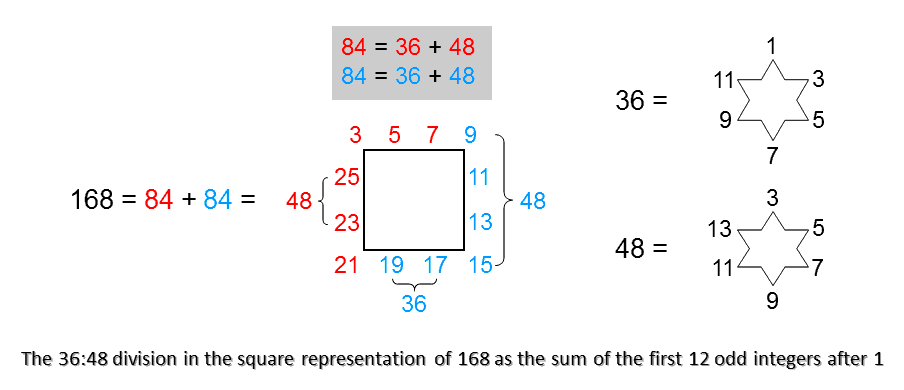 |
The sum of the first 12 odd integers after 1 assigned to the 12 yods on the boundary of the square is 168, which is the number of hexagonal yods at the centres of its 168 tetractyses. The sum of the remaining 12 odd integers assigned to the 12 internal yods surrounding the centre of the square is 456, which is the number of yods other than vertices that line the sides of the 168 tetractyses. The central integer 1 denotes the centre of the 16-cell. Here is a remarkable arithmetic representation of the number of yods needed to construct the 16-cell from Type A triangles. What is also remarkable is that the red and blue, L-shaped sides of the square array each add up to 84, the integers in either one naturally adding up to 36 and 48 to generate arithmetically the 36:48 division that is characteristic of this holistic parameter. Moreover, 36 is the sum of the first 6 odd integers, whilst 48 is the sum of the first 6 odd integers after 1. The number of yods needed to construct the 16-cell from Type A triangles is not only the number of hexagonal yods in the 7 separate Type B polygons making up the inner Tree of Life but also the sum of the 24 odd integers after 1 that can be assigned to the 24 yods surrounding the centre of a Type A square. Instead of these congruencies between number and sacred geometry being dismissed as just a coincidence, it is more plausible to see them as yet more evidence for the holistic nature of the 16-cell.
A remarkable property of the yod population (633) of the 16-cell is:
137 + 496 = 633.
Many physicists regard the number 137 as one of the most mysterious numbers because its reciprocal measures approximately what they call the "fine-structure constant," which, in electrostatic c.g.s. units, is defined as α = e2/ħc ≅ 1/137. Many sceptics of superstring theory view the dimension 496 of E8×E8 and SO(32) (the only two gauge symmetry groups that leave superstring interactions free of quantum anomalies) as equally mysterious because no one has ever convincingly proposed a theory that derives either number from fundamental principles. The latter emerges only from imposing consistency of these interactions with quantum mechanics. Both numbers are parameters of sacred geometries (e.g., the yod population of the inner Tree of Life with Type B polygons is 1370, which is the number of yods in 137 tetractyses; see here). There is, therefore, no longer any mystery about either number because both of them characterise all holistic systems, including superstrings. For examples of their presence in sacred geometries, see The holistic pattern under the headings "137" and "496 = 248 + 248."
Another remarkable property of the number 633 is that:
385 + 248 = 633,
where
385 = 12 + 22 + 32 +... + 102
is the 10th square pyramidal number and 248 is the dimension of E8. The first 10 Type A polygons have 75 sectors lined by 385 yods (see Table 2 in Article 58). As
496 = 248 + 248,
∴ 137 + 248 = 385.
The number 385 is another holistic parameter, although the number 384 is, usually, the more visible signature of its presence, the extra "1" denoting merely the centre of the system. As 632 yods surround the 16-cell,
384 + 248 = 632.
The number of yods surrounding the centre of the 16-cell is the sum of the holistic parameters 384 & 248.
Let us investigate what the first highlighted equation means for a 16-cell constructed from tetractyses. The diagram below depicts a Type A triangular face of an upper and a lower half of the 16-cell, together with a Type A internal triangle with an edge as one side and the centre of the polychoron as its interior corner:
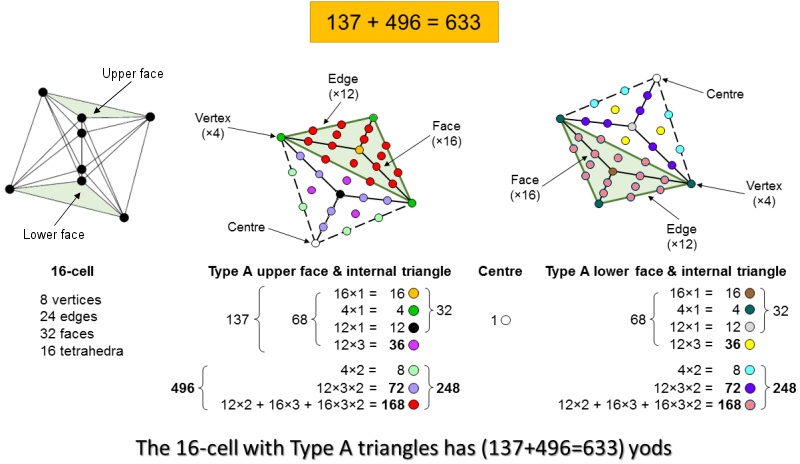 |
137
The upper half has 16 faces with 4 green vertices. Its 16 triangular faces have orange centres. Its 12 internal
Type A triangles has black centres, 3 violet hexagonal yods at the centres of the sectors of each one and 6
dark grey hexagonal yods lining their sides. The lower half has 16 faces with 4 dark green vertices and a
brown yod at the centre of each face. Its internal Type A triangles have light grey centres, 3 yellow
hexagonal yods at the centres of their sectors and 6 mauve hexagonal lining their sides. Each half has (3×12 +
3×16 = 84) tetractyses with 32 corners and 36 internal hexagonal yods (violet/yellow). Together
with the centre of the 16-cell, there are [1 + 2(32+36) = 137] yods that are either corners
(65) or hexagonal yods (72) at the centres of internal
tetractyses.
496
Four vertices in each half of the 16-cell are joined to the centre of the 16-cell by 4 sides with 8 hexagonal yods
(light green/turquoise). 72 hexagonal yods (dark grey/mauve) line the 3 tetractyses in each
internal Type A triangle and 168 hexagonal yods (red or dark green) either line the tetractyses in
the faces or are at their centres. Each half comprises
(8+72+168=248) yods that are not either corners or centres of
internal tetractyses. Both halves contain (248+248=496) such
yods. They correspond to the (248+248=496) roots of
E8×E8. The following correspondences exist between the 248 yods and the
248 roots of E8 (the properties refer to each half of the
16-cell):
 |
|
The hexagonal yod composition of the 16-cell is isomorphic to the 8:72:168 root composition of each E8 in E8×E8, each half of the 16-cell containing 248 yods that correspond to the 248 roots in E8. This is amazing but not unexpected, for the 16-cell is, after all, a holistic object, so that it must display all the parameters that characterise such objects, one of which is the number 496, whose origin is still so mysterious to superstring physics. Here we find it embodied in the 16-cell, along with the equally enigmatic number 137, whose reciprocal physicists have long known is approximately equal to the fine-structure constant, as discussed earlier. Their mystery vanishes once it is understood that they belong to a class of numbers that parameterise those geometrical objects (or, more generally, holistic systems) that embody the divine archetypes, such as certain sacred geometries of the world's religions. The numbers 137 and 496 appear in atomic and particle physics because they are signatures of holistic systems. The problem of their appearance there exists only for the philosophy known as "scientism." This refuses to countenance the possibility of the transcendental as the ultimate source and cause of all things, and it has no room for the notion of "holistic" as it confuses what it deems irrational with what is beyond the bounds of science because it is supra-rational and the divine source of all rationality.
The identity:
384 + 248 = 632
has the following interpretation in terms of the various classes of yods making up the 632 yods that surround the centre of the 16-cell:
384 = [16 centres of faces + 4×2 hexagonal yods] + 168 hexagonal yods in faces in one half + [16 centres of faces + 4×2 hexagonal yods] + 168 hexagonal yods in faces in the other half
= (24+168) + (24+168) = 192 + 192.
248 = 8 vertices + 24×3 hexagonal yods at centres of internal tetractyses + [24 centres of internal Type A triangles + 24×3×2 hexagonal yods on sides of internal tetractyses]
= 8 + 72 + 168.
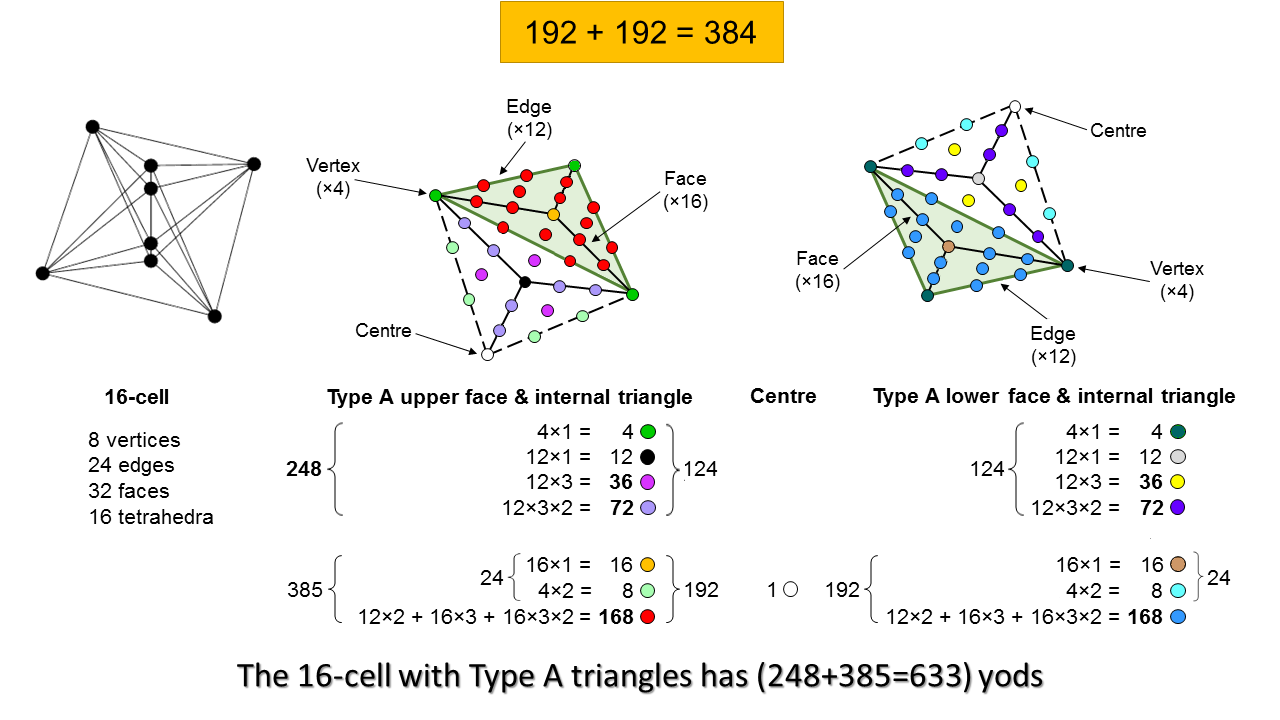 |
We find that the classes of yods in the 16-cell naturally make up a set of 384 yods (192 yods in each half) whose distribution in 4-dimensional space conforms to the archetypal pattern of division of a holistic system (see here). We also find that the remaining 248 yods naturally divide into a set of 8 yods corresponding to the 8 simple roots of E8, a set of 72 hexagonal yods corresponding to the 72 roots of E6 and a set of 168 yods corresponding to the remaining 168 roots of E8. There are too many correspondences to be attributable to chance. Its embodiment of the dimension 248 of E8, the dimension 496 of E8×E8 and the 192:192 pattern governing holistic systems found in sacred geometries amounts to convincing evidence for the holistic character of the 16-cell.
Paranormally-derived numbers do not appear by coincidence
in polychorons connected to the superstring symmetry group E8
Now let us
examine the 16-cell composition of the compound of two 600-cells that is the E8 Coxeter plane
projection of the 421 polytope. Each 600-cell is a compound of 5 24-cells, each 24-cell being a
compound of 3 16-cells. We found above that 56 yods line the 24 edges of a 16-cell when its faces are tetractyses.
Hence, (3×56=168) yods line the (3×24=72) edges of 3 16-cells in a 24-cell and
1680 yods line the 720 edges of the 30 16-cells in 10 24-cells (840 per 5 24-cells or
15 16-cells in a 600-cell). The number of boundary yods shaping all
the 16-cells in two 600-cells is the very number of circular turns in each helical whorl of the UPA, which has an
outer half comprising 840 turns and an inner half comprising 840 turns! Can anyone believe that
this is merely a coincidence? Well, perhaps one could do so with justification if two 600-cells had no connection
whatsoever to the symmetry groups describing superstring forces. But they do have a connection, for
their compound is the E8 Coxeter plane projection of the 240 vertices of the
421 polytope, which mathematicians know represents the 240 roots of E8, the very
symmetry group that appears (twice) in E8×E8 heterotic superstring theory! Moreover, the
factorisation of 840 here is 5×168, where "5" denotes the 5 24-cells. Compare this with
Leadbeater's account (summarised here), in which each whorl of the UPA revolves 5 times around its axis of
spin, making 5 half-revolutions in its outer spiralling and 5 half-revolutions in its inner windings. It would
seem that the natural conclusion is that the outer and inner halves of the UPA are the string manifestation of
the E8 gauge charges associated with the 120 vertices of each 600-cell, the 5 half-revolutions
of the 10 whorls in each half being the string manifestation of gauge charges associated with 5 24-cells.
However, this cannot be the entire explanation, because the UPA has 16800 turns in its 10 whorls, whereas the
number of boundary yods in the 30 16-cells is only 1680 (the number of turns in one whorl). The
reader should understand that it is not being claimed here that this correlation amounts to the whole story, for
the dynamic connection between circularly polarised, string-like oscillations and the yod composition of
16-cells has still to be elucidated. It is therefore more accurate to say that the 1680 boundary yods
correspond to the 1680 turns that make up — not a whorl — but a
half-revolution of all 10 whorls of the UPA. After all, its 10 whorls are what constitute the
E8×E8 heterotic superstring, not a single whorl. Despite two 600-cells
being a compound of 10 24-cells, a single 24-cell is not the basis in some still unexplained way
for each whorl of the UPA. After all, the 421 polytope merely represents through its 240
vertices the 240 roots of E8 in an 8-dimensional space; it does not map as well the 3-dimensional
structure of the UPA. Rather, because each whorl twists 10 times through an angle of 180°, every
one of the 10 24-cells is associated with a rotation through a half-circle of all 10 whorls of the UPA, each one
having the topology of a 1-torus. What is significant here is that, just as the E8 Coxeter plane
projection of the 421 polytope is a compound of 10 24-cells, so, too, the 10 whorls of the UPA
make 10 half-revolutions around its axis of spin. Both systems are 10-fold because
they are holistic objects. In fact, the UPA is the realisation in 10-dimensional space-time of
the E8-symmetric superstring force whose 240 gauge charges are mapped by the 240 vertices of the
421 polytope. The crucial point to be noted is that numbers like 168, 336, 840,
1680, 3360 & 6720, which the author points out quantify what he claims are
E8×E8 heterotic superstrings remote-viewed over a century ago,
naturally appear among the properties of objects known to be mathematically connected to the
symmetry group E8 describing the unified force between these very superstrings! Moreover, they
do so with a frequency that any reasonable person can see renders coincidence highly improbable. For the
16-cell, it is as obvious as its 168 triangles. Just how credible is it to attribute the
appearance of just this number to chance, let alone all the other numbers? How, otherwise, can we account for
the natural appearance in the 16-cell of all the Kabbalistic numbers except in terms of
transcendental, mathematical design, as revealed through gematria in the sacred ancient Hebrew alphabet? There
is no alternative, realistic explanation for how they quantify the properties of the 16-cell in
such an uncontrived way. Such numbers appear for the simple reason that — like
E8×E8 heterotic superstrings — the objects that embody them are all examples of
holistic systems expressing the divine archetypes — a concept which, of course, most
scientists deliberately exclude from consideration, although they do so for no better reason than
that they do not accept as a matter of principle that such systems can exist. Let us be plain:
there is only one sensible explanation for why certain numbers allegedly obtained by
remote-viewing subatomic particles turn up in the 421 polytope, E8 and its
exceptional subgroups so often as to make it highly improbable that this could happen by chance. It is that
the UPA described by Leadbeater really is an
E8×E8 heterotic superstring. It is as simple and as obvious as that! The
alternative explanation requires all these numerous appearances of numbers supposedly obtained by paranormal
means to be miraculous coincidences — a possibility which, statistically speaking, is so highly improbable that
no one with any common sense would take it seriously. Is it any more rational or
more reasonable to reject an ideologically problematic explanation, viz., UPAs are remote-viewed
E8×E8 heterotic superstrings, in favour of one that is more acceptable to one's
materialistic philosophy but requires having to believe that comments 1-11 listed above reveal nothing
more significant than the chance appearance of numerous Kabbalistic numbers? Why, for the sake of scientific
propriety, should we have to accept that this absurd explanation is preferable when it is preferred by sceptics
for no better reason than that it avoids their having to accept that the paranormal ability to remote-view
subatomic particles exists because of overwhelming evidence that it was successfully demonstrated by the
Theosophists Annie Besant and C.W. Leadbeater? Why should a personal ideology trump common sense as to what can
be plausibly attributed to coincidence?! Well, of course, it should not do so. But it will for
materialists who, faced with evidence that they cannot deny, try to salvage their cherished philosophy by
any means they can find, whether it is credible or not. However, a more sensible person unbiased by
philosophical viewpoints such as atheism or materialism will see the desperate appeal by sceptics to chance for
what it clearly is, viz., blatant confirmation bias exhibited by those who habitually refuse to recognise
any evidence — however strong — that discredits their ideological aversion towards the paranormal and the
transcendental and who resort to unreasonable explanations requiring multiple miracles of coincidence to occur
in order to provide themselves with any excuse — however flimsy — for rejecting this evidence. In
science, prima facie evidence for a phenomenon, whatever the implications of its
existence, must always trump personal presuppositions about what is — and what is not — possible,
otherwise its assessment ceases to be scientific as it becomes subjective. But that, unfortunately, is
not how every scientist thinks....
* Proper rotations are pure rotations about an axis unaccompanied by reflections. Improper
rotations are rotations about an axis followed by reflection in a mirror perpendicular to that axis. For more
details, see here.
** "Pythagorean intervals" are intervals that are equal to tone ratios of the 6 notes between the tonic and
octave of the Pythagorean scale.
| << Previous 1... 13 14 15 16 [17] Next >> |