#2 Introduction and Formulae

The inner form of the Tree of Life comprises two similar sets of seven enfolded, regular polygons, one set being the mirror image of the other set (Fig. 1):

The (7+7) enfolded polygons of the inner Tree of Life	The (7+7) separate, regular polygons
Figure 1. The inner Tree of Life comprises 7 types of regular polygons: triangle, square, pentagon, hexagon, octagon, decagon & dodecagon.

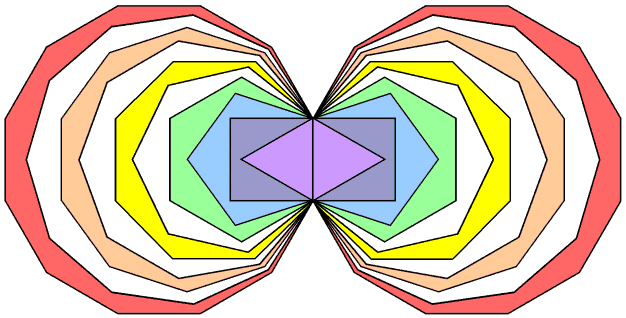
As the dodecagon is the tenth regular polygon, three polygons are absent from the inner Tree of Life: the 7-sided heptagon, the 9-sided nonagon & the 11-sided undecagon. They are shown coloured white in Figure 2, the seven other types of polygons belonging to the inner Tree of Life being coloured the seven colours of the rainbow. This absence of three polygons from the first 10 regular polygons suggests the following analogy between the first 10 regular polygons and the 10 Sephiroth of the Tree of Life:

• the three types of "absent polygons" → three Sephiroth belonging to the Supernal Triad, which express the subjective, 3-fold aspect of God (the triple Godhead) and which stand outside all levels of reality;  
• the seven types of polygons making up the inner Tree of Life → seven Sephiroth of Construction, which express the objective, 7-fold aspect of God and which manifest in His Creation.

Figure 2. The first (10+10) enfolded, regular polygons.

If we take this analogy seriously, it means that the two sets of heptagons, nonagons & undecagons express the geometric archetypes embodied in the Supernal Triad of Kether, Chokmah & Binah. They correspond in some religions to the triple Godhead (e.g., the Christian Trinity of the Father, the Son & the Holy Spirit, the Hindu trimûrti of Shiva, Vishnu & Brahma, the Three Pure Ones of Taoism and the first triad of the Ennead, the group of nine deities (neteru) in Egyptian mythology worshipped at Heliopolis (Fig. 3).

The heptagon. the nonagon and the undecagon are the three regular polygons in the first 10 polygons that are absent from the seven other types of polygons making up the inner form of the Tree of Life.	In Christianity, the triple Godhead is the Holy Trinity of God the Father, God the Son and God the Holy Spirit (symbolised in the painting above by a white dove),	The Hindu Trimûrti of Brahma the creator, Vishnu the maintainer or preserver and Shiva the destroyer or transformer. Sculpture on Elephanta Island, near Mumbai, India. Image source: commons.wikimedia.org Reference: en.wikipedia.org: Elephanta Caves Trimurti	The Three Pure Ones are the three highest gods in the Taoist pantheon. They emerge from the Tao. According to Daozang (the Taoist Canon), Loaze, the founder of Taoism, was one of the incarnations of Daode Tianzun, the third Pure One. Source: https://www.gutenberg.org/files/15250/15250-h/15250-h.htm#d0e2190	Atum is the first self-created god of the ancient Egyptian pantheon. He created Shu, the god of air, and Tefnut, the goddess of moisture. Author: Jeff Dahl. Source: https://commons.wikimedia.org/wiki/File:Atum.svg

Figure 3. As will be proved in the following pages, the analogy between the three aspects of the Godhead and the three polygons absent from the inner Tree of Life is more than formal; it is also mathematical. Although there is only one God,  the subjective nature of God is three-fold and the objective nature of God is seven-fold. The anthropomorphic representations of God in religions — whether monotheistic or polytheistic — are the representations of these divine attributes. At the exoteric level of religions, these representions are understood mostly in concrete terms as characters in a mythology; at the esoteric level, they are understood abstractly as cosmic principles, which these characters symbolise.

Which polygon should correspond to each Person of the Godhead is an issue that need not be resolved at this point. The geometrical and yod compositions of the first 10 regular polygons are analysed in Article 58.

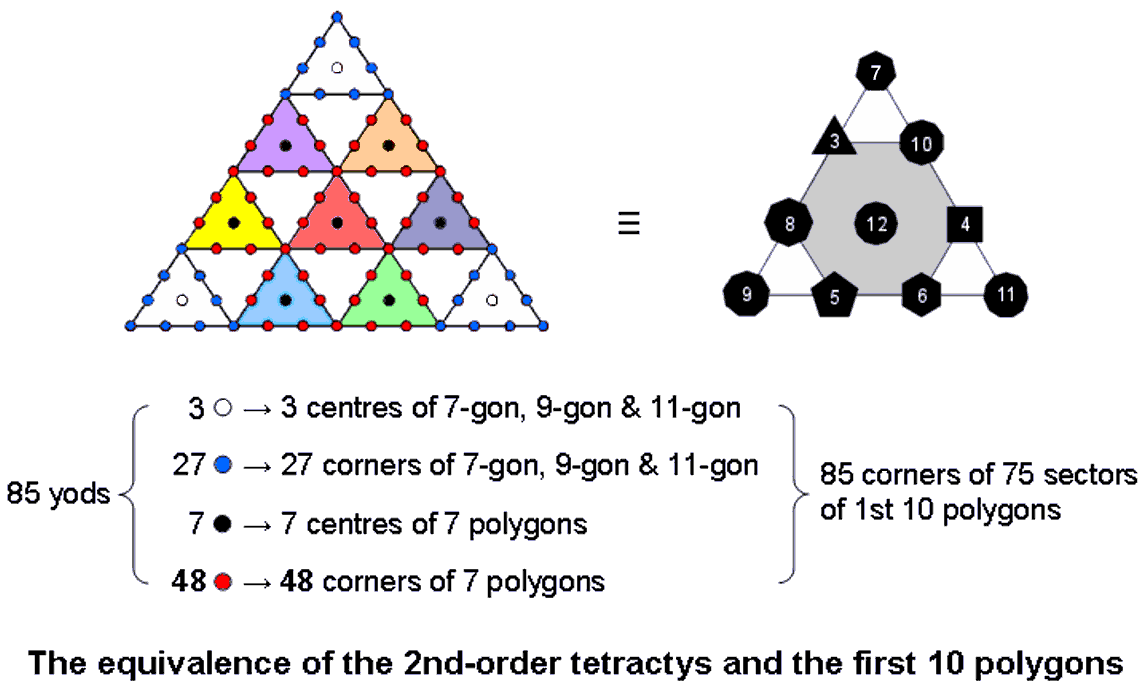
Figure 4. Parallels between the 2nd-order tetractys and the first 10 separate, regular polygons, proving their holistic character.

This section will explore the collective properties of these three regular polygons. We shall make the amazing discovery that they embody the same parameters as the (7+7) regular polygons that make up the inner form of the Tree of Life! It is as though information about all levels of reality, expressed through the seven Sephiroth of Construction by means of the seven types of polygons making up the inner Tree of Life, is encoded in a hidden geometry that represents the subjective Godhead. As initial confirmation of this, Figure 4 shows the remarkable set of correspondences between the 2nd-order tetractys and the first 10 enfolded polygons:

• 85 corners of the 75 sectors of the first 10 enfolded polygons → 85 yods in the 2nd-order tetractys;
• three centres of the three absent polygons → three centres of the three 1st-order tetractyses at the corners of the 2nd-order tetractys representing the Supernal Triad;
• 27 corners surrounding the centres of the three absent polygons → 27 yods lining the sides of the three 1st-order tetractyses;
• centres of the seven separate polygons → seven hexagonal yods at the centres of the seven 1st-order tetractyses representing the seven Sephiroth of Construction;
• 48 corners of the seven separate polygons → 48 yods lining the sides of (and intrinsic to) the seven 1st-order tetractyses.

They are too many to be all dismissed as due to coincidence. Table 1 lists formulae for the geometrical and yod compositions of an nth-order N-gon:

 Table 1. Geometrical & yod composition of the nth-order N-gon.

These formulae, which are derived in Article 65, may be used to determine below the global compositions of the three absent polygons when they are separate and when they are enfolded.

Three separate nth-order polygons (∑N = 27)

Number of corners of their triangles ≡ C_n = ∑c_n^N = ∑[1 + ½(3^n-1+1)N] = 3 + (27/2)(3^n-1+1) = ½(33+3ⁿ⁺²).

Number of sides of their triangles ≡ S_n = ∑s_n^N = ∑½(3ⁿ+1)N = (27/2)(3ⁿ+1).

Number of corners & sides = C_n + S_n = 30 + 2×3ⁿ⁺².

Number of triangles ≡ T_n = ∑t_n^N = ∑3^n-1N = 3^n-1×27 = 3ⁿ⁺².

Number of geometrical elements ≡ G_n = C_n + S_n + T_n = 30 + 3ⁿ⁺³, where "30" is the number of corners of the 27 sectors.

Number of hexagonal yods ≡ H_n = 2S_n + T_n = 3³ + 3ⁿ⁺² + 3ⁿ⁺³.

Number of yods ≡ Y_n = C_n + H_n = ½(87+3ⁿ⁺⁴), where 87 is the number value of Levanah, the Mundane Chakra of Yesod. As n→∞, Y_n/G_n→3/2. This is the arithmetic mean of the integers 1 & 2. In music it is the tone ratio of the perfect fifth, which is the primary division of the musical octave. This contrasts with Y_n/G_n = 3/2 for all values of n in the case of the 7 enfolded polygons of the inner Tree of Life (see comment after Table 3 here).

Three enfolded nth-order polygons

Number of corners ≡ C_n′ = C_n − 4 = ½(25+3ⁿ⁺²) = 2 + ½(21+3ⁿ⁺²), where "2" denotes the two endpoints of their shared side (the 'root edge').

Number of sides ≡ S_n′ = S_n − 2 = 1 + ½(21+3ⁿ⁺³), where "1" denotes the single, shared side.

Number of corners & sides ≡ C_n′ + S_n′ = C_n + S_n − 6 = 3 + 21 + 2×3ⁿ⁺², where "3" denotes the shared side and its two endpoints.

Number of triangles ≡ T_n′ = T_n = 3ⁿ⁺².

Number of geometrical elements ≡ G_n′ = C_n′ + S_n′ + T_n′ = G_n − 6 = 3 + 21 + 3ⁿ⁺³, where "3" denotes the three geometrical elements making up the root edge.

Number of hexagonal yods ≡ H_n′ = H_n − 4 = 2 + 21 + 3ⁿ⁺² + 3ⁿ⁺³, where "2" denotes the two hexagonal yods in the root edge.

Number of yods ≡ Y_n′ = Y_n − 8 = 4 + ½(63+3ⁿ⁺⁴), where "4" denotes the four yods in the root edge.

The ratio of the number of yods outside the root edge to the number of geometrical elements outside the root edge = (Y_n′−4)/(G_n′−3) = 3/2. The ratio is the same for every order n of the three N-gons absent from inner form of the Tree of Life. This contrasts with the ratio of the number of yods and the number of geometrical elements in the 7 enfolded nth-order polygons of the inner Tree of Life being 3/2 for all n (see discussion after Table 10 here). As n→∞, Y_n′/G_n′→3/2. We find that the tone ratio 3/2 of the musical perfect fifth is the asymptotic value of the ratio of the populations of yods and geometrical elements in the limit of infinite-order 7, -9- & 11-gons.

Table 2 shows the collective properties of the first four orders of the three absent polygons calculated with these formulae:

Table 2. Collective properties of the three absent polygons.

The next 10 pages will be devoted to explaining how the Kabbalistic Godnames of the 10 Sephiroth mathematically prescribe the properties of the three polygons absent from the inner Tree of Life — both separate and enfolded. The manner of their prescription is so natural that it ought to leave no doubt in an unbiased mind that the ancient Hebrew Divine Names operate at the level of Atziluth to determine the properties not only of the outer and inner forms of the Tree of Life (and, of course, all sacred geometries that are equivalent to them) but — amazingly — also the three polygons absent from the inner Tree of Life. The pattern of parameters that pervades holistic systems (see The holistic pattern) will then be shown to be embodied as well in these three polygons. This indicates that they must be understood as the abstract precursor within the Godhead of cosmic archetypes that are embodied in the seven Sephiroth of Construction and actualised by means of the seven types of regular polygons that make up the inner Tree of Life. Finally, this section will reveal direct, undeniable links between properties of the three absent polygons and group-theoretical aspects of superstring theory, which the pages of this website prove are represented in isomorphic sacred geometries like the Tree of Life, the Platonic solids, the Sri Yantra and the disdyakis triacontahedron.

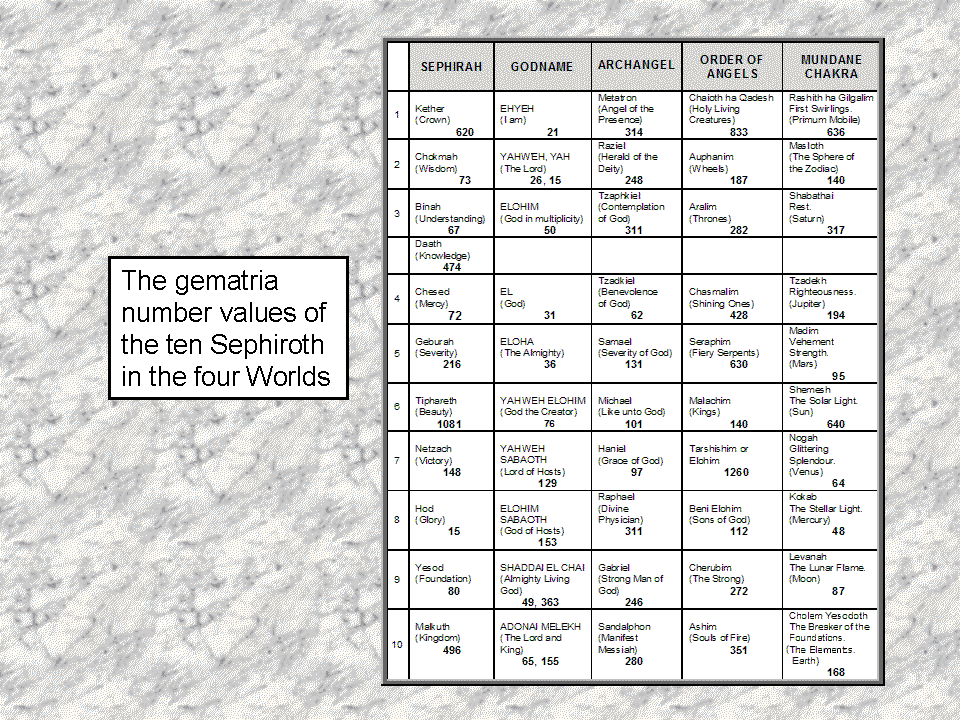
For ease of reference, the table of the gematria number values of the 10 Sephiroth (Godnames, Archangels, etc) are given below:

Table 3

<< Previous    1  [2]  3  4  5  ...17    Next >>

Home