Occult Chemistry Part 11

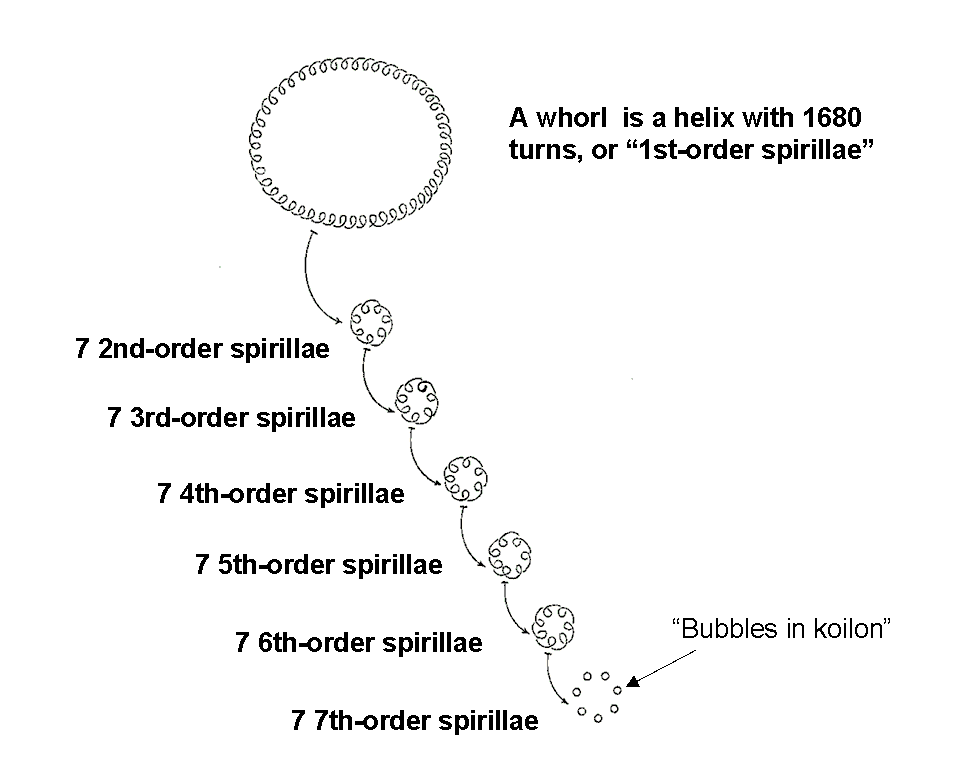
The positive and negative UPAs are mirror images of each other, their ten whorls each making five clockwise revolutions in the former and five anticlockwise revolutions in the latter. According to Leadbeater, who made a special study of the structure of the UPA, each whorl is a helical coil with 1680 circular turns, so that the UPA comprises 16800 turns of 10 helical coils. The helical nature of whorls was depicted in Babbitt's picture of the UPA (see here). We can feel certain that this number was not miscounted because Leadbeater checked it by counting the number of turns in a whorl in 135 different UPAs.* Each circular turn, or so-called "1st-order spirilla," is another coil made up of seven smaller, circular turns, or "2nd-order spirillae," which wind around a torus.

Each 2nd-order spirilla is another helical coil with seven still smaller turns, or "3rd-order spirilla," and so on. Leadbeater noticed seven orders of spirillae, each finer than the preceding one and made up of seven circular turns that form a turn of the next lower order of spirilla. Each spirilla winds in a circle whose plane is perpendicular to the direction in which the preceding order of spirilla winds at that point. According to Leadbeater, the 7th-order spirilla consists of seven spherical "bubbles" spaced evenly along the circumference of a circle. The diagram below, taken from the third edition of Occult Chemistry apart from the added text, depicts the helical winding of the fifth, sixth and seventh orders of spirillae. Rather than a soap bubble, whose film has both an inner and an outer surface, the bubbles making up the last order of spirilla are more like bubbles of air in a liquid, which have only one surface. Leadbeater said that space is filled with an invisible plenum or substance akin to the aether much loved by Victorian physicists before Einstein effectively banished it with his Special Theory of Relativity. Calling it "koilon,"** he claimed that both types of UPA are ultimately composed of bubbles or holes in this substance. In other words, the fundamental building blocks of matter are really a kind of void, an absence of the all-pervasive koilon. The bubbles seemed to contain nothing, as far as Leadbeater's highest magnifying powers could discern. Drawing an analogy with air bubbles (admittedly, not a perfect one because such bubbles still contain air), Leadbeater remarked: "Just as the bubbles are not water, but precisely the spots from which water is absent, so these units are not koilon but the absence of koilon — the only spots where it is not — specks of nothingness floating in it, so to speak, for the interior of these space-bubbles is an absolute void to the highest powers of vision that we can turn upon them."*** Leadbeater was saying, effectively, that the basic units of matter are made up of myriads of infinitesimally-small pockets of empty space, holes in a physical vacuum that is permeated by some kind of homogenous field, whose nature he could not discern.

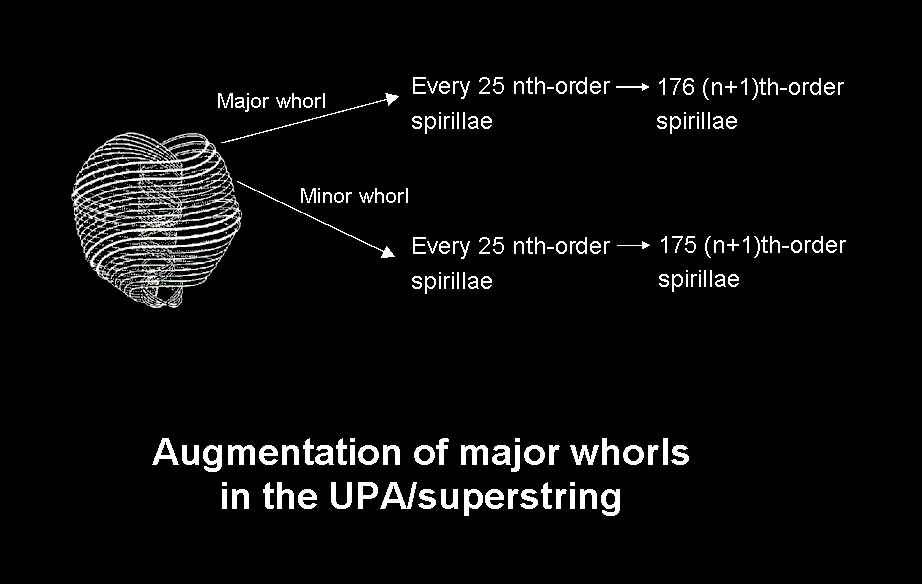
In a minor whorl, every spirilla of a given order is composed of seven spirillae of the next higher order, so that 100 nth-order spirillae consist of 700 (n+1)th-order spirillae. However, in the case of major whorls, Leadbeater noticed that 100 nth-order spirillae consist of 704 (n+1)th-order spirillae. In other words, four extra spirillae of the next higher order are present in every 100 spirillae of a given order. This addition continues in the same proportion for every order of spirilla up to the 7th-order spirilla, every 100 of which consist of 704 bubbles in koilon, whereas in a minor whorl every 100 7th-order spirillae comprise 700 bubbles because each 7th-order spirilla is a set of seven bubbles spaced evenly along a circle. Instead of being composed of exactly seven circular turns, each order of spirilla in a major whorl consists of 7.04 turns, an nth-order spirilla winding an extra 1/25th of a revolution by the time it forms 25 turns. The presence of extra spirillae of every order above the 1st-order spirillae is what made the major whorls appear thicker to Besant & Leadbeater. Every 25 nth-order spirillae in a minor whorl are composed of 175 (n+1)th-order spirillae, whereas in a major whorl they consist of 176 (n+1)th-order spirillae. A simple calculation based upon this information shows that the UPA contains approximately 14 billion bubbles, each major whorl having about 56 million more bubbles than a minor whorl. The number 1680 is, of course, not exactly divisible by 25, which means that the augmentation cannot be uniform everywhere along the length of a major whorl. Instead, there must be 67 sections of 25 1st-order spirillae, each composed of 176 2nd-order spirillae, and five remaining 1st-order spirillae that are composed of 175 2nd-order spirillae.

When we compare Leadbeater's description of the whorls and their spirillae with the picture of closed bosonic and heterotic superstrings discussed earlier, as well as with the 6-dimensional torus model of the compactified space that string theorists have considered, the following remarkable similarities emerge:

A whorl is a closed, 1-dimensional curve. It appeared to Leadbeater to be, ultimately, a string of empty, spherical bubbles;

The 2nd−7th orders of spirillae are the winding of a curve about the six circular dimensions of a 6-dimensional torus, the winding number N_n = 7 (minor whorl) or 7.04 (major whorl) for the nth circular dimension being independent of n;

The reported existence of spherical, i.e., 3-dimensional, bubbles in koilon spaced along circular 7th-order spirillae implies that whorls are projections of surfaces that extend beyond the sixth compactified, superstring dimension in at least two more dimensions. This means that space-time is neither 10-dimensional nor 11-dimensional, as predicted by M-theory, but 26-dimensional, as predicted by quantum mechanics for bosonic strings;

The UPA is the subquark state of a closed (therefore heterotic) superstring. However, instead of this being a single closed curve, it consists of a bundle of ten such curves, none of which touch or intersect another one.

The fourth feature of the basic unit of matter, namely, having a ten-fold structure, has profound religious and scientific significance. It will be discussed in the sections on sacred geometries and explained in the section 4-d sacred geometries.

As further evidence of the string-like nature of the UPA, compare the research paper below, written in 1982 by Michael Green, one of the principal developers of superstring theory, with a page from the third edition of Occult Chemistry in which Leadbeater described at least 74 years earlier the nature of a whorl (analogous sentences are underlined):

Leadbeater described here the six mutually orthogonal circles of a 6-torus, one of the 6-dimensional, compact spaces that string theorists have used as a model to explore various mathematical formulations of superstring theory. Notice how, in the last underlined sentence, Leadbeater likens all the bubbles in koilon to "an enormous circle of the tiniest imaginable dots lying like pearls upon an invisible string" (author's italics). Leadbeater uses the very word "string" as a metaphor for what he observed. He thereby declared^† about 74 years before this word started to appear in the journals of theoretical physics that the basic building blocks of matter revealed by micro-psi have a string-like nature! How can anyone dismiss this as yet another coincidence? Admittedly, the UPA is a bundle of ten closed curves, not a single one, as string theorists currently conceive superstrings to be. But the as yet undiscovered M-theory will have many new surprises, including the prediction that superstrings are constituents of quarks, not quarks themselves, and this compositeness of superstrings will be among them. It will be seen that the whorl is to the superstring as the superstring is to the hydrogen atom, namely, both are ten-fold systems, the sacred-geometrical reason for which is analyzed in depth in this website.

The sizes of each compactified dimension are defined by the radii of the circular spirillae. Leadbeater did not estimate their relative sizes (or, if he did, he did not specify them in any of the published investigations). Nor did he indicate whether successive orders of spirillae decrease by a constant or variable proportion. This would have been difficult to judge because any sense of relative size might have been lost when he shifted the focus of his micro-psi vision from the perspective of one compactified dimension to that of another. As he warned in Occult Chemistry, its diagrams are not to scale. They could never be so because of the wide disparity in sizes of, say, hydrogen triplets (quarks) and hydrogen triangles (nucleons). Nevertheless, it is significant vis-à-vis higher-dimensional theories of particle physics that Besant & Leadbeater reported their awareness of an aspect of the UPA which is higher-dimensional in the strict, mathematical sense of this word. Referring to the three major whorls and seven minor whorls, they said: "Each of the three coarser whorls, flattened out, makes a closed circle; each of the seven finer ones, similarly flattened out, makes a closed circle. The forces which flow in them again come from 'outside,' from a fourth-dimensional space."^††

In conclusion, the resemblance of the whorls of the UPA to closed strings and the similarity between the six mutually perpendicular orders of circular spirillae and the six orthogonal circular dimensions of the 6-torus — one of the many models of the 6-dimensional, compactified space predicted by superstring theory — are too close to have the conventional explanation that they are due to chance. Rather, this remarkable correspondence has no more credible explanation than that heterotic superstrings (it turns out that they were E₈×E₈ heterotic superstrings) were described paranormally over a century ago. Any alternative that appeals to lucky coincidence sacrifices credibility for the sake of scientific respectability. That is unacceptable. The skeptic might retort that a paranormal explanation is no more acceptable. Well, that is so for him, but only because he is ideologically committed to a materialist's belief in a universe where the paranormal cannot exist. For those who think this attitude is unscientific because it prejudges the truth, objective, empirical evidence must always trump personal ideology or philosophy.

* Occult Chemistry, 3rd edition, p. 23.
** A Greek word, meaning 'hollow.'
*** Occult Chemistry, 3rd ed., p. 17.
^† The page appearing in the 1952 edition was reproduced from the 1908 edition of Occult Chemistry.
^†† Ibid., p. 14.

WHORL	STRING
1. Closed curve;	1. Closed curve;
2. A circular (n+1)th-order spirilla winds seven times around a circular nth-order spirilla;	2. Winds N_n times around nth circular dimension (n = 1, 2, 3, 4, 5, 6). N_n = winding number for nth compactified dimension;
3. (n+1)th-order spirillae wind in circles whose planes are at right angles to plane containing circular nth-order spirillae (n = 1, 2, 3, 4, 5, 6);	3. Compactified 6-d torus has 6 perpendicular, circular dimensions.