Type A

Type B

Number of geometrical elements

Nonagon

Type A nonagon

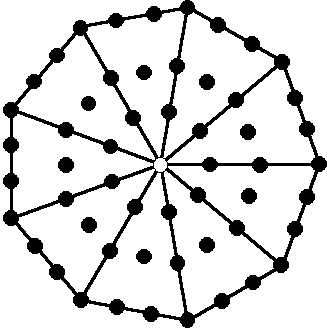
The Type A nonagon has 36 geometrical elements surrounding its centre, where

36 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8

is the 8th triangular number. It has 55 yods, where

55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9+ 10

is the 10th triangular number and the 10th Fibonacci number. This means that the nonagon is a polygonal representation of the 550 SLs belonging to the 91 Trees of Life in CTOL (see here) because, assigning the Decad to each of its 55 yods, the 54 yods surrounding its centre generates the number 540, which is the number of SLs down to the top of the lowest Tree of Life, after which there are 10 more SLs; these are denoted by the central yod that is weighted with the Decad.

The Type B nonagon has 91 geometrical elements. It embodies the number of Trees in CTOL. The two joined Type B nonagons have 176 geometrical elements outside their shared side. This is the number of geometrical elements in the 7 enfolded Type A polygons. They have 264 yods outside their shared side. This is the number of yods in the 7 enfolded polygons.

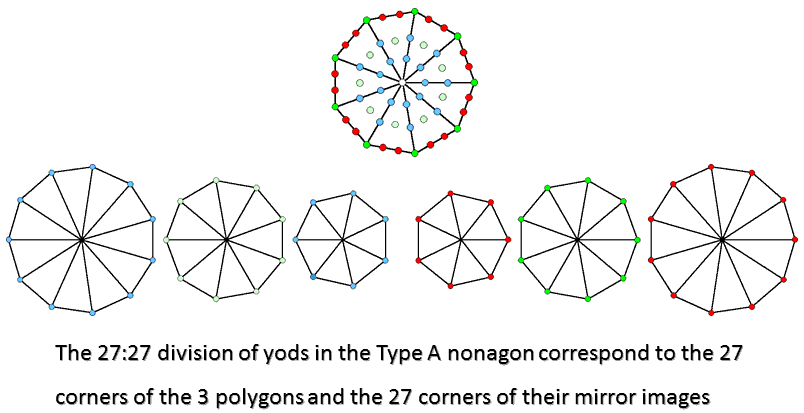
The (3+3) separate Type A polygons have (27+27=54) corners. In the right-hand set, they comprise the 18 red corners of the heptagon & undecagon and the 9 dark green corners of the nonagon. In the left-hand set, they consist of the 18 blue corners of the heptagon & undecagon and the 9 light green corners of the nonagon. The boundary of the Type A nonagon has 9 green corners & 18 red hexagonal yods; its interior has 9 light green hexagonal yods at the centres of tetractys sectors and 18 blue hexagonal yods on their sides. The 54 yods therefore correspond to the 54 corners of the (3+3) polygons; the 27 yods that line the sides of the nonagon correspond to the 27 corners of the right-hand set of polygons and the 27 yods in its interior correspond to the 27 corners of the left-hand set.

 Heptagon

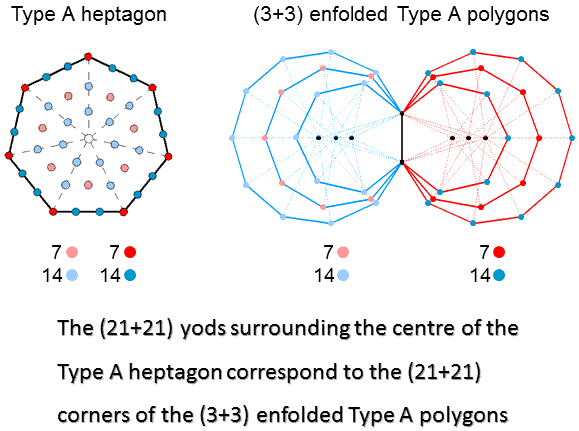
The Type A heptagon has 42 yods surrounding its centre. They comprise the 7 dark red corners, 14 dark blue hexagonal yods on its sides, 7 light red hexagonal yods at the centres of tetractyses & 14 light blue hexagonal yods on their sides. Compare this with the 42 corners outside the root edge of the (3+3) enfolded Type A polygons; they comprise the 7 red corners of the nonagon and the 14 dark blue corners of the heptagon & undecagon on the right-hand side and the 7 light red corners of the nonagon and the 14 light blue corners of the heptagon & undecagon on the left-hand side. The 21 yods on the boundary of the heptagon correspond to the 21 corners in the right-hand set of polygons and the 21 internal yods surrounding its centre correspond to the 21 corners in the left-hand set.

The two joined Type A heptagons have 55 geometrical elements, where

55 = 1 + 2 + 3 +... + 10.

50 geometrical elements outside the root edge surround their centres, where 50 is the number value of ELOHIM, the Godname of Binah. 26 geometrical elements are outside each heptagon, where 26 is the number value of YAHWEH, the Godname of Chokmah.

The Type B heptagon has 91 hexagonal yods. This polygon embodies the number of Trees of Life in CTOL. There are 49 coloured hexagonal yods that either line the sides of its sectors or are at centres of the 21 tetractyses. They symbolise the 49 Trees of Life that map the 49 subplanes of the cosmic physical plane. The 42 white hexagonal yods lining other sides of tetractyses symbolise the 42 Trees of Life that map the 42 subplanes of the 6 cosmic superphysical planes.

The two joined Type B heptagons have 139 geometrical elements. Surround their two centres are 137 geometrical elements, where 137 is the mysterious number whose reciprocal approximately equals the fine-structure constant known by physicists to measure the strength of the coupling of the electric charge of the electron to the electromagnetic field. 67 geometrical elements surround the centre of each Type B heptagon, where 67 is the number value of Binah.

206 yods surround the centres of the two joined Type B heptagons. This number is the number of bones in the adult human skeleton (see here).

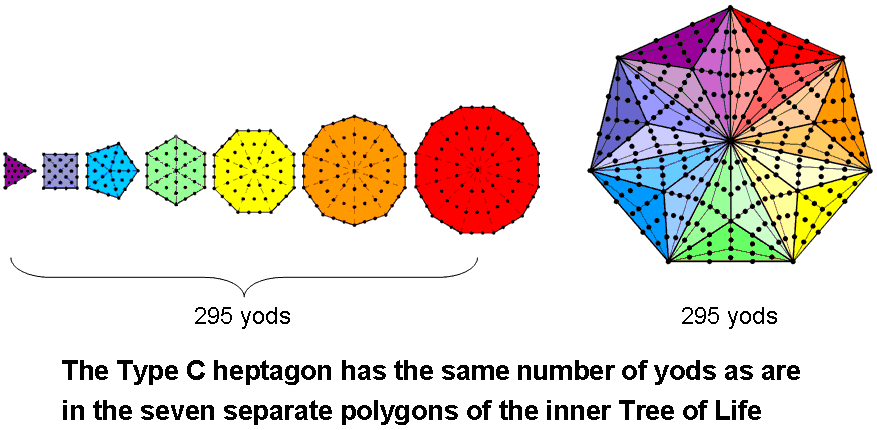
According to Table 1, the number of yods in the nth-order N-gon = (3/2)(3ⁿ+1)N + 1. The Type C heptagon (n=3, N=7) has 295 yods. The number of yods in the Type A N-gon = 6N + 1. The 7 separate Type A polygons of the inner Tree of Life have 48 corners. The number of yods = 6×48 + 7 = 295. The yod population of the Type C heptagon is equal to the number of yods in the 7 separate Type A polygons. This is the number of SLs in CTOL up to Chesed (the 1st Sephirah of Construction) of the 49th Tree mapping the highest subplane of the 7th plane of consciousness.

Undecagon

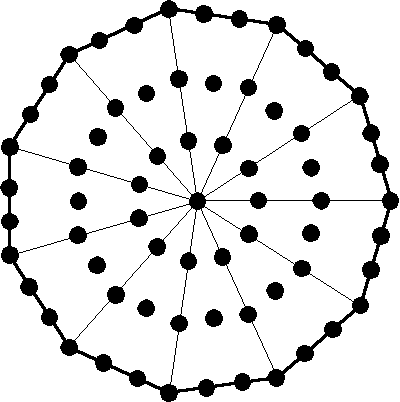
Type A undecagon

The Type A undecagon has 67 yods. This is the gematria number value of Binah, the third member of the Supernal Triad. There are 33 yods lining its boundary and 33 internal yods surrounding its centre, where 33 = 1! + 2! + 3! + 4!. The two joined Type A undecagons have 130 yods. 65 yods are associated with each undecagon, where 65 is the number value of ADONAI, the Godname of Malkuth.

The Type B undecagon has 165 yods surrounding its centre, where

165 = 1² + 3² + 5² + 7² + 9².

The two separate Type B undecagons have 220 geometrical elements surrounding their centres, where

220 = 2² + 4² + 6² + 8² + 10².

The two joined Type A undecagons have 87 geometrical elements, where 87 is the number value of Levanah, the Mundane Chakra of Yesod. 84 geometrical elements are outside their shared side.

The 66 yods surrounding the centre of the Type B undecagon consist of 33 yods lining its sides and 33 internal yods. The former consist of 11 dark red corners, 11 dark green hexagonal yods & 11 dark blue hexagonal yods. The latter consist of 11 light red hexagonal yods at centres of tetractyses, the sides of which are lined by 11 light green hexagonal yods & 11 light blue hexagonal yods.

Above or below the central horizontal axis passing through the centres of the (3+3) separate Type B polygons are 24 black corners & 24 white corners. The right-hand undecagon has 11 internal dark red corners & two dark blue corners lying on the axis, the nonagon has 11 dark green corners that are either internal or lie on the axis and the heptagon has 7 dark blue internal corners & two dark blue corners. Similarly for the corresponding light colours in the left-hand set of 3 polygons. The counterparts of the 11 dark red, 11 dark blue & 11 dark green corners are the yods lining the sides of the undecagon. The counterparts of the 11 light red, 11 light blue & 11 light green corners in the other set of polygons are the yods inside the undecagon. This Type A polygon displays the pattern found in the (3+3) separate Type B polygons.

260 yods lining tetractyses surround the centres of the two joined Type B undecagons

According to Table 4, the number of yods in the Type B undecagon is 166. It has 33 tetractyses, each with a central hexagonal yod, so that (166−33=133) yods line their 55 sides. 132 such boundary yods (128 outside the root edge) surround its centre. (128+128+4=260=26×10) boundary yods surround the centres of two joined Type B undecagons. This is the number of yods in 26 tetractyses, where 26 is the number value of YAHWEH, the Godname of Chokmah. It is also the yod population of the 7 enfolded Type A polygons outside their root edge. The number of boundary yods associated with each Type B undecagon = 130 = 7² + 9², i.e., the sum of the squares of the numbers of corners of the two other types of regular polygon absent from the inner Tree of Life! As there are 33 yods on the sides of the undecagon, (2×33 − 4 = 62) yods line the two joined undecagons, where 62 is the number value of Tzadkiel, the Archangel of Chesed. 31 such yods are associated with each undecagon, where 31 is the number value of EL, the Godname of Chesed.

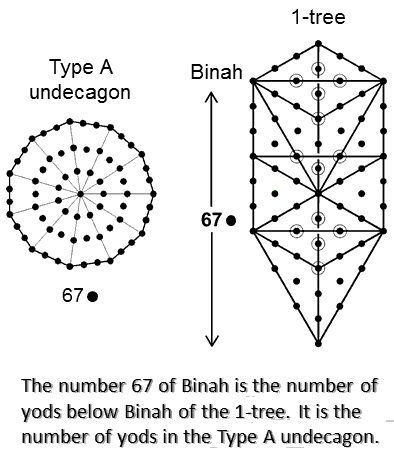
When the 19 triangles in the 1-tree are tetractyses, there are 67 yods below Binah, whose number value is 67. This is the number of yods in the Type A undecagon. The property is not sufficient reason, however, to associate the largest of the three polygons with the third member of the Supernal Triad. Which polygon should be associated with which Sephirah is a subtle issue that will be discussed later.

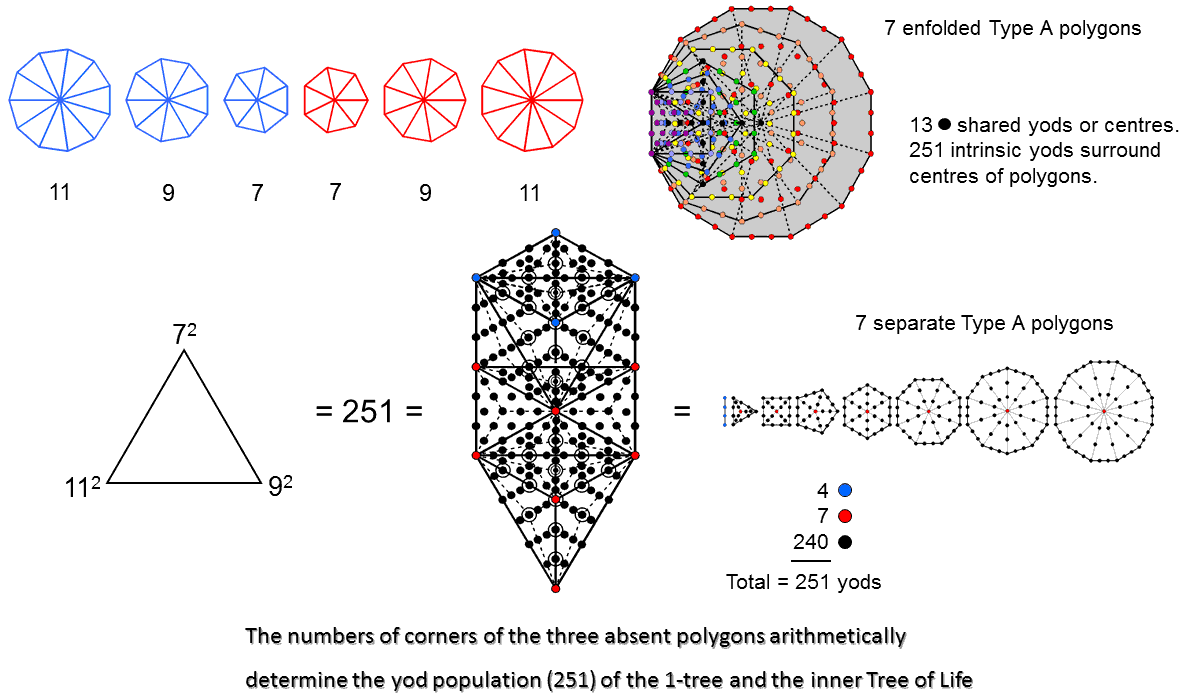
Amazingly, the heptagon, nonagon & undecagon determine arithmetically, as well as geometrically, various yod populations of the outer & inner Trees of Life. Here are examples:

• The (3+3) separate polygons have 54 corners. This is the number of yods lining the 16 triangles in the outer Tree of Life with 10 corners & 22 sides when they are tetractyses: 10 + 22×2 = 54.
• The (3+3) separate corners have 54 sectors with 60 corners. This is the number of hexagonal yods in the outer Tree of Life when its 16 triangles are tetractyses: 16 + 22×2 = 60.
• The sum of the squares of 7, 9 & 11 = 251:

7² + 9² + 11² = 251.

This is the number of yods in the 1-tree when its 19 triangles are Type A. It is also the number of yods unshared with the outer Tree that surround the centres of the 7 enfolded polygons.* There are 251 yods in the root edge and in the 7 separate Type A polygons that line its 48 tetractys sectors.**

• The sum:

7² + 9² = 130

is the number of hexagonal yods associated with each set of 3 enfolded Type A polygons.^† It is also the number of geometrical elements making up the first 6 enfolded polygons.^††

* Proof: the 7 black yods in the hexagon spaced along the vertical line joining its top and bottom are shared with the outer Tree of Life when its triangles are tetractyses because they lie on the Pillar of Mercy, which forms two sides of its triangles. One of these yods is the black centre of the hexagon, leaving 6 black centres of other polygons. The 7 enfolded polygons have 264 yods. (264−7−6=251) yods are unshared with the outer Tree of Life and surround the 7 centres.
** Proof: 5 yods per sector of a Type A polygon line its sides. Including the 7 red centres, the number of boundary yods in the 48 sectors = 5×48 + 7 = 247. Including the 4 blue yods lining the separate root edge, (247+4=251) yods line the root edge and the 48 sectors of the 7 separate Type A polygons.
† Proof: according to Table 2, the 3 enfolded Type A polygons have 131 hexagonal yods.129 are outside the root edge, which has two hexagonal yods. One of them is associated with each set of 3 polygons. Therefore, (129+1=130) hexagonal yods are associated with each set.
^†† Proof: The 7 enfolded Type A polygons comprise 176 geometrical elements. The Type A dodecagon has 49 geometrical elements (46 outside the root edge). The first 6 enfolded Type A polygons have (176−46=130) geometrical elements.