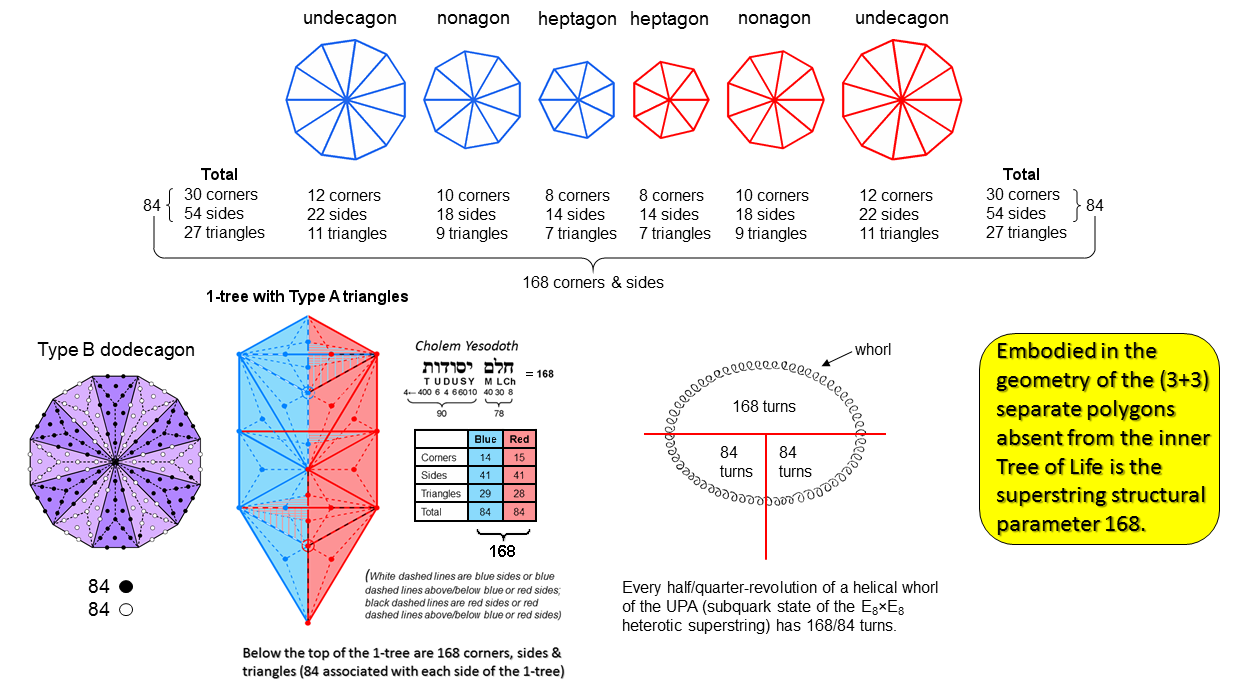
The separate Type A heptagon, nonagon & undecagon have 27 sectors with 30 corners & 54 sides, i.e., 84 corners & sides, where

84 = 1² + 3² + 5² + 7².

Both sets of polygons have (84+84=168) corners & sides. As discussed in the next picture, this number is the gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. The 84:84 division is characteristic of holistic systems, as illustrated in many places in this website (e.g., see here). It arises here as a mirror reflection that is distinct due to the fact that 7, 9 & 11 are odd numbers, so that the mirror images of the polygons with these numbers of corners are not identical to them.

The 84:84 division appears in the Type B dodecagon (the last of the first 10 types of polygons). The number of yods in a Type B n-gon = 15n +1, where "1" denotes its centre. Surrounding the latter are 14n yods other than polygonal corners. The Type B dodecagon (n=12) has (14×12=168) such yods. This is the number of yods added by the transformation of the dodecagon into a Type B dodecagon. Associated with 6 sectors are 84 black or white yods.

The 1-tree is the lowest of any set of overlapping Trees of Life. It comprises 19 triangles with 11 corners & 25 sides. When these triangles are Type A, there are 168 corners, sides & simple triangles below the apex of the 1-tree. Some of them are located in the left-hand side, some (the mirror images of the former) are in the right-hand side and some straddle the central Pillar of Equilibrium, so that they are their own mirror images. By self-consistently defining which of these should be associated with which half, the 1-tree may be divided into two "halves", each with 84 geometrical elements below its apex. For more details, see here.

A similar 84:84 division exists in the yod composition of the 1-tree. As discussed here, a root, trunk & branches can be defined for it. There are 168 yods in its branches, 84 yods being in their left-hand & right-hand halves.

The UPA remote-viewed by Annie Besant & C.W. Leadbeater (see here) is the subquark state of the E₈×E₈ heterotic superstring. Each of its 10 whorls is a helix with 1680 circular turns that revolves 5 times around its spin axis. One whole revolution of a whorl comprises 336 turns, a half-revolution comprises 168 turns and a quarter-revolution comprises 84 turns. The outer section of a whorl comprises 2½ revolutions with 840 (=84×10) turns; its inner section also comprises 2½ revolutions with 840 turns. The 84:84 pattern also appears in the context of superstring physics as the two base angles of 84° in each sector of a triacontagon, which is the Petrie polygon for the 4₂₁ polytope known to represent the 240 roots of the Lie group E₈ (see here).

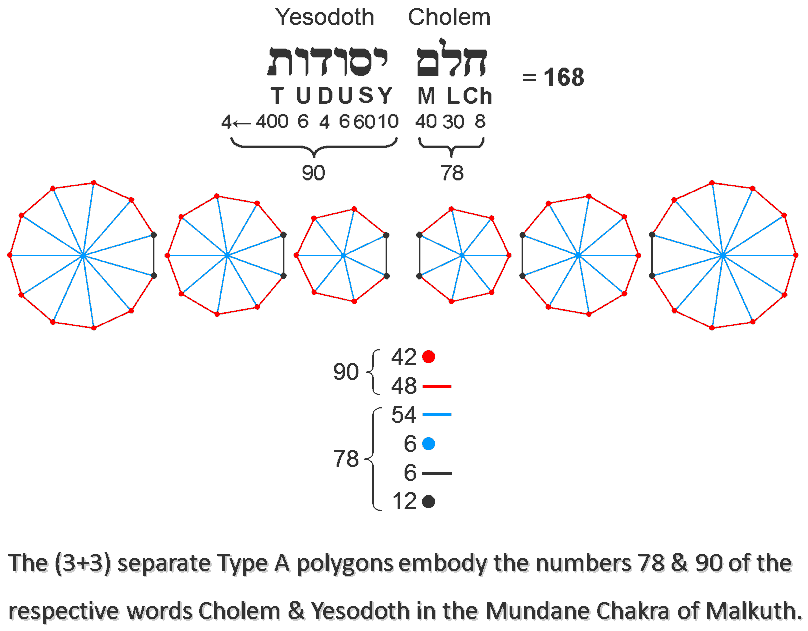
The boundaries of the (3+3) separate Type A polygons have (54+54=108) red corners & sides. The left sides (shown in black) of the right-hand set and the right sides of the left-hand set (also in black) become the root edge when all the polygons become enfolded. The root edge comprises two corners & one side. The number of corners & sides outside these sides = 108 − 6×3 = 90. (27+27=54) blue internal sides of sectors surround the blue centres of the 6 polygons. The number of corners & sides in both their root edges and inside the polygons = 6×3 + 54 + 6 = 78. The number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, is 168. The number 78 is the number value of Cholem and the number 90 is the number value of Yesodoth:

168 = 78 + 90.

The number 78 quantifies the shape-defining corners & sides making up the parts of the boundaries of the polygons that extends beyond their root edges. The number 90 quantifies the number of corners & sides that make up either the root edges or the inside of the polygons; these geometrical elements do not shape the polygons.

It is amazing that the number that resulted from Leadbeater's remote-viewing of the UPA, which he regarded as the basic constituent of atoms, should appear naturally and in such a minimal way as, simply, the number of points & lines making up the 3 absent polygons and their mirror images. Such a simple, uncontrived basis can leave no room for the sceptic to argue that the number has been obtained by cherry-picking. It clearly has not, for it refers to ALL the points & lines that make up the (3+3) separate polygons divided into their sectors. To attribute to chance the presence of the paranormally-derived number is to dismiss, likewise, the ways that the Godnames prescribe the properties of these polygons. This is not credible; it just beggars plausible belief. Is it really any more "rational" to explain away so many significant results as supposed miracles of chance than to accept them as evidence of divine design? Of course not!

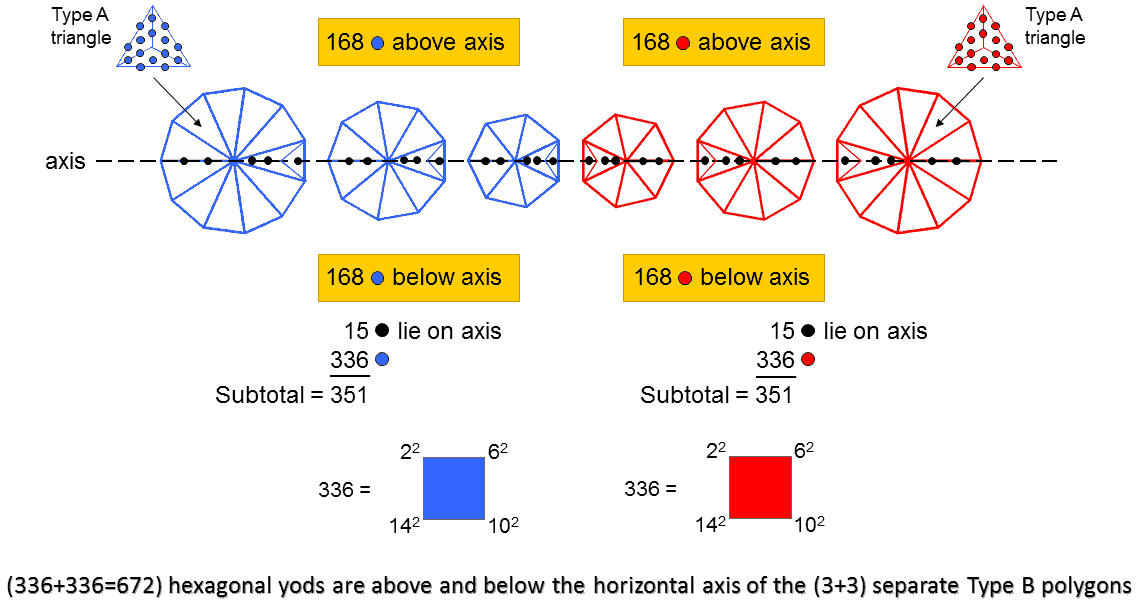
According to Table 2, the number of hexagonal yods (shown above as coloured red) in the 3 separate Type B polygons = 351. This is the number value of Ashim ("souls of fire"), the Order of Angels assigned to Malkuth. It is the 26th triangular number:

351 = 1 + 2 + 3 + ... + 26,

where 26 is the number value of YAHWEH, the Godname of Chokmah. It is a parameter of the 10-tree whose 65 SLs are prescribed by ADONAI with number value 65 (see here). This is because the 70 enfolded polygons making up the inner form of 10 overlapping Trees of Life have 351 corners (see here). Each of the 3 polygons has an odd number of corners. Despite this, each one can be divided into two halves that are mirror images of each other if the plane of the mirror is perpendicular to the plane containing the polygon and passes through its centre. Consider the axis formed by a straight line passing through the centres of the 3 separate polygons. Imagine a mirror perpendicular to the planes of the polygons and passing through this axis. Each yod in the polygons above the axis has a mirror image below it. Five hexagonal yods (coloured black) in each polygon lie on the axis and are their own mirror images. The number of red hexagonal yods above or below the axis = 351 − 3×5 = 336. Therefore, the 3 polygons contain 168 hexagonal yods on either side of the axis. Similarly, the mirror-image set of 3 polygons have 168 blue hexagonal yods on each side of the axis, 336 in total. The (3+3) separate Type B polygons have (336+336=672) hexagonal yods on both sides of the axis, which contain (15+15=30) black hexagonal yods. Notice that the number value 15 of YAH, the shorter form of the Godname YAHWEH, and the number 351 prescribed by this Godname, determine the number 336. This is a defining parameter of holistic systems (see the picture depicting the holistic pattern at the beginning of this page).

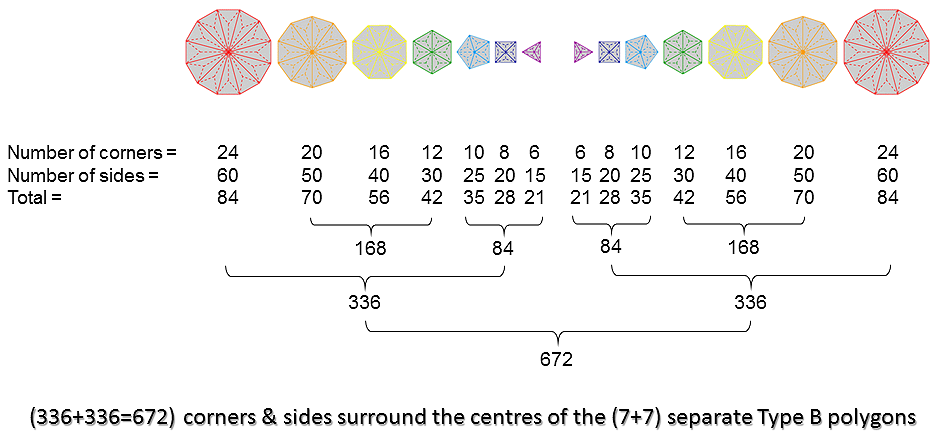
The inner Tree of Life counterpart of the 336:336 division displayed by the (3+3) separate Type B polygons is shown above. A Type B n-gon has 3n triangles with 2n corners and 5n sides surrounding its centre, i.e., 7n corners & sides. The 7 separate Type B polygons in the inner Tree of Life has 48 corners. Their 144 triangles have 96 corners 240 sides, i.e., 336 corners & sides. The (7+7) separate Type B polygons have 288 triangles with (336+336=672) corners & sides surrounding their (7+7) centres. The triangle, square, pentagon & dodecagon have 24 corners, as do the hexagon, octagon & decagon, that is, each of these two sets of polygons has half the numbers of corners, sides & triangles making up all 7 polygons. Therefore, each set has 168 corners & sides. The 4 sets of polygons. each with 168 corners & sides, correspond to the 168 hexagonal yods above and below the axis in each set of 3 separate polygons. Once again, we find that a pattern of distribution of yods in the (7+7) polygons of the inner Tree of Life has its counterpart in the three types of polygons that are absent from it. It is no coincidence that this happens. It has to occur because the blueprint for Creation represented by the inner Tree of Life has its precursor in the Godhead that exists outside of it. This is why we discover the very same holistic parameters forming patterns in the absent polygons that are analogous to those appearing in the 7 polygons, as well, of course, to isomorphic patterns in other sacred geometries (see here).

As explained in 4-d sacred geometries/Polychorons & the Gosset polytope, the number 672 is a parameter of all sacred geometries. For example:

• Surrounding the centres of the 7 Type C polygons of the inner Tree of Life are 672 sides of triangles. See here.
• Surrounding the centres of the two Type C dodecagons are 672, corners, sides & triangles. See here.
• The first 4 Platonic solids that represented for the ancient Greeks the Elements of Earth, Water, Air & Fire, have 672 yods when their faces and interior triangles are constructed from tetractyses. See here.
• Constructed from Type A triangles, the 3-d Sri Yantra contains 672 yods other than the corners of its 42 triangles. See here.
• 672 extra points, lines & triangles are needed to construct the faces of the 24-cell from Type A triangles. See here.

It manifests in the context of superstrings as the (672×10=6720) edges of the 4₂₁ polytope, the 8-dimensional polytope whose 240 vertices represent the 240 roots of E₈, the largest of the five exceptional Lie groups that describes the unified symmetry of the forces between E₈×E₈ heterotic superstrings. For details, see here.

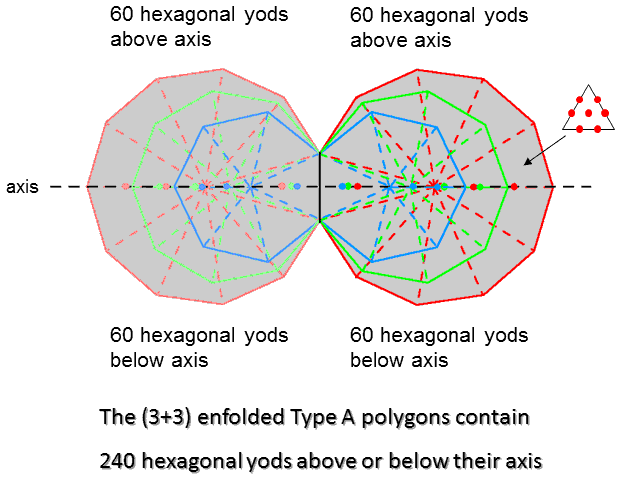
According to Table 2, the 3 enfolded Type A polygons have 131 hexagonal yods, where 131 is the number value of Samael, the Archangel of Geburah. Outside the root edge are (131−2=129) hexagonal yods, where 129 is the number value of YAHWEH SABAOTH, the Godname of Netzach. Straddling the horizontal axis (shown as a black dashed line) that passes through the centres of the (3+3) polygons are 3 sectors of each set of 3 enfolded polygons (coloured dark red, dark green & dark blue) joined at the root edge (also shown as a black line). Each of these 3 sectors is a tetractys that has either a dark red, a dark green or a dark blue hexagonal yod at its centre. For each polygon, two hexagonal yods lie on a side shared by two tetractyses that also lies on the axis. They are coloured dark red, dark green & dark blue. Three hexagonal yods belonging to each polygon lie on the axis. Similarly, 3 light red, 3 light green & 3 light blue hexagonal yods line the axis in the other set of enfolded polygons. Nine hexagonal yods in each set lie on the axis. Therefore, (129−9=120) hexagonal yods lie off the axis, 60 above it and 60 below it. Both sets of 3 polygons contain (120+120=240) hexagonal yods above and below the axis.

The number 240 is a parameter of holistic systems:

240 = 2⁴ + 2⁵ + 2⁶ + 2⁷.

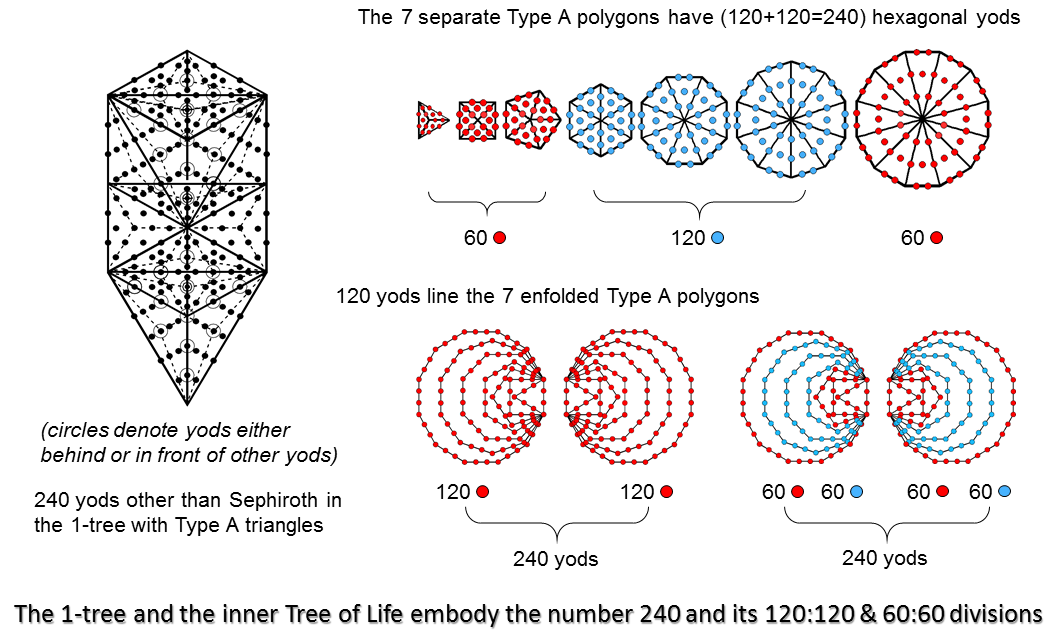
For example, the 1-tree is composed of 19 triangles. When they are Type A triangles, the 1-tree contains 251 yods. Eleven of them are the corners of these triangles, at which Sephirothic levels (SLs)* are located. Hence, (251−11=240) yods are not SLs. The 7 regular polygons of the inner Tree of Life have 48 sectors with 240 hexagonal yods when they are Type A. The triangle, square, pentagon & dodecagon with 24 sectors have 120 hexagonal yods (coloured red), as do the hexagon, octagon & decagon with 24 sectors (coloured blue). The first 3 polygons have 12 sectors with 60 hexagonal yods, as has the dodecagon. This 120:120 division of the parameter 240 is characteristic of holistic systems. It reappears in the two sets of 7 enfolded polygons as the 120 yods lining their sides. The 60:60 division of these 120 yods manifests as the 60 red yods lining the sides (including the root edge) of the triangle, square, pentagon & dodecagon and the 60 blue yods on the sides of the hexagon, octagon & decagon. The (3+3) enfolded Type A polygons comprise 4 sets of 60 hexagonal yods off their axis and outside the root edge. Likewise, the two separate sets of 7 enfolded Type A polygons have 4 sets of 60 hexagonal yods lining their sides.

The superstring significance of the number 240 is discussed widely in this website. It is the number of non-zero roots of the largest, exceptional Lie group E₈ appearing in E₈×E₈ heterotic superstring theory (see here). They are represented by the 240 vertices of the 8-dimensional polytope called the "4₂₁ polytope" (see here). The 120:120 division in the number 240 displayed in the geometry of the (3+3) enfolded Type A polygons and the further 60:60 division of the number 120 has remarkable counterparts in the geometry of this polytope, as will be explained shortly.

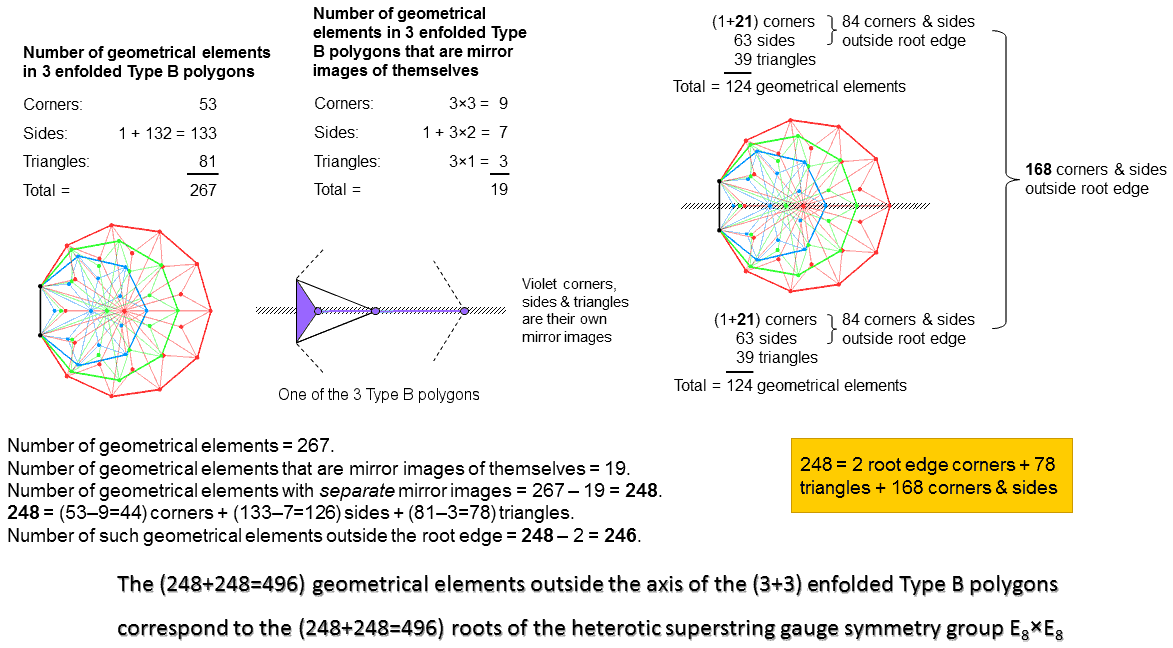
According to Table 2, the 3 enfolded Type B polygons have 267 geometrical elements. As pointed out on #13, the 264 geometrical elements outside their shared root edge correspond to the 264 yods making up the 7 enfolded Type A polygons. They are composed of 134 corners & triangles and 133 sides, so that 132 corners and 132 sides are outside the root edge. Outside the root edge of the (3+3) enfolded Type B polygons are 264 corners & triangles and 264 sides, so that the (3+3) enfolded polygons contain (3+264+264=531) geometrical elements.

Consider the axis passing through the centres of the 6 polygons. For each polygon, there are 3 corners & two sides of triangles lying in the axis, which is straddled by one triangle with the root edge as one of its sides. If we imagine the axis as a mirror, every geometrical element in the upper halves of the 3 polygons has a counterpart in their lower halves as their reflected image. But the 5 corners & sides that lie in the mirror are their own mirror images, as is the triangle and its root edge side at right angles to the mirror. Each polygon has 7 geometrical elements that are mirror images of themselves. But, when they are enfolded, they share one of them as the root edge, leaving 6 independent geometrical elements on the axis in each polygon. The total number of geometrical elements in the 3 enfolded polygons that are mirror images of themselves = 1 + 3×6 = 19. There are (267−19=248) geometrical elements: 124 elements and their distinct mirror images. Two of them are the endpoints of the root edge, leaving 246 geometrical elements outside it (123 in each half). 248 is the number value of Raziel, the Archangel of Binah, and 246 is the number value of Gabriel, the Archangel of Yesod. But the dimension of the largest exceptional Lie group E₈ is 248. Amazingly, each set of 3 enfolded Type B polygons has as many geometrical elements outside their root edge and axis as E₈ has roots! The pair of separate sets of polygons, one the mirror image of the other, contain (248+248=496) such geometrical elements, where 496 is the number value of Malkuth. Compare this with the discovery in 1984 that anomaly-free interactions between 10-dimensional superstrings require 496 Yang-Mills gauge fields, so that their symmetry group was either SO(32) or E₈×E₈. The two E₈ groups arise because the 3 enfolded polygons are chiral, each having an odd number of corners, and only a pair of 3 enfolded polygons, one the mirror image of the other, can be unchanged by reflection in a mirror. Article 59 discusses how the (3+3) enfolded polygons encode the root composition of E₈ & E₈×E₈.

There are 21 corners & 63 sides (i.e., 84 corners & sides) of 39 triangles outside the root edge in each half of the 3 enfolded polygons. Leadbeater's structural parameter of the UPA, namely, 168, is embodied in each set of 3 polygons as the (84+84=168) corners & sides of their (39+39=78) triangles outside their shared root edge. Including the two endpoints of the latter, there are 85 corners & sides in one half that have distinct mirror images in the other half, where

85 = 4⁰ + 4¹ + 4² + 4³

is the number of yods in the 2nd-order tetractys. Because of this, each half of the 3 enfolded polygons can be regarded as a whole in itself. The number of geometrical elements in the two joined sets of 3 polygons = 2 + 2×246 = 494. This is the number of yods lining the sides of the sectors of the (7+7) separate Type A polygons (see 2nd footnote in last diagram in #14). The 247 geometrical elements associated with each set correspond to the 247 boundary yods in each set of 7 separate Type A polygons.

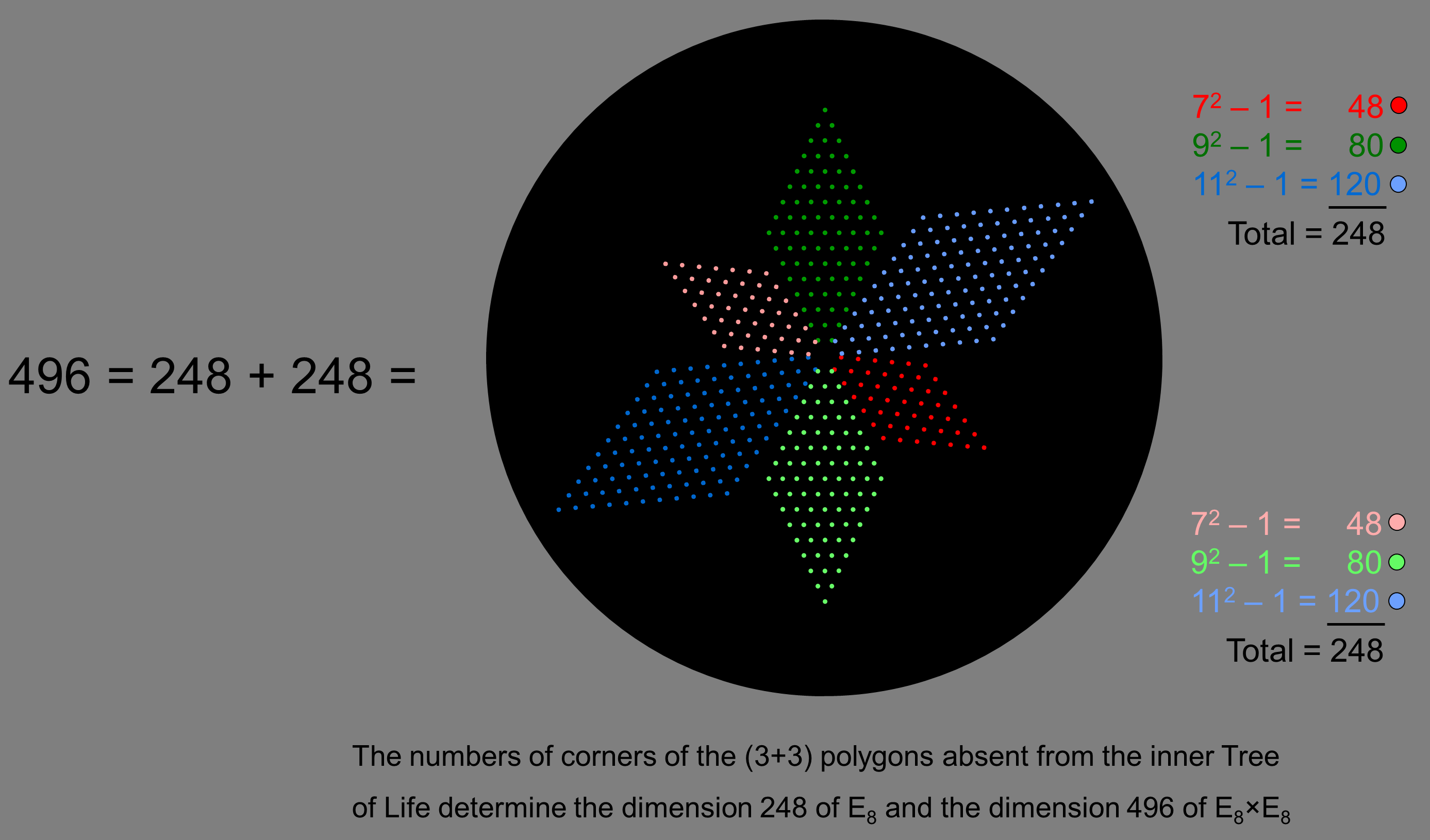
 As

7² + 9² + 11² = 251,

7² − 1 + 9² − 1 + 11² − 1 = 251 − 3 = 248.

This is the dimension of the rank-8, exceptional Lie group E₈. Imagine 3 parallelogram arrays of dots with 7, 9 & 11 dots spaced evenly along each side. Suppose that they are connected at one corner. There are 248 dots surrounding their shared corner. Similarly for a second set of 3 parallelogram arrays corresponding to the mirror images of the first set. If all 6 parallelograms are connected at a corner, there are (248+248=496) dots surrounding this shared corner. The 3 regular polygons absent from the inner Tree of Life have the remarkable property that their numbers of corners generate the dimension 248 of E₈, whilst the (3+3) sets of parallelograms corresponding to these 3 polygons and their mirror images generate the dimension 496 of E₈×E₈! As

n² = 1 + 3 + 5 +... + 2n−1,

for any positive integer n, (n²−1) is the sum of the (n−1) odd integers 3, 5, ... 2n−1. The number 248 is the sum of (6+8+10=24) odd integers, where 24 = 5² − 1 = 3 + 5 + 7 + 9 = 4! = 1×2×3×4, showing the power of the Tetrad (4) to express this parameter of holistic systems. It also expresses the number 496 because

496 = 1³ + 3³ + 5³ + 7³,

as well as the number (84) of corners & sides of the 27 sectors of the 3 separate polygons because

84 = 1² + 3² + 5² + 7².

The number of dots in the parallelograms with 7 & 11 dots along each side = 48 + 120 = 168. This is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, and the paranormally derived, superstring structural parameter widely discussed throughout this website because it is a primary parameter of sacred geometries. The 4 parallelograms corresponding to the heptagon, undecagon and their mirror images have (168+168=336) yods. This number always accompanies the parameter 168 in holistic systems.

The division:

248 = 80 + 168

generated by the parallelogram associated with the nonagon with 9 corners and the parallelograms associated with the heptagon and undecagon with 18 corners manifests in the root composition of E₈ as the 80 roots that comprise its 8 simple roots and the 72 roots of its exceptional subgroup E₆ and as the remaining 168 roots. The number 80 is the number value of Yesod ("Foundation"), the Sephirah that precedes Malkuth ("Kingdom) with number value 496. The counterpart of this division in the geometry of overlapping Trees of Life can be seen here.

Here is a simple, but remarkable, way in which the 3 polygons generate merely through their numbers of corners the group-theoretical numbers 248 & 496 that are central to E₈×E₈ heterotic superstring theory. It is yet more evidence that the 3 polygons absent from the inner Tree of Life represented by 7 types of polygons are analogous to the Supernal Triad of the outer Tree of Life in a way that is more than just formal, for they contain the same information (in terms of cosmic parameters) about the basic physics of matter as the 7 polygons — a repetition that would exceed all bounds of probability were the correspondence merely a formal one.

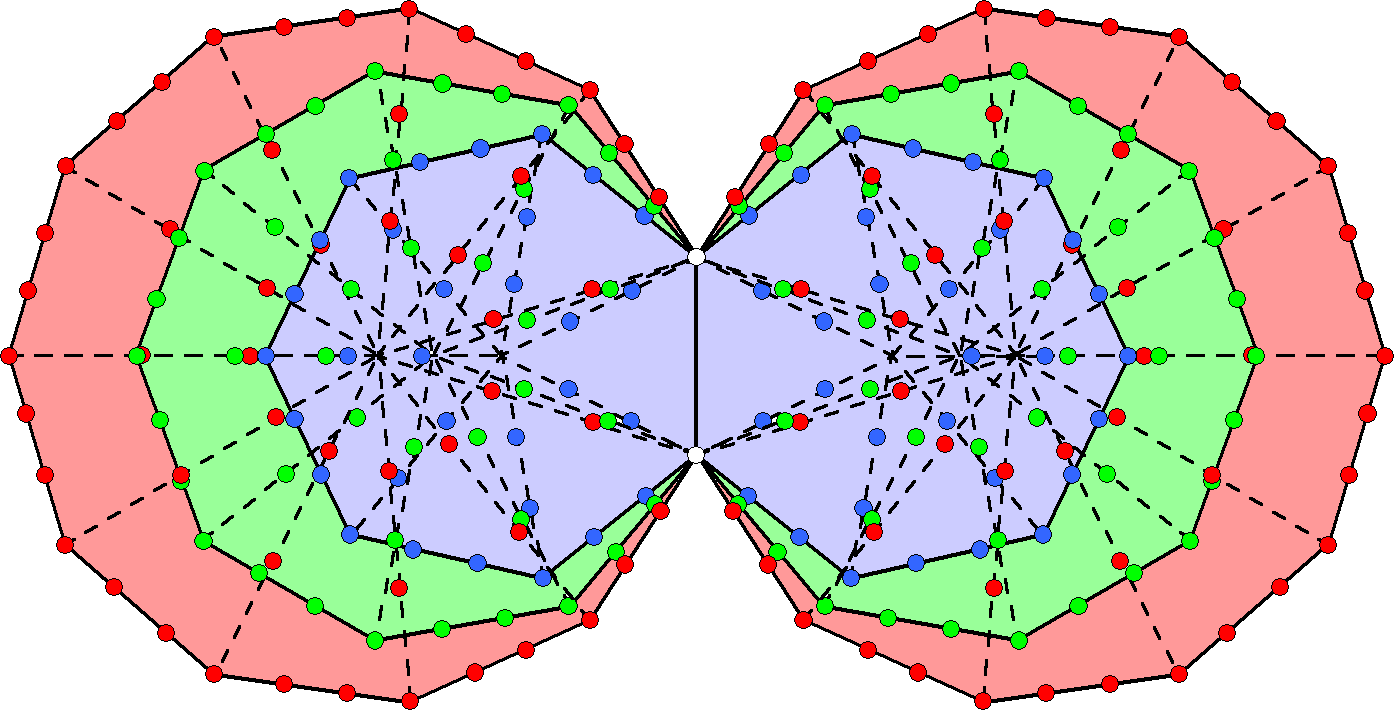
Surrounding the centres of the (3+3) enfolded polygons are 248 yods lining all sides of their (27+27) tetractys sectors outside their root edge. Each yod
denotes one of the 248 roots of the exceptional Lie group E₈, whose gauge fields transmit the unified force between E₈×E₈ heterotic superstrings.

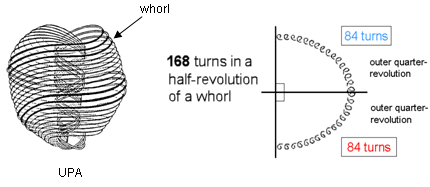
Each helical whorl of the UPA/subquark superstring conforms to the 84:84 division displayed by holistic systems
because each half-revolution of a whorl comprises 168 turns and each quarter-revolution comprises 84 turns.
Also, its 2½ outer revolutions consist of 840 (=84×10) turns, as do its 2½ inner revolutions.

Number of boundary yods in the three enfolded polygons.

(numbers refer to yods outside the root edge; numbers in brackets refer to both sets of polygons)

123 boundary yods outside the root edge surround the centres of the polygons. This is the tenth Lucas number, L₁₀. In terms of the Golden Ratio Φ = (1+√5)/2,

L₁₀ =  Φ¹⁰ + Φ^-10.

This demonstrates the influence of the Pythagorean Decad symbolised by the tetractys in expressing holistic parameters like 123. Including the four yods of the root edge, (123+4=127) yods line the three enfolded polygons. This is the 31st prime number, showing how EL, the Godname of Chesed with number value 31, prescribes the (3+3) enfolded polygons. Outside the root edge are 42 corners and 204 hexagonal yods on sides of tetractyses, i.e., 246 boundary yods, where 246 is the number value of Gabriel, the Archangel of Yesod. Including the two hexagonal yods of the root edge, the two sets of enfolded polygons contain 206 hexagonal yods on the sides of 54 tetractyses and 50 corners, totalling 256 boundary yods, where 256 = 4⁴. This demonstrates the amazing power of the Tetrad to express the beautiful, mathematical properties of sacred geometries. Including the two endpoints of the root edge, 248 boundary yods surround the centres of the six enfolded polygons and line sides of tetractyses outside the root edge. This is the number value of Raziel, the Archangel of Chokmah. It is the dimension of E₈, the rank-8, exceptional Lie group, i.e., the number of its roots and, therefore, the number of the spin-1 gauge fields coupled to their associated charges that transmit the unified force between E₈×E₈ heterotic superstrings. Embodied in the three types of polygons absent from the inner Tree of Life is the very master number 248 that determined what kind of matter came to compose the universe.

The yods at the 6 corners of sectors that lie on the axis of the (3+3) polygons denote the six simple roots of E₆, the rank-6 exceptional subgroup of E₈; the two endpoints (white yods) of the root edge denote the two extra simple roots of the latter. The following table shows the numbers of yods denoting the 240 roots of E₈:

Yods denoting the 240 roots of E₈.

E₈ has the following numbers of roots in its four exceptional subgroups:

(the numbers are underlined to indicate that each is a subset of its nearest right-hand neighbour because E₇⊃E₆⊃F₄⊃G₂). It means that there must exist a set of 126 yods that contains a subset of 72 yods, which contains a subset of 48 that, finally, contains a subset of 12 yods. This would be trivially true if we were allowed to choose the yods at random. But, of course, we cannot do this because we expect the yod populations of individual polygons, or combinations thereof, to determine the various dimensions of these subgroups. This severely limits possible choices of the combinations of the numbers shown in the table. In fact, analysis of all the possible combinations shows that only one is consistent with group-theoretical restrictions:

(the number 16 refers to the corners of the two undecagons);

72 = 48 + 8 + 16 = 8 + 12 + 16 + 16 + 20

and

126 = 72 + 14 + 18 + 22 = 8 + 12 + 14 + 16 + 16 + 18 + 20 + 22.

The 168 roots of E₈ that are not roots of E₆ have the yod counterparts:

168 = 16 + 28 + 24 + 36 + 44 + 20 = (16+24+44) + (28+36+20) = 84 + 84.

The chosen distribution satisfies the requirement, established by many analyses of sacred geometries presented in this website, that 168 = 84 + 84, reflecting the fact that holistic systems display two halves. As we found in the discussion of the first diagram, the 27 sectors of each set of 3 separate Type A polygons have 84 corners & sides. The (3+3) polygons manifest this archetypal division in both their geometrical and yod compositions. Its subatomic realisation is the UPA/subquark superstring. Each of its 10 whorls is a helix with 1680 (=168×10) circular turns. 840 (=84×10) turns in its outer half wind around its spin-axis and 840 turns in its inner half wind around it in a narrower spiral. As each half comprises 2½ revolutions of the helix, i.e., 10 quarter-revolutions, each of the latter comprises 84 turns.