| << Previous 1... 16 17 [18] 19 20 ...56 Next >> |
#18 Embodiment of the superstring structural parameters 1680 & 3360 in the inner form of 10 overlapping Trees of Life

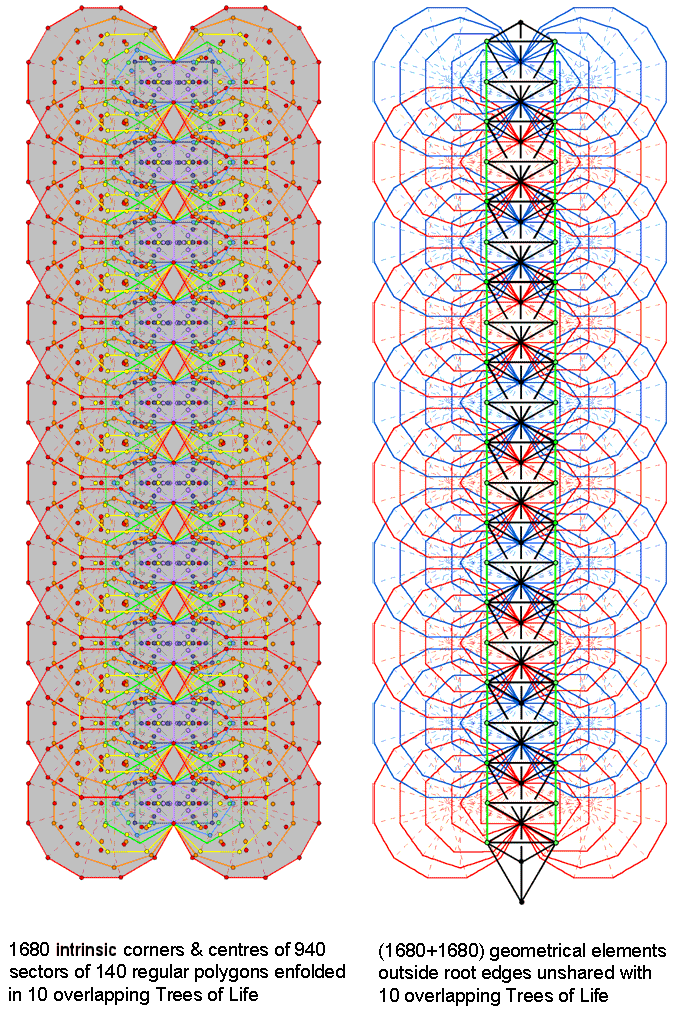
The 47 sectors of the seven enfolded polygons making up half of the inner Tree of Life have 41 corners and 88 sides. As the highest corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree, 40 corners are intrinsic to the set of seven polygons. The number of corners, sides & triangles in the 7n polygons enfolded in n overlapping Trees of Life = 40n + 1 + 88n + 47n = 175n + 1, where "1" denotes the highest corner of the hexagon enfolded in the nth Tree, which coincides with the lowest corner of the hexagon enfolded in the (n+1)th Tree. The root edge in each set of polygons has three geometrical elements (two endpoints & one line). Hence, (172n+1) elements are outside the n root edges. The (7n+7n) polygons enfolded in n Trees have (344n+2) elements outside their root edges, that is, including the n root edges, they have (344n + 2 + 3n = 347n + 2) elements. The 14 polygons enfolded in one Tree of Life have 349 geometrical elements. As this is the 70th prime number, it is remarkable that the geometrical composition of the inner Tree of Life is quantified by the last of the first 70 prime numbers that can be assigned to the 70 yods making up its outer form when it is constructed from tetractyses (see here)!
The number of corners & centres of sectors of the 47n sectors of the 7n polygons enfolded in n Trees of Life = 40n + 1 + 47n = 87n +1, where 87 is the number value of Levanah, the Mundane Chakra of Yesod. 85n corners & centres outside their root edges are intrinsic to the 7n polygons, where 85 = 40 + 41 + 42 + 43. Those in the polygons on the right include 2n corners that coincide with either Chesed or Netzach of each Tree. Those in the polygons on the left include 2n corners that coincide with either Geburah or Hod of each Tree. Hence, on each side of the n root edges are 83n corners & centres of sectors that are intrinsic to the polygons. Including the two endpoints of each root edge, there are (2×83n + 2n = 168n) corners & centres of the 94n sectors of the (7n+7n) polygons enfolded in n overlapping Trees, there being 84n corners & centres associated with each set of 7n polygons. The 940 sectors of the 140 polygons enfolded in 10 Trees have 1680 intrinsic corners & centres, 840 such points being associated with the 70 polygons on each side of the central Pillar of Equilibrium. Notice in the left-hand diagram that no green yods in the tetractyses of hexagons are shown at those corners & centres that coincide with Sephiroth on the Pillars of Mercy & Severity because, being shared with the outer Tree of Life, they are excluded from the count of corners & centres that are intrinsic to the inner Tree of Life.
Now let us separate shared geometrical elements from unshared ones. As well as the two corners in each set (outer corner of the triangle and the lower corner of the hexagon) that are shared with its outer Tree (indicated by green yods in the second diagram), the vertical diameters of each hexagon (i.e., two sides of sectors) are shared, too, with triangles of the outer Tree of Life; they are indicated by the green lines that are the Pillars of Mercy and Severity. As indicated above, the 7n polygons have (172n+1) corners, sides & triangles outside their n root edges. Of these, (4n+1) corners & sides are shared with the outer Tree of Life. Therefore, 168n corners, sides & triangles outside their root edges are intrinsic to each set of 7n polygons. The inner form of 10 overlapping Trees consists of (70+70) enfolded polygons with (1680+1680=3360) intrinsic corners, sides & triangles outside their 10 root edges (see also here).
All holistic systems display the division 168 = 84 + 84 (see The holistic pattern). Does this hold true for the geometrical composition of the seven enfolded polygons, which — par excellence — is a representation of such systems? Yes, as is now shown. We shall calculate the composition of individual polygons and then show that at least two combinations exist each of which has 84 geometrical elements. There is ambiguity over whether the corner of the pentagon that coincides with the centre of the decagon should be counted as though it belongs to the former or to the latter. Let us consider the former case for the moment. Below are tabulated the numbers of sectors of the seven polygons and their corners and sides that are outside the root edge and unshared with the outer Tree of Life:
Geometrical composition of the seven enfolded, regular polygons.
|
triangle |
square |
pentagon |
hexagon |
octagon |
decagon |
dodecagon |
Total | |
|
Corners |
1 |
3 |
4 |
2 |
7 |
8 |
11 |
36 |
| Sides |
5 |
7 |
9 |
7 |
15 |
19 |
23 |
85 |
| Triangles |
3 |
4 |
5 |
5 |
8 |
10 |
12 |
47 |
| Total = |
9 |
14 |
18 |
14 |
30 |
37 |
46 |
168 |
The dodecagon has the most geometrical elements, but there is no polygon or combination of polygons with 38 elements that add together with the 46 elements of the dodecagon to make 84 elements. So, regarding the centre of the decagon as one of the corners of the pentagon does not allow the division 168 = 84 + 84. Let us, instead, treat this corner of the pentagon as the centre of the decagon. Now, the numbers of intrinsic geometrical elements are:
|
Triangle |
Square |
Pentagon |
Hexagon |
Octagon |
Decagon |
Dodecagon |
|
9 |
14 |
17 |
14 |
30 |
38 |
46 |
We see that the decagon & dodecagon have 84 geometrical elements, as do the triangle, square, pentagon, hexagon & octagon — outside their root edge, of course. Moreover, no other combinations of polygons have 84 elements. The 168 geometrical elements in
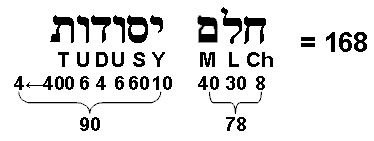
The gematria number value of Cholem Yesodoth is 168.
the seven enfolded polygons, therefore, divide uniquely into the 84 elements of the first five polygons and the 84 elements of the last two polygons. Not only that, the set of seven polygons also divides uniquely* into a subset (triangle, square, pentagon & decagon) that has 78 elements and a subset (hexagon, octagon & dodecagon) that has 90 elements, thereby reproducing the gematria number value 78 of "Cholem" and the number value 90 of "Yesodoth" in the Kabbalistic name of the Mundane Chakra of Malkuth (see diagram above). Alternatively, each set of seven enfolded polygons with 47 sectors have 34 corners outside the root edge, i.e., 31 corners other than those coinciding with Sephiroth (Chokmah, Chesed & Netzach for the right-hand set, Binah, Geburah & Hod for the left-hand set), so that outside the shared root edge of each set are (31+47=78) polygonal corners & triangles and 90 sides & centres of polygons.
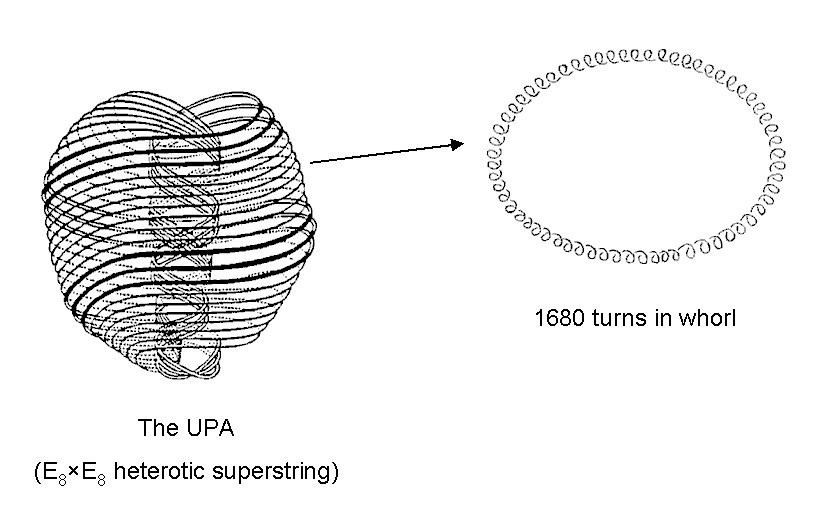
These properties demonstrate the remarkable analogy between the geometrical properties of the inner form of 10 overlapping Trees of Life and the helical form of the ten whorls of the basic unit of matter ("UPA") described by Besant & Leadbeater with the yogic siddhi called "anima" (see diagram above and here). The two halves of the inner form — the two sets of 70 polygons — correspond to the outer and inner halves of this particle; the 840 intrinsic corners & centres of sectors associated with each set corresponding to the 840 1st-order spirillae (circularly polarized oscillations) in each whorl. The 1680 intrinsic geometrical elements outside the root edges in each set correspond to the 1680 1st-order spirillae in the outer or inner half of the UPA. The 3360 intrinsic geometrical elements outside the root edges of both sets of 70 polygons correspond to the 3360 circular turns in one revolution of all ten whorls of the UPA. The subquark state of the E8×E8 heterotic superstring is the realization in the subatomic world of the sacred geometrical blueprint of the outer and inner forms of the Tree of Life.
This amazing property of the inner Tree of Life is one of the most convincing pieces of evidence presented in this website that sacred geometries embody the details of the basic units of matter paranormally observed by Besant & Leadbeater (see Occult Chemistry). Here is the meeting point of the sacred geometry of Kabbalah and paranormal information about these particles. The only desperate, alternative response that a skeptic could make in explaining why such a meeting occurs would be to suggest that the appearances of the numbers 1680 and 3360 are mere coincidence. But then, according to the skeptic, it would have to be just chance, too, that the 140 polygons enfolded in 10 Trees of Life have 940 sectors with (840+840=1680) corners & centres. No reasonable mind can accept such a highly improbable accumulation of coincidences for three numbers that appear in alleged, paranormal descriptions of subatomic particles. Indeed, we should add to them a fourth number, namely, 176, as the number of geometrical elements composing the seven enfolded polygons, for Leadbeater noticed that every 25 spirillae of a given order in a major whorl are composed of 176 spirillae of the next higher order (see here). For the minor whorls, the number is 175. The counterpart of this difference in the inner Tree of Life is the fact that the number of geometrical elements in the 7n polygons enfolded in the n-tree = 175n + 1. This means that 175 of the 176 elements are intrinsic to the seven polygons enfolded in each Tree, the "1" referring to the topmost corner of the hexagon — the only element that is shared between sets of seven polygons enfolded in successive Trees because it coincides with the lowest corner of the hexagon belonging to the set of polygons enfolded in the next higher Tree. That four numbers characterizing the paranormal descriptions could appear by chance in the same context would be a miracle of improbability. It has, therefore, to be discounted by any sensible person.
It was pointed out in comment 8 in the section "Parameters of Superstring & Bosonic String Physics" in Polygonal numbers that the sum of the first seven orders of the first 10 types of polygonal numbers is 3360:
7
∑ (Tn + Sn + Pn + Hn + hn + On + Nn + Dn + En + dn) = 3360.
n=1
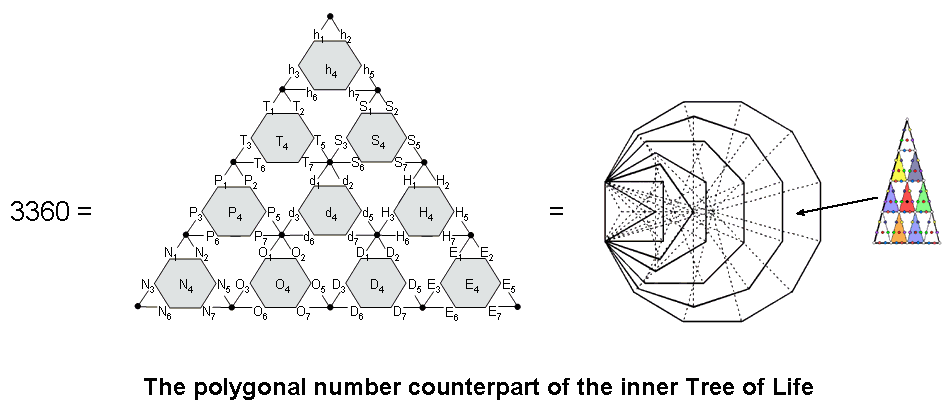
The superstring structural parameter 3360 is the sum of the 70 polygonal numbers that can be assigned to the 70 hexagonal yods of a 2nd-order tetractys, the 10 1st order tetractyses being associated with the first 10 types of polygonal numbers and the seven hexagonal yods in each tetractys being associated with their first seven orders. Here is the arithmetic counterpart to the geometrical embodiment of this amazing number in the inner form of 10 Trees of Life. It is embodied in the inner form of a single Tree of Life as the 3360 yods in the seven enfolded polygons when their sectors are 2nd-order tetractyses (for proof, see ref. 3 in Article 24).
* That is, apart from a residual ambiguity about whether the square or hexagon should contribute to each number, due to the fact that they both have the same number of geometrical elements. What is unique are the two combinations of numbers that sum to 78 and 90.
| << Previous 1... 16 17 [18] 19 20 ...56 Next >> |