Home
Polygonal Numbers
In this section we shall study a class of mathematical object known to
the ancient Greeks as ‘polygonal numbers.’ They are a generalisation of geometrically-based numbers, such as
the numbers of corners of polygons, their yod populations, etc. Remarkable relationships exhibiting
beautiful, mathematical harmonies will be shown to exist between polygonal numbers and parameters of the Tree
of Life, including those that are group-theoretical numbers of superstring/bosonic string theories. These
links turn out to be too closely attuned to Pythagorean mathematical notions to be plausibly explained
away as coincidental.
It is important to
realize that mathematics during the time of the Pythagorean School in Croton in southern Italy had not yet been
formalized into a subject for academic research. Instead, students were taught mathematics in this fraternity in
order to contemplate the divine immanent in nature. The mathematical doctrines of Pythagoras cannot be properly
understood without recognising that the modern dichotomy of science and religion did not exist then. Pythagoreans
believed that man could realise his divine nature by knowing the universal principle that governs the cosmos (a
word coined by Pythagoras himself, meaning “world-order,” a world ordered in a state of mathematical
harmony). This principle is Number, which is “the principle, the source and the root of all things.” For the
Pythagoreans, the spiritual and scientific dimensions of number were complementary and could not be separated.
Numbers were not merely measures of things but possessed a spiritual dimension. They believed that
understanding the relationship between these two aspects could lead the student to God.
Pythagoras was not only the first to call
himself a philosopher but also a priest-initiate of a mystery religion influenced heavily by Orphism, which
taught that the essence of the gods is defined by number. Numbers, indeed, expressed the essence of all created
things. According to the Pythagorean Philolaus: “All things which can be known have numbers, for it is not
possible that without number anything can either be conceived or known.” The Pythagoreans were the first to
assert that natural phenomena conformed to mathematical principles and so could be understood by means of
mathematics. In this sense, they may be considered the first physicists. However, their doctrine gradually
became distorted into the proposition that not only does number express the essence of things but also that,
ultimately, all things are numbers. Unconvinced by the peculiar emphasis Pythagoreans gave to
numbers because he was not privy to the secrets of their teachings, Aristotle said of them: “These thinkers seem
to consider that number is the principle both as matter for things and as constituting their attributes and
permanent state.”
The Pythagoreans thought that numbers had
metaphysical characters, which expressed the nature of the gods. The number one (the Monad) represented the
principle of unity — the undifferentiated source of all created things. The One was equated with the god Apollo
(a = not; pollon = of many). Pythagoras became associated with Apollo because he was named
after Pythios, the name of Apollo at Delphi, the most sacred place of his oracle. The Pythagoreans did not
even regard the number 1 as a number because for them it was the ultimate principle underlying all
numbers. The number 2 (Dyad) represented duality — the beginning of multiplicity, but not yet the possibility of
logos, the principle relating one thing to another. The number 3 (Triad) was called “harmony”
because it created a relation or harmonia (“joining together”) between the polar extremes of the
undifferentiated Monad and the unlimited differentiation of Dyad. These properties correspond in the Tree of
Life to the meaning of Kether, Chokmah and Binah. The number 4 corresponds to Daath (“knowledge”) because
impersonal, objective knowledge proceeds from principles only by standing outside the duality of subject and
object, thereby transcending their relativity.
Polygonal
Numbers
Pythagoras was the first to use geometrical diagrams as models of
cosmic wholeness and the celestial order. Numbers themselves were represented by geometrical shapes: triangles,
squares, pentagons, etc., and we have seen that tetractys-divided, regular polygons, the pentagram and the Star of
David provide natural representations of Godname numbers or parameters of the Tree of Life, CTOL, and superstring
theory. Any positive integer N can be represented by the corners of a regular, N-sided polygon. The ancient
Greek mathematicians, however, generalised such ‘figurative numbers’ by considering nests of n regular
polygons nested inside one another so that they share two adjacent sides. Dots denoting
the number 1 are spaced at regular intervals along the edges of the polygons, the edge of each polygon having
one more dot than the edge of its smaller predecessor. The total number PNn of dots in a
set of n nested regular polygons with N sides is called a “polygonal number.” The number 1 is the first
polygonal number, i.e., PN1 = 1. The second polygonal number, which is simply the
number of corners of an N-sided, regular polygon is PN2 = N, the third is
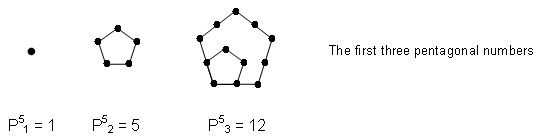
PN3, etc. The diagram below shows the first three pentagonal numbers:
P51 = 1, P52 = 5 and P53 = 12. Notice that
the second pentagonal number is depicted with two dots along each edge of the outermost pentagon and
that the third has three dots. In general, the
representation of the nth polygonal number PNn has n dots along each of the N sides of
the outermost, regular polygon.
can be represented by the corners of a regular, N-sided polygon. The ancient
Greek mathematicians, however, generalised such ‘figurative numbers’ by considering nests of n regular
polygons nested inside one another so that they share two adjacent sides. Dots denoting
the number 1 are spaced at regular intervals along the edges of the polygons, the edge of each polygon having
one more dot than the edge of its smaller predecessor. The total number PNn of dots in a
set of n nested regular polygons with N sides is called a “polygonal number.” The number 1 is the first
polygonal number, i.e., PN1 = 1. The second polygonal number, which is simply the
number of corners of an N-sided, regular polygon is PN2 = N, the third is
PN3, etc. The diagram below shows the first three pentagonal numbers:
P51 = 1, P52 = 5 and P53 = 12. Notice that
the second pentagonal number is depicted with two dots along each edge of the outermost pentagon and
that the third has three dots. In general, the
representation of the nth polygonal number PNn has n dots along each of the N sides of
the outermost, regular polygon.
It can be shown** that:
PNn = ½n[(N–2)n – (N–4)].
Table 1 list for future
reference formulae expressing the first ten types of polygonal numbers:
Table 1
| N |
PNn = ½n[(N-2)n − (N-4)] |
|
3
|
P3n ≡ Tn = ½n(n+1)
|
|
4
|
P4n ≡ Sn = ½n(2n-0)
|
|
5
|
P5n ≡ Pn = ½n(3n-1)
|
|
6
|
P6n ≡ Hn = ½n(4n-2)
|
|
7
|
P7n ≡ hn = ½n(5n-3)
|
|
8
|
P8n ≡ On = ½n(6n-4)
|
|
9
|
P9n ≡ Nn = ½n(7n-5)
|
|
10
|
P10n ≡ Dn = ½n(8n-6)
|
|
11
|
P11n ≡ En = ½n(9n-7)
|
|
12
|
P12n ≡ dn = ½n(10n-8)
|
Table 2 lists the values of PNn for 3≤N≤12 and
1≤n≤13:
Table 2. Values of PNn.
|
N
n
|
3
Tn
|
4
Sn
|
5
Pn
|
6
Hn
|
7
hn
|
8
On
|
9
Nn
|
10
Dn
|
11
En
|
12
dn
|
sn
|
∑n
|
bn
|
cn
|
sn− bn
|
∑n− cn |
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
10
|
10
|
7
|
7
|
3
|
3 |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
75 |
85 |
48 |
55 |
27 |
30 |
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
30
|
33
|
195
|
280
|
123
|
178
|
72
|
102 |
|
4
|
10
|
16
|
22
|
28
|
34
|
40
|
46
|
52
|
58
|
64
|
370
|
650
|
232
|
410
|
138
|
240 |
|
5
|
15
|
25
|
35
|
45
|
55
|
65
|
75
|
85
|
95
|
105
|
600
|
1250
|
375
|
785
|
225
|
465 |
|
6
|
21
|
36
|
51
|
66
|
81
|
96
|
111
|
126
|
141
|
156
|
885
|
2135
|
552
|
1337
|
333
|
798 |
|
7
|
28
|
49
|
70
|
91
|
112
|
133
|
154
|
175
|
196
|
217
|
1225
|
3360
|
763
|
2100
|
462
|
1260 |
| 8 |
36 |
64 |
92 |
120 |
148 |
176 |
204 |
232 |
260 |
288 |
1620 |
4980 |
1008 |
3108 |
612 |
1872 |
| 9 |
45 |
81 |
117 |
153 |
189 |
225 |
261 |
297 |
333 |
369 |
2070 |
7050 |
1287 |
4395 |
783 |
2655 |
| 10 |
55 |
100 |
145 |
190 |
235 |
280 |
325 |
370 |
415 |
460 |
2575 |
9625 |
1600 |
5995 |
975 |
3630 |
| 11 |
66 |
121 |
176 |
231 |
286 |
341 |
396 |
451 |
506 |
561 |
3135 |
12760 |
1947 |
7942 |
1188 |
4818 |
| 12 |
78 |
144 |
210 |
276 |
342 |
408 |
474 |
540 |
606 |
672 |
3750 |
16510 |
2328 |
10270 |
1422 |
6240 |
| 13 |
91 |
169 |
247 |
325 |
403 |
481 |
559 |
637 |
715 |
793 |
4420 |
20930 |
2743 |
13013 |
1677 |
7917 |
Also listed are:
a) the sums
sn of the first ten types of polygonal numbers for given n:
12
sn ≡ Σ PNn =
5n(11n−7)/2;
N=3
b) the running sums of sn:
n
Σn ≡ Σ
sr =
5n(n+1)(11n−5)/6;
r=1
c) the sums
bn of the seven polygonal numbers for given n corresponding to the seven types of regular polygons
making up the inner form of the Tree of Life, namely, the triangle (N=3), square (N=4), pentagon (N=5), hexagon
(N=6), octagon (N=8), decagon (N=10) & dodecagon (N=12):
bn ≡ Tn + Sn + Pn + Hn +
On + Dn + dn = n(17n−10);
d) the running sums
of bn:
n
cn ≡ Σ br =
n(n+1)(34n−13)/6;
r=1
The difference:
sn − bn = hn + Nn + En =
½n(21n−15),
which is the sum of the polygonal numbers corresponding to the
7-, 9- and 11-sided regular polygons not defined by the
geometry of the Tree of Life (notice the appearance here of the Godname numbers of Kether (21) and
Chokmah (15));
f) the running sums
of (sn − bn):
n
Σn − cn
= Σ
(sr−br) = n(n+1)(7n−4)/2.
r=1
The
best-known polygonal number is the Pythagorean Triangle, or tetractys:

As the
fourth triangular number T4 = 10, it is an equilateral, triangular
array of ten dots that denotes the Decad, which for the Pythagoreans was the perfect number, symbolising
wholeness and unity. The importance of the tetractys to them is
illustrated by their oath of fellowship:
“I swear by the discoverer* of the
Tetractys,
Which is the spring of all our wisdom,
The perennial fount and root of
Nature.”
It came to signify for the Pythagoreans an all-embracing
paradigm for whole systems. They believed that a four-fold pattern permeated the natural world, examples of
which are the four seasons, the point, line, surface and solid and the four
elements Earth, Water, Air and Fire. However, this alone does not explain why they valued the tetractys so
much. Its true significance is that it turns objects with sacred geometry into numbers having cosmic meaning,
some of which are relevant to theoretical physics. The Pythagoreans called the Tetrad, or number 4, “the
greatest miracle.” For this, indeed, is what it is, because it both prescribes and expresses the mathematical
description of all levels of reality, including the subatomic world.
The author has called the mathematical counterpart of the Pythagorean
metaphysical doctrine of the Tetrad the “Tetrad Principle.” This states:
|
TETRAD PRINCIPLE
An integer of significance to the physics of fundamental processes is always
either:
1) the 4th member of a class of numbers (sometimes the (42=16)th member of a class). If
the first member of this class is 1, it may be the 4th member after 1;
2) the sum of the first 4 members of a class of numbers;
3) the sum of 4 consecutive members of a class, starting with the 4th;
4) a property of either the 4th member or the first 4 members of a class of mathematical objects,
or of the square (symbol of the Tetrad) or square matrix array of integers or mathematical objects,
or of a tetractys array or geometrical pattern of integers with orthogonal symmetry.
|
It is discussed in more detail in
Article 1.
The most obvious example from
superstring theory of this principle is its prediction that space-time has 10 dimensions, where 10 is the
fourth triangular number:
10 = 1 + 2 + 3 + 4.
Another example from bosonic string theory is its prediction
that there are 16 higher dimensions beyond 10-dimensional space-time, where 16 = 42. Many more will be
encountered later and throughout this website. No claim is made for the converse of this principle, e.g., the
fourth (or 16th) member or the first four members of any class of mathematical objects always quantify
a parameter governing fundamental processes. The Tetrad Principle is a necessary, but not sufficient, condition for
a number to be of significance to the subatomic world. This means that a number which is predicted by a theory as
having fundamental significance in the subatomic world and which is consistent with the Tetrad Principle is not
necessarily an actual parameter of the physics of this world. The fact that examples to be discussed shortly can be
found which show how this principle prescribes parameters of the theories of superstrings and bosonic strings does
not indicate in itself that these theories are true. Taken individually, such examples merely demonstrate that they
satisfy a necessary criterion for being valid. What, however, turns this criterion into a potent principle is the
large degree to which these two theories support it. As the subsection entitled "Godname numbers" reveals, their
degree of consistency with the Tetrad Principle so exceeds what chance would lead one to expect that such detailed
conformity cannot, plausibly, be dismissed as coincidence. Instead, it is indicative of a powerful principle at
work hitherto unrecognised by science that prescribes the mathematics of fundamental phenomena. The Pythagoreans
appear to have sensed it by their emphasis on the importance of the number 4 to the study of nature. However, their
preoccupation with the Tetrad/tetractys was not taken seriously by scholars because the latter understood it only
in a secular sense that encompassed too wide a range of seemingly unrelated phenomena to make the principle
plausible.
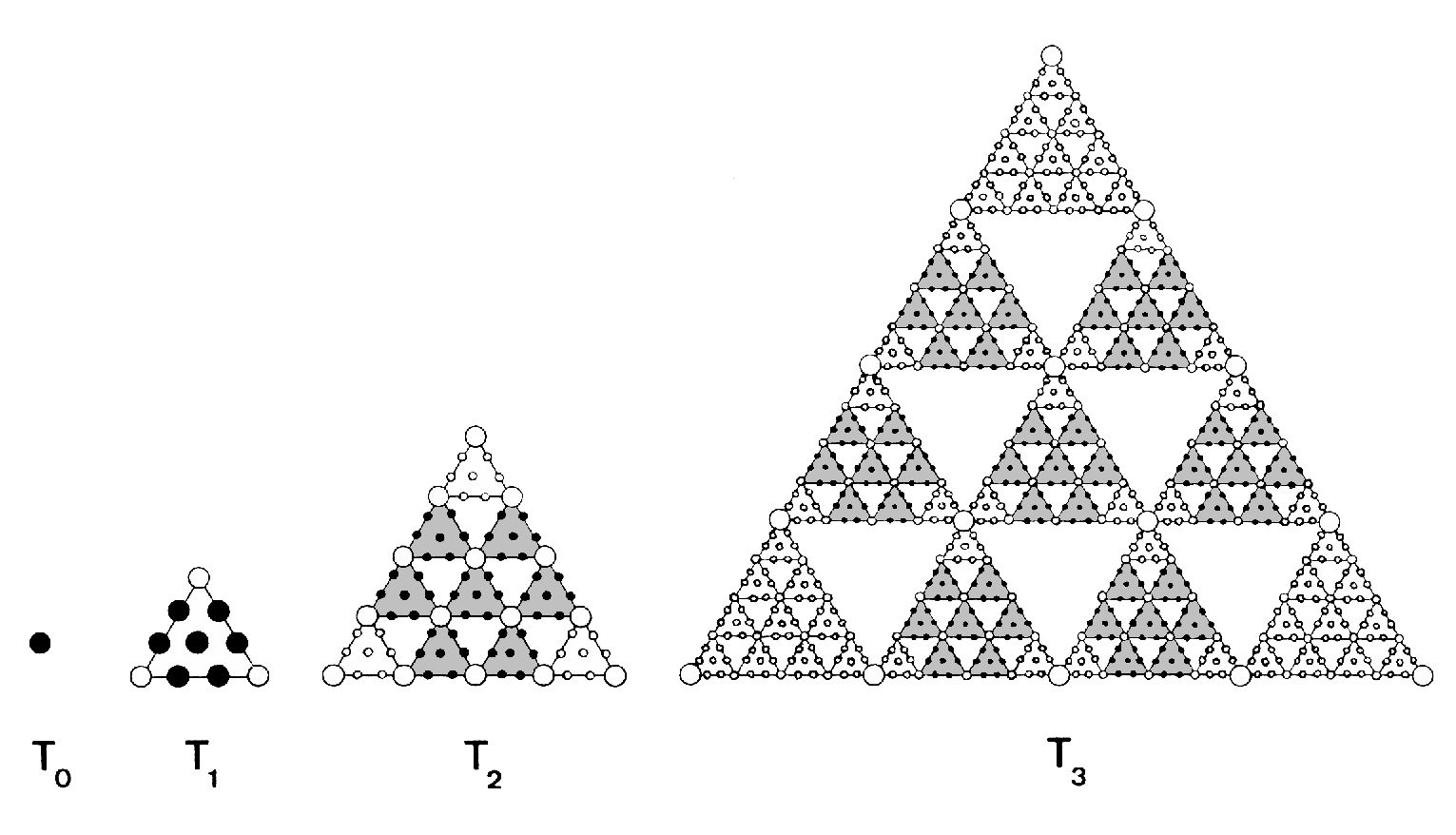
The tetractys is but one member of an infinite series of
tetractyses in which the nth member Tn is generated by replacing each yod in the (n−1)th member by a
tetractys, two adjacent yods being substituted by two tetractyses sharing a corner. The Pythagorean Monad —
the geometrical point — is the first member T0 of this series (the 0th-order tetractys), the Pythagorean
Triangle (1st-order tetractys) is the second member T1, the 2nd-order tetractys T2 is the
third, and so on. The Tetrad Principle prescribes properties of higher order tetractyses as well as T1
because they, too, are representations of spiritually whole systems, albeit more differentiated ones.
Because of its importance to our discussion, we illustrate below how the Tetrad Principle prescribes properties of
T2:
1) number of
yods = 85 = 40 + 41 + 42 + 43;
2) number of
yods surrounding its centre = 84 = 12 + 32 + 52 + 72;
3) number of
corners (○) of 1st-order tetractyses = 15 = 4th Mersenne number = 4th triangular number after
1;
4) number of
sides of 1st-order tetractyses = 30 = 12 + 22 + 32 +
42;
5) number of
hexagonal yods (•) = 70 = 10×7 = (1+2+3+4)×4th odd integer.
The polygonal
numbers in Table 2 will now be examined in the context of the Tree of Life and CTOL, the Godname numbers and
superstring group-theoretical numbers.
Tree of
Life
1) The fourth triangular number is 10
(=1+2+3+4). This is the number of Sephirothic corners of its 16 triangles, where 16 is the fourth
square number:
The fourth pentagonal number:
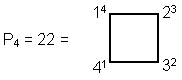
is the number of Paths in the Tree of Life forming the sides of
its triangles. This is an example of how the Pythagorean Tetrad defines structural parameters of the Tree of
Life. As shown here, the Tree of Life has 70 yods when constructed from tetractyses, where
70 = 7×10, 7 is the fourth odd integer and 10 (=1+2+3+4) is the fourth triangular number. The
1-tree has 80 yods, where 80 = 8×10 and 8 is the fourth even integer. Constructed from
Type A triangles, it has 171 more yods, where 171 = 19×9, 19 is the tenth odd integer and 9 is the
fourth odd integer after 1. The number of yods other than SLs = 240
| |
|
4!
|
|
|
|
| |
|
4! |
4! |
|
|
| = |
4!
|
4!
|
4!
|
|
|
| |
4! |
4! |
4! |
4! |
|
where 4! = 1×2×3×4.
2) The number of Paths in four overlapping Trees of Life,
which in Kabbalah represent the four Worlds of Atziluth, Beriah, Yetzirah
& Assiyah, is
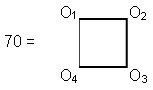
This is also the
number of corners of the (7+7) enfolded polygons and the number of yods in the tetractys-divided Tree of Life
(see here). A tetrahedral number is the number of points in a stack of
triangular numbers, each of which is a triangular array of points. They can be extended into 4-dimensional
space, forming 4-dimensional, tetrahedral numbers. 70 is the fourth such number after 1. In fact,
the first four of these numbers:
1, 5, 15, 35,
are the numbers of
yods in, respectively, the sequence:
point (1) → point+line
(1+4=5) → point+line+triangle (1+4+10=15) → point+line+triangle+tetrahedron
(1+4+10+20=35)
that constitutes the
"trunk" of the Tree of Life (see here), 70 being the number of yods in the whole Tree when its 16
triangles are turned into tetractyses.
The arithmetic mean
of the first n triangular numbers Tn is
tn = (n+1)(n+2)/6.
Therefore, t10 = 22 and
t19 = 70. Assigning the first 10 triangular numbers to the 10 yods of the tetractys and the first 19
triangular numbers to the 19 yods of a Type A triangle (see here), we see that the average of the former is the number of Paths in the Tree of Life
and that the average of the latter is the number of Paths in four Trees of Life, as well as the yod
population of the Tree of Life.
3) Polygonal numbers
possess a counterpart to how 35 and 70 can be expressed in terms of 4-dimensional, tetrahedral
numbers:
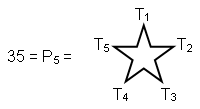
that is, 35 is the
fourth pentagonal number after 1 and 70 = P7;
4) the number of Trees in CTOL = 91 (see here)
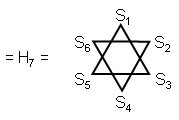
i.e., 91 is the sixth hexagonal number after 1. A Type B hexagon contains 91 yods (see
here).
5) The number of SLs in CTOL is
P1
55
T10
P2
P3 55
55
T10 T10
550 = P4
P5 P6
= 55 55 55
= T10 T10
T10
P7 P8 P9
P10 55 55 55
55 T10 T10
T10 T10.
where T10
= 55,
T1
T2 T3
55 + 55 + 55 +
55
=
T4 T5
T6
T7 T8
T9 T10,
and
●
S1
55
55
S2 S3
55 55
55
=
S4 S5 S6
● 55
55
●
S7
S8 S9 S10.
Also,
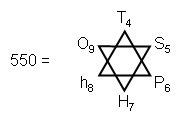
Notice that T4 is the Pythagorean tetractys and that H7 = 91. The
Star of David ‘defines' CTOL in terms of the 4th triangular number T4, the 5th square number
S5, the 6th pentagonal number P6, etc (notice how the order of the polygonal number
increases monotonically by 1 for all six numbers).
6) The number of SLs in the
49-tree representing the cosmic physical plane is
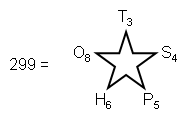
The order of each polygonal number is the number of corners of
the corresponding polygon. The triangle, square, pentagon, hexagon and octagon are the first five regular
polygons enfolded in the Tree of Life. They have 26 corners and contain 161 yods corresponding to the 161
SLs of the 26-tree that is the counterpart of 26-d space-time predicted by the quantum mechanics
of spinless strings. We see how the number of YAHWEH defines both space-time and the cosmic physical
plane.
7) The number
of yods surrounding the centres of the seven separate regular polygons generated by the Tree of Life
is
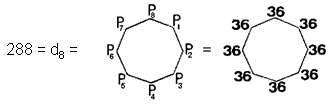 = 11 + 22 +
33 + 44.
= 11 + 22 +
33 + 44.
Once again, the octagon, whose 49
yods measure the number value of EL ChAI, the Godname of Yesod, represents a structural parameter of the
set of polygons.
Godname
Numbers
1) The fifth octagonal number, O5 = 65, is the number of ADONAI, the
Godname of Malkuth. This is the fourth octagonal number after 1, illustrating how the Tetrad Principle
defines this powerful number. 65 is the sum of the first 10 integers after 1:
| |
|
2
|
|
|
| |
|
3
|
4 |
|
|
65 =
|
5
|
6
|
7
|
|
| |
8 |
9 |
10 |
11 . |
This shows how the number 10, the Decad, determines the Godname number of the
tenth Sephirah. Using the identity:
n
Σ Pr =
nTn,
r=1
| |
P4
|
|
|
|
|
T1
|
|
|
| |
P3 |
P3 |
|
|
|
T2 |
T2 |
|
|
P2
|
P2
|
P2
|
|
= 65 =
|
T3
|
T3
|
T3
|
|
| P1 |
P1 |
P1 |
P1 |
|
T4 |
T4 |
T4 |
T4 . |
The sum of the first five nonagonal numbers:
defines the number of the complete Godname ADONAI MELEKH of Malkuth.
2) The remarkable mathematical
properties of the Pythagorean tetractys, Tetrad and Decad are illustrated by the equation
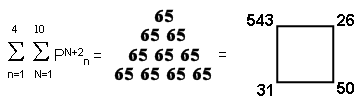
which relates the number of ADONAI and
the Godname numbers of the first four Sephiroth to the first four sets of ten polygonal
numbers.
3) The inverse of the
summation in (2) is
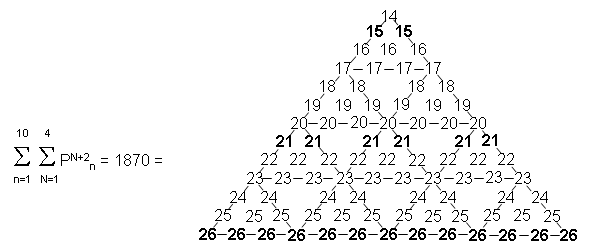
where the number at the centre of
this 2nd-order tetractys array of integers:
is the number of
Paths in the Tree of Life. 1870 = 187×10, where 187 is the number value of
Auphanim, the Order of Angels assigned to Chokmah. The number 26 of its Godname YAHWEH
forms the base of this array.
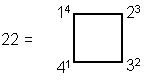
4) The number of the Godname YAHWEH
ELOHIM of Tiphareth is
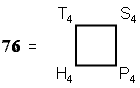
that is, it is the sum of the first four polygonal numbers of the
fourth order. It illustrates how the Tetrad defines this number. Notice that T4 +
S4 = 26, the number of YAHWEH, and that H4 + P4 =
50, which is the number of ELOHIM. The Tetrad also determines the latter because
50 is the sum of the first four triangular numbers and the first four square
numbers:
50 = (T1 + T2 + T3 +
T4) + (S1 + S2 + S3 + S4).
5) Compare (4)
with
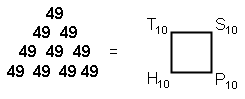
which relates the tenth triangular, square, pentagonal and hexagonal numbers — the
first four types of polygonal numbers — to the number 49 of the Godname EL ChAI of
Yesod.
6) The number of
SHADDAI EL ChAI, the complete Godname of Yesod, is
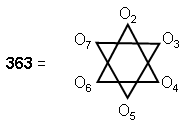
This summation of the first six
octagonal numbers after 1 relates the octagon with 49 yods prescribed by EL ChAI to the sixth
Sephirah of Construction.
7) The eighth, non-trivial
hexagonal number is H9 = 153, which is the number of the Godname ELOHIM SABAOTH of Hod, the
eighth Sephirah, counting from Kether.
8) The seventh, non-trivial
heptagonal number is h8 = 148, which is the number of Netzach, the seventh Sephirah,
counting from Kether.
9) The sum of
the first seven orders of polygonal numbers corresponding to the seven regular polygons of the inner Tree of Life
is
7
Σ (Tn + Sn + Pn +
Hn + On + Dn + dn) = 2100.
n=1
This illustrates the potency of the
Godname number 21 of Kether. Notice that the number 26 of YAHWEH forms the base of this tetractys
array.
10) The sum of the first seven orders
of non-trivial polygonal numbers (i.e., numbers larger than 1) corresponding to the seven regular
polygons of the inner Tree of Life is
8
Σ (Tn
+ Sn + Pn + Hn + On +
Dn + dn) = 3108
n=2
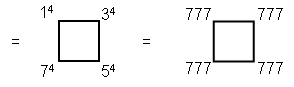
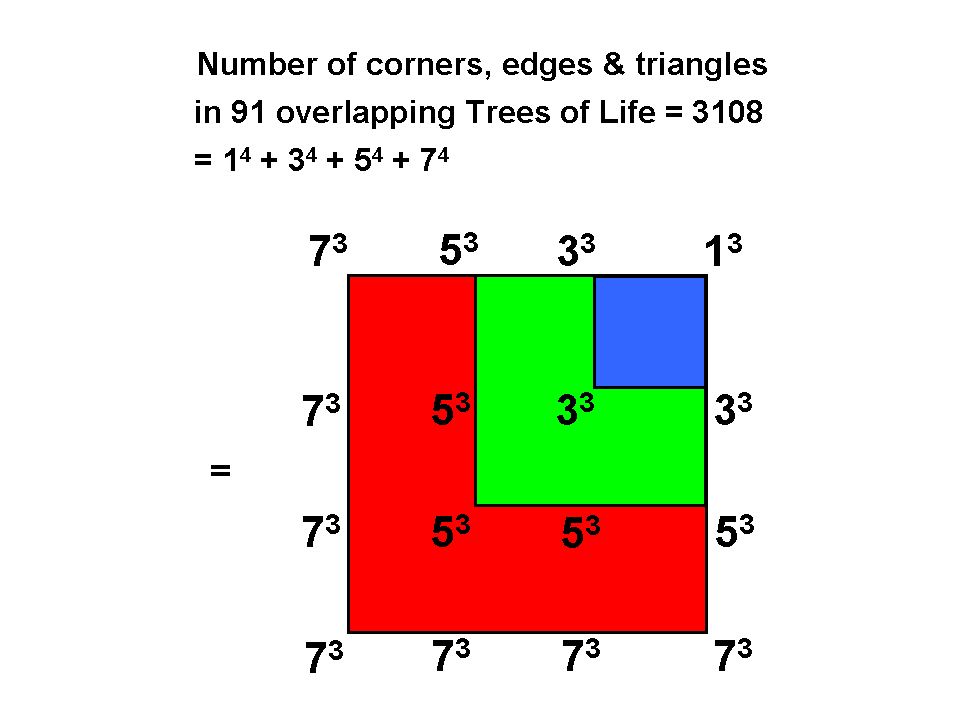
This demonstrates the beautiful symmetry inherent in these numbers based upon the
Pythagorean Tetrad, which defines the number 7 as the fourth odd integer. 3108 is the number of
geometrical elements making up the 91 Trees of Life in CTOL (for proof, see here). This parameter of CTOL is prescribed in a very remarkable way
by EL ChAI, the Godname of Yesod with number value 49, because 3108 is the sum of
(7×7=49) polygonal numbers. The fact that it is also the sum of the fourth powers of
the first four odd integers demonstrates par excellence the Tetrad Principle.
11) The sum of the first (10×10)
polygonal numbers is
10 12
Σ10 = Σ Σ
PNn = 9625 = 25×385
n=1 N=3
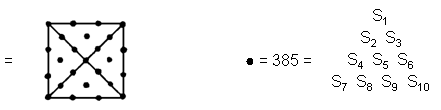
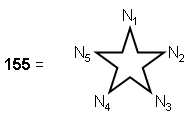
12) The sum of the first (10×10) array of polygonal numbers other than unity is
11 12
Σ Σ PNn = 12750 = sum of
15 integers 15, 25, 35, 45… 155 = 10×85×15,
n=2 N=3
where
This illustrates the powerful, archetypal nature of the Godname YAH with number 15. The sum of
the 10×10 square array of polygonal numbers determined by the Decad is the sum of 15 integers,
starting with 15 and spaced ten units apart. Notice that:
| |
|
11
|
|
|
| |
|
12 |
13 |
|
| 155 = |
14
|
15
|
16
|
|
| |
17 |
18 |
19 |
20 , |
that is, starting with the next integer after the tenth one, 155 is the sum of the
next ten integers having 15 at its centre when arranged as a tetractys. These two
properties serve to demonstrate how the Decad determines arithmetically not only the number 65
of ADONAI (as we saw in (1)) but also the number 155 of ADONAI MELEKH, the complete
Godname of Malkuth, the tenth Sephirah.
13) The sum of the first (10×5=50) polygonal numbers is
10
7
Σ
Σ
PNn = 2750 = 55×50,
n=1
N=3
where
| |
|
1
|
|
|
| |
|
2 |
3 |
|
| 55 = |
4
|
5
|
6
|
|
| |
7 |
8 |
9 |
10 |
(the tenth triangular number and the tenth Fibonacci number) is the
arithmetic mean of the first 50 polygonal numbers. This illustrates how the parameter 55 of CTOL,
which has 550 (=10×55) SLs (see here), is prescribed by the Godname ELOHIM with number value 50. The
55th SL from the bottom of CTOL is the 496th SL from its top, where 496 is the
number value of Malkuth and the dimension of both E8×E8 and SO(32), the two gauge symmetry
groups describing the unified forces between the two types of heterotic superstring (see under "Superstring
gauge symmetry group" here). The number 55, therefore, determines the number at the very heart
of superstring theory that was shown by physicists Michael Green and Gary Schwarz to be the dimension of a
symmetry group that generates interactions between superstrings that are free of quantum
anomalies.
14) The inverse of the summation in (13)
is the sum of the (5×10=50) polygonal numbers:
5 12
Σ
Σ
PNn = 1250 = 25×50
n=1 N=3

15) The sum of the first (7×7=49) polygonal numbers is
7
9
Σ
Σ
PNn = 1764 = 49×36.
n=1 N=3
The number 36 of ELOHA, the
Godname of Geburah, is the arithmetic mean of the first 49 polygonal numbers, where 49 is the number
value of EL ChAI, the Godname of Yesod.
16) The sum of the Godname numbers of
the seven Sephiroth of Construction is
8
539 = 31 + 26 +
76 + 129 + 153 + 49 +
65 = Σ
On.
n=2
Parameters of Superstring & Bosonic String Physics
(1) The dimension of superstring
space-time is
10 = T4,
the number of compactified dimensions of
bosonic strings beyond superstring space-time is
16 = S4,
and the total number of compactified
dimensions for bosonic strings is
22 = P4.
These numbers demonstrates the Pythagorean principle (referred to here as the "Tetrad
Principle") of a 4-fold pattern in these numbers characterizing the nature of matter, for they are the
fourth triangular, square & pentagonal numbers.
2) The dimension of the superstring
symmetry group E8 is
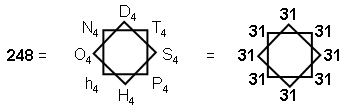
where 31 is the number value of EL, the Godname of Chesed, which is the
fourth Sephirah from the top of the Tree of Life. This demonstrates how the Pythagorean Tetrad
determines the symmetry group E8 at the heart of superstring theory (notice that
248 is the sum of the first eight polygonal numbers of the fourth order). Also,
the rank of E8 is 8, which is the fourth even integer. Notice that
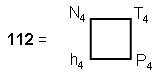
is the number of non-zero roots of
E8 of a certain kind. 112 is the number value of Beni Elohim, the Order of Angels
assigned to the Sephirah Hod.
3) The total number of non-zero
roots of E8 is
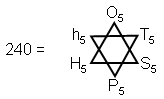
where T5, S5, etc. are the fourth triangular numbers, square numbers, etc.
after 1. Notice that the smallest polygonal number here is T5 = 15, the number of YAH, whilst
the largest number is O5 = 65, which is the number of ADONAI, the Godname of Malkuth. Also
notice from Table 2 that
and
i.e., the sum of the first four
orders of polygonal numbers corresponding to the three regular polygons (7-, 9- & 11-sided polygons) which are
not generated by the Tree of Life is equal to the number of non-zero roots of E8. Once again, the
Pythagorean Tetrad is seen to generate a group-theoretical parameter of this superstring symmetry group. The number
of ADONAI expresses the sum of the first four orders of the first ten types of polygonal
number.
4) The dimension of the anomaly-free gauge symmetry groups E8×E8 and SO(32) of
heterotic superstrings is
In other words, the number 31 of EL ("God"), the Godname of Chesed, prescribes
the dimension of this gauge group as the 31st triangular number. The arithmetic mean of the first n
pentagonal numbers is
n
(1/n) Σ Pr =
Tn.
r=1
Therefore, 496 is the arithmetic mean of the first 31 pentagonal numbers:
31
496 = (1/31) Σ Pn,
n=1
so that
31
Σ Pn =
31×496 = 31×(1+2+3+... + 31).
n=1
Since the tetractys-divided pentagon has 31 yods (see
here), it has the remarkable property that it generates not only the number
496 when the first 31 integers are assigned to its yods but also the same number when
496 is assigned to each yod as when the first 31 pentagonal numbers are
assigned to them! Moreover, this property is unique to the pentagon because assigning the (6n+1)th
triangular number T6n+1 to each of the (6n+1) yods of an n-sided regular polygon gives the same
sum as assigning the polygonal numbers PNr (r = 1, 2,... 6n+1) only for n = 5. The
pentagram has the equally important property that, if the 30 triangular numbers T1, T2,
...T30 are assigned to the (12 + 22 + 32
+ 42 = 30) yods along its boundary:
their sum is
In superstring theory, each of the 496 roots of the gauge group E8×E8 is
associated with a gauge charge that is the source of a vector gauge field having 10 components defined with
respect to the 10 dimensions of space-time. Therefore, the pentagram generates the number of space-time
components of all the gauge bosons responsible for the forces of nature other than gravity — truly an
amazing property of this ancient, religious symbol.
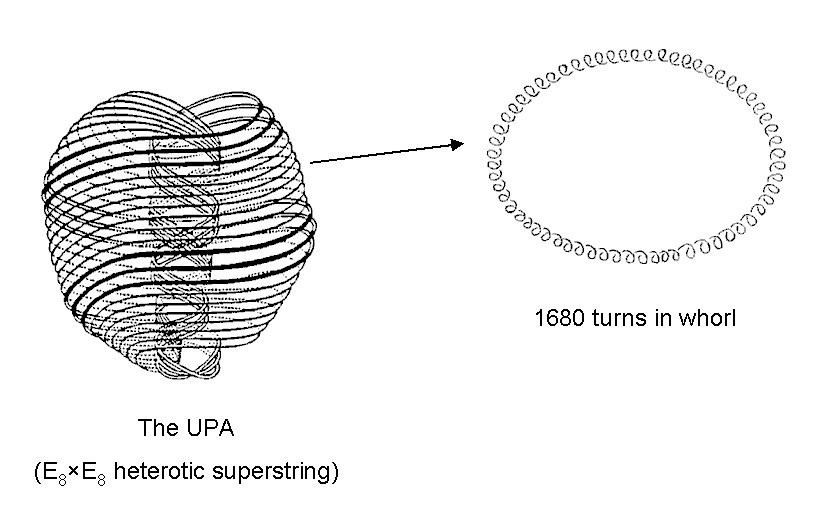
The 10 whorls of the UPA/subquark superstring make 50 revolutions around its axis of
spin. Each helical whorl comprises 1680 circular turns, there being 336 turns in each of its five revolutions.
The number 1680 is the 24th octagonal number: O24. Here are the first five octagonal numbers:
As 336 =
(12+22+32+42+...+312) ⁄31,
we see that this structural parameter of superstrings is the arithmetic mean of the first 31
square numbers. This shows how EL ("God"), the Godname of Chesed with number value 31,
prescribes the form of the UPA.
Using the
identity:
Hn = 4Tn-1 + n,
H16 = 4T15 + 16
= 480 + 16 = 496,
which compares with the fact that the 496 roots of E8×E8, one
of the two anomaly-free, gauge symmetry groups of superstrings, consist of 480 non-zero roots and 16 zero roots.
H16 is the 15th hexagonal number after the trivial hexagonal number: H1 = 1. This
shows how the number 15 of the Godname YAH of Chokmah determines the dimension 496 of
the two symmetry groups at the heart of superstring theory.
5) The 26th
triangular number is the sum of the sixth polygonal numbers of the first six types:
(notice the double role of the number 6). This number is the number of corners of the 70 polygons
enfolded in the inner form of 10 overlapping Trees of Life that represent 10-dimensional, superstring
space-time (see here).
6) The sum of the tenth polygonal numbers of the
first seven types is
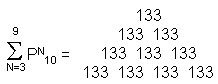
,
where 133 is the
dimension of E7, the rank-7 subgroup of E8. Notice that
| |
|
12
|
|
|
| |
|
32 |
52 |
|
| 1330 = |
72
|
92
|
132
|
|
| |
132 |
152 |
172 |
192 |
is the sum of 100 (=
13 + 23 + 33 + 43) odd integers comprising these 10 (=1+2+3+4) square
numbers. The sum of the tenth set of the first 10 polygonal numbers is
illustrating the representational power of the Pythagorean
Tetrad.
7) This is the
4th-order tetractys T4:

It
has
| |
|
240
|
|
|
| |
|
240 |
240 |
|
| 74 − 1 = 2400 = |
240
|
240
|
240
|
|
| |
240 |
240 |
240 |
240 |
hexagonal yods surrounding its centre that belong to
lower-order tetractyses corresponding to Sephiroth of Construction because each hexagonal yod in the
1st-order tetractys gets replaced in the 2nd-order tetractys by a 1st-order tetractys with seven hexagonal
yods, and so on, so that the numbers of such yods in higher-order tetractyses increases according to the
geometric series 71, 72, 73, 74, etc. The 5th-order tetractys
T5 has 16800 hexagonal yods surrounding its central set of seven hexagonal yods. The
fourth-order tetractys, T4, therefore expresses through its 2400 hexagonal
yods the number of space-time components of the gauge fields corresponding to the 240 non-zero roots of
E8, namely, 240×10 = 2400, whilst T5, the fourth higher-order tetractys beyond
the ordinary tetractys T1, embodies the number (16800) of coils in the 10 helical whorls of the
UPA/subquark superstring paranormally described by C.W. Leadbeater and Annie Besant (see here). In the former case, the Tetrad Principle prescribes a
dynamical parameter of superstrings; in the latter, it determines the tetractys representation of their
structural parameter.
8) The sum of the first seven orders of the first 10 types of
polygonal numbers is 3360:
7
∑ (Tn + Sn + Pn +
Hn + hn + On + Nn + Dn + En +
dn) = 3360.
n=1
This is a primary structural parameter of the subquark
superstring that is embodied in sacred geometries (see The holistic
pattern) because its 10 whorls make five complete revolutions around its axis of spin,
i.e., each of their revolutions on average comprises 16800/5 = 3360 circular turns of their
helices. Amazingly, this is the number of yods in the seven enfolded polygons of the inner Tree of Life
with 2nd-order tetractyses as their sectors (for proof, see Article 24, ref. 3) :
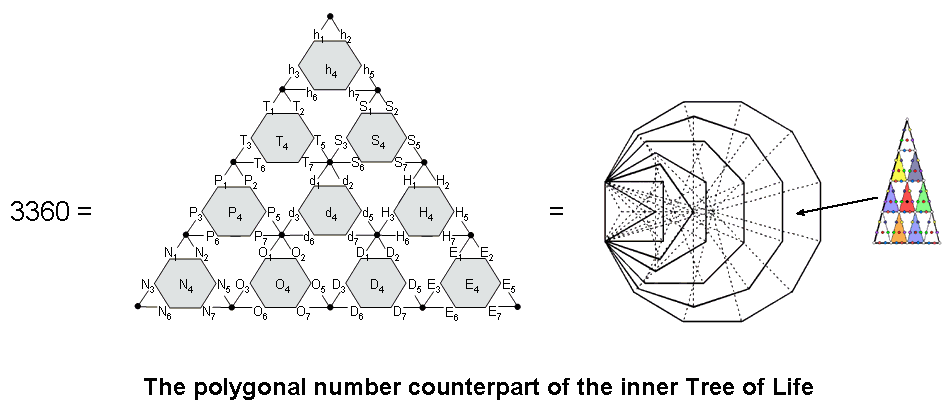
This
extraordinary property is illustrated by the 2nd-order tetractys array shown above with polygonal numbers assigned
to its 70 hexagonal yods. The seven orders of each type of polygonal number are assigned to the hexagonal yods
corresponding to Sephiroth of Construction. Polygonal numbers of the type corresponding to the seven enfolded
polygons of the Tree of Life are assigned to the 7×7 hexagonal yods of the seven tetractyses arranged at the
corners and centre of a hexagon. The dodecagonal numbers are assigned to the central tetractys because both the
dodecagon as the seventh of the regular polygons of the inner Tree of Life and the central yod of a
tetractys correspond to Malkuth, the seventh Sephirah of Construction. Polygonal numbers corresponding to
the three types of polygon not generated by the Tree of Life (7-, 9- & 11-cornered polygons) are
assigned to hexagons in the tetractyses at the corners of the 2nd-order tetractys. The sum of these (3×7=21)
numbers is
7
∑ (hn + Nn + En) =
1260
n=1
| |
|
126
|
|
|
| |
|
126 |
126 |
|
| = |
126
|
126
|
126
|
|
| |
126 |
126 |
126 |
126 , |
1260 is the number of Tarshishim, the Order of Angels
assigned to Netzach, the seventh Sephirah. It is remarkable that the number 126 is the sum of the
values of the four types of combinations of the letters of EHYEH (Hebrew: אהיה; English: AHIH), the Godname of Kether, whose number value is
21:
A = 1, H = 5, I = 10
| 1. A + H + I |
= 16 |
| 2. AH + HI + AI + HH |
= 42 |
| 3. AHI + HIH + AHH |
= 47 |
| 4. AHIH |
= 21 |
|
TOTAL
|
= 126 |
It is also
remarkable that it is the arithmetic mean of the first 26 triangular numbers and therefore
prescribed by YAHWEH, the Godname of Chokmah with number value 26:
26
126 = (1/26) Σ Tn.
n=1
The sum of the remaining (7×7=49) polygonal numbers in the hexagonal array of seven
hexagons is
7
∑ (Tn + Sn + Pn + Hn +
On + Dn + dn) = 2100
n=1
| |
|
210
|
|
|
| |
|
210 |
210 |
|
| = |
210
|
210
|
210
|
|
| |
210 |
210 |
210 |
210 , |
where
| |
210 |
210 |
210 |
210 |
| |
210 |
210 |
210 |
210 |
|
3360 =
|
210
|
210
|
210
|
210 |
| |
210 |
210 |
210 |
210 . |
This is
an example of the Tetrad Principle expressing a structural parameter of the superstring through the 4×4 square
array of the number value of a Godname, in this case, EHYEH.
This polygonal counterpart of the inner Tree of
Life demonstrates the beautiful harmony between number and sacred geometry. The number 3360 is the number
of circular turns in one revolution of the 10 whorls of the UPA/subquark superstring. The polygonal
representation of this structural parameter of the subquark state of a superstring reveals its
archetypal character in a remarkable way. How it is embodied in sacred geometries is discussed here [see under heading "3360 = 1680 + 1680 (or 336 = 168 + 168)"].
See also here.
A comment needs to be made concerning the significance of the properties of polygonal numbers
demonstrated above. Given a source of 100 numbers listed in Table 2 comprising the first ten orders of the
first ten types of polygonal numbers, as well as all their possible combinations, it is obvious that it would
not be too hard to pick at random certain combinations of them whose sum is equal to some given number.
Indeed, it would have been highly improbable, statistically speaking, if none of these polygonal numbers
or their combinations had turned out to be parameters of the Tree of Life and other sacred
geometries. Should, therefore, any significance other than coincidence be assigned to these results? The
answer is: yes, because there is in fact no randomness displayed in the examples actually discussed. In the
case of single polygonal numbers PNn, the order n is usually either 4 or 5 (both
being allowed according to the Tetrad Principle) or 10, or a number that corresponds to the order of
appearance in the Tree of Life of the Sephirah whose number or Godname number is PNn.
In the case of numbers that are sums of polygonal numbers, the number of terms in the sum may be 4, 5, 6, 8 or
10. But the crucial point is that the orders n of the summed numbers are either all the same or increase by
equal increments of 1 from term to term in the summation. This is not a random pattern indicative of deliberate
cherry-picking of polygonal numbers that add up to some required number. In other cases, the number of
polygonal numbers in the sum is a Godname number, 40, 70 or 100, these numbers having obvious Pythagorean
character vis-à-vis the Tetrad, 2nd-order tetractys (its number of hexagonal yods) or Decad. These
representations of parameters of the Tree of Life or CTOL, Godnames and group-theoretical numbers of string
theory are, therefore, not arbitrary, random sets of polygonal numbers of different orders. Instead, they
display definite patterns of progression. Admittedly, the choice of these examples was not prompted by any
underlying theory. But none was needed, as the purpose of the exercise was to demonstrate that a real,
substantive nexus exists between polygonal numbers and the archetypal numbers that are embodied in sacred
geometries analyzed in this website — a connection which displays a beautiful harmony between number
and sacred geometry engineered by the tetractys, Decad and Tetrad. Examples (9), (12), (13) & (15) in the
section entitled "Tree of Life" are spectacular evidence of how Godname numbers are connected to the properties
of sets of polygonal numbers either defined by the Decad or corresponding to the seven polygons of the inner
form of the Tree of Life, whilst the role played by the Tetrad in expressing the property given in (10) is
unmistakable. Example (7) discussed above, in which the Tetrad Principle defines orders of tetractyses
embodying both the dynamical parameter 2400 and the structural parameter 16800 of the superstring, is also
incontestable. What we have here is not chance at work. Instead, we are glimpsing the
transcendental Intelligence that turns number into form, namely, the superstring.
Such examples serve to demonstrate the Pythagorean doctrine
that number is the most fundamental principle of all because it expresses the beautiful harmonies underlying
the mathematics of the physical and spiritual cosmos. Moreover, they show that the properties of polygonal
numbers are intrinsically linked to the tetractys. It was clear to Pythagoras that number is the most important
principle of all because of his insight that the harmonies revealed in their relationships must be realized in
nature. The tetractys is the basic paradigm of the Divine Creation, encompassing every one of its sensory and
supersensory levels, and so it is the natural expression of these relationships. Through the discovery by
superstring theory that space-time must have ten dimensions, modern physics has discovered an example of this
paradigm.
The Fibonacci
connection
The sum of the first 10 nth-order polygonal numbers ≡ sn =
5n(11n−7)/2 = ½(55n2−35n).
The sum of the seven nth-order polygonal numbers whose shapes conform to the seven regular polygons making up
the inner Tree of Life ≡ bn = n(17n−10) = ½(34n2−20n).
The sum of the remaining three nth-order polygonal numbers = sn − bn =
½n(21n−15) = ½(21n2−15n).
Apart from the common factor of ½, the coefficients of n2 in each sum are 55, 34 &
21, which are the tenth, ninth & eighth Fibonacci numbers after 0 belonging to the
famous Fibonacci series:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ....
(see Article 50 (
Part 1 &
Part 2) for how Fibonacci numbers appear in sacred geometries; see
Article 51 for how they are connected to the Pythagorean musical scale).
Excluding the implausible possible that it is mere chance that the coefficients are consecutive Fibonacci
numbers, the question arises: why should the mathematical growth of the polygonal numbers be determined by
some of the
same numbers that manifest in the
phillotaxis of many plants and
Sunflower
flowers? An example is the sunflower (see above), which, typically, has 34 spirals of florets twisting in one
direction and 21 spirals twisting in the other, making a total of 55 spirals. Obviously,
the appearance of Fibonacci numbers in these sums of polygonal numbers arises from having chosen
particular sets of polygonal numbers, namely, the first 10 of any order, the seven of any order
that correspond to the seven types of regular polygons in the inner Tree of Life and the three of any order
that correspond to the three regular polygons absent from this archetypal set: the heptagon, nonagon &
undecagon. The numbers 55, 34 & 21 therefore arise from the 3:7 division of the
number 10, which manifests in the tetractys as its three corners and its seven hexagonal yods and in the Tree
of Life as the Supernal Triad and the seven Sephiroth of Construction. The 7-, 9- & 11-cornered polygons
are analogous to the former because they are not part of the geometry of the inner form of the Tree of Life —
just as the Supernal Triad stands outside objective Creation. The polygonal numbers corresponding to them have
sums that are determined by the number 21 of EHYEH, the Godname of Kether, the first
member of the Supernal Triad. The 3-, 4-, 5-, 6-, 8-, 10- & 12-cornered regular polygons making up the
inner Tree of Life are analogous to the seven Sephiroth of Construction, which have objective manifestation.
The polygonal numbers that correspond to them have sums determined by the number 34, the next Fibonacci number
after 21. Clearly, to dismiss the two subsets of polygonal numbers as lacking significance on
the grounds that there are six other possible pairs of subsets that generate the coefficients 34 and
21 in their sums is to miss the point. What is significant here is that the types of
polygonal numbers corresponding to the seven regular polygons in the inner Tree of Life and the types
corresponding to the three regular polygons absent from it create three successive Fibonacci numbers. Of the
120 possible combinations of three polygonal numbers drawn from a group of 10, seven combinations generate the
coefficient 21 in their sum, creating a chance of 1 in 17 that its appearance is a
coincidence. Add to this the non-trivial fact that the first ten polygonal numbers of a given order generate
the coefficient 55 in their sum and it is inescapable that the property of certain sums of polygonal numbers
displaying Fibonacci numbers is significant, statistically speaking, because it is unlikely that it could be
due to coincidence. Indeed, they manifest not only in each order of polygonal number as the sum of 10, sum of
seven and sum of three numbers but also in the sums of all the 7n polygonal numbers up to the nth order that
correspond to the seven types of regular polygons, for cn = n(n+1)(34n−13)/6 =
(n/6)(34n2+21n−13), where 13, 21 & 34 are
successive Fibonacci numbers!
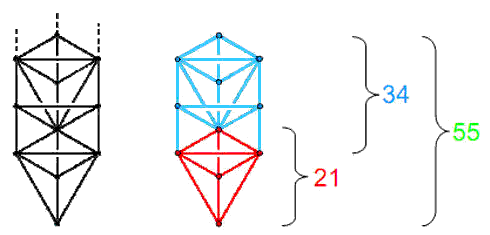
A similar 21:34 division appears in the geometry of the 1-tree, whose 55 geometrical elements
comprise 11 corners and 25 sides of 19 triangles:
The number of geometrical elements in the n-tree is given by
***:
N(n) = 34n + 21.
The Lower Face of the 1-tree is the red kite-shape in the diagram above at whose corners are located Tiphareth,
Netzach, Hod, Yesod & Malkuth. It consists of five corners, nine sides & seven triangles, i.e.,
21 geometrical elements. Six corners, 16 sides & 12 triangles, i.e., 34 elements
(those in the blue section in the diagram) are added by successive, overlapping Trees because N(n+1) − N(n) =
34. The counterpart of this in the seven separate polygons of the inner Tree of Life is the fact that their
48 triangular sectors have 55 corners, those in the triangle, pentagon & decagon
having 21
corners and those in the
square, hexagon, octagon & dodecagon having 34 corners.
Alternatively, 21 corners of the 48 sectors are either centres of
the seven polygons or endpoints of their root edges, leaving 34 corners outside these sides:
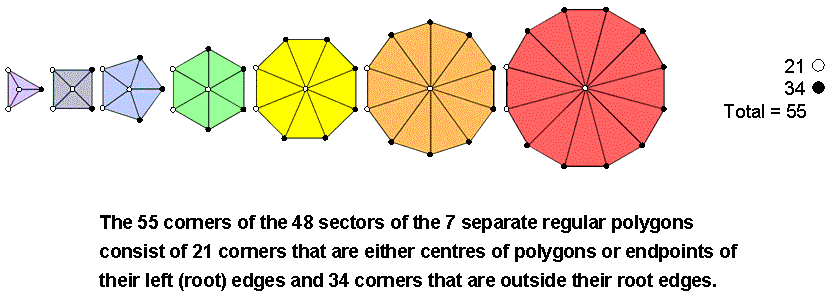
In fact, this
21:34 division is found in
all sacred geometries (see Article 50
(
Part 1 &
Part 2)). What is amazing is that it also manifests in the properties of
certain sets of polygonal numbers. However, given that these sets reflect the primary 3:7
division of the Tree of Life, it may not seem so surprising that the division should appear in polygonal
numbers
as well as in sacred geometries.
As sn = (n2/2)(55−35/n) and bn = (n2/2)(34−20/n),
sn/bn = (55−35/n)/(34−20/n), so that sn/bn → 55/34 as
n→∞. The ratio of successive numbers in the Fibonacci series tends to the limiting value of the Golden Ratio Φ
(= 1.618033...) as these numbers become larger and larger. 55/34 =1.61764... , which is already within 0.024%
of Φ, so that the ratio of sn/bn converges towards a limit of 55/34 that
approximates closely to the Golden Ratio. The same conclusion applies to the running sums of
sn and cn as n→∞ because Σn = 5n(n+1)(11n−5)/6 and cn = n(n+1)(34n−13)/6, so that
Σn/cn =
5(11n−5)/(34n−13) = (55/34)(1−5/11n)/(1−13/34n) → 55/34 as n→∞.

We can see where the numbers 55 and 34 originate by looking at the general formula for the nth polygonal number
P
Nn = ½n[(N−2)n − (N−4)]. The coefficient of n
2 is N − 2 (apart from the
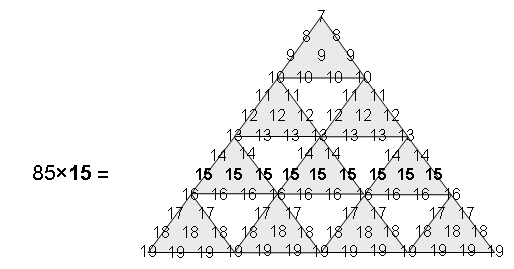
factor of ½). As the sum of the first 10 integers N = 3 + 4 + 5 +... + 12 = 75, the coefficient of
n
2 (apart from the factor of ½) in the sum of the first 10 polygonal numbers = 75 − 2×10 = 55.
As the sum of the seven different integers N corresponding to the seven regular polygons in the inner Tree of
Life = 3 + 4 + 5 + 6 + 8 + 10 + 12 =
48, the coefficient of n
2 in the sum of the
seven types of polygonal numbers that correspond to them =
48 − 7×2 = 34. The Fibonacci number
34 appears because the seven polygons 'happen' to have
48 corners, whilst the Fibonacci
number 55 appears because the three remaining polygons in the set of the first 10 polygons have
(75−
48=27) corners. There are seven different sets of three polygons drawn from the first
10 that have 27 corners: (4,11,12), (5,11,12), (6,9,12), (7,8,12), (6,10,11), (7,9,11) & (8,9,10).
Corresponding to them are seven sets of seven polygons with
48 corners, one of which is that
of the inner Tree of Life. The set (7, 9,11) that is absent from them is the only one of the seven sets of
three polygons for which all the polygons have
odd numbers of corners. In that sense, this set —and,
therefore, the seven polygons of the inner Tree of Life — are unique. If we impose the condition that there
should be seven polygonal numbers for given n whose sum has the Fibonacci constant 34 in the coefficient of
n
2, then their corresponding polygons
must have
48 corners. If,
alternatively, we impose the condition that the latter polygons have
48 corners,
then there must be seven of them. Kabbalistically speaking, the former condition amounts to the fundamental
distinction between the seven Sephiroth of Construction and the three members of the Supernal Triad, whose
counterpart in the inner Tree of Life is the presence of its seven regular polygons and the absence of the
three other polygons that complete the set of the first 10 polygons. The properties of these three absent
polygons and all 10 polygons are analysed
here.
* A reference to
Pythagoras.
** Proof: the
representation of PNn consists of the superposition of (n−1)
regular polygons with 2, 3, 4, ...n dots along each of their N edges. The rth polygon has r dots per edge. The
total number of dots in (n−1) separate polygons is
n−1
Σ Nr =
½nN(n−1).
r=1
Of these, there are
2 + 3 + 4 +... + n−1 =
½n(n+1) − 1
dots along one set of edges
and
1 + 2 + 3 +... + n−1 =
½n(n−1)
dots along the set of adjacent edges. The
total number of shared dots when the polygons are superimposed is
½n(n+1) − 1 + ½n(n−1) =
n2 −
1.
The total number of unshared yods
is
½nN(n−1) −
(n2−1) =
½n[[(N−2)n − N] + 1.
Superimposed, the (n−1) polygons have n dots
along one shared edge and (n−1) dots along the adjacent shared edge. The total number of dots in the
representation is
PNn = (n−1) + n + ½n[(N−2)n −
N] + 1
=
½n[(N−2)n − (N−4)].
*** Proof: the n-tree
has (12n+7) triangles with (6n+5) corners and (16n+9) sides. Number of corners, sides & triangles in the
n-tree = 34n + 21.
Home
 can be represented by the corners of a regular, N-sided polygon. The ancient
Greek mathematicians, however, generalised such ‘figurative numbers’ by considering nests of n regular
polygons nested inside one another so that they share two adjacent sides. Dots denoting
the number 1 are spaced at regular intervals along the edges of the polygons, the edge of each polygon having
one more dot than the edge of its smaller predecessor. The total number PNn of dots in a
set of n nested regular polygons with N sides is called a “polygonal number.” The number 1 is the first
polygonal number, i.e., PN1 = 1. The second polygonal number, which is simply the
number of corners of an N-sided, regular polygon is PN2 = N, the third is
PN3, etc. The diagram below shows the first three pentagonal numbers:
P51 = 1, P52 = 5 and P53 = 12. Notice that
the second pentagonal number is depicted with two dots along each edge of the outermost pentagon and
that the third has three dots. In general, the
representation of the nth polygonal number PNn has n dots along each of the N sides of
the outermost, regular polygon.
can be represented by the corners of a regular, N-sided polygon. The ancient
Greek mathematicians, however, generalised such ‘figurative numbers’ by considering nests of n regular
polygons nested inside one another so that they share two adjacent sides. Dots denoting
the number 1 are spaced at regular intervals along the edges of the polygons, the edge of each polygon having
one more dot than the edge of its smaller predecessor. The total number PNn of dots in a
set of n nested regular polygons with N sides is called a “polygonal number.” The number 1 is the first
polygonal number, i.e., PN1 = 1. The second polygonal number, which is simply the
number of corners of an N-sided, regular polygon is PN2 = N, the third is
PN3, etc. The diagram below shows the first three pentagonal numbers:
P51 = 1, P52 = 5 and P53 = 12. Notice that
the second pentagonal number is depicted with two dots along each edge of the outermost pentagon and
that the third has three dots. In general, the
representation of the nth polygonal number PNn has n dots along each of the N sides of
the outermost, regular polygon.

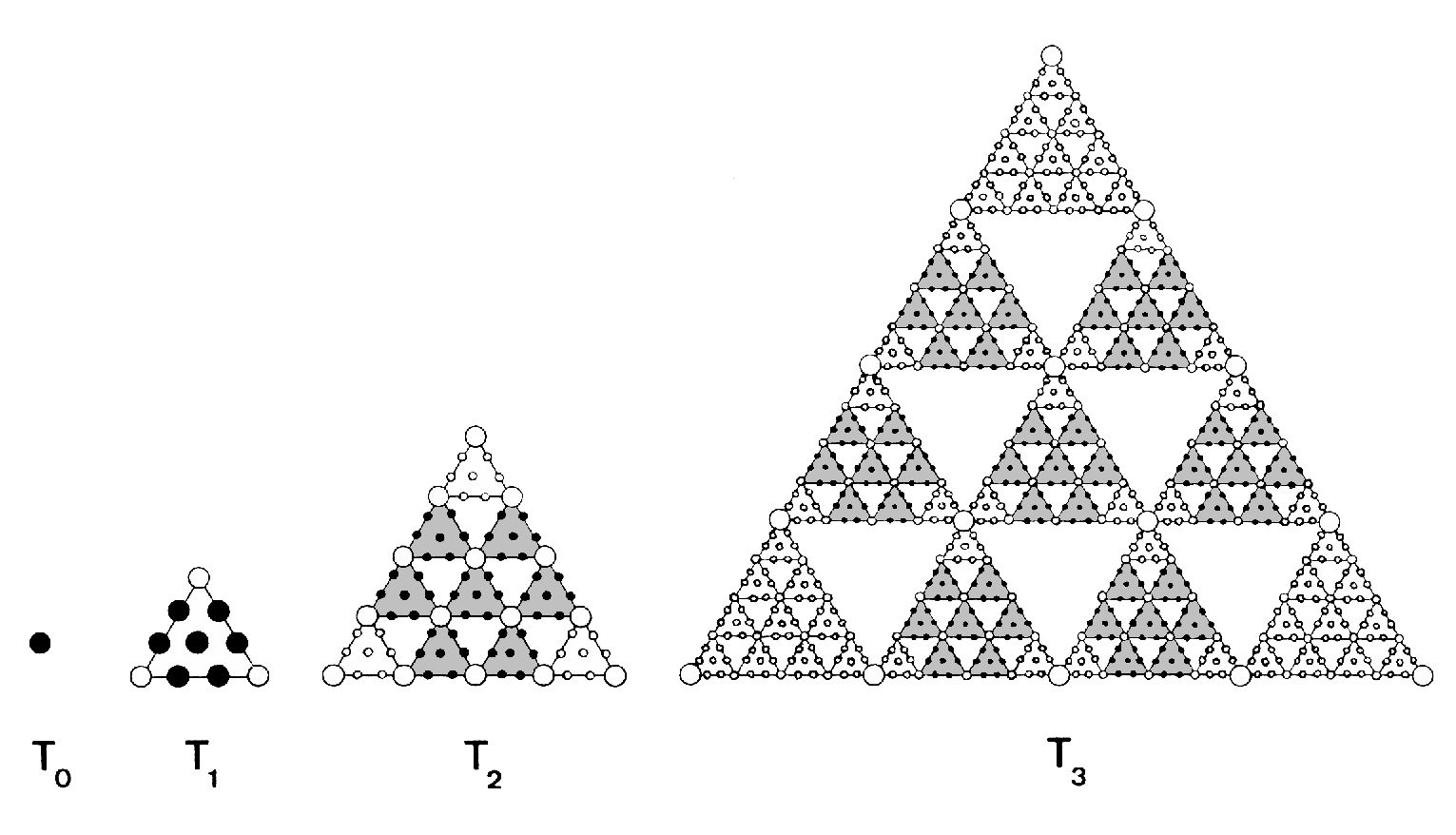
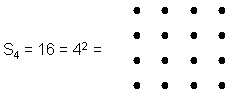
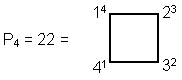
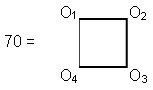

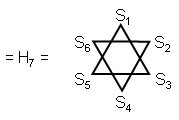


 = 11 + 22 +
33 + 44.
= 11 + 22 +
33 + 44.
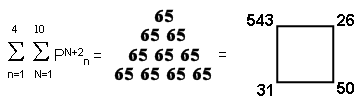
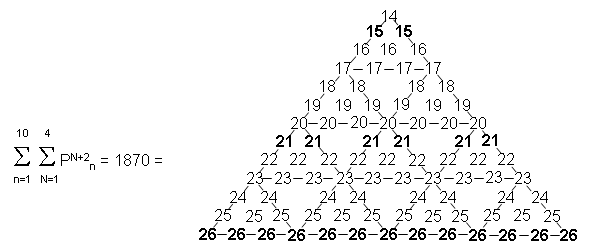


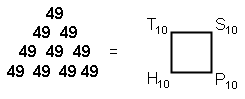

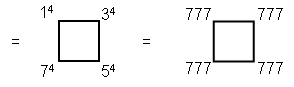

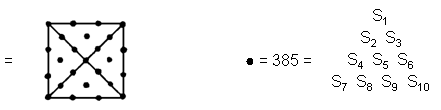


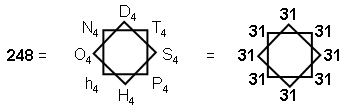
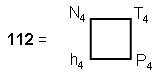
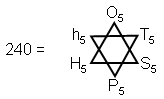
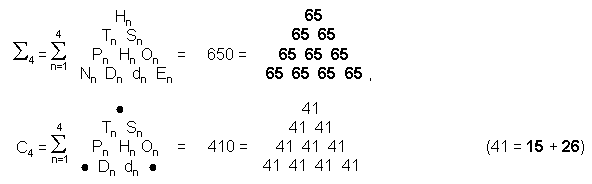
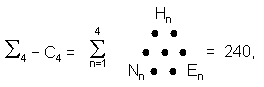
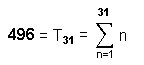

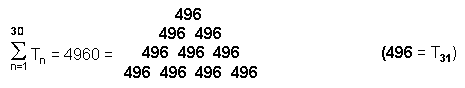


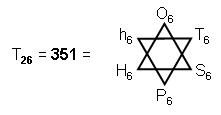
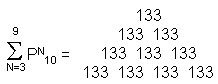 ,
,