| << Previous 1... 15 16 [17] 18 19 ...56 Next >> |
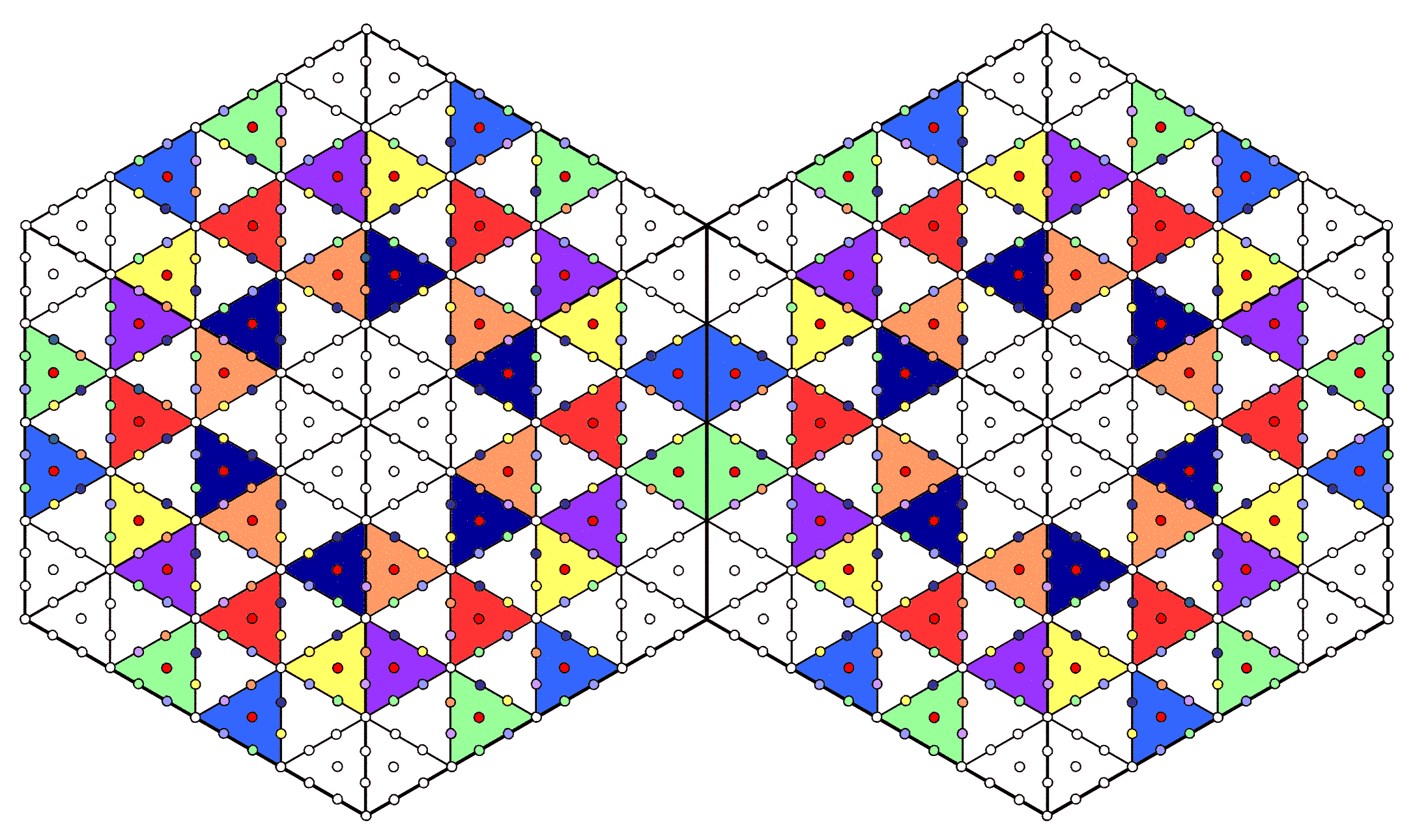
#17 The two joined hexagons with 2nd-order tetractyses as sectors embody the superstring structural parameter 840

A 2nd-order tetractys (see here) has 85 yods, where
85 = 40 + 41 + 42 + 43.
13 yods line each side. When the sectors of an n-gon are 2nd-order tetractyses, there are (85–13=72) yods per sector, where 72 is the number value of Chesed. The number of yods in such an n-gon = 72n + 1. A hexagon whose six sectors are 2nd-order tetractyses has 433 yods. For two joined hexagons, there are (433–13=420) yods in each one outside the root edge that is shared by them. Both hexagons have 840 yods outside their root edge. They are shown as either coloured in the seven 1st-order tetractyses in each sector that correspond to Sephiroth of Construction or as white in the 1st-order tetractyses at the corners of each 2nd-order tetractys corresponding to the Supernal Triad. The number 840 is a structural parameter of the subquark state of the E8×E8 heterotic superstring because, as described by Besant & Leadbeater (see here), each of the 10 whorls of the UPA is a helix with 1680 turns. They make 2½ revolutions around its spin axis in an outer spiral with 840 turns and 2½ revolutions around this axis in a narrower, inner spiral. We see that the pair of hexagons embodies not only the dynamics of the E8×E8 heterotic superstring (see previous page) but also the 4-dimensional space-time structure of its subquark state in up and down quarks.
The number 840 is the sum of the nine integers in the Lambda Tetractys (see here) that surround its central one when they are all multiplied by 10:
| 10 | |||
| 20 | 30 | ||
| 40 | 60 | 90 | |
| 80 | 120 | 180 | 270 . |
It is embodied in the disdyakis triacontahedron in the following way: when its faces are divided into their sectors and lines drawn inside it connecting its vertices to its centre, there are 1680 points, lines & triangles that surround any axis passing through two opposite vertices. 840 geometrical elements compose each half of the polyhedron (see here). It illustrates how this number is a parameter of holistic systems that possess sacred geometry.
The number 840 is also embodied in the 15 polygons formed by the vertices of the disdyakis triacontahedron. When their sectors are Type A triangles, 840 yods other than vertices surround their centres (see here).
| << Previous 1... 15 16 [17] 18 19 ...56 Next >> |