
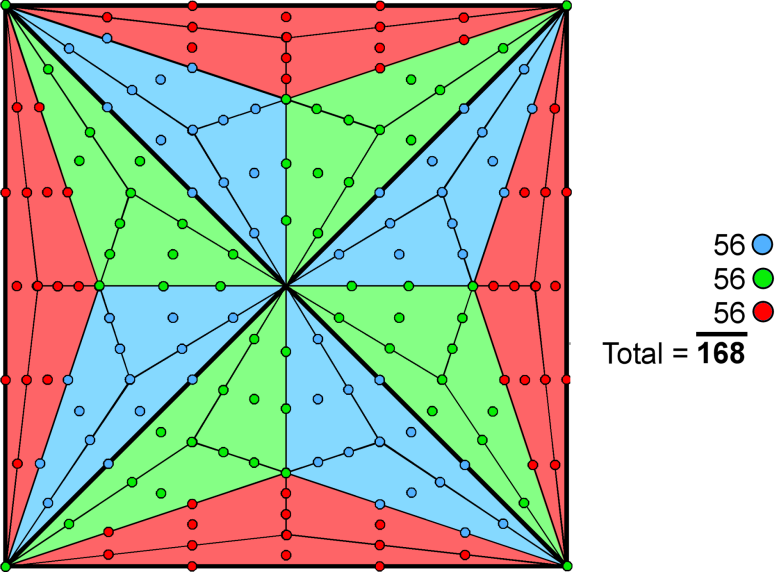
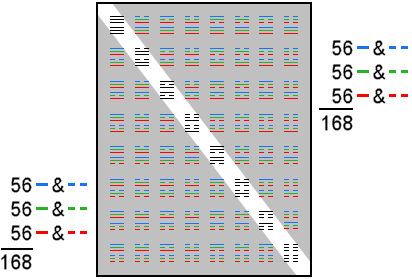
168 = 3×56
The 240 roots of the rank-8, exceptional Lie group E8 consist of
112 roots represented by 8-tuples with integer number components and 128
roots represented by 8-tuples with half-integral components, in both cases the sum of the
coordinates for each 8-dimensional root vector being even. The former comprise two sets of 28 roots
and one set of 56 roots. The latter comprise two sets of 28 roots, a set of 70 roots and a root at
(½,½,½,½,½,½,½,½) and its mirror image (½ → -½). The 72 roots that do not
form sets of 28 generate the 72 roots of the rank-6, exceptional group
E6. The remaining 168 roots comprise four sets of 28 and one set
of 56, i.e., three sets of 56.
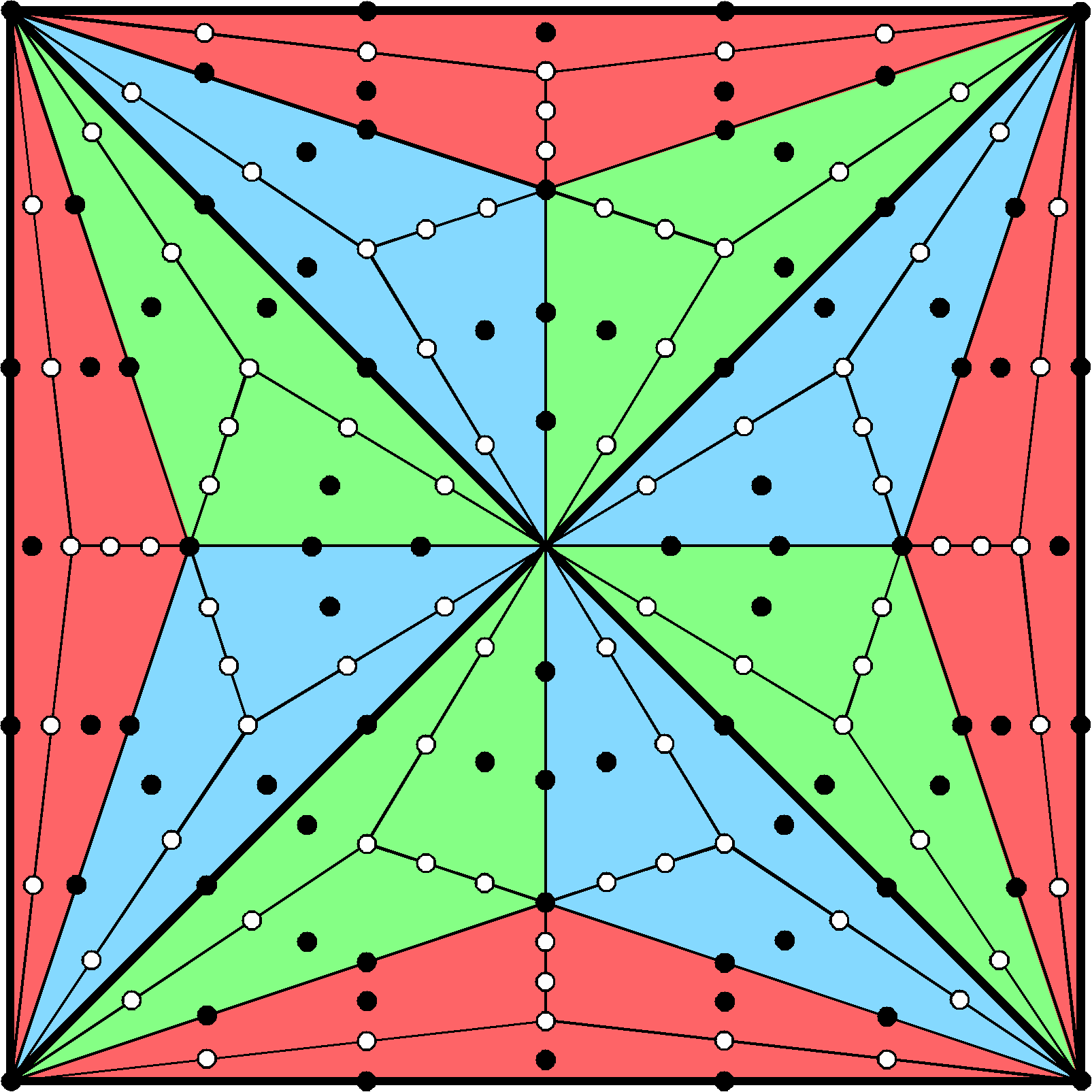
168 = 2×84
The 168 roots can be divided into three sets of 28 roots:
(1, 1, 0, 0, 0, 0, 0, 0) and all 28 permutations
(1, −1, 0, 0, 0, 0, 0, 0) and all 28 combinations
(−½, −½, ½, ½, ½, ½, ½, ½) and all 28 permutations
and their inversions:
(−1, −1, 0, 0, 0, 0, 0, 0) and all 28 permutations
(−1, 1, 0, 0, 0, 0, 0, 0) and all 28 combinations
(½, ½, −½, −½, −½, −½, −½, −½) and all 28 permutations.
The 168 roots comprise 84 roots and their 84 inversions.

The 240 roots of the rank-8, exceptional Lie group E8 are represented by 240 vectors in 8-dimensional, Euclidean space. These vectors all have the same length (by convention, it is taken to be √2). These vectors are the position vectors of the 240 vertices of the semi-regular polytope called the "Gosset polytope," or 421 polytope (this is discussed here). The 28 permutations of (−1, −1, 0, 0, 0, 0, 0, 0) are the mirror images of the 28 permutations of (1, 1, 0, 0, 0, 0, 0, 0). The 56 permutations of (1, −1, 0, 0, 0, 0, 0, 0) contain their mirror images, so that it contains 28 permutations and their 28 mirror images, in which +1→−1 & −1→+1. The 28 permutations of (−½, −½, −½, −½, −½, −½, ½, ½) are the mirror images of the 28 permutations of (−½, −½, ½, ½, ½, ½, ½, ½). There are 168 permutations that consist of three sets of 28 permutations and three sets of their mirror images. The remaining 72 roots consist of 70 permutations of (−½, −½, −½, −½, ½, ½, ½, ½), that is, 35 permutations and their mirror images, and two roots, namely, (½, ½, ½, ½, ½, ½, ½, ½) and its mirror image (−½, −½, −½, −½, −½, −½, −½, −½). The 72 roots comprise (35+1=36) roots and their 36 mirror images.
When their 47 sectors are tetractyses, the seven enfolded polygons making up each half of the inner Tree of Life have 120 yods lining their boundaries. They comprise 36 corners and 84 hexagonal yods. The topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life. It is the only corner of any of the seven polygons that is not intrinsic to them. It is coloured black in the diagram above, its counterpart in the mirror image set of polygons being coloured white. The 36 corners of each half of the inner Tree of Life consist of 35 intrinsic corners (coloured grey) and one corner shared with the inner form of the next higher Tree. Both separate halves contain 72 corners that comprise 70 intrinsic corners and two shared corners. 2×84 hexagonal yods line the 84 sides. They form three sets of 28 hexagonal yods lining each set of seven enfolded polygons, i.e., 3×56 hexagonal yods for both sets.
If the two hexagonal yods in the shared root edge are associated with the dodecagon, this polygon can be paired only with the triangle to create 14 sides with 28 hexagonal yods. This in turn means that the decagon can be combined only with the hexagon to create 14 sides, which means that the octagon can be combined only with the square and pentagon to create 14 sides with 28 hexagonal yods. If, instead. the two hexagonal yods are associated with one of the six other polygons, there are six possible combination schemes that can generate three sets of 28 hexagonal yods:
|
square + dodecagon |
square + dodecagon |
square + dodecagon |
||
|
hexagon + decagon |
or |
hexagon + decagon |
or |
hexagon + decagon |
|
triangle + pentagon + (root edge & octagon) |
|
triangle + (root edge & pentagon) + octagon |
(root edge & triangle) + pentagon + octagon |
|
square + dodecagon |
square + dodecagon |
(root edge & triangle) + dodecagon |
||
|
(root edge & pentagon) + decagon |
or |
pentagon + (root edge & decagon) |
or |
hexagon + decagon |
|
triangle + hexagon + octagon |
|
triangle + hexagon + octagon |
square + pentagon + octagon |
Such ambiguity in correspondence between hexagonal yods and roots of E8 is unattractive because, unless there is a plausible reason why it should exist (and there is none here), a unique, one-to-one correspondence should exist between hexagonal yods and these roots. Associating the root edge with the dodecagon is the most likely possibility because it leads to a unique, triple combination of polygons with 28 hexagonal yods in their 14 sides.
Comparing the six sets of 28 permutations of the 8-tuples with the sets of yods lining sides of the polygons in the two halves of the inner Tree of Life, the 72 corners correspond to the 72 8-tuples of the last three types listed in the diagram and the 168 hexagonal yods correspond to the 168 8-tuples of the first five types. The two chiral halves of the inner Tree of Life with 120 boundary yods correspond to the 120 8-tuples and their 120 mirror images. The two shared corners of the hexagons correspond to the root at (½, ½, ½, ½, ½, ½, ½, ½,) and its mirror image at (−½, −½, −½, −½, −½, −½, −½, −½).
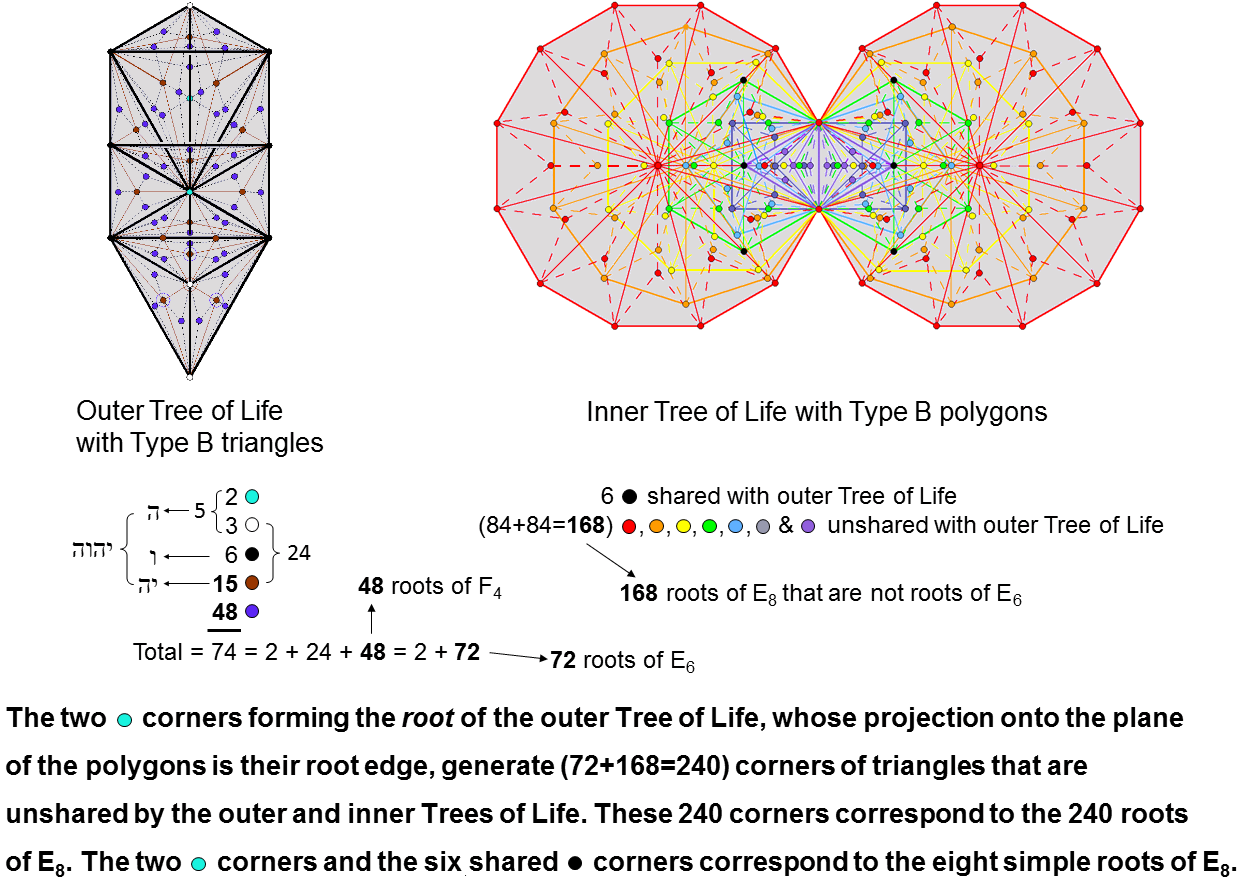
Outer Tree of Life
The outer Tree of Life is made up of 16 triangles with 10 corners. When they are Type B, each
triangle is composed of nine tetractyses with four internal corners, so that the number of corners
of the (16×9=144) tetractyses = 10 + 16×4 = 74. They comprise the 16 centres of the 16 original
triangles, the six black corners located at Sephiroth on the Pillar of Mercy and the Pillar of
Judgement, the turquoice corner at Tiphareth. the three white corners located at Kether, Yesod
& Malkuth and the 48 purple corners inside the 16 triangles. One of the
16 centres coincides with Daath. It is coloured turquoice because this yod and Tiphareth constitute
the "root" of the outer Tree, their projections onto the plane of the polygons of the inner Tree of
Life coinciding with the two endpoints of their shared root edge. Hence the outer Tree of Life
contains the two yods as its root and 72 corners.
Inner Tree of Life
The 14 regular polygons in the inner Tree of Life have (47+47=94) sectors with
80 corners. When the polygons are Type B, each sector consists of three tetractyses.
The inner Tree of Life has (94×3=282) tetractyses with (80+94=174) corners. The top,
centre & bottom of each hexagon coincides with the Sephiroth on the side pillars of the outer
Tree. This leaves 168 corners that are intrinsic to the inner Tree.
Outer & inner Trees of Life
As well as the root of the outer Tree, there are six shared corners, 72 corners
intrinsic to the outer Tree and 168 corners that are intrinsic to the inner Tree. The
combined Trees have (144+282=426) tetractyses with 248 corners. This is the
dimension of E8. The six shared corners and the two turquoice yods of the root
correspond to the eight simple roots of E8, the former corresponding to the six simple
roots of its exceptional subgroup E6, whilst the 72 corners intrinsic to the
outer Tree correspond to the 72 roots of E6 and the
168 corners intrinsic to the inner Tree correspond to the 168 remaining
roots of E8. The 84 roots and their 84 inversions correspond to the 84 corners
associated with (and intrinsic to) each chiral set of seven enfolded polygons.
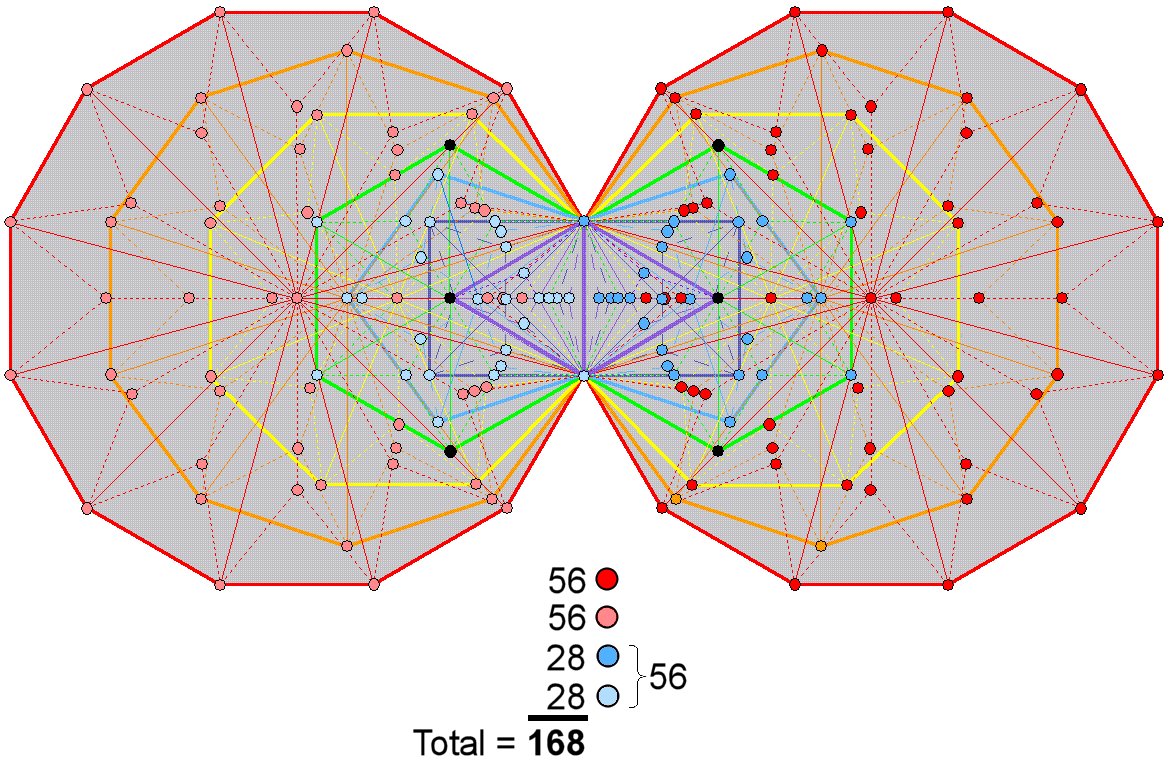
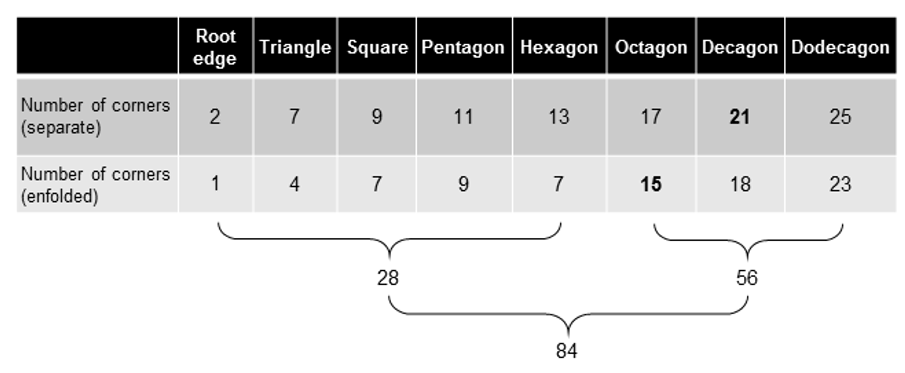
The 1st (4+4) enfolded Type B polygons have
(28+28= 56) corners of 102 triangles; the last (3+3) enfolded Type B polygons have
(56+56=112) corners of 180 triangles.
168 = 3×56
The first row in the table displays
the number of corners of triangles in each separate polygon of the inner Tree of Life.
The second row shows the number of corners of each enfolded polygon that belong to
the set of (84+84=168) intrinsic corners. The first (4+4) enfolded polygons have 56 corners
of 102 tetractyses; the last (3+3) enfolded polygons have (56+56=112) corners of
180 tetractyses. The 168 intrinsic corners group naturally into three sets of
56.
168 = 2×84
84 corners of 141 triangles are associated with each set of seven enfolded
polygons.
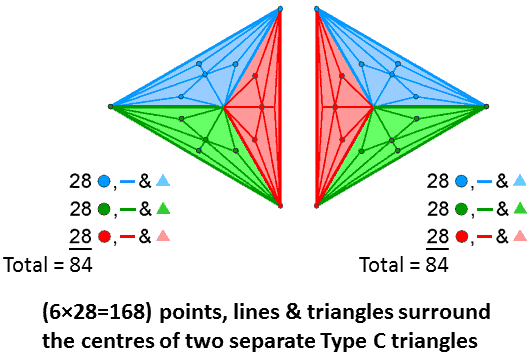
168 = 3×56
The number of corners, sides &
triangles that surround the centre of a Type C n-gon = 28n. A Type C triangle has 85 geometrical
elements, where
85 = 40 + 41 + 42 + 43,
of which 84 geometrical elements surround its centre, where
84 = 12 + 32 + 52 + 72.
There are 28 such elements per sector. There are 56 elements per sector and its counterpart in the mirror image triangle making up the (7+7) polygons of the inner Tree of Life. The two Type C triangles have (3×56=168) geometrical elements surrounding their centres.
168 = 2×84
84 points, lines & triangles
surround the centres of the two Type C triangles in the inner Tree of Life.
 84 black/white yods
84 black/white yods168 = 3×56
There are 42 yods per sector of a Type C square, so that 168 yods surround
its centre. There are 14 yods per blue, green or red Type A triangle in each Type B sector of the
Type C square. Colouring them respectively, blue, green & red, the four blue Type A triangles
contain 56 blue yods, the four green Type A triangles contain 56 green yods and the four red Type A
triangles contain 56 red yods.
168 = 2×84
The 14 yods of each colour in each
sector of the square consist of seven white yods and seven black yods. There are
(3×7=21) white yods and 21 black yods per sector, so that
the Type C square contains (4×21=84) white yods and 84 black yods. Alternatively,
84 yods can be associated with each diagonal half of the square.
 56 black & white yods in either red,
green or blue triangles
56 black & white yods in either red,
green or blue triangles
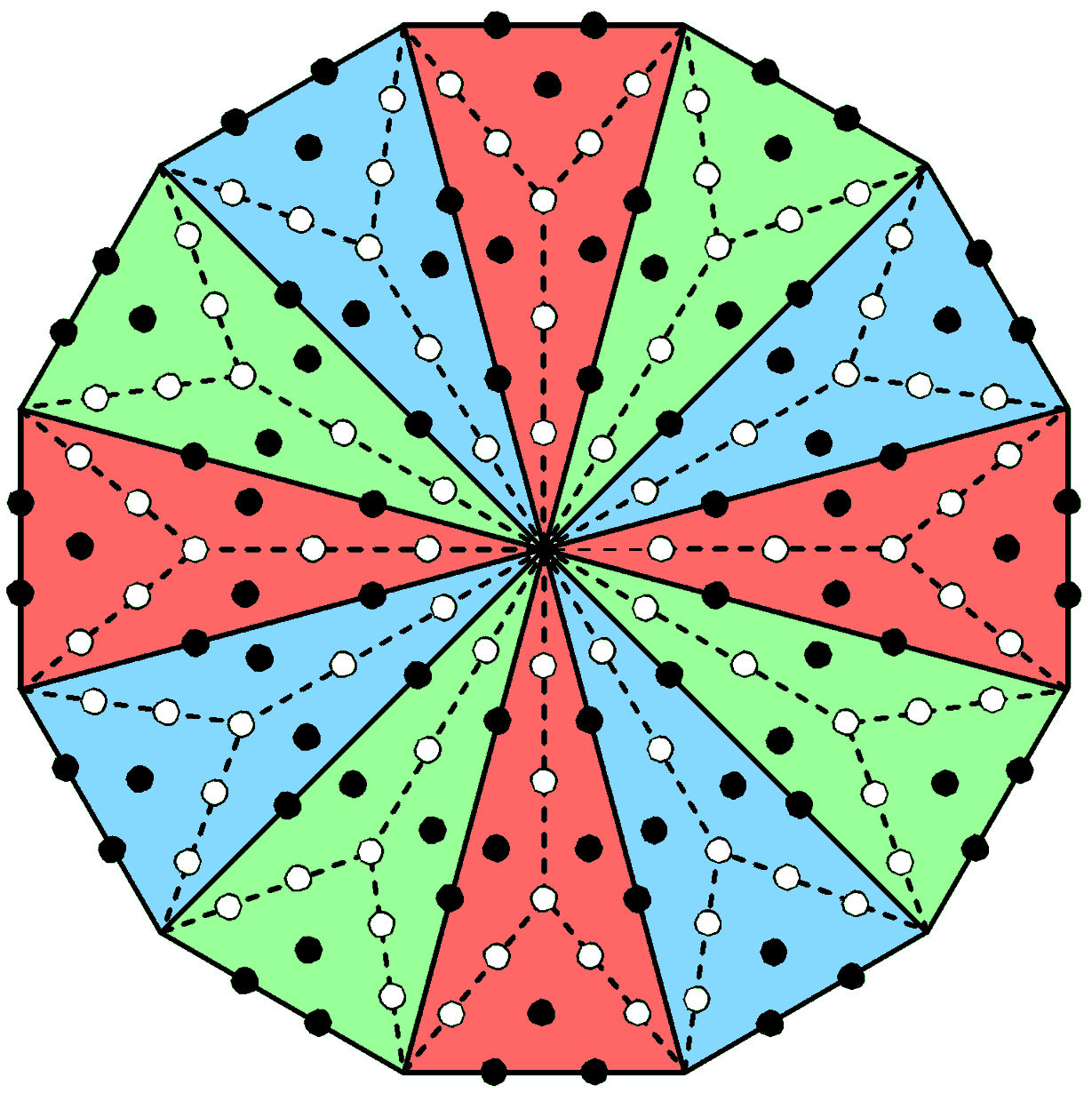
168 = 3×56
The 12 sectors of a dodecagon group
into three sets of four, each set (coloured either blue, green or red) being cross-shaped. There
are 14 yods per sector of a Type B dodecagon other than its corners, so that it has
168 such yods. They comprise (4×14=56) yods in red sectors, 56 yods in green
sectors and 56 yods in blue sectors.
168 = 2×84
The 14 yods per sector comprise seven black yods either on its sides or at centres of tetractyses
and seven white yods. The 168 yods other than corners of sectors consist of
(12×7=84) black yods and 84 white yods. Alternatively, 84 yods make up each half of the
dodecagon.
 The 64 hexagrams
The 64 hexagrams
168 = 3×56
The 8×8 square array of 64 hexagrams comprise eight hexagrams (16 trigrams)
forming its diagonal and 28 hexagrams (56 trigrams) on either side of them. Colouring the three
rows of a trigram blue, green & red, the 56 off-diagonal trigrams with
168 lines & broken lines consist of 56 blue lines & broken lines, 56
green lines & broken lines and 56 red lines & broken lines.
168 = 2×84
The 56 trigrams on either side of the diagonal set of eight basic trigrams are seven copies of the
latter, which comprise 12 lines and 12 broken lines. The 168 lines &
broken lines in each group of 56 off-diagonal trigrams consist of (7×12=84) lines and 84 broken
lines.
The three rows of a trigram correspond to the three types of 8-tuple:
(1, 1, 0, 0, 0, 0, 0, 0) and all permutations
(1, -1, 0, 0, 0, 0, 0, 0) and all combinations
(−½, −½, ½, ½, ½, ½, ½, ½) and all permutations
Interchanging lines & broken lines in a trigram corresponds to inverting the 8-d root vector, i.e., (+) signs → (−) signs and vice versa. Each off-diagonal line and broken line denotes one of the 168 8-tuples. The fact that they comprise 84 lines and 84 broken lines reflects the fact that these 8-tuples consist of 84 8-tuples and their 84 inversions, in which all (+) signs → (−) signs and vice versa. The 168 lines & broken lines in the 56 off-diagonal trigrams in the lower half of the 8×8 array of hexagrams denote the 168 8-tuples expressing those roots in the second E8′ group belonging to E8×E8′ that are not roots of its exceptional subgroup E6.
 The 3-dimensional Sri
Yantra
The 3-dimensional Sri
Yantra
168 = 3×56
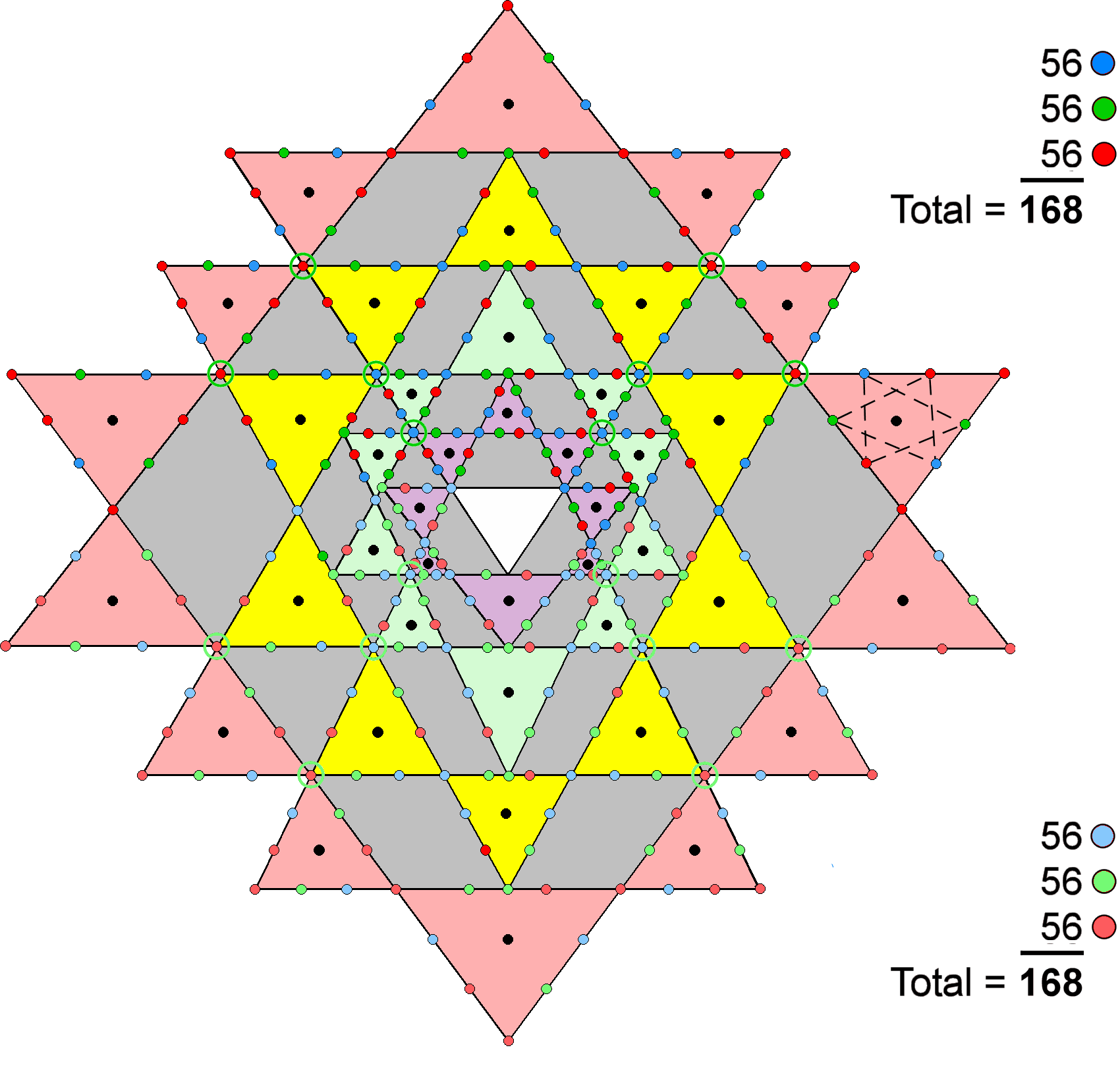
When the 42 triangles in the 3-d Sri
Yantra surrounding the central triangle (shown as white) are tetractyses, 336 yods line their
(42×3=126) sides. 168 yods line the 21 triangles in each half of the Sri
Yantra. Corners of tetractyses belonging to the layer of triangles next above a given layer are
denoted by circles; there are eight such corners in each half. The six hexagonal yods lining the
sides of each triangle are the corners of a 6-gon. They may be viewed as two intersecting,
triangular arrays of three hexagonal yods coloured blue, green & red that form an asymmetric
Star of David (shown in the diagram opposite as dashed lines in one triangle). The
21 tetractyses are lined by (21×2=42) hexagonal yods of each colour. The fourth
layer has 14 triangles. The seven tetractyses in each half of this layer have 14 corners. Suppose
that we colour them red. The 14 triangles in each half of the first, second & third layers have
28 corners. Suppose that we colour the outward-pointing corners green and the remaining corners
blue, so that they have 14 green corners and 14 blue corners. The (21×2=42) corners of the
42 triangles consist of 14 corners in each colour. Hence, the 168 boundary yods in each
half of the 3-d Sri Yantra consist of (42+14=56) yods of each colour. The 3-d Sri Yantra makes the
factorisation 168 = 3×56 geometrically possible through the tetractys template because
its first, second & third layers have 28 triangles, which is exactly twice the
number (14) of triangles forming the fourth layer.
168 = 2×84
Each half of the 3-d Sri Yantra has
21 tetractyses with 21 pairs of corners and
21 pairs of triangular arrays of three hexagonal yods. The
168 yods lining each half comprise 21 pairs of four yods that are either
corners or hexagonal yods, i.e., 84 pairs of yods. The factor of 2 derives from the fact that there
are two types of yods, namely, corners of tetractyses and hexagonal yods.
168 = 3×56
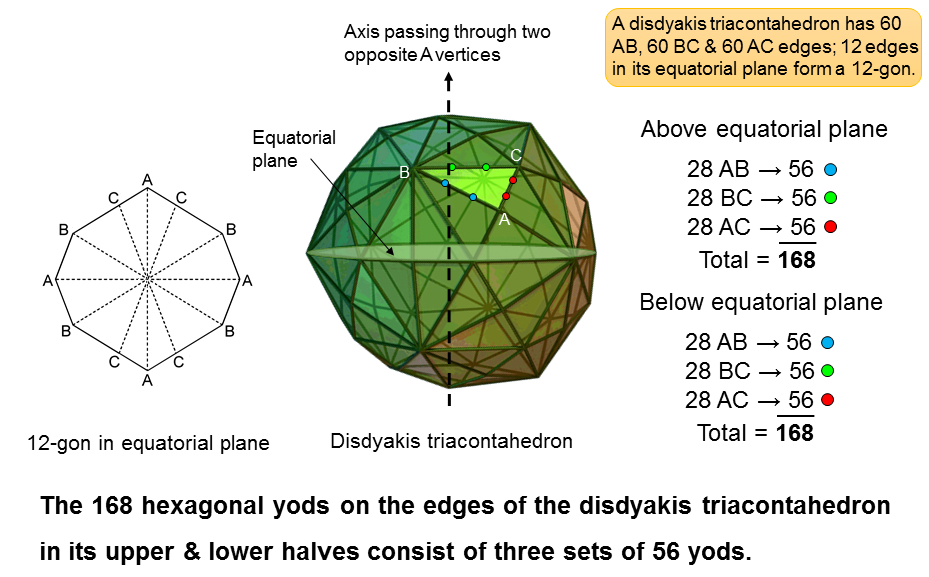
The disdyakis triacontahedron is a polyhedron with 62 vertices, 180 edges and 120
scalene triangles. Its vertices are of three types: A, B & C. They are connected by three types
of edges: AB, BC & AC. An axis of the polyhedron that passes through two diametrically opposite
A vertices is perpendicular to its equatorial plane containing a 12-gon formed by four AB, four BC
and four AC edges. This leaves (180−12=168) edges. 84 edges extend above its equatorial
plane and 84 edges extend below it. Each set of 84 edges consists of 28 AB, 28 BC and 28 AC edges.
Hence, the 168 edges consist of (2×28=56) AB, 56 BC and 56 AC edges.
If each triangular face is considered a tetractys, the 60 tetractyses either above or below the equatorial plane are lined by (84×2=168) hexagonal yods. Assigning blue hexagonal yods to AB edges, green hexagonal yods to BC edges and red hexagonal yods to AC edges, each set of 168 hexagonal yods comprises (28×2=56) blue yods, 56 green yods and 56 red yods.
168 = 2×84
84 edges extend above the equatorial plane and 84 edges extend below it. When faces are
tetractyses, two hexagonal yods line each edge, so that the 168 hexagonal yods on edges
above or below the equatorial plane consist of 84 pairs.
168 = 3×56
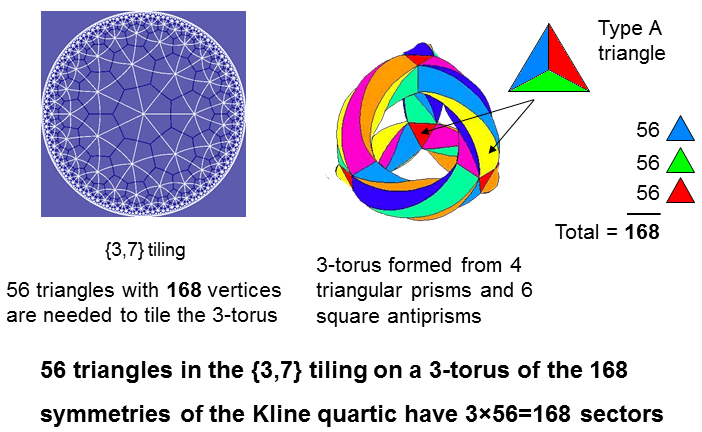
The 168 symmetries of the
Klein quartic:
X3Y + Y3Z + Z3X = 0
have a {3,7} tiling on the Poincaré disc. It consists of 56 triangles with 168 vertices. As the Klein quartic has genus 3, its 168 symmetries can be mapped onto the hyperbolic surface of a 3-torus. Regarded as Type A triangles (albeit distorted because they lie not on a plane but on a hyperbolic surface), the 56 triangles have 168 sectors.
168 = 2×84
The 56 triangles have 84 sides.
Considering each triangle as a tetractys, (84×2=168) hexagonal yods line their sides. The
factor of 2 derives from the pair of hexagonal yods on each side of the 56 tetractyses.
Including the 56 hexagonal yods at the centres of tetractyses and the 24 corners, (168+56+24=248) yods make up the 56 tetractyses. This is the dimension of E8. This is another indication that the {3,7} tessellation of the 3-torus constitutes sacred geometry. Together with its version turned inside it, 496 yods make up their 112 tetractyses. This is the dimension of E8×E8, one of the two symmetries that govern heterotic superstrings.
(For details, see Table 3 on p. 11 of Article 43).


168 = 3×56
There are 12 types of notes between
the tonic and the octave of the seven diatonic, musical scales. Six types with their tone ratios
written in red belong to the Pythagorean scale (the C major scale, or the Roman Catholic Church's
Hypolydian mode). They occur 26 times in the 42 notes between the tonic and
octave, where 26 is the number value of YAHWEH, the Godname of Chokmah. The
other six types are non-Pythagorean; they occur 16 times. Among the 27 intervals less than an
octave between the eight notes in each diatonic scale are Pythagorean intervals. Each scale has
certain numbers of different Pythagorean intervals, some of which are repeated in that scale. There
are 84 such repetitions of the Pythagorean intervals between notes in the seven scales. They
comprise 28 D intervals, 28 E & G intervals and 28 F & A intervals, i.e., 56 E, F, G &
A intervals. The (84+84=168) repeated, rising and falling Pythagorean intervals
between the notes in the seven diatonic scales comprise (28+28=56) rising and falling D intervals,
56 repeated, ascending E, F, G & A intervals and 56 repeated, descending E, F, G & A
intervals. The three sets of 28 repeated, Pythagorean intervals correspond to the three
combinations of polygons belonging to the set of seven enfolded polygons that are each lined by 28
hexagonal yods.
168 = 2×84
The seven diatonic scales have 84
repeated, rising Pythagorean intervals and 84 repeated, falling Pythagorean intervals.
There are (28+11=39) repeated D & E intervals and (23+17+5=45) repeated F, G & A intervals. Hence, the seven diatonic scales have (39+39=78) repeated, rising and falling D & E intervals and (45+45=90) repeated, rising and falling F, G & A intervals. The seven diatonic scales embody the gematria number values of Cholem (78) and Yesodoth (90), the two words in Cholem Yesodoth, the Kabbalistic name of the Mundane Chakra of Malkuth.
(For more details, see Article 16 and here).
The 84 repeated, rising and 84 repeated, falling, Pythagorean intervals are the counterparts of the 84 roots in E8 and their 84 inversions that are not roots of E6. Amazingly, in each case they form three sets of 28. This is because the seven diatonic scales constitute a holistic system that conforms to the archetypal pattern embodied in sacred geometries.
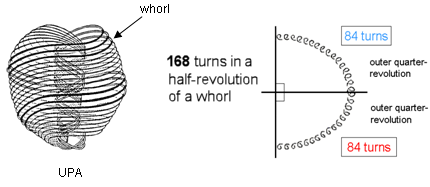 The 84:84 division in a helical
whorl of the UPA
The 84:84 division in a helical
whorl of the UPAWhen he observed the UPA with micro-psi, Charles W. Leadbeater counted 1680 circular turns in each of its 10 helical whorls. As a whorl twists five times around the spin axis of the UPA, one revolution of a whorl consists of 336 turns. A half-revolution consists of 168 turns and a quarter-revolution consists of 84 turns, where
84 = 12 + 32 + 52 + 72 = 41 + 42 + 43.
This 84:84 division (or its 840:840 counterpart in the outer and inner halves of each whorl) manifests in sacred geometries (see Article 64) and in the seven diatonic scales (see also here). The vibrational ground state of the E8×E8 heterotic superstring is the microscopic realisation of the archetypal pattern embodied in sacred geometries, whilst the seven diatonic scales are its macroscopic manifestation in music.