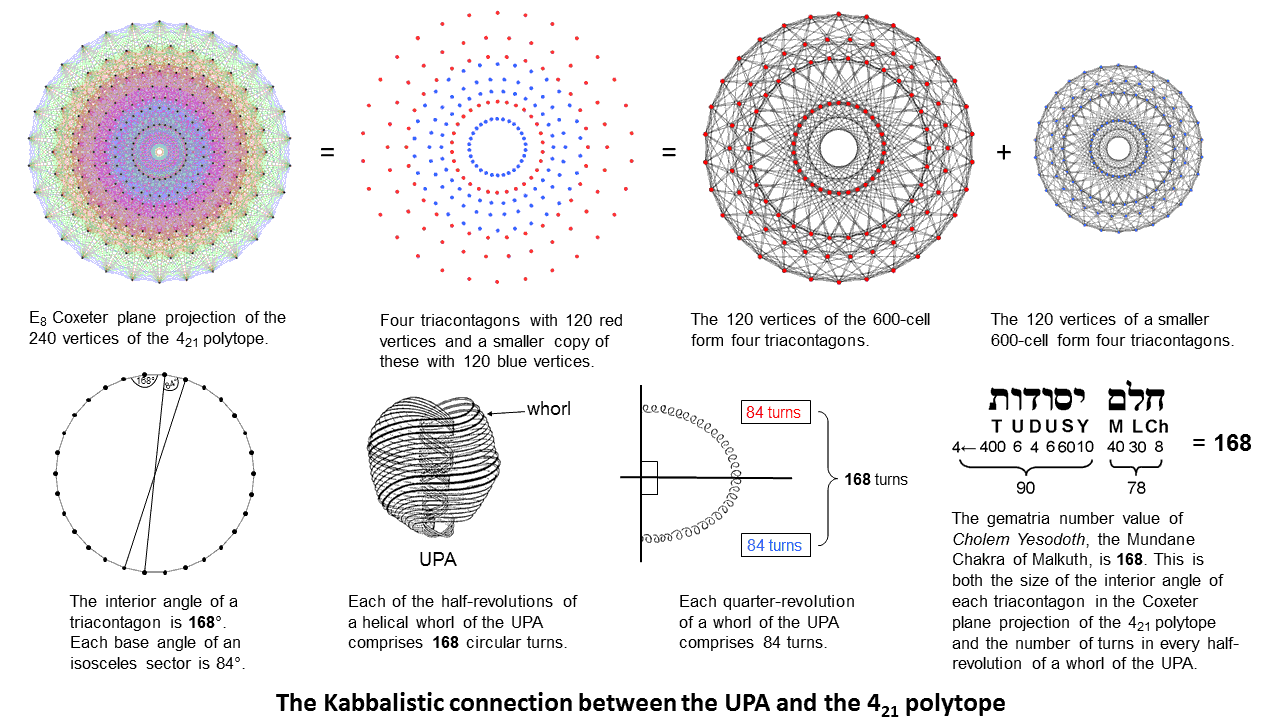
The superstring structural parameters 168 & 84 are, respectively, the interior angle of the Petrie polygon of the 421 polytope with E8 symmetry and the base angle of its sectors.
| << Previous [1] 2 3 4 5 ...17 Next >> |
1. The eight triacontagons in the E8 Coxeter plane projection of the 421 polytope.
 |
The superstring structural parameters 168 & 84 are, respectively, the interior angle of the Petrie polygon of the 421 polytope with E8 symmetry and the base angle of its sectors. |
When projected into 4-dimensional space, the 8-dimensional 421 polytope has a particular projection in which its vertices appear arranged at the 240 corners of eight concentric, similar regular polygons called triacontagons, each with 30 corners. The triacontagon is known to be the so-called "Petrie polygon" for the E8 Coxeter plane projection of the 421 polytope. The 120 red vertices in four triacontagons are the projected vertices of a 600-cell; the remaining 120 blue vertices of four other triacontagons are the projected vertices of another, smaller 600-cell. This polychoron is discussed in #1 of Polychorons & Gosset polytope.
A triacontagon has an interior angle of 168°. This is remarkable because the number 168 is the gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. Each of the 30 sectors of the triacontagon is an isosceles triangle with a base angle of 84° and an apex angle of 12°. This display of the 84:84 division of 168 is characteristic of sacred geometries, being part of the archetypal pattern that they represent (see here). It manifests in the UPA, the subquark state of the E8×E8 heterotic superstring remote-viewed over a century ago by Annie Besant & C.W. Leadbeater, as the 168 circular turns in every half-revolution of each of its 10 helical whorls. For a whorl with 1680 turns spirals 5 times around the axis of the UPA, making 2½ revolutions with 840 turns in its outer half and 2½ revolutions with 840 turns in its inner half. Every ¼ revolution of a whorl comprises 84 turns, where
84 = 12 + 32 + 52 + 72 = 41 + 42 + 43.
The fact that the Petrie polygon of the E8 Coxeter plane projection of the 421 polytope has an interior angle equal to the basic structural parameter 168 of the UPA cannot, plausibly, be dismissed as coincidence because the odds are extremely small that a number characterising the geometry of such a complex mathematical object would just happen by chance to be identical to that reported 109 years ago as a result of alleged remote-viewing of the basic constituents of matter! Instead, here is smoking gun evidence that the UPA described by Annie Besant & C.W. Leadbeater is a state of the E8×E8 heterotic superstring. There is no alternative explanation for the appearance of the numbers 84 & 168 in the group mathematics underlying superstring theory that is sensible because it does not invoke a miraculous coincidence that is too improbable to believe. Another piece of evidence is that the 421 polytope has 6720 edges. This number is discussed in the section Polychorons & Gosset polytope as the number of plane waves that make up one revolution of the ten whorls of the UPA. Its embodiment in the inner Tree of Life is analysed in #12 and #21 of that section. How other sacred geometries embody this structural parameter of the 421 polytope is discussed in pages 15-18 of this section.
| << Previous [1] 2 3 4 5 ...17 Next >> |