#28 How polygonal numbers & sacred geometries represent the superstring structural parameter 3360

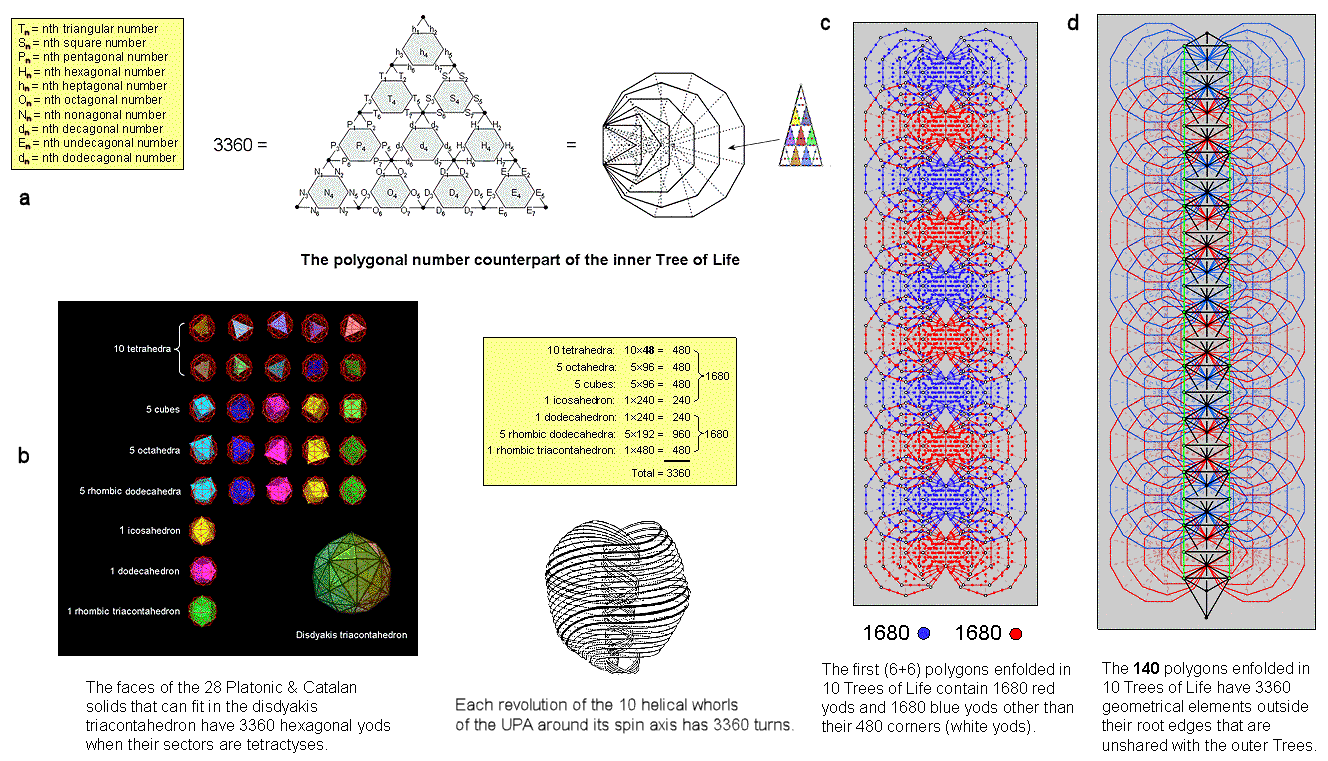
a) The first seven orders of the first 10 types of polygonal numbers can be assigned to the seven hexagonal yods in the 10 1st-order tetractyses making up the 2nd-order tetractys. Their sum is 3360 (see here). This is the number of yods in the seven enfolded polygons of the inner Tree of Life when their sectors are 2nd-order tetractyses (for proof, see Article 24, ref. 3);

b) The 62 vertices of the disdyakis triacontahedron can fit 28 Platonic and Catalan solids. They consist of ten tetrahedra, five cubes, five octahedra, five rhombic dodecahedra, one icosahedron, one dodecahedron and one rhombic triacontahedron. Turning the sectors of their faces into tetractyses generates 3360 hexagonal yods;

c) The first (6+6) enfolded polygons of the inner Tree of Life constitutes a holistic subset of the (7+7) enfolded polygons of the inner Tree of Life. When their 70 sectors are turned into tetractyses, the first (6+6) enfolded polygons have 336 yods other than their 50 corners. The 120 polygons enfolded in 10 overlapping Trees of Life have 3360 yods other than their corners (see also here);

d) There are 336 corners, sides & triangles outside the root edge of the (7+7) enfolded polygons that are intrinsic to them in the sense that none of these geometrical elements belong also to the triangles making up the outer form of the Tree of Life. The 140 polygons that are enfolded in 10 overlapping Trees of Life have 3360 such geometrical elements unshared with these Trees (see also here).

The 2nd-order tetractys array of 70 polygonal numbers is the arithmetic counterpart of these four sacred geometrical representations of the superstring structural parameter 3360 — the number of circular turns in one complete revolution of the ten helical whorls of the spin-½ UPA/subquark superstring around its axis of spin. Demonstrated here is the beautiful harmony between number and sacred geometry expressed through the template of the 2nd-order tetractys. It is discussed in detail in (8) at Polygonal numbers.

<< Previous    1...   26  27  [28]  29  30  ...56    Next >>

Home