|
ARTICLE 50 (Part 1)

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth.
Dorset BH2 5PH. England.
Website:
http://smphillips.mysite.com
Abstract
|
This article explores the presence and role of
the Golden Ratio, the Fibonacci numbers Fn and the Lucas
numbers Ln in the sacred geometries of the Platonic solids,
the outer & inner Trees of Life and their polyhedral counterparts —
the 144 Polyhedron and the disdyakis triacontahedron. F8 is
the number of geometrical elements in the Lower Face of the Tree and
F9 is the number of elements in its Upper Face,
F10 being the number of elements in the whole Tree.
L10 is the number of geometrical elements in the three
lowest Trees of Life mapping three-dimensional space. F10
measures the inner Tree of Life as the 55 corners of the 48 sectors of
its seven separate polygons. L9 is the number of corners of
the seven enfolded polygons that are not also their centres.
F9 (=34) is the number of corners associated with the seven
enfolded polygons enfolded in successive overlapping Trees of Life. It
is also the number of geometrical elements added by them. The length of
successive twists of the DNA molecule is about 34 angstroms. The 21:34
division of geometrical elements in the outer Tree of Life manifests in
the 21 vertices & centres of the first three Platonic solids and
the 34 vertices & centres in the last two. It also appears in the
first four Platonic solids as the 210 triangles, polyhedral vertices
& sides in their faces and as the remaining 340 elements in all
five solids. The former embody the dimension 248 of the exceptional Lie
group E8 describing superstring forces as the 248 corners
& sides of the 120 sectors of their 38 faces. This number is
embodied in the lowest Tree of Life as the 248 yods below its apex. The
(248+248) yods other than corners in the root edge and (7+7) separate
polygons symbolize the (248+248) roots of E8×E8.
The 1370 yods lining edges of the tetractyses needed to construct the
five Platonic solids is the counterpart of the 1370 yods in the inner
Tree of Life. L10 is the average number of geometrical
elements in each half of these solids. F10 is the average
number of elements in the faces of each half. The average number of
internal geometrical elements (including centres) is 137, showing how
the Platonic solids embody the number determining the fine-structure
constant in physics. The relation L10 = F10 +
2F9, which appears in the three Trees of Life mapping
three-dimensional space, manifests in the five Platonic solids - the
only regular polyhedra that can exist in such a space. These Trees
encode the 206 bones in the human skeleton and the 361 classical
acupuncture points. L10 is the number of Pythagorean
intervals between the notes of the seven musical scales.
|
Page Index
|
Part 1
|
|
|
Part 2
|
|
|
|
Page
|
|
|
Page
|
|
Table of number values of the Sephiroth in the four Worlds
|
|
|
Table of number values of the Sephiroth in the
four Worlds |
|
|
The Tree of Life
|
|
|
Geometrical properties of the 13 Archimedean & 13 Catalan
solids |
|
|
The Upper & Lower Faces of the Tree of Life
|
|
|
The polygonal Tree of Life encodes its polyhedral
counterpart |
|
|
Fibonacci & Lucas numbers
|
|
|
Construction of the polyhedral Tree of Life |
|
|
Fibonacci & Lucas numbers in the 1-, 2- & 3-tree
|
|
|
Isomorphism between the polygonal & polyhedral Trees of
Life |
|
|
The generation of the inner Tree of Life
|
|
|
√2 & Φ determine the polyhedral Tree of Life |
|
|
The outer & inner Tree of Life
|
|
|
Connection between the Tree of Life and the faces of the
rhombic dodecahedron & rhombic triacontahedron |
|
|
Fibonacci numbers in the geometry of the inner Tree of Life
|
|
|
The Golden Rhombus in the Fano plane |
|
|
Geometrical composition of the outer & inner Tree of Life
|
|
|
The 15 sheets of vertices in the disdyakis
triacontahedron |
|
|
The ninth Fibonacci number in the outer & inner Tree of Life
|
|
|
The disdyakis triacontahedron as the polyhedral representation
of CTOL |
|
|
Fibonacci numbers & the Golden Ratio in the DNA molecule
|
|
|
The 34 corners of the 27 sectors of the seven
polygons |
|
|
Comparison of the 64 codons & 64 anticodons with the 64 hexagrams
|
|
|
The two sets of 7 polygons are analogous to the two halves of
the inner Tree of Life and the trunk and branches of the outer Tree of
Life |
|
|
Comparison of the 384 geometrical elements of the 14 polygons with the 384
lines & broken lines in the 64 hexagrams
|
|
|
The ninth & tenth Lucas numbers determine the 15 sheets of
vertices |
|
|
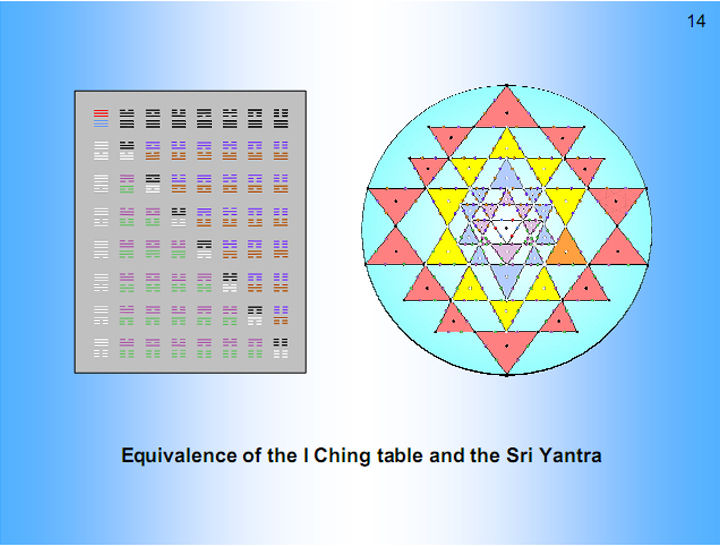
Comparison of the 64 hexagrams with the Sri Yantra
|
|
|
The disdyakis triacontahedron embodies the fine-structure
number 137 |
|
|
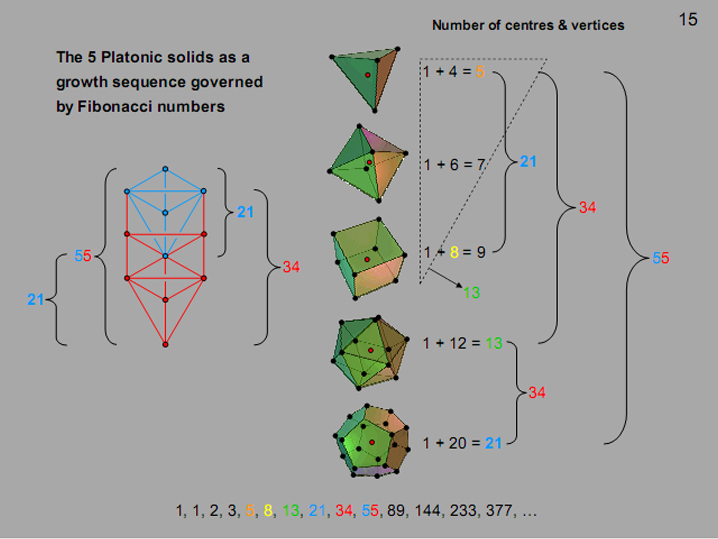
The five Platonic solids as a sequence governed by Fibonacci numbers
|
|
|
The equivalence of the outer Tree of Life and the Sri
Yantra |
|
|
F8, F9 & F10 in the five Platonic
solids
|
|
|
The equivalence of the inner Tree of Life and the Sri
Yantra |
|
|
The first four Platonic solids and the square embody the dimension 248 of
E8
|
|
|
The equivalence of the Sri Yantra and 7 overlapping Trees of
Life |
|
|
How the 1-tree embodies the dimension 248 of E8
|
|
|
The equivalence of the Sri Yantra and the 7-tree |
|
|
How the (7+7) separate polygons of the inner Tree of Life embody
E8×E8
|
|
|
The Sri Yantra embodies the superstring structural parameter
1680 |
|
|
1370 yods on edges of tetractyses in the five Platonic solids
|
|
|
Numbers of hexagonal yods in the faces of the Platonic
solids |
|
|
The inner Tree of Life contains 1370 yods
|
|
|
Correspondence between the outer and inner Trees of
Life |
|
|
Fibonacci, Lucas numbers and the Golden Ratio determine the geometrical
composition of the five Platonic solids
|
|
|
28 polyhedra fit into the disdyakis
triacontahedron |
|
|
The number 247 is a Tree of Life parameter
|
|
|
The faces of the 28 polyhedra have 3360 hexagonal
yods |
|
|
Properties of the five Platonic solids
|
|
|
The seven enfolded polygons of the inner Tree of Life have
3360 yods |
|
|
Counterpart of the internal geometrical composition of the Platonic solids
in the inner Tree of Life
|
|
|
EHYEH prescribes the superstring structural parameter
1680 |
|
|
Counterpart of the internal composition of the Platonic solids in the inner
form of ten Trees of Life
|
|
|
49 overlapping Trees of Life contain 1680 geometrical
elements |
|
|
The 3-tree determined by the tenth Lucas number encodes the human skeleton
|
|
|
1680 geometrical elements surround an axis of the disdyakis
triacontahedron |
|
|
The 3-tree encodes the 361 acupuncture points
|
|
|
The number value of Cholem Yesodoth is 168 |
|
|
The eight Church musical modes
|
|
|
Geometrical composition of the Archimedean & Catalan
solids |
|
|
Tone ratios of the notes in the seven octave species
|
|
|
The Godname ADONAI prescribes the 10-tree |
|
|
The tenth Lucas number is the number of Pythagorean intervals between notes
of the seven musical scales
|
|
|
1680 yods lie below the top of the 10-tree |
|
|
References
|
|
|
The 10-tree has 34 tree levels |
|
|
|
|
|
References |
|
Figure
1
In the ancient
practice of gematria, consecutive letters of an
alphabet are assigned the integers 1-10, 20-100
& 200-900. This means that words have
numerical values that are the sum of their
letter values. Words in religious texts with the
same number values, however different they were,
were considered to possess some kind of analogy,
implying that the textual passages in which
these words were located were connected in a
subtle way and allowing levels of meaning beyond
the literal to be uncovered in these sacred
writings. In Kabbalah, the ten Divine Qualities,
or Sephiroth, manifest in the four Worlds of
Atziluth (Archetypal World), Beriah (World of
Creation), Yetzirah (Formative World) and
Assiyah (World of Action). The divine names that
are assigned to the Sephiroth embodying the
archetypal essence of God function in Atziluth.
The Archangels assigned to each Sephirah operate
in Beriah, the ten orders of angels exist in
Yetzirah, whilst the Mundane Chakras are
regarded as the physical manifestations of the
Sephiroth, some being assigned one of the sacred
planets (to be understood in their astrological,
not astronomical, sense). The table in Figure 1
lists the gematria numbers of the Hebrew names
of the Sephiroth, the Godnames, Archangels,
Orders of Angels & Mundane Chakras. A few of
the numbers, such as those of Elohim, Elohim
Sabaoth and Cholem Yesodoth differ from those
stated by standard works on Hebrew gematria.
This is because these texts provide only numbers
that are the sums of their letter values. They
take no account of the possibility of
contraction, wherein a sum of such values, or
even an individual one, can be reduced to
another number if it is a multiple of 10. For
example, the letter value 40 of the Hebrew
letter mem (מ) can be reduced
to 4 because 4 + 0 = 4, as can the letter value
400 of tav (ת). Whether such
contraction is required depends upon the context
in which these words occur. Thirty years of
correlating the gematria number values of the
Sephiroth in the four Worlds with the properties
of sacred geometries and with the mathematics
underlying superstring theory has proved to the
author that contraction occurs in a few of these
number values. An example germane to superstring
structure will be discussed later on in this
article.
|
|
1
|
|
|
SEPHIRAH
|
GODNAME
|
ARCHANGEL
|
ORDER OF
ANGELS
|
MUNDANE
CHAKRA
|
| 1 |
Kether
(Crown)
620 |
EHYEH
(I am)
21 |
Metatron
(Angel of the
Presence)
314 |
Chaioth ha Qadesh
(Holy Living
Creatures)
833
|
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
636 |
| 2 |
Chokmah
(Wisdom)
73 |
YAHWEH, YAH
(The Lord)
26,
15
|
Raziel
(Herald of the
Deity)
248 |
Auphanim
(Wheels)
187 |
Masloth
(The Sphere of the Zodiac)
140 |
| 3 |
Binah
(Understanding)
67 |
ELOHIM
(God in multiplicity)
50
|
Tzaphkiel
(Contemplation
of God)
311
|
Aralim
(Thrones)
282
|
Shabathai
Rest.
(Saturn)
317 |
|
Daath
(Knowledge)
474 |
|
|
|
|
| 4 |
Chesed
(Mercy)
72 |
EL
(God)
31 |
Tzadkiel
(Benevolence
of God)
62 |
Chasmalim
(Shining Ones)
428
|
Tzadekh
Righteousness.
(Jupiter)
194 |
| 5 |
Geburah
(Severity)
216
|
ELOHA
(The Almighty)
36
|
Samael
(Severity of God)
131
|
Seraphim
(Fiery Serpents)
630
|
Madim
Vehement Strength.
(Mars)
95 |
| 6 |
Tiphareth
(Beauty)
1081
|
YAHWEH ELOHIM
(God the Creator)
76 |
Michael
(Like unto God)
101
|
Malachim
(Kings)
140
|
Shemesh
The Solar Light.
(Sun)
640 |
| 7 |
Netzach
(Victory)
148
|
YAHWEH SABAOTH
(Lord of Hosts)
129
|
Haniel
(Grace of God)
97 |
Tarshishim or
Elohim
1260
|
Nogah
Glittering Splendour.
(Venus)
64 |
| 8 |
Hod
(Glory)
15
|
ELOHIM SABAOTH
(God of Hosts)
153
|
Raphael
(Divine
Physician)
311
|
Beni Elohim
(Sons of God)
112
|
Kokab
The Stellar Light.
(Mercury)
48 |
| 9 |
Yesod
(Foundation)
80
|
SHADDAI EL CHAI
(Almighty Living
God)
49,
363
|
Gabriel
(Strong Man of
God)
246
|
Cherubim
(The Strong)
272
|
Levanah
The Lunar Flame.
(Moon)
87 |
| 10 |
Malkuth
(Kingdom)
496
|
ADONAI MELEKH
(The Lord and
King)
65,
155
|
Sandalphon
(Manifest
Messiah)
280 |
Ashim
(Souls of Fire)
351
|
Cholem Yesodoth
The Breaker of the Foundations.
The Elements.
(Earth)
168 |
|
|
The Sephiroth exist in the
four Worlds of Atziluth, Beriah, Yetzirah and
Assiyah. Corresponding to them are the Godnames,
Archangels, Order of Angels and Mundane Chakras
(their physical manifestation).
This table gives their number
values obtained by the ancient practice
of gematria, wherein a number is assigned to
each letter of the alphabet, thereby giving a
number value to a word that is
the sum of the numbers associated with its letters.
When some of these numbers are
referred to in the article, they
will be written in
boldface.
|
|
Figure
2
At the heart of the Jewish mystical tradition
called ‘Kabbalah’ is the Tree of Life,
or
Otz Chiim
. It represents Adam Kadmon, or “heavenly man.”
The ten “Divine Qualities,” or Sephiroth
(singular: Sephirah) are represented by ten
circles. The first three — Kether (Crown),
Chokmah (Wisdom) and Binah (intelligence) —
constitute the Supernal Triad. They head the
Pillars of Equilibrium (central column), Mercy
(right-hand column) and Judgement (left-hand
column). The seven remaining Sephiroth are
called the Sephiroth of Construction. They are
Chesed (Mercy), Geburah (Severity), Tiphareth
(Beauty), Netzach (Victory), Hod (Glory), Yesod
(Foundation) & Malkuth (Kingdom). Between
Binah and Chesed on the Pillar of Equilibrium
is Daath (knowledge). It is not a Sephirah but
a stage of transition from the subjective level
of God to the seven Sephiroth of Construction
expressing the objective nature of God. The
Sephiroth are connected by 22 straight lines,
or Paths.
As a three-dimensional object, the Tree of Life
consists of 16 triangles with 22 edges and ten
corners. Traditional Kabbalah considers only
the generic single Tree of Life and the four
overlapping Trees that represent the Archetypal
World (the domain of the Divine Names), the
Creative World (the archangelic level), the
Formative World (the angelic realms) and the
World of Action (physical universe). However,
it has been shown in earlier articles that 91
overlapping Trees of Life (called the "Cosmic
Tree of Life," or CTOL) map all levels of
physical and superphysical reality.
Figure 2
shows the lowest seven Trees. They map
26-dimensional
space-time predicted by string theory and which
is prescribed by YAHWEH, the Godname Chokmah
whose number value is
26.
|
|
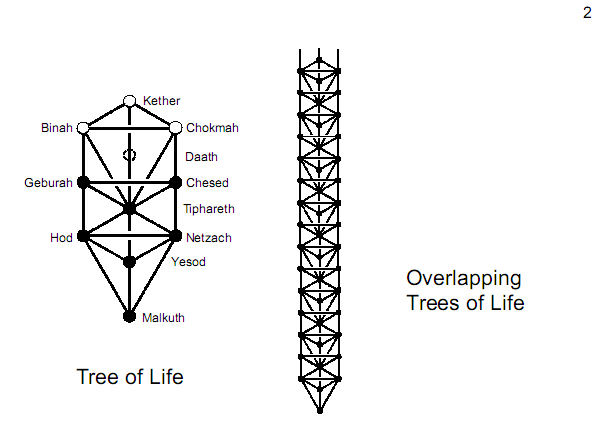
Figure
3
The kite-shaped group of Sephiroth of
Construction:
Tiphareth-Netzach-Hod-Yesod-Malkuth
is called the ‘Lower Face’ of the Tree of Life.
Its ‘Upper Face’ is the five Sephiroth above
Tiphareth. Here, the names will be meant to
refer not only to the corners of triangles but
also to the space enclosed by the triangles
themselves, as well as to their edges (Paths).
This means that the triangular space with
Chesed, Tiphareth & Netzach at its corners
belongs to the Upper Face even though the
dotted line joining Tiphareth & Netzach is
a Path that belongs to the Lower face.
Similarly, the space within the triangle with
Geburah, Tiphareth & Hod at its corners
belongs to the Upper Face, which comprises
every corner, edge & triangle
outside
the Lower Face.
|
|
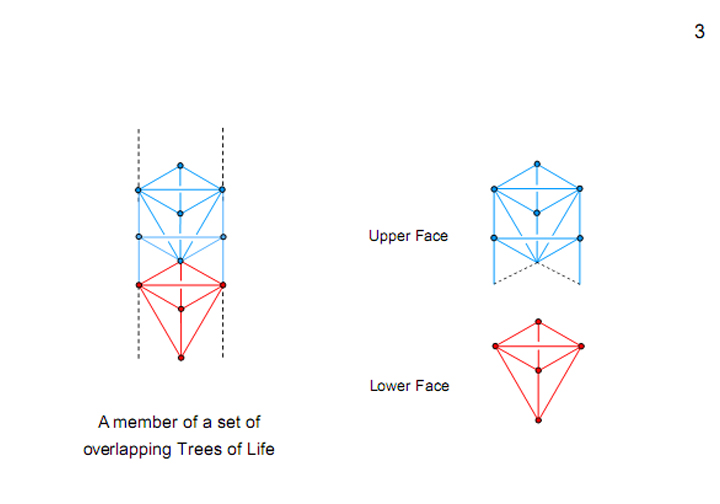
Figure
4
The
nth Fibonacci number (1) is defined
as:
Fn =
Fn−1 +
Fn-2, if
n>1,
where
F0 = 0
& F1 = 1.
They belong to the infinite series:
0, 1, 1,
2, 3, 5, 8, 13, 21, 34, 55, 89, 144,….
Each
integer is the sum of the previous two numbers. The
French mathematician, François Édouard Anatole Lucas
(1842-1891), who gave this series of numbers the
name of Fibonacci Numbers, found a similar series
occurs often when investigating Fibonacci number
patterns:
2, 1, 3,
4, 7, 11, 18, 29, 47, 76, 123, 199, 322, ...
The
Fibonacci rule of adding the previous two to get the
next is kept, but here we start from 2 and 1 (in
this order) instead of 0 and 1 for the (ordinary)
Fibonacci numbers. Called the Lucas numbers after
him, the nth number in this series is defined
as:
Ln =
Ln−1 +
Ln-2, for
n>1
where
L0 = 2 & L1
= 1. To
emphasis their presence, all Fibonacci and Lucas
numbers will henceforth be written in
colour.
The
Lower Face of any Tree of Life in a set of
overlapping Trees contains 21
points,
lines & triangles. This
is F8. It is
also the number value of EHYEH, the Godname of
Kether (see Fig.
1). Its Upper Face contains
34
geometrical
elements. This is F9.
A
whole Tree of Life has 55
elements.
This is the tenth Fibonacci
number F10. Thirty-four
more elements are needed to construct successive,
overlapping Trees. Two overlapping Trees have
89
elements.
This is F11. Three
overlapping Trees possess 123
elements.
This is the tenth Lucas number L10.
The
significance of this particular set of Trees will be
revealed later.
The
natural appearance of both Fibonacci and Lucas
numbers in the geometrical composition of the Tree
of Life and its two basic components that become
replicated in successive Trees is the first
indication of how these numbers, which manifest in
the philotaxis of plants and flowers, are also
intrinsic to the growth of the Tree of Life as a
geometrical object. The general relationship between
them:
Ln
= Fn−1 +
Fn+1
Is
actualised geometrically in the three overlapping
Trees of Life as
123
=
34
+
89,
because
34
is the
number of geometrical elements in the Upper Face of
the third Tree and 89
is the
number of elements below it.
|
|
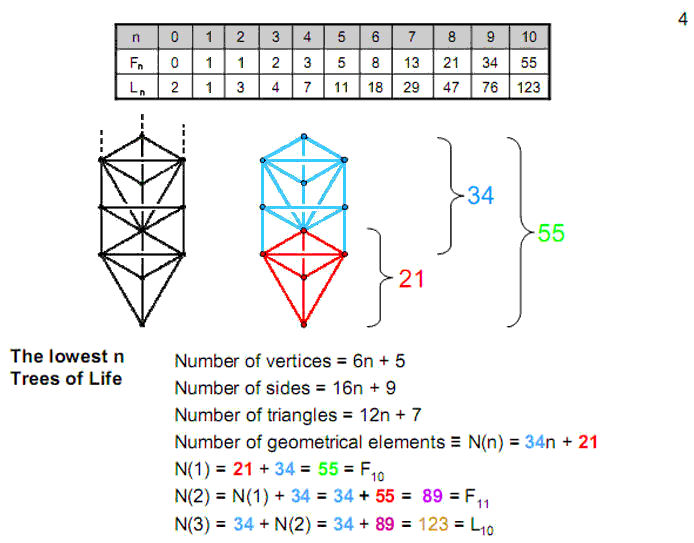
Figure
5
The lowest three Trees serve to illustrate
another relationship between Fibonacci and
Lucas numbers. The nth numbers obey the
equation:
L
n
= Fn
+ 2Fn−1.
This follows from the equation just
discussed:
Ln = Fn−1
+ Fn+1
because
Fn+1 = Fn−1
+ Fn
.
For n = 10, L10 =
F10 + 2F9
= 55 + 2×34.
This has the natural meaning in the context of
the three lowest overlapping Trees of Life as
the 55 geometrical
elements of either the lowest or highest one
and as the
34
elements added by each of the next two Trees.
This relation between Lucas and Fibonacci
numbers, illustrated for n = 10, will be shown
to apply to the total geometrical composition
of several other holistic systems that possess
sacred geometry. Earlier articles proved the
equivalence of these systems, so that it is
safe to infer that all such systems conform to
this equation, at least for n = 10, if not for
all n<10.
|
|
Figure
6
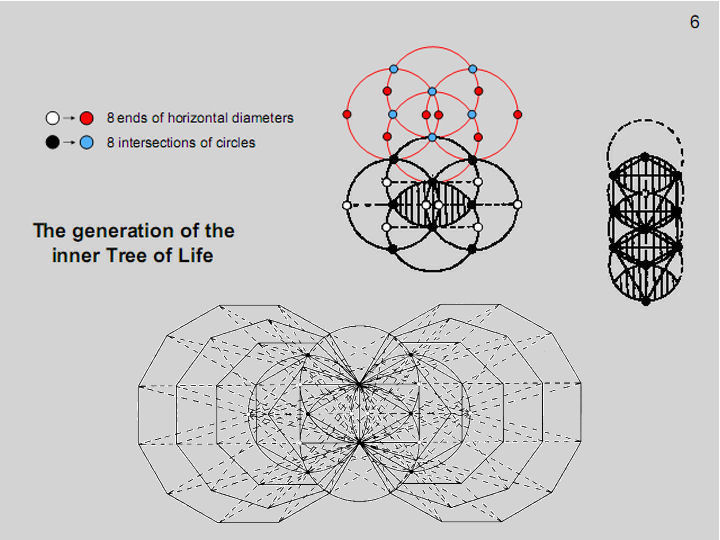
Two
similar circles that overlap centre to circumference
create the Vesica
Piscis.
As four overlapping circles generate the locations
of the ten Sephiroth of the Tree of Life, the latter
is created by the extremities of a vertical stack of
four Vesica
Piscis (shown
shaded). Their horizontal extremities can be
regarded as the centres of two more circles. The
eight ends (white dots) of the horizontal diameters
of the four overlapping circles are not points of
intersection of any two circles, unlike the eight
black dots. If we stack more
Vesica Piscis so
as to form the next higher Tree of Life, the black dots
are translated into blue dots and the white dots are
shifted to red dots. The black and white dots
constitute two independent sets of eight points. They
possess the amazing property that straight lines
passing through any two dots intersect at the corners
of two similar sets of seven regular
polygons:
triangle,
square, pentagon, hexagon, octagon, decagon,
dodecagon.
Those
in one set are the mirror image of their
counterparts in the other set. They share one edge —
the vertical “root edge,” as it has been called in
previous articles.
This
geometrical object is implicate in the geometry of
the circles whose intersection create overlapping
Trees of Life. They represent a hidden geometrical
potential that is possessed not only by a single
Tree but by every overlapping Tree because, when
straight lines are drawn through the blue and red
dots of the circles generating the next higher Tree,
they intersect at the corners of another set of 14
regular polygons.
|
|
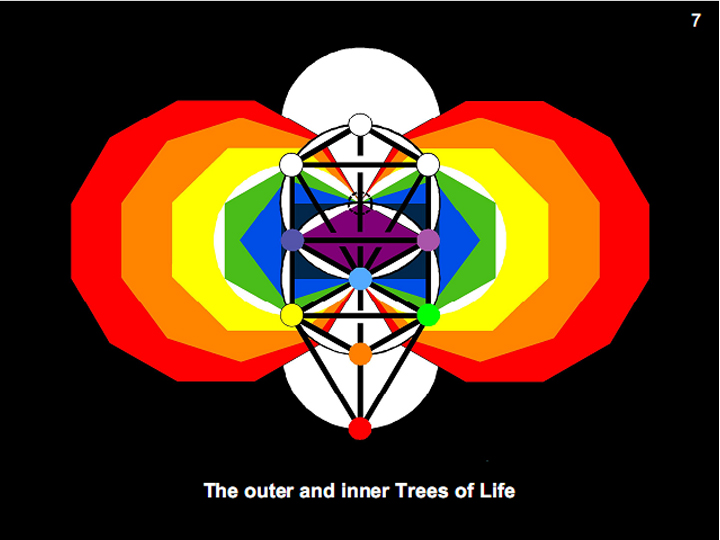
Figure
7
The form of the Tree of Life known to
Kabbalists is but its outer form. The 14
regular polygons constitute its inner form.
They have 70 corners. Their 94 sectors
have
80
corners, where
80
is the number value of Yesod. Notice that the
corners of the triangles coinciding with Chesed
and Geburah are the centres of the two
hexagons. Also, the outermost corners of the
two pentagons coincide with the centres of the
decagons. This means that the sectors of the 14
polygons have
76
corners that are not also centres of
polygons.
76
is the number value of YAHWEH ELOHIM, the
Godname of Tiphareth. It is also the ninth
Lucas number.
|
|
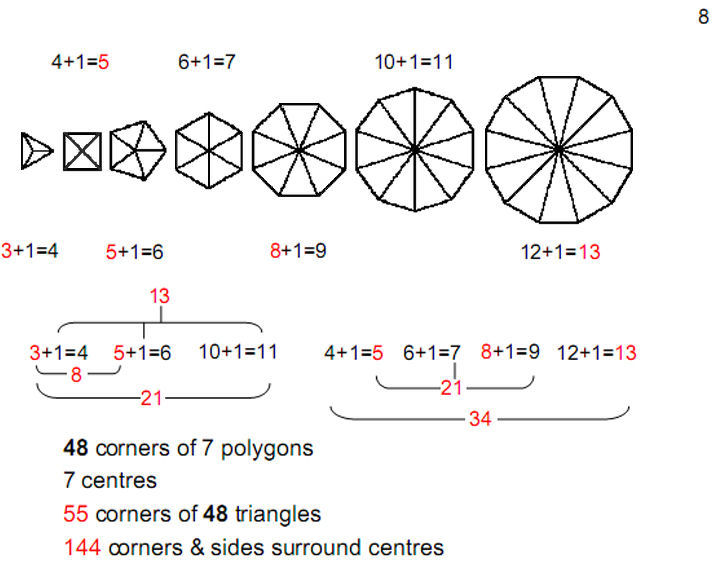
Figure
8
When separated, each set of seven polygons
have
48
corners. According to the table of gematria
number values of the Sephiroth shown in
Fig. 1,
this is the number value of
Kokab
, the Mundane Chakra of Hod. It is not
coincidental that this number appears in this
context because many previous articles have
demonstrated that the inner Tree of Life is
prescribed by the Godnames and manifests all
the number values of the Sephiroth in the four
Worlds.
Including the centres of the seven polygons,
their
48
sectors have (48+7=
55)
corners.
55
is the tenth Fibonacci number F10.
This is the counterpart in the inner Tree of
Life of the
55
geometrical elements in its outer form. In
either case, it is a measure of the
form
or
shape
of a holistic system.
The numbers in the Fibonacci series less
than
55
can be identified by distinguishing between the
corners of each polygon and its centre (denoted
“1” in Fig. 1).
The sectors of the triangle, pentagon &
decagon have
21
corners and the sectors of the square, hexagon,
octagon & dodecagon have
34
corners. Each Fibonacci number divides into
smaller Fibonacci numbers that measure subsets
of polygons.
The twelfth Fibonacci number
144
is the number of corners and sides of
the
48
sectors of the seven separate
polygons.
|
|
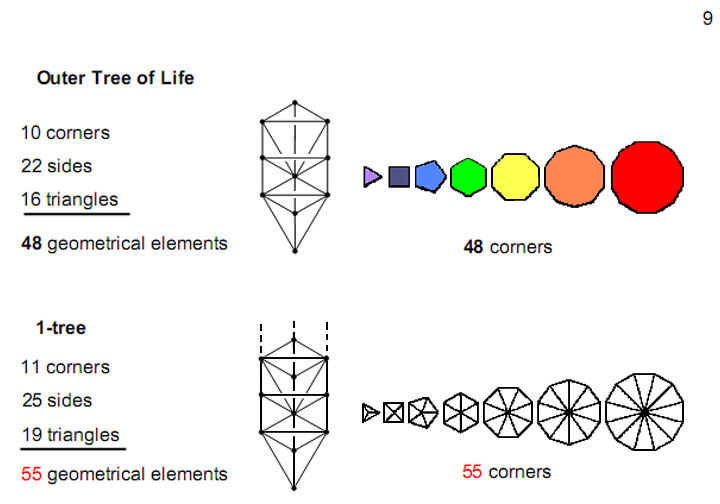
Figure
9
The outer Tree of Life has 16 triangles with
ten corners and 22 edges. These
48
geometrical elements are the counterpart of
the
48
corners of the seven separate polygons. Just as
seven elements are added when the Tree of Life
becomes the lowest Tree of Life, so seven
corners are added by dividing the seven
polygons into their sectors.
|
|
|
The topmost corners of the two hexagons enfolded in the
inner Tree of Life coincide with the lowest corners of
the two hexagons enfolded in the next higher Tree.
There are 68 corners per set of 14 polygons,
34
per set of seven polygons. This is the counterpart of
the addition of
34
geometrical elements in the Upper Face of every higher
Tree of Life. In algebraic terms, the number of
geometrical elements in the lowest n Trees of Life
(what has been called the ‘n-tree’ in previous
articles) is:
N(n) = 34n +
21,
so that N(n+1) – N(n) = 34.
Compare this with the fact that the number of corners
of the 14n polygons enfolded in the n-tree
is:
C(n) = 68n + 2,
so that the number of corners associated with each set
≡ C'(n) = C(n)/2 = 34n +
1 and
C'(n+1) – C'(n) = 34.
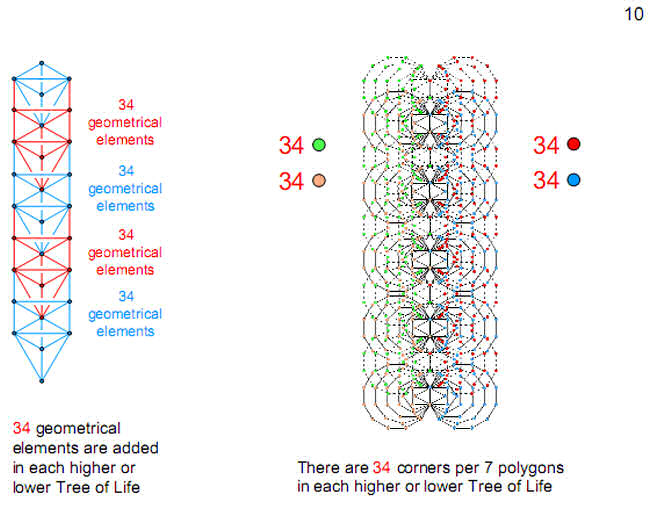
The ninth Fibonacci
number
34 measures the geometrical composition of
successive Trees of Life and the corners associated
with the seven polygons enfolded in them.
|
| |
|
|
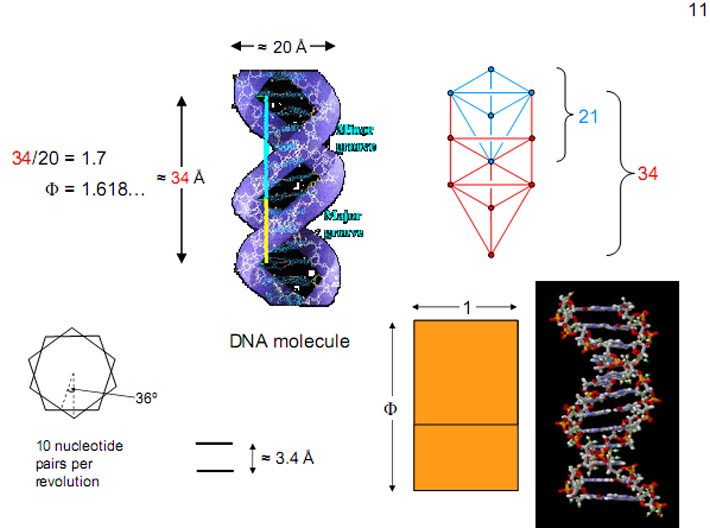
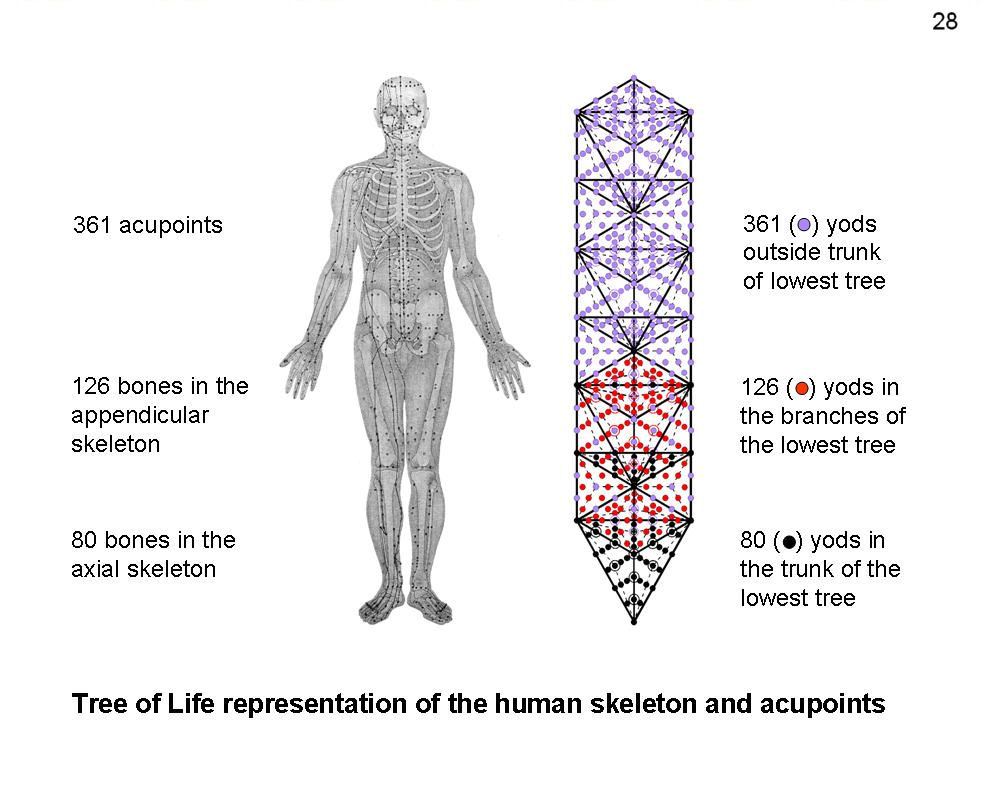
The width of the DNA molecule is 20 angstroms, to the
nearest integer (1 angstrom = 10-8 cm). One
360 degree turn of DNA measures about
34
angstroms in the direction of the axis. These lengths,
34:20, are
in the ratio of the Golden Mean Φ
within the limits of the accuracy of the measurements
(compare 1.7 with 1.618… ). It is remarkable that its
two dimensions, rounded off to the nearest integer, are
so close to two Fibonacci numbers. Each DNA strand
contains periodically recurring phosphate and sugar
subunits. There are ten such phosphate-sugar groups in
each full 360 degree revolution of the DNA spiral, the
average vertical distance between base pairs being 3.4
angstroms. The amount of rotation of each of these
subunits around the DNA cylinder is therefore
36
degrees. This is exactly half the pentagon rotation,
showing a close relation of the DNA sub-unit to the
Golden Mean and refuting the suggestion that the
closeness of the length and width of one helical turn
of the DNA double helix is merely
coincidental.
The coiling of the two helical strands of the DNA
molecule creates a major groove 22 angstroms wide and a
minor groove 12 angstroms wide. Their relative
proportion is 22/12 ≈ 1.545… . This differs from the
Golden Ratio
Φ
only by about 4.5%.
|
|
The two strands of the DNA molecule are held together
by non-covalent hydrogen bonding between pairs of
nitrogen bases. There are four types: adenine (A),
thymine (T), guanine (G) & cytosine (C). They form
the rungs of a ladder whose sides are alternating sugar
and phosphate groups and which spiral around each other
in opposite senses. Base A always pairs with base T and
base C always pairs with base G. When a cell prepares
to divide, the DNA helix splits down the middle and
becomes two strands. These single strands serve as
templates for building two new, double-stranded DNA
molecules - each a replica of the original DNA
molecule. In this process, an A base is added wherever
there is a T base, a C where there is a G, and so on
until all the bases once again have
partners.
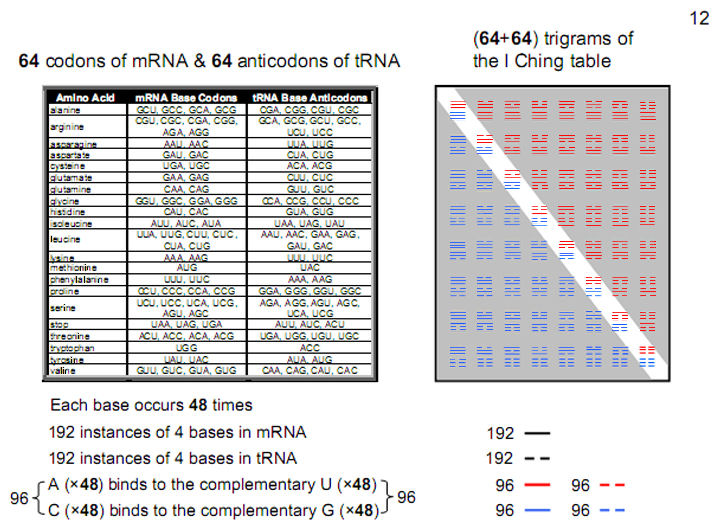
The
genetic code consists of (4×4×4
= 64)
triplets of nucleotides called codons
(64 i
s the number value
Nogah
, the Mundane Chakra of Netzach). With three
exceptions, each codon encodes for one of the 20
standard amino acids used in the synthesis of proteins.
RNA is a single-strand molecule with a much shorter
chain of nucleotides than DNA. Instead of thymine, the
complementary base to adenine is uracil (U), an
unmethylated form of thymine. Figure 12 shows
the
64
codons of messenger RNA (mRNA). An anticodon is a
sequence of three adjacent nucleotides in transfer RNA
(tRNA) that correspond to the three bases of the codon
on the mRNA strand. An anticodon is complementary to
the codon in mRNA that binds to it and designates a
specific amino aid during protein synthesis. For
example, the anticodon GUA is the complement of the
codon CAU because G is the complement of C and U is the
complement of A. The four bases appear
(64×3 = 192)
times in each set
of
64 codons or anticodons. Each base
appears (192/4 = 48)
times,
where 48 is the number
value of
Kokab
, the Mundane Chakra of Hod, the next Sephirah after
Netzach. There are 96 instances of A & C that bind
to the 96 instances of their respective complements U
& G.
Compare this pattern with the table
of
64
hexagrams that form the basis of the ancient Chinese
system of divination known as ‘I Ching.’ Each hexagram
is a pair of trigrams (triplets of all combinations of
lines & broken lines denoting the polarities of
yang & yin). The
64
trigrams in one diagonal half of the 8×8 array comprise
192 lines & broken lines (96 yang lines & 96
yin lines). The
64
trigrams in the other half of the array similarly
consist of 192 lines and broken lines. The 32 hexagrams
in this half are the inversions of those in the other
half, so that they comprise
the
same
set of
64
trigrams. The
64
trigrams in one diagonal half of the table
correspond to the
64
mRNA codons and the
64
trigrams in its other half correspond to
the
64
tRNA anticodons. The yang/yin duality of lines &
broken lines manifests in RNA as pairs of complementary
bases, which create
64
codons and
64
anticodons. The 96 lines in each half correspond to the
96 instances of the non-bonding A & C. The 96
broken lines in each half correspond to the 96
instances of their non-bonding complements U & G
(for more details, see ref. 2).
|
|
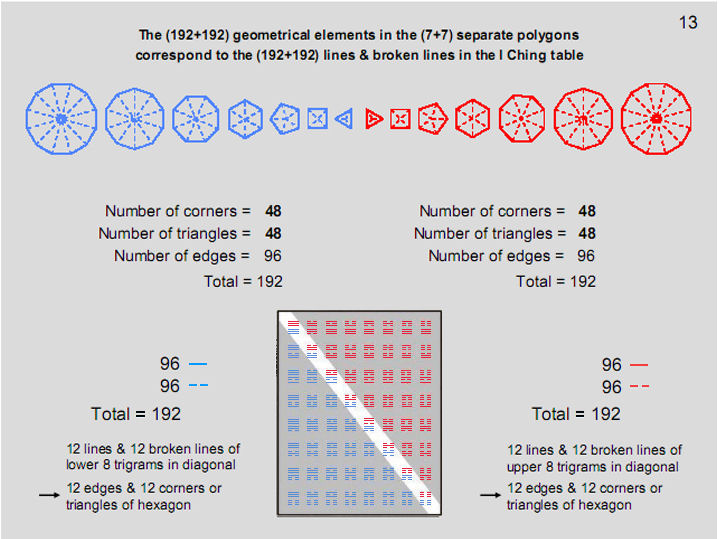
Figure
13
The
counterpart in the inner Tree of Life of
the 48
instances
of each of the four types of bases in the DNA
molecule is the four types of geometrical
elements making up the 48
sectors
of the seven separate regular polygons. There
are 48
vertices,
48
external
sides, 48
internal
sides & 48
triangles.
The pair of geometrical elements
(repeated 48
times)
forming the boundaries of the polygons
correspond to either the non-bonding pair (A,C)
or (G,U) and the pair of internal elements
(repeated 48
times)
correspond to, respectively, either (G,U) &
((A,C).

The
192 geometrical elements in one half of the
inner Tree of Life are the geometrical
counterpart of the 192 instances of the four
bases making up the 64
codons
in mRNA and the 192 lines & broken lines in
a diagonal half of the I Ching table. The 192
elements in the mirror image half of the inner
Tree of Life are the counterpart of the 192
instances of the four bases making up the
64
anticodons
in tRNA and the 192 lines & broken lines in
the other half of the table. The mirror
reflection of each element belonging to one set
of polygons into its counterpart in the other
set corresponds to replacing A, C, U & G in
the 64
codons
by their respective complements U, G, A & C
in the 64
anticodons
(for more details about the geometrical
counterpart of the 64
hexagrams
and the 64
codons
& anticodons, see ref. 2).
|
|
Figure
14
Yantras
are the yogic equivalent of mandalas, used by
Hindus and Buddhists as objects of meditation.
The Sri Yantra is the most revered of these
plans or charts that map Man’s inward journey
from physical existence to spiritual
enlightenment. It is generated from nine primary
triangles. Five downward-pointing triangles
symbolizing the feminine, creative energy of the
Goddess Shakti intersect four upward-pointing
triangles symbolizing the masculine, creative
energy, popularly conceived in India as the God
Shiva. Their overlapping generates 43 triangles.
Forty-two triangles arranged in four layers of
eight, ten, ten & 14 triangles surround a
downward pointing triangle whose corners denote
the triple Godhead, or Hindu Trimûrti of Shiva,
Brahma & Vishnu. At its centre is a point,
or bindu, representing the Absolute, or
transcendental Unity.
When
the 43 triangles in the 3-dimensional Sri Yantra
are tetractyses, 378 yods surround the central
tetractys (note that the outward-pointing
corners of the triangles in the highest three
layers lie above
the
joined corners in the layer next below the
triangle in question. These corners are
represented by circles that are split into two
differently coloured halves; one half denotes a
corner of a triangle in one set and the other
half denotes a corner in the adjacent set ). The
two triplets of red and blue hexagonal yods in
the central tetractys correspond to the two
trigrams of the Heaven hexagram in the top
left-hand corner of the I Ching table. Each pair
of triplets of hexagonal yods in a triangle (one
displays dashes connecting a pair) corresponds
to a pair of trigrams in a hexagram. The 384
yods composing the Sri Yantra other than the
corners and centre of the central triangle
correspond to the 384 lines & broken lines
of the 64
hexagrams
(3).
|
|
Figure
15
There are only five regular polyhedra. Known as the
Platonic solids because of Plato’s reference to
them in
Timaeus
, his cosmological treatise expounding Pythagorean
doctrine, they are:
tetrahedron
octahedron cube
icosahedron
dodecahedron
They have
50
vertices (black dots) and five centres (red dots),
so that the 180 sectors of their faces and the 90
interior triangles formed by their edges
have 55
corners.
This is F10. The tetrahedron has
5
centres & vertices, where
5
is F5. The first three solids
have
21
centres & corners and the icosahedron &
dodecahedron have
34
centres & vertices.
21
is F8 and
34
is F9. The icosahedron has
13
centres & vertices. This is F7. The
dodecahedron has
21
centres & vertices. This is F8. We
see that the five Platonic solids display five of
the first ten Fibonacci numbers. The other five are
present as well, although less explicit because
they mix points in several solids. As
21
=
8
+
13,
F6 appears as the
8
points that are either centres of the octahedron
& cube or vertices of the former, whilst
F7 appears as the
5
centres & vertices of the tetrahedron and as
the
8
vertices of the cube. The
5
points of the tetrahedron are further reducible to
its centre (F1), an apex (F2)
(this pair makes F3 (=
2
)) and the
3
vertices of its base (F4).
Comparing this pattern with the geometrical
composition of the lowest Tree of Life, the
55
points in the set of five Platonic solids
corresponds to the 55
points, lines & triangles making up the Tree,
the
21
points in the first three solids correspond to
the
21
geometrical elements in the kite-shape that is part
of the Upper Face and the
34
points in the icosahedron and dodecahedron
correspond to the
34
elements in the remainder of the Tree.
|
|
The sum of the 180 angles subtended by the 90 edges
of the five Platonic solids is 14400. This is the
square of the sum of the squares of the first four
even integers. The average of these angles
is 80º.
The sum is equivalent to 40 circles, where 40 = 4 +
8 + 12 + 16, and to
80
half-circles, where
80
is the number value of Yesod. These properties
illustrate the Tetrad Principle (4), which
states that the fourth member of a class of
mathematical object, or the sum of the first
four members, quantifies the properties of
holistic systems that display sacred geometry,
such as the Platonic solids.
When the
50
faces of the five Platonic solids are divided into
their sectors, there are 550 points, lines &
triangles. This is
ten
times the sum of the first
ten
integers, showing how the Decad determines the
geometrical composition of the faces. Also, 550 =
10F10,
where F10 (=
55)
is the
tenth
Fibonacci number.
The first four Platonic solids have 210 triangles
and polyhedral vertices & sides making up their
faces, leaving 340 elements distributed amongst all
five solids. Hence,
550 = 210 + 340 = 10×(
21
+
34).
21
is the eighth Fibonacci number and
34
is the ninth such number. As the Lower Face of the
lowest Tree of Life has
21
geometrical elements (Fig. 4) and
the Upper face has
34
elements, this is their regular polyhedral
counterpart.
|
|

The
first four Platonic solids have
248
vertices
& sides in the 120 sectors of their 38
faces. This is the dimension of the rank-8,
exceptional Lie group E
8 that
plays a fundamental role in superstring theory. It
demonstrates that the four regular polyhedra
believed by the ancient Greeks to be the shapes of
the particles of the elements Earth, Water, Air
& Fire do, indeed, embody the physics governing
all basic subatomic particles.
248
is
the number value of Raziel,
the Archangel of Binah (see table in Fig.
1).
The
square is the symbol of the Pythagorean Tetrad,
or number 4. When its sectors are so-called
‘2nd-order tetractyses’ (tetractyses generated
by replacing the ten points of a tetractys by a
tetractys), there are 248
points
(shown coloured) other than corners of
tetractyses. The seven coloured points in each
tetractys formally symbolize the seven Sephiroth
of Construction and its corners denote the
Supernal Triad of Kether, Chokmah &
Binah.
|
|
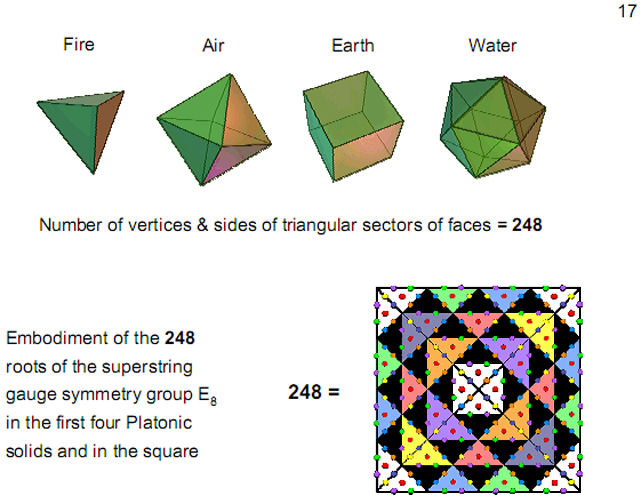
Figure 18
We saw earlier that the lowest
Tree of Life has
55
geometrical elements. When its 19 triangles are
divided into their 57 sectors and each sector then
turned into a tetractys, there are 240 (black) yods
generated by this transformation, i.e., yods other
than the original 11 corners of the 19 triangles. A
similar transformation of triangles outside this
Tree generates eight (red) yods below its top. The
240 yods symbolise the 240 (non-zero) roots
of E8 and
the eight yods denote its eight simple (zero)
roots.
The E8
root system consists of 240 vectors in an
eight-dimensional space. Those vectors are the
vertices (corners) of an eight-dimensional object
called the Gosset
polytope 421.
In the 1960s, Peter McMullen drew (by hand) a
two-dimensional representation of the Gosset
polytope 421.
The image shown here was computer-generated by John
Stembridge, based on McMullen's drawing. (Credit:
Image courtesy of American Institute of
Mathematics).
|
|
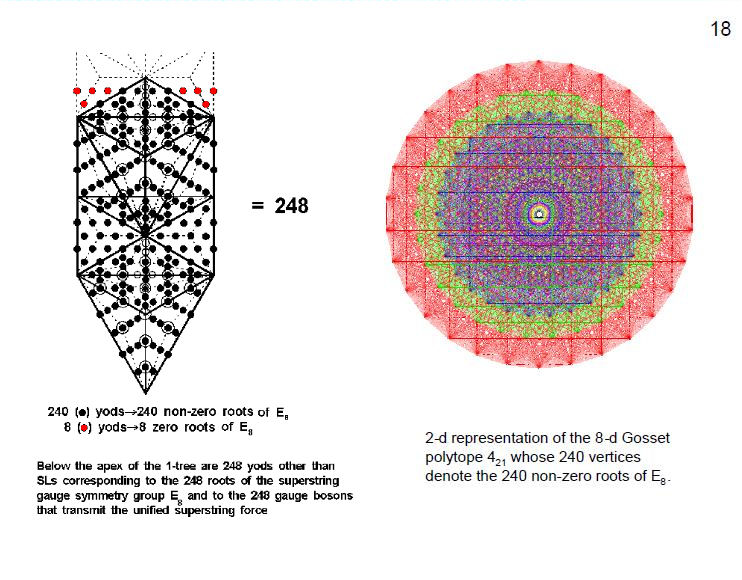
Figure 19
When the
48
sectors of the seven separate regular polygons in
one half of the inner Tree of Life are converted
into tetractyses, there are 247 yods other than the
given
48
corners of the polygons, i.e., 247 new yods appear.
Four yods lie along each edge, so that two extra
yods appear when the root edge, now regarded as a
separate straight line, is turned into such an
edge. One of them is associated with one set of
polygons and the second is associated with the
other set. Hence,
248
yods are associated with each set and the root edge
separating the two sets of polygons. They symbolise
the
(248+248=496)
roots
of E8×E8. The
se
ven centres of each set and its associated yod on
the root edge denote the eight simple roots of
E8
and the 240 other yods (called ‘hexagonal yods’ in
previous articles because they are located at the
corners and centre of hexagons) symbolise its 240
roots. The 240 yods belong to a geometrical object
with
55
corners. They are the counterpart to the 240 yods
that belong to the lowest Tree of Life that
possesses
55
geometrical elements. This is how the tenth
Fibonacci number F10
determines the superstring gauge symmetry group
E8.
|
|
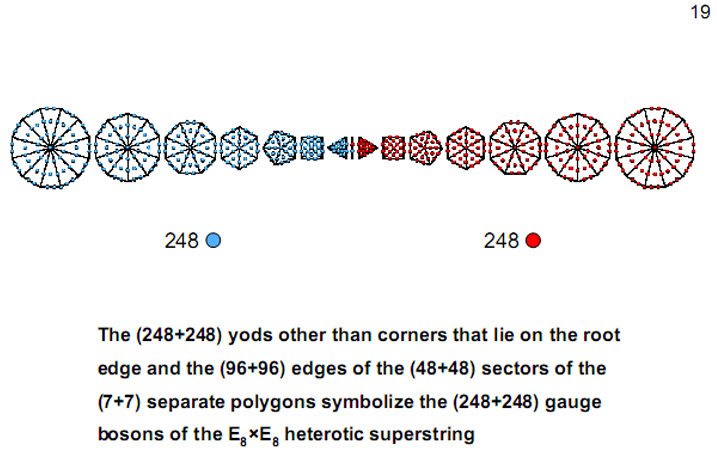
Figure 20
Suppose
that the 50
faces of
the five Platonic solids are divided into their
180 sectors and that their 90 internal
triangles, created by joining vertices to their
centres, are divided into their 270 sectors.
Then suppose that these 450 sectors with 190
vertices surrounding the centres of Platonic
solids are each turned into a tetractys. Four
yods lie along every one of their 590 sides, two
yods being between the ends of every side. The
number of yods surrounding the centres of the
five solids and lining the sides of their 450
tetractyses = 190 + 2×590 = 1370. This is the
number of yods in 137 tetractyses. The number
137 shapes the archetypal set of five regular
polyhedra. It is one of the most important
numbers in modern physics, being the number
whose reciprocal is approximately equal to the
dimensionless fine-structure constant α
= e2/ħc ≈
1/137, where e is the electric charge of the
electron, ħ (=h/2π)
is
the reduced Planck’s constant & c is the
speed of light in
vacuo. Its
magnitude remains a mystery no more. The
number 137 is a defining parameter of
holistic systems, being embodied in all
sacred geometries .
|
|

Figure
21
When the
94 sectors of the 14 enfolded, regular polygons
making up the inner Tree of Life are themselves
divided into their sectors and the latter then
turned into tetractyses, the resulting
282
tetractyses
have 1370 yods. This is the number of yods in
137 tetractyses. It is the same as the number of
yods surrounding the centres of the five
Platonic solids that line all the tetractyses
needed to construct their faces and interiors.
It is a remarkable illustration of how different
holistic systems embody analogous
properties.
The 14
enfolded polygons have 70 corners. This leaves
1300 yods that are added by the construction of
the inner Tree of Life from tetractyses. The
integers 1, 2, 3 & 4 symbolized by the four
rows of dots in the tetractys express this
number as
1300
= 15 + 25 +
35 + 45.
It is an
example of the beautiful, mathematical
properties of the inner Tree of Life.
|
|
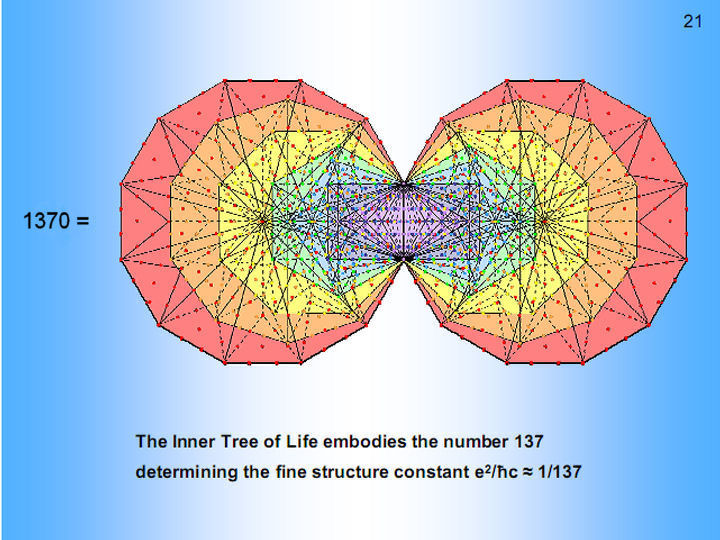
Figure 22
There are 90
triangles inside the five Platonic solids formed
by their 90 polyhedral edges and by the
50
straight
lines joining their 50
vertices and
their five centres. They can be further divided
into their 270 sectors. This generates
(3×90=270) new sides, 90 new corners and 270
internal triangles. The number of points, lines
& triangles inside the five solids that
surround their centres = 90 +
50
+ 270 +
270 = 680. According to Fig. 16, the
number of points, lines & triangles in
the 50
faces of the
solids is 550. Therefore, the number of
geometrical elements surrounding their centres =
550 + 680 = 1230 = 10L10, where
L10 (123) is the tenth
Lucas number. There are 340 internal elements in
each half of the five solids. 340 =
10F9, where
F9 (34) is the ninth
Fibonacci number. The relation
Ln =
Fn + 2Fn-1
is
geometrically realised for n = 10:
1230 = 550 +
680
10L10 =
10F10 + 10×2F9.
The factor
‘2’ expresses the two halves of each solid. The
factor ’10’ expresses the ten halves of the five
solids. L10 (=123) is the average
number of geometrical elements in each half that
surround the centres of the five solids and
F10 (=55) is the average
number of geometrical elements in each half of
their faces. The Golden Ratio
Φ
determines
the average geometrical composition of a
Platonic solid because L10
= Φ10 +
Φ−10.
This
beautiful property shows how the Decad
measures their geometrical
composition.
The
55:68
distinction
generated by the faces and the interior of
the five Platonic solids corresponds in
Fig. 5 to
the 55
geometrical
elements in the lowest Tree of Life and the 68
elements added in the second and third
Trees.
|
|

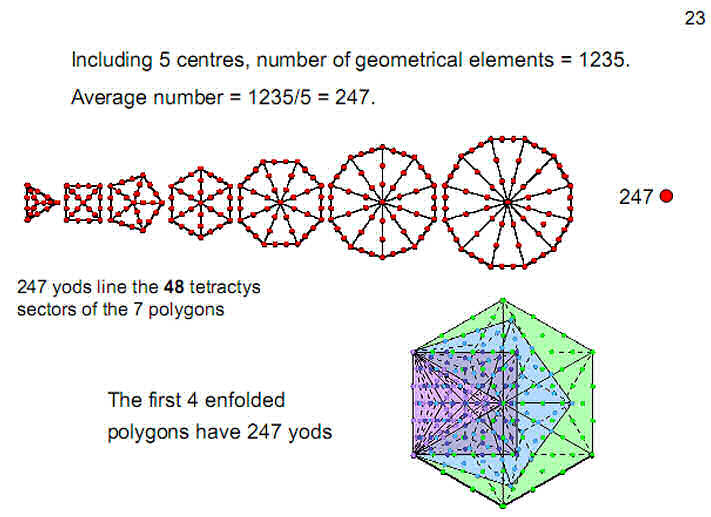
Figure 23
The five Platonic solids
are made up of 1235 points, lines &
triangles, including their centres. The average
number of geometrical elements is 247. This is
the number of yods lining the
48
tetractyses
that make up the seven regular polygons of
the inner Tree of Life. It is also the number
of yods in the first four enfolded polygons
when their sectors are divided into three
tetractyses.
The average number of
geometrical elements that surround the centres
of the five Platonic solids is 1230/5 =
246.
This is the number value
of Gabriel,
the Archangel
of Yesod.
|
|
|
24
Average
number
of
geometrical
elements
in
faces
of each
half of
a
Platonic
solid =
550/10
=
55
=
F10.
Average
number
of
geometrical
elements
in each
half of
a
Platonic
solid =
1230/10
=
123
=
L10.
Average
number
of
internal
elements
in each
half =
L10
–
F10
= 68 =
2F9.
Number
of
internal
elements
(including
centres)
= 680 +
5 =
685.
Average
number
of
elements
(including
centres)
inside
5
Platonic
solids
= 685/5
=
137.
Number
of
internal
elements
surrounding
centres
= 680 =
10(L
10
–
F10)
=
12
+
32
+
52
+
72
+
92
+
112
+
132
+
15
2.
15
is the
number
value
of YAH,
the
older
Godname
assigned
to
Chokmah.
|
|
|
Figure 25
We saw in
Fig. 21 that
the 14 enfolded polygons of the inner Tree of
Life have 1370 yods. Each set of seven enfolded
polygons has 687 yods. Therefore, 680 yods
surround their centres. This is the counterpart
of the 680 geometrical elements inside the five
Platonic solids that surround their centres.
Their interior constitutes a Tree of Life
pattern characterised by the same parameter 680,
which is determined by the ninth Fibonacci
number 34.
|
|
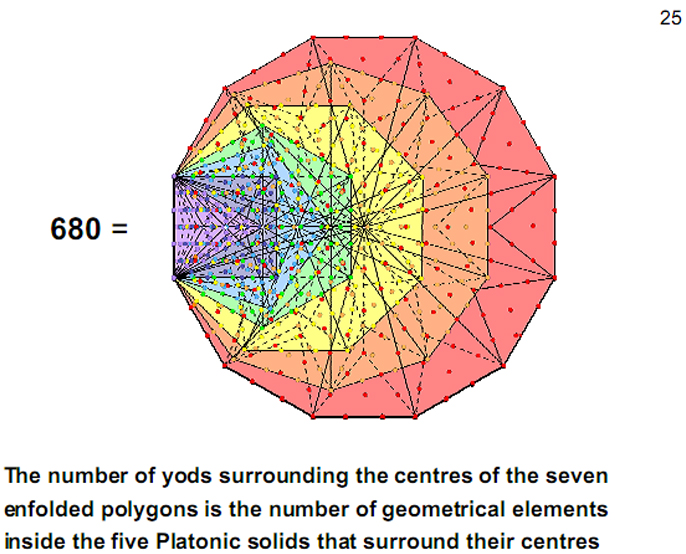
Figure 26
We saw in Fig. 10 that
the set of 14 polygons enfolded in each
overlapping Tree of Life has 68 corners (two of
the 70 corners coincide with corners of the two
hexagons enfolded in the next higher Tree).
The 140
polygons
enfolded in ten overlapping Trees of Life have
680 corners that belong alone to those polygons.
Ten such Trees are a representation of a single
Tree, with each Sephirah replaced by a Tree of
Life. This indicates that the five Platonic
solids and ten Trees of Life are analogous
sacred geometries. 140
is the number
value of
Masloth, the Mundane Chakra of
Chokmah.
|
|
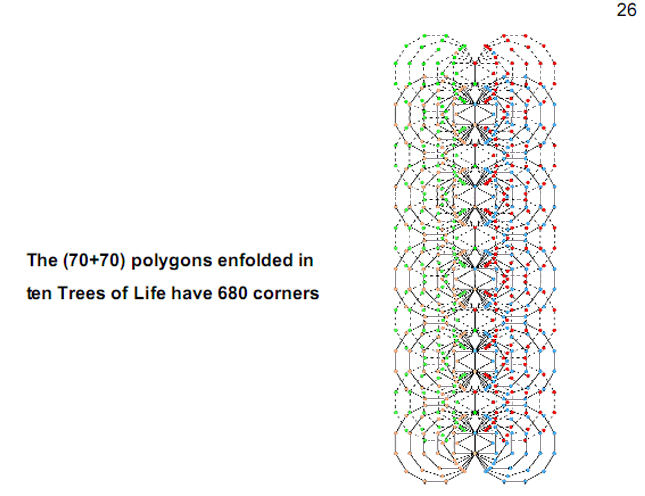
Figure 27
The two sets
of 21
polygons
enfolded in the lowest three Trees of Life have
206 corners. These Trees map the 3-dimensional
aspect of Adam Kadmon, which for a human being
is his or her physical body, its skeleton having
206 bones. This is why L10 measures
the geometrical composition of these Trees (see
Fig. 5).
L10 also measures the geometry of
their inner form because each set of
21
polygons
has 123
sides outside
their root edges.
The
80
bones of the
axial skeleton comprise 34
single bones
and 23 pairs of bones, one on the left of the
body and one on the right.
34
is
F9. 80
is the
number value of Yesod, whose meaning,
“foundation,” aptly describes this core set
of bones.
|
|
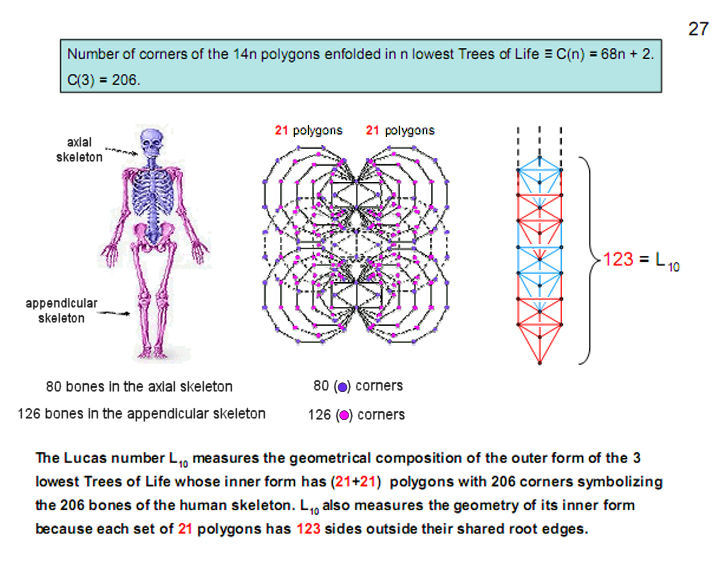
Figure 28
Number of corners of
triangles in the lowest n Trees ≡ S(n) = 6n
+5.
Number of sides of
triangles ≡ E(n) = 16n + 9.
Number of triangles ≡ T(n)
= 12n + 7.
Suppose that the three
sectors of each triangle are tetractyses. Each
triangle then has ten yods inside it.
Number of yods in the
lowest n Trees = S(n) + 10T(n) + 2E(n) = 158n +
93.
The three lowest Trees have
567 yods, of which 206 yods symbolize the 206
bones of the human skeleton and 361 yods denote
the 361 classical acupuncture points (5,6).
|
|
Figure
29
For centuries the music of
the Roman Catholic Church has been based upon
eight ‘modes.’ Four modes:
Dorian, Phrygian, Lydian &
Mixolydian
are called ‘authentic’ and
four:
Hypodorian, Hypophrygian,
Hypolydian & Hypomixolydian
are called ‘plagal.’ They
are seven different musical scales with distinct
orderings of intervals between their notes, the
first (Dorian) and last (Hypomixolydian) having
the same pattern of intervals but a
different dominant
(reciting note)
and finalis
(ending note)
(7).
|
|

Figure 30
The pitches of the notes in
the church modes are those of the modern
equal-tempered scale. However, this is an
invention by musicians to make their playing of
music more convenient with more notes available
than the ancient seven note Pythagorean
scale:
T T
L T T
T L
where T is the tone
interval of 9/8 and L (leimma) is the interval
of 256/243 (the Pythagorean counterpart of the
modern half-tone). Figure 30
shows the tone ratios of the seven types of
musical scale (the C scale is the Pythagorean
scale). Coloured cells denote notes belonging to
the C scale and white cells denote
non-Pythagorean notes. There are 12 types of
notes between the tonic with tone ratio 1 and
the octave with tone ratio 2. The last seven
notes with tone ratio n are the inversions of
their partners in the first seven notes with
tone ratio m, where mn = 2. The thick vertical
line separates notes and their inversions. Bold
tone ratios refer to notes of the Pythagorean
musical scale.
|
|
|




























