
The octagon
TYPE A OCTAGON
(1) The octagon has 49 yods, of which

2
4
3 3
4 4 40 = 4
4
4
= 4
4
4
5 5 5 5 4 4 4 4 yods are hexagonal, 24 (= 1×2×3×4) are boundary yods and 25 are internal yods. The octagon embodies the Godname number 49 of Yesod. The 49th odd integer is the sum:
97 = 21 + 26 + 50
of the Godname numbers of the Supernal Triad. The number 97, which is the number of Haniel, the Archangel of Netzach, defines the Godname of Malkuth:
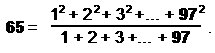
(2) The sum of the first 49 integers = 1225 = 49×25. The seven separate polygons and their associated endpoint of the root edge have 49 corners. The 25-tree prescribed by the complete Godname of Malkuth generates 25 sets of seven polygons and root edges with 1225 corners. Hence, the Godname of Yesod prescribes the 49th triangular number and thus the 25-tree that is the counterpart of the 25 spatial dimensions of the physical universe predicted by quantum mechanics for spinless strings. In other words, arithmetically embodied in the octagon is the number of spatial dimensions of matter. It is the arithmetic mean of the integers 1–49 that can be assigned to its yods.
(3) If the first 24 (= 1×2×3×4) integers are assigned to the boundary yods of the octagon and the next 25 integers are assigned to its internal yods, then
1 + 2 + 3 +... + 24 = 300 = (1 + 2 + 3 + 4)(12 + 22 + 32 + 42)
and the sum of their squares is 4900 = 702. Just as the sum of the squares of the first 12 integers on the boundary of a square is 650 (that is, the square encodes the Godname number 65 of Malkuth), so, too, the sum of the squares of the first 24 integers on the boundary of an octagon (two squares rotated through 45º) is 4900 (that is, the octagon encodes the Godname number of Yesod both arithmetically and through its division into tetractyses). Notice that:
|
1 |
15 |
||||||||
| 1 | 1 | 25 | 25 | ||||||
| 4900 = |
1 |
1 |
1 |
+ |
35 |
35 |
35 |
||
| 1 | 1 | 1 | 1 | 45 | 45 | 45 | 45 | ||
|
|
|
+ |
|
||||||
(4) Sum of squares of first 49 integers = 49×15×55 = 40425 = 5×15×539

where
539 = 31 + 36 + 76 + 129 + 153 + 49 + 65
is the sum of the Godname numbers of the seven Sephiroth of Construction.
(5) Sum of first 49 odd integers = 492 = 2401. Assigning
these integers to the yods of the octagon with the number 1 at its centre, the sum of the 48 surrounding
odd integers is
|
240 |
||||
| 240 | 240 | |||
| 2400 = |
240 |
240 |
240 |
|
| 240 | 240 | 240 | 240 . |
The octagon therefore embodies the number of
space-time components of the 240 ten-dimensional gauge fields of E8
corresponding to its non-zero roots. The sum of the 96 odd integers surrounding the centres of the pair of
octagons generated by the Tree of Life = 2400 + 2400 = 4800, which is the number of space-time components of the
480 ten-dimensional gauge fields associated with the (240+240=480) non-zero roots of
E8×E8. As a set of seven polygons has 240 hexagonal yods, 2400 is also the number of
hexagonal yods in 70 separate, Type A polygons generated by the 10 Trees in the 10-tree counterpart of
superstring space-time. Through this arithmetic property, the octagon determines not only the number of spatial
dimensions of bosonic strings as the mean of the first 49 integers but also the dimensionality
of superstrings.
(6) Assigning the first 40 odd integers after 1 to
the 40 hexagonal yods of the octagon, their sum = 412 − 1 = 3 + 5 +... + 81 = 1680 =
168×10. The octagon (and therefore the Godname of Yesod) embodies the structural parameter of
the superstring. The sum of the next eight odd integers 83–97 that can be assigned to
the corners of the octagon = 720 = 72×10. Sacred geometries are always found to embody the
number 240 as the sum of 72 and 168. Its group-theoretical counterparts are
the 240 roots of E8, which comprise the 72 roots of its exceptional subgroup
E6 and the 168 remaining roots. The octagon displays its arithmetic counterpart as
the sum 2400 = 240×10 = 168×10 + 72×10.
(7) The sum of the numbers of the complete Godnames of the 10 Sephiroth is represented by
an octagonal array of the fourth powers of 1, 2, 3 & 4:
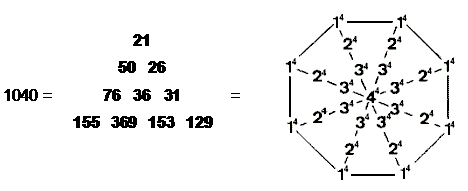
Also:
65 65 65 65 1040 = 65 65 65 65 65 65 65 65 65 65 65 65 ,
where 65 is the number of ADONAI. These are remarkable and beautiful illustrations of the fundamental connection between Godname numbers and the Pythagorean integers 1, 2, 3 & 4.
(8) There are 260 hexagonal yods in separate pairs of triangles, squares, pentagons, hexagons and octagons, that is, in the first (5+5) separate polygons. This is the number of yods outside the root edge in seven enfolded Type A polygons. This and properties (5) & (6) illustrate the meaning of the word “foundation” translating the Hebrew name Yesod. The octagon is the geometrical representation of the Godname EL ChAI, which prescribes what manifests at the level of Malkuth as the physical form of the Tree of Life. In prescribing the fifth polygon, this Godname also determines the yod population of all seven enfolded polygons, namely, the inner form of the Tree of Life, whilst it prescribes the forces of nature in property (5) and the form of a whorl in (6) — the manifestation of this blueprint. The fourth octagonal number after 1 is 65:
1 8 21 40 65
The octagon therefore determines mathematically the number values of the Godnames of the last two Sephiroth of the Tree of Life. This is an example of the Tetrad Principle (discussed in Article 1) governing classes of numbers, whereby parameters of sacred geometry, including the gematria numbers of the 10 Sephiroth in the four Worlds, are expressed by either the sum of the first four members after 1 of a class of numbers or its fourth member.
(9) The meaning of Yesod is further elucidated by the fact that a pair of octagons constructed from tetractyses has 80 hexagonal yods, thereby embodying the number of Yesod. They also have (24+24=48) boundary yods, so that the 10 pairs of octagons generated by the 10-tree counterpart of 10-dimensional space-time have (240+240=480) boundary yods. This is the number of hexagonal yods in the (7+7) polygons generated by a single Tree of Life. 80 is also the number of corners of the 10 octagons belonging to half of the inner form of the 10-tree representing the 10 Sephiroth of the Tree of Life. The significance of the connection between the number 65 of ADONAI, the Godname of Malkuth, and the (240+240=480) boundary yods of the 10 pairs of octagons in the 10-tree is that the anomaly-free symmetry group E8×E8 describing the forces between one of the two types of heterotic superstrings has (240+240=480) roots. This root structure therefore manifests in the pairs of octagons enfolded in the 10 Trees that map either the 10 dimensions of space-time or the 10 whorls of the UPA, the subquark state of the E8×E8 heterotic superstring remote-viewed by Annie Besant & C.W. Leadbeater. Malkuth is the physical form of the Tree of Life (in this case, the superstring) that is determined by these forces, and so the presence in this context of the Godname of this Sephirah is very relevant, particularly as it also prescribes the very 10 Trees themselves, which have 65 Sephirothic emanations.
TYPE B OCTAGON
(1) The octagon contains 121 yods. 121 is the 61st odd integer and the square of the tenth integer after 1: 121 = 112. There are 120 yods surrounding the centre, where
|
3 |
10 |
||||||||
| 5 | 7 | 11 | 11 | ||||||
| 120 = |
9 |
11 |
13 |
= |
12 |
12 |
12 |
||
| 15 | 17 | 19 | 21 | 13 | 13 | 13 | 13 |
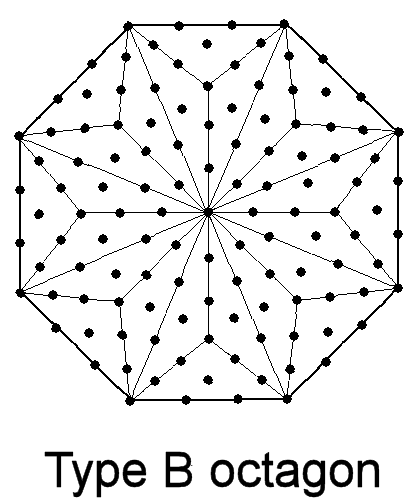
is the sum of the first ten odd integers after 1. This is a parameter of the inner Tree of Life because 120 yods line the 42 sides of the seven enfolded polygons when their 47 sectors are tetractyses (see here). The number of internal yods is
97 = 21 + 26 + 50.
As pointed out in the discussion of the Type A octagon, this is both the 49th odd integer and the number value of Haniel, the Archangel of Netzach. The number of hexagonal yods is 104.
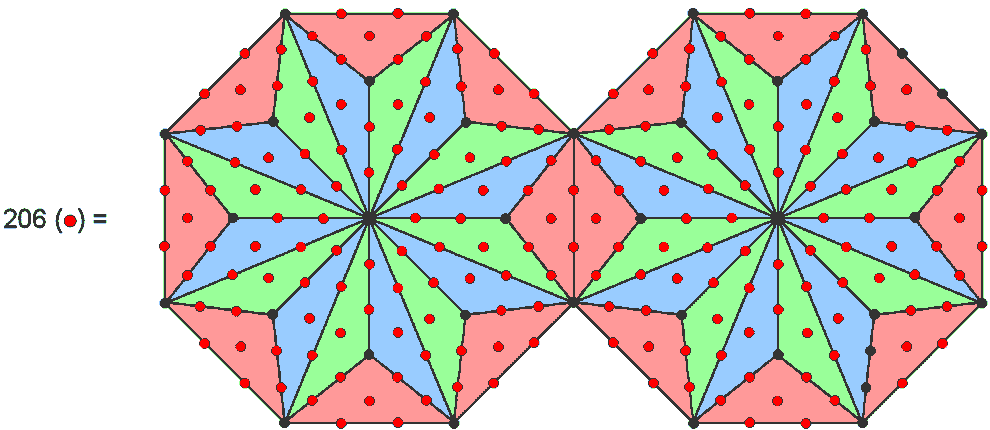
(2) A pair of separate Type B octagons has 240 yods surrounding their centres. The number of non-zero roots of the rank-8 Lie group E8 is embodied in a single Type B octagon. The number 240 is a parameter of holistic systems because it is embodied in all sacred geometries (see under heading "240 = 72 + 168" here). Two enfolded octagons contain 238 yods, of which 206 yods are hexagonal, i.e., associated with each octagon are 103 hexagonal yods, where 103 is the number of SABAOTH. The two enfolded octagons, therefore, embody the 206 bones in the human skeleton:
 |
 |
They have 236 yods surrounding their centres, each having 120 yods surrounding them. This is the
number of yods lining the sides of the (7+7) enfolded polygons of the inner Tree of Life, each having 120 yods
lining the seven enfolded polygons (see here), as well as the number of geometrical elements making up the
42 triangles that surround the centre of the 2-dimensional Sri Yantra (see here). The pair of Type B octagons embodies two numbers (120 & 236) that
quantify the shapes of two sacred geometries. The simplest example of how the octagon embodies
such numbers is the fact that 48 yods surround the centre of a Type A octagon, where
48 is the number of Kokab, the Mundane Chakra of Hod, which is the eighth
Sephirah. This is the number of corners of the seven separate polygons that make up the inner Tree of Life (see
here).
(3) Sum of the first 121 integers = 7381 = 121×61. Assigning these integers to the
yods of the octagon with the number 1 at its centre, the sum of the first 97 integers inside the
octagon = 4753 = 97×49 = 13 + 33 + 53 + 73 +
93 + 113 + 133
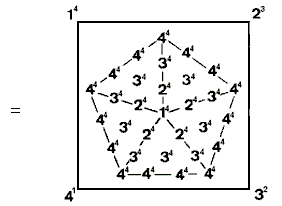
where 49 = 1 + 3 + 5 + 7 + 11 + 13. The sum of the 24 boundary integers is
(4) Sum of squares of the first 97 integers = 308945 = 97×49×65.
TYPE A + TYPE B OCTAGONS
(1) A pair of separate octagons has 170 yods (168 surrounding their
centres). Enfolded, they contain 166 yods, that is, 160 (= 42(1+2+3+4))
yods outside their root edge surround their centres. The pair of octagons encodes the number 168 of
Cholem Yesodoth, the Mundane Chakra of Malkuth. It quantifies the form of the subquark state
of the superstring as the number of circularly polarized waves in half a revolution of a
whorl.
(2) A pair of separate octagons contains
| 10 | 20 | 30 | 40 | |
| 11 | 21 | 31 | 41 | |
| 144 = | 12 | 22 | 32 | 42 |
| 13 | 23 | 33 | 43 |
hexagonal yods. Enfolded, they contain 142 hexagonal yods, of which 140 are outside the root edge, where 140 is the number value of Malachim, the Order of Angels assigned to Tiphareth.
OCTAGON WITH 2ND-ORDER TETRACTYSES AS SECTORS
.png)
In the discussion of the square whose sectors are 2nd-order tetractyses, it was pointed out that there are 62 hexagonal yods per sector, where 62 is the number value of Tzadkiel, the Archangel of Chesed. Hence, an octagon has (8×62=496) hexagonal yods. This is the dimension of the two Lie groups SO(32) and E8×E8 that describe superstring forces free of the quantum anomalies that afflict field theories based upon point-like particles. Each coloured yod denotes one of the 496 quantum states of the messenger particles that transmit the unified force between superstrings (see also here). Surrounding the centre of the octagon are 80 white yods at the corners of the 80 1st-order tetractyses, where 80 is the number value of Yesod. There are 72 yods per sector, where 72 is the number value of Chesed (notice the appearances of the numbers of both Chesed and its Archangel). Hence, (8×72 = 576 = 242 = 12×22×32×42) yods surround the centre of the octagon, illustrating how the integers 1, 2, 3 & 4 symbolized by the four rows of dots in the tetractys express the yod population of an octagon with 2nd-order tetractyses as its sectors. How these integers express the number 496 is illustrated here.
TYPE C OCTAGON
|
|
The Type C octagon embodies the superstring structural
parameter 336 because 336 yods (168 yods and their diametric opposites) surround its centre. |
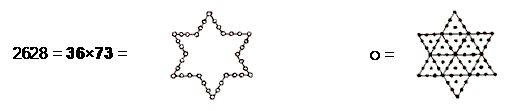
The Type C octagon has Type B triangles as its sectors. The number of yods in a Type C n-gon = 42n + 1. Surrounding the centre of a Type C octagon are (8×42=336) yods. This is the number of turns in each of the five revolutions of a whorl of the UPA/subquark superstring about its spin axis (see also Article 60). Two joined Type C octagons have 666 yods outside the root edge. Including the latter, they have 670 (=67×10) yods. This is how the number 67 of Binah is connected to the superstring structural parameter 336. It is connected to it in the following, equally amazing way: the number of yods in n overlapping Trees of Life whose triangles are tetractyses = 50n + 20. The tetractys with Kether, Chokmah & Binah of the nth Tree contains 10 yods. Below Binah of the nth tree are (50n+10) yods. Below Binah of the 67th Tree are (50×67 + 10 = 3360 = 336×10) yods. This is the number of turns in each revolution of all 10 whorls of the UPA.
Each sector of the Type C octagon has 9 tetractyses, each of which has a central hexagonal yod. The number of yods lining the (8×9=72) tetractyses in a Type C octagon and surrounding its centre = 336 − 72 = 264. This is the number of yods in the 7 enfolded Type A polygons making up each half of the inner Tree of Life:
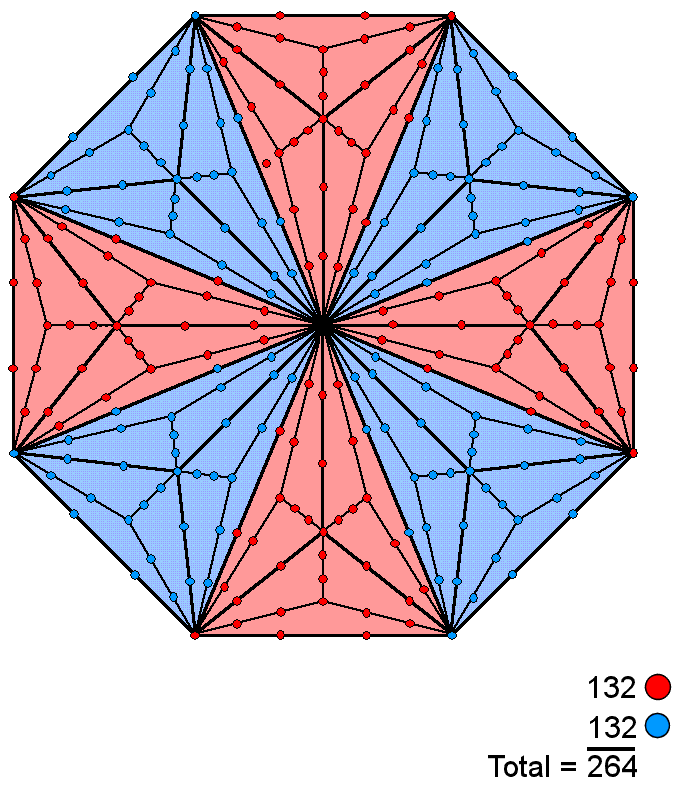 |
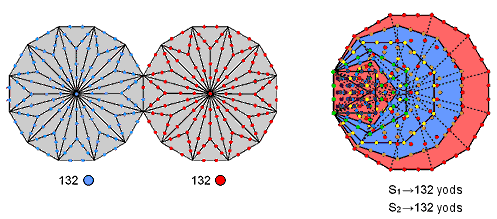 |
The set of polygons (S1) consisting of the triangle, square, pentagon & dodecagon (coloured red) contain 132 yods outside the root edge, as do the set of polygons (S2) consisting of the hexagon, octagon & decagon (coloured blue) when the root edge is included (for proof, see Table 5, p. 5 in Article 64). This is the number of yods (red or blue) lining sides of tetractyses in 4 red or blue sectors of the Type C octagon. Remarkably, 132 yods lining tetractyses are associated with each dodecagon present in the (7+7) enfolded, Type B polygons. This illustrates how the pair of dodecagons constitutes the single, polygonal version of the inner Tree of Life (see the discussion in this section of the dodecagon).
According to Table 1 in Polygonal numbers, the nth octagonal number On = ½n(6n−4) = n(3n−2). Therefore, O24 = 24×70 = 1680. We see that the primary superstring structural parameter 1680 recorded by C.W. Leadbeater in his book Occult Chemistry (see here) is the 24th octagonal number, showing how it is generated arithmetically by the number 24, as well as dynamically by it because the 1680 circular turns of each helical whorl in the UPA (subquark state of the E8×E8 heterotic superstring) are the manifestation of 24 gauge charges of the rank-8, exceptional Lie group E8 spread along the closed curve. Remarkably, the eighth octagonal number O8 = 176, which, according to Occult Chemistry, is the number of (n+1)th-order spirillae in every 25 nth-order spirillae in each major whorl (see here). This number is a inner Tree of Life parameter because: