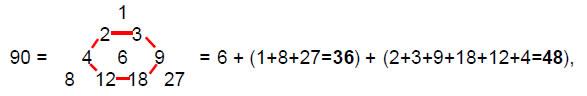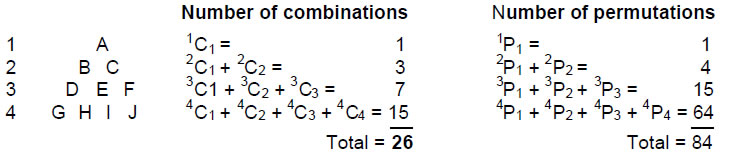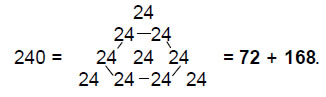ARTICLE 37

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

1

Table 1. Gematria number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

(Numbers in this table referred to in the article will be written in boldface).

2

1. The seven octaves of the seven musical scales
The Pythagorean musical scale consists of five tone intervals of 9/8 (T) and two leimmas of 256/243 (L):

By starting with successive notes to generate scales of eight notes and then normalising the tone ratios so that the tonic in each scale has a tone ratio of 1, the pattern of intervals is repeated at the eighth sequence, thus generating seven distinct octave species:

These are the musical modes¹ used for hundreds of years in the plainsong of the Roman Catholic Church. Mode 8 (Hypomixolydian) is the D scale with different ‘dominant’ and ‘finalis’ notes. Table 2 displays the values of their tone ratios.

Table 2. Tone ratios of the seven musical scales.

Musical scale	Tone ratio
B scale	1	256/243	32/27	4/3	1024/729	128/81	16/9	2
A scale	1	9/8	32/27	4/3	3/2	128/81	16/9	2
G scale	1	9/8	81/64	4/3	3/2	27/16	16/9	2
F scale	1	9/8	81/64	729/512	3/2	27/16	243/128	2
E scale	1	256/243	32/27	4/3	3/2	128/81	16/9	2
D scale	1	9/8	32/27	4/3	3/2	27/16	16/9	2
C scale	1	9/8	81/64	4/3	3/2	27/16	243/128	2

Tone ratios belonging to the Pythagorean scale are written in black and non-Pythagorean tone ratios are written in red. The 42 notes between the tonic and the octave comprise 26 notes with Pythagorean tone ratios and 16 with non-Pythagorean values. Table 1 indicates that 26 is the gematria number value of YAHWEH, the Godname of Chokmah. As 42 is the 21st even integer, EHYEH, the Godname of Kether with number value 21, prescribes the notes of the seven musical scales between the tonic and the octave.

The seven species of octaves comprise 14 different notes. In order of increasing tone ratios, they are:

1     256/243     9/8     32/27     81/64     4/3     1024/729     729/512     3/2     128/81     27/16     16/9     243/128     2

There are six Pythagorean intervals and six non-Pythagorean intervals between the tonic and octave. Defining the inversion of a note with tone ratio n as a note with tone ratio m, where nm = 2, the 14 notes form seven pairs of notes and their inversions:

3

1	1	2	1×2 = 2
2	256/243	243/128	256/243×243/128 = 2
3	9/8	16/9	9/8×16/9 = 2
4	32/27	27/16	32/27×27/16 = 2
5	81/64	128/81	81/64×128/81 = 2
6	4/3	3/2	4/3×3/2 = 2
7	1024/729	729/512	1024/729×729/512 = 2

The inversion of a note is equal to the interval between it and the octave.

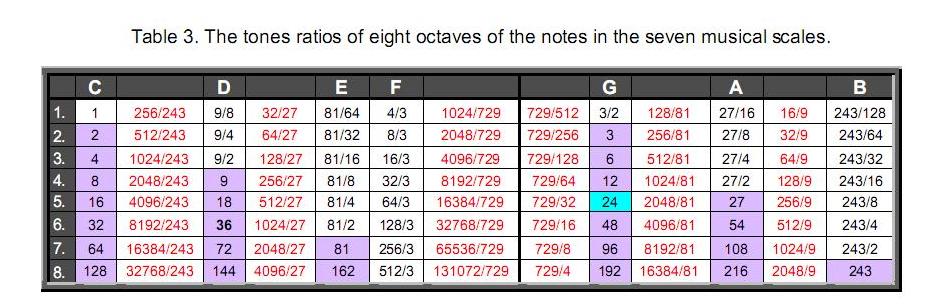
Now imagine the 14 notes as composing a new musical scale. It is, of course, not similar to the modern equal-tempered scale because this has 13 notes with 12 equal half-tone intervals. Table 3 shows the tones ratios of eight successive octaves of these notes. For future discussion, it is unnecessary to regard these 14 notes as an actual musical scale because we will be analysing seven octaves of the seven scales and it is more convenient to group their notes and their higher octaves in order of increasing tone ratios in a scale-like sequence than to consider them in their separate scales. 2⁷ = 128 is the seventh octave. Table 3 indicates that it is the 92nd note, the 91st interval, the 49th Pythagorean interval, the

(Purple cells indicate overtones, black tone ratios are Pythagorean and red tone ratios are non-Pythagorean. The turquoise cell is 24, the perfect fifth of the fifth octave).

50th Pythagorean note and the 21st overtone. The appearance of the number values of the Godnames ELOHIM (50), EL CHAI (49) and EHYEH (21) is the first sign that these seven octaves constitute a Tree of Life pattern defines by the Godnames of the Sephiroth. Each ‘octave’ group of 13 notes has six Pythagorean notes other than octaves and non-Pythagorean notes, so that below the seventh octave there are 90 intervals made up of six octaves, (7×6=42) Pythagorean notes and 42 non-Pythagorean notes, that is, (42+42=84) intervals other than octaves. As discusses later, the fact that there are 90 intervals is a sign that the seven octaves of the notes in the seven musical scales constitutes a holistic pattern.

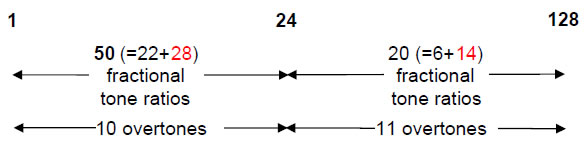
Now let us consider the tone ratio 24 in the turquoise cell of Table 3. It is the 33rd Pythagorean note, the 32nd Pythagorean interval, the 10th overtone, the 61st note and the 60th interval. As 32 is the 31st integer after 1 and 61 is the 31st odd integer, the Godname EL with number value 31 picks out the tone ratio 24 in the sequence of monotonically increasing tone ratios of the notes of the seven scales and their higher octaves. There are 22 Pythagorean notes with fractional tone ratios and 28 fractional, non-Pythagorean notes up to 24, that is, 50 notes with fractional tone ratios. Hence, the

4

Godname ELOHIM with number value 50 also picks out this note. There are 14 fractional, non-Pythagorean notes, 6 fractional, Pythagorean notes (that is, 20 fractional notes) and 11 overtones above the tone ratio 24 to 128, that is, (20+11=31) notes. EL therefore also defines the number of notes above it to 128. The fact that EL picks out 24 in not just one but three ways makes coincidence implausible as the reason why two Godname numbers describe its position in the sequence of notes.

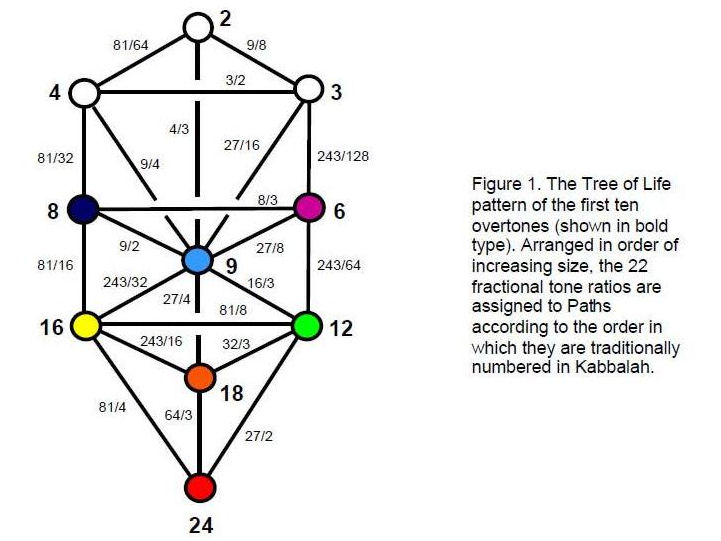
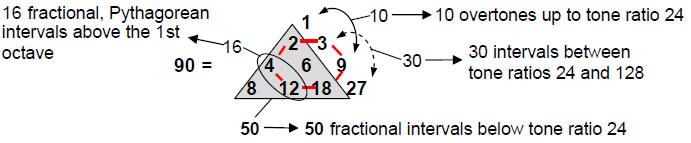
The reason why such Godnames appear is that the 32 intervals and the ten overtones up to the tone ratio 24 form a Tree of Life pattern, which is always prescribed by all the Godnames. The 10 overtones correspond to the ten Sephiroth and the 22 notes with fractional, Pythagorean tone ratios correspond to the 22 Paths of the Tree of Life (Fig. 1).

The implication of this correspondence is that, in corresponding to Malkuth, the last Sephirah, the tenth overtone 24 plays some role in the physics of matter. This will be explored later.

 

24 is the tone ratio of the 61st note as well as the tenth overtone. A decagon whose

5

sectors are tetractyses has 61 yods (Fig. 2). Called “All perfect” by the ancient Pythagoreans, the number 10 completes the sequence of natural integers because all integers above it are simply the sum of integers smaller than it and integer multiples of 10 that are similarly reducible. Assigning to its central yod the tone ratio 1 as the first note, the ten overtones up to 24 can be assigned to the corners of the decagon and the 50 notes below it with fractional tone ratios can be assigned to the 50 hexagonal yods. This is another reason for regarding the tone ratio 24 as special — it is defined

by the tetractys-divided decagon symbolizing the perfect number 10.

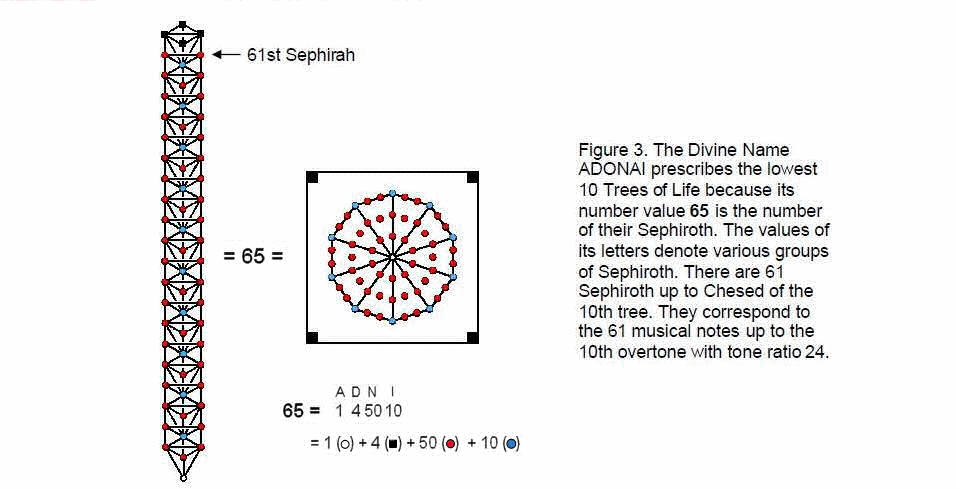
The Godname ADONAI with number value 65 prescribes the ten lowest Trees of Life because they have 65 Sephiroth (Fig. 3). The values of its letters denote various groups of Sephiroth. Assigning the musical notes of the seven scales to the Sephiroth, starting with Chesed of the tenth tree — the first Sephirah of Construction — the note assigned to

6

the lowest Sephirah is 24 because it is the 61st. Here is further evidence that this tone ratio has physical significance, for ADONAI is the Godname of Malkuth, the physical universe. The 10-tree is the representation of the Tree of Life with each Sephirah represented by a tree. Remarkably, they both define the tone ratio 24 — in the former case as the 32nd interval and in the latter case as the 61st note.

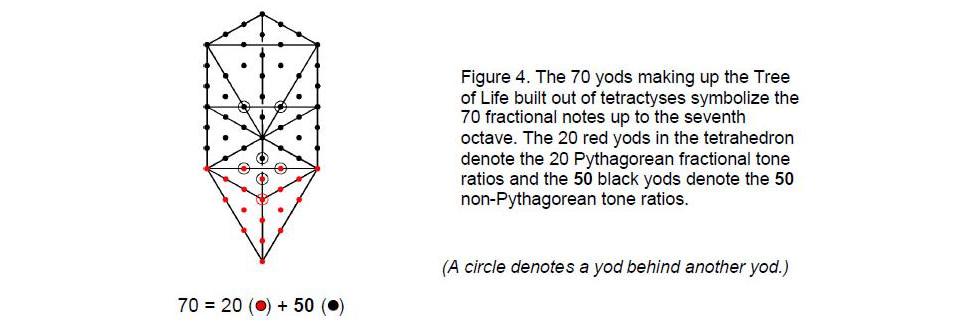
The note 24 divides the 70 fractional notes up to 128 into 50 below it and 20 above it, the 22 integer notes into 11 up to it and 11 above it and the 92 notes up to 128 into 60 below and 31 above it:

The 50:20 division of fractional notes up to the seventh octave demonstrates that this sequence of 70 notes constitutes a Tree of Life pattern. This is because, when the 16 triangles of the Tree of Life are tetractyses, it has 70 yods made up of 20 yods in the tetrahedron whose vertices coincide with the four lowest Sephiroth of Construction and 50 yods in the rest of the tree (Fig. 4). The division 50:20 of its yods has its counterpart in the inner Tree of Life as the 20 corners of the two dodecagons and the 50 corners of the two sets of six polygons. As we shall show later, the dodecagon marks the tone ratio 24 in another way.

The 91 intervals up to 128 consist of 21 overtones and 70 fractional notes comprising 28 Pythagorean notes and 42 non-Pythagorean notes. The 91 intervals therefore comprise (21+28=49) Pythagorean notes and 42 non-Pythagorean notes. Seven of the former are the notes of the Pythagorean scale above the tone. Hence, 91 = 7 + 84, where 84 is the number of other notes in the seven octaves. 84 = 6 + 78, where 6 = the number of non-Pythagorean notes in the first octave and 78 = 42 + 36, where 42 is the number of Pythagorean notes above the first octave and 36 is the number of non- Pythagorean notes above the first octave. Therefore, the 84 notes are divided into 42 Pythagorean notes above the first octave and 42 non-Pythagorean notes (six in the first octave and 36 above it). Alternatively, 84 intervals are not octaves.

Below is summarised how some Godnames prescribe either the seven octaves of the seven musical scales as a Tree of Life pattern or the tone ratio 24 (the brackets enclose their number values):

EHYEH (21):	21 overtones up to 128. 42 Pythagorean notes above the 1st octave (42 = 21st even integer). 42 non-Pythagorean notes in the seven octaves.
YAH (15):	A 15-sided polygon with tetractys sectors has 91 yods. 128 is the 91st interval.
YAHWEH (26):	24 is the 26th note, counting from the 2nd octave.
ELOHIM (50):	128 = 50th Pythagorean note. 50 notes below 24 with fractional tone ratios.
EL (31):	24 = 32nd Pythagorean interval (32 = 31st integer after 1). 31 notes above 24 to 128.
ELOHA (36):	36 non-Pythagorean notes and 36 Pythagorean notes other than octaves above the 1st octave.

7

 

YAHWEH ELOHIM (76):	76 notes above 1st non-Pythagorean note of 2nd octave.
EL CHAI (49):	128 = 49th Pythagorean interval.

2. Comparison with the last four enfolded polygons
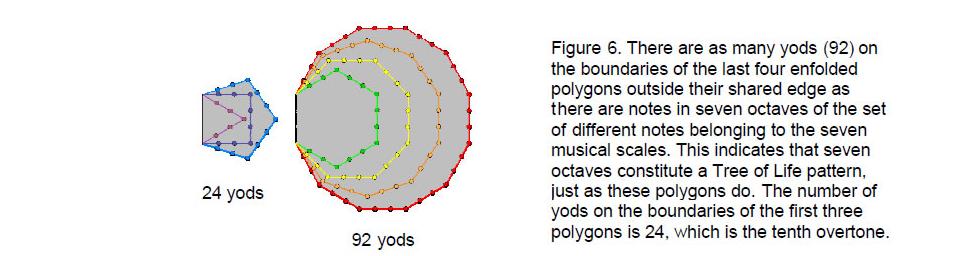
The inner form of the Tree of Life (Fig. 5) consists of two similar sets of seven regular polygons that are enfolded in one another, all 14 polygons sharing the same ‘root edge.’ The last four polygons are the hexagon, octagon, decagon and dodecagon. 92 yods lie on their 32 sides outside their root edge (Fig. 6). Of these, 32 red yods lie on the 11 sides of the

dodecagon outside the root edge and 60 yods lie on the 21 edges of the hexagon, octagon and decagon. The Godname EHYEH with number value 21 prescribes the first three polygons with 60 yods on their edges, whilst the Godname EL with number value 31 prescribes all seven polygons with 32 sides because 32 is the 31st integer after 1. As the 32nd Pythagorean interval is 24 and the 92nd note is 128, the 92 yods in the last four polygons symbolize the 92 notes in the seven octaves. The ten vertices of the dodecagon symbolize the ten overtones up to 24, the 22 yods on its edges
 

between vertices denote the 22 Pythagorean intervals up to 24 and the 60 yods of the hexagon, octagon & decagon denote the 60 remaining intervals. The dodecagon defines the tone ratio 24 in terms of the correspondence between its boundary yods and the notes in the Pythagorean scale up to 24. Alternatively, as 24 is the 61st note in the sequence of notes and as there are 31 notes above it to the seventh octave, the 60 yods in the first three polygons may be thought to symbolize the 60 notes below 24, whilst the 32 yods in the dodecagon denote 24 and the remaining 31 notes above 24. Whichever correspondence one chooses (as it reproduces the order of sequence of notes, the latter is more natural), it is clear that the tone ratio 24 is marked out either by the first three polygons as the transition point to the last polygon or by the last one itself as having special significance. The increase of pitch from note to note over seven octaves has its exact counterpart in the sacred geometry of the last four polygons. Why? Because both conform to a Tree of Life pattern.

This conclusion is given support by the fact that the first three polygons of the inner Tree of Life — the triangle, square and pentagon — have 24 yods on their edges

8

outside the root edge (see Fig. 6). Once again, the part of the inner Tree of Life supplementing a part that is itself a Tree of Life pattern defines the very same number 24! It is highly implausible that this is merely coincidental. It speaks powerfully of design — of a universal blueprint of which the seven musical scales and their seven octaves are a manifestation and in which the tenth overtone plays a fundamental role, as indicated previously by the fact that the Godname ELOHIM assigned to Binah in the Tree of Life prescribes the number of fractional notes below 24 and the Godname EL of Chesed, the next Sephirah, prescribes the 31 notes above it to 128.

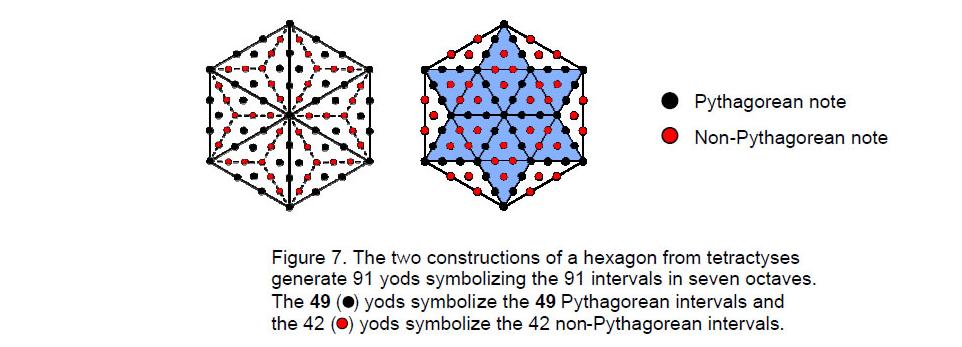
As the first of the last four polygons with 92 yods on their edges, the hexagon embodies the 91 intervals. This is because, when its six sectors are each divided into three tetractyses, it has 91 yods (Fig 7). This is true also for the alternative construction out of a Star of David. The 49 yods either delineating the edges of the tetractyses or at their centres symbolize the 49 Pythagorean notes. The

42 yods inside each sector symbolize the 42 non-Pythagorean intervals. This is a remarkable example of how the tetractys generates Tree of Life parameters like the number 91.

3. The Cosmic Tetractys pattern of the seven octaves
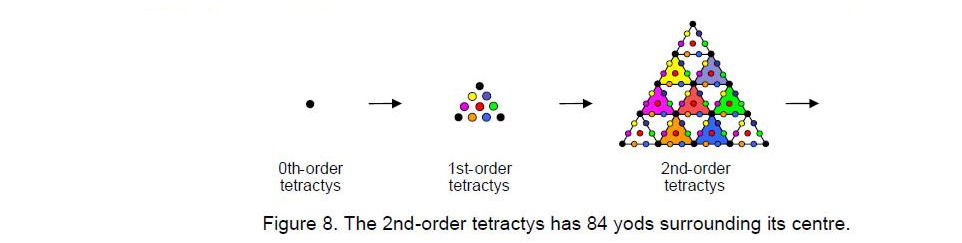
As many previous articles have demonstrated, Pythagoras’ tetractys reveals numbers of cosmic significance embodied in objects possessing sacred geometry when they are constructed from this building block. This remains true for its next higher-order differentiation — the 2nd-order tetractys (Fig. 8), formed by replacing each yod in the (1st-order)

tetractys by a tetractys of the same order. It has 85 yods, where

85 = 4⁰ + 4¹ + 4² + 4³.

9

10

84 yods surround its centre, where

84 = 1² + 3² + 5² + 7².

They symbolize the 84 collective degrees of freedom or variables characterising a holistic system’s physical manifestation, which is symbolized by the yod at the centre of the central 1st-order tetractys. It represents the Malkuth aspect of the Tree of Life, whilst the six coloured yods at the corners of a hexagon symbolize the six Sephiroth of Construction above Malkuth.

In the context of the seven musical scales, the central yod denotes the seven Pythagorean intervals of the first octave and the 84 yods surrounding it denote the 42 Pythagorean notes above the first octave, the six non-Pythagorean notes in the first octave and the 36 non-Pythagorean notes above the first octave. The lattermost are symbolized by the 36 yods on the boundary of the 2nd-order tetractys.

Suppose that the central tetractys in the 2nd-order tetractys is replaced by another 2ndorder tetractys. Its seven coloured tetractyses have (7×7=49) hexagonal yods, whilst the six coloured tetractyses surrounding it that belong to the original 2nd-order tetractys have (6×7=42) hexagonal yods. The new kind of tetractys has (49+42=91) hexagonal yods. This is the Cosmic Tetractys (Fig. 9). It maps all the levels of consciousness of the physical and spiritual cosmos, as now explained. The seven Sephiroth of Construction are the objective ‘qualities’ of God that have been anthropomorphized into the gods and goddesses of ancient religions. They define seven modalities of being. The great Swiss psychologist Carl G. Jung explored the lowest four of these when he identified the four ‘psychic functions’ of sensing, feeling, thinking and intuiting as ways of apprehending the world. In Theosophical terms, the seven Sephiroth of Construction appear as the seven ‘principles’:

They also define as modalities of being the seven cosmic planes of consciousness:

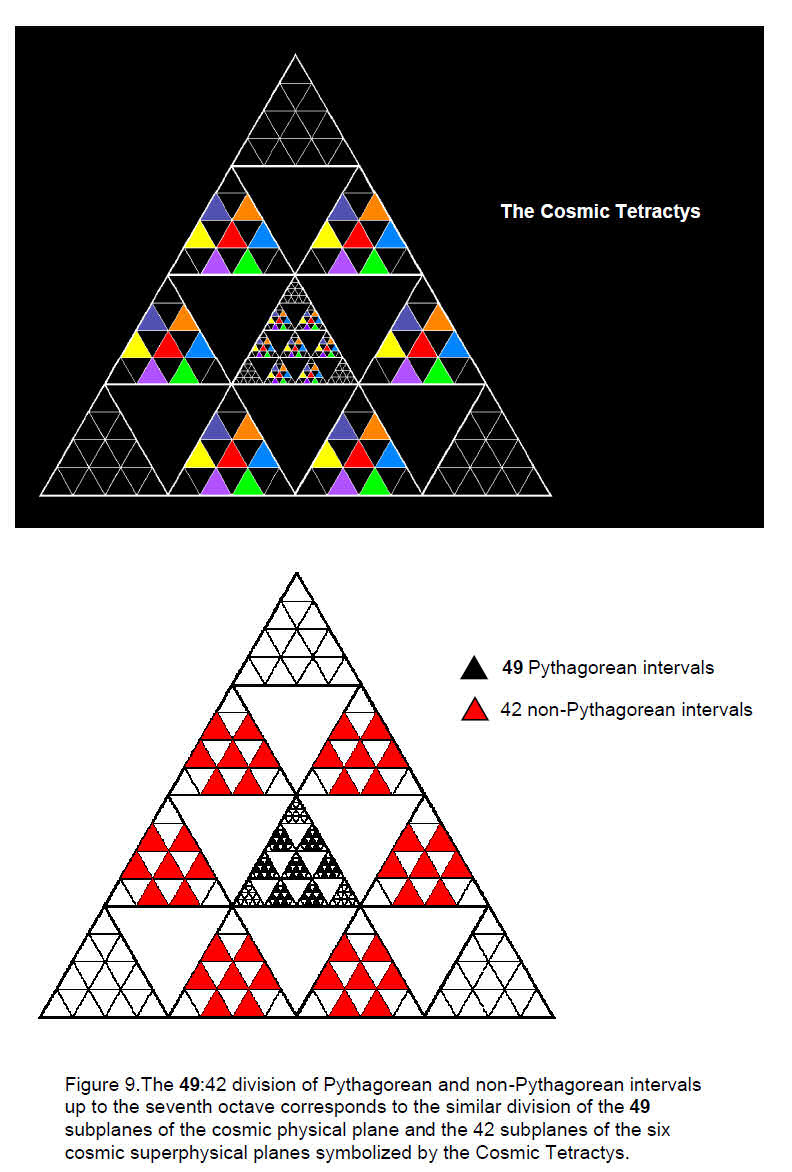
The six cosmic superphysical planes are each divided into seven subplanes, totalling 42 subplanes. The cosmic physical plane is divided into seven planes (they have the same names as above), each of which is further divided into seven subplanes, so that it consists of 49 subplanes. There are therefore (42+49=91) subplanes in the seven cosmic planes. This is the number of hexagonal yods in the Cosmic Tetractys. Each yod symbolizes a subplane, the 49 hexagonal yods in the central 2nd-order tetractys denoting the 49 subplanes of the cosmic physical plane and the 42 hexagonal yods surrounding it denoting the 42 subplanes of the six cosmic superphysical planes. Each hexagon containing seven yods denotes a plane of consciousness that is divided into seven subplanes.

11

For future discussion, it will be useful to factorise 91 as 7×13, where 13 = 7 + 6 (the reason for the red colour will be apparent shortly). Then 91 = 7(7+6) = 7×7 + 7×6 = 49 + 42. This factorisation reveals the fact that 91 is the sum of the first 13 integers:

91 = 1 + 2 + 3 + … + 13,

i.e., it is the thirteenth triangular number. As 28 is the seventh triangular number:

28 = 1 + 2 + 3 +… + 7,

the number 91 is the sum of 28 and 63. We found earlier that the 91 tone intervals up to the seventh octave comprise 28 notes with fractional, Pythagorean tone ratios and 63 others (21 overtones & (7×6=42) non-Pythagorean notes — the reason for writing in red). The number 7 defines through its triangular number the division of the 91 intervals into 28 intervals with fractional Pythagorean tone ratios and 63 intervals that are either non-Pythagorean or overtones. Notice that the tone ratio 24 also defines this 28:63 division, for we found earlier that 28 fractional, non-Pythagorean notes are below it.

Comparing the seven planes of consciousness with the seven octaves, the following correspondences appear:

	7 planes	7 octaves
1.	91 subplanes	91 intervals
2.	49 subplanes of the cosmic physical plane	49 Pythagorean intervals
3.	42 subplanes of the cosmic superphysical plane	42 non-Pythagorean intervals
4.	28 subplanes of the 4 lowest planes in the cosmic physical plane	28 Pythagorean intervals with fractional tone ratios
5.	21 subplanes of the 3 highest planes in the cosmic physical plane	21 overtones

Each subplane has a corresponding interval as its musical counterpart. The counterpart of the cosmic physical plane with 49 subplanes is the set of 49 Pythagorean intervals. 28 of them have fractional tone ratios. Their counterpart is the set of 28 subplanes comprising the four lowest planes of consciousness — physical, astral, mental and buddhic — that correspond in Kabbalah to the four lowest Sephirah of Construction — Malkuth, Yesod, Hod & Netzach. 21 of the 49 Pythagorean intervals are overtones. Their counterpart is the set of 21 subplanes of the three highest planes of

the cosmic physical plane — the Atmic, Anupadaka and Adi planes.

4. The Lambda Tetractys pattern of the seven octaves
In his Timaeus, his treatise on Pythagorean cosmology, Plato gave an account of how the Demiurge formed the celestial bodies. He blended the three ingredients of the World Soul — Sameness, Difference and Existence — into a kind of malleable

12

substance, took a strip of it, bent it at some point and marked out sections measured by the numbers forming the first four terms of the two geometric series 1, 2, 4, 8, 16,… and 1, 3, 9, 27, 81, … . This became known as Plato’s Lambda because of its resemblance to Λ, the Greek letter lambda (Fig. 10). The powers of 2 and 3 are, however, but two sides of a tetractys array of integers, the three extra integers shown in blue in Fig. 10 being created by the rule of multiplication of 2 and 3 along diagonal rows of numbers. This ‘Lambda Tetractys’ and its extrapolation by the Pythagorean mathematician Nichomachus of Gerasa (c. 60 C.E. – c. 120 C.E.), using more terms in the two geometric series, was known to generate the tone ratios of the Pythagorean musical scale as ratios of these numbers. It was thought, however, to have no significance beyond this musical context. Articles 11² & 12³ discussed deeper aspects of this pattern of numbers and their generalisation, whilst subsequent articles have shown that it plays a fundamental role in defining the properties of any holistic system that conforms to the divine archetype or universal paradigm, the seven musical scales being just one example.

The sum of the ten integers is 90, the sum of the integers at the corners of the tetractys is 36, the sum of the seven remaining integers at the centre and six corners of a hexagon the red, dotted boundary in Fig. 10) is 54, the sum of the six integers at these corners being 48. That the Lambda Tetractys has 90 as its sum immediately suggests a connection with the seven octaves of the seven musical scales, for they have 91 intervals up to 128, i.e., 90 intervals up to its predecessor, the seventh octave of note B with tone ratio 243/2, which is the 49th Pythagorean note. The following properties confirm this suggestion: the 90 intervals below the seventh octave with tone ratio 128 comprise 20 overtones, 28 fractional, Pythagorean notes (that is, (20+28=48) Pythagorean intervals) and 42 non-Pythagorean intervals, all with fractional tone ratios. The latter consist of the 6 non-Pythagorean intervals below the first octave and the 36 non-Pythagorean notes of higher octaves. Compare these numbers with the three main groupings of numbers belonging to the Lambda Tetractys:

where ‘6’ = 6 non-Pythagorean intervals in the first octave, ‘36’ = non-Pythagorean intervals of higher octaves and ‘48’ = Pythagorean intervals. We see that the numbers of Pythagorean and non-Pythagorean intervals below the seventh octave conform to the archetypal pattern of the Lambda Tetractys. As this defines holistic systems, it must be concluded that the 90 notes between the tonic of the first octave and the seventh octave constitute a holistic system.⁴

24 is the 60th interval and the 10th overtone. Below it are 50 fractional intervals made up of 22 Pythagorean intervals and 28 non-Pythagorean intervals. 50 is the sum of the triangular array of six integers in the Lambda Tetractys with 8 at one corner:

Six Pythagorean intervals symbolised by the central number 6 belong to the first octave. Hence, (22–6=16) fractional Pythagorean intervals belong to higher octaves. This is the

13

sum of the integers 12 and 4. The other integers 2, 8 and 18 in the triangular array add up to 28 and signify the number of non-Pythagorean integers. There are 10 overtones up to the tone ratio 24. This is the sum of the integers 1 denoting the tone ratio 24 itself) and 9. Above it are 30 intervals below the tone ratio 128. This is the sum of 3 and 27. Different sets of integers belonging to the Lambda Tetractys therefore add up to the numbers of Pythagorean and non-Pythagorean intervals below the seventh octave.

That the Lambda Tetractys describes so many aspects of the intervallic composition of seven octaves of the 14 basic notes cannot be coincidental. Instead, it shows that they constitute a holistic, or Tree of Life, system. Moreover, the Lambda Tetractys clearly flags the tenth overtone 24, just as we saw both the outer and inner Trees of Life did.

5. The seven octaves & the seven 3-tuples of octonions
The integers 1, 2, 4 & 8 forming one side of the Lambda Tetractys are the dimensions of the four only classes of numbers that have division algebras: real numbers, complex numbers, quaternions and octonions (also called ‘Cayley numbers’). An octonion has the form:

N = a₀e₀ + a₁e₁ + a₂e₂ + …. + a₇e₇,

where the a_i (i = 0-7) are real numbers, e₀ is the identity element 1 and the seven unit octonions e_i (i = 1-7) are imaginary numbers: e_i² = -1. Their multiplication is anticommutative:

e_ie_j = - e_je_i (i≠j)

non-associative:

e_i(e_je_k) ≠(e_ie_j)e_k

and follows the rule

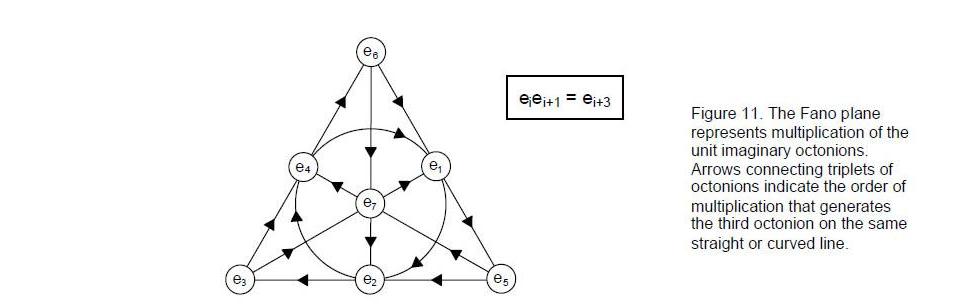
e_ie_i+1 = e_i+3.

Every unit imaginary octonion has an inverse, or conjugate, e_i* = -e_i, where e_ie_i* = 1.
Similarly, the conjugate of an octonion N is N*, where

N* = a₀ - a₁e₁ - a₂e₂ - … - a₇e₇.

The norm of an octonion is ││N││= √N*N, where

││N││² = a₀² + a₁² + a₂² + … + a₇².

The inverse of N is N^–1 ≡ N*/││N││², so that N^–1N = NN^–1 = 1. It was shown in Article 28 that there are 13 classes of real, linear combinations of two or more unit imaginary octonions. This means that there are 13 classes of their inverses. Their polyhedral counterparts are the 13 Archimedean solids and their duals — the 13 Catalan solids. Their musical counterparts are the 13 different intervals above the tonic found in the notes of the seven musical scales. This section will explore further the analogy between the scales and the multiplicative properties of the unit imaginary octonions.

Raising a note with tone ratio p by an interval m and then raising it by its complementary interval n (mn = 2) creates the note pmn = 2p, which is the same as the original note, only one octave higher. The second operation is in this sense the inverse of the first because it reverts the note to the same kind of note that it was originally, only an octave higher. Therefore, the complement of a note is the musical counterpart of the inverse of a unit imaginary octonion. Just as the seven imaginary octonions e_i have seven inverses e_i^-1= e_i* = -e_i, so the 14 different notes of the seven scales are divided into seven notes and their complements:

14

 

imaginary octonion	inverse	musical notes	complement
e1	e1–1	tonic (= 1)	octave T5L2 (= 2)
e2	e2–1	L	T5L
e3	e3–1	T	T4L2
e4	e4–1	TL	T4L
e5	e5–1	T2	T3L2
e6	e6–1	T2L	T3L
e7	e7–1	T2L2	T3

(As previously done for their tone ratios, Pythagorean notes are written in black and non-Pythagorean notes are written in red).

The Fano plane (Fig. 11) is a useful way of representing the non-associative and noncommutative multiplication of the seven unit imaginary octonions.

In mathematics, a projective plane consists of a set of “lines” and a set of “points” with the following properties:

Given any two distinct points, there is exactly one line incident with both of them.

Given any two distinct lines, there is exactly one point incident with both of them.

There are four points such that no line is incident with more than two of them.

The last condition simply excludes some degenerate cases.

A projective plane is an abstract mathematical concept, so the "lines" need not be anything resembling ordinary lines, nor need the "points" resemble ordinary points. It can be shown that a projective plane has the same number of lines as it has points. This number can be infinite (as for the real projective plane) or finite. A finite projective plane has (n²+n+1) points, where n is an integer called the order of the projective plane.

15

A projective plane of order n has (n+1) points on every line, and (n+1) lines passing through every point. For all known finite projective planes, the order is a prime power. The smallest possible projective plane has only seven points and their duals — seven lines. This is the Fano Plane. It has order 2 because 2² + 2 + 1 = 7.

Each line in the Fano plane joins three octonions that form a 3-tuple (e_i, e_i+1, e_i+3), where the index is defined modulo 7. The seven 3-tuples are:

(e₁, e₂, e₄)
(e₂, e₃, e₅)
(e₃, e₄, e₆)
(e₄, e₅, e₇)
(e₅, e₆, e₁)
(e₆, e₇, e₂)
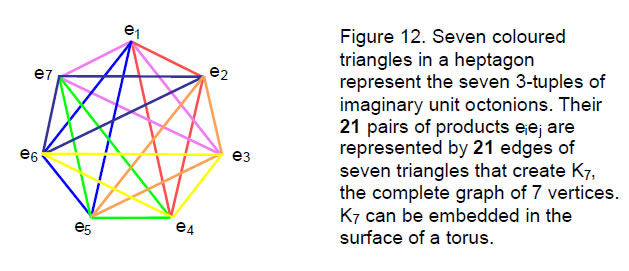
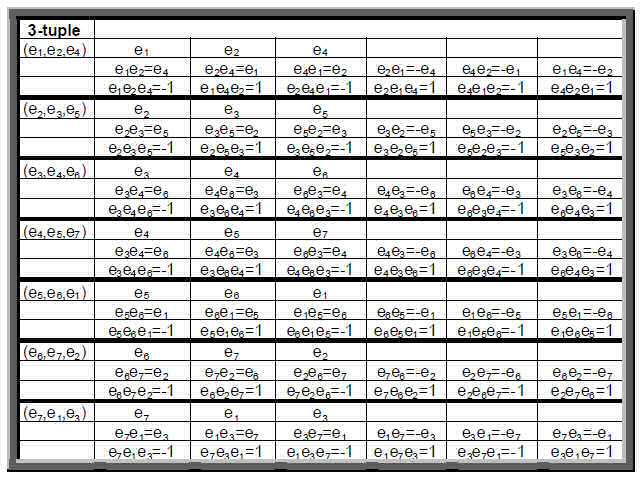
(e₇, e₁, e₃)

They can be represented by seven triangles whose vertices are the vertices of a heptagon (Fig. 12). Table 4 displays the multiplication of pairs of octonions. For each 3-tuple, there are seven combinations of one, two or three unit octonions:

e_i, e_i+1, e_i+3
e_ie_i+1, e_i+1e_i+3, e_i+3e_i (6 permutations)
e_ie_i+1e_i+3 (6 permutations)

Each 3-tuple has 12 permutations of two or three imaginary octonions. Similarly, as e_ie_i+1 = e_i+3 = -e_i+1e_i = -(-e_i+1)(-e_i) = -e_i+1^–1e_i^–1, then e_i+1^–1e_i^–1 = -e_i+3 = e_i+3^–1, that is, the inverses of the octonions in a 3-tuple also form a 3-tuple with 12 permutations of pairs or triplets. Their multiplication is represented by the Fano plane with each e_i replaced by e_i^–1 and with the directions of all arrows reversed to take account of the reverse ordering of. The seven octonions therefore have (7×12=84) permutations, as do their inverses. The seven 3-tuples and their inverses display (84+84=168) permutations of their members. The octonion algebra can be represented by the Fano plane because SL(3,2), the simple group of automorphisms (incidence-preserving bijections) of

the latter, is of dimension 168. The significant factorisation of 168 is 7×24, where 24 is the sum of the number of permutations of two or three octonions and the number of permutations of their inverses. We shall discuss in Section 8 how this factorisation manifests in one of the most beautiful and important objects in mathematics — the Klein Configuration.

In each of the seven 3-tuples, there are seven permutations of the seven octonions taken one at a time, 42 permutations of them taken two at a time and 42 permutations taken three at a time. They are shown in Table 5:

16

Table 5. Permutations of the unit imaginary octonions in each 3-tuple.

The permutations of single octonions create three sets of seven octonions, the permutations of two octonions create three sets and three sets of their negatives and the permutations of three octonions create three sets of seven ‘1’s and three sets of seven ‘-1’s. The 84 permutations of two or three octonions consist of  42 positive numbers (21 octonions, 21 ‘1’s) and 42

negative numbers (21 octonions, 21 ‘-1’s). Similarly for the 84 permutations of two or three inverse unit octonions. Hence, the seven 3-tuples and their inverses have 84 positive numbers and 84 negative numbers as permutations.

The real unit octonion corresponds to the tonic of a scale, the seven unit imaginary octonions correspond to the seven octaves and the 84 permutations of two or three octonions correspond to the 84 other intervals up to the seventh octave. Each 3-tuple corresponds to an octave of the set of 12 different notes between the tonic and octave of the seven musical scales.

Divided into tetractyses, a heptagon contains 42 yods surrounding its centre (Fig. 13). Each sector signifies a musical scale, the six yods per tetractys sector symbolizing the six notes above the tonic in each one. In the context of octonions, the central yod denotes ‘1’, the real unit octonion, each sector symbolizes a 3-tuple and the six yods symbolize the three octonions and their three pairings. With each sector divided into

17

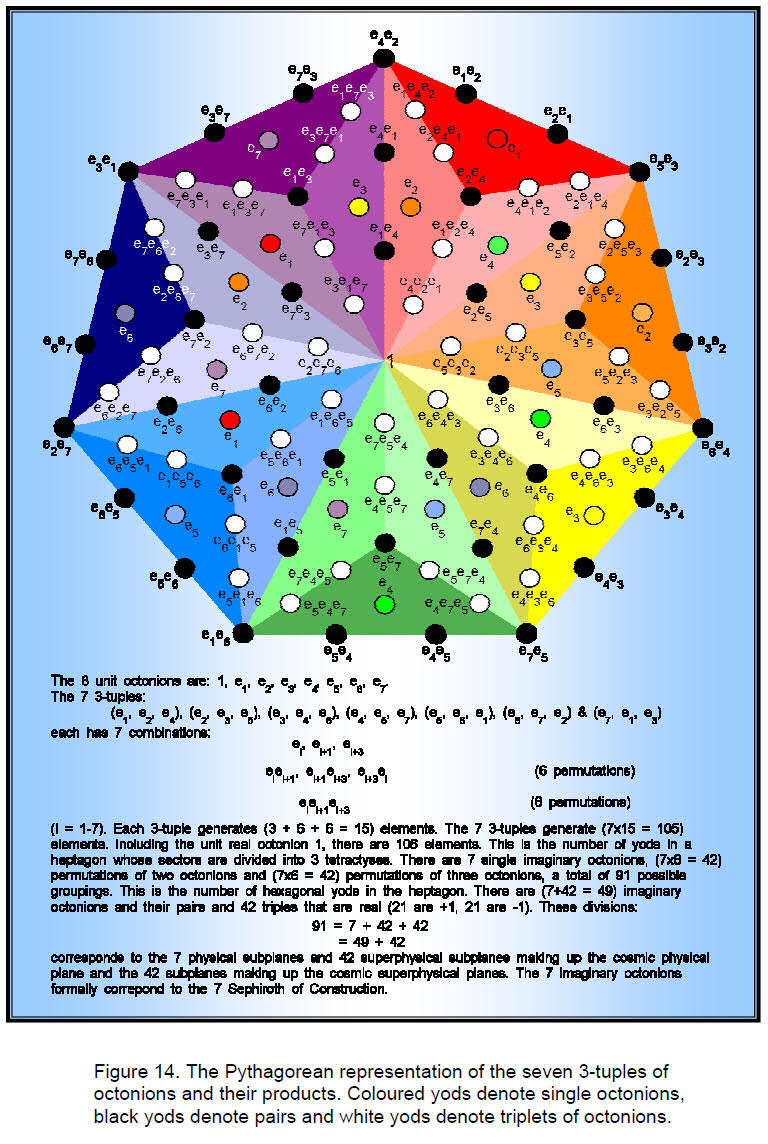
18

three tetractyses, the centre of a heptagon is surrounded by 105 yods,¹ or 15 yods per sector (Fig. 14). The three octonions in each 3-tuple form three combinations of one octonion (denoted by the coloured yods), three combinations of two octonions with six permutations (denoted by the black yods) and one combination of three octonion with six permutations (denoted by the white yods). In other words, the seven different combinations for each 3-tuple (e_i, e_i+1, e_i+3) generate 15 permutations if we regard each octonion in it (say, e_i) as 1×e_i = e_i×1. The seven 3-tuples therefore possess (7×15=105) permutations. Each yod symbolizes a permutation, the central yod denoting the real unit octonion. The three combinations of one octonion are symbolized by the yods at the centres of the three tetractyses in each sector. The six black yods on the edges of the sector and at its centre denote the six permutations of pairs of octonions and the six white yods on the edges of the tetractyses  inside the heptagon symbolize the six permutations of the three octonions in a 3-tuple.

Fourteen octonions are just copies of the basic set of seven octonions, so that there are 91 distinct permutations of the octonions in the seven 3-tuples. The 13 such permutations per sector correspond to the 13 tone intervals in each octave of the notes belonging to the seven musical scales. As they comprise six Pythagorean intervals, six non-Pythagorean intervals and the octave, we find the following correspondences:

Single octonion		octave note
Six permutations of two octonions		six Pythagorean intervals
Six permutations of three octonions		six non-Pythagorean intervals
3-tuple		one octave

Just as the fourth class of 8-dimensional numbers constitute a holistic system with 91 distinct permutations of their, so, too, the 91 intervals in seven octaves of the notes belonging to the seven musical scales make up a holistic system. The identity element 1 corresponds to the first note of the first octave.

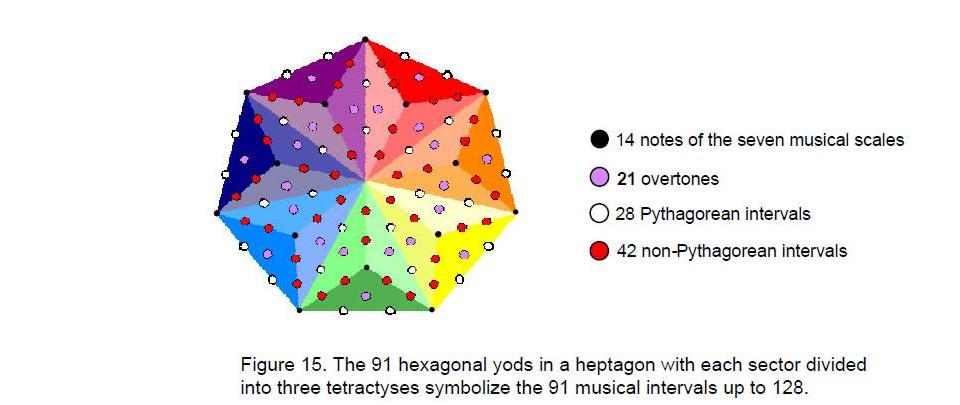
A heptagon whose sectors are each divided into three tetractyses has 91 hexagonal yods (Fig. 15). The 13 intervals per octave can be assigned to the 13 hexagonal yods per sector. Alternatively, the 14 notes in the seven scales can be assigned to its corners

________________________________

¹ An n-sided, regular polygon with its n sectors divided into three tetractyses has (15n+1) yods.

19

and to the centres of its sectors, with the 21 yods at centres of tetractyses symbolizing the 21 overtones up to 128, the 28 other yods on edges of sectors symbolizing the 28 Pythagorean intervals and the 42 yods on edges of tetractyses inside the heptagon denoting the 42 non-Pythagorean intervals. The intervals of the seven musical scales are reproduced in the Pythagorean geometry of the heptagon.

6. Comparison with the disdyakis triacontahedron
There are (10+22=32) Pythagorean intervals and 28 non-Pythagorean intervals up to the note with tone ratio 24. Compare this with the 60 vertices surrounding the A-A axis of the disdyakis triacontahedron, of which 32 are either B or C vertices and 28 are A vertices (Fig. 16). It is as if the 60 vertices surrounding its A-A axis symbolize the 60 intervals up to 24, the A vertices symbolizing the non-Pythagorean intervals and the B and C vertices symbolizing the Pythagorean intervals. The B vertices cannot symbolize just the overtones themselves because there are 10 overtones but 12 B vertices. Similarly, there are 22 fractional Pythagorean intervals but only 20 C vertices. The B-B axis would allow the 10 B vertices surrounding it to correspond to the 10 overtones, but there would be two few C vertices to correspond to the 22 Pythagorean intervals and two too many A vertices to correspond to the 28 non-Pythagorean intervals. The C-C axis surrounded by 18 C vertices, 12 B vertices and 30 A vertices does not permit any obvious correspondence. Hence, only the A-A axis generates a correlation between the surrounding types of vertices and the numbers of Pythagorean and non-Pythagorean intervals up to 24. It indicates that the rhombic triacontahedron with 32 vertices, which underlies the disdyakis triacontahedron, is what is significant here, not the fact that the former is a compound polyhedron formed by joining the vertices of the dodecahedron and icosahedron. It is further evidence of the special significance of the tenth overtone. Previous articles⁵

proved that the disdyakis triacontahedron is the polyhedral version of the inner (polygonal) Tree of Life. In particular, it was shown in Article 27 that it has 1680 vertices, edges and triangles surrounding an A-A axis when its interior triangles are each divided into three tetractyses and its triangular faces each turned into a single tetractys.⁶ This is the structural parameter of the E₈×E₈ heterotic superstring, being the number of circularly polarized oscillations in each of the ten closed curves making up this type of superstring (see Fig. 25). That fact that the 60 vertices surrounding the axis create 1680 geometrical elements and symbolize the 60 intervals up to the tenth overtone suggests that the former is connected to the number 24 in some way. It is also significant that the fourth type of polygon in the seven layers of vertices of the disdyakis triacontahedron — the polygon forming its equatorial plane — is a 12-sided polygon with 12 corners and 12 edges on its boundary, i.e., 24 geometrical elements. Once again, the arrangement of the vertices of the disdyakis triacontahedron reveals the presence of the number 24. Is the Pythagorean mathematics of music therefore intrinsic to the physics of the vibrations of superstrings?

Here is further evidence that it is: Article 16⁷ showed that the seven musical scales

20

have 84 rising intervals between their notes that repeat the basic set of seven intervals of the Pythagorean scale. They also have 84 falling intervals. The number of rising and falling Pythagorean intervals varies from scale to scale:

C scale	D scale	E scale	F scale	G scale	A scale	B scale
2×13=26	2×12=24	2×13=26	2×12=24	2×11=22	2×11=22	2×12=24
Total = 2×84 = 168.
Average = 168/7 = 24.

However, the average number of rising and falling Pythagorean intervals per scale is 24. Once more, we find the number 24 characterising the seven musical scales! In the context of the tetrahedral generalisation of the Lambda Tetractys discussed in Articles 11 and 12, the number that replaces the number 6 at its centre is 24. As discussed earlier, the products of two and three octonions in a 3-tuple have 12 permutations, their inverses having 12 permutations as well. Therefore, a 3-tuple of octonions and a 3-tuple of their inverses have 24 permutations of two and three octonions. Finally, given that the ancient Greeks regarded the eight notes in a scale as two groups of four notes, or tetrachords, it is remarkable that the number of broken chords of four notes that can be played with eight notes is ⁸P₄ = ⁸C₄×4! = 1680, the superstring structural parameter.

As well as being the number of yods surrounding the centre of a 2nd-order tetractys and the number of notes other than octaves in the seven octaves of notes in the seven musical scales, the number 84 is the number of permutations of 1, 2, 3 and 4 objects arranged in a tetractys:

They have 26 combinations, the last row having 15 combinations, which shows how the Godnames YAHWEH with number value 26 and YAH with number value 15 prescribe the Pythagorean representation of holistic systems. It illustrates how the number 84 characterises holistic systems like the seven musical scales and the seven 3-tuples of octonions. The 84 permutations comprise (1!+2!+3!+4!=33) permutations of all the objects in each row, i.e., 32 permutations of sets of two, three and four objects, 10 permutations of single objects and 42 permutations of two and three objects. The 84 permutations therefore naturally divide into (10+32=42) permutations of single objects and all objects in a row and 42 permutations of two and three objects. The counterparts of this 42:42 division of permutations in the seven octaves are the 42 Pythagorean notes other than octaves and the 42 non-Pythagorean notes below the seventh octave.

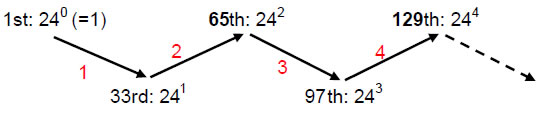
Counting from the tonic of the first octave, the tone ratio 24 (=1×2×3×4) is the 33rd Pythagorean note (33=1!+2!+3!+4!) and the perfect 5th of the fifth octave. Starting from this note, the 33rd note is 576 = 24²and still the perfect 5th of the new fifth octave. This is the 65th note from the tonic of the first octave, where 65 is the 33rd odd integer.

21

The Godname ADONAI with number value 65 prescribes sequences of 33 Pythagorean notes whose last note has a tone ratio always 24 times that of the first one. Only the first sequence (1) has ten overtones. The second sequence (2) has 24 overtones in addition to the first overtone with tone ratio of 24. In general, the nth sequence terminates in the note with tone ratio 24ⁿ. Notice that the Godname of Netzach, the fourth Sephirah of Construction, with number value 129, determines the end of the fourth sequence with tone ratio 24⁴, that is, 4! raised to the fourth power. This illustrates the Tetrad Principle⁸ at work. Indeed, as 24 = 5² – 1 = 3 + 5 + 7 + 9, 24 is the sum of the first four odd integers after 1. Furthermore, starting from a point, 24 more yods are needed to construct a square, symbol of the number 4, from tetractyses (Fig. 17). The central yod denotes the octave, the 12 yods inside the square denote the 12 intervals below the octave and the 12 yods on its boundary denote the 12 intervals between the 13 notes of the octave above the tonic. The square represents all the notes in the seven musical scales and the intervals between them.

Given that the note with tone ratio 24 is the 61st note, it is a remarkable illustration of the power of the Tetrad Principle to define numbers of scientific significance (as the number 24 will prove to be) that there are 61 yods in a square whose sectors are divided into three tetractyses (Fig. 18). The central, white yod symbolizes the tonic, the 32 black yods on the sides and diagonals and at centres of tetractyses denote the 32 Pythagorean intervals up to tone ratio 24 and the 28 red yods on the internal edges of tetractyses denote the 28 fractional, non-Pythagorean intervals up to this note.

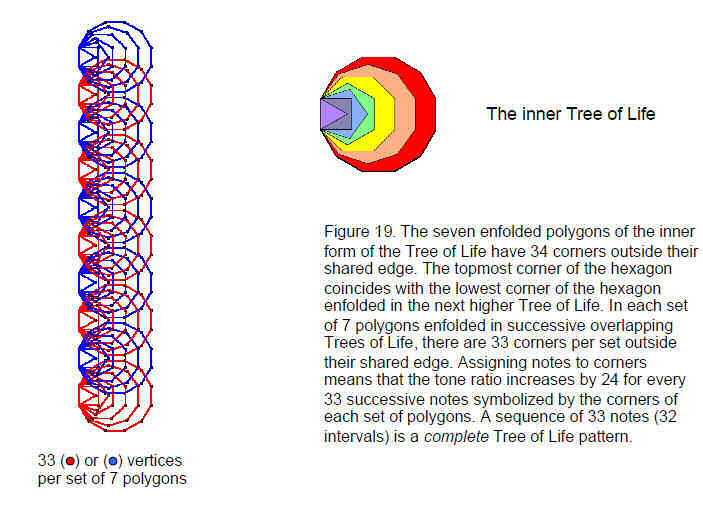
That the number 33 truly measures holistic cycles is demonstrated par excellence in the inner form of the Tree of Life. Its seven enfolded polygons (Fig. 19) have 36 corners i.e., 34 corners outside their shared edge. In any set of overlapping Trees of Life, a set

22

of these polygons are enfolded in each tree. The corners of polygons enfolded in successive Trees of Life touch at only one point, namely, the topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher tree. There are n sets of seven polygons enfolded in n trees with (33n+1) corners outside their root edges. There are therefore 33 corners per tree outside their shared edge. The 70 polygons enfolded in the lowest ten Trees of Life have 351 corners. This is the number value of Ashim, the Order of Angels assigned to Malkuth (see Table 1).

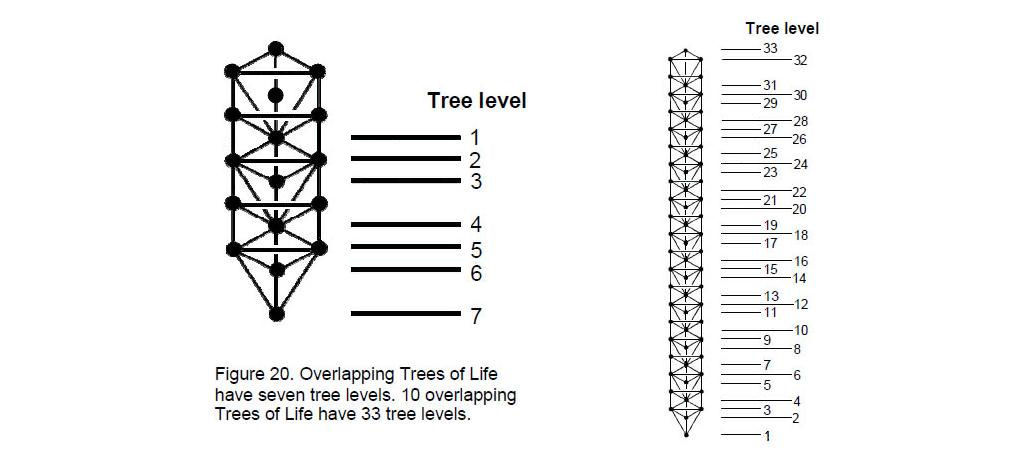
When Trees of Life overlap, all Sephirah except Chesed and Geburah are shared by adjacent trees. Defining a ‘tree level’ as a horizontal striation of one or two such Sephiroth, the lowest Tree of Life has seven tree levels and ten overlapping trees have 33 tree levels (Fig. 20). As ten overlapping Trees of Life are the Tree of Life representation of the ten Sephiroth, it demonstrates that the number 33 is a parameter of a holistic system.

The number of yods in the lowest n overlapping Trees of Life when all their triangles are turned into tetractyses can be shown⁹ to be:

Y(n) = 50n + 30.

As Y(n+1) – Y(n) = 50, the Godname ELOHIM with number value 50 determines the increase in number of yods with successive trees. The number of yods in the lowest 33 trees is Y(33) = 1680. This connects the superstring structural parameter 1680 to the number 33. The 91 subplanes in the seven cosmic planes can each be represented by a Tree of Life. Assigning each successive Pythagorean note in the seven octaves to a tree, the lowest 49 trees mapping the cosmic physical plane are correlated with the 49 Pythagorean notes above the tonic, whilst the next 42 trees correlate with the 42 non-Pythagorean notes. As the 33rd note, the tenth overtone 24 is assigned to the 33rd tree. This indicates a connection between at least the number 24 and the superstring structural parameter 1680, if not this number as a musical tone ratio as well. The number of yods in the lowest 49 trees is Y(49) = 2480, i.e., the number of yods in 248

23

tetractyses. 248 is the dimension of the superstring symmetry group E₈ and 2480 is the number of space-time components of the 248 10-dimensional gauge fields of E₈. Therefore, the tenth overtone determines the number defining the structure of the superstring and the number of Pythagorean notes in the seven octaves determines the nature of the unified superstring force — a very remarkable conclusion.

As 1680 = 70×24 and as the Tree of Life contains 70 yods when its triangles are turned into tetractyses (see Fig. 4), it can be regarded as embodying the number 1680 when the number 24 is assigned to each yod. It further demonstrates the significance of this number for the physics of superstrings.

24

7. The dodecagon defines all intervals in the seven octaves
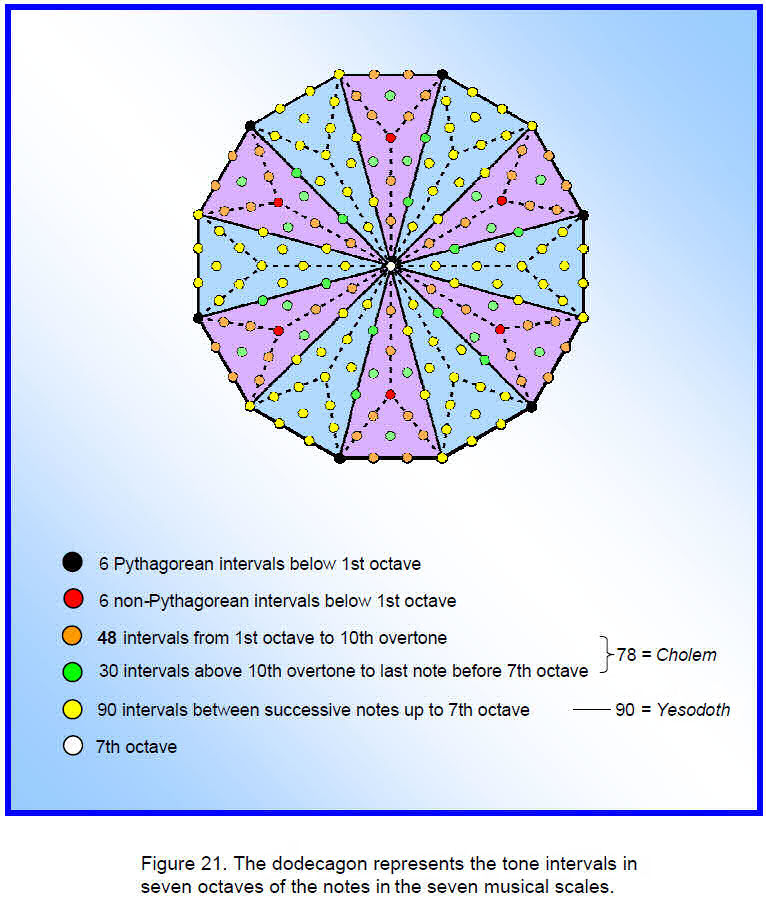
The tetractys-divided hexagon with 91 yods was shown in Section 2 to embody the 91 intervals in seven octaves of the set of 14 different notes that make up the seven musical scales. There are 90 intervals between the 91 notes above the tonic of the first octave. (91+90=181) intervals can therefore be defined either between this note and all the other notes or between successive notes. This fact is symbolized by the 181 yods in the dodecagon — the last of the regular polygons forming the inner Tree of Life — when its sectors are divided into three tetractyses (Fig. 21). The six

Pythagorean notes between the tonic and the first octave can be assigned to alternating corners of the dodecagon, with the red yod at the centre of six sectors denoting the six non- Pythagorean intervals. The 48 intervals above the first octave up to the tenth overtone with tone ratio 24 are denoted by orange yods arranged in pairs on edges of tetractyses inside the dodecagon. The 30 intervals above the tenth overtone up to the penultimate note of the seventh octave are denoted by the 30 green yods lying on radial edges or at centres of tetractyses. The 90 intervals between successive notes are symbolized by the 90 yellow yods in alternating sectors. Finally, the yod at the centre of the dodecagon denotes the seventh octave. There are (48+30=78) intervals from the

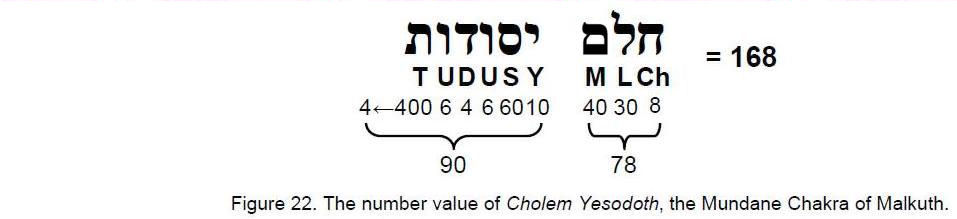
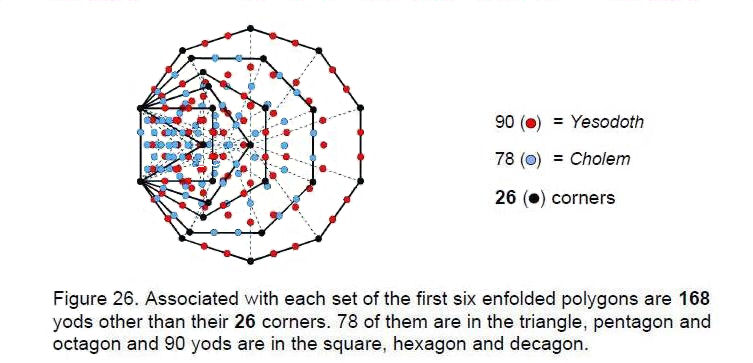
first octave to the seventh octave and 90 intervals between successive notes in the seven octaves, starting from the second note. There are therefore 168 intervals other than the basic set of 12 intervals below the first octave and the seventh octave. Quite apart from it being the number of permutations of two and three octonions belonging to the seven 3-tuples and of their inverses, this reproduces the number values of the two Hebrew words ‘Cholem’ and ‘Yesodoth’ in the name of the Mundane Chakra of Malkuth, which has the number value 168 (Fig. 22). This is a very remarkable illustration of how the gematria number values of the Godnames, Archangelic Names, etc listed in Table 1 quantify aspects of a holistic system like the seven octaves of the notes belonging to the seven musical scales.

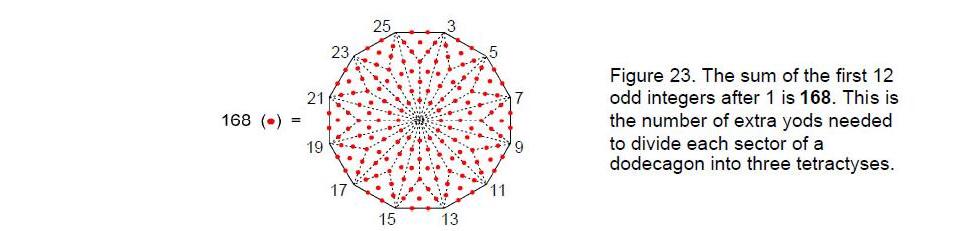
As 13² – 1 = 168 = 3 + 5 + 7 + … + 25, the number 168 is the sum of the 12 odd integers after 1 that can be assigned to the 12 corners of a dodecagon (Fig. 23). The dodecagon therefore embodies this number both arithmetically and geometrically. The pair

25

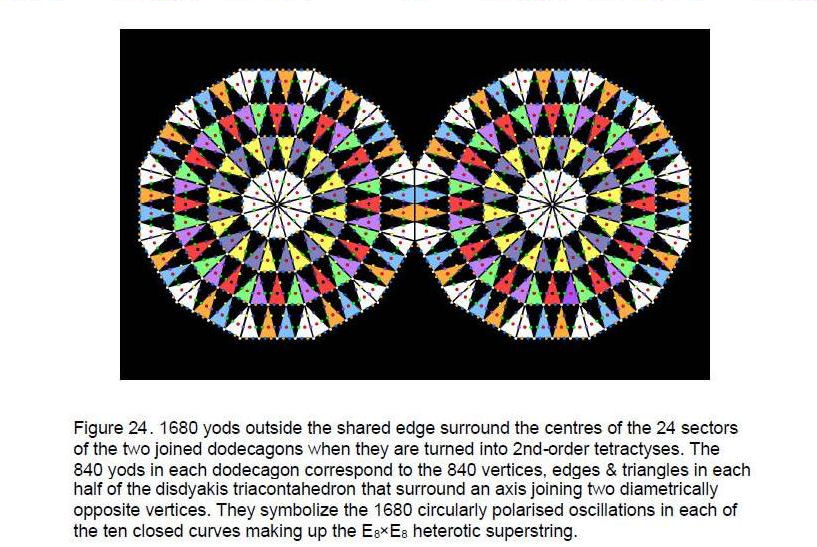
of joined dodecagons embodies the superstring structural parameter 1680 in a way that directly connects this fundamental number to the number 24. A 2nd-order tetractys has 85 yods (see Fig. 8). As there are 13 yods along each side, there are 72 yods per sector. Hence, a dodecagon has, including its centre, (12×72 + 1 = 865) yods. (865–13=852) yods are outside the edge one dodecagon shares with the other. (852–12=840) yods outside this edge surround the centres of the 12 2nd-order tetractyses. The pair of dodecagons has(840+840=1680) such yods surrounding these 24

centres (Fig. 24). The 840 yods in each dodecagon correspond to the 840 vertices, edges and triangles needed to construct each half of the disdyakis triacontahedron from triangles.

26

 

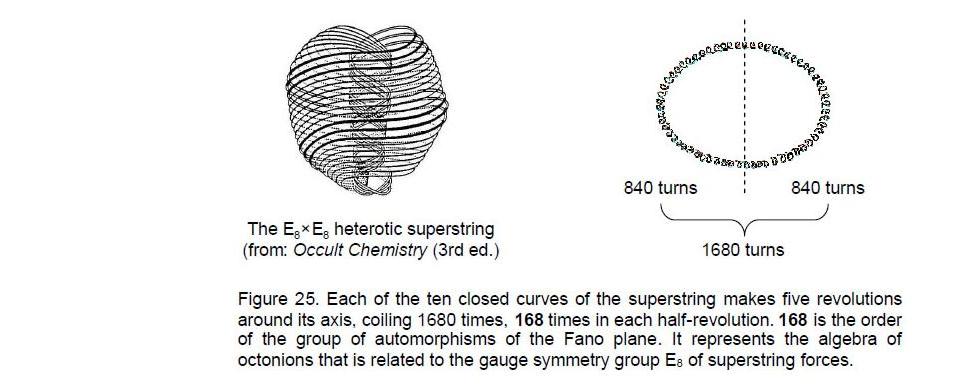
This is a remarkable example of the power of the sacred geometry of the Tree of Life to represent numbers of scientific significance. Several previous articles has proposed that along each of the ten curves comprising the E₈×E₈ heterotic superstring are spread 24 gauge charges of E₈ associated with its non-zero roots, so that all ten curves carry the gauge charges associated with its 240 non-zero roots. Each 2nd-order tetractys in the two dodecagons would then represent an E₈ gauge charge. The heterotic superstring has waves that travel clockwise in 10-dimensional space-time mixed with waves that travel anticlockwise in 26-dimensional space-time. A string in the latter space-time can oscillate in 24 transverse directions. The 24 vibrational degrees of freedom of the closed curves making up the superstring manifest in the Tree of Life blueprint as the 24 sectors of the two dodecagons. The heterotic superstring described by Annie Besant and C.W. Leadbeater¹⁰ with the use of a yogic siddhi called ‘anima’ consists of a set of ten closed curves (Fig. 25). Each revolves 2½ times in an outer spiral, making 840 circularly polarised oscillations as it twists down to its lowest point. It

then revolves 2½ times in a narrower helix towards the starting point at the top, making 840 more oscillations. This separation of its form into an outer half and an inner half corresponds in the polygonal form of the Tree of Life to the pair of similar dodecagons, each containing outside their shared edge 840 yods that surround the centres of their sectors. In its polyhedral form, it corresponds to the 840 vertices, edges and triangles in each half of the disdyakis triacontahedron, half of it being the mirror image of the other half.

As further evidence that the seven octaves constitute a Tree of Life pattern, Fig. 26 shows the 194 yods associated with a set of the first six enfolded polygons. These form a Tree of Life pattern prescribed by Godnames. For example, the Godname YAHWEH with number value 26 prescribes their 26 corners, whilst the Godname ELOHIM with number value 50 prescribes the 50 corners of both sets of polygons (for details of how the other Godnames prescribes them, see Article 4¹¹). When their sectors are turned into tetractyses, 168 yods need to be added to the 24 yods at their corners. Of these, 78 yods are in the triangle, pentagon and octagon, and 90 yods are in the square, hexagon and decagon. Once again, we see that the number 24 is associated with the number 168. It is as if, as more basic degrees of freedom, the former generates the latter as new variables. In the context of superstrings, there are 240 roots of the gauge

27

symmetry group E₈ and eight simple roots. Arranging this number as a tetractys array of the number 24,

There are 72 non-zero roots of its exceptional subgroup E₆ and 168 roots of E₈ that do not belong to E₆. This is the group origin of the number 168. Its factorisation 7×24 is a manifestation of fundamental symmetries whose nature has yet to be determined and which generate the gauge group E₈ describing the unified superstring interaction.

The very same three numbers 24, 78 & 90 define the geometry of the disdyakis triacontahedron. Surrounding its axis are 1680 corners, edges and triangles, created when its 180 internal triangles are formed by joining its vertices to its centre and are then divided into three tetractyses. This is easily seen from the table below:

		Corners		Edges		Triangles
surface:		62		180		120
interior:		180	62 + 3×180 =	602	3×180 =	540
	Total =	242		782		660
minus:		–2 (two poles)		–2 (two internal edges)
	Grand total =	240	+	780	+	660 = 1680.

There are 780 (=78×10) edges and 900 (=90×10) corners and faces, totalling 1680 (=168×10) geometrical elements. Built from triangles, the geometrical composition of the disdyakis triacontahedron manifests the number value 168 of Cholem Yesodoth, the first word expressing the number of edges surrounding its axis and the second word the number of corners and triangles that surround it.

Let us now compare the geometrical composition of the disdyakis triacontahedron with the interval composition of seven octaves. The 780 edges correspond to the 78 intervals from the first octave to the last note before the seventh octave and the 900 vertices and triangles correspond to the 90 intervals between successive notes from the second octave up to the seventh octave. We pointed out in Section 6 that the 60 vertices surrounding the axis symbolise the 60 intervals up the tenth overtone. As there are 30 intervals beyond it to the last note before the seventh octave and 90 intervals between successive notes, (30+90=120) intervals correspond to the 120 faces of the disdyakis triacontahedron. Its 180 edges can alone be thought to symbolize the 90 intervals between the tonic and the last note before the seventh octave and the 90 intervals between successive notes, starting with the first note after the tonic. The 90:90 division reflects the inversion symmetry of the disdyakis triacontahedron, every edge having its mirror image. The 12 edges between the 12 vertices in its equatorial plane correspond to the 12 intervals below the first octave and the remaining 168 edges correspond to the 168 notes and intervals between notes from the first octave up to the seventh octave. Music is number experienced in time. The geometry of the disdyakis triacontahedron manifests in space the holistic pattern of seven octaves of

 

 

28 

the seven musical scales. It expresses all possible intervals between these scales.

8. The 24 heptagons of the Klein Configuration
In 1878, the great mathematician Felix Klein, known as one of the nineteenth century’s finest geometers and to students of mathematics as the discoverer of the one-sided, closed surface called the “Klein bottle," discovered that the quartic equation:

x³y + y³z + z³x = 0

has the 336-fold symmetry of the group SL(2,7). This curve is known to mathematicians as the “Klein quartic.” Its Riemann surface is mapped onto itself by 168 analytic transformations (automorphisms). Curves of genus g that display the maximum number of automorphisms 84(g–1) and the same number of anti-automorphisms are known as Hurwitz curves.¹² As 168 = 84×2, the   

Klein quartic is a Hurwitz curve mapped onto a surface of genus 3, i.e., the 3-torus (Fig. 27). If triangles are joined together so that three of them meet at a corner, a tetrahedron is formed. If squares are joined so that three meet at a corner, a cube results. Pentagons can be joined to form a dodecahedron. However, hexagons cannot be joined to form a Platonic solid. Instead, they form a tiled

29

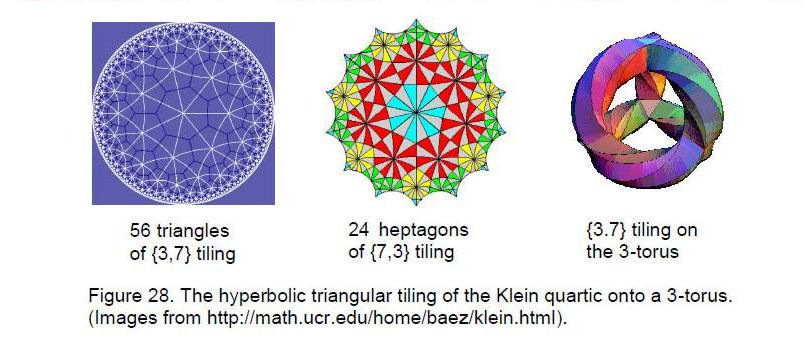
plane looking like honeycombs. If heptagons are joined so that three meet at a corner, the tiling can be done only on a hyperbolic surface with negative curvature because the sum of the angles of the three corners of a heptagon is now greater than 360 degrees. Tessellations are represented by the Schläfli symbol {p,q}, which means that q regular polygons with p vertices surround each vertex. Fig. 28 displays the {3,7} tessellation with 56 triangles. Its so-called ‘Poincaré dual’ is the {7,3} with 24 heptagons. The rings of heptagons around the central one in Fig. 26 appear smaller but that is just the distortion created by their being drawn on the hyperbolic surface. The tessellation of the Riemann surface of the Klein quartic can be done only on the 3-torus. However, not any number of heptagons can be cut out and wrapped around the 3-torus. Only 24 heptagons can be. They are shown in Fig. 28 with their hyperbolic triangular sectors in different colours. The seven sectors are made up of two different slices, each with 12 triangles. There are 84 triangles in seven slices made up of 28 red, 28 yellow and 28 green triangles. The seven slices of the other type have 84 triangles made up of 21 yellow, 21 green, 21 red and 21 cyan triangles. The 168 symmetries of the Klein quartic arise from the sevenfold symmetry of the Klein Configuration, the 12 rotational symmetries of the tetrahedron into which it can be deformed and the 12 reflection symmetries of the latter. Here is an explicit meaning of the number 24: the order of the tetrahedral (and cubic) symmetry group.

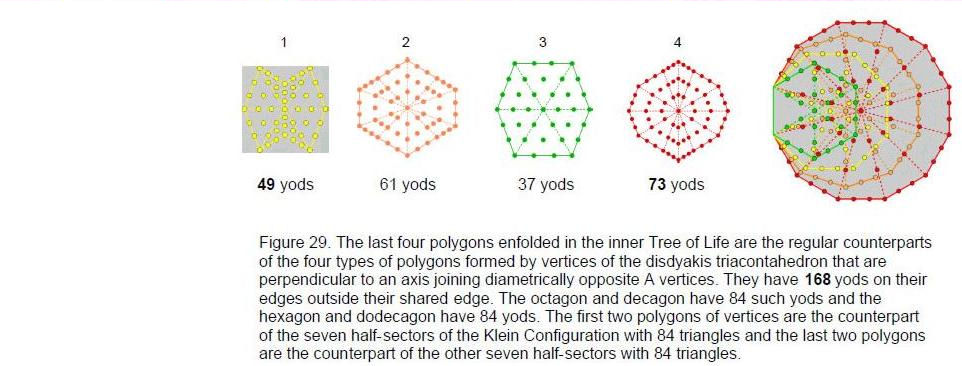
The 168 automorphisms of the Klein quartic represented by the 168 triangles of the Klein Configuration manifest in the disdyakis triacontahedron as follows: Article 34 proved¹³ that the regular counterparts in the inner Tree of Life of the 8-sided, 10-sided, 6-sided and 12-sided polygons formed by the 36 vertices in one half of this polyhedron have 168 yods on their edges outside their shared edge (Fig. 29). The octagon and decagon have 84 such yods, as do the hexagon and dodecagon. This reveals the character of the number 168 as the parameter defining the shape of a

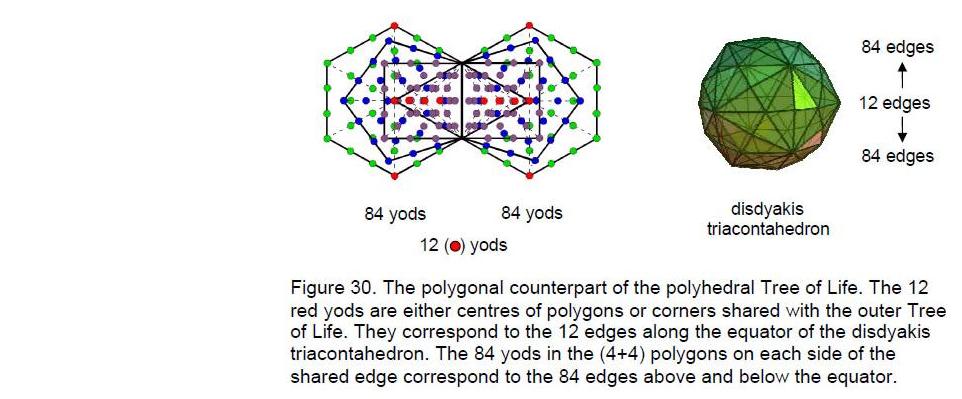
Tree of Life pattern for these yods delineate the shapes of the four polygons. The polyhedron has 180 edges, of which 12 edges of the fourth polygon shape its equatorial plane, leaving 168 edges, of which 84 edges are above the plane and 84 edges below it. The counterpart of this geometry in the polygonal form of the inner Tree of Life is the fact that, the first four polygons in each half of it have 84 yods outside the shared edge other than centres of polygons or yods that are shared with the outer Tree of Life (Fig. 30).

30

 

31

Musically speaking, the 12 centres or shared yods of the first (4+4) polygons and the 12 edges of the disdyakis triacontahedron symbolise the 12 different notes in the seven musical scales between the tonic and the octave, whilst the (84+84) yods or edges denote the 84 rising intervals and the 84 falling intervals between their notes.¹⁴

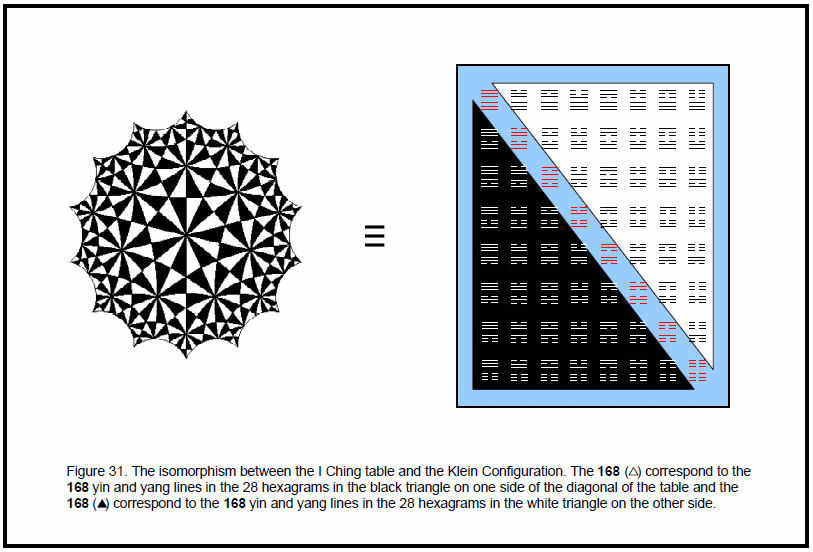
The number 24 plays a fundamental role in the I Ching table (Fig. 31) as the number of lines and broken lines in the eight basic trigrams. There are 28 hexagrams above the diagonal row of eight hexagrams shown in red. They comprise 56 trigrams with (56×3=168) lines and broken lines. They correspond to the 56 hyperbolic triangles, each with three vertices, of the {3,7} tiling of the Riemann

surface of the Klein quartic onto a 3-torus. The 56 off-diagonal trigrams with 168 lines and broken lines below the diagonal of the table correspond to the 168 anti-automorphisms of the Klein quartic.

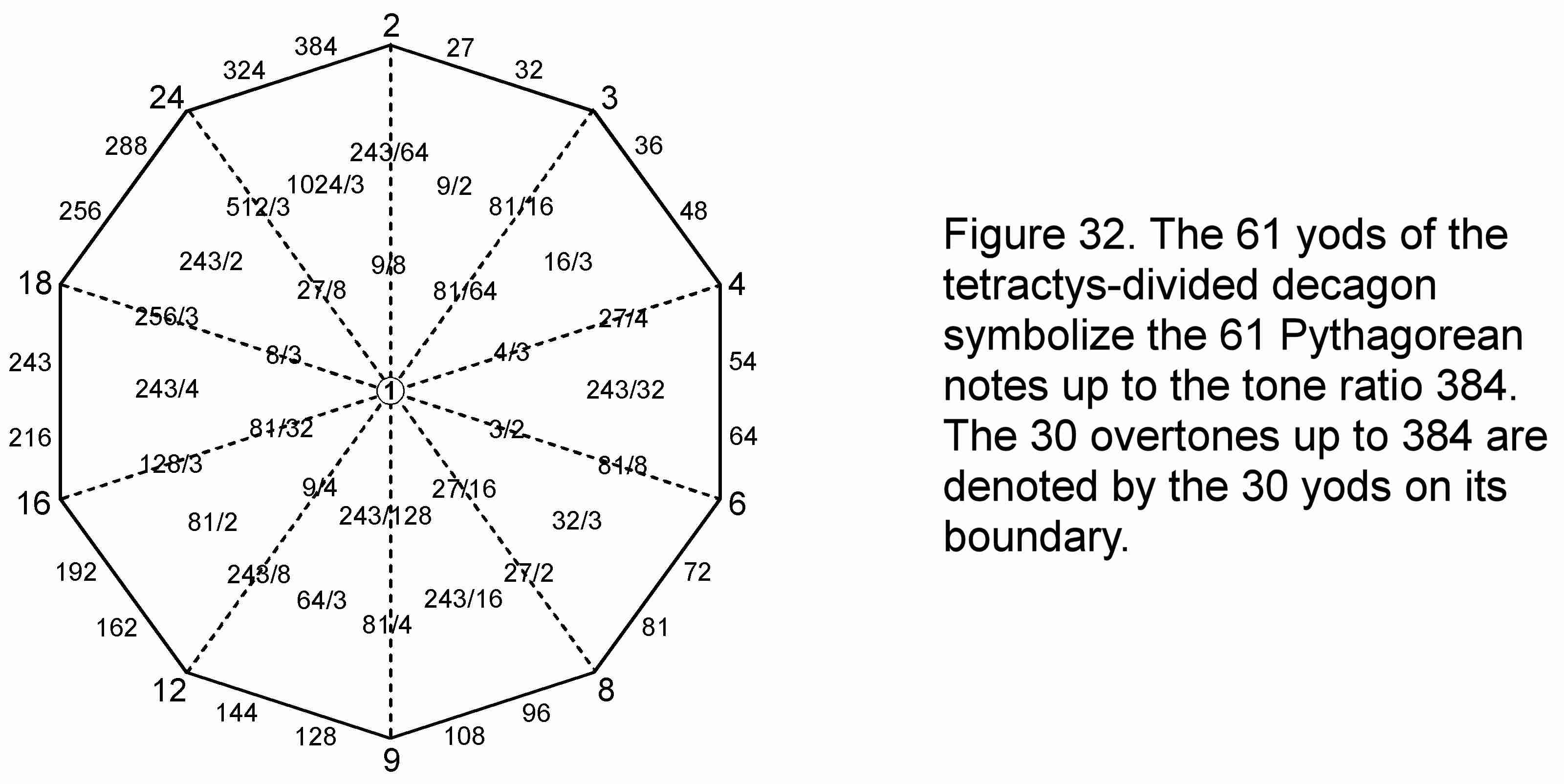
Just as the tone ratio 24 is the 61st note in the ascending sequence of notes in the seven musical scales, so the tone ratio 384 is the 61st Pythagorean note (Fig. 32). What is remarkable is that 384 is the number of lines and broken lines in the 64 hexagrams of the I Ching table, which are all possible pairings of the eight trigrams with 24 lines and broken lines! This is not coincidental. Nor is it coincidental that there are 128 trigrams, where 128 is the seventh octave completing a holistic system of the notes of the seven musical scales.

In I Ching, the lines are so-called ‘stable Yang

 32

lines’ and the broken lines are ‘stable Yin lines.’ If we suppose that Yang lines represent different phases of an oscillation with a positive amplitude and that Yin broken lines represent phases that differ by180 degrees from the former, then the 168 lines and 168 broken lines belonging to off-diagonal hexagrams of the I Ching table represent a system of 24 oscillators, each with seven different positive phases and seven different negative phases. The lines and broken lines of the diagonal hexagrams represent oscillators in a state of zero amplitude with all their phases cancelled out. Each trigram appears seven times in the set of 56 trigrams above or below the diagonal, that is 14 times altogether. As shown in Article,¹⁵ the I Ching table is isomorphic to the Klein Configuration, the 168 lines corresponding to the 168 automorphisms of the Klein quartic and the 168 broken lines corresponding to its 168 anti-automorphisms. The 56 trigrams correspond to the 56 triangles in the {3,7} tiling. The 24 lines and broken lines in the eight trigrams correspond to the 24 triangles in each of the seven sectors in the {7,3} tiling of the Klein Configuration, their 14 (2×7)-fold repetition corresponding to its 14 half-sectors. The pairing of trigrams in a hexagram corresponds to the two halves of each sector.

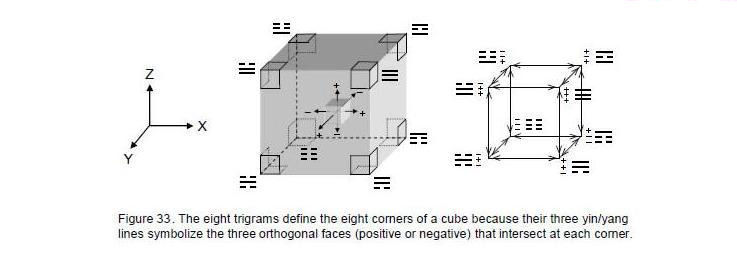
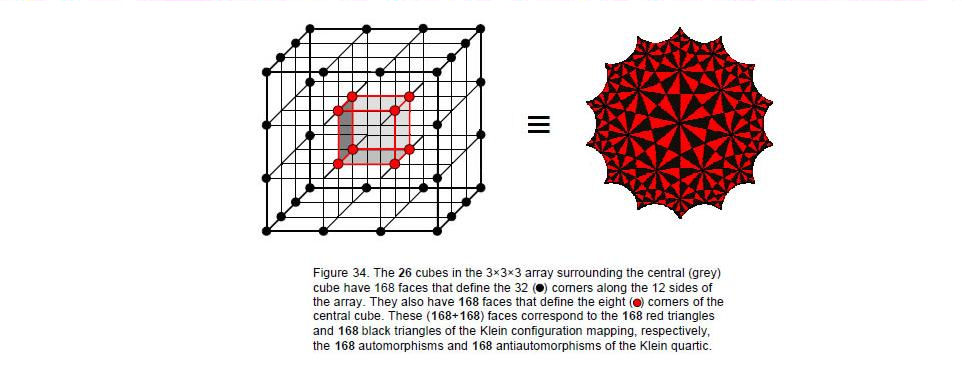
It was shown in Article 21¹⁶ that the I Ching table is also isomorphic to a 3×3×3 array of cubes. The proof is summarized here: a face of a cube can point along the positive or negative directions of the X, Y & Z axes. By replacing the yang line by a positive sign and the Yin broken line by a negative sign, the eight trigrams:

become ordered sets of three signs, each symbolizing three orthogonal faces that intersect at the eight corners of a cube (Fig. 33). A hexagram is a permutation of two trigrams and can be represented by an arrow joining the two corners of the cube defined by its trigrams. As pairs of similar trigrams, the hexagrams along the diagonal of the I Ching table denote the eight corners. A point in 3-dimensional space such as the corner of a cube is also the corner of seven other contiguous cubes, three in the same plane as this cube and four above it. This means that the corner is defined seven times, so to speak, by the three orthogonal faces of seven other cubes surrounding it. The eight corners of a cube are therefore defined by (8×7×3=168) faces, 84 of them directed

33

34

in positive directions of the axes and 84 in negative directions. The 24 faces of the cube that define its eight corners are symbolised by the 24 Yang/Yin lines of the eight upper trigrams in the diagonal hexagrams and the 168 Yang/Yin lines of the 28 hexagrams above the diagonal symbolize the 168 faces of the seven adjacent cubes. By then considering a 3×3×3 array of cubes so that each corner of the central cube is surrounded by seven contiguous cubes, it is simple to show¹⁷ that there are 168 faces defining the 32 corners of the 26 cubes that lie along the outer edges of the 3×3 array (Fig. 34). The other 288 faces define the four corners within each face, which do not form the boundaries of the array. There are (168+168=336) faces defining those corners that shape both the central cube and the cubes surrounding it. The 168 faces defining the former correspond to the 168 automorphisms of the Klein Configuration, whilst the 168 faces defining the latter correspond to its 168 antiautomorphisms. The 168 Yang/Yin lines above the diagonal of the I Ching table correspond to the 168 faces defining the eight corners of the central cube and the 168 lines below the diagonal correspond to the 168 faces defining the 32 corners lying along the edges of the array.

In the factorisation 168 = 7×8×3, the number ‘7’ denotes in the I Ching table the number of copies of each trigram in the off-diagonal hexagrams, in the Klein Configuration the number of sectors and in the 3×3×3 array the seven other cubes meeting at the corner of a cube. The number ‘8’ denotes in the table the number of different trigrams, in the Klein configuration the number of triangles in each sector (see Fig. 28) and in the 3×3×3 array the eight corners of the central cube. The number ‘3’ denotes in the table the number of lines in each off-diagonal trigram, in the Klein Configuration the number of half-sectors of each heptagon in each triangle and in the 3×3×3 array the number of orthogonal faces needed to define a point. The I Ching table, the Klein Configuration and the 3×3×3 array of cubes all display the factor 7 and the factor 24. These isomorphic objects show that the number 24 determines the number 168. For the table, it is the number of lines and broken lines in the eight trigrams. For the Klein Configuration, it is the 24 possible rotations that leave the tetrahedron unchanged, the 3-torus that it can cover being topologically equivalent to a tetrahedron with three holes bored through it. For the 3×3×3 array, the number 24 signifies the basic set of 24 faces defining the eight corners of the central cube, these being repeated for the seven cubes contiguous with any given corner. For the octonions represented by the Fano plane with the seven-fold symmetry of its seven points and seven lines, it is the 12 permutations of pairs and triplets of octonions in a 3-tuple and the 12 permutations of their inverses. For the seven musical scales, 24 is the number of repeated intervals belonging to the basic set of 14 notes averaged over the scales. For their seven octaves, it is the number of basic rising and falling tone intervals in each octave.

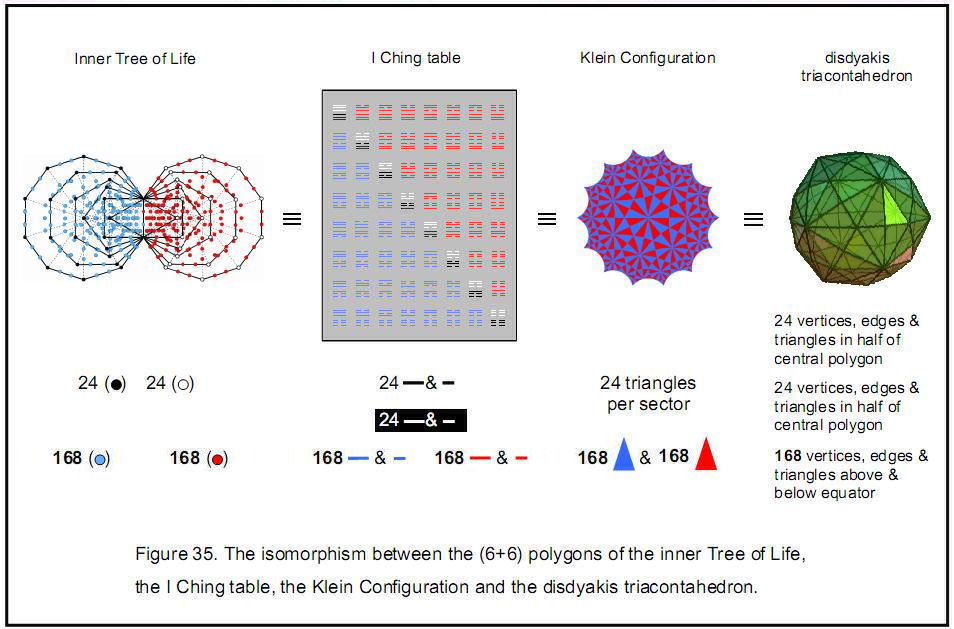
Figure 35 shows the equivalence between the inner Tree of Life, the I Ching table, the Klein Configuration and the disdyakis triacontahedron in representing the (168+168) formative degrees of freedom of a holistic system. They manifest in space-time as the 168 circularly polarised oscillations made by each of the ten closed curves of the E₈×E₈ heterotic superstring as it winds 180° about the axis in either an outer or an inner half of the superstring. Each holistic system exhibits 24 independent, higher order degrees of freedom that generate 168 structural elements. In the heterotic superstring, they reflect the 24 transverse modes of vibration of a string in 26-dimensional space-time.

References
¹ Phillips, Stephen M. Article 14: “Why the Greek Musical Modes are Sacred,” (WEB, PDF).

35

² Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).

³ Phillips, Stephen M. Article 12: “New Pythagorean Aspects of Music and Their Connection to Superstrings,” (WEB, PDF).

⁴ As the set of 14 notes constituting the seven scales is a holistic set, it, too, is defined by the Lambda Tetractys. There are (14×13/2 = 91) intervals between them, that is, 90 intervals other than the octave. This is the sum of the ten numbers of the Lambda Tetractys. There are six Pythagorean intervals below the first octave. This is denoted by the number 6 at the centre of the Lambda Tetractys. There are 84 intervals other than these notes. This is the sum of the nine integers surrounding the central integer. There are (6×6=36) intervals between the six Pythagorean notes and the six non-Pythagorean notes. This is the sum of the integers 1, 8 and 27 at the corners of the tetractys. There are (6×5/2=15) intervals between the six Pythagorean notes and 15 intervals between the six non-Pythagorean notes. There are six intervals between the octave and each set of six notes, making 12 intervals. The number of intervals other than Pythagorean notes and those between each set of six notes = 15 + 15 + 6 + 6 + 6 = 48. This the sum of the six integers in the Lambda Tetractys arranged at the corners of a hexagon.

⁵Phillips, Stephen M. Articles 22–24.

⁶ Phillips, Stephen M. Article 27: “How the Disdyakis Triacontahedron Embodies the Structural Parameter 1680 of the E₈×E₈ Heterotic Superstring,” (WEB, PDF), p. 6.

⁷ Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence with Octonion Algebra and Superstrings,” (WEB, PDF), p. 17.

⁸ Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 5.

⁹ Proof of Y(n) = 50n + 30: 6 Sephiroth are added per tree to the lowest 5 Sephiroth. The number of corners of the triangles in the lowest n Trees of Life ≡ S(n) = 6n + 5. 16 Paths are added in successive trees to the lowest 9 Paths joining the 5 lowest Sephiroth. The number of edges of triangles in the lowest n trees ≡ E(n) = 16n + 9. Each successive tree adds 12 triangles to the lowest 7 triangles. The number of triangles in the lowest n trees ≡ T(n) = 12n + 7. When each triangle is a tetractys, there are (6n+5) yods at corners, two yods between the ends of each edge, i.e., 2E(n) yods, and one yod at the centre of each triangle, i.e., T(n) yods. The number of yods in the n lowest trees = S(n) + 2E(n) + T(n) = 50n + 30.

¹⁰ Besant, Annie, and Leadbeater, Charles W. Occult Chemistry, Theosophical Publishing House, Adyar, Chennai, India, 1951.

¹¹ Phillips, Stephen M. Article 4: “Godnames Prescribe Inner Tree of Life,” (WEB, PDF), p. 4.

¹² It was Hurwitz who first proved in 1898 that n = 1, 2, 3, 4 are the only possible values that allow for division algebras the norm condition: |A|²|B|² = |C|², where A = (a₁, a₂, … a_n), B = (b₁, b₂, … b_n) and C = (c₁, c₂, … c_n).

¹³ Phillips, Stephen M. Article 34: “The Seven Layers of Vertices in the Disdyakis Triacontahedron Encode the 206 Bones of the Human Skeleton, the Superstring Symmetry Groups E₈ & E₈×E₈ and the Superstring Structural Parameters 168, 336, 840 & 1680,” (WEB, PDF), p. 20.

¹⁴ Ref. 7, p. 17.

¹⁵ Phillips, Stephen M. Article 18: “Encoding of Planetary Distances and Superstring Structural Parameters in the I Ching Table,” (WEB, PDF), p. 31–33.

¹⁶ Phillips, Stephen M. Article 21: “Isomorphism Between the I Ching Table, the 3×3×3 Array of Cubes and the Klein Configuration,” (WEB, PDF), p. 6–9.

¹⁷ Ibid, p. 11.

36