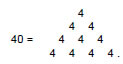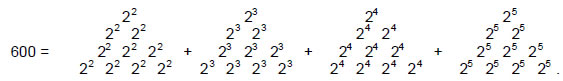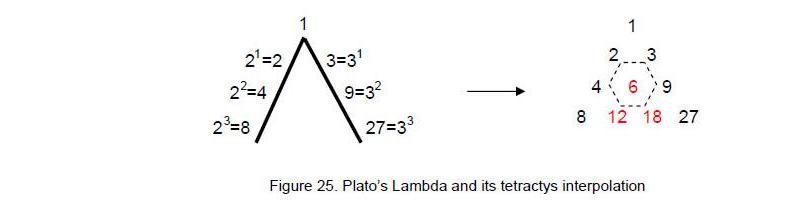ARTICLE 34

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

1

Table 1. The number values of the Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters. Numbers from this table will be written in boldface in the article.

2

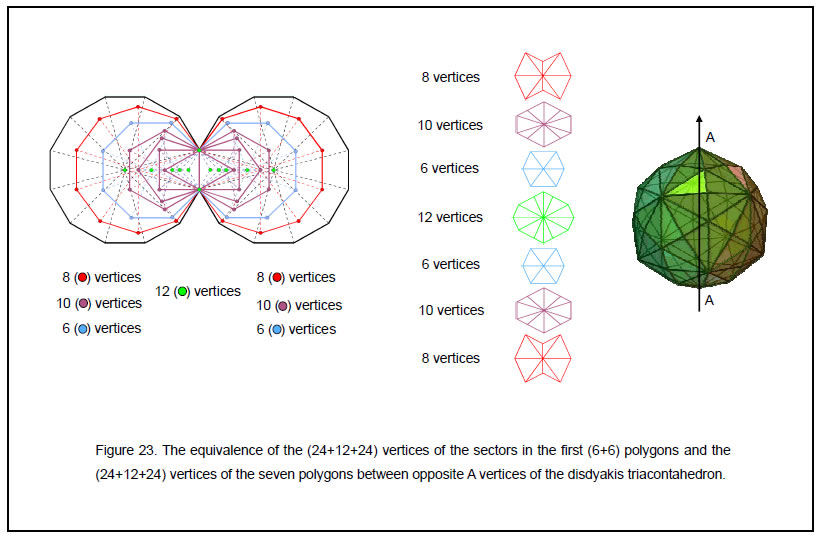
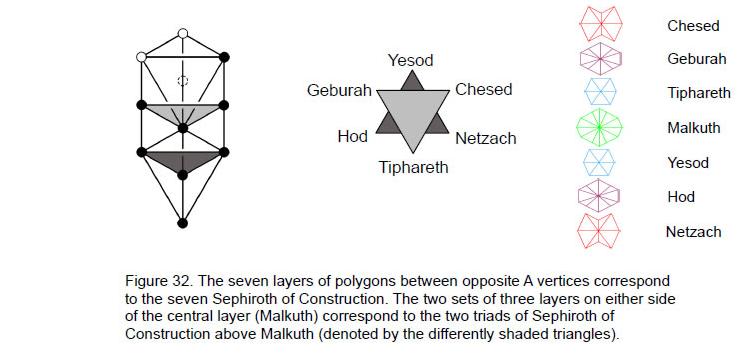
1. The seven layers of vertices in the disdyakis triacontahedron

Articles 22-30 provided evidence that the disdyakis triacontahedron (Fig. 1) — the Catalan solid with the most faces — is the polyhedral version of the polygonal, inner Tree of Life. It has 62 vertices, 180 edges and 120 triangular faces, that is, 362 geometrical elements in its faces. Therefore, 360 elements surround the central axis joining any two diametrically opposite vertices. Because it is the polyhedral counterpart of the inner form of the Tree of Life, it constitutes sacred geometry par excellence. This means that the geometrical (indeed, all mathematical) properties of this polyhedron are prescribed by the gematria number values of the Hebrew names of the ten Sephiroth of the Tree of Life, their Hebrew Godnames, Archangelic Names, Orders of Angels and Mundane Chakras. Table 1 lists the English versions of these names (their literal English translations appear within brackets) and the number values of all the Hebrew names. It indicates the remarkable fact that ELOHA,^* the Godname of Geburah with a number value of 36, prescribes the shape of the polyhedron because the number of geometrical elements surrounding its axis is 360, which is the number of yods in 36 tetractyses. The Godname EL (“God”) of Chesed with number value 31 also prescribes it because every one of 31 vertices in one-half of the polyhedron has its mirror image diametrically opposite it. Remarkably, the gematria number value of Tzadkiel, the Archangel of Chesed, is 62 — the number of vertices in the disdyakis triacontahedron. Other ways in which the Godnames, etc define its properties were discussed in previous articles. This article will explain how they characterise the layering of vertices.

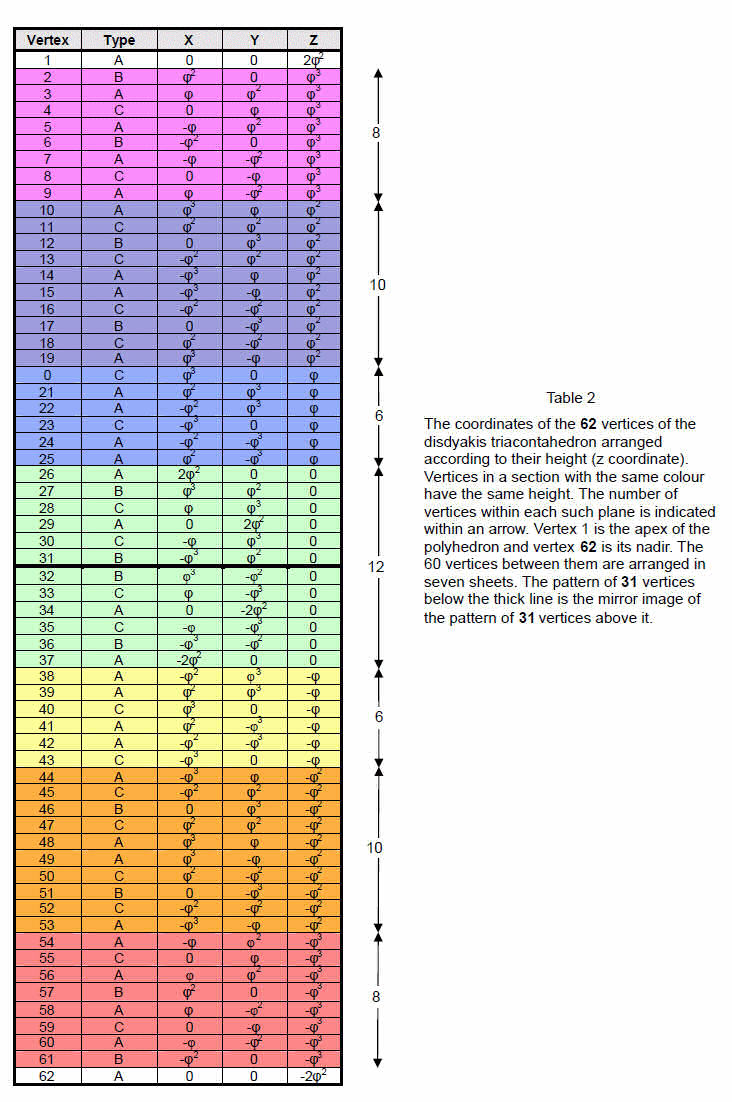
The 62 vertices are of three types: 12 B vertices of an icosahedron, 20 C vertices of a dodecahedron (these form the 32 vertices of a rhombic triacontahedron (Fig. 2)) and 20 A vertices  created  by  raising  the  centres  of  the  Golden  Rhombic  faces  of  the latter  polyhedron.  Table 2  displays  the x-, y- & z-coordinates of the 62 vertices of the disdyakis triacontahedron. All coordinate values belong to the set (0, ±φ, ±φ², ±φ³,

±2φ²), where φ = 1.6180…. is the Golden Ratio. The topmost vertex A is at a height z = 2φ² above the XY plane. Eight vertices are at a height φ³, 10 vertices are at a height φ² and six vertices are at a height φ. Counterparts of these three layers of vertices lie below the XY plane, which contains 12 vertices. The vertices of the polyhedron are arranged in seven layers. In Fig. 2, each layer is assigned one of the seven colours in white light. Vertex 1 is the apex of the polyhedron and vertex 62 is its nadir. The dark line divides the first 31 vertices from their mirror images. Vertices are ordered so that the nth vertex at (a,b,c) is the mirror image of the (63–n)th vertex at (–a,–b,–c).

Whether viewed along the X-, Y- or Z-axes, the polyhedron has seven layers of vertices between the A vertices at its apex and nadir. Counting from the top, the numbers of vertices in the layers are:

1. 8 (4A, 2B & 2C);
2. 10 (4A, 2B & 4C);
3. 6 (4A, 2C);
4. 12 (4A, 4B & 4C);
5. 6 (4A, 2C);
6. 10 (4A, 2B & 4C)
7. 8 (4A, 2B & 2C).

__________________________________

^* Godnames will be written in upper case and Archangelic Names, Angelic Names & Mundane Chakras will be italicized.

3

4

5

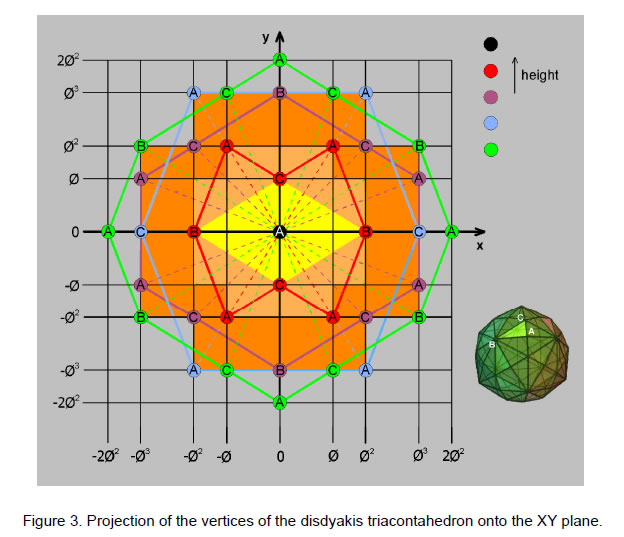
The four uppermost layers have 36 vertices made up of 16 A vertices, eight B vertices and 12 C vertices. The three lowest layers have 24 vertices comprising 12 A vertices, four B vertices and eight C vertices. Figure 3 shows the projection of the uppermost four layers onto the XY plane, looking downwards along the Z-axis. The apex is shown as a black circle. The uppermost layer of eight vertices is in red, the next layer of 10 vertices is in violet, the third layer of six vertices is in blue and the fourth layer of vertices lying in the XY plane is in green. The black gridlines mark distances ±φ, ±φ, ±φ² & ±2φ². Four A vertices in the first layer are at the corners of a Golden Rectangle, as are four A vertices in the third layer, although the size of the rectangle is different. Similarly, four B vertices in the fourth layer lie at the corners of the same sized Golden Rectangle rotated by 90°. No four vertices in the second layer form a Golden Rectangle. The seven layers therefore contain five Golden Rectangles. Because of the mirror symmetry of the disdyakis triacontahedron, there is a vertex below every one shown in Fig. 3 that belongs to one of the three layers below the XY plane.

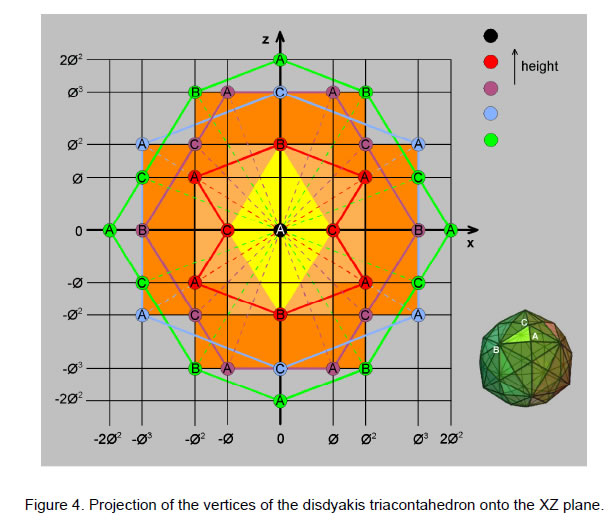
Figure 4 displays the projection of the vertices onto the XZ plane as viewed in the positive direction of the Y-axis. The distribution of vertices is the same as that seen along the Z-axis after rotating the disdyakis triacontahedron through 90°. The projection of vertices onto the YZ plane as viewed along the positive X-axis is identical to the projection onto the XY plane shown in Fig. 3. Hence, (3×5=15) Golden Rectangles are formed by vertices in the three perpendicular sets of seven layers totalling 21 layers. This shows how the Godname EHYEH of Kether with number value 21 and the Godname YAH with number value 15 prescribe the orthogonal layering of vertices in the disdyakis triacontahedron.

2. Encoding of the human skeleton in the seven layers
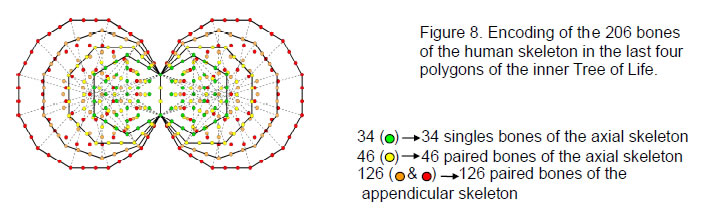
According to Kabbalah, Adam Kadmon, or Heavenly Man, is the universal prototype for all holistic systems, whether a subatomic particle or a human being. Genesis 1, verse 27, states: “So God created man in his own image, in the image of God created he him; male and female created he them.” This ‘image’ is the Tree of Life. It is the cosmic blueprint governing matter, man and the universe. As the representation of God, it manifests in the four Worlds of Atziluth (Archetypal World), Beriah (Creative World), Yetzirah (Psychological World) and Assiyah (Physical World). Godnames, Archangels, Angels and Mundane Chakras are the Sephiroth of the four overlapping Trees of Life mapping these worlds, which, of course, are not literally places but functional divisions of the Divine Life. A human being at the Assiyatic level is the body composed of bones, flesh and vital organs. The Tiphareth of the body viewed as the lowest of the four Trees of Life is the central nervous system, a highly complex organisation of nerves that allow two-way communication between the brain (representing Kether) and all the parts of the body. Its Malkuth is the skeleton, which in the adult is composed of 206 bones. They form two groups: the 80 bones of the axial skeleton (bones of the head, vertebral column, ribs and breastbone or sternum) and the 126 bones of the appendicular skeleton (the upper and lower limbs and their attachments, or girdles) (Fig. 5).

Some bones occur singly and others exist in pairs, with one belonging to the left side of the body and the other belonging to its right side. Listed below are the numbers of single bones and pairs of bones:

	Single	Pairs
Axial skeleton (80 bones)
Skull	6	11
Hyoid:	1
Vertebral column:	26
Thoracic cage:	1	12
Subtotal:	34	23
Appendicular skeleton (126 bones)
Pectoral girdles:		2
Upper extremity		30
Pelvic girdle:		1
Lower extremity:		30
Subtotal:	0	63
Total:	34	86

The human skeleton is composed of 34 bones that occur singly and 172 bones that appear in pairs. The

6

80 bones of the axial skeleton consist of 34 single bones and 46 bones that occur in pairs. The 126 bones of the appendicular skeleton comprise 63 pairs of bones.

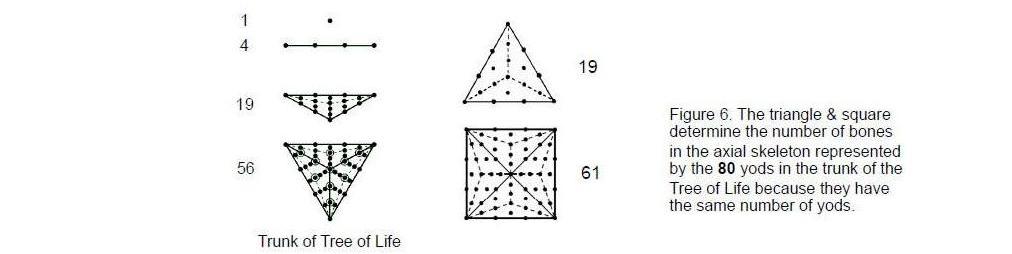
It was shown in Articles 32¹ and 33² that the axial skeleton is the manifestation of the ‘trunk’ of the Tree of Life. This is the downward sequence of point, line, triangle and tetrahedron — what mathematicians call the first four ‘simplexes.’ With its triangles constructed from three tetractyses, the trunk is made of 80 yods, each one denoting a bone of the axial skeleton. The rest of what is the lowest of the four Trees mapping the human body — what may be called its ‘branches’ — has 171 yods, 126 of which denote the 126 bones of the appendicular skeleton. The 34 types of single bones are encoded in the inner Tree of Life as the

34 yods in its pair of triangles. The 23 types of pairs of bones are encoded as the 23 pairs of yods in the pair of squares. With their sectors transformed into three tetractyses, the pair of joined triangles and the pair of joined squares contain 206 yods — the number of bones in the human skeleton, whilst a separate triangle and a square contain 80 yods when similarly transformed, which is the number of bones in the axial skeleton (Fig. 6).

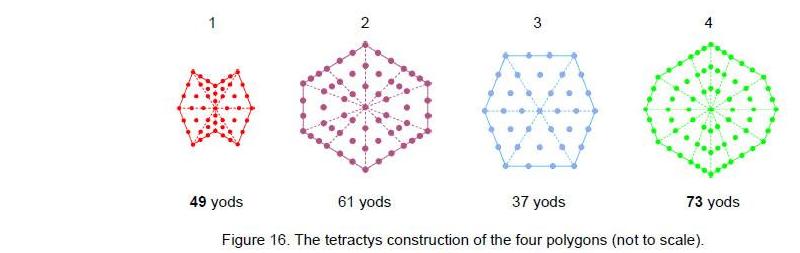
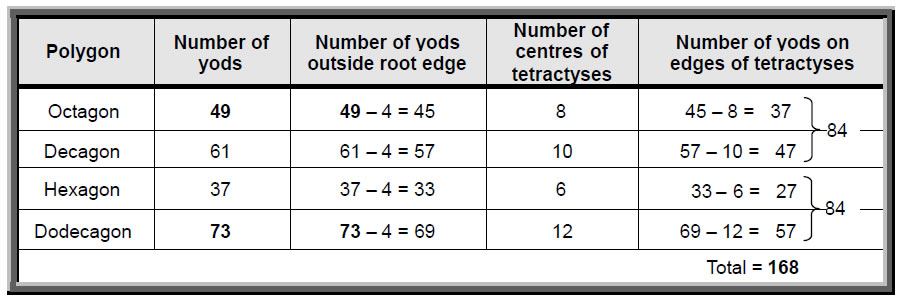
Let us return to the seven layers of polygons in the disdyakis triacontahedron. They are of four types: an 8-sided polygon, a 10-sided polygon, a 6-sided polygon and a 12-sided polygon. They correspond in the polygonal Tree of Life (Fig. 7) to the octagon, decagon, hexagon and dodecagon, although the polygons formed by the layers of vertices are not regular. It is trivial to prove that the number of yods in an n-sided polygon (regular or irregular) whose n triangular sectors are tetractyses with four yods on each side is 6n+1. The hexagon (n=6) has 37 yods, of which (37–4=33) yods are outside the root edge,^* the octagon (n=8) has 49 yods (45 outside the root edge), the decagon (n=10) has 61 yods (57 outside the root edge) and the dodecagon (n=12) has 73 yods (69 outside the root edge). The hexagon and octagon have (33+45=78) yods outside the root edge. Two yods of the latter are associated with one set of seven polygons and the two other yods of the root edge are associated with the other set of seven polygons (Fig. 8). (78+2=80) yods are associated with the hexagon and octagon on each side of the root edge. They consist of (33+1=34) yods associated with each hexagon and (45+1=46) yods associated with each octagon. They symbolize, respectively, the 34 single bones of the axial skeleton and its 46 bones that exist as pairs, one on the left-hand side of the body and the other on the right-hand side. The (57+69=126) yods of the decagon and dodecagon symbolize the 126 bones of the appendicular skeleton.

_________________________________

^* The root edge is the vertical edge shared by all the 14 polygons of the inner Tree of Life.

7

Layers 1 and 3 of the disdyakis triacontahedron have 14 vertices arranged as an 8-sided polygon and as a 6-sided polygon. They correspond in the inner Tree of Life to, respectively, the octagon and the hexagon associated with which are 80 yods symbolizing the 80 bones of the axial skeleton. Layers 2 and 4 have 22 vertices arranged as a 10-sided polygon and as a 12-sided polygon. Their counterparts in the inner Tree of Life are the decagon and the dodecagon, which have 126 yods outside the root edge symbolizing the 126 bones of the appendicular skeleton. The odd-numbered layers therefore determine the axial skeleton and the even-numbered layers determine the appendicular skeleton. Layers 5, 6 & 7 are the respective mirror images of layers 3, 2 &1.

Of the 264 yods in the seven enfolded polygons, the 206 yods associated with the last four polygons symbolize bones, leaving 58 yods in the first three enfolded polygons. The last (4+4) enfolded polygons have 58 corners, showing how this number defines the last four polygons in two different ways. Eight of these corners coincide with Sephiroth of the lowest tree mapping the human body (Fig. 9), leaving 50 corners that are unshared with it. This shows how the Divine Name ELOHIM with number value 50 prescribes the last (4+4) polygons and therefore the number of bones in the human skeleton. The 70 triangular sectors of the last (4+4) enfolded polygons have 66 corners, where 66 is the 65th integer after 1. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes these polygons embodying information about the human body — the Malkuth aspect of Adam Kadmon. 33 such corners are associated with each set of the last four polygons. The centre of the hexagon is a corner of the triangle and the centre of the decagon is a corner of the pentagon. This leaves (33–2=31) corners of the 35 sectors of the last four polygons that are intrinsic to them alone because they do not belong to the first three polygons. EL, the Godname of Chesed with number value 31, therefore prescribes the last four polygons of the inner Tree of Life that encode the bone composition of the human skeleton.

The 35 sectors of the last four enfolded polygons have 34 corners and 69 sides, totalling 138 geometrical elements. The number of elements associated with each set of four polygons is 137. This integer defines the fine-structure constant e²/ħc ≈ 1/137.036, making it perhaps the most important number in physics because its reciprocal measures the strength of the coupling of the electromagnetic field to electric charges and thus the size of atoms and the energy scale of their chemical bonding. 137 is the 33rd prime number. As mentioned earlier, 33 corners of sectors are associated with the last four polygons, where 33 = 1! + 2! + 3! + 4!, i.e., the sum of the numbers of permutations of 10 objects arranged in the four rows of a tetractys. Of the 34 corners, eight are either centres of polygons, shared with the Tree of Life or both.  This leaves 26 corners, showing how YAHWEH, the Godname of Chokmah with number value 26 prescribes  the last four enfolded polygons. 26 = 1 + 3 + 7 + 15, where

Table 3. Geometrical composition of the seven polygons (single triangles as sectors).

		n	Number of vertices n+1	Number of edges 2n	Number of triangles n	Total 4n+1
1		8	8+1	16	8	32+1
2		10	10+1	20	10	40+1
	Subtotal	18	18+2	36	18	72+2
3		6	6+1	12	6	24+1
4		12	12+1	24	12	48+1
	Subtotal	36	36+4	72	36	144+4
5		6	6+1	12	6	24+1
6		10	10+1	20	10	40+1
7		8	8+1	16	8	32+1
	Total	60	60+7	120	60	240+7

‘1’ is number of combinations of one object, ‘3’ is the number of combinations of two objects, ‘7’ is the number of combinations of three objects and ‘15’ is the number of combinations of four objects. The

8

9

permutational and combinatorial properties of ten objects arranged in the form of a tetractys are therefore connected to the shapes of the last four of the seven enfolded polygons that make up the inner Tree of Life. When regarded as separate polygons, the last four polygons have (6+8+10+12=36) corners, where 36 is the number value of ELOHA, the Godname of Geburah. Their 36 sectors have (36+4=40) corners, where

This demonstrates the basic role of the Tetrad (4) in defining properties of any geometrical object that conforms to the universal pattern of the Tree of Life — in this case the 40 corners of the 36 sectors of the first four layers of vertices of its polyhedral form — the disdyakis triacontahedron.

3. Geometrical composition of the seven polygons
Table 3 tabulates the numbers of vertices, edges and triangles making up each polygon in the seven layers of the disdyakis triacontahedron. The seven polygons comprise 67 vertices, where 67 is the number value of Binah. This is very appropriate in view of the meaning of the Sephirah Binah as embodying the archetype of form, for this number does, indeed, quantify the shapes of the seven polygons when constructed from tetractyses. In fact, when the 19 triangles of the 1-tree are 

converted into tetractyses, there are 67 yods below the horizontal path joining Binah to Chokmah (Fig. 11). They include the seven yods that coincide with the seven Sephiroth of Construction, leaving 60 other yods. This 60:7 division in the 1-tree constructed from tetractyses parallels the division of vertices in the seven polygons into 60 vertices that surround their seven centres. The correspondence is striking evidence of the Tree of Life nature of the disdyakis triacontahedron.

According to Table 3, there are 247 geometrical elements in the seven polygons. 240 of these elements surround the seven centres. This important property, the superstring significance of which will be discussed later, corresponds in the polygonal form of the inner Tree of Life to the 240 hexagonal yods of the seven separate polygons that surround their seven centres (Fig. 10. The second subtotal row in the table above for the four layers of vertices making up half of the

disdyakis triacontahedron shows that they comprise 148 elements. 148 is the number value of Netzach, the fourth Sephirah of Construction. 144 of these elements surround the centres of the four polygons, where 144 = 12² = 12th Fibonacci number. 36 of them are vertices of polygons, showing how the Godname ELOHA with number value 36 prescribes

10

the shapes of the four polygons, just as we saw earlier that it does for their separate, regular counterparts in the inner Tree of Life. The four polygons have 72 edges and 36 triangles, where 72 is the number value of Chesed, the fourth Sephirah from the top of the Tree of Life. Including the apex of the disdyakis triacontahedron (an A vertex), there are 41 vertices from this ‘North pole’ to the equatorial plane containing the 12 vertices. 41 is the 21st odd integer, showing how EHYEH, the Godname of Kether with number value 21, prescribes the number of vertices in half of the disdyakis triacontahedron when the polygons of

vertices in its layers are constructed from tetractyses.

The two uppermost layers are made up of an 8-sided polygon and a 10-sided polygon. They contain 36 edges. 72 geometrical elements surround their two centres. The five lowest layers are made up of an 8-sided polygon, a 10-sided polygon, two 6-sided polygons and a 12-sided polygon. They have 47 vertices, where 47 is the 15th prime number, showing how the Godname YAH of Chokmah with number value 15 prescribes the polygons in the five lowest layers. 42 of these vertices surround their five centres, where 42 is the 21st even integer, showing how EHYEH, Godname of Kether with number value 21, prescribes these five polygons. They have 84 edges, where 84 = 1² + 3² + 5² + 7², and 42 triangles. They also have (42+42=84) vertices and triangles surrounding their centres. The lowest five polygons therefore have (84+84=168) geometrical elements, where 168 is the number value of the Mundane Chakra of Malkuth. This division of the number of elements into two sets of 84 is highly significant. It has been encountered in previous articles such as:

1. Article 15,³ which discussed the 84 permutations of pairs and triplets of octonions belonging to the seven triples of octonions (e_i, e_i+1, e_i+3) and the 84 permutations of their inverses;

2.Article 18,⁴ which discussed the I Ching table of 64 hexagrams and the 28 hexagrams on either side of its diagonal. Each hexagram is a pair of trigrams, so that each set of 28 off-diagonal hexagrams has (28×2×3=168) lines and broken lines. Each set comprises 84 lines and 84 broken lines;

3. Article 21,⁵ which discussed the 84 hyperbolic triangles in the two types of seven similar slices of the Klein Configuration, the diagram whose 168 hyperbolic triangles represent the 168 automorphisms of the equation known to mathematicians as the Klein Quartic;

4. Article 16,⁶ which discussed, firstly, the 84 repetitions of the Pythagorean-valued, rising intervals between the notes of the seven types of musical scales and their 84 falling intervals (pp. 17–18), and, secondly, the 84 yods belonging to the first four enfolded polygons enfolded in each half of the inner Tree of Life that either are not centres of polygons or do not coincide with Sephiroth (pp. 23–24).

Such correspondences demonstrate powerfully that the lowest five layers of the disdyakis triacontahedron form a Tree of Life pattern in themselves. This could have already been anticipated, because the number 168 is the structural parameter of the superstring — the manifestation in the subatomic world of the Tree of Life blueprint. Indeed, this is why the number 168 is the number value of the Mundane Chakra of Malkuth, the Sephirah of the Tree of Life denoting the physical universe of space and time.

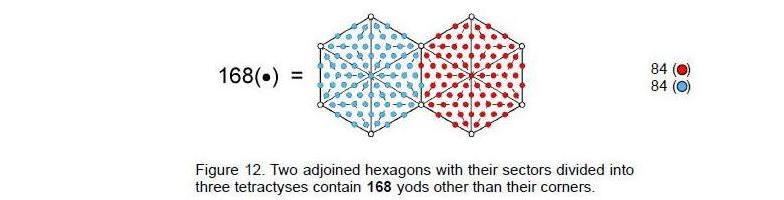
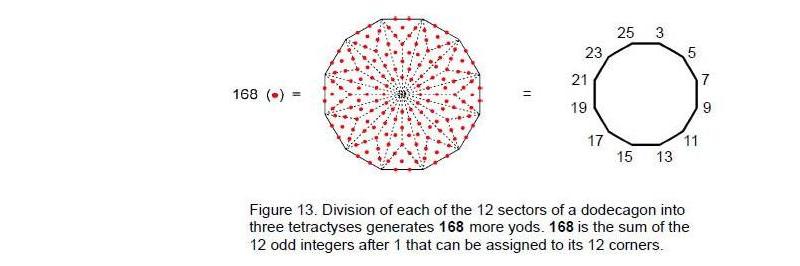
The 84:84 division of geometrical elements in the last five polygons of vertices, which start with the 6- sided polygon, has its counterpart in the pair of joined hexagons belonging to the polygonal form of the inner Tree of Life. 168 more yods (84 per hexagon) are needed to transform their sectors into three tetractyses (Fig. 12). Furthermore, it is remarkable that the 12-sided polygon in the middle of the seven layers of vertices requires 168 more yods to construct its sectors from three tetractyses. Figure 13 shows this property for the dodecagon. The fact that the sides of the 12-sided polygon are unequal in length is irrelevant. As 13² – 1 = 168 = 3 + 5 + 7 + … + 25, assigning the first 12 odd integers after 1 to the vertices.

11

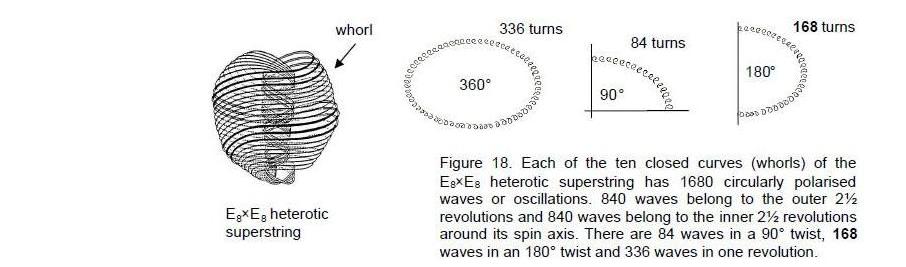
of this central 12-sided polygon generates the number 168 as their sum. This is an example of the beautiful coherence between number and sacred geometry. It also illustrates the Tetrad Principle because the four-fold sequence of 8-sided, 10-sided, 6-sided and 12-sided polygons ends with one that embodies a number of universal significance, namely, the very number 168 that defines the form of an E₈×E₈ heterotic superstring because each of its 10 curves makes 168 circularly polarized oscillations during one half of a revolution around its spin axis. It manifests in the disdyakis triacontahedron as its 168 edges above and below its equator that give it a 3-dimensional shape.

4. The seven polygons encode the roots of E₈
The seven polygons have 240 geometrical elements surrounding their centres, of which 72 belong to the uppermost two layers and 168 belong to the five lowest layers. This 72:168 division appears in the structure of the non-zero roots of the superstring gauge symmetry group E₈. The roots of the E₈ algebra can be described in terms of eight orthonormal unit vectors {u_i}. Eight zero roots correspond to points at the centre of the root diagram and 240 non-zero roots all have length √2. They are given by:

±u_i ±u_j (i, j = 1, 2, …, 8)

and

½(±u₁, ±u₂, …±u₈)                                                                     (even number of +’s)

Their explicit forms as 8-tuples and their numbers are listed below:

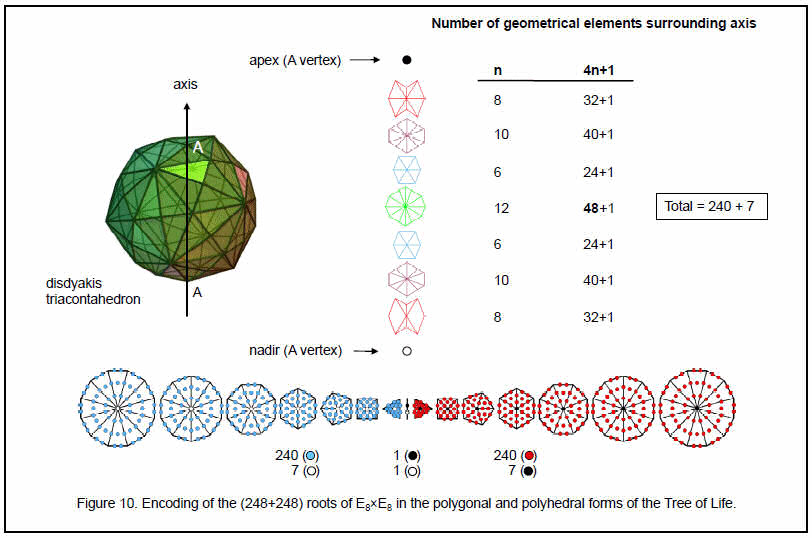
The 240 non-zero roots of E₈ comprise 168 non-zero roots made up of four sets of 28 and one set of 56 and 72 non-zero roots comprising one set of 70 and two single ones. Remarkably, surrounding the seven centres of the polygons are as many geometrical elements (240) as there are non-zero roots of E₈, the first two polygons having as many elements (72) as there are non-zero roots of E₆, an exceptional subgroup of E₈ of much interest to physicists seeking to extend the Standard Model of particle physics using superstring theory. This provides highly convincing evidence that superstring physics is encoded in the pattern of vertices belonging to the seven layers of the disdyakis triacontahedron.

The 2:5 division of layers generating the 72:168 division of geometrical elements surrounding centres of polygons reflects the distinction in the Tree of Life between the two Sephiroth of Construction — Chesed and Geburah, which lie outside its Lower Face, and the remaining five Sephiroth of Construction that span it. The eight zero roots of E₈ consist of seven zero roots of one kind and one zero root of another kind. The former are denoted by the seven centres of the polygons and the latter is denoted by the topmost A vertex of the disdyakis triacontahedron (see Fig. 10).

The 72:168 division was encountered in Article 267 in discussion of the construction of the disdyakis triacontahedron from tetractyses. When its 180 internal triangles formed by its centre and each edge of the polyhedron are divided into three tetractyses and its 120 triangular faces are turned into single tetractyses, there are 1680 (=168×10) geometrical elements surrounding the axis that joins two diametrically opposite A vertices. When each of its 120 faces is constructed from three tetractyses, there are 2400 (=240×10) such elements, i.e., an extra 720 (=72×10) elements are added. What is being represented geometrically here are the root structures of the superstring gauge symmetry group E₈ and its exceptional subgroup E₆, for E₈ has 168 non-zero roots that do not belong to E₆, which has 72 such roots.

12

Every simple root of E₈ is associated with a Yang-Mills gauge charge — the source of a 10-dimensional Yang-Mills gauge field. The factor of 10 in these properties therefore encodes the information that each gauge field has ten space-time components. The layers of the disdyakis triacontahedron encode the number of 10-dimensional gauge fields defining the unified superstring force, whilst the various numbers of geometrical elements making up the interior and exterior of this polyhedron are the numbers of components of these fields. They represent the number of bits of information needed to define the gauge fields of the superstring in 10-dimensional space-time. In the context of the disdyakis triacontahedron, the additional 720 elements correspond to the (240×3=720) components of these fields in 3-dimensional space.

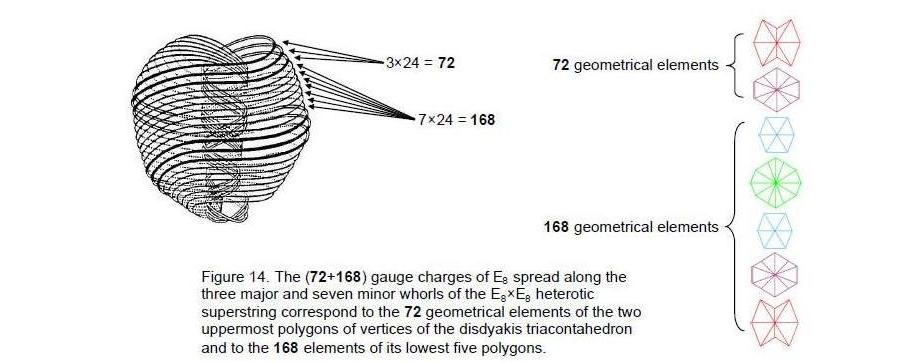
The 72:168 division of the non-zero roots of E₈ appears in the E₈×E₈ heterotic superstring as the distinction between the three major whorls and the seven minor whorls in the object described over a century ago by Annie Besant and C.W. Leadbeater⁸ as being the basic unit of matter (Fig. 14). As the manifestation in the space-time continuum of the Tree of Life blueprint, the major whorls correspond to the Kether, Supernal Triad of Chokmah and Binah, whilst the minor whorls

correspond to the seven Sephiroth of Construction. Besant & Leadbeater connected them to the three “solar Logoi” and to the seven “Planetary Logoi:”

“The Anu is a sun in miniature in its own universe of the inconceivably minute. Each of the seven whorls is connected with one of the Planetary Logoi, so that each Planetary Logos has a direct influence playing on the very matter of which all things are constructed. It may be supposed that the three conveying electricity, a differentiation of Fohat, are related to the Solar Logos.”⁹

Although each whorl is a separate closed curve that never intersects itself or touches one another, this separateness is an illusion, existing only in ordinary 3-dimensional space. The curves are the 3-dimensional cross-sections of a hyper-dimensional object embedded in a higher, 15-dimensional space with a topology such that its cross-section is a set of ten closed curves topologically equivalent to circles, each one twisting 2½ times in an outer circuit and 2½ times in a tighter revolution around the spin axis of the spin-½ superstring. A 1-dimensional curve embedded in 26-dimensional space-time has 24 transverse vibrational degrees of freedom. These generate generalised 24 Kaluza-Klein gauge fields that, on compactification of the 16 dimensions beyond superstring space-time, become 24 Yang-Mills gauge fields of E₈ existing in 10-dimensional space-time. Their charges are spread along each curve, 24 to each one. The three major whorls have 72 E₈ gauge charges and the seven minor whorls have 168 charges. The former are the gauge charges of E₆, an exceptional subgroup of E₈, and the latter are the remaining gauge charges of E₈. They correspond in the seven polygons of vertices of the disdyakis triacontahedron to the 72 geometrical elements surrounding the centres of the two uppermost polygons and to the 168 elements around the centres of the lowest five polygons. The first of these polygons has 24 elements, the second has 24 edges and 24 vertices and triangles, the third has 24 elements and the last two polygons have 72 elements. These sets of 24 elements are the polygonal counterpart of the 24 gauge charges

13

spread along each of the ten curves of the superstring.

Of the 72 elements in the two uppermost polygons, 18 elements are vertices of the disdyakis triacontahedron (eight A, four B & six C vertices). Hence, these polygons have (72–18=54) elements that are not polyhedral vertices. Of the 168 elements in the lowest five polygons, 42 elements are vertices of the disdyakis triacontahedron (20 A, eight B & 14 C vertices). This leaves (168–42=126) elements in the lowest five polygons that are not polyhedral vertices. Including their

five centres, there are (126+5=131) elements that are not polyhedral vertices. 131 is the number value of Samael, the Archangel of Geburah. All seven polygons have 180 edges and triangles. Including the seven centres of polygons, there are 187 geometrical elements that are not polyhedral vertices. This is the number value of Auphanim, the Order of Angels assigned to Chokmah.

The counterpart in the outer Tree of Life of the 240 geometrical elements surrounding the centres of the seven polygons is the 240 extra yods needed to construct the 1-tree when its 19 triangles are each divided into three tetractyses (Fig. 15). The counterpart of the centres of the seven polygons is the locations of the seven Sephiroth of Construction.

Suppose now that the 60 sectors of the seven polygons are each divided into three tetractyses instead of single ones. Table 4 lists the number of vertices, edges and triangles in each polygon.

Table 4. Geometrical composition of polygons (three triangles as sectors).

		n	Number of vertices 2n+1	Number of edges 5n	Number of triangles 3n	Total 10n+1
1		8	16+1	40	24	80+1
2		10	20+1	50	30	100+1
	Subtotal	18	36+2	90	54	180+2
3		6	12+1	30	18	60+1
4		12	24+1	60	36	120+1
	Subtotal	36	72+4	180	108	360+4
5		6	12+1	30	18	60+1
6		10	20+1	50	30	100+1
7		8	16+1	40	24	80+1
	Total	60	120+7	300	180	600+7

The seven polygons have 120 vertices surrounding their centres. This is a beautiful property because it indicates that the disdyakis triacontahedron has the same number of triangular faces as there are vertices in the 180 triangles making up the polygons in its seven layers of vertices. 60 of them are polyhedral ones, leaving 67 non-polyhedral vertices, where 67 is the number value of Binah. The numbers 120 and 60 conform to the Tetrad Principle¹⁰ because

120 = 2² + 4² + 6² + 8² = 2³ + 2⁴ + 2⁵ + 2⁶

14

and

60 = 2² + 2³ + 2⁴ + 2⁵.

The 8-sided polygon at the base of the disdyakis triacontahedron has 80 vertices, edges & triangles surrounding its centre. 80 is the number value of Yesod, the penultimate Sephirah. Its meaning — ‘foundation’ — is appropriate, given that this is the lowest polygon. The first two polygons have 36 vertices, 90 edges and 54 triangles surrounding their centres, which total 180 geometrical elements. The last five polygons have 84 vertices, 210 edges & 126 triangles surrounding their five centres, totalling 420 elements. With single triangles as sectors, the last five polygons have 84 edges. Once again, the heterotic superstring structural parameter 84 appears. The number of edges & triangles in the lowest five polygons = 210 + 126 = 336. This, too, is a structural parameter of the superstring, being the number of circularly polarized oscillations in one revolution of each whorl of the UPA/superstring. Both numbers are consistent with the Tetrad Principle governing Tree of Life parameters because

84 = 1² + 3² + 5² + 7²

and

336 = 4×84 = 2²×84 = 2²(1² + 3² + 5² + 7²)
     = 2² + 6² + 10² + 14².

As

10 = 1 + 2 + 3 + 4

and

30 = 1² + 2² + 3² + 4²,

the number of edges of the 180 triangles is

300 = 10×30 = (1+2+3+4)(1²+2²+3²+4²).

The number of edges and triangles is

480 = 2×240 = 2(2⁴ + 2⁵ + 2⁶ + 2⁷) = 2⁵ + 2⁶ + 2⁷ + 2⁸.
              = 4×120 = 2²(2² + 4² + 6² + 8²) = 4² + 8² + 12² + 16².

This property again illustrates the Tetrad Principle.

The number of geometrical elements surrounding the seven centres is 600, which has the tetractys representation:

Remarkably, this is the number of geometrical elements surrounding the axis of the disdyakis triacontahedron, for it has 60 vertices surrounding this axis, each joined internally to its centre as an edge of an internal triangle, 180 edges, each the edge of an internal triangle, and 120 triangles — a total of (60+60+180+180+120=600) elements.

The Divine Name EL assigned to Chesed with number value 31 prescribes the seven layers of vertices because the total number of vertices is 127, which is the 31st prime number. In view of the fact that there are seven layers, it is fitting that 127 is the seventh Mersenne prime number! EL prescribes the disdyakis triacontahedron also because it consists of 31 vertices and their mirror images. The Divine Name YAH assigned to Chokmah with number value 15 prescribes the vertex composition of the polygons because 120 vertices surround their centres and 120 is the 15th triangular number:

120 = 1 + 2 + 3 + … + 15.

Including the apex and nadir of the disdyakis triacontahedron, there are 129 vertices. This is the number value of YAHWEH SABAOTH, the Godname of Netzach, showing how the Godname of the seventh Sephirah prescribes the seven layers of vertices in the disdyakis triacontahedron.

We saw earlier that the 8-sided polygon at the base of the disdyakis triacontahedron comprises 80 vertices, edges & triangles when its sectors are divided into three triangles. With these triangles regarded as tetractyses, the polygon has 120 yods around its centre. In other words, it has as many yods around

15

its centre as all seven polygons have vertices surrounding their centres! When each sector is regarded as a tetractys, the 8-sided polygon has 49 yods. This shows how EL CHAI, Godname of Yesod with number value 49, prescribes the seven polygons, which begin and end with this one.

Table 5. Yod composition of the seven polygons (single tetractys).

		n	Number of vertices n+1	Number of yods 6n+1	Number of hexagonal yods 5n
1		8	8+1	48+1	40
2		10	10+1	60+1	50
	Subtotal	18	18+2	108+2	90
3		6	6+1	36+1	30
4		12	12+1	72+1	60
	Subtotal	36	36+4	216+4	180
5		6	6+1	36+1	30
6		10	10+1	60+1	50
7		8	8+1	48+1	40
	Total	60	60+7	360+7	300

Table 4 indicates that the four polygons in each half of the disdyakis triacontahedron have 360 geometrical elements surrounding their centres (including 36 polyhedral vertices), the fourth polygon having 36 triangles. This demonstrates how the Godname ELOHA assigned to Geburah with number value 36 prescribes the polygons formed by the 60 vertices of the disdyakis triacontahedron. They have 72 vertices (36 polyhedral vertices, 36 non-polyhedral vertices).

Including their four centres, the first four polygons have 76 vertices. This is the number value of YAHWEH ELOHIM, the Godname of Tiphareth, showing how this Godname prescribes each half of the disdyakis triacontahedron

The first four polygons have 36 internal vertices surrounding their centres and 180 edges in their tetractyses, that is, 216 vertices & edges. This is the number value of the Sephirah Geburah, whose Godname has the number value of 36.

5. The yod composition of the seven polygons
Table 5 lists the yod populations of the seven polygons when their sectors are turned into tetractyses. Figure 16 displays the yods in the first four polygons. The polygon in the second layer has 10 vertices and therefore is 10-sided even though its boundary has six straight lines. Similarly, the polygon in the fourth layer is 12-sided because it has 12 vertices, even though it is bounded by eight straight lines. The seven polygons have 67 yods at the corners of their 60 tetractyses, the first two polygons have 20 yods at corners of their 18 tetractyses and the last five polygons have 47 yods at the corners of their 42 tetractyses. As 47 is the 15th prime number, this shows how the Godname YAH with number value 15 prescribes the last five polygons. They have 210 (=21×10) hexagonal yods, showing how the Godname EHYEH with number value 21 prescribes the last five polygons. The first four polygons have 36 yods at corners of their 36 tetractyses surrounding their centres, showing how the Godname ELOHA of Geburah with number 36 prescribes these polygons. They have 216 yods surrounding their centres, where 216 is

16

the number value of Geburah. All seven polygons have 360 (=36×10) yods surrounding their centres, yet again demonstrating how ELOHA prescribes the seven polygons. The number of yods in the fourth polygon is 73, which is the number value of Chokmah. It has 72 yods surrounding its centre. This is the number of Chesed, the Sephirah next below Chokmah on the right-hand Pillar of Mercy. The number values of Chokmah, Binah, Chesed and Geburah measure in a natural way different groups of yods in the seven polygons. EHYEH also prescribes the central layer of the disdyakis triacontahedron because 73 is the 21st prime number.

There are 307 yods on the edges of the 60 tetractyses. ELOHIM SABAOTH with number value 153 prescribes the shapes of the polygons because 307 is the 153rd odd integer after 1. Formally including the two A vertices above and below the sheets, 309 yods shape the nine layers of vertices.

ADONAI MELEKH with number value 155 prescribes them as 309 is the 155th odd integer after 1. 247 new yods are needed to delineate the edges of the tetractyses (240 hexagonal yods on their 120 edges and seven centres). We found earlier that they are composed of 247 geometrical elements, seven of which are their centres (see Table 1). Remarkably, the 240:7 division exists for both yods and geometrical elements.

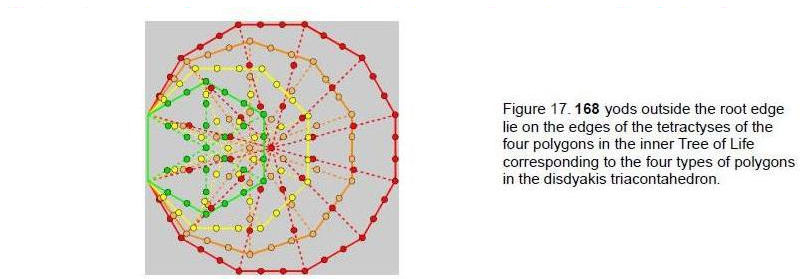
Now consider the last four regular polygons enfolded in the inner Tree of Life that are the counterparts of the polygons in one-half of the disdyakis triacontahedron. Tabulated below is the number of yods in each polygon outside the root edge, the number of centres of their tetractyses and the number of yods on the edges of tetractyses:

Table 6. Yod composition of the last four enfolded, regular polygons.

There are 168 yods in the four polygons outside the root edge on the edges of their 36 tetractyses (Fig. 17). The number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, defines the shapes of all the tetractyses that form the four polygons having counterparts in the disdyakis triacontahedron. It demonstrates the meaning of this Mundane Chakra: it expresses the form that the Tree of Life takes in the physical world. This form is the heterotic superstring and 168 is its structural parameter, as many previous articles have discussed. The first two polygons have the same number of yods (84) as the last two. Thus, there is the same 84:84 division as that which appears in the 84 edges and 84 vertices and triangles of the tetractyses in the last five polygons. This distinction manifests in the superstring as the

17

840 circularly polarised waves in the outer half of each of its 10 curves and the 840 oscillations in its inner half (Fig. 18).

We saw earlier that, associated with the first two regular polygons — the hexagon and the octagon — are 80 yods symbolizing the 80 bones of the axial skeleton, whilst the decagon and dodecagon has 126 yods symbolizing the 126 bones of the appendicular skeleton. Now we find that two pairs of polygons in a different order display an 84:84 division of yods on the boundaries of tetractyses that has significance for superstrings.

According to Table 6, the first four polygons of vertices in the disdyakis triacontahedron have 184 yods on the edges of their tetractys sectors and the 

last three polygons have 123 such yods. The seven polygons therefore have 307 yods lining their tetractyses. 307 is the 153rd odd integer after 1. This shows how the Godname ELOHIM SABAOTH of Hod with number value 153 prescribes the seven polygons of vertices.

Table 7 lists the yod populations of the seven polygons when their sectors are turned into three tetractyses:

Table 7. Yod populations of the seven polygons (three tetractyses).

		n	Number of vertices 2n+1	Number of yods 15n+1	Number of hexagonal yods 13n
1		8	16+1	12+1	104
2		10	20+1	150+1	130
	Subtotal	18	36+2	270+2	234
3		6	12+1	90+1	78
4		12	24+1	180+1	156
	Subtotal	36	72+4	540+4	468
5		6	12+1	90+1	78
6		10	200+1	150+1	130
7		8	16+1	120+1	104
	Total	60	120+7	900+7	780

120 yods are vertices surrounding their seven centres, where 120 is the 15th triangular number. The Godname YAH with number 15 also prescribes the number of yods per sector surrounding their centres. Including the seven centres and the A vertices at the apex and nadir of the disdyakis triacontahedron, there are (120+7+2=129) vertices altogether. The Godname YAHWEH SABAOTH with number value 129 therefore prescribes the disdyakis triacontahedron.

The seven polygons have 900 yods surrounding their seven centres. Article 26¹¹ showed that, when both the internal and external triangles formed by the edges of the disdyakis triacontahedron are divided into three tetractyses, it has 900 triangles. The yod population of the seven polygons is equal to the number of triangles needed to build the disdyakis triacontahedron.

An n-sided polygon has (15+1) yods when its sectors are constructed from three tetractyses. Three yods

18

19

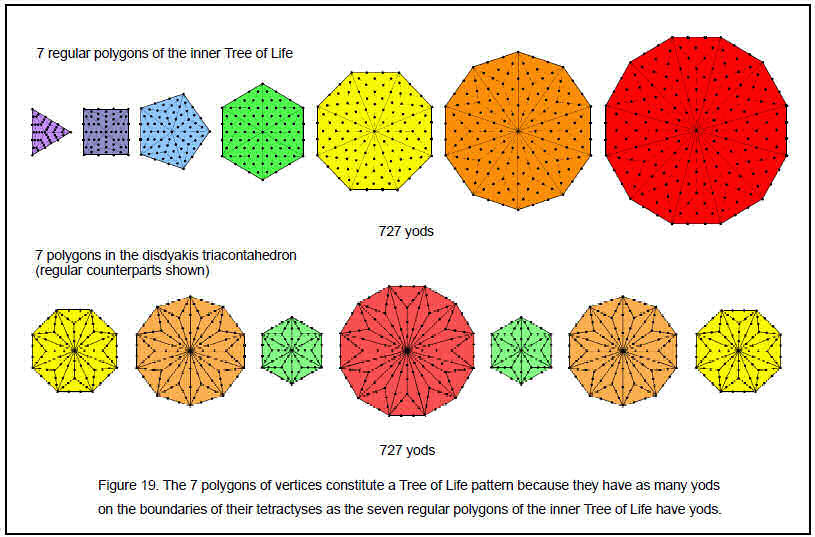
in each sector are at the centres of tetractyses, so that (12n+1) yods lie on the boundaries of the 3n tetractyses. The seven polygons have (12×60+7=727) boundary yods. 727 is the 129th prime number, showing the remarkable way in which YAHWEH SABAOTH, the Godname of Netzach (the seventh Sephirah) with number value 129, prescribes the seven layers of vertices in the disdyakis triacontahedron. 720 boundary yods surround the seven centres. This constitutes a Tree of Life pattern because the seven separate, regular polygons of the inner Tree of Life have 720 yods surrounding their seven centres when their sectors are constructed from three tetractyses. The two sets of polygons are compared in Fig. 19 (for the sake of clarity, the regular counterparts of the polygons in the seven layers are shown). It is yet more proof that the disdyakis triacontahedron is the polyhedral form of the Tree of Life.

The first four polygons have (12×36+4=436) yods on the edges of tetractyses. Of these, 76 are vertices, where 76 is the number value of YAHWEH ELOHIM, Godname of Tiphareth, leaving 360 (=36×10) yods. YAHWEH ELOHIM prescribes the first four polygons in terms of their vertices and the Godname ELOHA with number 36 prescribes those yods that are not vertices.

The first or last three polygons with 24 vertices have (12×24+3=291) yods lying on edges of tetractyses. 288 yods surround their three centres, where 288 = 1¹ + 2² + 3³ + 4⁴, showing how the integers 1, 2, 3 & 4 symbolized by the tetractys express properties of Tree of Life patterns. They have 240 geometrical elements surrounding their centres. As the seven separate polygons of the inner Tree of Life have 288 yods surrounding their centres and 240 hexagonal yods, this indicates that each set of three polygons constitute a Tree of Life pattern, just as the first four polygons do.

Table 7 indicates that the seven polygons need 907 yods to build them out of tetractyses. 907 is the 155th prime number, where 155 is the number value of ADONAI MELEKH, the Godname of Malkuth. This is a truly sublime property, for it powerfully demonstrates how the Godname of the most material Sephirah — Malkuth — arithmetically prescribes the number of yods needed to construct all seven polygons from tetractyses. ADONAI MELEKH also prescribes the fourth polygon because it has 156 hexagonal yods, where 156 is the 155th integer after 1. Article 26 showed¹² that the number of yods other than polyhedral vertices needed to construct each of its 120 faces from three tetractyses is 1560 (= 156×10), so that ADONAI MELEKH prescribes the shape of the surface of the disdyakis triacontahedron as well as its interior polygons.

The last three polygons have 363 yods. This is the number value of SHADDAI EL CHAI, the complete Godname of Yesod. It differentiates between the first four layers forming half of the polyhedron and its remaining three layers. The latter have 48 vertices surrounding their centres, that is, they have 51 vertices. 51 is the 50th integer after 1, showing how ELOHIM, the Godname of Binah with number value 50, differentiates the first four layers of vertices from the last three layers. The first two polygons have 272 yods. This is the number value of Cherubim, the Order of Angels assigned to Yesod.

The seven polygons have 187 yods that lie on internal edges of tetractyses. This is the number value of Auphanim, the Order of Angels assigned to Chokmah. The first four polygons have 112 such yods. This is the number value of Beni Elohim, the Order of Angels assigned to Hod. 36 of these are vertices, leaving 76 radial yods that are not vertices of the disdyakis triacontahedron. YAHWEH ELOHIM therefore prescribes the four layers of each half of the disdyakis triacontahedron. The number of yods other than polyhedral vertices that lie on the 300 edges of the 180 tetractyses in the first four polygons is 400 = (2+4+6+8)². This is another beautiful illustration of the Tetrad Principle because 400 is the square of the sum of the first four even integers.

6. Encoding of the superstring structural parameter 336
The disdyakis triacontahedron has 60 vertices, 180 edges and 120 triangular faces (360 geometrical elements) surrounding any axis passing through two diametrically opposite vertices. The fourth polygon of vertices forming its equator has 12 vertices and 12 edges, totalling 24 geometrical elements. (360– 24=336) elements lie above and below the equator, 168 on either side. As the polyhedron has 180 edges, there are (180–12=168) edges above and below its equator, 84 on either side. There are 48 vertices above and below the equator, 24 vertices on either side. Furthermore, there are 60 triangles on each side of the equator. Therefore, the 168 geometrical elements on each side comprise 24 vertices, 84 edges and 60 triangles, that is, 84 edges and (24+60=84) vertices and triangles. Once again, we find the 84:84 division in the superstring structural parameter 168. It is created by the mirror symmetry of the disdyakis triacontahedron whereby every geometrical element has its mirror image, both 84’s referring to the same upper or lower half of the polyhedron. Its inversion symmetry divides the 336 elements into two sets of 168 geometrical elements, one the mirror image of the other.

20

21

22

The number 336 has the beautiful property:

336 = 4×84 = 2²×(1² + 3² + 5² + 7²) = 2² + 6² + 10² + 14².

It is an illustration of the Tetrad Principle, which determines parameters of any system designed according to the blueprint of the Tree of Life.

The 12-sided polygon in the equator has 24 vertices and edges on its boundary and 24 edges and triangles in its sectors (12 edges & 12 triangles). Using the results obtained above, the pattern of elements in the disdyakis triacontahedron is set out below:

	vertices	internal edges	external edges	internal triangles	external triangles	Total
First 3 layers:	24	24	84	24	60	216
Equator:	6+6	6+6	6+6	6+6	0	48
Last 3 layers:	24	24	84	24	60	216
Total =	60	60	180	60	120	480

The first three layers have 216 internal and external geometrical elements, where 216 is the number value of Geburah. Similarly for the last three layers. The fourth polygon has 48 elements (24 internal, 24 external) surrounding its centre, totalling 49 elements. This shows how the Godname EL CHAI of Yesod with number value 49 prescribes the central polygon. 48 is the number value of Kokab, the Mundane Chakra of Hod. The seven layers have 480 geometrical elements made up of 240 elements and their 240 mirror images. Each set of 240 elements consists of 168 external ones (24 vertices, 60 triangles & 84 edges) belonging to the three layers and 72 elements comprising six vertices and six external edges of the fourth polygon, 30 internal edges and 30 internal triangles. This 72:168 division corresponds to the division of non-zero roots of the superstring gauge symmetry group E₈. The 72 elements correspond to the 72 non-zero roots of its subgroup E₆ and the 168 elements correspond to the 168 roots of E₈ that are not also roots of E₆. The geometry of the disdyakis triacontahedron therefore encodes the 480 non-zero roots of the E₈×E₈ heterotic superstring, the direct product of the two identical groups reflecting the inversion symmetry of the polyhedron, not the distinction between its exterior and interior, which creates a 120:360 division. One-half of the polyhedron encodes the forces between superstrings of ordinary matter, its mirror image half encodes the forces between superstrings of shadow matter.

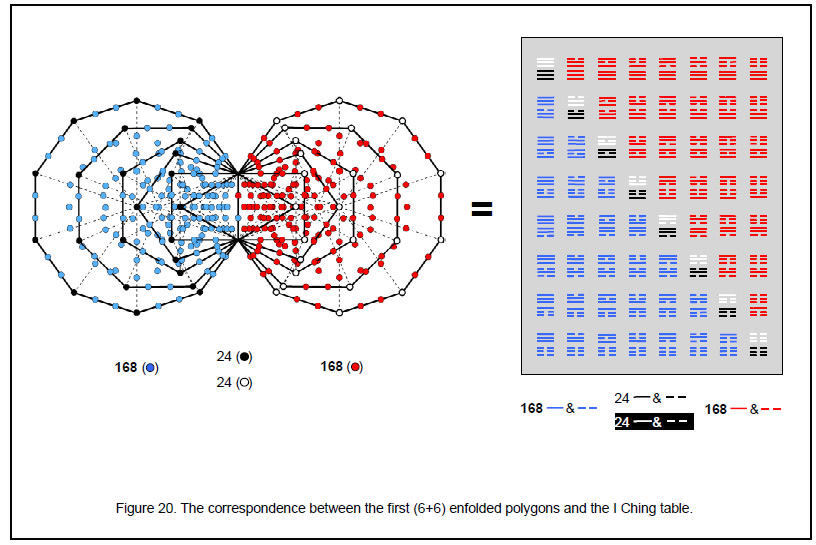
The 168:24:24:168 pattern of yods in the (6+6) polygons of the inner Tree of Life appears in the I Ching table (Fig. 20). The 24 corners outside the root edge of the first six polygons on one side correspond to

23

 

24

the 24 lines in the upper trigrams of the eight diagonal hexagrams and the 24 corners on the other side correspond to the 24 lines in the lower trigrams. The 168 yods associated with each set of polygons that are not corners correspond to the 168 lines and broken lines in the 28 hexagrams on either side of the diagonal. The fourth polygon in the disdyakis triacontahedron has (6+6) polyhedral edges, (6+6) polyhedral vertices, (6+6) internal edges and (6+6) internal triangles, that is, eight groups of six geometrical elements. They correspond to the eight diagonal hexagrams, each with six lines/broken lines. The disdyakis triacontahedron is the polyhedral counterpart of the ancient I Ching table of 64 hexagrams, each line or broken line denoting a geometrical element of its faces and internal polygons. The 12 lines and 12 broken lines in the lower trigrams of the diagonal hexagrams correspond to the 12 vertices and 12 edges of the fourth polygon. The 168 lines and broken lines in the 28 off-diagonal hexagrams in the lower half of the table correspond to the 168 geometrical elements in the faces either above or below the equator. The 12 lines and 12 broken lines in the upper trigrams of the diagonal hexagrams correspond to the 12 internal edges and 12 triangular sectors of the 12-sided polygon, whilst the 168 lines and broken lines in the hexagrams above the diagonal correspond to the 168 elements that are the mirror images of the other set. There are (48+168+168=384) elements in the faces of the disdyakis triacontahedron and in its central polygon, i.e., lines and broken lines in the I Ching Table. This is the 383rd integer after 1. 383 is the 76th prime number, showing how YAHWEH ELOHIM, Godname of Tiphareth, prescribes the disdyakis triacontahedron.

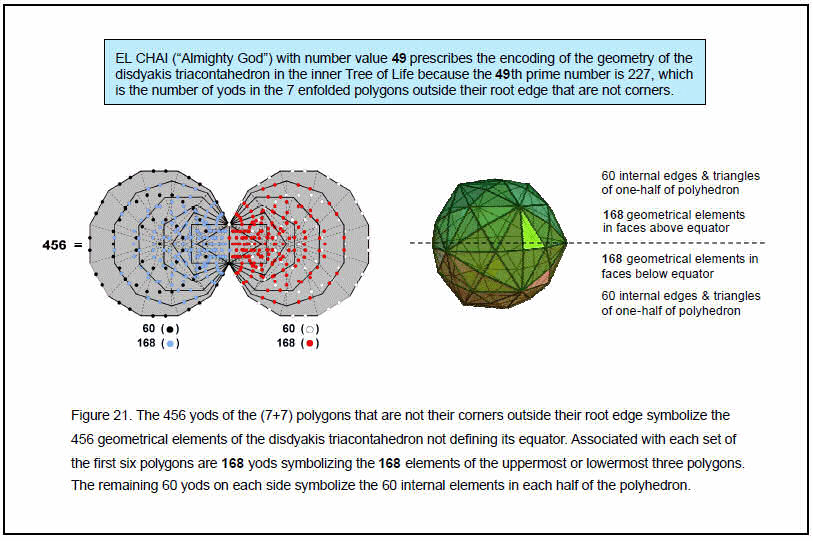
The seven polygons in the disdyakis triacontahedron have 60 internal edges and 60 internal triangles (30 edges and 30 triangles per half). Including the 168 external elements in the first three layers and similarly for the last three layers, there are (30+30+168=228) elements and their mirror images other than the 12 vertices and 12 edges in the equator of the disdyakis triacontahedron. Including the top and bottom A vertices, there are 229 elements in each half of the disdyakis triacontahedron other than its equator. 229 is the 50th prime number, showing how ELOHIM with number value 50 prescribes the disdyakis triacontahedron. Figure 21 depicts the inner Tree of Life counterpart of this. There are 228 yods other than external corners of polygons 

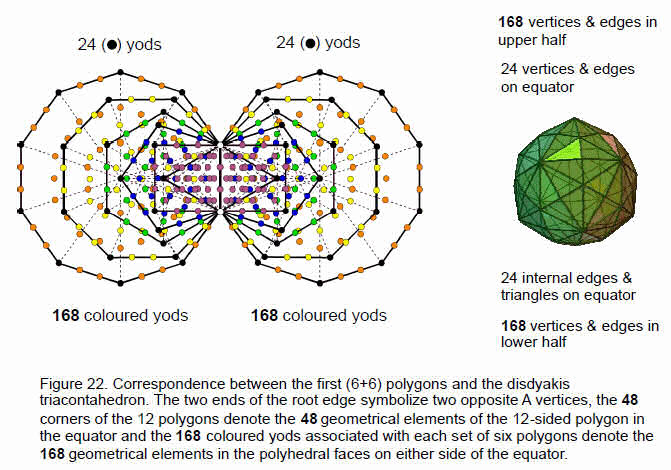
associated with each set of seven polygons (456 yods in total). Outside the root edge are 227 yods in each set of polygons other than their corners. The Divine Name EL CHAI of Yesod with number value 49 prescribes this set of yods symbolizing the geometrical elements of the seven polygons because 227 is the 49th prime number and 228 is the 227th integer after 1. Associated with either set of the first six enfolded polygons are 168 yods symbolizing the 168 elements in the three polygons above or below the equator. 60 yods symbolizing the 60 elements inside each half of the disdyakis triacontahedron are associated with each dodecagon. The first six polygons in the Tree of Life and their mirror images, reflected across the root edge, are the counterpart in the disdyakis triacontahedron of the first three layers of polygons and their mirror images, inverted through the centre of the polyhedron.

The (6+6) enfolded polygons constitute a Tree of Life pattern in themselves because they are prescribed by the ten Godnames. The simplest example of this is the fact that they have 50 corners, where 50 is the number value of ELOHIM, Godname of Binah (the complete prescription is given in Article 4).¹³ As before, the 168 yods associated with each set of the first six polygons symbolize the 168 geometrical elements in each set of three polygons, whilst the 24 corners on each side of the root edge denote the 24 vertices and edges on the equator and the 24 edges and triangles inside the polyhedron (Fig. 22). These degrees

25

of freedom mark out the boundary of the new Tree of Life pattern just as the 48 elements create the polygon that completes the sequence of polygons forming half of the disdyakis triacontahedron — a Tree of Life pattern in itself as the remainder of the polyhedron is merely its mirror image.

Figure 23 displays the equivalence between the seven layers of polygons with 60 vertices and the first (6+6) regular polygons of the inner Tree of Life. The six vertices of the fourth polygon and their mirror images correspond to the five centres and one end of the root edge on either side of the root edge. The eight vertices of the first polygon correspond to the eight external corners of the decagon. The 10 vertices of the second polygon correspond to the 10 external corners of the first four regular polygons. The six vertices of the third polygon correspond to the six external corners of the octagon. The mirror symmetry of the inner Tree of Life corresponds to the invariance of the disdyakis triacontahedron under the operation of inversion.

Figure 18 shows that each curve of the E₈×E₈ heterotic superstring makes 1680 circularly polarised oscillations as it twists five times around its axis. 336 oscillations occur during one complete revolution, 168 in each half revolution. They correspond to the 168 geometrical elements defining the shape of each set of three polygons. The 24 polyhedral vertices and edges on the equator correspond to the 24 E₈ gauge charges that are spread along each curve.

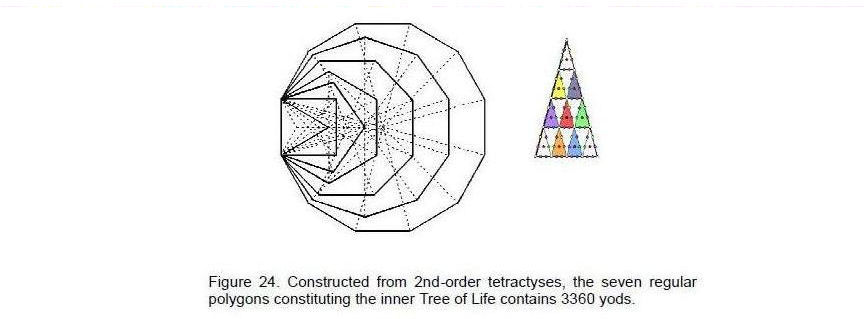
E₈×E₈ has 336 non-zero roots that do not belong to the subgroup E₆ in each factor. Their associated gauge charges are sources of 10-dimensional vector gauge fields, which therefore have 3360 components. As discussed in Article 31,¹⁴ there are 28 regular and semi-regular solids defined by the vertices of the disdyakis triacontahedron. When their faces are constructed from tetractyses, they have 3360 hexagonal yods that symbolize the seven Sephiroth of Construction. This

amazing property shows how the superstring parameter 3360 is present in the geometrical potential of the disdyakis triacontahedron as a number characterizing the forms of all the possible polyhedra within it. It is a Tree of Life parameter because, when the seven enfolded polygons of the inner Tree of Life are constructed not from the tetractys but from its next higher order — the 2nd-order tetractys — it is found to have exactly 3360 yods (Fig. 24). This is the number of circularly polarized oscillations made by all ten curves of the E₈×E₈ heterotic superstring during one complete revolution. Following through with the analogy with the 168 elements in the 60 faces of the disdyakis triacontahedron above or below its equator, it would be more accurate to associate each set with the inner or outer half of the superstring curves, so that the 168 elements in one set correspond to 168 oscillations in an outer half-revolution and the 168 elements in the other set correspond to the 168 oscillations made as the curve winds in a half revolution in the core of the

26

superstring. It is truly remarkable that the same number 168 should be encoded not only in the faces above or below the equator but also in the fourth polygon forming the equatorial plane as the extra number of yods needed to construct its 12 sectors from three tetractyses!

6. The Platonic Lambda
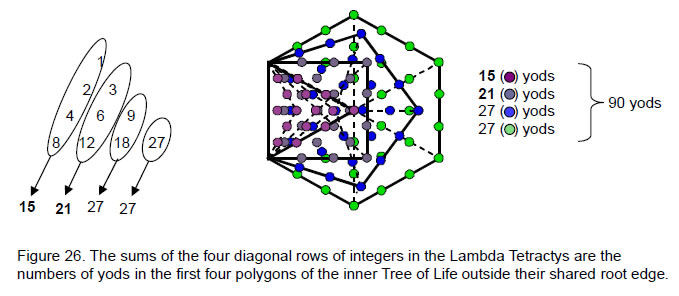
In his Timaeus, Plato described how the Demiurge measured the World Soul, or substance of the spiritual universe, as a strip divided according to the simple proportions of the first three squares of 2 and 3. This is traditionally represented by his ‘Lambda,’ so-called because of its resemblance to the Greek letter Λ (Fig. 25). These numbers line two sides of a tetractys array of ten numbers from whose relative proportions the scientists and musicians of ancient Greece worked out the frequencies of the notes of the now defunct Pythagorean musical scale.¹⁵ The numbers missing from the Lambda are shown in red in Fig. 25. The sum of the 10 integers is 90 and the sum of the integers 1, 8 and 27 at the corners of the tetractys is 36. The seven integers at the centre and corners of the hexagon shown in Fig. 25 with dashed edges add up to 54 and the sum of the integers at the corners of the hexagon is 48.

The archetypal nature of this arrangement of integers was demonstrated in previous articles. It is known today for how it generates the tone ratios of the notes of the Pythagorean musical scale, the ancient father of the modern equal-tempered scale. What is not realised by historians of music and mathematics is that it has connections to the I Ching table,¹⁶ superstrings,¹⁷ the seven musical scales¹⁸ and the nature of the spiritual cosmos.¹⁹ This is because it is the arithmetic representation of the universal Tree of Life pattern underlying these examples of holistic systems. The first four enfolded polygons in the inner form of the Tree of Life have 90 yods outside their shared edge (Fig. 26). This is the sum of the ten numbers of the Lambda Tetractys. This cannot be coincidental because the yod

populations of the individual polygons are also the sums of diagonal rows of integers in the Lambda! Indeed, the individual numbers in each diagonal row can be seen to denote different sets of yods in each polygon (Fig. 27)! They are listed below:

Triangle
1 centre;
2 2 hexagonal yods on horizontal edge of tetractys;
4 4 hexagonal on 2 internal edges;
8 8 yods on edges of triangle & at centres of 3 tetractyses.

Square
3 centre & 2 corners;
6 6 hexagonal yods on sides of square;
12 12 internal hexagonal yods.

Pentagon
9 9 yods at corners & centres of 5 tetractyses;
18 18 hexagonal yods.

Hexagon
27 27 yods.

Article 26²⁰ showed how the Lambda Tetractys matches the tetractys composition of the disdyakis

27

triacontahedron. Constructed from tetractyses, its 120 triangular faces divide into (120×3=360) tetractyses. Each of its 180 edges is the side of an internal triangle formed by two vertices and its centre. They are constructed from (180×3=540) tetractyses. The total number of tetractyses forming the disdyakis triacontahedron = 360 + 540 = 900. The following correspondences appear:

Lambda Tetractys		Disdyakis triacontahedron
Sum of 10 integers = 90		number of tetractys = 900 = 90×10;
Sum of integers at corners = 36		number of tetractyses in faces = 360 = 36×10;
Sum of integers at centre and corners of hexagon = 54		number of internal tetractyses = 540 = 54×10;
Integer at centre = 6		number of internal tetractyses having edges of rhombic triacontahedron = 60 = 6×10;
Sum of integers at corners of hexagon = 48		number of internal tetractyses without edges of rhombic triacontahedron = 480 = 48×10;
Sum of integers surrounding centre = 84		number of tetractyses without edges of rhombic triacontahedron = 840 = 84×10.

The numbers 1³, 2³ and 3³ at the shape-defining corners of the Lambda Tetractys add up to 36, which is the number of tetractyses whose yod population is the number of tetractyses creating the shape of the disdyakis triacontahedron. The seven numbers located at the centre and corners of a hexagon add up to 54 — the number of tetractyses whose yod population is the number of tetractyses inside the disdyakis triacontahedron. Notice that the number 36 — the number value of the Godname ELOHA — defines the external shape in both cases and that the number 54 in both cases defines the interior. Moreover, the largest of the seven integers in the hexagon is 18, whilst the number of internal tetractyses creating the 180 edges is 180 = 18×10. Lastly, of the 900 tetractyses in the disdyakis triacontahedron, 60 (=6×10) are tetractyses having edges that are edges of the rhombic triacontahedron, leaving 840 (=84×10) tetractyses other than these. The integer 6 at the centre of the Lambda Tetractys therefore corresponds to the 60 internal tetractyses of the disdyakis triacontahedron sharing edges with the rhombic triacontahedron, whilst the sum (84) of the integers on the boundary of the Lambda Tetractys correspond to the 840 additional tetractyses needed to construct the disdyakis triacontahedron. Six arithmetic properties of the Lambda Tetractys correlate precisely with the geometry of the disdyakis triacontahedron. This cannot be coincidental. Instead, it demonstrates that the Lambda Tetractys and the disdyakis triacontahedron are, respectively, arithmetic and geometric expressions of the same universal archetype expressing the holistic nature of God.

Table 7 indicates that the seven polygons formed by the vertices of the disdyakis triacontahedron have 900 yods surrounding their centres, that is, the number of yods in 90 tetractyses. The first four polygons in half the disdyakis triacontahedron have 540 yods surrounding their centres. This is the number of yods in 54 tetractyses. The remaining three polygons have 360 yods surrounding their centres — the number of yods in 36 tetractyses. This 54:36 division is identical to that displayed by the Lambda Tetractys. 60 yods of the fourth (12-sided) polygon other than its centre lie on its sides and on radial edges of tetractyses — the number of yods in six tetractyses. They correspond to the number 6 at the centre of the Lambda Tetractys. There remain 480 yods surrounding the centres of the first four polygons — the number of yods in 48 tetractyses. They correspond to the sum (48) of the integers at the corners of the hexagon in the Lambda Tetractys. There are (900–60=840) yods in the seven polygons not lying on the sides of the fourth polygon and radial edges of tetractyses. They correspond to the sum of the integers surrounding the integer 6 at the centre of the Lambda Tetractys.

As

29² – 1 = 840 = 3 + 5 + 7 + 9 + … + 57,

the second perfect number 28 defines the number 840 because the latter is the sum of the first 28 odd integers after 1. The third perfect number 496 is the dimension of the two possible gauge symmetry groups of superstrings (SO(32) and E₈×E₈). As discussed in Section 5, 840 is also the number of circularly polarised oscillations made during 2½ revolutions in an outer or inner half of each of the ten closed curves making up the heterotic superstring (see Fig. 18). As the seven polygons have 900 yods around their centres, of which 60 are vertices of the disdyakis triacontahedron, 840 yods surround their centres that are not polyhedral vertices. In other words, 840 extra yods are needed to construct the seven polygons from tetractyses. The appearance of the superstring structural parameter 840 in the polygons formed by the vertices of the disdyakis triacontahedron is astounding and demonstrates the form-creating character of this number. It was encountered earlier in the analysis of the disdyakis triacontahedron, when it was found to have 840 tetractyses not sharing edges with the 60 edges of the rhombic triacontahedron formed by B and C vertices. The seven polygons therefore collectively encode both the

28

form of the superstring and its gauge symmetry group E₈. As we saw earlier, the central polygon needs 168 extra yods to construct it from tetractyses. It, too, embodies a superstring structural parameter, for each closed curve of the heterotic superstring makes 168 oscillations during half of a complete revolution around its spin axis.

To summarise, the following remarkable correspondences exist between the Lambda Tetractys, the disdyakis triacontahedron and the seven polygons formed by its vertices:

Lambda Tetractys		Disdyakis triacontahedron		7 Layers
Sum of 10 integers = 90		900 (=90×10) tetractyses		900 (=90×10) yods surround 7 centres;
Sum of integers at corners = 36		360 (=36×10) tetractyses in 120 faces		360 (=36×10) yods in lowest 3 polygons surround 7 centres;
Sum of integers at centre and corners of hexagon = 54		540 (=54×10) tetractyses inside polyhedron		540 (=54×10) yods in first 4 polygons surround 7 centres;
Integer at centre = 6		60 (=6×10) internal tetractyses with edges of rhombic triacontahedron		60 (=6×10) yods on edges of sectors of 4th polygon surround 7 centres;
Sum of integers at corners of hexagon = 48		480 (=48×10) internal tetractyses do not share edges of rhombic triacontahedron		480 (=48×10) other yods in first 4 polygons surround 7 centres;
Sum of integers surrounding centre = 84		840 (84×10) tetractyses do not share edges of rhombic triacontahedron		840 (=84×10) yods surround centres other than those on edges of 4th polygon

The amazing parallels demonstrate the holistic nature of the disdyakis triacontahedron because the construction of both its external shape and its seven interior polygons from tetractyses conforms to the archetypal Lambda Tetractys array of integers, whose ratios determine the tone ratios of the notes of the Pythagorean musical scale.

The corners of a tetractys symbolize the Supernal Triad and its seven hexagonal yods denote the seven Sephiroth of Construction. The former correspond to the three lowest layers and the latter correspond to the first four layers in half the polyhedron. The yod at the centre of a tetractys symbolizes Malkuth, the lowest Sephirah signifying the material aspect of the Tree of Life, e.g., the physical universe. Its counterpart in the seven layers of the disdyakis triacontahedron is the form-generating boundary of the 12 sectors of the polygon in the central layer of vertices.  This is delineated by 60 yods (36 yods on the edges of the 

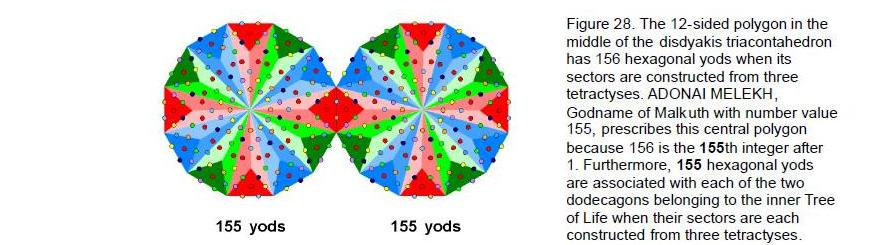
polygon and 24 yods inside it). Division of these sectors into three tetractyses requires 168 more yods (see Fig. 13). This is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, confirming the correspondence with Malkuth of the number 6 at the centre of the Lambda Tetractys and the 12-sided polygon as the middle layer of the disdyakis triacontahedron. The 12-sided polygon has 156 hexagonal yods, where 156 is the 155th integer after 1, showing how ADONAI MELEKH, the Godname of Malkuth, prescribes this polygon. 155 is also the number of hexagonal yods associated with each

29

dodecagon in the inner Tree of Life when each of its 12 sectors is divided into three tetractyses (Fig. 28). The number 156 is also the sum of the first 12 even integers that can be assigned to the vertices of a 12-sided polygon (Fig. 29). Remarkably, it is the sum of the letter values of all possible combinations of the Divine Name YHVH assigned to Chokmah with number value 26:

		Y = 10, H = 5, V = 6
Y + H + V	=	21
YH + HV + YV + HH	=	52
YHV + HVH + HYH	=	57
YHVH	=	26
TOTAL	=	156

This illustrates the mathematical power in a Godname, for the disdyakis triacontahedron is the 26th of the family of 13 Archimedean solids and their duals — the 13 Catalan solids, and so it is chosen by YAHWEH as the mother shape encoding the archetypal pattern of the form of the Tree of Life.

According to Table 7, the number of hexagonal yods in the seven polygons is 780. This is the sum of the first 12 multiples of 10 that can be assigned to its 12 corners:

780 = 10 + 20 + 30 + … + 120.

The 12-sided dodecagon is the tenth regular polygon and 120 is the sum of the first ten odd integers:

120 = 3 + 5 + 7 + … + 21.

The number 10 or Decad was called “All Perfect” by the ancient Pythagoreans. We see that it defines 1. the 120 vertices surrounding the centres of the seven polygons when they are constructed from tetractyses, 2. the 780 hexagonal yods that these tetractyses contain and 3. — through the Lambda Tetractys, when its numbers are multiplied by 10 — the 900 yods that surround their centres. Truly, 10 is the measure of divine perfection, whose polyhedral manifestation is the

disdyakis triacontahedron.

7. Encoding of the superstring parameters 840 & 1680
Considered as tetractyses, the 60 sectors of the seven polygons are made up of 360 yods surrounding their seven centres. Four of their 60 edges connect pairs of A vertices (see the 10-sided polygon in Figures 3 & 4). These are not edges of the disdyakis triacontahedron. The seven polygons share 56 sides with it, leaving (180–56=124) unshared edges. Each one has two hexagonal yods. The 124 unshared edges have (124×2=248) hexagonal yods. This is the dimension of the superstring gauge symmetry group E₈. There are nine hexagonal yods inside each of the 120 faces of the disdyakis triacontahedron when divided into three tetractyses, i.e., (120×9=1080) hexagonal yods, and 120 vertices, totalling 1200 yods. The polygons have four sides with eight hexagonal yods unshared with the faces of the disdyakis triacontahedron. They have (360–8=352) yods that are either inside them or lying on edges shared with the polyhedron. The faces and internal polygons of the disdyakis triacontahedron have (248+1080+120+352=1800) such yods. Of these, (1800–120=1680) are yods that are not vertices inside faces. Other than the vertices of the polyhedron, they are all hexagonal yods. Its mirror symmetry means that every one of the 840 yods in one half of the polyhedron has a yod that is its mirror image. This 840:840 division manifests in the E₈×E₈ heterotic superstring as the 840 circularly polarized waves in its outer half and the 840 waves in its inner half (see Fig. 18). Divided into three tetractyses, a face of the disdyakis triacontahedron has three internal edges, three triangles and a vertex, making seven geometrical elements. The 120 faces therefore have (7×120=840) elements inside them. The appearance again of the number 840 is further evidence that the disdyakis triacontahedron encodes the oscillatory form of the E₈×E₈ heterotic superstring.

30

A polygon with n sides has (15n+1) yods, that is, 14n yods other than its internal corners of tetractyses and centre. The first three polygons with 24 edges have (14×24=336) such yods, as have the last three polygons. The fourth polygon with 12 sides has (14×12=168) yods other than internal corners and centres. All seven polygons have (336+168+336=840) such yods (60 vertices of polygons and 780 hexagonal yods). Once again, we see this structural parameter of the heterotic superstring encoded in the seven polygons. The 240 vertices and edges of the disdyakis triacontahedron create 840 geometrical elements making up

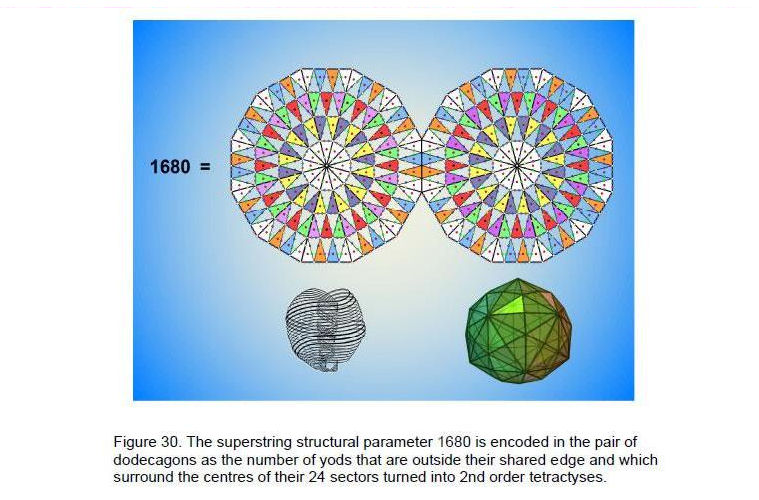
the interior of the faces of the disdyakis triacontahedron and 840 yods other than its vertices making up its seven layers of polygons. Figure 30 shows the counterpart in the inner Tree of Life of this representation of the inner and outer halves of the heterotic superstring. When the 24 sectors of the pair of dodecagons are changed into 2nd-order tetractyses, there are 1680 yods outside their root edge surrounding their centres, 840 yods in each polygon. The two dodecagons correspond to the two halves of the disdyakis triacontahedron. The (12+12=24) sectors signify the 24 gauge bosons of E₈ whose charges are spread along each curve as 1680 circularly polarised waves. They correspond in the disdyakis triacontahedron to the 12 vertices and 12 edges on its equator.

The 840 yods in the seven polygons include the eight hexagonal yods of the four A-A edges of the 10-sided polygon on the second level that are not shared with the polyhedron and which are excluded from the 1680 hexagonal yods and polyhedral vertices calculated above. The seven polygons therefore have (840–8=832) yods made up of 60 polyhedral vertices and 772 hexagonal yods other than the unshared hexagonal yods on the four edges, that is, 833 yods when the topmost A vertex is included. 833 is the number value of Chaioth ha Qadesh (“Holy Living Creatures”), the Order of Angels assigned to Kether. Starting from a point, 833 more yods are needed to construct from tetractyses the seven sheets of vertices and the lowest A vertex. Kether is the seed point from which the Tree of Life grows.

31

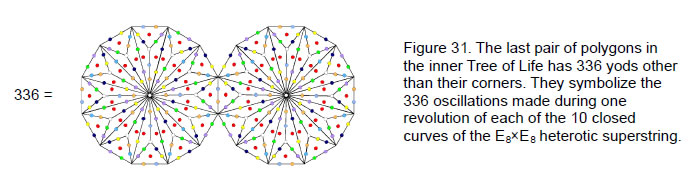
The 56 edges of the polygons shared with the disdyakis triacontahedron define 56 tetractyses with (6×56=336) yods surrounding their centres. 168 yods are in the 28 tetractyses in each half of the polyhedron. 84 yods lie on their edges and 84 yods are inside them. The 168:168 pattern is the same as that displayed by the edges of the disdyakis triacontahedron above and below its equator. The four shared edges not included in the counting have 24 yods, just as the 12 edges in the 12-sided polygon in the equator have 24 hexagonal yods. In fact, the pair of dodecagons in the inner Tree of Life has 336 yods other than their corners, 168 in each one (Fig. 31).

The 56 sectors of the polygons whose edges are shared with the disdyakis triacontahedron have 840 yods surrounding their centres when they are divided into three tetractyses. This is the same as the number of yods other than corners in all 60 sectors of the seven polygons. In the former case, we have 56×15 = 840, where 15 is the number of yods per sector; in the latter, we have 60×14=840, where 14 is the number of yods per sector other than corners. Amazingly, both cases encode the same superstring parameter 840. However, as each sector has 10 geometrical elements (two vertices, five edges and three triangles), the 56 sectors have (56×10=560) elements. Each set of 28 sectors has 280 elements. 280 is the number value of Sandalphon, Archangel of Malkuth. This is a remarkable conjunction in the same context of the number values of an Archangel and Mundane Chakra of the same Sephirah, for we have just seen that the 28 sectors have 168 yods surrounding the centres of their polygons and 168 is the number value of the Mundane Chakra of Malkuth.

The 56 shared edges have (2×56=112) hexagonal yods. 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod. There are also 112 hexagonal yods on the 56 radial edges of the 56 sectors. Including the seven centres, 119 yods line the sectors. The disdyakis triacontahedron has 180 edges and 62 vertices, so that (180×2+62=422) yods lie on its edges. (119+422=541) yods line the edges of the polyhedron and the 56 sectors of its polygons. Two of these are the top and bottom A vertices. (541–2=539) yods other than these vertices therefore line the (180+56=236) edges. Amazingly, 539 is the sum of the Godname numbers of the seven Sephiroth of Construction:

31 + 36 + 76 + 129 + 153 + 49 + 65 = 539.

This demonstrates the constructive power of the Divine Names.

The faces of the disdyakis triacontahedron have the top and bottom A vertices, 124 edges and 120 triangles that it does not share with the seven polygons, that is, 246 geometrical elements. This is the number value of Gabriel, the Archangel of Yesod.

There are 127 yods on the internal edges of all 60 sectors of the polygons. There are (422+127=549) yods lining both polyhedral edges and polygonal sectors. Excluding the centres of the three polygons on each side of the equatorial plane, there are 543 boundary yods. This is the number value of EHYEH ASHER EHYER (“I am that I am”), the complete Godname assigned to Kether.

With its faces constructed from three tetractyses, the disdyakis triacontahedron has seven yods lying on edges of tetractyses inside each face.

   

32

There are (120×7=840) such yods. Together with its 62 vertices and 360 hexagonal yods lying on its edges, the polyhedron has (840+62+360= 1262) boundary yods, that is, 1260 yods other than its two opposite A vertices. This is the number value of Tarshishim, the Order of Angels assigned to Netzach.

Of the 541 yods lining the edges of the polyhedron and the 56 sectors with edges shared with it, 67 are vertices of the polygons. (541–67=474) yods other than vertices lines these edges, creating their shapes. 474 is the number value of Daath (“knowledge”), the non-Sephirah. The number 539 is the sum of 474 and 65, the number value of ADONAI, Godname of Malkuth. It measures “knowledge of the Lord”.

8. The two sets of three polygons
The seven Sephiroth of Construction of the Tree of Life are grouped above Malkuth into two triads: Chesed–Geburah–Tiphareth and Netzach–Hod–Yesod (Fig. 32). In terms of human psychology, they represent, respectively, the transpersonal levels of human consciousness and the incarnated personality (loosely, “Spirit” and “Soul,” respectively). The two sets of three polygons above and below the equatorial plane of the disdyakis triacontahedron correspond to this 3:3 pattern, with the Malkuth aspect represented by the 12-sided polygon, the last of the enfolded polygons of the inner Tree of Life, which we saw earlier embodies the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth (see Fig. 13). A polygon and its mirror image are the counterpart of two Sephiroth of Construction on the same pillar.

9. The Godnames prescribe the seven layers of polygons
Below are listed the ways in which the Godnames of the ten Sephiroth mathematically define properties of the seven layers of vertices in the disdyakis triacontahedron between two diametrically opposite A vertices:

 

Kether	EHYEH: 21	disdyakis triacontahedron has 21 layers in 3 perpendicular sets of 7; 21 A and B vertices in first 4 polygons and their 21 mirror images; 41 vertices of sectors in first 4 polygons (including top A vertex). 41 = 21st odd integer after 1; 5 lowest polygons with 168 geometrical elements have 42 sectors. 42 = 21st even integer; 210 (=21×10) hexagonal yods in last 5 polygons; 73 yods in 4th polygon. 73 = 21st prime number;
	EHYEH ASHER EHYEH: 543	543 yods other than centres of 1st three polygons on each side of equator lie on the edges of the disdyakis triacontahedron and sectors of 7 polygons.
Chokmah	YAH: 15	15 Golden Rectangles in 3 perpendicular sets of 5; 15 sets of seven layers created by 15 opposite pairs of A vertices; 15 A vertices in half of disdyakis triacontahedron and their 15 mirror images; 47 vertices of sectors of lowest 5 polygons. 47 = 15th prime number; 120 vertices of 180 tetractyses in 7 polygons surround their centres. 120 = 1 + 2 + 3 + … + 15;
	YAHWEH: 26	26 A and B vertices (or A and C vertices) in first 4 polygons; 51 vertices in first (or last) 3 polygons. 51 = 26th odd integer.
Binah	ELOHIM: 50	229 geometrical elements in each half of polyhedron (including top or bottom A vertex). 229 = 50th prime number; 51 vertices in first (or last) 3 polygons. 51 = 50th integer after 1.
Chesed	EL: 31	31 vertices in each half of polyhedron; 127 vertices of sectors of 7 polygons. 127 = 31st prime number
Geburah	ELOHA: 36	360 (=36×10) geometrical elements in faces surround axis; 36 vertices of first 4 polygons; 36 yods along perimeter of 4th polygon; 360 (=36×10) geometrical elements surround centres of first 4 polygons with 36 vertices/sectors; 360 (=36×10) yods surround centres of 7 polygons; 360 (=36×10) hexagonal yods on boundaries of 108 tetractyses in first 4 polygons.
Tiphareth	YAHWEH ELOHIM: 76	76 vertices of tetractyses in first 4 polygons; 384 elements in faces of disdyakis triacontahedron and in central, 12-sided polygon. 384 = 383rd integer after 1. 383 = 76th prime number.

33

Netzach	YAHWEH SABAOTH: 129	129 vertices in 180 tetractyses of 7 polygons, including the top and bottom A vertices; 727 yods on boundaries of 180 tetractyses in 7 polygons. 727 = 129th prime number.
Hod	ELOHIM SABAOTH: 153	307 yods on boundary of 60 sectors of 7 polygons. 307 = 153rd integer after 1.
Yesod	EL CHAI: 49	49 geometrical elements in 4th polygon; 49 yods in first (or last) polygon.
	SHADDAI EL CHAI: 363	363 yods in first (or last) 3 polygons
Malkuth	ADONAI: 65 ADONAI MELEKH:155	129 vertices in 180 tetractyses of 7 polygons. 129 = 65th odd integer; 907 yods in seven polygons. 907 = 155th prime number.

The last property is perhaps the most remarkable of these demonstrations of the power of Godnames to define properties of a Tree of Life system such as the disdyakis triacontahedron. Very aptly, the number value of the Godname of the Sephirah Malkuth signifying the outer form of the Tree of Life defines a prime number that is the very number of yods creating the complete form of the seven polygons!

References
¹ Phillips, Stephen M. Article 32: "Derivation of the Bones & Classical Acupoint Compositions of the Human Body and Their Relationship to the Seven Musical Scales,” (WEB, PDF).

² Phillips, Stephen M. Article 33: "The Human Axial Skeleton is the Trunk of the Tree of Life,” (WEB, PDF).

³ Phillips, Stephen M. Article 15: “The Mathematical Connection Between Superstrings and Their Micro-psi Description: a Pointer Towards M-theory,” (WEB, PDF), p. 13.

⁴ Phillips, Stephen M. Article 18: “Encoding of Planetary Distances and Superstring Structural Parameters in the I Ching Table," (WEB, PDF), p. 19.

⁵ Phillips, Stephen M. Article 21: “Isomorphism Between the I Ching Table, the 3×3×3 Array of Cubes and the Klein Configuration,” (WEB, PDF), pp. 3–4.

⁶ Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence With Octonion Algebra and Superstrings,” (WEB, PDF).

⁷ Phillips, Stephen M. Article 26: “How the Seven Musical Scales Relate to the Disdyakis Triacontahedron,” (WEB, PDF), p. 15.

⁸ Besant, A. and Leadbeater, C.W. Occult Chemistry, 3rd ed., Theosophical Publishing House, Adyar, Chennai, India, 1951.

⁹ Ibid, p. 14.

¹⁰ Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 5.

¹¹ Ref. 7, p. 20.

¹² Ibid, p. 16.

¹³ Phillips, Stephen M. Article 4: “Godnames Prescribe Inner Tree of Life,” (WEB, PDF), pp. 2–5.

¹⁴ Phillips, Stephen M. Article 31: “The Musical Nature of the Polyhedral Tree of Life,” (WEB, PDF), pp. 30–31.

¹⁵ Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).

¹⁶ Phillips, Stephen M. Article 20: “Algebraic, Arithmetic and Geometric Interpretations of the I Ching Table,” (WEB, PDF), pp.18–22.

34

¹⁷ Ref. 14, p. 7.

¹⁸ Ibid, pp. 2–3, and Article 12, “New Pythagorean Aspects of Music and Their Connection to Superstrings,” (WEB, PDF), pp. 2–4.

¹⁹ Ibid, pp. 3–7.

²⁰ Ref. 7, pp. 28–29.

35