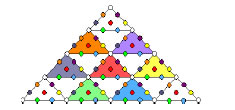
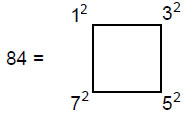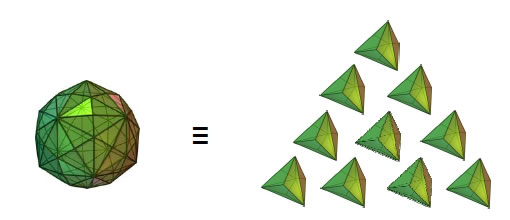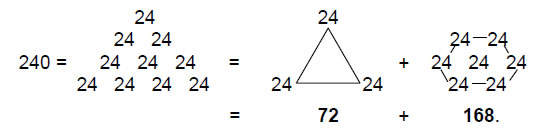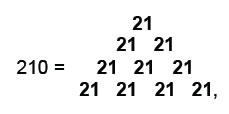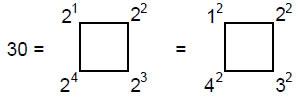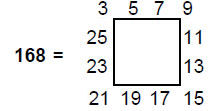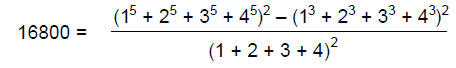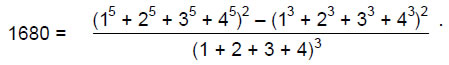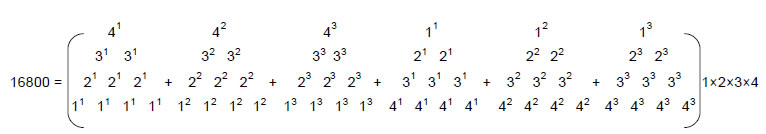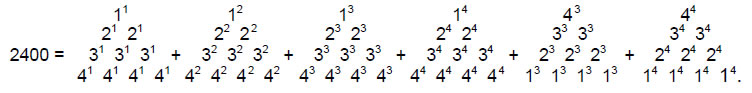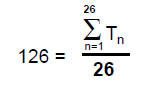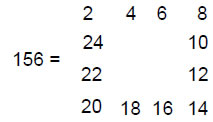ARTICLE 27
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.Website: http://smphillips.mysite.com
Abstract
|
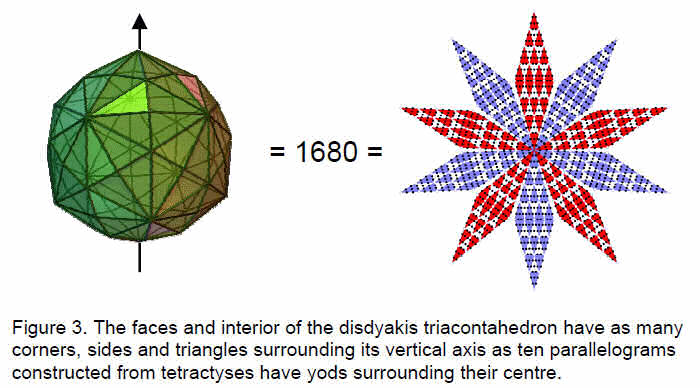
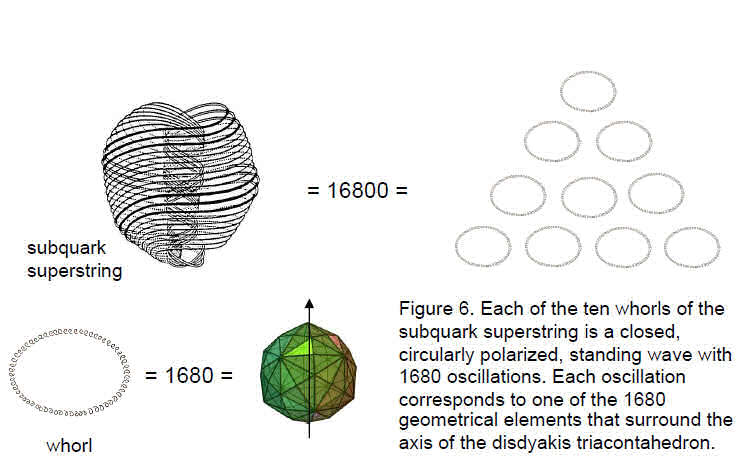
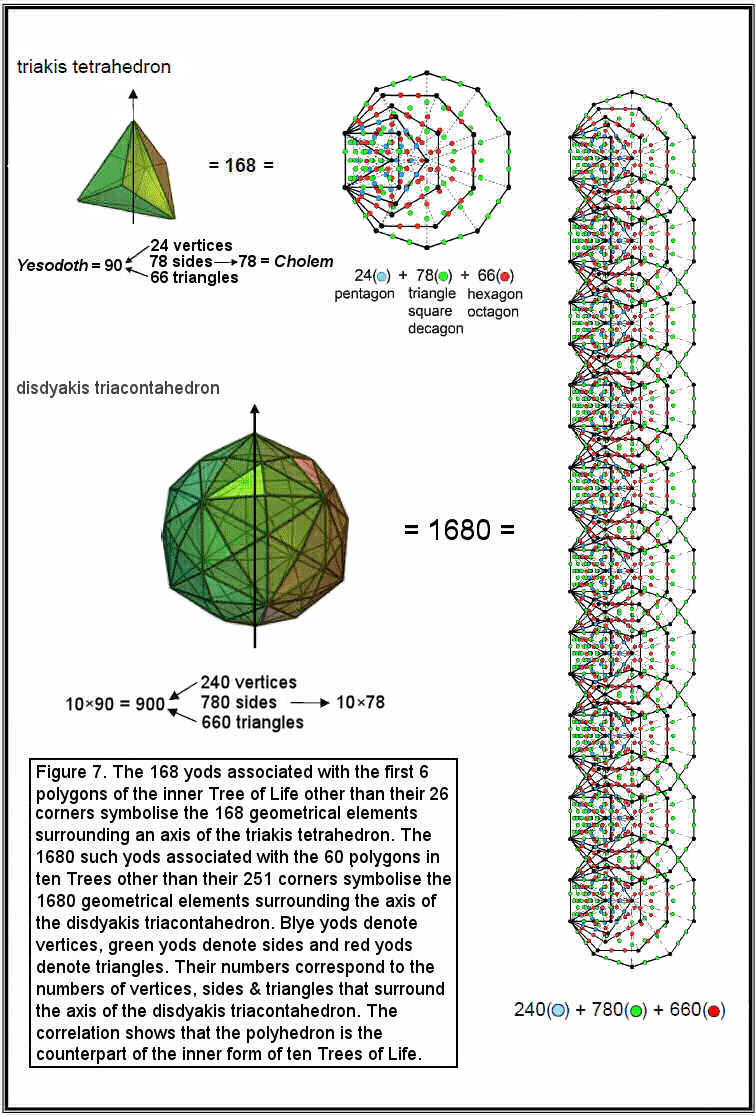
The Pythagorean tetractys of ten points (‘yods’) symbolises the geometrical sequence: point, line, triangle and tetrahedron. Its next higher-order differentiation has 85 yods that denote the 85 geometrical elements needed to construct the tetrahedron from tetractyses. The 15 Archimedean solids and their duals — the 15 Catalan solids — can likewise be constructed from this template. Starting from its centre, the construction of the truncated tetrahedron requires 248 geometrical elements. The simplest Archimedean solid therefore embodies the dimension 248 of the superstring gauge symmetry group E8. Its dual, the triakis tetrahedron, has 168 geometrical elements surrounding the axis passing through two opposite vertices. The simplest Catalan solid therefore embodies the superstring structural parameter 168 discussed by the author in many previous articles. Its 78 edges and 90 vertices and triangles correspond to the gematria number values of the Hebrew words ‘Cholem’ and ‘Yesodoth’ in the Kabbalistic Mundane Chakra of Malkuth. This geometrical composition has its exact counterpart in the yod population of the first six regular polygons of the inner Tree of Life. When its faces are constructed from three tetractyses, the triakis tetrahedron has 240 elements surrounding its axis, i.e., 72 extra ones. E8 has 240 non-zero roots, of which 72 are also non-zero roots of its exceptional subgroup E6. The disdyakis triacontahedron has 1680 geometrical elements surrounding its axis. This is the number of circularly polarised oscillations in each of the ten whorls of the ‘ultimate physical atom’, the basic unit of matter described paranormally 105 years ago by Annie Besant and C.W. Leadbeater and identified in earlier work by the author as the spin-½ subquark state of the E8×E8 heterotic superstring. The most complex Catalan solid therefore embodies in its geometry the number characterising the oscillatory form of the superstring. The geometrical composition of this solid is represented by the yod population of the first six polygons enfolded in ten Trees of Life. The disdyakis triacontahedron is their polyhedral counterpart. The numbers of geometrical elements in the triakis tetrahedron are the numbers of non-zero roots of E8, E7 and E6. The disdyakis triacontahedron has corresponding numbers that are ten times as large, demonstrating its ten-fold Tree of Life nature. |
1
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living Creatures)
833
Rashith ha Gilgalim
First Swirlings
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation of God)
311
Aralim
(Thrones)
282
Shabathai
Rest
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness
(Jupiter)
1945 Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength
(Mars)
956 Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light
(Sun)
6407 Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97Tarshishim or Elohim
1260
Nogah
Glittering Splendour
(Venus)
648 Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light
(Mercury)
489 Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame
(Moon)
8710 Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351
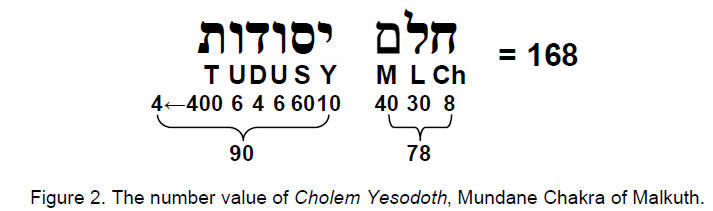
Cholem Yesodoth
The Breaker of the Foundations
The Elements.
(Earth)
168
2
1. Introduction
The Pythagorean tetractys is a triangular array of ten dots:
These dots will be called ‘yods.*The six yods at the corners of a hexagon and the yod at its centre will be called ‘hexagonal yods.’ They are shown above as coloured circles.
The four rows of points in the tetractys symbolise the sequence of what mathematicians call the first four “simplexes”:
As the 3-simplex, the tetrahedron consists of 4 vertices (0-simplexes) and 6 edges (1-simplexes) (i.e., ten simplexes), 4 triangles and one tetrahedron (i.e., 5 simplexes), totalling 15 simplexes. The simplest regular polyhedron is prescribed by the Godname YAH (YH) assigned to Chokmah in the Tree of Life (Table 1) with number value 15,1 the value 10 of Y (yod) denoting the number of 0-simplexes and 1-simplexes and the value 5 of H (he) denoting the number of 2-simplexes and 3-simplexes. The complete Godname YAHWEH (YHVH) prescribes the sequence of the first four simplexes because it contains 26 vertices, edges, triangles and tetrahedra:
The letter values of Y and H are as above, the value 6 of V (vav) is the number of 0-simplexes in the first three simplexes (shown encircled above) and the value 5 of the second letter H is the number of 1- and 2-simplexes in the 1-simplex and the 2-simplex.
Any polyhedron can be constructed from tetractyses by dividing its polygonal faces into triangular sectors and then changing the latter into tetractyses — it does not matter whether these sectors are equilateral or isosceles triangles. The edges of the polyhedron are also sides of internal triangles formed by joining its centre to two adjacent vertices. These triangles can be constructed from three tetractyses. For consistency, a polyhedron that has both triangular faces and faces of other shapes must have the former divided into three tetractyses rather than be considered as single ones. However, if all its faces are triangular, there are two possible constructions: either each face is a tetractys (case A) or each face is divided into three tetractyses (case B).
With its faces and internal triangles formed by its edges single tetractyses (case C), the tetrahedron contains also one internal corner (its centre) and 4 internal sides of triangles (totalling 5 elements) and 6 triangles, a total of 11 geometrical elements. This is the same as the number of elements in the first three simplexes, as shown above. Starting from a point (centre), 24 more points, lines and triangles have to be put in place before the interior and exterior of the tetrahedron can be constructed from triangles.
____________________________________________
* The tenth letter of the Hebrew alphabet is yod ( י), which looks somewhat like a dot.
3
With its faces and internal triangles divided into three tetractyses (case B), the geometrical composition of the tetrahedron is:
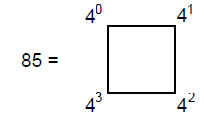
+ + = + + = + + = It has 15 vertices prescribed by YAH with number value 15 and 26 corners & sides in its faces defined by YAHWEH with number value 26. It has 70 sides & triangles and 85 corners, sides & triangles. This property proves its wholeness and perfection as the fundamental building block of solid geometry, for the next higher order tetractys — the 2nd-order tetractys:
has 85 yods. Each yod symbolises a geometrical element needed to construct the tetrahedron. The 15 (white) yods at the corners of the ten tetractyses denote the 15 vertices of the tetractyses forming the tetrahedron and the 70 hexagonal (coloured) yods denote the 70 sides & triangles. The Godname ELOHA with number value 36 prescribes this symbol of the simplest regular polyhedron because 36 yods lie on its boundary. It is prescribed by the Godname EL CHAI assigned to Yesod with number value 49 because 49 yods are inside its boundary.
The Tetrad Principle2 expresses this measure of a holistic system as
The number of geometrical elements surrounding the centre of the tetrahedron and symbolised by the 84 yods surrounding the central one is 84, where
i.e., 84 is the sum of the squares of the first four odd integers. The tetrahedron is the polyhedral realisation of the 2nd-order tetractys.
2. The Archimedean & Catalan solids
There are 13 Archimedean solids (polyhedra with two or more types of regular polygons as faces). Two have different mirror images (chiral partners). Their duals (vertices replaced by faces and faced replaced by vertices) are the Catalan solids. The two sets have 26 members, showing how YAHWEH prescribes this family of polyhedra, whilst YAH with number value 15 prescribes each set with the enantiomorphic members included. Their properties will now be calculated and then discussed.Definitions: C = number of vertices of polyhedron.
E = number of polyhedral edges.
4
F = number of polyhedral faces.
C, E and F are related by Euler’s equation for a convex polyhedron:
number of triangular sectors of a face with m edges. number of faces with m sides in polyhedron. Σmn(m) = number of triangular sectors of faces. m The internal triangles formed by the centre of the polyhedron and two ends of an edge are divided into three tetractyses; any triangular faces are either considered as single tetractyses (case A) or divided into three tetractyses (case B).
Surface
Number of corners in faces = C (case A)= C + F = 2 + E (case B).
Number of sides in faces = E (case A)
= E + Σmn(m) = E + L (case B).
mNumber of triangles in faces = F (case A)
= L (case B).
Number of corners, sides & triangles = C + E + F = 2E + 2 (case A)
= C + F + E + 2L = 2E + 2L + 2 (case B).
Table 2. Population of geometrical elements in the Archimedean & Catalan solids.
F
E
C
Archimedean solid
8
18
12
truncated tetrahedron 14
24
12
cuboctahedron 14
36
24
truncated cube 14
36
24
truncated octahedron 26
48
24
rhombicuboctahedron 38
60
24
snub cube 38
60
24
snub cube (chiral partner)
32
60
30
icosidodecahedron 26
72
48
truncated cuboctahedron 32
90
60
truncated icosahedron 32
90
60
truncated dodecahedron 62
120
60
rhombicosidodecahedron 92 150
60
snub dodecahedron 92
150 60
snub dodecahedron
(chiral partner)62 180 120 truncated icosidodecahedron
Catalan solid
F
E
C
triakis tetrahedron 12
18
8
rhombic dodecahedron 12
24
14
triakis octahedron 24
36
14
tetrakis hexahedron 24
36
14 deltoidal icositetrahedron 24
48
26
pentagonal icositetrahedron 24
60
38 pentagonal icositetrahedron
(chiral partner)24
60
38
rhombic triacontahedron 30 60
32 disdyakis dodecahedron 48
72
26
triakis icosahedron 60
90
32 pentakis dodecahedron 60
90
32 deltoidal hexacontahedron 60
120 62 pentagonal hexacontahedron 60
150 92 pentagonal hexacontahedron
(chiral partner)60
150 92 disdyakis triacontahedron 120
180 62 Interior
Number of corners = E + 1.
Number of sides = C + 3E.
Number of triangles = 3E.
Number of corners, sides & triangles = C + 7E + 1.5
Number of corners, sides & triangles = 2C + 8E + F + 1 = C + 9E + 3 (case A)
= 2C + 8E + F + 2L + 1 = C + 9E + 2L + 3 (case B)
The axis is made up of five geometrical elements (three corners, two sides). In case A, the number of elements surrounding the axis ≡ N = 2C + 8E + F + 1 – 5
= 2C + 8E + F – 4 = C + 9E – 2.
In case B, the number ≡ N' = 2C + 8E + F + 2L + 1 – 5 = C + 9E + 2L – 2.
Table 2 gives values of N and N' for the Archimedean and Catalan solids (as none of the former have just triangular faces, only values of N' can be listed for them). We find that the simplest Catalan solid — the triakis tetrahedron — has 168 geometrical elements surrounding an axis through two vertices, when its triangular faces are tetractyses (case A), and 240 elements if they are divided into three tetractyses (case B), that is, 72 more elements are needed to construct the faces from three tetractyses instead of from one. We also see that the most complex Catalan solid — the disdyakis triacontahedron — has 1680 (=168×10) geometrical elements in case A and 2400 (=240×10) elements in case B, i.e., 720 (=72×10) more elements are needed. Numbers of elements for the last Catalan solid are exactly ten times their counterparts for the first one. The first and last Catalan solids are equivalent in this sense. The division:
240 = 168 + 72
corresponds in the group mathematics of the Lie group E8 appearing in superstring theory to the fact that, of its 240 non-zero roots, 72 are non-zero roots of its exceptional subgroup E6 leaving 168 simple roots.
Table 3. Number values of the Sephiroth in the four Kabbalistic Worlds.
Sephirah
Angels
ChakraKether Chokmah Binah Chesed Geburah Tiphareth Netzach Hod Yesod Malkuth Notice that 168, 240, 1680 and 2400 do not appear in the table of numbers for the Archimedean solids. Notice also that the tenth Catalan solid — the triakis icosahedron — has 840 geometrical elements surrounding its axis, whilst the 15th solid has 1680 such elements. This corresponds to the fact that the 1680 circularly polarized oscillations of each whorl of a subquark superstring comprise 840 oscillations making 2½ outer revolutions around its axis and 840 oscillations making 2½ revolutions in the core of the superstring (see Fig. 6). This division is prescribed by the Godname YAH (YH) of Chokmah. Its number 15 (see the
6
upper orange cell in Table 2) prescribes the disdyakis triacontahedron as the 15th Catalan solid, whilst the letter value Y = 10 in YH defines that Catalan solid which has 840 elements surrounding its axis. 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth (see the last cell in Table 2).
The twelve faces of the triakis tetrahedron are isosceles triangles with one long side and two short sides. They are arranged as three-sided pyramids of height √6/15 constructed on the four faces of a regular tetrahedron with unit edge length (Fig. 1).
The geometrical composition of the triakis tetrahedron in case A is given below:
|
Corners
|
Sides
|
Triangles
|
|
| surface: |
8
|
18
|
12
|
| minus: |
–2 (poles)
|
||
|
Subtotal =
|
6
|
||
| interior: |
18
|
8 + 3×18 = 62
|
3×18 = 54
|
| minus: |
–2 (two
sides)
|
||
|
__
|
Subtotal = 60
|
__
|
|
|
Total =
|
24
|
+
78
+
|
66 =
168
|
Compare these numbers with the geometrical composition of the disdyakis triacontahedron in case A:
|
Corners
|
Sides
|
Triangles
|
|
| surface: |
62
|
180
|
120
|
| minus: |
–2 (poles)
|
||
|
Subtotal =
|
60
|
||
| interior: |
180
|
62 + 3×180 = 602
|
3×180 = 540
|
| minus: |
–2 (two sides)
|
||
|
___
|
Subtotal
= 600
|
___
|
|
| Total = |
240
|
+
780
+
|
660 = 1680
|
7
Every number of elements of a given type in the exterior and interior of the disdyakis triacontahedron is exactly ten times the corresponding number in the same colour in the triakis tetrahedron. The triakis tetrahedron is made up of 78 sides and 90 corners & triangles, whilst the disdyakis triacontahedron is composed of 780 sides and 900 corners & triangles. This division of the geometrical elements comprising the basic Catalan solid reflects the number value of Cholem Yesodoth, the Hebrew name of the manifestation in Assiyah, the fourth Kabbalistic World, of the Sephirah Malkuth (Fig. 2).
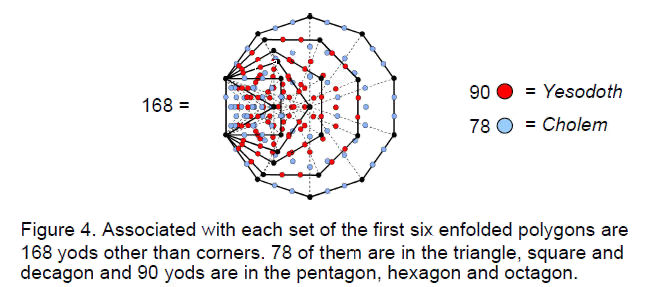
The ten-fold difference between the composition of the first and last Catalan solids can be represented by a star with ten points, each one a parallelogram formed from 32 tetractyses with 168 yods below its point at the centre of the star (Fig. 3). The division:
168 = 90 + 78
reflects the 90 yods in one half of the parallelogram and the 78 yods in the other half. It is encoded in the inner form of the Tree of Life (Fig. 4).
Associated with each set of its first six enfolded, regular polygons are 168 yods other than corners of the 35 tetractyses into which the six polygons can be divided. 90 of these representing the number of Yesodoth are in the square, hexagon and decagon, and 78 yods representing the number value of Cholem are in the triangle, pentagon and octagon.
8
The fact that the numbers of geometrical elements in the faces and interior of the last Catalan solid are ten times the numbers of corresponding elements in the faces and interior of the first Catalan solid is further evidence of the unique status of the disdyakis triacontahedron as the completion of the Catalan solids. For the Pythagorean tetractys symbolises holistic (that is, whole) systems — systems that are complete in themselves rather than mere intermediate members of some developing sequence. The triakis tetrahedron is the unit, or yod, of a tetractys representing the disdyakis triacontahedron:
Viewed as part of the complete sequence of 35 solids:
5 Platonic solids → 15 Archimedean solids → 15 Catalan solidsthe triakis tetrahedron is the 21st member, whilst the disdyakis triacontahedron is the 31st member when the enantiomorphic versions of solids are excluded. This shows how the Godname EHYEH of Kether with number value 21 prescribes the first Catalan solid with 168 geometrical elements surrounding the axis joining two opposite vertices and how the Godname EL of Chesed with number value 31 prescribes the last Catalan solid with 1680 geometrical elements surround its axis. The Godname YAHWEH with number 26 prescribes the number of Archimedean solids and their duals, the Catalan solids, when enantiomorphs are excluded, whilst its older version, YAH, with number value 15, is the number of each type when their enantiomorphs are included.
Figure 5. The pentagram represents the Godname EL with number value 31 because 31 yods define its boundary and centre. The 30 yods on the former divide into two alternating sets of 15 yods, one set symbolising 15 Platonic/Archimedean solids and the other set symbolising their duals. The central yod denotes the self-dual tetrahedron.
The 31 solids comprise the tetrahedron, 15 Platonic/Archimedean solids and their duals. This 1:30 pattern is reflected in the name EL, where E = 1 and L = 30. It is also represented by the pentagram because 30 yods lie on its edge when each side of the star's point is made up of four yods (Fig. 5). The central yod denotes the self-dual tetrahedron and the three yods on each side of a point symbolise Platonic or Archimedean solids and their duals.
9
The tetractys pattern of ten triakis tetrahedra that is equivalent to the disdyakis triacontahedron has its counterpart in the subquark superstring, which consists of ten closed standing waves, each with 1680 circularly polarised oscillations (Fig. 6). These vibrations are the subatomic counterpart of the 1680 geometrical elements surrounding the axis of the disdyakis triacontahedron. The correspondence exists because the former is the manifestation of the Tree of Life in the 10-dimensional space-time of superstrings and the latter is its polyhedral manifestation in the 4-dimensional spacetime of the large-scale universe.
The fact that the triakis tetrahedron has 168 geometrical elements surrounding its axis in case A and 240 elements in case B, i.e., 72 extra elements, itself reflects the tetractys arrangement of the number 24, where 24 = 1×2×3×4:
The first Catalan solid is constructed by what mathematicians call “cumulation” of a tetrahedron by a pyramid. Constructed from tetractyses, the tetrahedron in case B has 15 corners, 40 sides & 30 triangles (70 sides & triangles), totalling 85 geometrical elements. It conforms to the next higher differentiation of the tetractys:
because this consists of 85 yods, of which 15 are corners of the ten tetractyses and 70 are hexagonal yods (shown coloured). These 85 yods signify degrees of freedom. For the tetrahedron, the 15 corners symbolise the 15 corners of its 30 triangles and the 70 hexagonal yods denote its 70 sides & triangles. The geometrical sequence:
10
point → line → triangle → tetrahedron
has its Pythagorean counterpart:
So the 2nd-order tetractys symbolises the geometrical composition of the tetrahedron — the simplest regular polyhedron.
Ignoring enantiomorphic Archimedean solids, the 21st solid in the sequence:
5 Platonic solids → 15 Archimedean solids → 15 Catalan solids
is the triakis octahedron. It has F = 24, E = 36, C = 14 and N = 336. Comparing these values with the values F = 120, E = 180, C = 62 and N = 1680 for the disdyakis triacontahedron, we see that the latter has five times as many faces and five times as many edges, whilst the number of polyhedral vertices surrounding an axis passing through two opposite ones = 62 – 2 = 60, comparing with (14–2=12) such vertices for the former, that is, five times as many vertices of this type. The disdyakis triacontahedron has therefore five times as many elements of each variety surrounding its axis as the triakis octahedron has surrounding its axis. This difference of a factor of 5 appears in the subquark superstring described by Annie Besant and C.W. Leadbeater (Fig. 6). Each of its ten whorls make five revolutions about its spin axis, the number of oscillations made in one revolution being 1680/5 = 336, which is the number of geometrical elements surrounding the axis of the triakis octahedron.
Three Platonic solids (tetrahedron, octahedron & icosahedron) have all triangular faces. None of the Archimedean solids has this property, whilst seven of the 15 Catalan solids have all triangular faces: the triakis tetrahedron, the triakis octahedron, the tetrakis hexahedron, the disdyakis dodecahedron, the triakis icosahedron, the pentakis dodecahedron and the disdyakis triacontahedron. Ten of the 31 different solids have faces that are all triangular, and 21 have either non-triangular faces or a combination of both, showing that the Godname EHYEH with number value 21 prescribes the latter. The ten polyhedra with triangular faces form a tetractys array:
The Platonic solids are at the corners and the seven Catalan solids are at the corners and centre of a hexagon (shown in grey above), the disdyakis triacontahedron occupying the latter position because this corresponds to the Sephirah Malkuth, whose superstring manifestation the polyhedron embodies. The ten solids have 210 polyhedral vertices, where
11
12
showing how EHYEH prescribes this set of polyhedra.
We found earlier that, in case A, where its faces are single tetractyses, the triakis tetrahedron has 66 triangles with 24 corners and 78 sides surrounding its axis, these numbers generating the number values of the Hebrew words ‘Cholem’ and ‘Yesodoth’ in the name of the Mundane Chakra of Malkuth. They are symbolised in Fig. 7 by the 168 yods other than corners associated with the first six regular polygons enfolded in the inner Tree of Life. The 24 corners are denoted by the 24 yods of the pentagon outside the shared edge. The 78 sides are symbolised by the 78 yods of the triangle, square & decagon and the 66 triangles correspond to
the 66 yods of the hexagon & octagon. We also found that, in case A, the disdyakis triacontahedron has 660 triangles with 240 corners and 780 sides surrounding its axis. As the first Catalan solid, the triakis tetrahedron is the polyhedral manifestation of the first six polygons enfolded in the inner Tree of Life. As the last Catalan solid, the disdyakis triacontahedron is the polyhedral version of the 60 polygons enfolded in ten overlapping Trees of Life, each yod symbolising a corner, side or triangle. Because each Sephirah of the Tree of Life is itself ten-fold, the complete, expanded version of the latter is the set of ten overlapping Trees of Life. This
illustrates the holistic nature of the disdyakis triacontahedron: its remarkable geometry makes it the counterpart of the holistic system of ten Trees of Life. Table 2 indicates that none of the Archimedean solids has the property that the number of geometrical elements surrounding an axis passing through two vertices is ten times that of another polyhedron of this type. The disdyakis triacontahedron is unique in this regard for the Catalan solids as well.
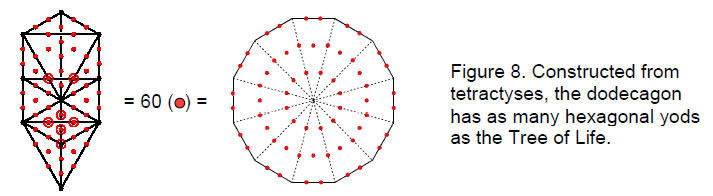
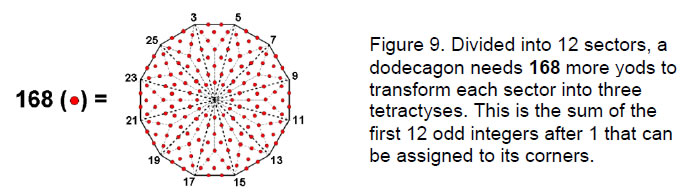
When constructed from tetractyses, the dodecagon has 73 yods. Twelve of these are at its corners and one is at its centre, so that 60 extra yods are needed to turn its sectors into tetractyses (Fig. 8). This is the number of hexagonal yods in the 16 triangles of the Tree of Life — a sign (which will be confirmed shortly) that the last of the seven regular polygons making up the inner Tree of Life embodies properties of its outer form. With its sectors divided into three tetractyses, the dodecagon has 181 yods, i.e., 168 yods other than its corners and centre (Fig. 9). As
132 –1 = 168 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25,
13
this is the sum of the twelve odd integers after 1 that can be assigned to the corners of the dodecagon. Just as there are 168 yods other than corners associated with the first six enfolded polygons, so there are 168 yods other than corners associated with the last polygon enfolded on each side of the central Pillar of Equilibrium. The dodecagons enfolded on one side of ten overlapping Trees of Life have 1680 such yods — exactly the same number of yods as in the first six
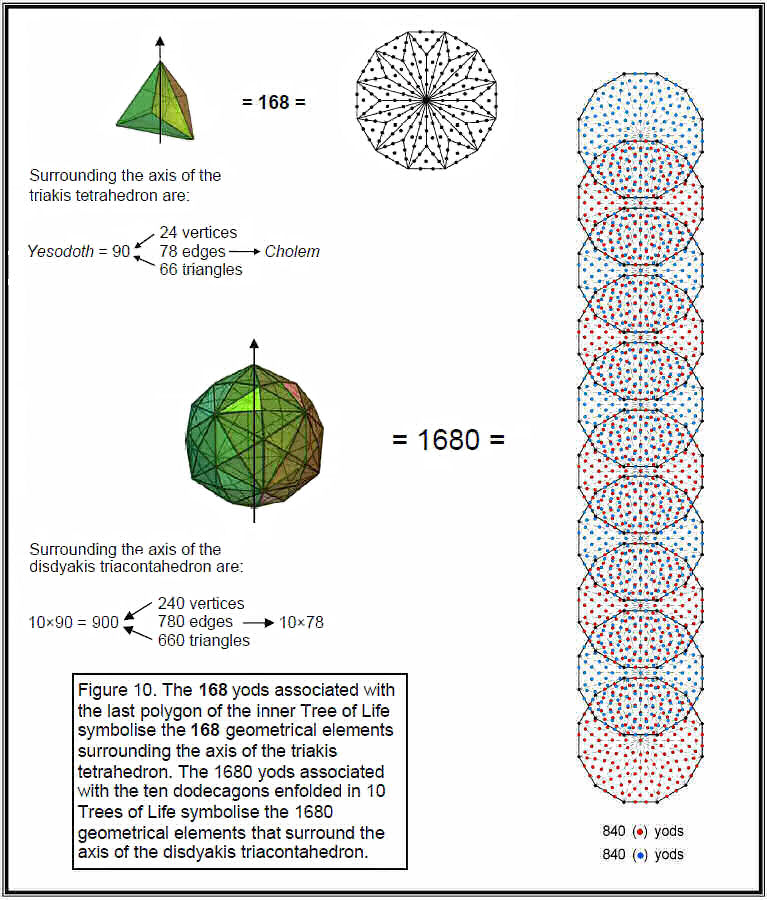
polygons enfolded in ten Trees of Life. What is embodied in the first six polygons as potential degrees of freedom manifests in the seventh polygon as the yods needed to be added to express its form. Fig. 10 indicates
14
the correspondence between the triakis tetrahedron and the dodecagon and the correspondence between the disdyakis triacontahedron and the dodecagons enfolded in ten Trees of Life.
We found earlier that, in case B, when its faces are constructed from three tetractyses, 72 more geometrical elements are added to the 168 elements surrounding the axis of the triakis tetrahedron. The counterpart of this in the inner Tree of Life is that there are 168 yods other than corners associated with the first six polygons and 72 yods associated with the dodecagon. Likewise, 720 more geometrical elements are added to the 1680 elements surrounding the axis of the disdyakis triacontahedron when its faces are constructed from three tetractyses. Its counterpart in the inner Tree of Life is that there are 720 yods associated with the ten dodecagons enfolded in ten Trees of Life. Construction of both Catalan solids according to Case A generates the counterpart of the first six regular polygons and construction according to case B creates the polyhedral counterpart of all seven polygons. The 240 geometrical elements of the triakis tetrahedron are symbolised by the 240 hexagonal yods belonging to the seven separate polygons (Fig. 11).
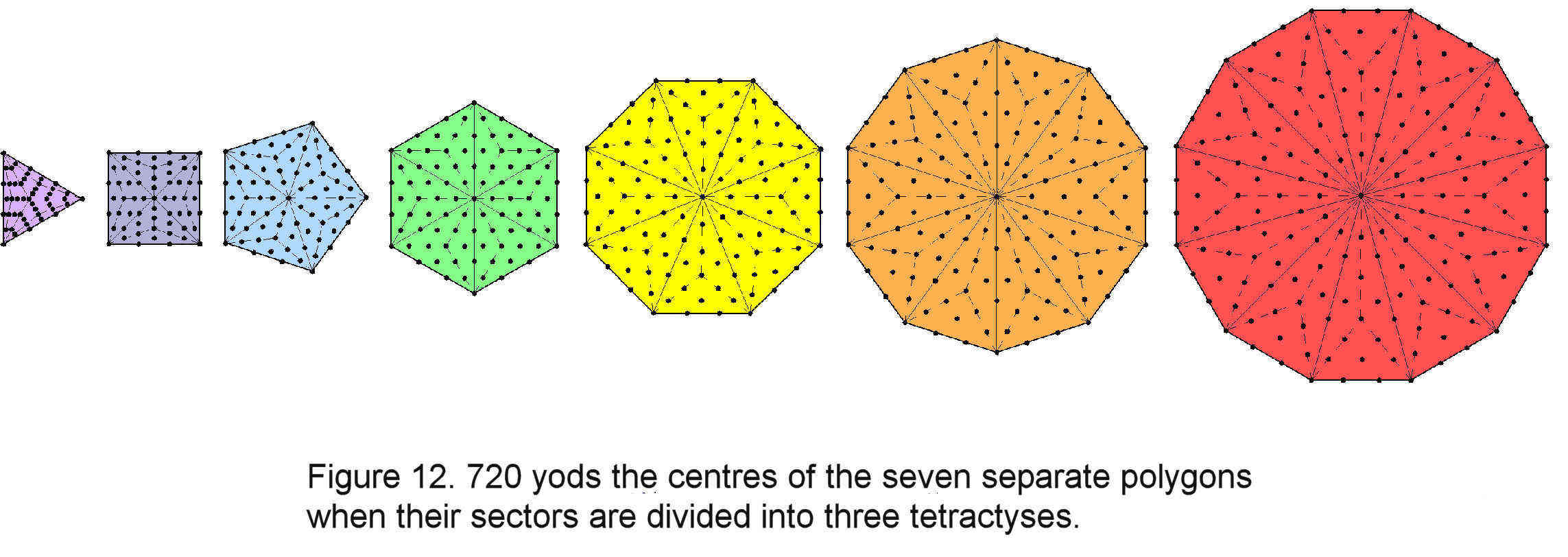
The extra 720 geometrical elements in the 120 faces of the disdyakis triacontahedron for case B are symbolised by the 720 yods in the seven separate polygons that surround their centres when their 48 triangular sectors are each turned into three tetractyses (Fig. 12).
It cannot be coincidence that the same number should appear in contexts where the polygonal and polyhedral forms of the inner Tree of Life are transformed in the same way. When constructed from tetractyses, the five Platonic solids have 820 yods in their 50 faces, of which 720 are hexagonal yods.3 The very surfaces of the five regular polyhedra embody this number as well.
It cannot also be coincidence that the disdyakis triacontahedron has 62 vertices (31 vertices and their inversions), in view of the facts that the number value of Chesed, the first Sephirah of Construction, is 72, its Godname EL has the number value 31 and its Archangel Tzadkiel (“Benevolence of God”) has number value 62 (Table 2).
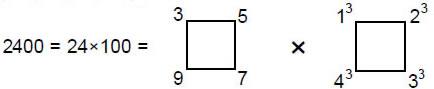
As 492 – 1 = 2400 = 3 + 5 + 7 + 9 + … + 97, the number (2400) of geometrical elements
15
in the disdyakis triacontahedron in case B is the sum of the first 48 odd integers after 1. As Table 2 indicates, Kokab, the Mundane Chakra of Hod, has the number value 48 and Haniel (“Grace of God”), the Archangel of Netzach, has the number value 97.
The integers 1, 2, 3 & 4 symbolised by the tetractys express the number 2400 as:
2400 = 1×2×3×4(13 + 23 + 33 + 43) = 1×2×3×4(1 + 2 + 3 + 4)2.
As 24 = 52 – 1 = 3 + 5 + 7 + 9,
illustrating how the Tetrad Principle4 determines this number.
The disdyakis triacontahedron has 30 polyhedral vertices and their 30 inversions surrounding its axis, where
This again shows how the Tetrad Principle determines the properties of this solid.
We found earlier that, as the first Catalan solid, the triakis tetrahedron has 168 geometrical elements surrounding its axis, where
This further illustrates the Tetrad Principle, for the odd integers 3, 5, 7, etc are arranged along the sides of a four-sided square, four to a side.
Since 168 = 132 – 1,
16800 = 100×168 = 102×(132 – 1) = 1302 –100.
But
1300 = 15 + 25 + 35 + 45
and
100 = 13 + 23 + 33 + 43 = (1 + 2 + 3 + 4)2.
Therefore,
and
This shows how the integers 1, 2, 3 & 4 express the superstring parameters 16800 and 1680. The former number has also the remarkable representation:
16
The number 2400 has the representation:
There are 240 gauge fields corresponding to the 240 non-zero roots of the superstring gauge symmetry group E8. Each of these fields has ten components because superstring space-time is 10-dimensional. This means that the 240 fields have 2400 components. Their counterparts in the disdyakis triacontahedron are the 2400 geometrical elements surrounding its axis that are needed to define its shape when it is constructed from the building block of the tetractys.
Table 1 shows that the truncated tetrahedron — the dual of the triakis tetrahedron — has 244 geometrical elements surrounding its axis, which consists of five elements (three vertex points and two edges). The total number of elements is therefore 249. Surrounding the centre of the solid are 248 elements. Starting from the mathematical point, 248 more geometrical elements are needed to build the simplest Archimedean solid. Remarkably, this is the dimension of the superstring gauge symmetry group E8! The tetractys therefore reveals the following beautiful properties of four solids that speak eloquently of their archetypal nature:
It was because of its power to describe the nature of the universe that the followers of Pythagoras swore the following oath:
“I swear by the discoverer of the tetractys
Which is the spring of all our wisdom,
The perennial fount and root of Nature.”They would have been delighted by the connections between superstring physics and solid geometry that the tetractys uncovers. This universal template has application both on a metaphysical level as the symbol of the ten-fold nature of God and on a physical level as the representation of holistic systems such as the superstring and — in its higher-order version — the tetrahedron, the basic unit of solid geometry.
Let us now calculate how many yods make up the Archimedean and Catalan solids
17
when they are constructed from tetractyses. Formulae are simplified by making use of Euler’s equation connecting the number of vertices (C), edges (E) and faces (F) in a convex polyhedron:
C – E + F = 2.
Surface
Number of corners surrounding axis ≡ Vs = C + F – 2 = E;
Number of hexagonal yods surrounding axis ≡ Hs = 2E + 3L;
Number of yods surrounding axis ≡ Ns = Vs + Hs = 3E + 3L;Interior
Number of corners surrounding axis ≡ Vi = E;
Number of hexagonal yods surrounding axis ≡ Hi = 2C + 9E – 4 = 11E – 2F;
Number of yods surrounding axis ≡ Ni = Vi + Hi = 12E – 2F;
Total number of corners surrounding axis ≡ V = Vs + Vi = 2E;
Total number of hexagonal yods surrounding axis ≡ H = Hs + Hi = 13E – 2F + 3L;
Total number of yods surrounding axis ≡ N = Ns + Ni = 15E – 2F + 3L.Table 3. Populations of non-axial yods in the Archimedean and Catalan solids.
Archimedean solid truncated tetrahedron cuboctahedron truncated cube truncated octahedron rhombicuboctahedron snub cube icosidodecahedron truncated cuboctahedron truncated icosahedron truncated dodecahedron rhombicosidodecahedron snub dodecahedron truncated icosidodecahedron
Catalan solid triakis tetrahedron rhombic dodecahedron triakis octahedron tetrakis hexahedron deltoidal icositetrahedron pentagonal icositetrahedron rhombic triacontahedron disdyakis dodecahedron triakis icosahedron pentakis dodecahedron deltoidal hexacontahedron pentagonal hexacontahedron disdyakis triacontahedron
Table 3 lists the various non-axial yod populations of the Archimedean and Catalan solids (enantiomorphic partners are excluded because their numbers are the same). The disdyakis triacontahedron has V = 360 (=36×10) corners surrounding its axis, showing how the Godname ELOHA of Geburah with number value 36 prescribes this solid. It also prescribes the triakis tetrahedron because it has 36 corners surrounding its axis18
and 354 yods surrounding its axis made up of seven yods, i.e., it has 361 yods in total, 360 (=36×10) of them surrounding its centre. As there are three vertices on the axis, the total number of corners in the disdyakis triacontahedron is 363. This is the number value of SHADDAI EL CHAI (“Almighty Living God”), the Godname of Yesod, the penultimate Sephirah (see Table 1). If its faces are single tetractyses, it has 2460 (=246×10) yods surrounding its axis. 246 is the number value of Gabriel (“Strong Man of God”), the Archangel of Yesod.
We found earlier that the numbers of vertices, edges and triangles surrounding the axis of the disdyakis triacontahedron are ten times the corresponding numbers for the triakis tetrahedron. Table 3 indicates that the numbers of corners or hexagonal yods in its faces and interior that surround the axis are ten times the corresponding numbers for the triakis tetrahedron. This is true only for surrounding numbers, not for the total numbers. It is also true only for the first and last members of the Catalan solids, not for the first and last members of the Archimedean solids, although some of their corresponding numbers do have this property.
The number of boundary yods in the faces of a polyhedron surrounding its axis = C + 2E + 2L + F – 2 = 3E + 2L. The triakis tetrahedron with 12 triangular faces has 126 such yods on the boundaries of its (12×3=36) tetractyses in its faces, and the disdyakis triacontahedron has 1260 boundary yods in the (120×3=360) tetractyses of its 120 faces, i.e., ten times as many yods. The number of boundary yods inside a polyhedron surrounding its axis = 2C + 7E – 4 = 9E – 2F. The triakis tetrahedron has 138 such yods and the disdyakis triacontahedron has 1380 such yods.
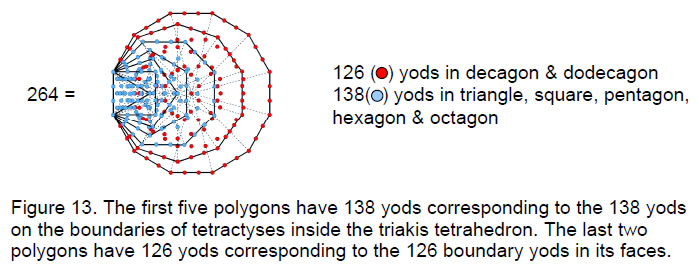
The former has (126+138=264) boundary yods and the latter has (1260+1380=2640) boundary yods. We see that the numbers of yods on the boundaries of tetractyses inside the disdyakis triacontahedron and on its faces are ten times the corresponding numbers for the triakis tetrahedron. The division: 264 = 126 + 138, created by the surface and interior of the triakis tetrahedron, appears in the inner form of the Tree of Life as the 126 yods of the last two enfolded polygons and as the 138 yods of the first five enfolded polygons! The fact that the number of boundary yods in the disdyakis triacontahedron is ten times that for the triakis tetrahedron and ten times the yod population of the inner Tree of Life is further evidence that this solid is the polyhedral counterpart of the inner Tree of Life.
1260 is the number of yods in 126 tetractyses. It is remarkable that the number 126 is the sum of the number values of the four types of combinations of the letters A, H and I in EHYEH (AHIH), the Godname of Kether:
A = 1, H = 5, I = 10
1. A + H + I = 16 2. AH + HI + AI + HH = 42 19
3. AHI + HIH + AHH = 47 4. AHIH = 21 Total = 126 This shows how EHYEH prescribes the population of yods that shape the 360 tetractyses in the faces of the disdyakis triacontahedron. It is further evidence of the way the Godnames of the ten Sephiroth prescribe the disdyakis triacontahedron as the polyhedral form of the inner Tree of Life.
The number 126 has the remarkable property that it is the arithmetic mean of the first 26 triangular numbers, where 26 is the number value of YAHWEH:
This shows how YAHWEH prescribes the shape of the disdyakis triacontahedron by mathematically determining the number of yods on boundaries of tetractyses in its surface.
According to Table 3, the number of yods in its faces that surround its axis is 1620. Of these, 60 are vertices of the polyhedron, leaving 1560 (=156×10) extra yods needed to create its faces. 156 is the sum of the number values of the four types of combinations of the letters Y, H and V in YHVH, the Godname of Chokmah:
Y = 10, H = 5, V = 6
1. Y + H + V = 21
2. YH + HV + YV + HH = 52 3. YHV + HVH + HYH = 57 4. YHVH
= 26 Total = 156 It illustrates the creative quality embodied in this well-known Godname, for the yods in 156 tetractyses are needed to form the faces of the disdyakis triacontahedron marked out by its 62 vertices. 156 is the 155th integer after 1, showing how ADONAI MELEKH, the Godname of Malkuth with number value 155 (see Table 1), prescribes this polyhedron.
156 is the sum of the first 12 even integers that can be arranged in a square:
This illustrates how the Tetrad Principle determines this number as a square array of even integers, starting with 2, the first even integer.
Let us now consider a polyhedron whose faces and internal triangles are single tetractyses (case C). The number of internal yods = 2C + E + 1. The number of yods in its faces = C + 2E + F = 3E + 2. The total number of yods = 2C + 4E + 3. The triakis tetrahedron has 91 yods, that is, 84 yods surround its axis made up of seven yods. The disdyakis triacontahedron has 847 yods, that is, 840 yods surround its axis. Once again, we see that the yod population of the last Catalan solid is ten times that of the
20
first one. The number 840 was encountered in Article 26 as the number of geometrical elements inside the faces of the disdyakis triacontahedron in case B.5 It is also the number of circularly polarised oscillations in an outer or an inner half of each whorl of the E8×E8 heterotic superstring (Fig. 6). The triakis tetrahedron with single tetractyses as its faces has as many yods surrounding its axis as the tetrahedron has geometrical elements surrounding its centre (case B).
For case C:
Number of corners ≡ V = C + 1. Number of corners surrounding axis ≡ V' = V – 3 = C – 2.
Number of sides ≡ e = C + E. Number of sides surrounding axis ≡ e' = e – 2 = C + E – 2.
Number of triangles ≡ T = E + F. Number of triangles surrounding axis = E + F.
Total number of geometrical elements ≡ N = 2C + 2E + F + 1 = C + 3E + 3.
Number of geometrical elements surrounding axis ≡ N' = C + 3E – 2.Table 4. Numbers of geometrical elements in the Catalan solids.
Catalan solid triakis tetrahedron rhombic dodecahedron triakis octahedron tetrakis hexahedron deltoidal icositetrahedron pentagonal icositetrahedron rhombic triacontahedron disdyakis dodecahedron triakis icosahedron pentakis dodecahedron deltoidal hexacontahedron pentagonal hexacontahedron disdyakis triacontahedron
Table 4 lists the various numbers of elements in the Catalan solids with triangular faces. The triakis tetrahedron has 26 sides prescribed by YAHWEH and 65 geometrical elements prescribed by ADONAI, Godname of Malkuth, because its number value is 65 (see Table 1). The latter property is remarkable because, together with the 168 elements surrounding its axis in case A, the solid embodies number values of the same Sephirah (Malkuth) in two Kabbalistic worlds — Atziluth and Assiyah. This is yet another indication that the simplest Catalan solid, which is prescribed by the Godname EHYEH of Kether with number value 21 because it is the 21st member of the set of Platonic, Archimedean and Catalan solids, is one that possesses a Tree of Life pattern.21
This is confirmed by the fact that the disdyakis triacontahedron has numbers of geometrical elements that — once again — are ten times their counterparts in the triakis tetrahedron. As was discussed in Article 26,6 ADONAI prescribes the lowest ten Trees of Life of an extended sequence of trees because they have 65 Sephirothic emanations or levels (what in previous articles were called ‘SLs’). The 65 bits of geometrical information needed to define the triakis tetrahedron are signalling these ten trees, the properties of their enfolded polygons being embodied in the disdyakis triacontahedron.7
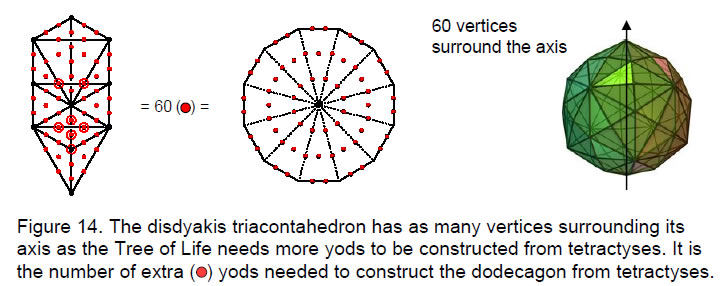
The 60 vertices surrounding the axis of the disdyakis triacontahedron are degrees of freedom symbolised by the 60 extra yods needed to construct the Tree of Life from tetractyses (Fig. 14). As the last of the seven regular polygons constituting the inner Tree of Life, the dodecagon — the tenth regular polygon — has 60 hexagonal yods symbolising these degrees of freedom.
3. The triakis tetrahedron as the Cosmic Tree of Life
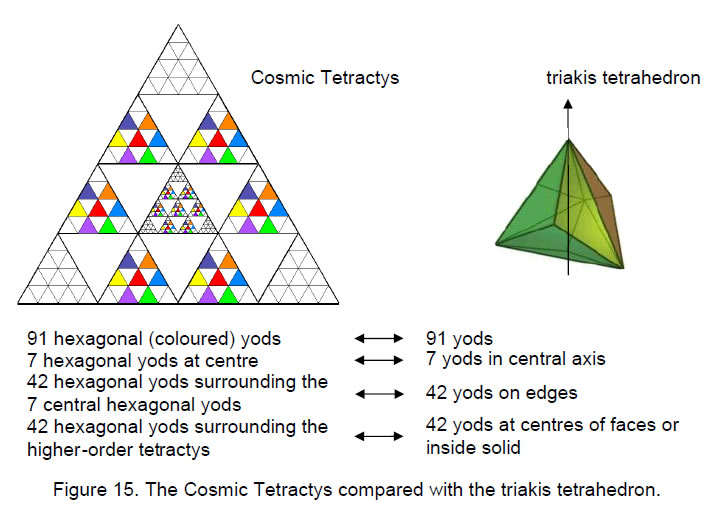
Because the superphysical and physical cosmos constitute a whole, they are together represented by the tetractys. Or, rather, following the ancient hermetic axiom “as above, so below,” a tetractys that is modified to express this statement. This is accomplished by replacing the tetractys at the centre of the next higher-order tetractys by another such tetractys (Fig. 15). This is the ‘Cosmic Tetractys.' It maps what the author has called the ‘Cosmic Tree of Life,’ namely, 91 overlapping Trees of Life, each tree representing a possible jump in evolutionary consciousness.8 This map of all levels of consciousness is encoded in the inner Tree of Life. The seven hexagonal yods at the centre of its central tetractys (shown coloured in Fig. 15)
symbolise the seven physical subplanes of consciousness discussed in Theosophical literature. The (6×7=42) hexagonal yods in the central higher-order tetractys that surround the central, 1st-order tetractys denote the 42 subplanes of the six planes of consciousness above the physical plane: astral, mental, buddhic, atmic,
22
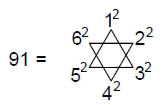
anupadaka and adi planes. The 42 hexagonal yods surrounding those in the central 2nd-order tetractys denote the 42 subplanes of the six cosmic superphysical planes. The 91 hexagonal yods in the Cosmic Tetractys symbolise the 91 subplanes. 91 is the sum of the squares of the first six integers:
Let us now compare this map of consciousness with the pattern of yods in the triakis tetrahedron. It has 91 yods, of which seven yods lie along its axis. They are surrounded by 84 yods distributed as 42 yods on the edges of the solid (6 vertices, 36 hexagonal) and 42 hexagonal yods either at the centre of its faces or inside the solid. We see that the axis of the solid with seven yods corresponds to the central tetractys with seven hexagonal yods symbolising the seven physical subplanes. The 42 yods lying on the boundary of the solid correspond to the 42 subplanes above the physical plane and belonging to the cosmic physical plane (hence their function in defining the shape of the solid). The 42 hexagonal yods not delineating its faces (and therefore playing an invisible role) correspond to the 42 subplanes of the cosmic superphysical planes (notice the aptness of the correspondence). The triakis tetrahedron may be regarded as the polyhedral version of CTOL. The three vertices and four hexagonal yods making up the central axis symbolise what in Theosophy are called, respectively, the three “dense physical” subplanes and the four “etheric” subplanes. Just as the physical universe (including the world of shadow matter or mirror matter) is the final product of Divine Thought issuing down through all higher realms of consciousness, so this axis is the fulcrum for the polyhedron.
The ‘case C’ type of transformation of the triakis tetrahedron creates a polyhedral map of all levels of consciousness, and the similar transformation of the disdyakis triacontahedron generates the superstring structural parameter 840. The transformation according to case A generates for these polyhedra the superstring structural parameters 168 and 1680. Transformation according to case B generates the group-theoretical parameters 240 and 2400 of the superstring gauge symmetry group E8.
4. Equivalence of Plato’s Lambda and the triakis tetrahedron
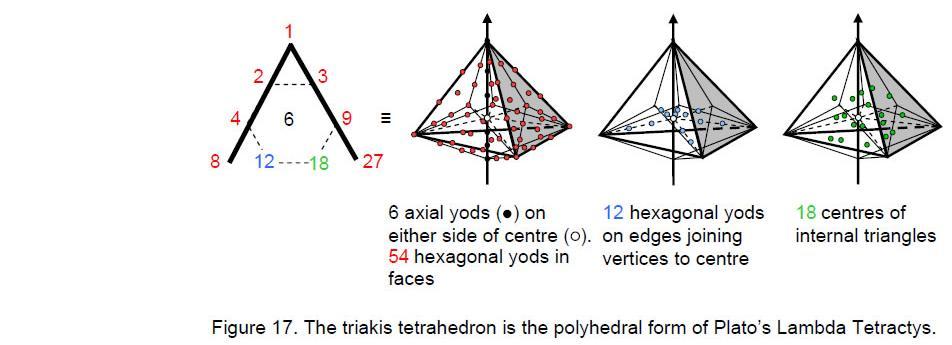
Article 26 discussed the remarkable correspondence between the tetractys of numbers extrapolated from Plato’s so-called ‘Lambda’ and the various numbers of tetractyses in the disdyakis triacontahedron (case B).9 As the latter are ten times the corresponding numbers in the triakis tetrahedron for the same kind of transformation, it might be expected that a correspondence also exists for case C, where the faces and internal23
triangles are single tetractyses. This, indeed, is true. 90 yods surround its centre (Fig. 16). This is the sum of the ten integers in the ‘Lambda Tetractys’ formed from the Lambda by extrapolating the three numbers shown in red. The six yods on the axis on either side of its centre correspond to the number 6 at the centre of the tetractys. The 18 edges of the solid have 36 hexagonal yods, and there are 12 hexagonal yods at centres of its faces. The 48 hexagonal yods in its faces correspond to the sum of the six integers in the Lambda Tetractys at the corners of a hexagon: 2 + 3 + 9 + 18 + 12 + 4 = 48. The remaining 36 yods (6 vertices and 30 internal yods) correspond to the sum of the integers at the corners of the tetractys: 1 + 8 + 27 = 36.
An alternative correspondence would have the central integer corresponding to the six vertices surrounding the axis and the sum 36 of the integers at the three corners corresponding to the 36 internal yods. As the number 6 is the musical proportion of the tonic, the lowest note of the musical scale, and as its position in the Lambda tetractys corresponds to Malkuth, the physical universe of seven subplanes symbolised (as we found earlier) by the seven yods on the axis, the correspondence that is more consistent with the analogy between the Cosmic Tetractys and the triakis tetrahedron is the one discussed first in which the central
integer 6 denotes the six yods on the axis on either side of its centre.
Another alternative correspondence scheme would have, firstly, the sum (54) of the seven integers making up the Lambda denoting the number of yods in the faces of the solid that surround its axis (6 vertices, 48 hexagonal yods) and, secondly, the sum (36) of the three extrapolated integers (shown in red in Fig. 17) denoting the number of yods in its interior. As before, the central integer 6 would signify the number of yods on the axis on either side of its centre, but now the extrapolated number 12 would denote the 12 internal hexagonal yods on the lines joining the centre to vertices surrounding the axis and the number 18 would denote the 18 hexagonal yods at the centres of the triangles formed by the centre and 18 edges of the triakis tetrahedron. This is intuitively appealing because the three extrapolated (i.e., hidden) numbers would then determine the number of interior yods, although the correspondence is not perfect because the number 6 would also determine the two vertices at the ends of the axis and these are external, not internal, yods.
Whatever scheme is favoured, this correspondence exists because the Lambda Tetractys and the triakis tetrahedron are, respectively, the arithmetic and geometric
24
expressions of mathematical archetypes working through a law of correspondence to link the psychological qualities of the notes of the musical scale to the pattern of varieties of consciousness in the spiritual cosmos.
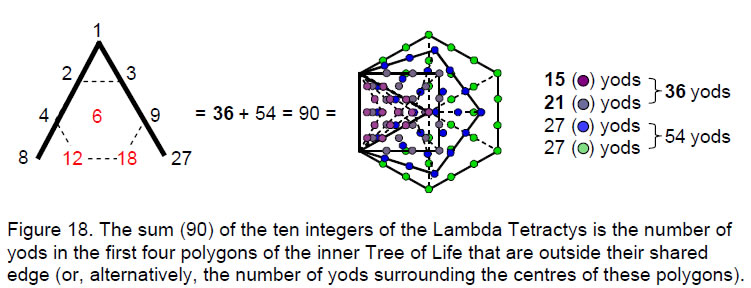
It was pointed out in Article 2610 that the sums of the integers in the four diagonal rows of the Lambda Tetractys are the numbers of yods in the first four polygons of the inner Tree of Life that are outside their shared edge (Fig. 18). As if this 1:1 correlation between the numbers and the geometry were not remarkable enough, it is further extraordinary that:
-
the sum (36) of the integers at the corners of the tetractys is the number of yods outside the root edge in the triangle and square. This is also the number of vertices and internal yods of the triakis tetrahedron;
-
the sum (54) of the integers arranged at the corners and centre of a hexagon is the number of external yods in the pentagon and hexagon. This is the number of hexagonal yods on the faces of the triakis tetrahedron and yods on its axis on either side of its centre.
25
side of its centre.
5. Root structures of E8, E7 & E6 and their polyhedral representation
The superstring gauge symmetry group E8 has 248 roots made up of eight zero roots and 240 non-zero roots. Its largest exceptional subgroup E7 has 133 simple roots made up of 7 zero roots and 126 non-zero roots. E7 has the rank-6, exceptional subgroup E6 with 78 simple roots that comprise six zero roots and 72 non-zero roots. Let us compare this root structure with the geometrical composition of the triakis tetrahedron. Fig. 17 shows that, when we start with case C, in which the faces and internal triangles are single tetractyses, the solid has 60 geometrical elements surrounding its axis.
Construction of the triangular faces from three tetractyses adds 72 new elements. Construction of the internal triangles from three tetractyses requires adding three sides within each triangle, i.e., 54 for the interior of the solid, therefore adding (72+54=126) elements for its interior and faces. As well as adding 54 more sides, division of each internal triangle into three tetractyses adds one corner and two triangles, creating 54 more elements. The total number of elements = 60 + 72 + 54 + 54 = 240. Constructed from tetractyses, the triakis tetrahedron has as many geometrical elements surrounding its axis as E8 has non-zero roots. The 72 new elements needed to construct its faces from three tetractyses correspond to the 72 non-zero roots of E6, whilst the minimal number of 126 new elements needed to construct both faces and internal triangles from tetractyses correspond to the 126 non-zero roots of E7. The remaining (60+54=114) elements correspond to the (240–126=114) non-zero roots of E8 that do not belong to E7. The simplest Catalan solid embodies the non-zero root structure. As we saw earlier, the simplest Archimedean solid — the truncated tetrahedron — has, when constructed from tetractyses, 248 geometrical elements surrounding its centre (eight corners at the centres of its faces, 240 other elements). This solid represents the eight zero roots and 240 non-zero roots of E8; its dual expresses the non-zero root structure of E8.
26
Fig. 18 displays the same type of calculation for the disdyakis triacontahedron as that given in Fig. 17 for the triakis tetrahedron. It shows a representative face and an internal triangle divided into three triangles. Amazingly, all corresponding numbers differ by a factor of 10. The non-zero root structures of the superstring gauge symmetry group E8 and its exceptional subgroups E7 and E6 are embodied in the geometrical composition of the disdyakis triacontahedron. E6 is determined by its faces and E7 encompasses both faces and its interior.
The superstring parameter 168 is the number of geometrical elements in the triakis tetrahedron in case A. In terms of the corresponding non-zero roots:
168 = 54 + 114,
where the first number is the number of non-roots of E7 that do not belong to E6 and the second term is the number of non-zero roots of E8 that do not belong to E7. In terms of corners, sides and triangles, there are in the triakis tetrahedron 24 corners (six external, 18 internal), 78 sides (18 external, 60 internal) and 66 triangles (12 external, 54 internal). The total number of 168 elements is the number value 168 of Cholem Yesodoth. The number value 78 of the word ‘Cholem’ measures the 78 sides and the number value 90 of the word ‘Yesodoth’ measures the number of corners & triangles. The triakis tetrahedron is composed of 36 geometrical elements in its faces (six vertices, 18 edges & 12 triangles) that surround its axis and 132 internal elements (18 corners, 60 sides & 54 triangles). This shows how ELOHA, the Godname assigned to Geburah with number value 36 (see Table 2), prescribes this solid and thus the superstring parameter 168 as the number of geometrical elements surrounding its axis. Surrounding the axis of the disdyakis triacontahedron are 360 elements in its faces (60 vertices, 180 edges & 120 triangles) and 1320 elements in its interior (180 corners, 600 sides & 540 triangles). Both the oscillatory structure and the E8-symmetric forces of the E8×E8 heterotic superstring are represented in the geometry of this remarkable polyhedron.
The 1680 circularly polarised oscillations of each whorl of the E8×E8 heterotic superstring are the string manifestation of the 240 gauge charges of E8 associated with the 240 generators defined by its non-zero roots. These gauge charges are spread along the ten whorls, 24 to a whorl. The seven minor whorls of the subquark superstring carry 168 gauge charges of E8 and the three major whorls carry (3×24=72) gauge charges that are also the gauge charges of its subgroup E6. The distinction between the two types of whorl amounts to a difference in how each turn in their helices is compounded from helices formed by the winding of each stringy whorl around six successively smaller circular dimensions of a 6-torus and does not need to be discussed here. Their difference indicates symmetry breaking of E8 into E6. Its counterpart in the disdyakis triacontahedron is the topological distinction between the interior of the polyhedron and its exterior, which requires 720 extra geometrical elements to construct it in order to make its outer fashioned in the same way from tetractyses as its inner. Analogous to a hypothetical universe where only superstring physics governed by E6 operates (this symmetry is further reduced for the real world) would be one allowing only the faces of polyhedra to be visible, so that their interiors never played any noticeable role, despite always being present. It would be one in which, like an ant crawling over the surfaces of things, one could be conscious only of surfaces, never of depth. The form of superstrings is determined, however, not by E6 or any of its subgroups (this determines only the difference between the major and minor whorls) but by that part of E8 that is not also its subgroup E6. In this sense, the analogy between the disdyakis triacontahedron and the E8×E8 heterotic superstring indicates that what is now visible as matter is determined by what is now unobservable
27
because the physics operated in a former time when the universe was, momentarily, one of perfect E8 symmetry and is locked out by the lesser symmetry of E6 and its subgroups that survived. It is not that the universe today is less perfect in a mathematical sense than before. It is just that the perfection of the complete symmetry is hidden from view — as the interior of a disdyakis triacontahedron would be to an ant crawling over it. Only when consciousness has the attribute of recognising spatial depth can the mathematical beauty of its solid structure be appreciated and its archetypal meaning discerned.
References
1 All numbers from the table appearing in the text will be written in boldface.2 Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 5.
3 Phillips, Stephen M. Article 3: “The Sacred Geometry of the Platonic Solids,” (WEB, PDF), Table 1, p. 20.
5 Phillips, Stephen M. Article 26: “How the Seven Musical Scales Relate to the Disdyakis Triacontahedron," (WEB, PDF), p. 29.
8 Phillips, Stephen M. Article 5: “The Superstring as Microcosm of the Spiritual Macrocosm,” (WEB, PDF).
28