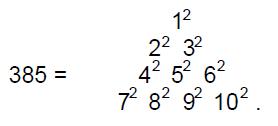ARTICLE 36

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

1

1. The 15 layers of polygons in the disdyakis triacontahedron
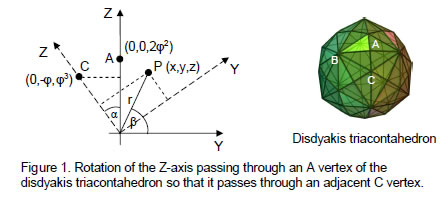
The position vector of the vertex A (Fig. 1) at (0,0,2φ²) is inclined at an angle α to the position vector of the vertex C at (0,-φ,φ³), where tanα = φ/φ³ = 1/φ². As φ – 1 = 1/φ,

1/φ² = 1 – 1/φ = 1 – (φ–1) = 2 – φ.

Therefore, tanα = 2 – φ

1 + tan²α = 1/cos²α = 1 + (2–φ)² = 1 + 4 +φ² – 4φ = 6 – 3φ = 3(2–φ) = 3/φ² .

Therefore, cosα = φ/√3.

1 – cos²α = sin²α = 1 – φ²/3 = (3–φ² )/3 = (3–(1+φ))/3 = (2–φ)/3 = 1/3φ² .

Therefore, sinα = 1/φ√3.

An anticlockwise rotation of α° about the X-axis of the Y- and Z-axes makes the positive Z-axis pass through vertex C at (0,φ,φ³) instead of the vertex A at (0,0,2φ²). A point P has rectangular coordinates (x,y,z) and polar coordinates (R,θ,ψ), where

y = rcosβ, z = rsinβ, and r² = y² + z² = R²(cos²ψ + sin²ψsin²θ).

and r is the projection of the position vector R of P onto the Y-Z plane. Its coordinates (x’,y’,z’) with respect to the new coordinate system with a C vertex on the Z-axis are given by:

x' = x,
y' = rcos(β–α) = rcosβcosα + rsinβsinα = (yφ+z/φ)/√3,
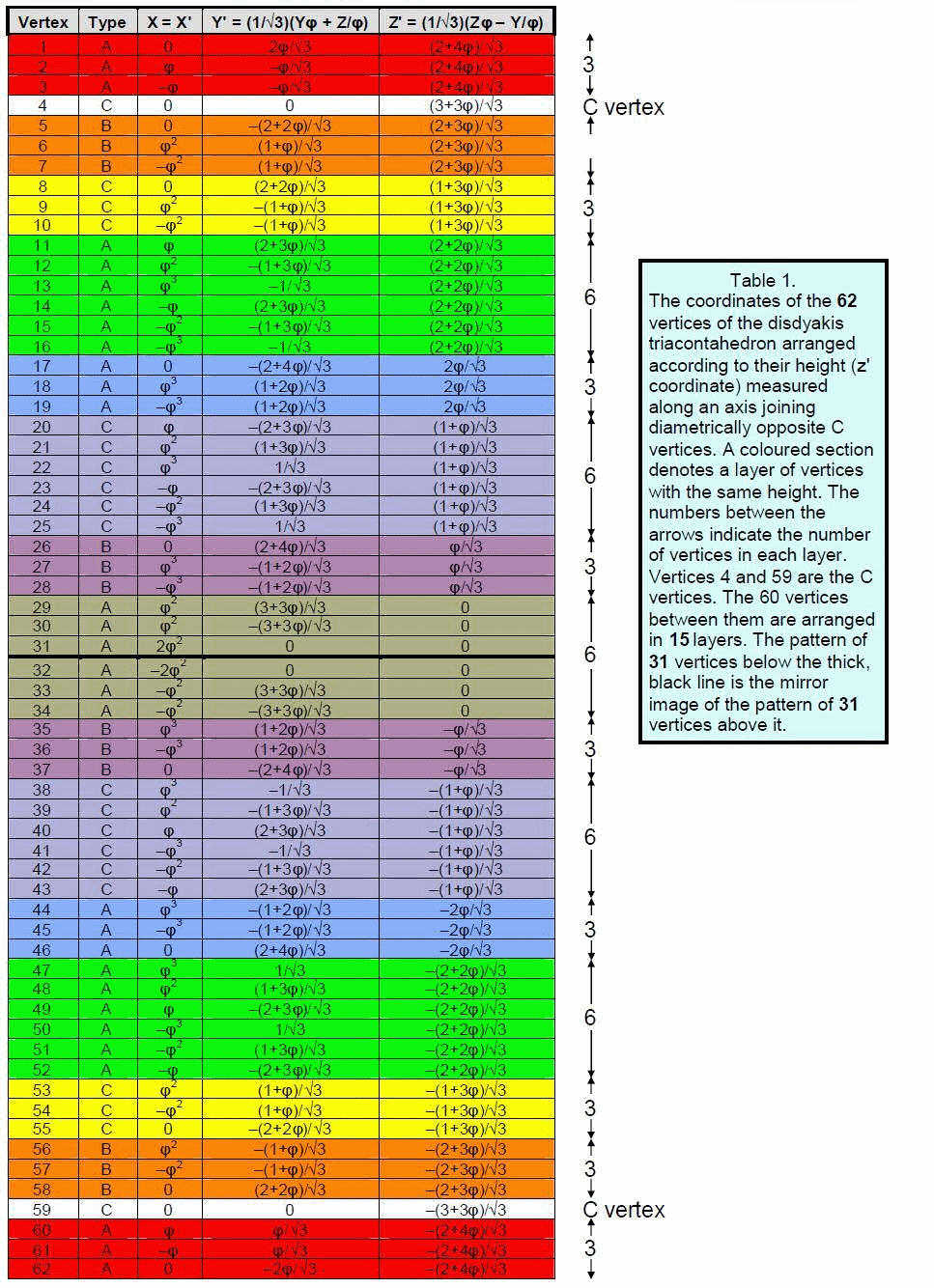
z' = rsin(β–α) = rsinβcosα – rcosβsinα = (zφ–y/φ)/√3,

where x, y & z are listed for each vertex of the disdyakis triacontahedron in Table 1 of Article 25. The new coordinates are listed here in Table 1.

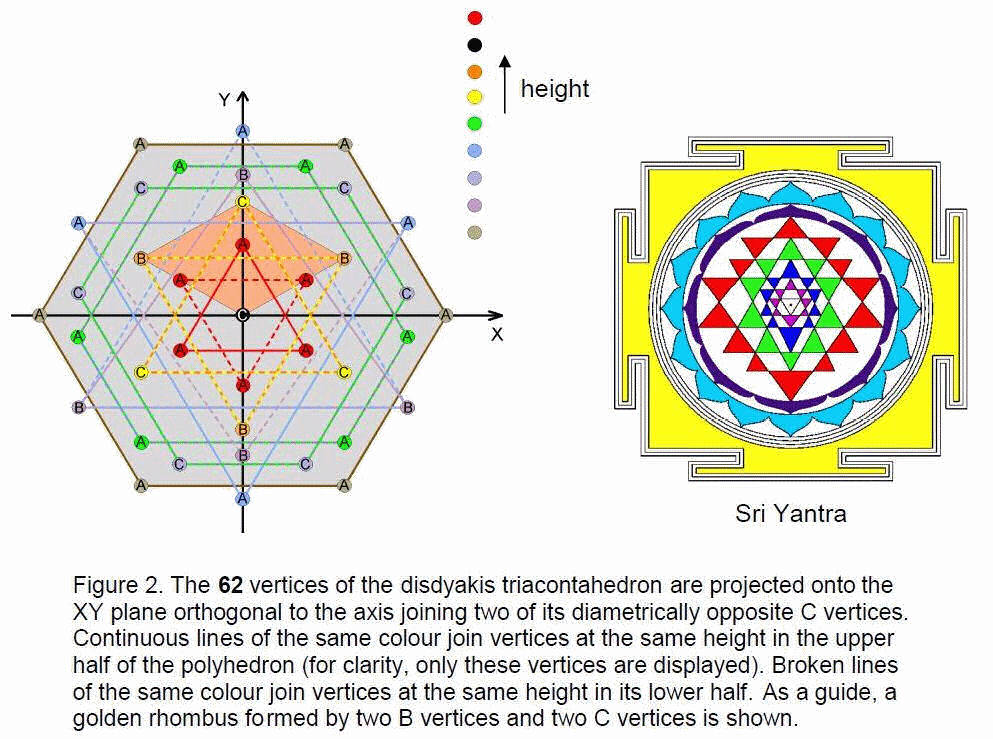
Fig. 2 shows that the rotation of the Z-axis creates above the XY plane three upward pointing triangles (red, yellow & violet) and two downward pointing triangles (orange & blue), whilst below the plane are two upward pointing triangles (orange & blue) and three downward pointing triangles (red, yellow & violet). There are five upward pointing triangles and five downward pointing triangles, whereas the Sri Yantra is formed from five downward pointing triangles and four upward pointing ones. However, the two pairs of triangles forming a Star of David with B (orange) vertices and C (yellow) vertices at their tips are identical in size and shape. This means there are four distinct, upward pointing triangles (red, yellow, violet & blue) and four distinct, downward pointing ones (red, orange, violet & blue), thus matching the two sets of four triangles of the Sri Yantra. Alternatively, the projection of the 10 triangles onto the XY plane (the central

2

3

Table 2. Gematria number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Orders of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters. Numbers from the table are written in boldface in the article.

4

layer of six vertices) creates four different pairs of intersecting triangles. There is nothing in the projection corresponding to the downward pointing central triangle, although it may be argued that the C vertex formally plays its role, being the starting point for the generation of the polyhedron, just as the triple Godhead symbolised by the innermost triangle in the Sri Yantra is the source of all manifestation.

The eight distinct triangles have 24 vertices. There are five 6-sided polygons but only three differently shaped ones with 18 vertices. This because one of the polygons with A vertices is the inversion of the other with C vertices on the same side of 

the XY plane, whilst the two others in the lower half of the polyhedron are the inversions of these. When projected onto the XY plane, they become two polygons, one the mirror image of the other. Hence, there are 42 vertices of distinct polygons. This is the number of triangles in the four layers of the Sri Yantra. 36 vertices originate in the layers above and below the XY plane. ELOHA, Godname of Geburah, prescribes them because its gematria number value is 36 (Table 2). 21 vertices and their 21 mirror images are in the XY plane. This shows how EHYEH, Godname of Kether with number value 21, prescribes the cross-section of the disdyakis triacontahedron viewed along a C-C axis.

Five vertices above the XY plane on either side of the X-axis do not have counterparts directly beneath them in the lower half. Starting from above the X-axis in Fig. 2, they are the B vertex on the Y-axis, the three A vertices forming a triangle and the lowermost A vertex. Similarly, five vertices below the XY plane have no vertices above them. Starting from above the X-axis, they are the A vertex, the three A vertices forming a triangle and the B vertex. Of the remaining 52 vertices, six vertices belong to the central hexagon, leaving 23 pairs of vertices, one of which is directly above the other in the pair. One of

5

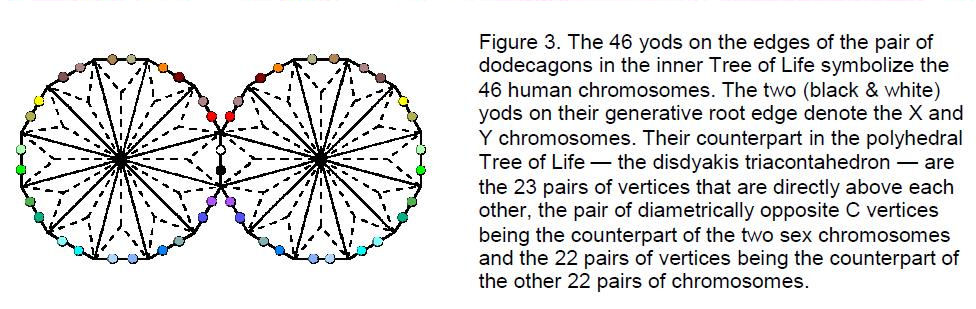
them is the pair of C vertices forming the apex and nadir of the disdyakis triacontahedron. These (22+1) pairs of vertices can be regarded as reproducing the pattern of the two sex chromosomes and the 22 pairs of chromosomes in the nucleus of the human cell. Given that this polyhedron is the cosmic blueprint — the “image of God” according to which humans were designed, according to Genesis 1:27, this pattern needs serious consideration. This view is reinforced by the fact that the same division appears in the polygonal form of the inner Tree of Life because there are 23 pairs of hexagonal yods on the edges of the pair of dodecagons, with one

pair belonging to the shared root edge (Fig. 3). Hexagonal yods signify hidden degrees of freedom, and the 23 pairs are the minimal number of degrees of freedom needed to delineate the boundary of the pair of dodecagons — the Malkuth aspect of the Tree of Life corresponding to the human body. The pairing of chromosomes is signalled not by the pairs of hexagonal yods on each edge in a dodecagon but by the mirror image pair of dodecagons, so that there is in one dodecagon a mirror image counterpart of each yod in the other dodecagon.

2. Geometrical composition of the 15 polygons
Consider the 15 polygons divided into their sectors. Table 3 lists the numbers of vertices, edges & triangles in the eight polygons in half the disdyakis triacontahedron.

Table 3. Number of vertices, edges & triangles in the eight polygons.

	Number of vertices	Number of edges	Number of triangles	Total
	3 + 1 = 4	6	3	12 + 1 = 13
	3 + 1 = 4	6	3	12 + 1 = 13
	3 + 1 = 4	6	3	12 + 1 = 13
	6 + 1 = 7	12	6	24 + 1 = 25
	3 + 1 = 4	6	3	12 + 1 = 13
	6 + 1 = 7	12	6	24 + 1 = 25
	3 + 1 = 4	6	3	12 + 1 = 13
Subtotal =	27 + 7 = 34	54	27	108 + 7 = 115
	6 + 1 = 7	12	6	24 + 1 = 25
Total =	33 + 8 = 41	66	33	132 + 8 = 140

6

The first seven polygons have 108 geometrical elements surrounding their centres. The hexagon in the XY plane has 24 elements surrounding its centre. The eight polygons have (108+24=132) elements surrounding their centres. They comprise 33 vertices and 33 triangles, where 33 (=1!+2!+3!+4!) is the number of layers of vertices that are orthogonal to A-A, B-B and C-C axes.¹ The total number of geometrical elements is 140. This is the number value of Malachim, the Order of Angels assigned to Tiphareth, and of Masloth, the Mundane Chakra of Chokmah (the Zodiac). It includes 41 vertices, where 41 is the 21st odd integer. This shows how EHYEH, the Godname of Kether with number value 21, prescribes the shapes of all the polygons orthogonal to a C-C axis. The eight polygons have 66 edges. As 66 is the 65th integer after 1, the Godname ADONAI with number value 65 prescribes the eight types of polygons.

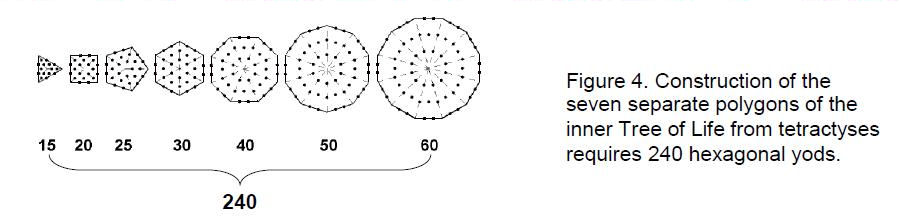
The two sets of seven polygons have (2×108=216) elements surrounding their centres, where 216 is the number value of Geburah, the sixth Sephirah. All 15 polygons have 60 vertices, 120 edges & 60 triangles surrounding their centres, i.e., 240 geometrical elements. This number is highly significant vis-à-vis the inner Tree of Life because it is the number of hexagonal yods in its seven separate polygons (Fig. 4). Moreover, the first three of these polygons have 60 hexagonal yods, comparing with the 60 vertices surrounding centres of the 15 polygons, the next three polygons have 120 hexagonal yods, comparing with their 120 edges, and the last polygon has 60 hexagonal yods, comparing with their 60 triangles. The correlation shows that the 15 polygons constitute a Tree of Life pattern. The 3:3:1 division of polygons generates the pattern of their vertices, edges and triangles. It reflects the fact that the seven Sephiroth of Construction are grouped in the Tree of Life as two triads and a single one — Malkuth.

The superstring gauge symmetry group E₈ has 240 roots and eight simple roots. The geometry of the 15 polygons embodies this group parameter describing the unified symmetry of superstring interactions. The centres of the eight types of polygons correspond to the eight simple roots. As each gauge field is 10-dimensional, the number of space-time components of the gauge fields corresponding to the generators associated with these roots is 2400. This was found in Article 27² to be the number of vertices, edges and triangles in the faces and interior of the disdyakis triacontahedron when the former are divided into three triangles and when the interior triangles formed by edges are likewise divided. The remarkable conclusion is that this polyhedron embodies the number of components of the 240 gauge fields of E₈ associated with its roots, whilst the 15 polygons formed by its vertices embody this number of gauge fields.

Just as the 2-dimensional form of the Sri Yantra was considered in Article 35, let us now imagine the 60 vertices in the 15 layers projected onto the X-Y plane. The two pairs of intersecting triangles forming Stars of David become one pair, losing eight vertices, 12 edges and six triangles. The four 6-sided polygons become two such polygons, losing 14 vertices, 24 edges and 12 triangles. Two A vertices and two B vertices of triangles disappear. Also, two edges of triangles disappear. 18 triangles disappear altogether, leaving (60–18=42) triangles. This is the number of triangles in

7

8

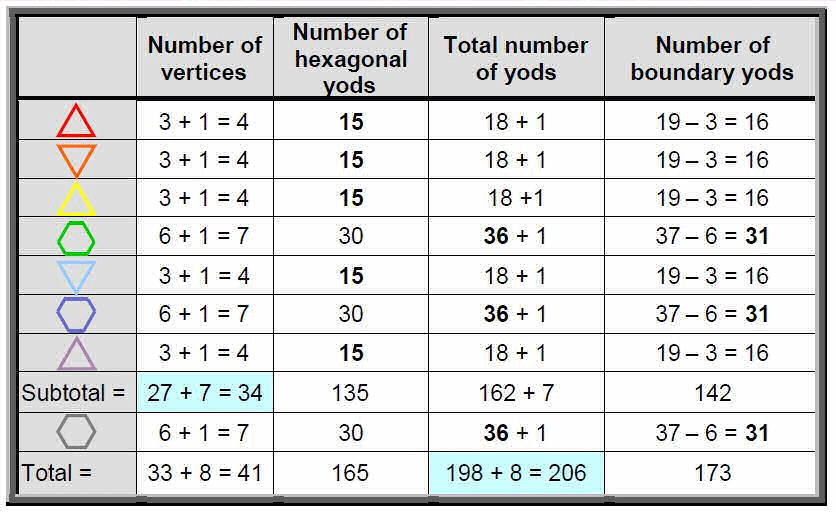
Table 4. Number of yods in the eight polygons (sectors as single tetractyses).

the Sri Yantra that surround the central one. 26 vertices disappear, leaving (75–26=49) vertices. 26 is the number value of YAHWEH, the Godname of Chokmah, and 49 is the number value of EL CHAI, the Godname of Yesod.

3. Yod composition of the 15 polygons
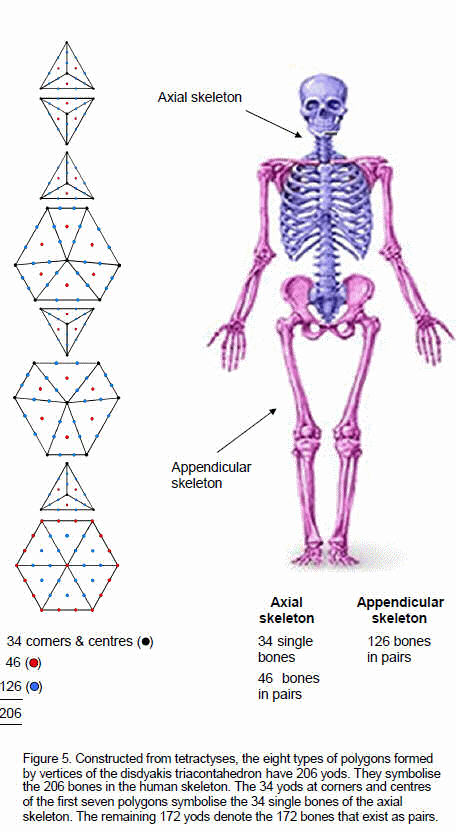
Now let us consider the triangular sectors of the polygons as tetractyses. Table 4 shows the numbers of yods in the eight polygons in one half of the disdyakis triacontahedron. There are 41 yods at the corners of their 33 tetractyses, 165 hexagonal yods and 206 yods altogether. The latter is made up of 34 vertices of the 27 tetractyses in the first seven polygons and 172 yods that are either hexagonal yods (165) or vertices of the tetractyses in the central hexagon (7). Compare this with the facts that the axial skeleton of the human body has 34 single bones and that 172 bones in the axial and appendicular skeletons exist in pairs (Fig. 5). The corners and centres of the seven polygons above the XY plane symbolise the single bones of the axial skeleton. It is truly remarkable that the bone composition of the body should be defined by the yods needed to construct the eight polygons in one half of the disdyakis triacontahedron from tetractyses! It is evidence that the human body is designed according to the blueprint of the Tree of Life, of which this Catalan solid is the polyhedral realisation.

The 60 tetractyses in the 15 polygons have 60 vertices other than centres of polygons and 300 hexagonal yods, totalling 360 (=36×10) yods that surround their 15 centres. This shows how ELOHA, the Godname of Geburah with number value 36, prescribes the yod population of the 15 layers of vertices. The central hexagon also has 36 yods surrounding its centre. There are 10 triangles and five 6-sided polygons. The numbers 10 and 5 are the values of, respectively, the letters yod (י) and heh (ה) making up the Divine Name YAH (יה) with number value 15, demonstrating how it prescribes the layers of vertices in the disdyakis triacontahedron.

The first six polygons have 142 yods on the edges of their 27 tetractyses. Both sets of six polygons have 284 boundary yods. The central hexagon has 31 yods on the edges

9

10

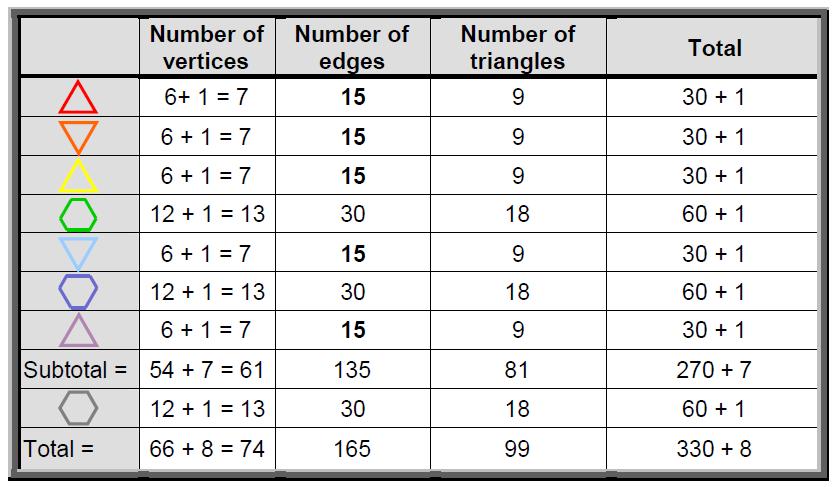
Table 5. Geometrical composition of the eight polygons (sectors as three triangles).

of its six tetractyses, showing how EL, the Godname of Chesed, prescribes the shape of the polygon in the middle of the 15 layers of vertices. The 15 polygons have (284+31=315) boundary yods. Of these, 75 are vertices, leaving 240 hexagonal yods on the edges of tetractyses. We found earlier that the 15 polygons have 240 geometrical elements surrounding their centres. The two numbers agree because each sector of a polygon adds four geometrical elements, whilst, considered as a tetractys, it adds four hexagonal yods on the two edges associated with it. Both properties demonstrate that the number 240 characterises the shape of the 15 polygons. Many previous articles have discussed it in the context of the E₈×E₈ heterotic superstring, whose 16800 circularly polarized oscillations about its spin axis are the space-time manifestation of the 240 gauge charges associated with the non-zero roots of E₈. Likewise, there are 240 geometrical elements surrounding the centres of the 15 polygons. The disdyakis triacontahedron embodies the structure of the superstring.

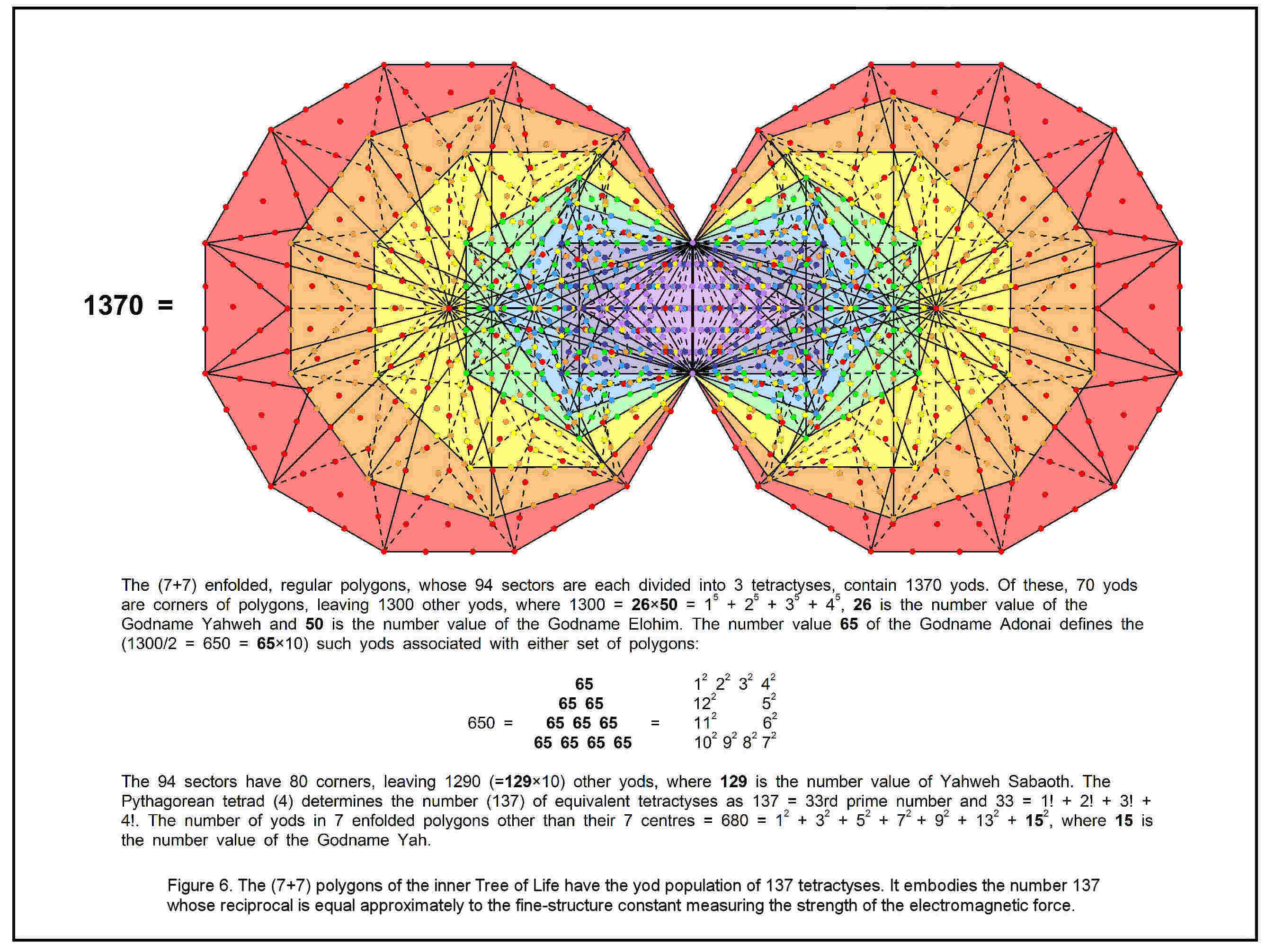
Now consider the sectors of the polygons divided into three triangles. Table 5 lists their geometrical composition. The first seven polygons have 61 vertices of their 81 triangles. Both sets of seven polygons have 122 vertices. The hexagon in the XY plane has 13 vertices. The 15 polygons have (122+13=135) vertices. Including the two C vertices, the disdyakis triacontahedron has 137 vertices. This is the 33rd prime number, where 33 is the number of corners of the eight polygons in one-half of the polyhedron. Its reciprocal is approximately the fine-structure constant α ≡ e²/ħc ≈ 1/137 that measures the coupling of the electric charge of an electron to the electromagnetic field. One of the most important numbers in physics is encoded in the geometry of the 15 layers of vertices of this polyhedron! It is encoded in the inner Tree of Life as the 1370 yods in its 14 polygons when their 94 sectors are each constructed from three tetractyses (Fig. 6).

The first seven polygons have 270 geometrical elements surrounding their centres. The central hexagon has 60 elements surrounding its centre. Surrounding the centres of the 15 polygons are (270+60+270=600) elements made up of 120 vertices, 300 edges and 180 triangles. Constructed from triangles, the disdyakis triacontahedron has 600 geometrical elements (60 vertices, 240 edges and 300 triangles) surrounding any axis

11

that joins two diametrically opposite vertices.³ It is remarkable that the same number of geometrical elements should be displayed by both the polyhedron and its 15 layers.

Table 6. Number of yods in the eight polygons (sectors as three tetractyses).

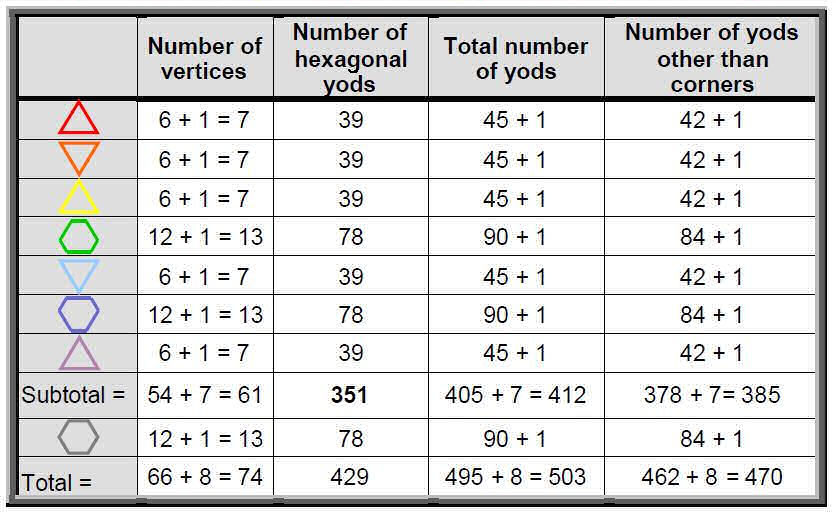
Table 5 also indicates that the eight polygons have 165 edges & 99 triangles, that is, 264 edges & triangles. This demonstrates that they constitute a Tree of Life pattern described by the structural parameters of the inner Tree of Life, whose seven enfolded polygons contain 264 yods when constructed from tetractyses (Fig. 7).

Now suppose that each triangle is a tetractys. Table 6 lists the yod populations of the eight polygons. The 99 sectors of the eight polygons in one-half of the polyhedron have 74 vertices. Including the two C vertices, there are  76  vertices. This  shows  how  YAHWEH ELOHIM, the Godname of Tiphareth with number value 76, prescribes the polyhedron through its 15 layers of vertices. The two 6-sided polygons above the XY plane have 26 vertices, leaving 50 vertices (two C vertices and 48 vertices of sectors). 26 is the number value of YAHWEH and 50 is the number value of ELOHIM.

Surrounding their centres are 66 yods at vertices of tetractyses. 66 is the 65th integer after 1, showing how ADONAI, the Godname of Malkuth with number value 65, prescribes the shapes of the polygons through the vertices of their 99 tetractyses. The first seven polygons have 351 hexagonal yods. 351 is the number value of Ashim, the

12

Order of Angels assigned to Malkuth. It is also the sum of the first 26 integers:

351 = 1 + 2 + 3 + …. + 26.

This shows how YAHWEH, the Godname of Chokmah, determines the population of hexagonal yods in the seven polygons above or below the XY plane. There are 385 yods other than polygonal corners in the 81 tetractyses making up the first seven polygons, where

This demonstrates the mathematical beauty intrinsic to the disdyakis triacontahedron. The Decad determines the number of extra yods needed to construct the polygons in either half of the polyhedron above or below its central plane.

All eight polygons have 495 yods surrounding their centres. As 495 = 9×55 = 3²×(1²+2²+3²+4²+5²) = 3² + 6² + 9² + 12² + 15², we see how the Godname YAH with number value 15 prescribes the yod population of these polygons. It also prescribes the 470 yods on the edges of their 99 tetractyses, for 47 is the 15th prime number. All 15 polygons have 135 vertices, 780 hexagonal yods (that is, ten times the number of hexagonal yods in the central hexagon) and 915 yods in all. 900 yods surround the 15 centres, where 900 = 30² = (1²+2²+3²+4²)² = 3²(1+2+3+4)² = (3+6+9+12)². This illustrates the Tetrad Principle⁴ at work in expressing the mathematical 

properties of holistic systems. When the 180 interior triangles formed by the edges of the disdyakis triacontahedron are each divided into three tetractyses, they form 540 tetractyses. When its 120 faces are each divided into three triangles, they form 360 tetractyses. Therefore, the construction of the polyhedron requires (540+360=900) tetractyses. Remarkably, the same number of tetractyses creates the polyhedron as there are yods surrounding the centres of the polygons in its 15 layers! Earlier, we found that it also has the same number (600) of geometrical elements as the 15 polygons.

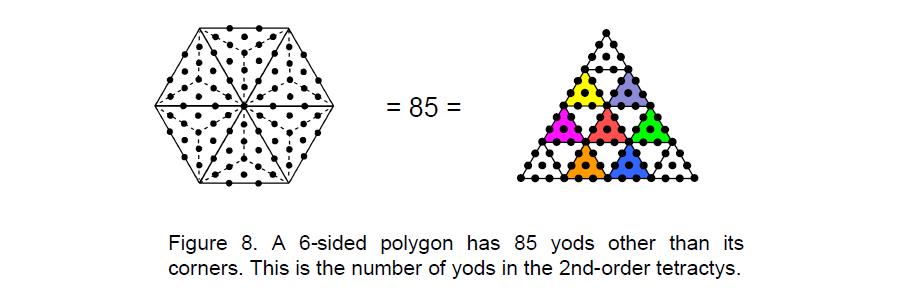
There are 85 yods in the central hexagon (Fig. 8) other than its six corners, where

85 = 4⁰ + 4¹ + 4² + 4³.

84 yods other than these corners surround its centre, where

84 = 1² + 3² + 5² + 7².

These are more examples of how the Tetrad Principle determines properties of holistic systems, e.g., the disdyakis triacontahedron. The seven polygons above the XY plane

13

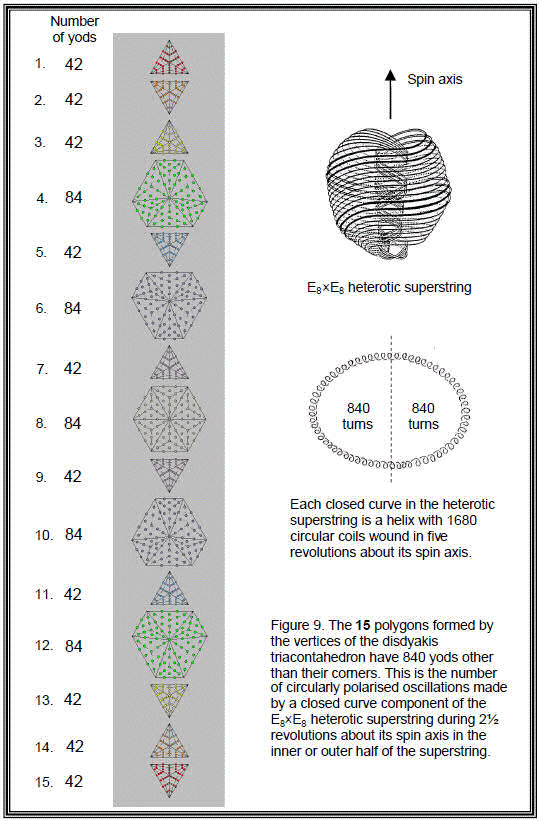
14

have 378 yods other than corners that surround their centres. The 15 polygons have (378+84+378=840) such yods (Fig. 9). Remarkably, they have ten times the corresponding number in the central hexagon. This number is a structural parameter of the heterotic superstring, being the number of circularly polarized oscillations in an outer or inner half of each of the ten closed curves that comprise it.

The arithmetic reason for this very important encoding of superstring structure in the 15 layers of vertices is simple. The number of yods in an n-sided polygon whose sectors are each divided into three tetractyses is 15n + 1. The number of yods other than corners of the polygon that surround its centre is 14n. The number of such yods in the 15 polygons = 14Σn = 14×60 = 840. The five 6-sided polygons have 30 corners and (14×30=420) yods other than corners, as do the ten triangles with 30 corners. This equal division of 420 yods is prescribed by the Godname YAH (YH) because the letter value 5 of H (heh) specifies the number of 6-sided polygons and the letter value 10 of Y (yod) specifies the number of triangles.

It was shown in Article 27 that, when constructed from tetractyses, the disdyakis triacontahedron has 840 yods surrounding any axis joining diametrically opposite vertices.⁵ Once again, it is remarkable that the same yod population appears in both contexts. The 840 yods in the 15 polygons other than their 60 corners consist of 60 vertices of tetractyses and 780 hexagonal yods. 

Similarly, the 840 yods surrounding the axis of the disdyakis triacontahedron comprise 60 polyhedral vertices and 780 hexagonal yods. The same 60/780 composition of yods exists in each context as well.

A 120:720 division in the number 840 occurs as well. The 15 polygons have (60×2=120) hexagonal yods along their 60 edges and 720 yods inside them. The latter comprise 360 hexagonal yods along the three edges inside each sector and 360 yods made up of 120 hexagonal yods along edges of sectors, 60 vertices and 180 hexagonal yods at centres of tetractyses. The disdyakis triacontahedron has 120 hexagonal yods at centres of its faces and 720 yods that comprise 360 hexagonal yods along its 180 edges and 360 yods made up of 120 hexagonal yods on 60 internal edges of triangles, 60 vertices and 180 hexagonal yods at centres of 180 internal tetractyses.

4. The Lambda Tetractys pattern of the 15 polygons
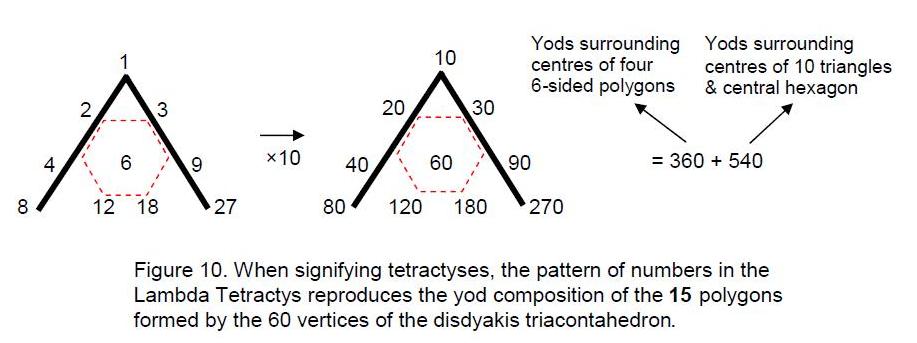
The total number of yods surrounding the centres of the 15 polygons = 15Σn = 15×60 = 900, that is, the number of yods in 90 tetractyses. They consist of the 60 vertices of the disdyakis triacontahedron (the yods of six tetractyses) and the 840 remaining yods surrounding the centres of these tetractyses (the yods of 84 tetractyses). This 6:84 division appears in the Lambda Tetractys (Fig. 10). This is the interpolated form of

15

Plato’s Lambda, the ratios of whose numbers have been known for over 2,000 years to define the tone ratios of the notes of the Pythagorean musical scale.⁶ If we consider its integers as denoting numbers of tetractyses, then the integer 6 denotes six tetractyses whose 60 yods correspond to the 60 vertices of the disdyakis triacontahedron, whilst the sum of its nine other integers is 84, and 84 tetractyses have 840 yods, which is the number of yods other than these vertices. This is intuitively appealing because, in terms of the equivalence between the Tree of Life and the tetractys, the central yod symbolizes Malkuth, so that the 60 vertices in the 15 polygons constitute the Malkuth aspect of the disdyakis triacontahedron as the polyhedral Tree of Life as they create its form, whilst the other yods constitute its higher aspect.

The Lambda Tetractys was encountered in a previous article⁷ in the context of the disdyakis triacontahedron as the 900 tetractyses needed to build its faces and interior triangles when each one is divided into three tetractyses. The 120 faces comprise (120×3=360) tetractyses and the 180 interior triangles formed by its 180 edges comprise (180×3=540) tetractyses. The former correspond to the sum (36) of the integers at the corners of the Lambda Tetractys and the latter correspond to the sum (54) of the integers at the centre and corners of a hexagon. Both the disdyakis triacontahedron and its 15 layers of polygons conform to the archetypal pattern of the Lambda Tetractys.

Another way of comparing the 15 polygons to the Lambda Tetractys is as follows: the ten triangles and the central hexagon have 36 sectors with (36×15=540) yods surrounding their 11 centres. This is the number of yods in 54 tetractyses. The four 6-sided polygons have 24 sectors with (24×15=360) yods surrounding their 4 centres. This is the number of yods in 36 tetractyses. The sum of the ten integers is 90, which is the number of tetractyses whose yod population equals that of the 15 polygons. The four 6-sided polygons with

360 yods correspond to the integers at the corners of the Lambda, whose sum is 36, whilst the ten triangles and the central hexagon correspond to the seven remaining integers, whose sum is 54.

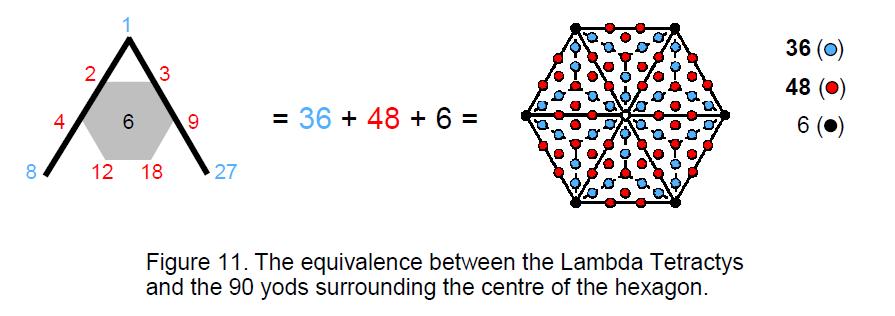
The central hexagon itself displays the 36:54 division in the Lambda Tetractys. Regarded as a single tetractys, each sector contributes six yods, so that 36 yods surround its centre. Regarded as three tetractyses, a sector contributes nine more yods (all hexagonal), so that 54 more yods are added to the hexagon. However, unlike the Lambda Tetractys with the number 6 at its centre, a group of six yods cannot be distinguished in this addition. The only way the comparison may be extended is to consider the six hexagonal yods lying on edges of tetractyses inside each sector as contributing to the number 36 and the remaining nine yods as contributing to the number 54. In this way, the central number 6 denotes the number of corners of the

16

hexagon (Fig. 11), as one would expect, intuitively, as the corners are the shape-defining yods, a quality consistent with the meaning of Malkuth symbolized by the yod at the centre of a tetractys and therefore with the number 6 that occupies this position in the Lambda Tetractys. The hexagon in the XY plane with A vertices at its corners is therefore analogous to the complete set of 15 polygons. As found several times earlier, the properties of the latter are exactly ten times the corresponding ones of the former. The whole is contained in another whole. The simple, arithmetic reason for this is that the central hexagon has six sectors, whilst the 15 polygons have 60 sectors, that is, ten times as many, so that any property of the sectors of the hexagon become multiplied by 10 for the corresponding properties of the complete set of polygons.

References

¹ Phillips, Stephen M. Article 25: “The 33 Vertex Sheets of the Disdyakis Triacontahedron Signify the 33 Tree Levels of Ten Overlapping Trees of Life,” (WEB, PDF).

² Phillips, Stephen M. Article 27: “How the Disdyakis Triacontahedron Embodies the Structural Parameter 1680 of the E₈×E₈ Heterotic Superstring,” (WEB, PDF), pp. 4–5.

³ Ibid., p. 20, Table 4.

⁴ Phillips, Stephen M. Article 1: The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 5.

⁵ Ref. 2, p. 19.

⁶ Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF), and Article12: “New Pythagorean Aspects of Music and Their Connection to Superstrings,” (WEB, PDF).

⁷ Phillips, Stephen M. Article 26: “How the Seven Musical Scales Relate to the Disdyakis Triacontahedron,” (WEB, PDF), p. 29.

17