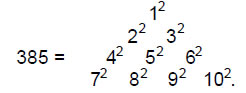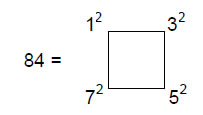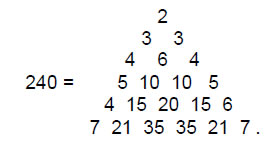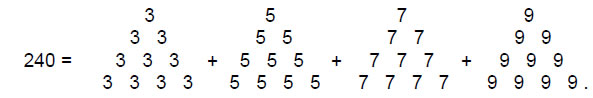ARTICLE 25

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

1

1. Tree levels as space-time dimensions
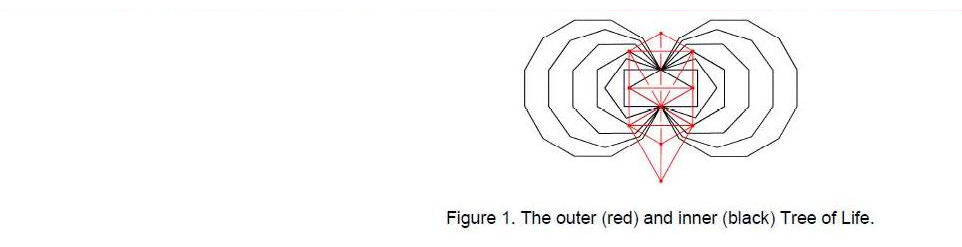
Just as the DNA molecule in the nucleus of a cell encodes the properties of the biological organism made up of such cells, so the inner form of the Tree of Life (Fig. 1) encodes how its outer form replicates to represent the whole cosmos — both physical and superphysical. By exploiting the isomorphism between a regular, n-sided polygon divided into tetractyses and n overlapping Tree of Life up to Chesed of the nth tree, the author has proved rigorously that the two sets of seven separate polygons contain a unique subset of 12 polygons that is isomorphic to a whole number of overlapping Trees of Life. One set of seven polygons is isomorphic to 49¹such trees and the remaining five polygons (the pentagon, hexagon, octagon,

decagon and dodecagon of the second set of polygons) are isomorphic to 42 trees. Encoded, therefore, in the regular polygons making up the inner Tree of Life are 91 overlapping Tree of Life. The 49 trees represent the 49 subplanes of the seven planes of consciousness — one of the teachings of Theosophy that can now be mathematically proved. These seven planes represent the outer evolutionary journey of the soul from one incarnation to another towards absorption in the inner Divine Life. They constitute but the lowest physical plane of seven cosmic planes of consciousness, the six higher planes of which are similarly divided into seven subplanes, making a total of 42 subplanes. These are represented by the 42 trees encoded in the five polygons belonging to the second set of seven polygons. Accordingly, the two halves of the inner Tree of Life signify the physical and superphysical domains of the spiritual cosmos, which the author has called the ‘Cosmic Tree of Life’ (CTOL). The boundary between these two domains is prescribed by EL CHAI, the Godname of Yesod, which has number value 49 (the other Godnames also prescribe it in ways that need not be described here).

The seven lowest trees in CTOL represent the seven levels of biological consciousness. In their normal physical activity, humans are focussed in the third tree but are evolving as well into ‘etheric’ realms of consciousness that are mapped by the next four trees. Defining the ‘n-tree’ as the lowest n trees in CTOL, physical consciousness can, potentially, extend over the 7-tree. When trees overlap, all the Sephirothic emanations (called ‘Sephirothic levels,’ or SLs) of one tree are SLs of the next higher and lower tree except Chesed and Geburah. These two types of SLs play a pre-formative role in the manifestation of the next lower tree as a level of consciousness. They represent gaps, or critical jumps, in the spectrum of awareness as it shifts from one modality to the next represented by the SLs of the next higher tree.

 

2

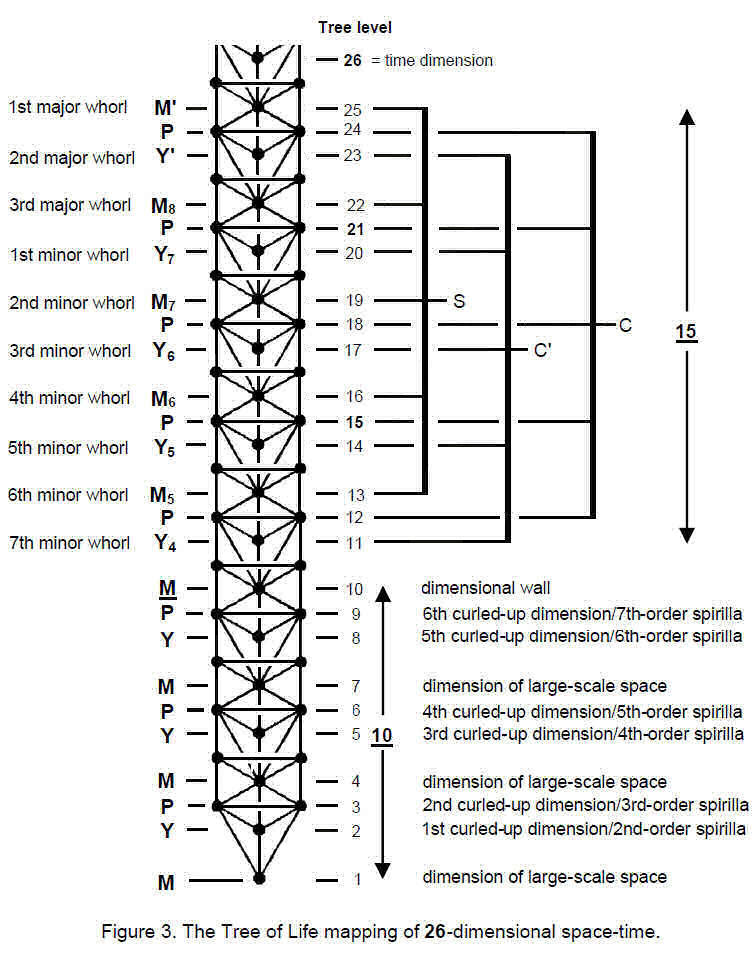
Each level of consciousness is a band of types of awareness characterised by the seven fundamental Sephiroth of Construction. The lowest four relate to what Carl Jung called the four ‘psychic functions’ of sensing, feeling, thinking and intuiting. These Sephirothic variations define seven ‘tree levels’ within each tree/level of consciousness (Fig. 2). The fourth has special evolutionary significance because it expresses the quality of Tiphareth. As the central Sephirah of the Tree of Life, it is the interface between the ego-centred and transpersonal, ego-less levels of being. The number of tree levels in the n-tree ≡ T(n) = 3n + 4. Hence, T(7) = 25. They

3

denote the 25 spatial dimensions of the 26-dimensional space-time predicted by quantum mechanics for spinless strings. The 26th tree level (the lowest one above the 7-tree) maps the time dimension. It is marked by Yesod of the ninth tree, the 50th SL. This shows how ELOHIM, Godname of Binah with number value 50, prescribes the 26 dimensions of space-time, which are prescribed directly by YAHWEH, Godname of Chokmah, because it has number value 26. YAH, the older version of YAHWEH, has number 15. It prescribes the 25 dimensions of space because the top of the seventh tree marked by the 25th tree level is the 47th SL, where 47 is the 15th prime number. The Godname EL of Chesed also prescribes these 25 dimensions because its number value 31 is the number of stages of vertical descent of what Kabbalists call the ‘Lightning Flash’ from the apex of the seventh tree to the nadir of CTOL, namely, Malkuth of the first tree.

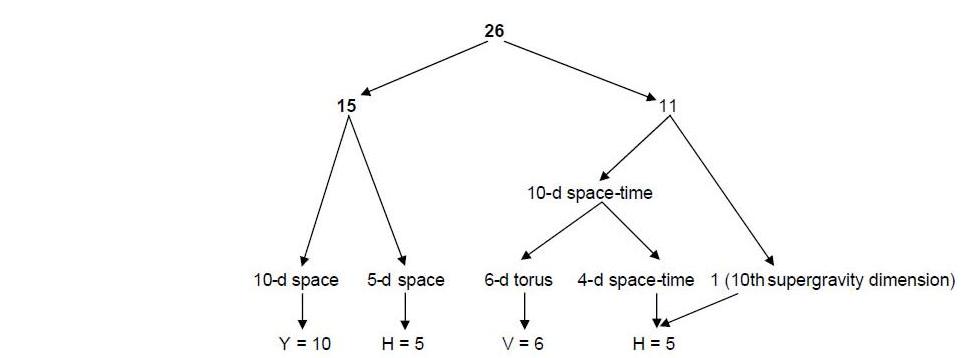
There are three types of tree levels: Malkuths (M) of trees, Yesods (Y) and Hod- Netzach Paths (P) (apart from the lowest tree, the lattermost are Binah-Chokmah Paths of the next lower tree). Article 2 explained the role of these tree levels in creating the ten whorls of the UPA described by Annie Besant and C.W. Leadbeater in their book Occult Chemistry. The author has identified the UPA as a heterotic E₈×E₈' superstring,² each of its ten whorls resulting from the curling into a circle of a dimension represented by a tree level (Fig. 3). Five M and five Y tree levels belonging to the uppermost four trees define a 10-dimensional space S×C' whose curling up generates the 10 whorls. Five P tree levels define a 5-dimensional space C whose symmetries generate the E₈ gauge symmetry group. The remaining 10-dimensional space is that of supergravity theories, one of the dimensions being a finite segment between the two 10-dimensional space-times of ordinary and shadow matter superstrings.³

The dimensionalities of the various spaces into which the author’s theory predicts 26-dimensional space-time bifurcates are the letter values of YHVH (YAHWEH), the

later version of the Godname of Chokmah given by God to the Jewish people, according to their religious beliefs. The value 10 of Y (yod) denotes the 10 dimensions of S×C' whose curling up creates the ten whorls of the UPA, the value 5 of H (he) denotes the 5-dimensional space C whose geometrical symmetries generate E₈, the value 6 of V (vav) denotes the curled-up, 6-dimensional space of superstrings and the value 5 of the second H denotes the Einsteinian, 4-dimensional space-time and the dimensional segment separating the two superstring space-times. According to Leadbeater’s description of the UPA, each whorl is a closed helix with 1680 turns

4

(“1st-order spirillae”). Each turn is a helix with seven circular turns (“2nd-order spirillae”); each of the latter is a smaller helix with seven turns (“3rd-order spirillae”) and so one. The six higher orders of spirillae described by Leadbeater represent the winding of strings around successively smaller, compact, 1-dimensional spaces, i.e., the 6- dimensional, compactified space of superstrings is a 6-d torus. Figure 3 shows that tree levels of type P and Y define these curled-up dimensions.

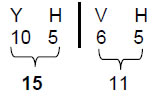
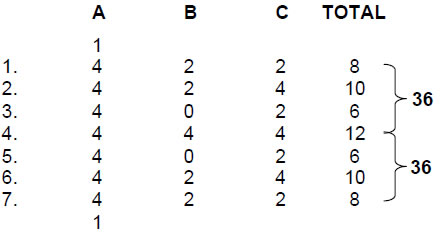
The superstrings of ordinary and shadow matter are confined to two space-time sheets separated by a gap. This tenth dimension acts as a wall that prevents either kind of superstring entering the other’s universe. It is represented by the tenth tree level (M in Fig. 3). This is Malkuth of the fourth highest tree in the 7-tree mapping the physical plane, that is, 26-dimensional space-time). This 15:11 division between the dimensionalities of supergravity space-time and the higher, 15-dimensional space that generates both the ten string-like whorls of the UPA/heterotic superstring and its gauge symmetry group E₈ has its counterpart in the combinatorial properties of ten objects labelled A, B, C…. J when arranged in the pattern of a tetractys:

The four objects G, H, I and J have (2⁴–1=15) combinations. The three objects D, E and F have (2³–1=7) combinations, the two objects B and C have (2²–1=3) combinations and the single object A has one combination. The six objects A–F therefore form 11 combinations. When arranged in a tetractys, all ten objects have 26 combinations when only objects from the same row are considered.

This has a simple geometrical realisation. Letting the objects be points in space, the four rows of the tetractys of ten points signify the sequence of point, line, triangle and tetrahedron. Combinations of two points denote the line joining them, combinations of three points signify the triangles with these points as their corners and the combination of four points signifies the tetrahedron with these points as its vertices. There are 26 vertices, lines, triangles and tetrahedra in the 4-stage sequence of generation from the point of the simplest Platonic solid — the tetrahedron. This illustrates in a very simple way the mathematical archetype embodied in the Divine Name YAHWEH.

n objects have n! permutations. The permutations of the objects in a tetractys are:

5

There are 26 combinations and 33 permutations of the objects arranged in the four rows of a tetractys when only objects in the same row are grouped together.

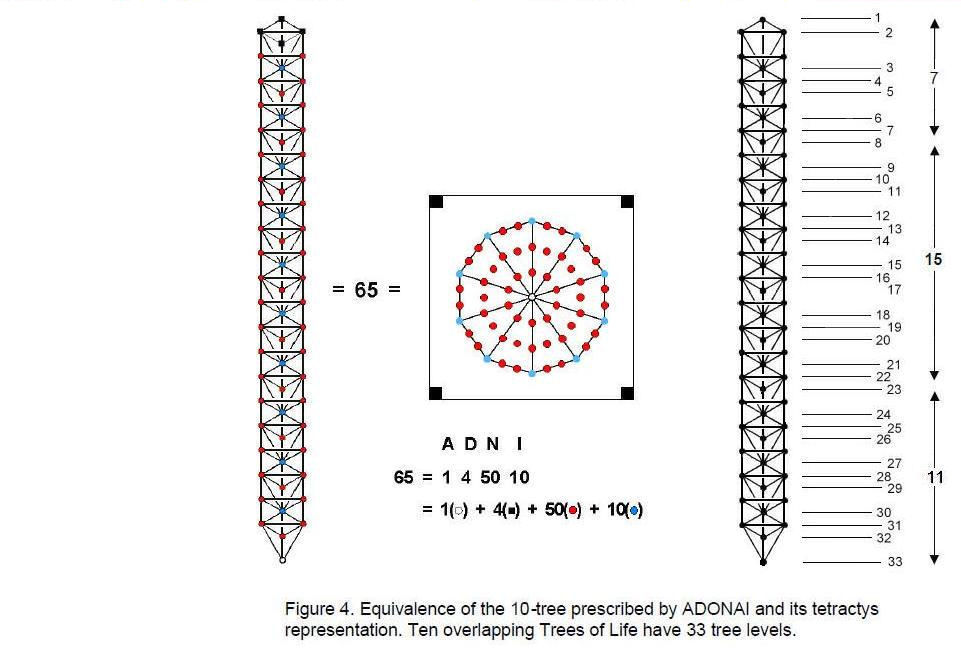
The tetractys and the Tree of Life are different representations of the 10-fold nature of holistic systems designed according to the universal blueprint. Each Sephirah of the Tree of Life has in turn a 10-fold differentiation, so that ten overlapping Trees of Life is the next higher differentiation of a single Tree of Life. In the same way, the 10-tree is the next higher

differentiation of the 1-tree. It has 65 SLs (Fig. 4). 65 is the number value of the Godname ADONAI assigned to Malkuth. In fact, its very letter values signify the numbers of various types of SLs in the 10-tree. This is borne out by the representation of the 10-tree as a decagon divided into 10 tetractyses and surrounded by a square, the letter values denoting the yods that are counterparts of the SLs. The 64 SLs of the ten overlapping trees span 33 tree levels. We saw earlier that the lowest 50 SLs span 26 tree levels signifying the 26 dimensions of space-time predicted by quantum mechanics for spin-0 strings. The 7-tree mapping the physical plane and the 25 spatial dimensions/tree levels emanates from the 50th SL, which, as Daath, represents in Kabbalah the ‘Abyss’ between the Supernal Triad represented by the three uppermost trees of the ten overlapping trees and the seven Sephiroth of Construction represented by the seven lowest trees. Hence, the division of tree levels in ten overlapping Trees of Life:

33 = 7 + 26

6

expresses in Kabbalistic terms the distinction between the seven Sephiroth of Construction and the triple Godhead of Kether, Chokmah and Binah.

The number of corners of the 7n regular polygons enfolded in n overlapping Trees of Life is

C(n) = 35n + 1,

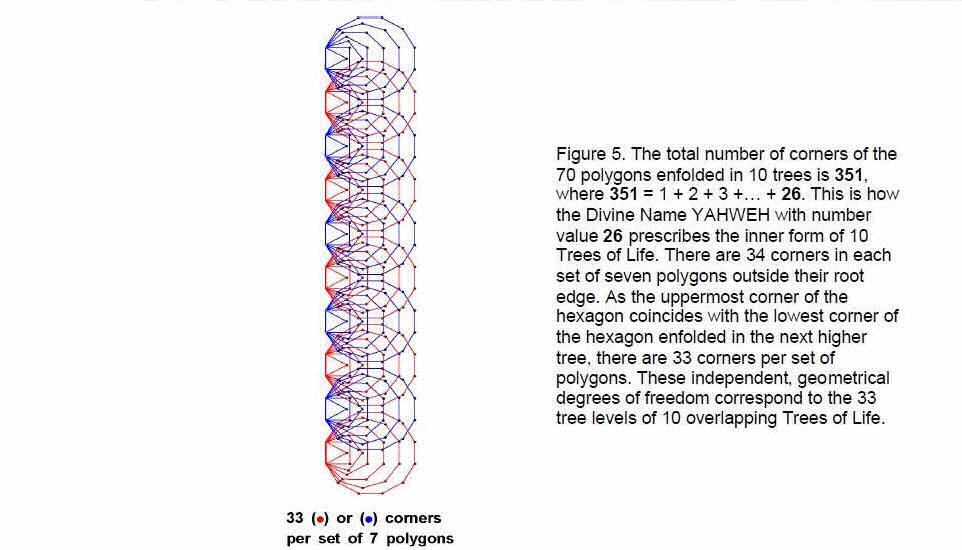
where “1” denotes the uppermost corner of the hexagon enfolded in the tenth tree (the hexagon is the only one of the seven regular polygons that shares its corners with polygons enfolded in adjacent trees. It results in its being picked out by the above formula). Therefore, C(10) = 351 = 1 + 2 + 3 +…. + 26. This shows how YAHWEH with number value 26 prescribes the inner form of ten overlapping Trees of Life. 351 is the number value of Ashim (“Souls of Fire”), the Order of Angels assigned to Malkuth. The number of corners of 

the 7n polygons outside their n root edges ≡ C'(n) – 2n = 33n + 1. C'(n+1) – C'(n) = 33. In other words, there are 33 corners per set of polygons outside their root edge (Fig. 5). The emanation of successive Trees of Life generates 33 new geometrical degrees of freedom associated with their inner form. The significance of this property for the disdyakis triacontahedron will be discussed in the next section.

The 10-tree has 34 tree levels, whilst ten overlapping Trees of Life have 33 tree levels. Their counterparts in the inner Tree of Life are its 34 corners outside the root edges, 33 per set of polygons. Any system or structure that conforms to the blueprint of the Tree of Life possesses 33 independent degrees of freedom. The counterpart of this in the tetractys is the 33 permutations of objects in its four rows.

The seven polygons enfolded on one side of the central Pillar of Equilibrium have corners shared with Chokmah, Daath, Chesed and Netzach. The other seven polygons

7

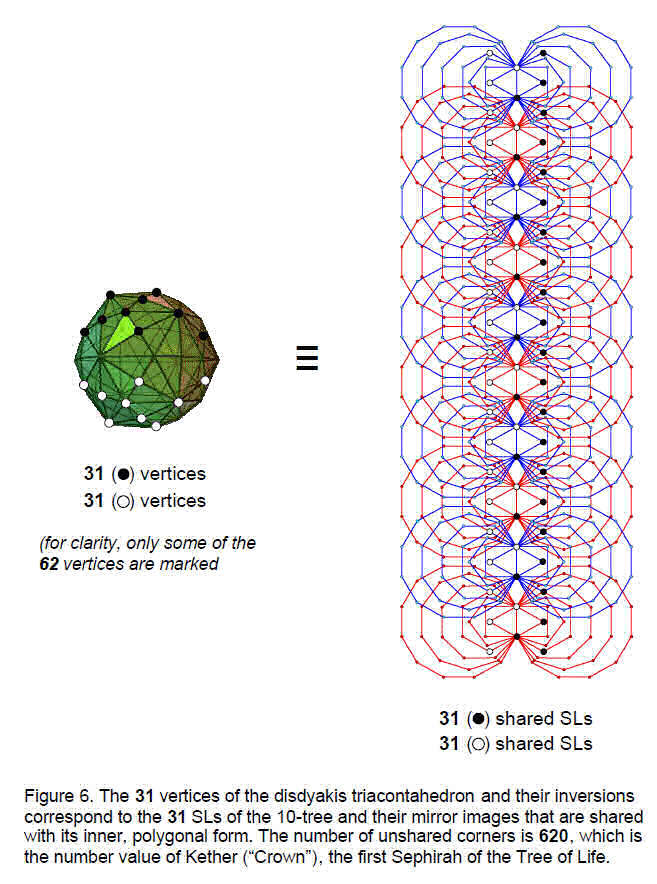
have corners shared with Binah, Tiphareth, Geburah and Hod. The top corner of the hexagon is the bottom corner of the hexagon enfolded in the next higher tree. This means that there are (3+1) corners associated with each set of polygons, “1” denoting the shared, top corner of the hexagon. Enfolded in n overlapping Trees of Life are 7n polygons on either side of the central pillar with (3n+1) corners that coincide with SLs. The 10-tree has 70 polygons on each side with 31 corners shared with it. Hence, there are 62 SLs of the 10-tree that are shared with its inner form. The 62 vertices of the disdyakis triacontahedron correspond to these SLs (Fig. 6), the 31 independent vertices and their 31 inverted images corresponding to the 31 SLs that coincide with corners of each set of polygons. 31 is the number value of EL (“God”), the Godname of Chesed, and 62 is the number value of Tzadkiel (“Benevolence of God”), the Archangel of Chesed — the same Sephirah.

8

2. Vertex planes in the disdyakis triacontahedron
The following evidence was presented in Article 22 that the disdyakis triacontahedron is the 3-dimensional realisation of the 2-dimensional (polygonal) form of the inner Tree of Life:

1. the 120 shape-forming yods on the boundaries of the seven enfolded polygons symbolise the 120 faces of this polyhedron;

2. the disdyakis triacontahedron completes the 10-step sequence of generation of polyhedra from the mathematical point:

3. the 480 hexagonal yods in the 120 faces of the disdyakis triacontahedron correspond to the 480 hexagonal yods in the two sets of seven regular polygons constituting the inner Tree of Life;

4. the 62 vertices of the disdyakis triacontahedron correspond to the 62 SLs of 10 overlapping Trees of Life that coincide with corners of their 140 enfolded polygons and to the 62 corners of the 14 polygons enfolded in one Tree of Life that do not coincide with its Sephiroth;

5. the seven polyhedra in the above sequence are made up of 1680 hexagonal yods — the number of yods below the top of the 10-tree when its triangles are divided into three tetractyses. This is the structural parameter of the E₈×E₈' heterotic superstring, as established in many previous articles and in the author’s books;

6. the hexagonal yod population of the 28 Platonic and Archimedean solids in the disdyakis triacontahedron is 3360. This is the yod population of the seven enfolded polygons when constructed from 2nd-order tetractyses.⁴

Further evidence in support of this conclusion is provided by the patterns of planes of vertices of the disdyakis triacontahedron. Its 62 vertices are made up of the 32 vertices of a rhombic triacontahedron, which form 30 Golden Rhombi, and 30 raised centres of the latter. The long diagonals of each Golden Rhombus are the edges of an icosahedron and its short diagonals

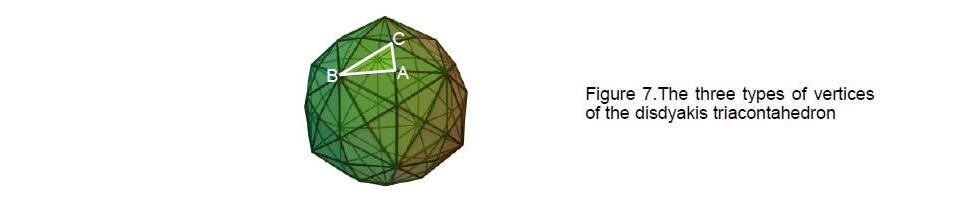
are the edges of a dodecahedron. Labelling the vertices of the 120 triangular faces A, B & C (Fig. 7), there are 30 A vertices, 12 B vertices (corners of the icosahedron) and 20 C vertices (corners of the dodecahedron).

9

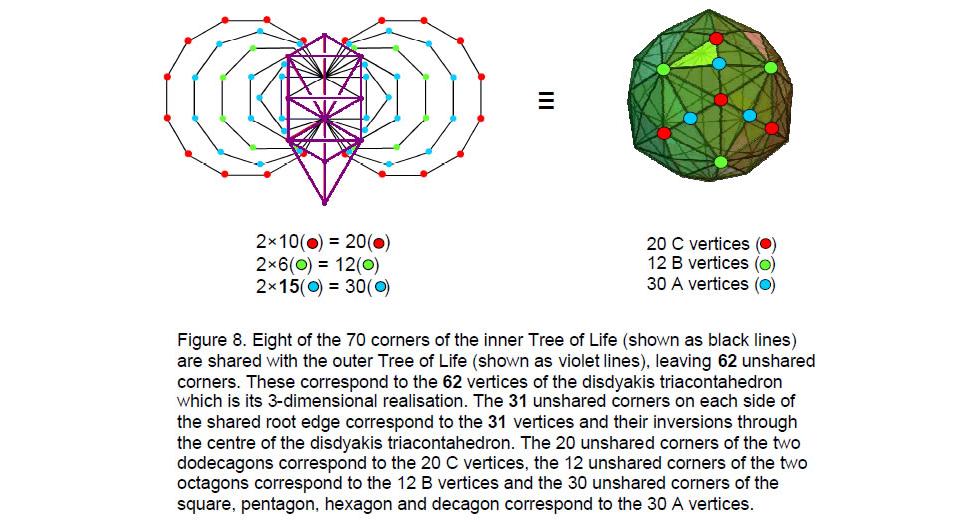
Remarkably, this pattern of types of vertices appears also in the inner Tree of Life in the 62 corners of the two sets of enfolded polygons that are unshared with Sephiroth of its outer form (Fig. 8). The two dodecagons have 20 corners (red yods) outside the root edge. The pair of octagons has 12 corners outside the root edge and the pair of squares, pentagons, hexagons

and decagons have 30 corners outside the root edge. We find the following correspondence:

30 corners of squares, pentagons, hexagons and decagons 30 A vertices
12 corners of octagons 12 B vertices
20 corners of dodecagons 20 C vertices

For the sake of clarity, only three representative A, B and C vertices are shown in the disdyakis triacontahedron in Fig. 7. It may be argued that the numbers of unshared corners in pairs of polygons:

square	pentagon	hexagon	octagon	decagon	dodecagon
4	6	4	12	16	20

allow other combinations of polygons to generate the numbers 30, 12 and 20, e.g., the pair of squares, pentagons and dodecagons have 30 corners. This is not true of the number 12, which can be associated only with the pair of octagons because it is not the sum of any of the above numbers. The dodecagons are the simplest choice for the number 20 because other choices require combinations of two or three polygons. Any argument over uniqueness, however, misses the point being demonstrated here, namely, that correspondence can be established not only between the numbers of vertices of the disdyakis triacontahedron and the corners of the inner Tree of Life but also between the numbers of each type of vertex and numbers of corners of different

10

11

polygons. Such precise correspondence cannot be dismissed as due to chance. It is further evidence that the disdyakis triacontahedron is the 3-dimensional form of the inner Tree of Life.

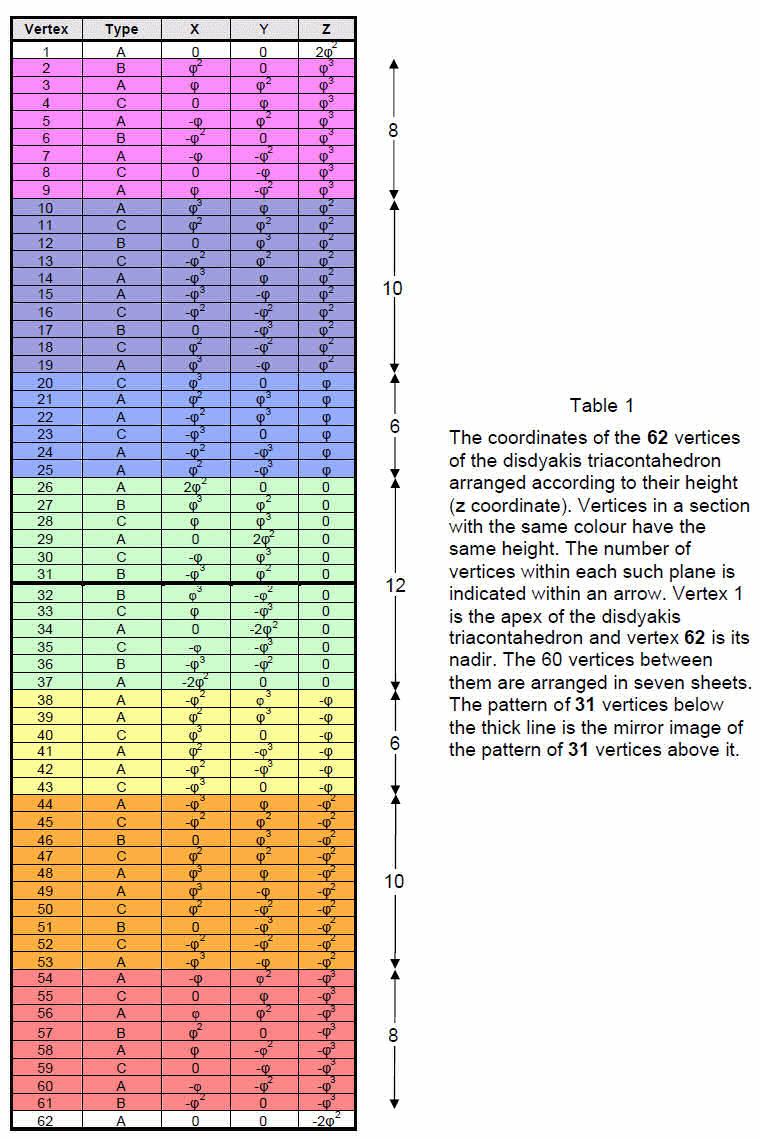
Table 1 lists the Cartesian coordinates of the 62 vertices. Their coordinates are the first three powers of φ, the Golden Ratio. They are arranged in nine vertical layers, the 

vertical axis being defined as the line joining the top and bottom A vertices indicated by the two white rows. The 60 vertices between them are distributed in seven horizontal planes

coloured according to the seven prismatic colours. The 62 sets of three coordinates are really 31 sets, as the other 31 vertices are the inversions of those in the first set, the coordinate values of one vertex being the negatives of its inverted counterpart. This is a clear example of the prescriptive power of the

 

12

 

mathematical archetype embodied in the Godname EL (“God”) associated with Chesed, the first Sephirah of Construction. Its letter vales E = 1 and L = 30 denote, respectively, the topmost vertex and the 30 vertices below it that have mirror image counterparts.

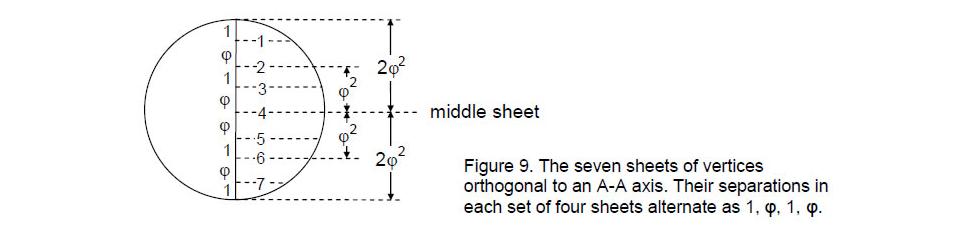
Fig. 9 indicates that the 30 A vertices are arranged in nine layers. The seven sheets between the outermost vertices are separated by distances that alternate as 1, φ, 1, φ, this pattern being reversed for the last four sheets.

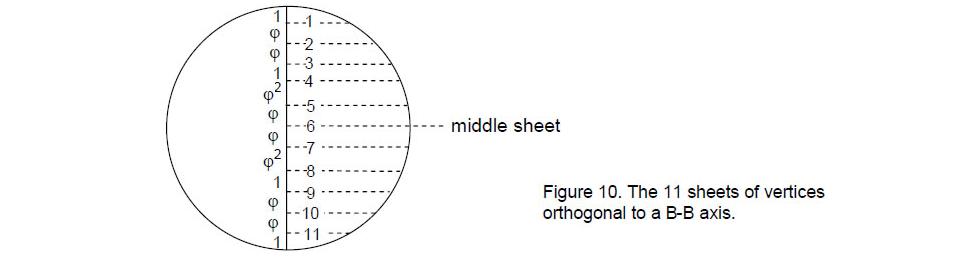
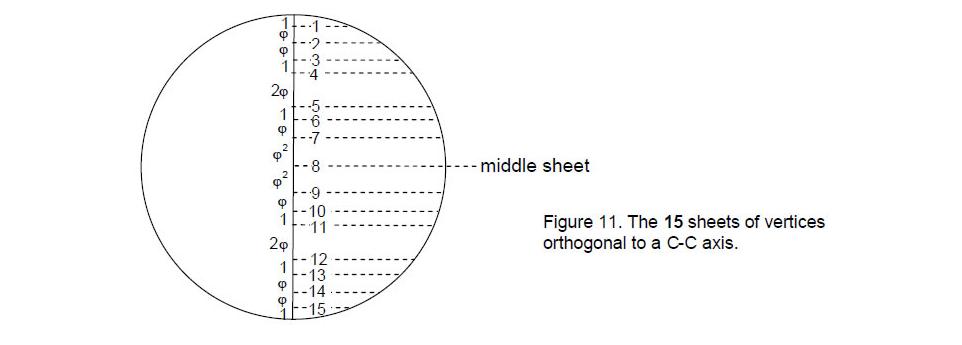
Fig. 10 indicates that the 12 B vertices (the corners of an icosahedron) are arranged in 11 sheets between the opposite B vertices defining the axis at right angles to them. Fig. 11 shows that the 20 C vertices (corners of a dodecahedron) belong to 15 sheets between the opposite C vertices defining the axis. The disdyakis triacontahedron has therefore (7+11+15=33) sheets.

3. Tree levels signify sheets of vertices
Comparing the sheet patterns of the three types of vertices with the tree levels of 10 overlapping Trees of Life shown in Fig. 4, we see that there are as many sheets as there are tree levels. Moreover, there are as many sheets (7) perpendicular to an A-A axis as there are tree levels in 10 overlapping Trees of Life above the 26th tree level marking the 50th SL, there being 26 sheets perpendicular to a B-B and a C-C axis. This is the number value of YAHWEH. The distinction between the 11 B-B sheets and the 15 C-C sheets is expressed in the letter values of YAHWEH:

It prescribes the distribution of vertices perpendicular to B-B and C-C axes, whilst YAH, the older version of this divine name with number value 15, prescribes the distribution of vertices perpendicular to a C-C axis.

The fact that the same three numbers 7, 15 and 11 appear in the contexts of 10 overlapping Trees of Life and the disdyakis triacontahedron is additional confirmation that the latter is equivalent to the inner form of the Tree of Life, its 62 corners unshared with its outer form being the counterpart of the 62 SLs of 10 trees that are

13

unshared with its enfolded polygons.

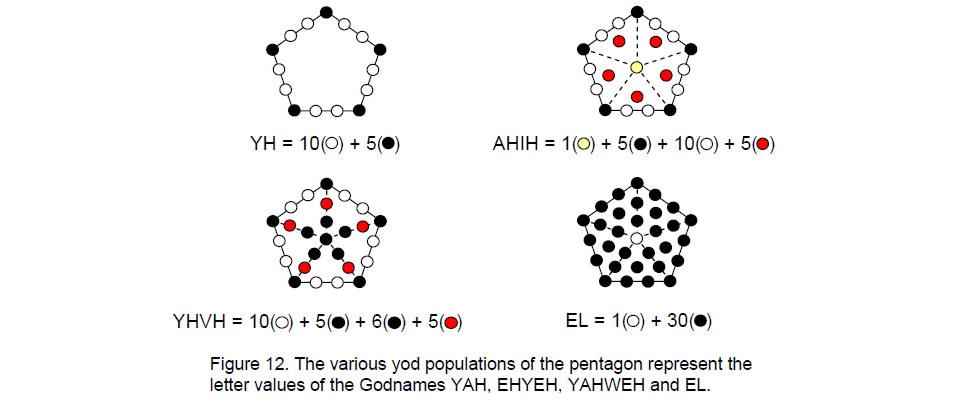
The pentagon is the polygonal representation of the Godnames of the four highest Sephiroth (Fig. 12). Constructed from tetractyses, it comprises 31 yods. This is the representation of EL, Godname of Chesed, because its central yod symbolises the letter value 1 of E (aleph) and the 30 yods surrounding its centre symbolise the letter value 30 of L (lamed). YAH is

represented by the boundary of the pentagon because the letter value 10 of Y (yod) is the number of hexagonal yods between its five corners, which denote the number value 5 of H (heh). The number value 26 of YAHWEH is the number of radial and boundary yods. The number value 21 of EHYEH is the number of yods on the boundary of the pentagon, at its centre and at the centres of its five sectors.

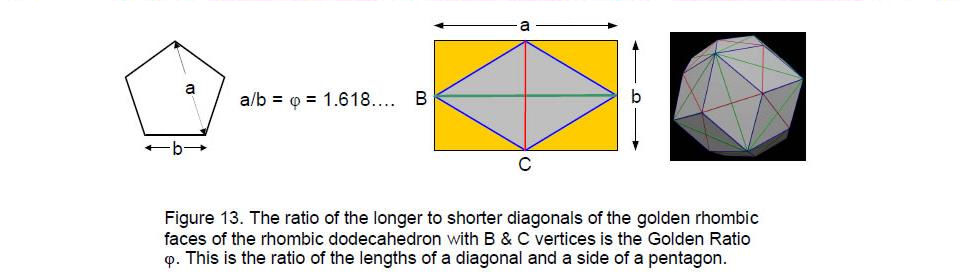
It is well-known that the pentagon contains the Golden Proportion as the ratio of the lengths of its diagonal and side (Fig. 13). The very regular polygon whose proportions define the shape of the faces of the rhombic triacontahedron underlying the disdyakis triacontahedron embodies the Godname numbers 15 and 26 that characterise the numbers of sheets of B and C vertices defining the shape of these faces.

Listed below are the numbers of A, B and C vertices within each of the seven planes between two outermost A vertices:

The fourth, central plane contains 12 vertices (six vertices and their images inverted through the centre of the disdyakis triacontahedron). There are (1+8+10+6+6=31) independent vertices in the uppermost vertex and the four planes containing half of the polyhedron. This is how the Godname EL of Chesed with number value 31 prescribes its vertex population. The other 31 vertices are their mirror images. The total number of vertices in the four planes = 8 + 10 + 6 + 12 = 36. This shows how the Godname ELOHA of the next Sephirah with number value 36 prescribes the polyhedron.

14

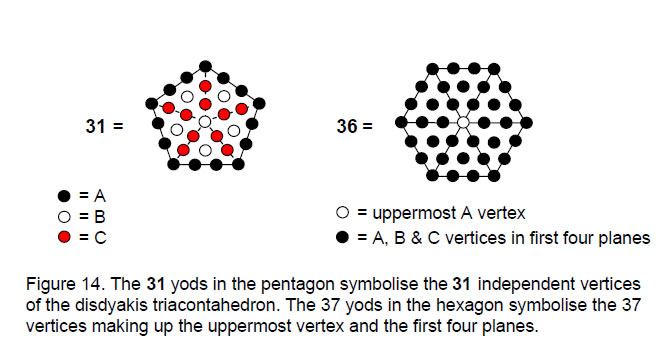
The 31 vertices are made up of 15 A vertices, six B vertices and 10 C vertices. In a pentagon divided into five tetractyses, there are 15 yods on its boundary, six yods at the centres of the tetractyses or the pentagon and 10 yods on the sides of tetractyses

15

inside it (Fig. 14). Half of the polyhedron contains 37 vertices. This is the number of yods in a hexagon constructed from tetractyses, its central yod corresponding to the uppermost A vertex. The tetractys therefore reveals how these two polygons embody numbers defining the disdyakis triacontahedron as the inner form of the Tree of Life.

The number of vertices needed to create the disdyakis triacontahedron is not the number that actually constitutes it. The former is 31; these vertices are symbolised by the 31 corners of the seven enfolded polygons unshared with the outer Tree of Life (see Fig. 8). The number constituting the first or last four planes is 36; these are symbolised by all 36 corners of the seven enfolded polygons forming the inner Tree of Life.

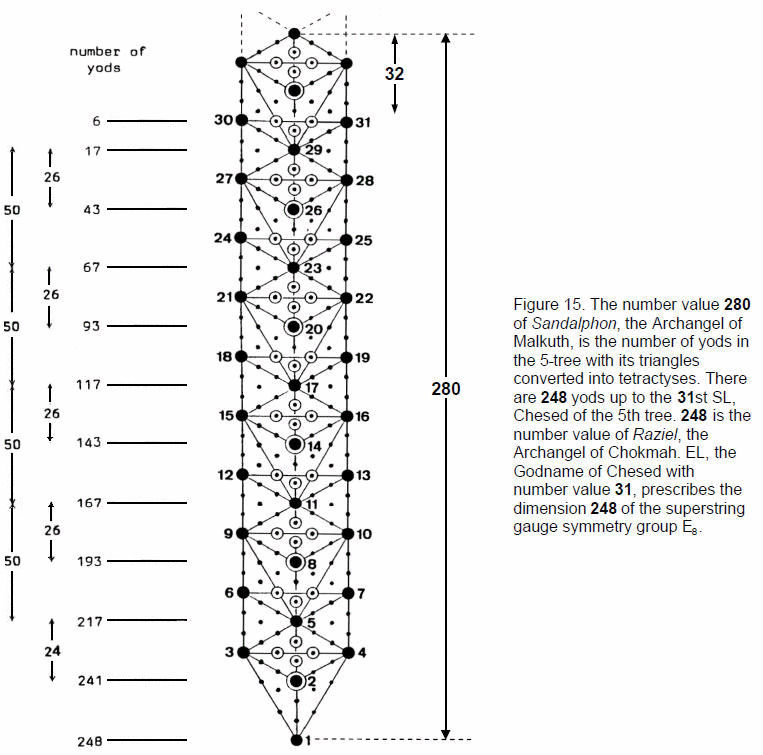
n overlapping Trees of Life consist of (12n+4) triangles. Transformed into tetractyses, they contain (50n+20) yods, where 50 is the number value of ELOHIM. 10 Trees of Life have 520 yods in 124 tetractyses. The n-tree consists of (12n+7) triangles. Changed into tetractyses, they contain (50n+30) yods. The 5-tree has 280 yods (Fig. 15). This is the number value of Sandalphon, Archangel of Malkuth. As the apex of the 5-tree is Malkuth of the seventh tree, we see that Sandalphon prescribes the 7-tree representing the physical plane, the 25 tree levels of which are the 25 spatial dimensions predicted by quantum mechanics (hence the appropriateness in this context of the Sephirah Malkuth). The number value 26 of YAHWEH is the number of yods between successive SLs on the central pillar and the number value 50 of ELOHIM is the
  

16

number of yods between corresponding SLs on this pillar. Chesed of the 5th tree — the first Sephirah of Construction — is the 31st SL. Fig. 15 shows that there are 248 yods up to the level of the 31st SL. This is how the Godname EL with number value 31 prescribes the dimension 248 of the superstring gauge symmetry group E₈. Each yod up to the 31st SL denotes a physical particle — a gauge boson of E₈. The 1-tree contains 80 yods, where 80 is the number value of Yesod. There are, therefore, (248–80=168) yods above the 1-tree up to the 31st SL. This is the number value of Cholem Yesodoth, (“Breaker of the Foundations”), the Mundane Chakra of Malkuth. As pointed out in Section 1 and as discussed in many previous articles, 168 is the structural parameter of the E₈×E₈' heterotic superstring, being the number of circularly polarised oscillations of each of its whorls during one-half revolution.

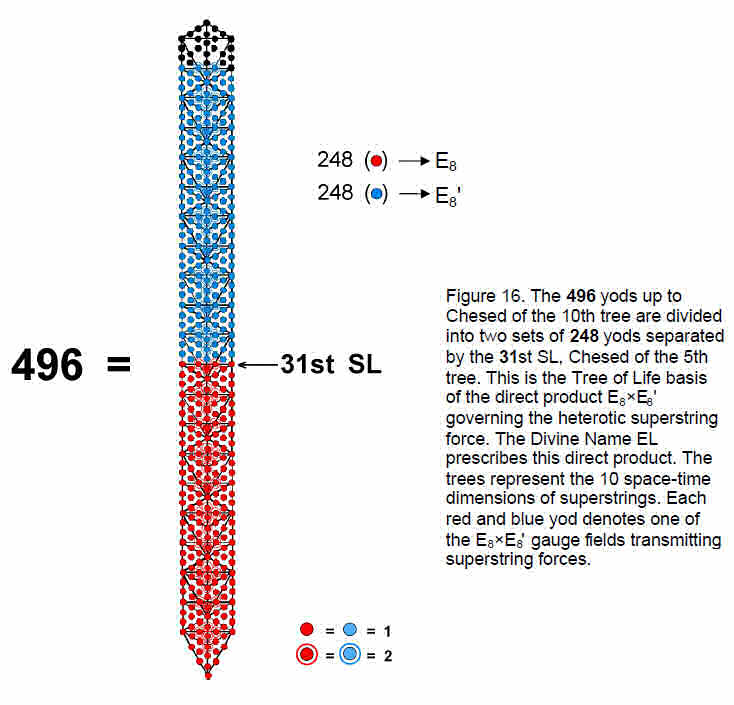
The number of yods in n overlapping Trees of Life up to the level of Chesed of the nth tree = 50n – 3.⁵ There are 496 yods up to (but not including) Chesed of the tenth tree (Fig. 16). They include 60 SLs, of which the lowest 31 SLs have 248 yods associated with them. Therefore, there are 248 yods above the 31st SL up to Chesed of the tenth tree. The E₈×E₈' heterotic superstring has a unified interaction transmitted by 496 gauge bosons, of which 248 particles are the gauge bosons of the first E₈ group and 248 particles are the gauge bosons of the second E₈' group. The Godname EL prescribes the direct product structure of the gauge symmetry group governing the interactions of heterotic superstrings. The product reflects the division of the ten Sephiroth of the Tree of Life into the five Sephiroth of its Lower Face and the five Sephiroth of its Upper Face.

It was found in Article 22 that the disdyakis triacontahedron has 480 hexagonal yods in its 120 faces. This is the number of yods in the 9-tree, which has 31 tree levels, showing how the Divine Name EL prescribes the 480 hexagonal yods in the disdyakis triacontahedron that symbolise the 480 non-zero roots of E₈×E₈'.

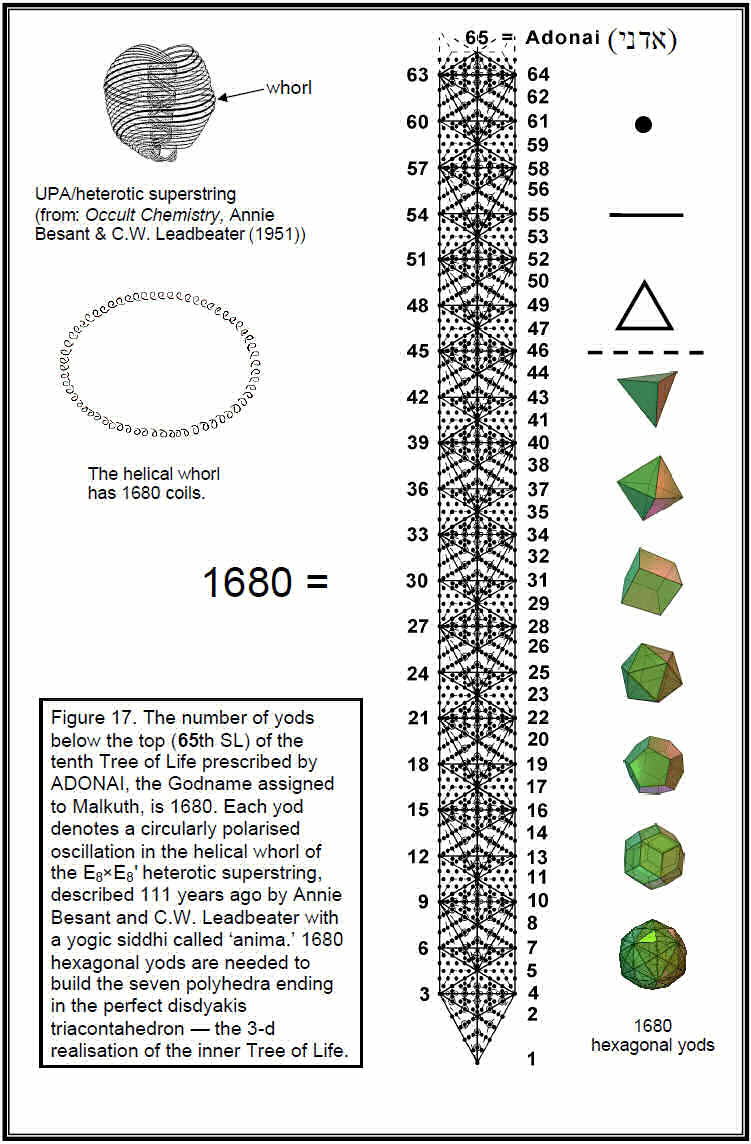
There are 15 sheets of vertices orthogonal to a C-C axis and 26 sheets of vertices perpendicular to A-A & B-B axes, totalling 33 sheets. Against the backdrop of CTOL— the map of physical and superphysical reality — the 15-tree has 780 yods, i.e., the yods in 78 tetractyses, and the 26-tree has 1330 yods, i.e., the yods in 133 tetractyses. 78 is the dimension of E₆, the rank-6 exceptional group, and 133 is the dimension of E₇, the rank-7 exceptional group. The two numbers 15 and 26 that specify the number of sheets of vertices that create the shapes of the faces of the disdyakis triacontahedron define the dimensions of two exceptional subgroups of the exceptional group E₈. The 33-tree has 1680 yods. As pointed out in Article 22, this is the number of hexagonal yods in the sequence of seven polyhedra that evolve into the perfect disdyakis triacontahedron:

It is the number of 1st-order spirillae in a whorl of the UPA. Here, therefore, is the scientific meaning of the numbers 15, 26 and 33 defining the three types of groups of sheets of vertices. It is revealed by representing sheets by Trees of Life. Malkuth of the 33rd Tree of Life in CTOL is the 65th SL on the central Pillar of Equilibrium. This is

17

18

how the Godname ADONAI of Malkuth with number value 65 prescribes the number 1680. Another way whereby ADONAI determines this fundamental structural parameter of the E₈×E₈' heterotic superstring is as follows: as proved in Article 22, when the (12n+7) triangles of the n-tree are each divided into three tetractyses, the number of yods below the top of the nth tree is⁶

N(n) = 158n + 100.

The number of yods below Kether of the tenth tree (the 65th SL) is N(10) = 1680, that is, the number of yods in 168 tetractyses, where 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth (Fig. 17). This is how ADONAI prescribes the structural parameter 1680. The astounding result involves both the Godname and the Mundane Chakra of the same Sephirah and so it is implausible that it is coincidental. Instead, it reveals the amazing nature of the Tree of Life as the blueprint that determines the nature of microscopic as well as macroscopic reality. Moreover, as shown in Article 22,⁷ the 1680 yods belong to 385 tetractyses, where

Such a simple, yet beautiful, mathematical property is not an accident. Instead, it is an eloquent expression of mathematically perfect design.

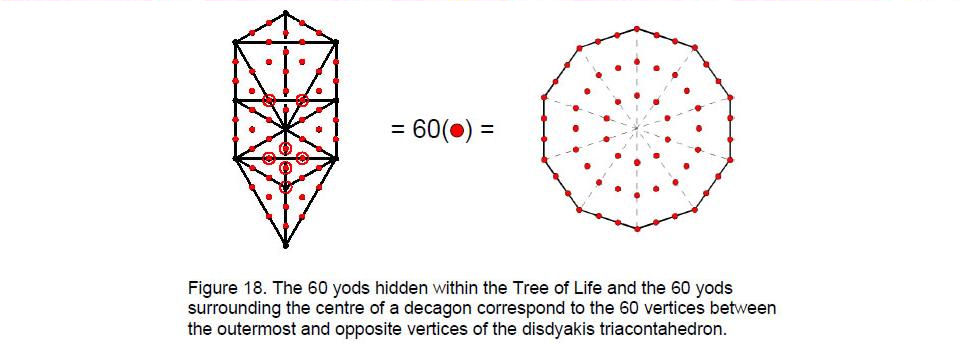
There are 33 sheets of vertices in the disdyakis triacontahedron between its diametrically opposite and outermost vertices. They contain 60 vertices. This is the 3-dimensional counterpart of the outer Tree of Life having 60 yods generated when its 16 triangles are turned into tetractyses. A decagon with its ten sectors turned into tetractyses has 60 yods surrounding its centre (Fig. 18). In other words, starting with the mathematical point, 60 more points are needed in 2-dimensional space to construct a decagon from tetractyses. Similarly, starting with ten

points as Sephiroth, 60 more points are required to create their arrangement in space as the 16 triangles of the Tree of Life. These 60 formative degrees of freedom appear in the disdyakis triacontahedron as the 60 vertices between any two outermost A vertices that are diametrically opposite. This is yet more evidence for its Tree of Life nature. It is truly remarkable that there should be as many yods (1680) spanning 33 tree levels below the 65th SL

19

when the triangles of the trees are divided into three tetractyses as there are in the 33-tree with its triangles turned into tetractyses and with 65 SLs on the central pillar up to Malkuth of the 33rd tree. The reason for this correspondence is that the geometry of the Tree of Life has a fractal-like quality of being characterised by the same set of parameters whenever it maps sections of CTOL that are counterparts of each other in a way that need not be discussed here.

 

20

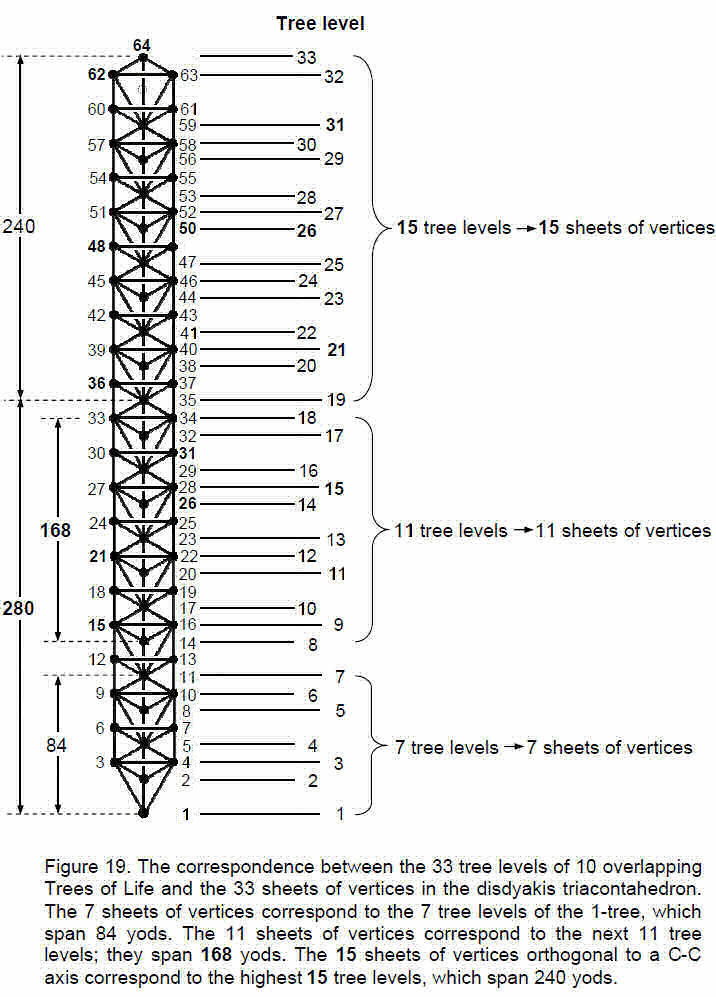
We have seen that the 33 sheets of vertices in the disdyakis triacontahedron correspond to the 33 tree levels of 10 overlapping Trees of Life. The question now arises: how should the three types of groups of sheets be ordered when correlating them with tree levels? We know that the 1-tree has seven tree levels (Fig. 1), so it seems natural to correlate them with the 7 sheets of vertices perpendicular to an A-A axis. The 1-tree is the Malkuth level of 10 overlapping Trees of Life representing the 10 Sephiroth. The seven sheets of vertices represent the lowest tree and therefore the Malkuth aspect of the disdyakis triacontahedron as the polyhedral counterpart of these ten trees. There are 80 yods in the 1-tree and, as Fig. 15 indicates, there are four yods outside the 1-tree up to the level of its apex. The seven tree levels therefore span 84 yods (Fig. 19), where

is the sum of the squares of the first four odd integers. The 5-tree has 280 yods, of which seven yods are above the Binah-Chesed path of the 5th tree. This leaves 273 yods in the five

trees up to the level of Chokmah of the 5th tree — the 18th tree level. Below Yesod of the 3rd tree are 105 yods (see Fig. 15). There are (273–105=168) yods in the 11 tree levels from the 8th to the 18th. Finally, as the 10 overlapping Trees of Life have 520 yods, there are (520–280=240) yods in the 15 tree levels between the 5-tree and the top of the 10th tree.

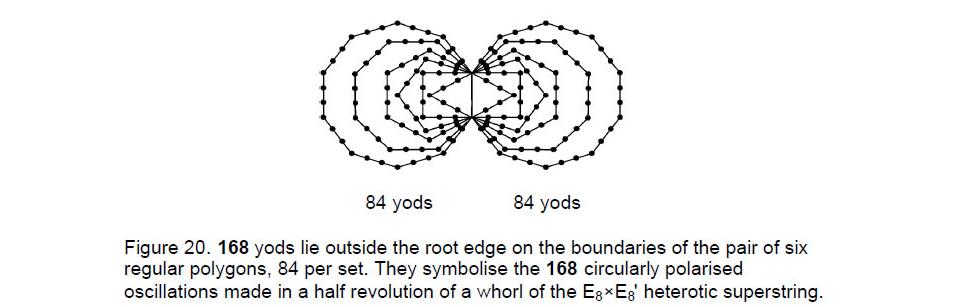
The superstring significance of the numbers 84, 168 and 240 is as follows: each whorl of the heterotic superstring twists five times around its central axis (see Fig. 17), making 1680 circularly polarised oscillations. There are 1680/5 = 336 oscillations per revolution, 168 oscillations per half-revolution and 84 oscillations per quarter-revolution. The 84:84 pattern manifests in the inner form of the Tree of Life as the 84 yods that line the first six polygons outside the root edge on each side (Fig. 20). This pattern has been discussed in the context of octonions⁸ and the Klein Configuration.⁹ The seven sheets of vertices between diametrically opposite A vertices of the disdyakis triacontahedron define the 84 oscillations made by a whorl in a quarter of a revolution. The 11 sheets of vertices perpendicular to a B-B axis define the 168 oscillations in half a revolution. According to heterotic string theory, its E₈ gauge charges are spread around its length. However, it is the 240 charges corresponding to its non-zero roots that are spread

21

around the 10 whorls, 24 per whorl. There are 168 such charges along the seven minor whorls and 72 carried by the three major whorls. The former correspond to the 168 nonzero roots of E₈ that are not also non-zero roots of E₆, one of its exceptional subgroups, whilst the latter correspond to the non-zero roots of E₆. The 15 sheets of vertices perpendicular to a C-C axis correspond to the 15 tree levels spanning the 240 yods between the top of the 5-tree and the top of the 10th tree. These yods denote the gauge charges corresponding to the 240 non-zero roots of E₈ that are spread around the heterotic superstring. Information about the dynamics and oscillatory form of the heterotic superstring is thus encoded in the sheets containing the three types of vertices. The sheets of vertices perpendicular to an A-A axis and a B-B axis encode through their Tree of Life counterparts the numbers of circularly   

 

polarised oscillations made in, respectively, a quarter-revolution and a half-revolution of a whorl, whilst the C-C sheets encode the number of E₈ gauge charges that are spread around all ten whorls.

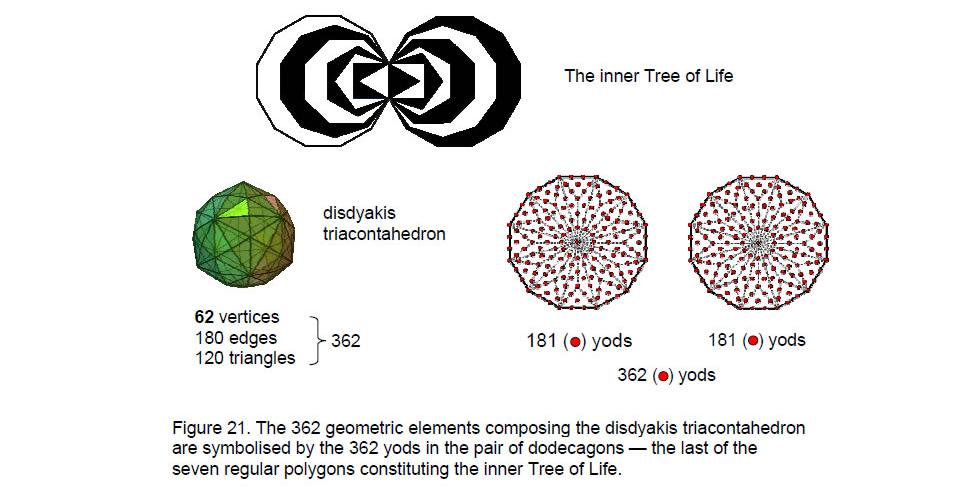
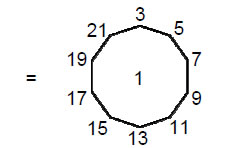
The disdyakis triacontahedron is made up of 62 vertices, 180 edges and 120 triangles, that is, 362 geometric elements. This attribute is encoded in the pair of dodecagons — the last of the regular polygons making up the inner Tree of Life — because the division of their 24 sectors into three tetractyses produces 362 yods (Fig. 21). Each yod denotes a geometric element of the disdyakis triacontahedron. The two centres denote any pair of diametrically opposite A vertices and the 360 yods surrounding them denote the 60 vertices, 180 edges and 120 triangles between these opposite poles. The archetypal ‘form’ quality of the Godname ELOHIM assigned to Binah in the Tree of Life is illustrated by the fact that its number value 50 is the number of corners of the 72 tetractyses in the pair of dodecagons. The same applies to the Godname ELOHA assigned to Geburah below Binah in the Tree of Life because its number value is 36, which is the number of tetractyses in a dodecagon. Each one has 25 corners and 60 edges, a total of 121 geometric elements, where 121 = 11²

22

“1” denotes the centre of the dodecagon. This shows how the decagon symbolising the perfect Pythagorean Decad expresses the tetractys-divided dodecagon.

As well as the Godname YAH assigned to Chokmah, the Godname EHYEH of Kether with number value 21 prescribes the superstring group-theoretical number 240. It is the sum of the first 21 binomial coefficients other than 1 in Pascal’s Triangle:

As 24 = 5² – 1 = 3 + 5 + 7 + 9, the number has the tetractys representation:

In terms of the integers 1, 2, 3 & 4 symbolised by the tetractys, 240 = (1+2+3+4)1×2×3×4, whilst 33 (=1!+2!+3!+4!) is the number of tree levels in 10 overlapping Trees of Life, the counterparts of which in the disdyakis triacontahedron are the 33 sheets of its three types of vertices.

These arithmetic expressions for geometrical parameters of holistic objects such as this polyhedron are examples of the Tetrad Principle at work.¹⁰ It also determines the E₈×E₈' heterotic superstring structural parameter 84 because

84 = 1² + 3² + 5² + 7.²

Indeed, the fact that the disdyakis triacontahedron has 120 vertices is a clear illustration of this fundamental mathematical principle because the 30 Golden Rhombic faces of the rhombic triacontahedron are each divided into four faces to produce 120 faces, where

30 = 1² + 2² + 3² + 4²

and

120 = 4×30 = 2²×(1² + 2² + 3² + 4²)        
              = 2² + 4² + 6² + 8².         

As 248 = 4×62, the disdyakis triacontahedron with the Tetrad assigned to each of its 62 vertices represents the 248 E₈ gauge fields that transmit superstring forces, two diametrically opposite A vertices signifying the eight gauge fields that correspond to the eight zero roots of E₈ and the 60 vertices in the seven sheets between them generating the number 240 as the 240 non-zero roots of E₈ and therefore signifying their corresponding 240

23

Table 2. The gematria number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations The Elements (Earth)                  168

 

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

24

gauge fields. Constructed from tetractyses, the disdyakis triacontahedron has 422 yods on the 180 edges of the 120 tetractyses,¹¹ that is, 420 yods between polar-opposite A vertices are needed to define the edges of these tetractyses. Assigning the number 4 to these yods generates the number 1680. This is the number of oscillations in each whorl of the heterotic superstring. It is also the number of hexagonal yods symbolising the seven Sephiroth of Construction needed to build the sequence of seven polyhedra completed with the disdyakis triacontahedron. This is a profound meaning of the disdyakis triacontahedron: if we imagine it built with the integer 4 as each vertex, its seven sheets of vertices express both the number of particles transmitting the unified superstring force and the number of circularly polarised oscillations in each whorl of the heterotic superstring. Moreover, the arithmetic connection between 240 as the sum of the integers 4 assigned to the 60 vertices between opposite A vertices and 1680 — the sum of these integers assigned to the yods between them — is 1680 = 7×240. Remarkably, this factorisation is identical to the seven sets of 240 hexagonal yods in the sequence of seven polyhedra (see page 17). The disdyakis triacontahedron embodies numbers that characterise both fundamental force and form. It does so simply because, as shown in Articles 22-24 and as further demonstrated here, it is the 3-dimensional version of the universal blueprint called the ‘Tree of Life.’ No wonder that the ancient Pythagoreans gave to the number 4 the title of “holding the key of nature”!

References
¹ All numbers written in boldface are the number values of the ten Sephiroth, their Godnames, Archangels, Orders of Angels and Mundane Chakras. They are listed above in Table 2.

² Phillips, Stephen M. “ESP of Quarks & Superstrings,” New Age International, New Delhi, India, 1999.

³ Horava, Petr and Witten, Edward. “Heterotic and type 1 string dynamics from eleven dimensions,” Nucl. Phys. B460 (1996), pp. 506-524.

⁴ For the definition of the 2nd-order tetractys, see p. 4 of Article 24: “More Evidence for the Disdyakis Triacontahedron as the 3-dimensional Realisation of the Inner Tree of Life & its Manifestation in the E₈×E₈ Heterotic Superstring,” by Stephen M. Phillips, (WEB, PDF).

⁵ The n-tree has (50n+30) yods. Therefore, the number of yods in the (n–1)-tree = 50(n–1) + 30 = 50n – 20. There are 17 yods beyond the (n–1)-tree up to the level of Chesed of the nth tree. The number of yods in n overlapping tree up to Chesed of the nth tree = 50n – 20 + 17 = 50n – 3.

⁶ Phillips, Stephen M. Article 22: “The Disdyakis Triacontahedron as the 3-dimensional Counterpart of the Inner Tree of Life,” (WEB, PDF), ref. 5.

⁷ Ibid, p. 16.

⁸ Phillips, Stephen M. Article 15: “The Mathematical Connection between Superstrings and Their Micro-psi Description: a Pointer Towards M-theory,” (WEB, PDF), p. 11.

⁹ Ibid, p. 27, and Phillips, Stephen M. Article 21: “Isomorphism between the I Ching table, the 3×3×3 Array of Cubes and the Klein Configuration,” (WEB, PDF), p. 6.

¹⁰ Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF), p. 5.

¹¹ Ref. 6, p. 9.

25