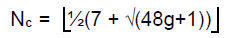1. Introduction
121 years ago, the two Theosophists Annie Besant and Charles W. Leadbeater claimed to undertake a series of investigations into the nature of atoms, using one of the siddhis, or paranormal abilities, that can, according to yogic tradition, be gained intentionally or unintentionally through meditation. Called ‘anima’ in Sanskrit and discussed over 2000 years ago in the Yoga Sutras of Patanjali, this supposed ability to experience highly magnified images of microscopic objects has been given by the author the modern name of ‘micro-psi.’ In parapsychological terms it is a type of ‘remote viewing,’ although a more accurate term is ‘clear cognition,’ as the objects being scanned need be only a few inches from the micro-psi observer, who does not need to have his eyes open because he does not ‘see’ with them. Besant & Leadbeater published their observations of atoms in 1908 in their book Occult Chemistry.¹ All the material that had

accumulated over 38 years of intermittent study finally appeared in 1951 in its third edition.

 According to Besant & Leadbeater, atoms are ultimately made up of indivisible units that they called ‘ultimate physical atoms,’ or UPAs. They had two forms (Fig. 1). Each consisted of ten closed, non-intersecting curves that spiralled 2½ times around the axis about which the UPA spun, maintaining parallel paths, and then twisted 2½ times in tighter spirals upwards through the core of the UPA, each curve completing its circuit at the top. In the ‘positive’ variety, the curves, or ‘whorls,’ spiralled clockwise when viewed from the top; the ‘negative’ type spiralled anticlockwise. For the purpose of the present discussion, the most important details that Leadbeater gave

 

2

about the UPA were:

1. each whorl in either type was essentially a closed, helical coil (Fig. 2) with 1680 turns. Leadbeater meticulously checked this number by examining 135 different UPAs. It was the same whatever the element whose atoms he thought he was observing;
2. each whorl made five revolutions about the axis of the spinning UPA, twisting 2½ times in an outer spiralling movement and 2½ times in an inner circuit. This means that a whorl coils (1680/5 = 336) times each time it completes one revolution, that is, 168 times in every half-revolution through 180°.

By analysing self-consistently the many thousands of details recorded in Occult Chemistry for 111 purported atoms, the author proved² in a model-independent way that the UPA is an as yet undiscovered constituent of the up and down quarks making up the protons and neutrons in atomic nuclei. He also pointed out features of the UPA that are consistent with their interpretation as closed superstrings. This article will focus on those features listed above in order to establish rigorous mathematical contact with group-theoretical aspects of the unified superstring force and their connection to octonions, the Fano plane and the Klein Quartic, an equation well-known to mathematicians. Through the pivotal role of the number 168, it will establish mathematically the ten possible links between the following five subjects:

Their validity does not depend on the invoking of dubious, metaphysical ideas or speculations based upon some untested model or theory other than superstring theory itself. Reference to the Jewish mystical doctrine of Kabbalah will make use only of mathematical aspects of the Tree of Life diagram at the heart of its teachings. This article represents work in progress and does not offer any final ‘theory of everything.’ Rather, it provides a few paving stones for the path that will lead to it.

2. Octonions

In 1878 and 1880, Frobenius and Peirce³ proved that the only associative⁴ real division

3

algebras are real numbers, complex numbers, and quaternions. Adams⁵ proved that n-dimensional vectors form an algebra in which division (except by 0) is always possible only for n = 1, 2, 4, and 8. Bott and Milnor⁶ proved that the only finite-dimensional real division algebras occur for dimensions n = 1, 2, 4, and 8. Each gives rise to an algebra with particularly useful physical applications (which, however, is not itself necessarily nonassociative), and these four cases correspond to real numbers, complex numbers, quaternions, and Cayley numbers, respectively. The Cayley algebra is the only nonassociative algebra. Hurwitz⁷ proved in 1898 that the algebras of real numbers, complex numbers, quaternions, and Cayley numbers are the only ones where multiplication by unit "vectors" is distance-preserving. These most general numbers are also called “octonions.” The mathematical fact that n-dimensional, division algebras are allowed only for n = 2⁰ = 1, 2¹ = 2, 2² = 4 and 2³ = 8 gives meaning to these powers of 2 on one slope of the Platonic Lambda (Fig. 3). It

is a powerful example of the ‘Tetrad Principle’ formulated by the author⁸ wherein the fourth member of a class of mathematical object (in this case, even numbers) has fundamental significance to physics (in this case, the relevance of octonions to superstring theory). In the musical context of Plato’s cosmological treatise, Timaeus, the numbers of his Lambda generate the musical proportions of the Pythagorean musical scale, successive octaves of which have pitches 2⁰, 2¹, 2², 2³, etc. This demonstrates the archetypal role played by these powers of 2, for they define not only successive musical octaves but also the dimensions of the four possible division algebras. It intimates a connection between the Pythagorean basis of music and octonions and therefore with superstring theory, as was discussed in Article 13. This will be explored in Section 7

An octonion has the form:

N = a₀+ a₁e₁ + a₂e₂ + a₃e₃ + a₄e₄ + a₅e₅ + a₆e₆ + a₇e₇,

where the a_i (i = 0, 1, 2, 3, 4, 5, 6, 7) are real numbers, the unit octonions e_i (i = 1-7) are

4

imaginary numbers:

e_i² = -1                                                                               (i = 1-7)

and are anticommutative:

e_i e_j = -e_je_i                                                                                (i ≠ j)

Shown below is the multiplication table for the 8-tuple of unit octonions: (1, e₁, e₂, e₃, e₄, e₅, e₆, e₇):

It comprises (8×8=64=4³) entries, of which eight are diagonal and real (8 = fourth even integer) and (64–8=56) are off-diagonal and imaginary (28 on one side of the diagonal and 28 on the other side with opposite signs due to their anticommutativity). 28 is the seventh triangular number, where 7 is the fourth odd integer and the fourth prime number. There are 36 entries with a positive sign (one real and 35 imaginary) and 28 entries with a negative sign (7 real and 21 imaginary). 36 is the sum of the first four even integers and the first four odd integers:

36 = (2+4+6+8) + (1+3+5+7).

This illustrates how the Pythagorean Tetrad (4) defines the properties of the octonion multiplication table. The 35 positive imaginary entries consist of five copies of each of the seven imaginary unit octonions and the 21 negative entries comprise three copies of these, that is, the multiplication table contains (ignoring their signs) eight copies of each imaginary octonion. Multiplication yields seven new copies, that is, (7×7=49) imaginary octonions made up of 28 positive in four sets and 21 negative in three sets. Multiplication also generates seven, new, identical, negative numbers -1, so the 56 new entries comprise equal numbers with positive and negative signs (four positive sets of

5

seven and (3+1) negative sets).

As the realisation of the most general type of numbers showing neither associativity nor commutativity, the eight unit octonions are the mathematical counterpart in the Tree of Life of Daath and the seven Sephiroth of Construction:

The differentiation between the non-Sephirah Daath and the Sephiroth of Construction corresponds to the distinction between the real unit octonion 1 and the seven imaginary octonions. The 1:3:4 pattern of new numbers created by their multiplication in pairs (see

previous paragraph) corresponds, respectively, to Daath, the triangular array of Chesed, Geburah and Tiphareth and the quartet of

6

 Netzach, Hod, Yesod and Malkuth situated at the corners of the tetrahedron at the base of the Tree of Life (Fig. 4).

The multiplication table for the seven, imaginary, unit octonions (e₁-e₇) (Table 2) has (7×7=49) entries, of which 42 are imaginary (21 in three positive copies and 21 in three negative copies of the set) and seven are real (-1). As (-e_i )×(-e_j ) = (e_i )×(e_j ), the multiplication table for the negative, imaginary unit octonions is the same as Table 2. This 7:42 pattern conforms to the tetractys, the Pythagorean archetypal pattern of wholeness, for the following reason: the set (e₁-e₇) can be assigned to what the author calls the seven ‘hexagonal yods’* of the tetractys (Fig. 5), the sets (e₁, e₂, e₃ ) and (e₄, e₅, e₆)  

 

_______________________________
* So-called because they are located in the tetractys at the corners and centre of a hexagon.

7

being located at the corners of the two intersecting equilateral triangles forming a Star of David, whilst e₇ is at the centre of the tetractys because it corresponds to Malkuth, which the rules of correspondence between the Tree of Life and the tetractys require to be the central yod of the tetractys. The tetractys of the next higher order (Fig. 6) contains yods, of which 15 (the fourth triangular number after

85 = 4⁰ + 4¹ + 4² + 4³

1 and the sum of the first four powers of 2 in the Lambda) are corners of tetractyses and (85–15=70) are hexagonal yods. The seven hexagonal yods of the tetractys now become (7×7=49) such yods belonging to their corresponding seven tetractyses. The 49 entries of the multiplication table for the seven imaginary unit octonions can be assigned to them in a way consistent with their 7:42 pattern. The set (-1,-1,-1,-1,-1,-1,-1) corresponds to the central set of seven hexagonal yods, the three sets (-e₁,-e₂,-e₃,-e₄,-e₅,-e₆,-e ₇) correspond to one triangular array of seven yods and the three sets (-e₁,-e₂,-e₃,-e₄,-e₅,-e₆,-e ₇) correspond to the other triangular array of seven yods. The original set of seven octonions, represented by the Pythagorean symbol of wholeness, yields on multiplication another pattern that is really just a more differentiated form of the latter: unity remains unity as new levels of complexity emerge.

3. Fano projective plane

In mathematics, a projective plane consists of a set of "lines" and a set of "points" with the following properties:

Given any two distinct points, there is exactly one line incident with both of them.
Given any two distinct lines, there is exactly one point incident with both of them.
There are four points such that no line is incident with more than two of them.

The last condition simply excludes some degenerate cases.

A projective plane is an abstract mathematical concept, so the "lines" need not be anything resembling ordinary lines, nor need the "points" resemble ordinary points.

It can be shown that a projective plane has the same number of lines as it has points. This number can be infinite (as for the real projective plane) or finite. A finite

 

 

 

8

projective plane has (n²+n+1) points, where n is an integer called the order of the projective plane. A projective plane of order n has (n+1) points on every line, and (n+1) lines passing through every point. For all known finite projective planes, the order is a prime power. The existence of finite projective planes of other orders is an open question. The smallest possible projective plane has only seven 

points and seven lines. It is often called the “Fano plane,” and is shown in Figure 7. The seven points are shown as small blobs, and the seven lines are shown as six line segments and a circle. However, we could equally consider the blobs to be the "lines" and the line segments and circle to be the "points" — this is an example of the duality of projective planes: if the lines and points are interchanged,
 

the result is still a projective plane. The Fano plane with seven points therefore has order 2 because 2² + 2 + 1 = 7.

The Fano plane is known to generate the multiplication table for the seven imaginary

9

unit octonions if they are assigned to its points in the way shown in Figure 8. The multiplication of two units is the third on the same straight or curved line provided that their multiplicative ordering follows the arrow on the line. Their product is minus the third if multiplication is opposite to the sense of the arrow. For example, e₅e₂ = e₃ and e₁e₂ = e₄. But e₆e₄ = -e₄ and e₁e₄ = -e₂.

Having pointed out earlier that a fundamental correspondence exists between the seven imaginary octonions and the seven Sephiroth of Construction of the Tree of Life, it should come as no surprise that the geometry of the Fano plane representing the algebra of octonions is implicit in the construction of the Tree of Life from identical circles overlapping centre to circumference (Fig. 9). They are inscribed by the same circle. It is a simple exercise in trigonometry to prove that the straight line passing through the two points of intersection of the black and red overlapping circles shown in Figure 9 meets the larger circle at a point such that the middle point divides the straight line in the Golden Ratio 1:φ = 1: 1.618… . The path joining Chesed to Geburah is the base of a Golden Rectangle whose sides are collinear with the Pillars of Mercy and Judgement and extend slightly above the path joining Chokmah to Binah. The dashed lines in Figure 9 are the upper side of the Golden Rectangle and the sides of the squares adjoining its vertical side. It is of great significance to the relevance of octonions to elementary particle physics that the Golden Ratio, which appears in the growth patterns of many living things, should be so naturally present in the geometry of the representation of these numbers. It is evidence that, as the fourth and last class of division algebras, octonions are nature’s numbers.

Each line in the Fano plane joins three octonions that form a 3-tuple (e_i , e_i+₁, e_i+₃), where the index is defined modulo 7. Each of these seven 3-tuples (Fig. 10) is a quaternionic triple, obeying the same algebra as the three quaternions I, j & k:

{i, j} = {j, k} = {k, i} = 0

and ij = k, jk = I and ki = j, where i² = j² = k² = -1. A 3-tuple has seven combinations:

A.	ei, ei+1, ei+3
B.	eiei+1, ei+1ei+3, ei+3ei	(6 permutations)
C.	eiei+1ei+3	(6 permutations)

 

10

Associated with each 3-tuple are (3+6+6=15) elements that are made up of the three original octonions (A), one copy of them and their negatives (B) arising from anticommutativity of pairs, three 1’s and three -1’s (C), that is, 12 new elements. The seven 3-tuples have (7×7=49) combinations of their 21 elements, among which are three of each octonion from all the 3-tuples, that is, two new copies of the seven octonions, so that there are really (49 – 2×7 = 35) distinct combinations. Seven of these are the octonions themselves and 28 are new combinations (three pairs and one triple for each 3-tuple) generating (7×12=84) new elements made up of 42 imaginary numbers and 42 real ones, or alternatively, 42 positive elements (21 real, 21 imaginary) and 42 negative elements (21 real, 21 imaginary). They are made up of 16 distinct elements: (±1, ±e₁, ±e₂, ±e₃, ±e₄, ±e₅, ±e₆, ±e₇).

As e_i+3e_i+1 = -e_i = (-e_i+3)(-e_i+1), (-e_i+3, -e_i+1, -e_i ) is a 3-tuple. This means that there are 35 distinct combinations:

A.	(e1), (e2),(e3), … (e7)
B.	(e1)(e2), (e2)(e4), etc	(7×6 = 42 permutations)
C.	(e1)(e2)(e4), (e2)(e4)(e1), etc	(7×6 = 42 permutations)

with (42+42=84) permutations of two or three octonions, and 35 distinct combinations:

A.	(-e1), (-e2), … (-e7)
B.	(-e4)(-e2), (-e2)(-e1), etc	(7×6 = 42 permutations)
C.	(-e4)(-e2)(-e1), (-e2)(-e1)(-e4), etc	(7×6 = 42 permutations)

with (42+42=84) permutations of two or three negative octonions. There are (35+35=70)

11

combinations of one, two and three octonions from the two sets of seven 3-tuples with (84+84=168) possible orderings of the pairs and triplets in them. As 1/e_i = -e_i , each 3- tuple in one set is the inversion of its counterpart in the other. Both set of results may be summarised by saying that there are 84 permutations of pairs and triples of octonions obeying e_i e_j = e_k and 84 such permutations for the inverse octonions obeying (1/e_i )(1/e_j ) = 1/e_k, that is, e_i e_j = -e_k, where the indices i, j & k are in cyclic order. The seven 3-tuples and their inverses display (84+84=168) permutations of their members. The octonion algebra can be represented by the Fano plane because SL(3,2) the simple group of automorphisms (incidence-preserving bijections) of the latter is of order 168.

Figure 11 shows the isomorphism between the outer and inner forms of the Tree of Life. Constructed from 16 triangles, the outer form contains 70 yods when these triangles are turned into tetractyses. 35 () yods belong to the sequence of the first four simplexes: point, line, triangle and tetrahedron that constitute the ‘trunk’ of the Tree of Life, leaving 35 () yods belonging to the 11 other triangles. The inner form of the Tree of Life is two identical sets of seven regular polygons: triangle, square, pentagon, hexagon, octagon, decagon and dodecagon. They are enfolded in one another and share the same ‘root edge.’ The 14 polygons possess 70 corners, 35 of them being associated with one set of seven polygons and the remaining 35 corners being associated with the mirror image set of seven polygons on the other side of the root edge. We see that both the outer and inner forms of the Tree of Life have 70 degrees of freedom represented by yods or corners of polygons and that these are divided up into two sets of 35. This 35:35 division corresponds to the octonions in the seven 3-tuples having 35 combinations and their inverses also having 35 combinations. Once more, the analogy

is evidence that the mathematics of octonions is an intrinsic aspect of the cosmic blueprint of the Tree of Life.

12

The same 35:35 division is displayed by the first six polygons, each set of which has 35 triangular sectors (Fig. 12). When the latter are converted into tetractyses, one finds that there are 168 yods on their boundaries outside their root edge, 84 creating the edges of 35 tetractyses on one side and 35 forming the edges on the other side. So the 12 polygons with (35+35) sectors have (84+84) yods on their edges outside their shared edge. The tetractyses in one set of polygons symbolise distinct combinations of octonions in the seven 3-tuples, their 84 boundary yods signifying the possible permutations of two and three octonions, whilst the tetractyses in the mirror image set of regular polygons represent combinations of the seven inverse (negative) octonions, all their 84 boundary yods denoting corresponding permutations of two and three such octonions.

Each 3-tuple (e_i, e_i+1, e_i+3) forms three pairs with six permutations and one triplet with six permutations, i.e., a total of 12 permutations. Similarly for each inverse 3-tuple (-e_i+3, -e_i+1, -e_i). A 3-tuple and its inverse provide (12+12=24) permutations. All seven 3-tuples and their inverses create (7×24=168) permutations of two and three octonions. That this number includes permutations of the inverses of imaginary unit octonions reflects the fact that every automorphism of the Fano plane must have its own inverse because PSL(3,2) is a group. As will be discussed later, the factorisation 7×24 is of fundamental significance to the structure of superstrings.

According to Kabbalah, everything is the coming into being of the perfection of Adam Kadmon, or ‘Heavenly Man,’ as symbolised by the ten ‘divine qualities,’ or ‘Sephiroth,’  

 

 

13

of the Tree of Life. There are four great stages in the physical realisation of this universal blueprint. They are the ‘worlds’ of Atziluth (archetypal level embodied in the divine names), Beriah (archangelic level), Yetzirah (angelic hierarchies) and Assiyah (physical universe). Every Sephirah exists at each level as the Godname, Archangel, Angelic Order and Mundane Chakra, which is its cosmic, physical manifestation. The Mundane Chakra of Malkuth, the outer, physical form of Adam Kadmon, is Cholem Yesodoth (“breaker of the foundations”), traditionally referred to as the four elements of earth, water, air and fire. In the ancient practice of gematria, numbers were assigned to letters of the alphabet in order to identify words or phrases in religious texts that have hidden connections because they have the same number values. Table 3 lists the 27 letters of the Hebrew alphabet and their associated numbers. The

sum of the values of the letters of Cholem Yesodoth is 168 (Fig. 13). Had this been any of the 39 other number values of the Godnames, Archangelic Names, Angelic Names and Mundane Chakras of the ten Sephiroth, its appearance might plausibly be attributed to chance. But the Mundane Chakra of Malkuth signifies the most physical, cosmic aspect of the Tree of Life. So a number that characterises the Fano plane representation of the

14

algebra of octonions and which may be related to the group theory of superstrings is found to be the gematria number value of the Kabbalistic term for the most appropriate level of the most appropriate Sephirah!

Confirmation that this is not coincidental but indicative of the transcendental truths contained in Kabbalah is the fact that the sum of the letter values of Malkuth is 496 (Fig. 14). This is the very number discovered in 1984 by physicists Michael Green and John Schwarz to be the number of non-abelian gauge fields transmitting the unified force between 10-dimensional superstrings if it is free of quantum anomalies⁹. Again, it is not merely that this number appears among the number values of the Kabbalistic words for the manifestations of the ten Sephiroth in each of the four Kabbalistic worlds. Given that there are 40 such numbers, this, arguably, could be coincidental on purely statistical grounds. What makes the presence of the number 496 so highly significant is that this dynamical parameter of 

superstrings refers in the context of physics to the most appropriate Sephirah, namely, Malkuth — the physical universe of subatomic particles and their forces. Had it been the number value of any other Sephirah or of its aspect in one of the four worlds, it would have been difficult to argue the case for its appearance being non-coincidental. The joint association of 496 and 168, which we pointed out in Section 1 is the structural parameter of superstrings, with the most apt Sephirah is amazing evidence for the mystical doctrine of Kabbalah possessing scientific truths.

As each 3-tuple obeys the multiplication rule:

e_ie_i+1 = e_i+3,

the seven imaginary, unit octonions, when assigned to the corners of a heptagon, form

15

seven triangles whose corners are the members of each 3-tuple (Fig. 15). Successive clockwise rotations of a triangle by 2π/7 turn it into triangles representing successive

16

3-tuples. The fourth (green) triangle is the turning point in the 7-fold cycle of rotation because the last octonion e₇ is at its corner and further rotation generates triangles that include the octonions that started the cycle.

Divided into tetractyses, a heptagon contains 42 yods surrounding its centre (Fig. 16). In other words, starting from unity symbolised by the central yod, 42 ‘bits of information’ and degrees of freedom express the 7-fold differentiation of unity. Each tetractys represents a 3-tuple and the six yods per tetractys symbolise the six permutations of products of imaginary unit octonions within each 3-tuple. With each sector divided into three tetractyses, a heptagon contains 106 yods,* that is, 15 per sector surround its centre. We saw earlier that multiplication of the octonions in each 3-tuple generates 12 permutations of pairs and triplets, so that a 3-tuple can be associated with (12+3=15)

___________________________________________________

* An n-sided regular polygon with its n sectors divided into three tetractyses has 15n + 1 yods.

17

elements. The seven 3-tuples therefore possess (7×15=105) elements. Amongst these are three copies of each octonion. Assigning the real octonion 1 to the central yod, Figure 17 demonstrates that an isomorphism exists between the yods within each sector of the heptagon and the octonions within each 3-tuple and their permutations. The octonion indices 1, 2, 3, 4, 5, 6, 7 follow the sequence of colours of the rainbow, starting with red. To every one of the 91 hexagonal yods in the heptagon there corresponds an octonion, a pair of octonions or a triplet of octonions. The 49 coloured yods denote singles or pairs and the 42 white yods denote triplets.

Work by the author reported in previous articles proved that the inner form of the Tree of Life encodes the self-replication of the latter to span 91 trees. They comprise the 49 trees that map the 49 subplanes of the cosmic physical plane and the 42 trees that map the 42 subplanes of the six cosmic superphysical planes. Figure 16 is their tetractys representation, coloured triangles signifying subplanes. A remarkable parallelism exists between this 49:42 pattern and the 49:42 pattern of octonions and their pairs and triplets:

It exists because the seven imaginary unit octonions are the algebraic counterpart of the seven Sephiroth of Construction, which define the seven planes of consciousness and their seven-fold division into subplanes. Thought by physicists untilrecently to have no relevance to subatomic particle physics, these constructs of the largest possible division algebra are the mathematical realisation of the seven-fold objective nature of God. Their grouping into seven 3-tuples represented by the Fano plane is another manifestation of the seven Divine qualities. We have shown how 168 — the kernel of the number 1680 — the number of circularly polarised oscillations that Leadbeater counted in a whorl of what the author interpreted as a superstring constituent of quarks — is the order of the symmetry group SL(3,2) of the Fano plane representing the imaginary octonions. What, if at all, is the octonion basis of 1680 itself? Imagine the number 1, the real octonion, at a point directly above the centre of a heptagon to whose

 

18

corners the seven imaginary octonions are assigned. It is shown in Figure 19 connected by dotted lines to these corners. The number of combinations of four octonions from the set of eight is [⁸₄] = 70. They comprise [⁷₃] = 35 combinations of three imaginary octonions and the real octonion 1 at the corners of a tetrahedron, as well as [⁷₄] = 35 combinations of four imaginary octonions at the corners of a quadrilateral in the plane of the heptagon. Each combination of four octonions has (4!=24) permutations. The 70 combinations of four octonions have (70×24=1680) permutations. In terms of graph theory, there are 1680 ordered 3-simplexes made up of (35×24=840) ordered simplexes in the plane of the heptagon and 840 non-planar, ordered 3-simplexes. In fact, there are 70 3-simplexes in a

7-simplex made up of eight points and therefore 1680 ordered 3-simplexes. Notice the appearance once again of the number 70 and its split into two 35’s, one providing 840 permutations of the set (1, e_i, e_j, e_k) (i ≠ j ≠ k) and 840 permutations of the set (e_i, e_j, e_k, e_l) (i ≠j ≠k≠l), just as we found earlier that the seven 3-tuples have 35 distinct combinations with 84 different permutations and the seven 3-tuples made up of the negative octonions have 35 combinations with 84 permutations. But now the inclusion of the real octonion 1 and the consideration of permutations of any three or four octonions instead of just the seven 3-tuples have replaced the factor of 7 by 7×10. In other words, there are five times as many combinations of three octonions as 3-tuples and five times as many combinations of four octonions. Compare these results with the following details about the UPA:

1. each whorl has 1680 turns;

19

seen by some physicists to underlie M-theory.

4. Encoding of 168 in Tree of Life

We found in Section 3 that the Fano plane representation of the octonions implied the factorisation:

168 = 7×24,

where 7 is the number of 3-tuples and 24 is the number of permutations of pairs and triplets within each 3-tuple and their negatives. This may be expressed more precisely as:

168 = 7×12 + 7*×12*,

where ‘7’ is the number of 3-tuples (e_i, e_i+1, e_i+3), 7* is the number of 3-tuples (-e_i, -e_i+1, -e_i+3) and 12 and 12* are their respective numbers of permutations. Therefore,

336 = 2×168 = 14×12 + 14*×12*,

where 14* = 2×7*. This factorisation of 336 is encoded in the inner form of the Tree of

21

Life in the following way: the dodecagon is the seventh and last of the regular polygons making up this inner form (see Fig. 11). Transformation of the 12 sectors of each dodecagon into three tetractyses generates 181 yods, that is, 169 yods other than their corners. There are therefore 168 yods associated with each dodecagon sharing one side, 14 per sector* (Fig. 21). This is the

factorisation given above. Hidden within the pair of dodecagons sharing one side are 336 new degrees of freedom revealed by their construction from tetractyses — the template that builds sacred geometry.

That this is not due to chance is proved by the construction of all seven enfolded polygons from the higher-order tetractys shown in Figure 6. This is what the author has called the “2nd-order tetractys,” the 1st-order one being the well-known tetractys and the 0th-order tetractys being the mathematical point. When each of their 48 sectors are turned into this type of tetractys, one finds that they contain 3360 yods, that is, the number of yods in 336 tetractyses (Fig. 22). The very order of SL(3,2) or PSL(2,7) is embodied in the sacred geometry of the inner form of the Tree of Life! Moreover, as the UPA is made up of 1680 turns in each of its ten helical whorls, which revolve five times around its axis, the number of turns in each revolution of all ten whorls is 10×1680/5 = 3360. What this is telling us is that one revolution of the UPA constitutes a whole in

_________________________________________
* Of the 15n + 1 yods in an n-sided polygon with its sectors divided into three tetractyses, n are corners, leaving 14n + 1 yods, 14 per sector surrounding its centre.

22

some sense that is repeated five times but that this whole is itself a doubling of a basic pattern characterised by the number 168, itself quantifying another whole. In terms of group theory, this is simply the fact that SL(2,7) is the double cover of PSL(2,7), which is isomorphic to SL(2,3), the group of automorphisms of the Fano plane.

We found earlier that there are 1680 permutations of the 70 sets of four octonions that can be selected from the eight octonions, each set having 24 permutations. The factorisation:

1680 = 70×24

is geometrically realised in the pair of dodecagons. The 2nd-order tetractys contains 85 yods, where

85 = 4⁰ + 4¹ + 4² + 4³.

Surrounding its centre are

84 = 1² + 3² + 5² + 7²

yods. We saw earlier that this is the number of permutations of octonions belonging to

23

---

the seven 3-tuples. As 13 yods lie along each edge of a 2nd-order tetractys, there are (71n+1) yods in an n-sided polygon surrounding its sectors when they are turned into 2nd-order tetractyses, that is, (71n+1–13=71n–12) such yods outside one edge. A dodecagon (n=12) has 840 such yods and two dodecagons sharing one side have (2×840=1680) yods outside it surrounding the centres of their 24 sectors (Fig. 23). Once again the number 1680 is found to be associated with the number 24, 70 being the average number of yods per sector surrounding its centre (average only because counting yods outside the shared edge means that the two sectors sharing it do not have the same number of yods as the 22 other ones). Another association of the number 168 with the number 24 will be discussed in the next section.

5. The Klein Quartic

The mathematician Felix Christian Klein (1849–1925) is well-known to mathematicians for his work in group theory, function theory, non-Euclidean geometry and on the connections between group theory and geometry. The one-sided, closed surface called

the “Klein bottle” is named after him. In 1878, he discovered that the curve

x³ y + y³ z + z³ x = 0

has the 336-fold symmetry of the group SL(2,7). This curve is known to mathematicians as the “Klein Quartic.” It is a specific occurrence of a quartic curve, whose general form for two variables x & y is

Ax⁴ + By⁴ + Cx³y + Dx²y² + Exy³ + Fx³ + Gy³ + Hx²y + Ixy² + Jx² + Ky² + Lxy + Mx + Ny + O = 0,

where the letters are real numbers. The “Klein surface” is the Riemann surface of the Klein quartic (Fig. 24). Klein showed that it is mapped onto itself (hence “automorphisms”) by 168 analytic transformations. Schwarz¹⁰ proved at the end of the nineteenth century that the automorphism group of a compact Riemann surface of

24

genus g≥ 2 is finite. Hurwitz¹¹ showed that this surface has at most 84(g-1) automorphism and the same number of antiautomorphisms. A Riemann surface with the maximum number of automorphisms is called a “Hurwitz curve of genus g (g≥3). A Hurwitz curve of genus 3

has (84(3–1) = 84×2 = 168) automorphisms. The Klein curve is the Hurwitz curve with the smallest genus g = 3. Accola and Maclachlan¹² found a lower bound for the number μ(g) of automorphisms for a surface of genus g:

8g + 8 ≤ μ(g) ≤ 84(g-1)

More recently, Belolipetsky and Jones¹³ showed that, for every g≥2, there is a compact arithmetic Riemann surface of genus g with at least (4g-1) automorphisms, the least value of g attaining the lower bound being g = 24.

Macbeath showed that there is an infinite number of Hurwitz curves.¹⁴ No curves other than the Klein curve with g = 3 and one with genus 7 have equations known to mathematicians.¹⁵ The Riemann surface of the Klein Quartic. It can also be represented by the Klein Configuration (Fig. 25). It has 168 coloured, hyperbolic triangles and 168 grey triangles. Each of the 14 slices shown numbered has 12 coloured triangles. They can be grouped in groups of seven, each group forming one of 24 heptagons:

25

three heptagons are coloured cyan — the central heptagon (1) and two (2) composed of the 14 outermost, cyan triangles; seven red heptagons (7) ; seven yellow heptagons (sets of four (4) and three (3) triangles in each sector); seven green heptagons (sets of four (4) and three (3) triangles in each sector);

This composition can be represented as:

168 coloured triangles = 7×24,

where

24 = (1+2) + (4+3) + (4+3) + (4+3).

The numbers within each bracket denote the triangles in the two slices of each sector of the Klein configuration. Each sector is made up of two different slices, each with 12 triangles, i.e., the 168 triangles can be sorted into 84 from one type of slice and 84 from the other type. This 84:84 division is the same as that shown in Figure 12 to be embodied in the first six polygons of the inner form of the Tree of Life. It is mirrors the 84 permutations in the seven 3-tuples, 12 per 3-tuple, and the 84 permutations of the negative octonions, 12 per 3-tuple. In other words, the triangles correspond to permutations of octonions, the two slices of each of the seven sectors corresponding to a 3-tuple and the 3-tuple of its negative octonions. An exact parallel exists between the permutation properties of the octonions and the automorphisms of the Riemann surface of the Klein Quartic. This is, of course, simply because the former belong to the group SL(2,3) and the latter belong to PSL(2,7), which is isomorphic to SL(2,3).

Because the Klein Quartic is a Riemann surface of genus 3, it can be realised as a regular map in an orientated 2-manifold of genus 3, i.e., the 3-torus (Fig. 26), either with 24 heptagons, three meeting at each of its 56 vertices, or with 56 triangles, seven meeting at each of its 24 vertices. According to the Heawood Conjecture, the maximum number of colours sufficient to colour a map on a surface of genus g is

 

 

where denotes the floor function.* Ringels and Young proved in 1968¹⁶ that this

______________________________

* The floor function is the largest integer less than or equal to x.

26

number is also sufficient except for the sphere (and plane) and the Klein Bottle. Nine colours are needed to colour maps on the 3-torus.

6. Connection between Klein Configuration and E₈

Let us now examine the 14 slices of the Klein Configuration in more detail and compare the composition of coloured triangles with the root structure of the Lie algebra of the superstring gauge symmetry group E₈. The 168 automorphisms of the Klein Quartic represented by the 168 coloured hyperbolic triangles of the Klein configuration are:

168 = 7×24 = 7×[(1+2) + (4+3) + (4+3) + (4+3)] = 7(4+4+4) + 7(3+3+2) + 7(3+1)

= (28+28+28) + (56+28) = 84+84.

Seven slices of one type have 84 triangles made up of 28 red, 28 yellow and 28 green triangles and the seven slices of the other type have 84 triangles made up of 21 yellow, 21 green, 21 red and 21 cyan triangles. The roots of the E₈ algebra can be described in terms of eight orthonormal unit vectors {u_i}. Eight zero roots correspond to points at the centre of the root diagram and 240 nonzero roots all have length √2. They are given by

The 240 non-zero roots of E₈ comprise 168 made up of four sets of 28 and one set of 56, one set of 70 and two single ones. There are as many sets of 28 and 56 in the 168

27

non-zero roots as there are groups of 28 and 56 coloured triangles in the Klein configuration. This is not a coincidence, for the 168 automorphisms of the Klein Quartic are in one-to-one correspondence with the group of 168 automorphisms of the Fano plane that represents the 8-dimensional octonion algebra, which in turn is connected to the 8-dimensional Lie algebra of E₈. It, too, may not be coincidental that E₈ has 168 more non-zero roots than E₆ (240 compared with 72) because E₆ is an exceptional subgroup of E₈ that has been shown to accommodate the Standard Model of particles and their interactions other than gravity.

7. The octonions & Pythagorean octaves

Compare the eight notes of the Pythagorean musical scale:

C	D	E	F	G	A	B	C'
1	9/8	(9/8)2	4/3	3/2	27/16	243/128	2

with the eight unit octonions:

1

e1

e2

e3

e4

e5

e6

e7

Although it is tempting to make the correspondence between the tonic with tone ratio 1 and the real octonion 1, this is incorrect because the first seven notes correspond to the seven Sephiroth of Construction,¹⁷  the octave C' being a musical repetition of the

Table 4. Table of tone ratios of the notes in the seven church modes.

Lydian	1	9/8	81/64	729/512	3/2	27/16	243/128
Phrygian	1	256/243	32/27	4/3	3/2	128/81	16//9
Dorian	1	9/8	32/27	4/3	3/2	27/16	16/9
Hypolydian	1	9/8	81/64	4/3	3/2	27/16	243/128
Hypophrygian	1	256/243	32/27	4/3	1024/729	128/81	16/9
Hypodorian	1	9/8	32/27	4/3	3/2	128/81	16/9
Mixolydian	1	9/8	81/64	4/3	3/2	27/16	16/9

sequence that they underlie, whilst, as was pointed out earlier, the real octonion corresponds to Daath in the Tree of Life and the seven imaginary octonions correspond to the seven Sephiroth of Construction. Hence, note C corresponds to e₁, D corresponds to e₂, etc. Each type of church mode¹⁸ has five tone intervals and two leimmas. They are generated¹⁹ by starting with successive intervals of the Pythagorean scale until one completes the cycle of seven intervals by returning to the first sequence:

28

1.

T

T

L

T

T

T

L

2.

T

L

T

T

T

L

T

3.

L

T

T

T

L

T

T

4.

T

T

T

L

T

T

L

5.

T

T

L

T

T

L

T

6.

T

L

T

T

L

T

T

7.

L

T

T

L

T

T

T,

where the Pythagorean whole tone ratio T = 9/8 and the Pythagorean leimma L = 256/243. Table 4 shows the tone ratios of the (7×7=49) notes of the seven modes. Similarly, successive rotation through 2π/7 of the triangles shown in Figure 15 moves through the seven 3-tuples, creating (7×7=49) elements:

Just as each mode has eight notes separated by seven intervals, i.e., it comprises 15 notes and intervals, so each 3-tuple is associated with three octonions, six permutations of pairs of them and six permutations of all three, i.e., 15 elements. The 3-tuples can be regarded as the octonion counterpart of the seven Greek musical modes, the seven combinations of octonions within each 3-tuple being

analogous to the seven notes of its corresponding mode. Figure 27 compares the seven notes of the Pythagorean musical scale and the seven imaginary octonions.

We saw earlier that the Klein Configuration factorises the 168 automorphisms of the

29

Klein Quartic as 7×24. We also saw that the 8-tuple (1, e₁, e₂, e₃, e₄, e₅, e₆, e₇) has 70 combinations of four octonions with (70×24=1680) permutations. The number 24 appears in the Pythagorean musical scale as the tenth overtone (Table 5).

The Pythagorean significance of the number 10 is that it is the fourth triangular number — the tetractys.

This overtone is also the 33rd tone, where

30

33 = 1! + 2! + 3! + 4! = 33,

that is, it is the sum of the permutations of 10 objects arranged in the pattern of a tetractys. In other words, starting from the number 1, the sequence of successive integers: 1, 12, 123, 1234 has 33 permutations such that the 33rd one 1234 for which the integers are monotonically ascending has the value 24 when the integers are multiplied by one another. That this is not just a coincidence but an indication of deep connections between the Pythagorean basis of both music and superstrings is the fact that the ten overtones and 22 fractional tone ratios up to the perfect fifth of the fifth octave shown in Table 5 correspond precisely to the 10 Sephiroth and 22 Paths of the Tree of Life (Fig. 28), whilst we saw in Figure 11 that the Tree of Life has 16 triangles which, when turned into tetractyses, contain 70 yods. In other words, the geometry of the Tree of Life embodies both the factors 70 and 24 of the number 1680 — the number of circularly polarised oscillations made by each whorl of the UPA. What this remarkable correlation between Pythagorean tone ratios and the structure of the Tree of Life is indicating²⁰ is that, as the tenth overtone and the 32nd note, the tone ratio 24 must have physical significance because it corresponds to Malkuth, which is the tenth and last Sephirah, as well as the 32nd Path in the Kabbalistic sense. The number 24 certainly does have such significance in the context of the octonions underlying the superstring gauge symmetry group E₈ and in the context of the Klein Configuration. A spinless string in the 26-dimensional space-time predicted by quantum mechanics for such strings can oscillate in 24 orthogonal directions that are transverse to its length at any point. These 24 vibrational degrees of freedom in the bosonic string field are known to play a role in heterotic superstring theory. Their full significance for M-theory awaits elucidation. The musical counterpart of the number 24 as the tenth overtone would indicate that the 10-fold Tree of Life paradigm becomes fully realised in space-time with the generation, relative to the vacuum ground state of a string (the first overtone of one full oscillation) of 24 independent waves. Each oscillation creates a non-abelian gauge charges of E₈ in a way that generalises to the non-abelian context Kaluza’s identification of oscillation along a circular, fifth dimension with the electric charge of a particle. The 240 such charges, which are spread as separate oscillations along the ten string-like projections of a certain brane²¹ into 4-dimensional space-time, 24 to a string (namely, the ten whorls of the UPA), would then correspond to the 240 non-zero roots of E₈.

31

Conclusion

A continuous chain of mathematical connections has been established between the group E₈ describing superstring interactions and the number 168 implicit in the paranormal, 108-years old description of the building blocks of matter by Annie Besant and C.W. Leadbeater. Remarkable confirmation that this number is a structural parameter of the superstring is provided by the Kabbalistic system of knowledge, whilst the fact that the number value of the very Sephirah signifying the physical universe is the very dimension of a gauge group describing anomaly-free interactions between superstrings removes any doubt concerning whether the Kabbalistic appearance of 168 could be a coincidence.

E₈: rank-8 exceptional group describes superstring forces

Octonions: eight unit octonions form a division algebra isomorphic to E₈

SL(3,2): group of automorphisms of Fano plane representing
octonions is of order 168

PSL(2,7): group of 168 automorphisms of Klein Quartic is isomorphic to SL(3,2)

One half-revolution of the whorl of UPA has 168 turns

The form of the UPA reflects the holistic nature of the M-theory currently being sought by many theoretical physicists throughout the world. As the author has proved²² that the UPA is not a quark but its subquark constituent, their search is being hampered by their placing false constraints on M-theory, namely, to find a theory that not only unifies the five superstring theories and supergravity but also predicts the existence of three generations of quarks with interactions that conform to the gauge symmetry of U(1)×SU(2)×SU(3). But neither quarks nor this gauge symmetry are fundamental , and the correct M-theory will make this revolutionary prediction. This article has discussed some of its ingredients, particularly, octonions, the Klein Quartic and PSL(2,7).

References

¹ Besant, Annie, and Leadbeater, Charles W. Occult Chemistry, Theosophical

32

Publishing House, Adyar, Chennai, India, 1951.

² Phillips, Stephen M. Extra-sensory Perception of Quarks, Theosophical Publishing House, Wheaton, Ill. USA, 1980; Anima: Remote Viewing of Subatomic Particles, Theosophical Publishing House, Adyar, Chennai, India, 1996; ESP of Quarks and Superstrings, New Age International, New Delhi, India, 1999.

³ Mishchenko, A. and Solovyov, Y. “Quaternions.” Quantum 11, 4-7, and 18, 2000.

⁴ An associative algebra is one for which a(bc) = (ab)c. If this is untrue, it is non-associative.

⁵ Adams, J. F. “On the Non-Existence of Elements of Hopf Invariant One.” Ann. of Math. 72, 20-104, 1960.

⁶ Bott, R. and Milnor, J. “On the Parallelizability of the Spheres.” Bull. Amer. Math. Soc. 64, 87-89, 1958.

⁷ Hurwitz, A. “Ueber die Composition der quadratischen Formen von beliebig vielen Variabeln.” Nachr. Königl.

⁸ Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,” (WEB, PDF).

⁹ Green, M.B. & Schwarz, J.H. “Anomaly cancellations in supersymmetric d = 10 gauge theory and superstring theory.” Physics Letters, B149, 117.

¹⁰ Schwarz, H.A. “Ueber diejenigen algebraischen Gleichungen zwischen zwei veränderlichen Grössen, welche eine Schaar rationaler, eindeutig umkehrbarer Transformationen in sich selbst zulassen.” J. reine angew. Math. 87, 139–145; Ges. Math. Abh. II, pp. 285–291 (1890, reprinted Chelsea, 1972).

¹¹ Hurwitz, A. “Über algebraische Gebilde mit eindeutigen Transformationen in sich,” Math. Ann. 41 (1893), 403-442.

¹² Accola, R.D. “On the number of automorphisms of a closed Riemann surface.” Trans. Amer. Soc. 131 (1968), 398-408; Maclachlan, C. “A bound for the number of automorphisms of a compact Riemann surface.” J. London Math. Soc. 44 (1968), 265-272.

¹³ Belolipetsky, Mikail and Jones, Gareth. “A bound for the number of automorphisms of an arithmetic Riemann surface.” http://arxiv.org/PS_cache/math/pdf/0306/0306105.pdf.

¹⁴ Murray Macbeath, A. “On a theorem of Hurwitz.” Proc. Glasgow Math. Assoc. 5 (1961), 90-96.

33

¹⁵ Murray Macbeath, A. “Hurwitz groups and surfaces.” The Eightfold Way. MSRI Publications, vol. 35, 1998, 11.

¹⁶ Ringel, G. and Youngs, J.W.T. “Solution of the Heawood Map-Coloring Problem.” Proc. Nat. Acad. Sci. USA 60, 438-445, 1968.

¹⁷ Phillips, Stephen M. Article 14: “Why the Ancient Greek Musical Modes are Sacred,” (WEB, PDF).

¹⁸ Ibid.

¹⁹ Ibid.

²⁰ See also Article 13: “The Music of Superstrings,” (WEB, PDF).

²¹ This is discussed in detail in the author’s book The Mathematical Connection between Religion and Science (Antony Rowe Publishing, 2009) and in Article 2 (WEB, PDF).

²² Reference 2.

34