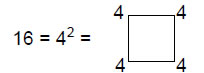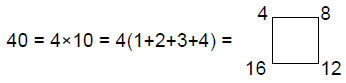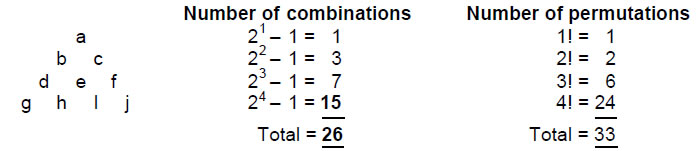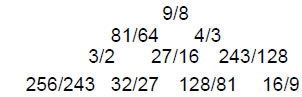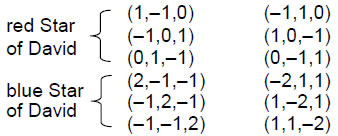ARTICLE 31
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.Website: http://smphillips.mysite.com
Abstract
|
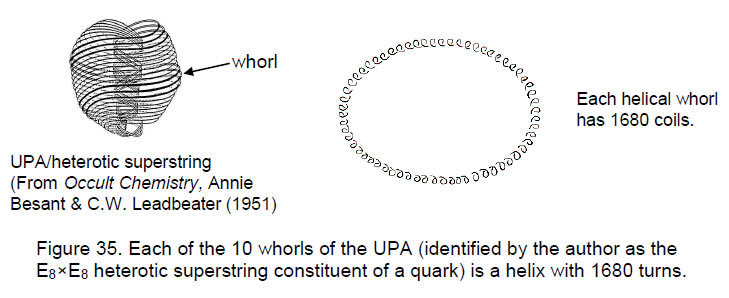
The polyhedral Tree of Life is correlated with the eight Church musical modes. These musical scales, which start and finish with the D scale, comprise 48 notes between the tonic and octave — a set of 50 notes that is represented by the 50 corners of the first (6+6) regular polygons of the inner Tree of Life. They comprise 14 different notes (eight with tone ratios of the Pythagorean scale, six with non-Pythagorean tone ratios). The eight scales have 168 rising intervals and 168 falling intervals between notes above the tonic. These intervals are symbolised by the (168+168) yods in the first (6+6) polygons other than their corners. These are the musical and Tree of Life counterparts of the 168 automorphisms and 168 antiautomorphisms of the Klein Quartic. Its symmetry group PSL(2,7) is isomorphic to the symmetry group SL(3,2) of the Fano Plane representing the multiplication of octonions. Their group of automorphisms is the exceptional group G2. Its seven pairs of roots correlate with the seven pairs of notes in the seven musical scales, explaining why the correspondence exists, viz. Pythagorean music and physics based upon octonions share the same principles. The 48 vertices of the 144 Polyhedron that stem from the 48 faces of the underlying disdyakis dodecahedron express the 48 basic degrees of freedom manifested by a holistic system. In the context of the musical modes, these are notes, which can be grouped into eight sets of six notes between the tonic and octave. The icosahedron with 12 B vertices in the disdyakis triacontahedron represents the 12 different notes between the tonic and octave of these scales. Eight of them consist of fours pairs of notes and their complements, one of which is Pythagorean and the other non-Pythagorean. The 216 edges of the 144 Polyhedron represent the 216 intervals other than octaves between the notes of the eight Church musical modes. The 180 edges of the disdyakis triacontahedron represent the 12 basic notes and the 168 intervals other than octaves between notes above the tonic. The 13 rising intervals and the 13 falling intervals between the tonic and the other types of notes in the Church modes are the musical counterparts of the 13 Catalan solids and their duals. Just as the disdyakis triacontahedron has 26 sheets of vertices that are perpendicular to either B-B or C-C axes and 33 sheets perpendicular to A-A, B-B & C-C axes, so it is the 26th member of the family of Archimedean and Catalan solids and the 33rd stage in the development of polyhedra. The disdyakis triacontahedron contains 1680 vertices, edges & triangles, where 1680 is the number of yods in the lowest 33 Trees of Life constructed from tetractyses. The 28 polyhedra defined by its 62 vertices have 3360 hexagonal yods in their faces. This is the number of yods needed to construct the inner Tree of Life from 2nd-order tetractyses. It is also the number of helical turns in one revolution of the ten whorls of the basic unit of matter described over a century ago by Annie Besant & C.W. Leadbeater, showing how the disdyakis triacontahedron embodies geometrically the structural parameter of this object, identified in earlier work by the author as the E8×E8 heterotic superstring constituent of up and down quarks. |
1
1. The ancient musical scales/Church modes
Historically speaking, musical scales were always divided into eight notes because the ancient Greeks regarded them as composed of two tetrachords (sets of four notes). If the pitch, or ‘tone ratio,’ of the starting note (‘tonic’) of a scale is given the value of 1, the eighth note of the scale (‘octave’) has a tone ratio of 2, that is, it has twice the frequency of the tonic and is the tonic of the next higher set of eight notes. The arithmetic mean of these two frequencies is (1+2)/2 = 3/2. This is the tone ratio of the ‘perfect fifth,’ so-called because it is the fifth note in the ascending scale, counting from the tonic. The musical scale based entirely on octaves and fifths is called the ‘diatonic scale.’ The tone ratios of the eight notes making up an octave of this scale are:1 9/8 (9/8)2 4/3 3/2 27/16 243/128 2
This diatonic scale is also called the ‘Pythagorean scale' because Pythagoras is generally thought to have discovered its mathematical basis. It comprises five tone intervals (T) of 9/8 and two intervals (L) of 256/243, called in Greek the leimma, or ‘left over,’ which corresponds to the modern semi-tone, although slightly less than it. The interval pattern of the Pythagorean scale is:
tone–tone–leimma–tone–tone–tone–leimma.
T T L T T T LIn the C scale, the tonic is labelled ‘C’ and subsequent notes in the scale are labelled D, E, F, G, A & B, the octave being written as C'. Their tone ratios are:
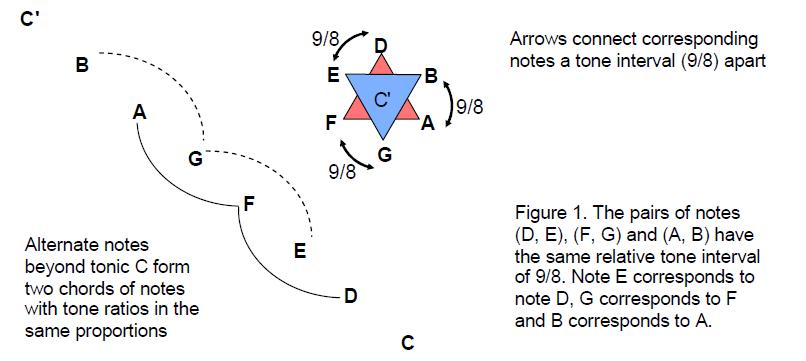
As proved in Article 14,1 the six notes above the tonic of the C scale can form only two triplets of notes with the same proportions of their tone ratios. They are (D, F, A) and (E, G, B), corresponding members of which are separated by a tone interval (Fig. 1).
The seven notes D–C' above the tonic of the C scale therefore comprise three pairs of notes (D, E), (F, G) & (A, B) and the octave C' as well as a (3:3:1) pattern. The two triplets (D, F, A) and (E, G, B) correspond in the Tree of Life (Fig. 2) to the two triads of Sephiroth of Construction: Chesed-Geburah-Tiphareth and Netzach-Hod-Yesod, whilst the last note of the C scale, the octave C', corresponds to Malkuth, the last Sephirah of Construction, which completes the emanation of the Tree of Life. The three pairs of notes (D, E), (F, G) & (A, B) separated by a tone interval correspond to the pairs of Sephiroth of Construction on the three pillars of the Tree of Life. This parallelism
2
suggests that the musical scales, both collectively and in their mathematically perfect version — the Pythagorean scale, conform to the Tree of Life, the Kabbalistic representation of Adam Kadmon, or ‘Heavenly Man.’
This article will add to the evidence presented in Article 14 for this bold assertion by showing that a remarkable similarity exists between the intervallic composition of the musical scales and the disdyakis triacontahedron, the most complex of the Catalan solids, which was proven in Articles 22-30 to be one of the two polyhedra that make up the polyhedral representation of what the author has called the “inner Tree of Life” (to be discussed later).
Many modern musical scholars hold the view that the ancient Greek musical modes, such as the Dorian and Phrygian modes, were not different octave species but different
3
keys of the same scale. Article 16 refuted this belief with two arguments:
1. the ancient Greeks would not have used two different musical terms — ‘harmonia’ and ‘tonos’— to mean the same thing, namely, key, instead of scale and key;
2. the Pythagorean mathematician Nichomachus stated2 (quoting Pythagoras and Plato) that the ancient Egyptians ascribed 28 sounds to the universe, indicating that they were aware of the seven octave species, which have 28 notes with tone ratios belonging to the Pythagorean scale. As it is known3 that many musicians of ancient Greece, as well as learned men like Pythagoras and Plato, studied music with the Egyptians, it is highly unlikely that they neither learnt of the existence of the seven octave species nor heard music played in various modes based upon them.
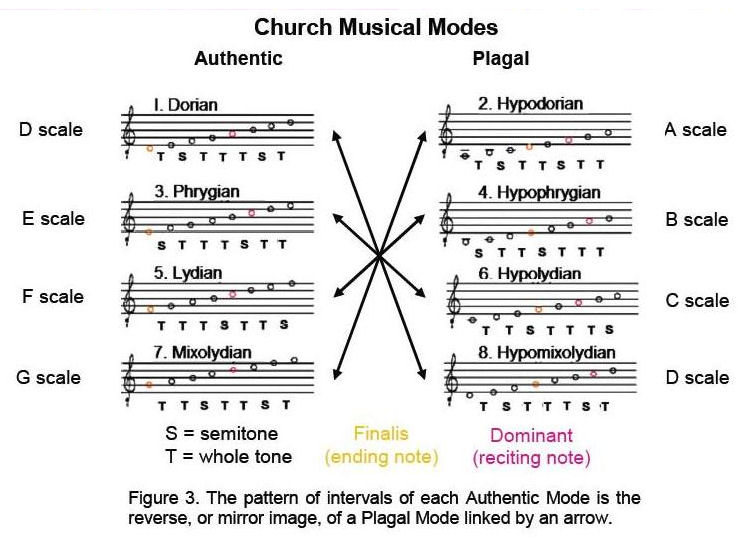
The musical modes that have served as the basis of plainsong in the Roman Catholic Church originated not from the
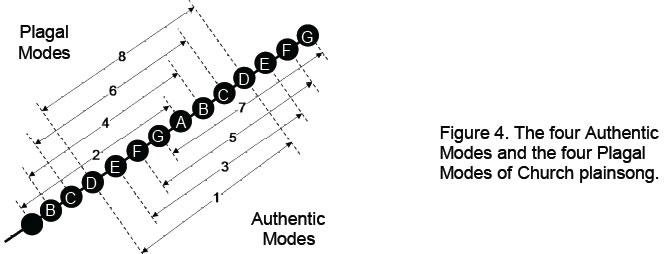
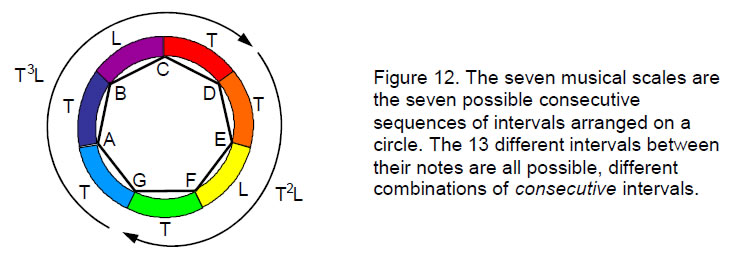
ancient Greek modes described by Plato and Aristotle but from the Byzantine octoechoi, which were four pairs of melodic motives that expressed different feelings, or ethos. The church modes consist of four ‘Authentic Modes’ (so-called because they were given the ancient Greek names of Dorian, Phrygian, Lydian and Mixolydian) and four ‘Plagal Modes’ (Fig. 3). The latter are separated from the former by a perfect fourth (Fig. 4). By dividing a circle into seven arcs (Fig. 5) representing successive intervals of the Pythagorean scale and selecting consecutive sequences of seven intervals as each scale, it is readily seen that there can be only seven different musical scales because there are seven intervals between successive notes in a scale and so the eighth sequence merely repeats the first one:
Moreover, as all intervals are selected, their sequences do not depend upon the starting
4
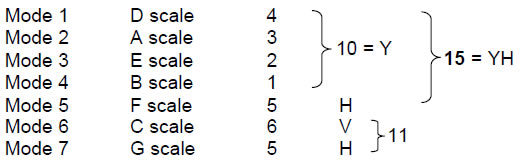
point on the circle. The eight Church modes are labelled 1–8 (see Fig. 4) and start with the D scale. It is called the ‘Dorian mode,’ although whether it was what the ancient Greeks understand as this mode is unknown. It turns out that the numbering of modes is not arbitrary because, starting with the tonic of the D scale, the last of the different scales is the Pythagorean scale (C scale), the only scale with all its notes having tone ratios with Pythagorean values. As it displays the most mathematical harmonies, it is intuitively natural that the last of any sequence of these scales should be the Pythagorean scale. The D scale, however, is the only scale whose pattern of intervals is symmetric. Fig. 3 indicates that it is the same as its mirror image and that Modes 3, 5 & 7 are the mirror image of Modes 6, 4 & 2. This unique property of the D scale gives it a pivotal role in establishing the connection between the musical scales and the polyhedral Tree of Life, as will be explained later. If each rising interval in a scale is replaced by its falling counterpart, i.e., T
T–1 and L
L–1, an ascending scale, e.g., TLTTLTT, becomes T–1L–1T–1T–1L–1T–1T–1, which is the descending version of the scale TTLTTLT. Inverting each interval of a scale creates another scale whose pattern of intervals is its mirror image. Only the D scale is unchanged when its intervals are inverted.
The eight C–C' scales shown above (or eight consecutive scales starting with any note) span 15 successive notes C–C'' and 14 intervals, showing how the Godname YAH with number value 154 prescribes the range of notes needed to define the complete set of four Authentic Modes and four Plagal Modes. Their (8×7=56) intervals comprise 16 leimmas (L) and 40 whole tones (T), where
and
This demonstrates how the Tetrad (4) symbolised by the square expresses the tone interval and leimma composition of the eight scales. Notice that, as each scale has the same number of tone intervals and the same number of leimmas, this composition is the same whatever the scale chosen to start the sequence, e.g., 40 whole tones and 16 leimmas are spanned by the eight scales that start and end with the D-scale.
Table 1. The tone ratios of the eight scales C–C'.
Musical scale C' scale B scale A scale G scale F scale E scale D scale C scale (White cells denote Pythagorean notes; red cells denote non-Pythagorean notes).
5
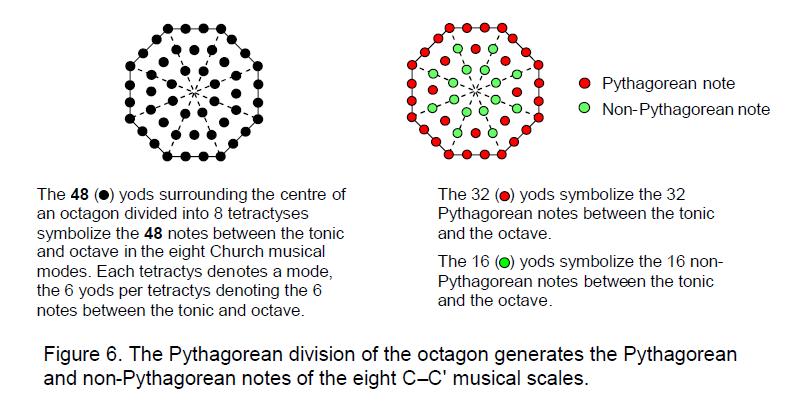
The eight C–C' musical scales have 48 notes with Pythagorean tone ratios (white cells in Table 1) and 16 notes with non-Pythagorean tone ratios (red cells). Table 2 lists their numbers in each scale. These notes can be represented by an octagon whose sectors are tetractyses (Fig. 6) because 48 yods surround its centre.
The Pythagorean notes consist of eight tonics (1), eight octaves (2) and 32 notes between the tonic and octave with intermediate tone ratios. They comprise 26 notes of the seven scales C–B and the six notes of the repeated C' scale.
Table 2. Number of Pythagorean/non-Pythagorean tone ratios in the eight modes.
Musical scale
tone ratios (white cells)Number of non-Pythagorean
tone ratios (red cells)C' scale
B scale
A scale
G scale
F scale
E scale
D scale
C scale
Total = 48 Total = 16
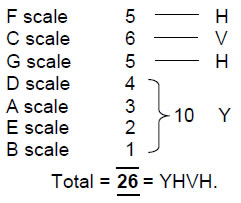
The number of independent (non-repeated) Pythagorean notes is 26, which is therefore prescribed by the Godname YAHWEH (YHVH), the values of the letters of the Godname denoting the numbers of tones with tone ratios of two possible values:
The letter values of YAHWEH also define the numbers of Pythagorean notes between
6
the tonic and octave of the seven independent scales:
Including their octaves, there are 33 Pythagorean notes above the tonic of the seven scales. The numbers 26 and 33 measure, respectively, the number of combinations and the number of permutations of 10 objects a, b, c, ...j arranged in a tetractys:
Indeed, Table 1 indicates that those types of Pythagorean and non-Pythagorean tones above the tonic that occur more than once are themselves 10 in number:
The seven distinct octave species have notes above the tonic with 13 different tone ratios listed below in increasing order of magnitude:
256/243 9/8 32/27 81/64 4/3 1024/729 729/512 3/2 128/81 27/16 16/9 243/128 2
(Numbers in red denote notes not belonging to the Pythagorean scale (C-scale)). Including the tonic, they consist of seven pairs that, as intervals, span an octave. In order of increasing magnitude, they are:
1 2 3 4 5 6 7
The 14 notes consist of two pairs of Pythagorean notes, four pairs of a Pythagorean and a non-Pythagorean note and one pair of non-Pythagorean notes. The significance of this structure will emerge later.
As demonstrated in Article 165, every one of the 28 intervals between two notes belonging to each of the seven different musical scales is equal to the tone ratio of one of the 13 different notes above the tonic that can be found in these scales. In other words, all their intervals are just repetitions of this basic set.
Table 3 lists the tone ratios of the eight D–D' scales. They comprise 30 Pythagorean
7
notes and 18 non-Pythagorean notes. Table 4 compares the number of notes in the C–C' scales and the D–D' scales.
Table 3. The tone ratios of the notes of the eight D–D' musical scales.
Musical scale D' scale C scale B scale A scale G scale F scale E scale D scale (White cells denote Pythagorean notes; red cells denote non-Pythagorean notes).
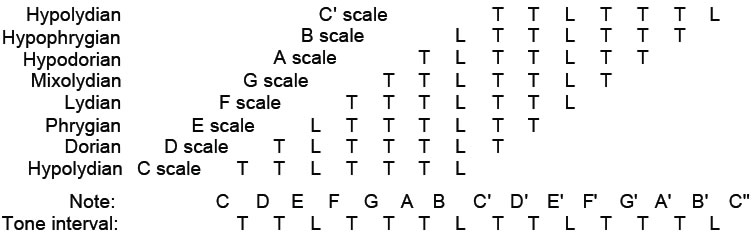
Both have the same numbers of notes (24) and their octave complements (24). It is straightforward to verify that all of the other scales except the F scale (Lydian mode) exhibit this symmetry possessed by the C scale (Pythagorean) and D scale (Dorian musical mode). The latter is unique among the scales in that its pattern of intervals — TLTTTLT — is its own mirror reflection.
Table 4. Numbers of different notes in the eight C–C' and the eight D–D' scales.
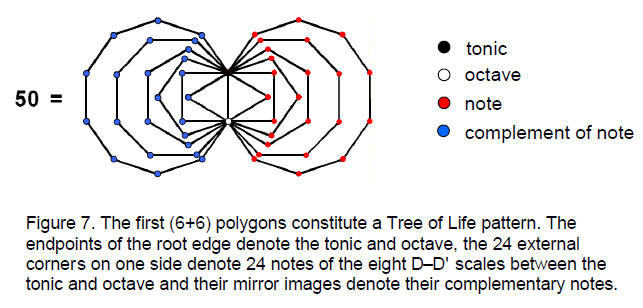
The tonic, octave and the 24 pairs of notes and their complements can be assigned to the 50 corners of the first (6+6) regular polygons of the inner Tree of Life (Fig. 7). Article 4 showed that this set of polygons constitute a Tree of Life pattern because the number values of the ten Godnames define its geometrical properties.6 The two endpoints of the shared root edge denote the tonic and the octave, and a corner and its mirror image in
8
the other similar set of polygons denote a note and its complement.
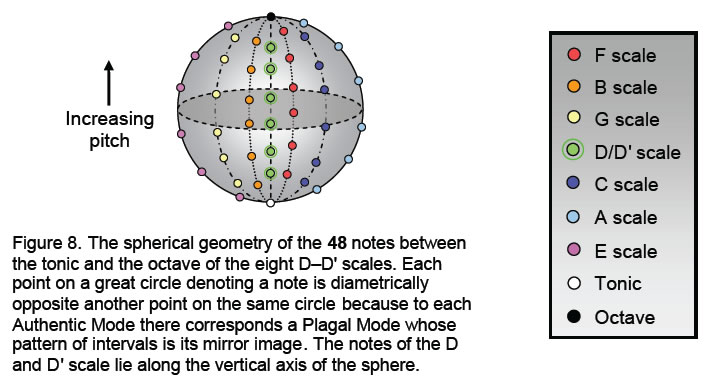
Suppose that the eight notes of a scale are denoted by points on a great circle of a sphere passing through the South Pole (tonic) and North Pole (octave) (Fig. 8). As the intervals of the E, F & G scales are the mirror images of, respectively, the C, B & A scales, a note is diametrically opposite every other note on the circle. As the pattern of intervals of the D scale is its own mirror image, its notes can be represented by points on the central vertical axis of the sphere, each point being the same distance from the centre as its mirror image. This means that the eight scales
D–D' can be represented by (2+8×6 = 50) notes on the sphere and its axis, 12 of them lying on the latter as six different pairs of identical notes assigned to the six points between the North and South Poles. It demonstrates how the Godname ELOHIM with number value 50 prescribes this sequence of scales. It also demonstrates the power of the Tetrad (4) to express properties of holistic systems such as the seven musical scales, for the number of points symbolising their notes is 44. The Divine Name ELOHA assigned to Geburah with number value 36 prescribes the (6×6=36) notes between the tonic and the octave of the E–C scales that lie on the surface of the sphere and surround the 14 notes on its axis.
The 42 notes between the tonics and octaves of the seven different musical scales consist of the following pairs:
The Godname EHYEH (AHIH) with number value 21 prescribes the 21 notes and their 21 complements, its letter values specifying different combinations of notes. As pointed out earlier, the Godname YAHWEH prescribes the 26 Pythagorean notes in this set of 42 notes.
The 50 notes of the eight scales D–D' represented in Fig. 8 consist of seven sets of
9
notes and their seven sets of complementary notes:
There have to be at least seven pairs of complementary notes because there are seven notes in a scale below the octave. The fact, however, that the eight scales contain only seven pairs is non-trivial, because, although they comprise 14 different notes when the tonic is included, there is
no obvious reason why they should group into seven pairs of complementary notes. It becomes obvious only when all possible intervals between the notes in each scale are calculated and found to consist of the same set of tone ratios of their notes.7 This is because every interval has its complementary interval and therefore 14 different intervals must be grouped into seven pairs. As there is a note in the seven scales whose tone ratio equals one of these intervals, all their types of notes can be grouped into seven pairs.
As pointed out earlier, the D scale is uniquely symmetric in its sequence of intervals. It is also the only scale whose 36 intervals have the values of 26 Pythagorean tone ratios.8 This prescription by the Godnames ELOHA with number value 36 assigned to Geburah and YAHWEH with number value 26 assigned to Chokmah reflects its status in Church music as the Dorian Mode, labelled Mode 1 to indicate that it is the scale from which all the other scales (ending with Mode 7, the mathematically most harmonious Pythagorean scale) can be generated by shifting one interval at a time. Furthermore, the D scale is the only one with 10 intervals with non-Pythagorean values.9 As the seven octave species have 66 non-Pythagorean intervals,10 the eight D-D' scales have (66+10=76) non-Pythagorean intervals. This is how the Godname YAHWEH ELOHIM with number value 76 prescribes the set of eight Church musical modes: it measures all its non-Pythagorean intervals.
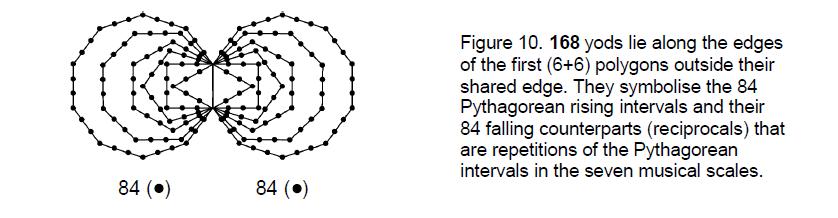
Excluding the interval 1 between a note and itself, the seven different scales D–C have 130 Pythagorean intervals.11 Excluding their seven octaves, they have 123 Pythagorean intervals. The eight notes of the D scale have 26 Pythagorean intervals. They include eight ‘1’s and one '2', that is, (26–8–1=17) such intervals between 1 and 2. The number of intervals between 1 and 2 in the eight scales D–D' = 123 +17 + 76 = 216, which is the number value of Geburah. 48 of these are their notes between their tonic and octave, leaving 168 intervals between the notes of the eight D–D' scales above the tonic. This is the number of Cholem Yesodoth, the Mundane Chakra of Malkuth. It is the superstring structural parameter discussed in many previous articles. They are symbolised in the first six enfolded, regular polygons as the 168 yods within them other than their 26 corners (Fig. 9), which, as we saw in Fig. 7, symbolise notes of the eight
10
scales. They are symbolised in the spherical representation of the eight D–D' scales as the 168 intervals between the seven notes above the tonic in each scale.
We found in Article 1612 that the seven scales D–C have 84 rising, Pythagorean intervals that are repetitions of the six Pythagorean notes between the tonic and the octave. They have 84 falling intervals as their counterparts, making 168 in total. They are symbolised by the 84 yods along the edges of the first six enfolded polygons and their 84 mirror images in the other set of polygons (Fig. 10). Mirror symmetry of corresponding corners denotes the difference between a rising and a falling interval. In terms of notes of the C scale, the composition of the 84 rising,
Pythagorean intervals is
D E F G A
28 11 23 17 5Therefore, there are (2×(28+11) = 78) rising and falling seconds and thirds and 2×(23+17+5) = 90 rising and falling fourths, fifths and sixths (the seventh never appears more than once in a scale). 78 is the number value of the Kabbalistic word ‘Cholem’ and 90 is the number value of the word ‘Yesodoth.’
The seven different scales have 12 basic notes with different tone ratios between 1 and 2. All the intervals between notes in these scales have values found in this set. Hence, there are in the eight scales (216–12=204) repetitions of these notes and intervals. Including the tonic and the octave, the 50 notes of these scales arranged as in Fig. 8 and starting with the same note have 206 notes/intervals other than the basic set. Of these, 136 are Pythagorean notes/intervals and 70 are non-Pythagorean notes/intervals. It was shown in Article 2913 that the triakis tetrahedron, the simplest Catalan solid, has 136 vertices, edges and triangles surrounding its centre when its internal triangles are regarded as single tetractyses and its faces are divided into three tetractyses. There are as many geometrical elements surrounding this polyhedron as there are Pythagorean notes and intervals in the eight scales in addition to its basic set. The reason for this correspondence is that both the eight D–D' musical scales and the triakis tetrahedron conform to the archetypal pattern of the Tree of Life, as proved for the latter in Article 29, and therefore must display properties that numerically correspond to each other.
Ten Pythagorean notes (tonic, octave & two identical sets of the four notes E, G, A & B of the D scale) lie on the central axis of the spherical representation of the eight D–D' scales. Hence, the 206 intervals consist of (136–10=126) Pythagorean intervals of the six scales other than the two D scales and 80 intervals made up of 70 non-Pythagorean intervals and 10 Pythagorean notes arranged along the axis. As, according to Table 2 of Article 29, the triakis tetrahedron has 132 geometrical elements surrounding its axis, six of which are its vertices, 126 other vertices, edges and triangles surround its axis.
11
Once again, correspondence appears between different features of each system.
The counterpart in the triakis tetrahedron of the fact discussed above that 168 intervals exist between the notes above the tonic of the eight D–D' scales is that, when its internal triangles are divided into three tetractyses, it has 168 geometrical elements surrounding its axis. As the Pythagoreans taught, “music is geometry.”
As commented upon earlier, the 14 different notes of the seven musical scales consist of seven pairs of notes and their complements:
1 2 3 4 5 6 7 (The ordering is in terms of increasing size of the first member of each pair). Let us write, firstly, the octave 2 as ‘1’ (using boldface to remind ourselves that 1 is not the number 1), secondly, each note of one set as ai (i = 1–7) and, thirdly, its complement as ai–1. The product of an interval and its complement may then be expressed as:
aiai–1 = 1.
The complement of a given note is as far below the octave as that note is above the tonic — they are equally spaced from each end of the scale (Fig. 11). The complement can be regarded as the inverse of a note in the sense that their intervals span the octave. A rising musical interval a = n (n>1) has a complement with interval 2/n, not 1/n, which is the value of the falling interval. Every member of the set of 14 notes has a complement, or inverse, which is also a member of that set. As the D scale is unique in having a pattern of intervals that is identical to its mirror image, this means that it alone amongst the scales is made up of four pairs of notes and their complements:
In terms of the Pythagorean tone T and leimma L, the seven pairs of notes making up the musical scales have the form:
1 1 T5L2 (= 2) 2 L T5L 3 T T4L2 4 TL T4L 5 T2 T3L2 6 T2L T3L 7 T2L2 T3 12
Eight notes are Pythagorean and six notes (written above in red) are non-Pythagorean. By arranging the intervals between successive notes of the Pythagorean scale on a circle (Fig. 12), all possible scales are the sequences of seven intervals generated by starting at successive intervals until all of them have been selected. Their notes and intervals are all possible different combinations of consecutive intervals. They have the forms listed above. The complement of any note represented by an arc of the circle in Fig. 12 is that created by the opposing arc that completes the
circular pattern of intervals. Just as every colour has its complementary colour, so, too, do the notes.
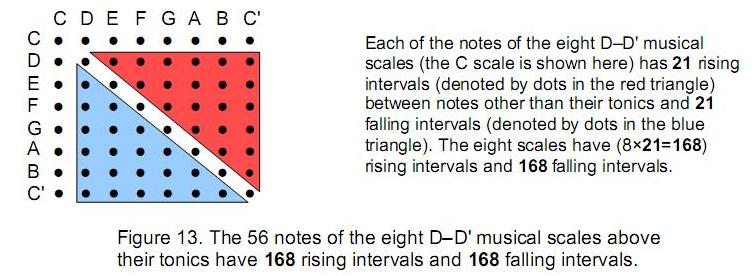
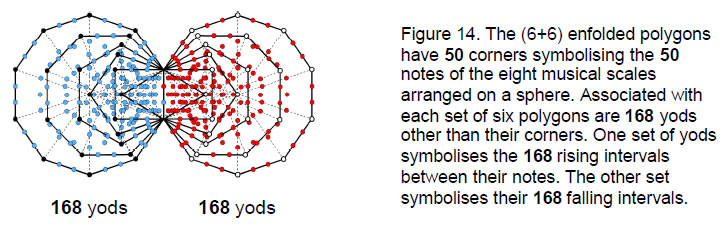
The eight notes of a musical scale have 8C2 = 28 intervals. They include the seven notes above the tonic. There are 21 intervals between these notes (Fig.13). The eight D-D′ scales have (21×8=168) such rising intervals between their (8×7=56) notes:
Similarly, there are 168 falling intervals. They are symbolised in the inner Tree of Life by the 168 yods in each set of the first six enfolded polygons (Fig. 14), whose corners denote the 50 notes of the eight D–D' scales arranged on the surface of the sphere and along its axis, as discussed earlier and shown in Fig. 8.
13
This remarkable analogy between the intervallic composition of the eight church musical modes and the inner Tree of Life would remain valid whatever set of eight scales was considered. The eight scales starting with the D scale have been chosen because: 1. it was the Dorian mode that was, historically speaking, made the first of the Authentic Modes, and 2. starting with the D scale means that the Pythagorean scale is the last different scale that can be generated from it — a sequence that is natural in view of its special significance as the most mathematically harmonious scale and its historical importance as the basis of Western musical theory. The interval composition of the scales does, of course, depend upon which set of eight scales is considered.
The seven pairs of notes and their complements consist of two pairs of Pythagorean notes (tonic/octave & perfect fourth/fifth) and five pairs of notes that each includes at least one non-Pythagorean note. The 2:5 division is another example of the basic pattern that starts in the seven
scales, each with five tone intervals T with magnitude 9/8 and two leimmas L with magnitude 256/243.
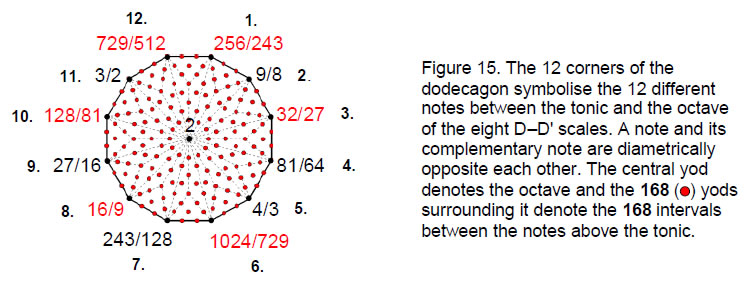
The last of the regular polygons in the inner Tree of Life is the dodecagon. As the tenth regular polygon, it represents the completion of the Pythagorean paradigm of wholeness symbolised by the tetractys. When its 12 sectors are each divided into three tetractyses, it contains 181 yods (Fig. 15). 13 yods are at the corners and centre of the dodecagon and 168 yods are generated by this transformation. The 12 types of musical notes between the tonic and the octave in the seven types of scales can be assigned to its corners, with the octave assigned to its centre. The
168 rising intervals between them can be assigned to the 168 yods. The 168 yods in the other dodecagon symbolise the 168 falling intervals. This demonstrates the remarkable connection between the sacred geometry of the inner Tree of Life and the musical potential of the eight scales.
As
132 – 1 = 168 = 3 + 5 + & + … + 25,
168 is not only the number of yods in a dodecagon other than its centre and corners but also the sum of the first 12 odd integers that can be assigned to its corners (Fig. 16).
14
This shows the arithmetic, geometric and musical connection between the numbers 12 and 168. It appears in the first four Platonic solids ending with the icosahedron with 12 vertices as the average number of yods needed to build them out of tetractyses.14
Inspection of Tables 3, 4, 5, 7, 8 & 9 in Article 1615 shows that the C, E, F, G, A & B scales have (including octaves) 112 Pythagorean intervals and 56 non-Pythagorean intervals, that is, 168 intervals. Once again, the number value of Cholem Yesodoth measures the number of intervals — this time for the six scales other than the D scale and including octaves.
2. Connection between the 144 Polyhedron and the eight scales
We found earlier that the eight D–D' scales have 216 intervals other than octaves between their 64 notes. We also found that they have 12 types of notes other than the octave and 168 intervals between notes above the tonic, totalling 180 intervals other than the octave. Compare this with the facts that the 144 Polyhedron has 216 edges and that the disdyakis triacontahedron has 180 edges (Fig. 17). In the first case, there are (8×6 + 168 = 216) intervals. The (8×6=48) notes between the tonic and octave of the eight scales contain the basic set of 12 notes, that is, there
are 36 repetitions of some of these notes, where 36 is the number value of ELOHA, Godname of Geburah. These repetitions are represented by the 36 extra edges of the 144 Polyhedron. We see that the edges of the 144 Polyhedron represent all possible intervals other than octaves between the notes of the eight Church musical modes and that the edges of the disdyakis triacontahedron represent the basic set of 12 intervals and their 168 repetitions:
15
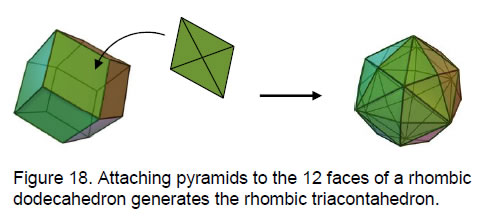
The disdyakis dodecahedron that generates the 144 Polyhedron is itself generated from the rhombic dodecahedron by attaching pyramids to its 12 rhombic faces (Fig. 18). This increases the number of vertices from 14 to (14+12=26), the number of edges from 24 to (24+12×4=72) and the number of faces from 12 to (12×4=48). The change in the number of edges: 24→(24+48=72)→(72+144=216), has its counterpart in the eight Church modes, whose 216 intervals below the octave comprise the 48 notes between the tonic and octave, (8×3=24) intervals between the octave and the second, third and fourth notes in each scale, and 144 other notes (Fig. 19).
Notice that the 216 intervals split also into the 48 notes and 168 other intervals, where 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth and a basic structural parameter of the E8×E8 heterotic superstring. The number 48 is represented in the 144 Polyhedron as the 48 peaks of the tetrahedra that have to be added to the faces of the disdyakis dodecahedron in order to create it. The 24 notes and their 24 complements correspond to the 24 peaks and their 24 mirror images. The latter originate in the four faces of a pyramid that is attached to each of the (6+6) faces of the rhombic dodecahedron. This means that each set of 24 peaks is six sets of four. Similarly, the 24 notes and their 24 complements can be regarded as six sets of eight notes, one note from each of the four Authentic Modes and one note from each of the four Plagal Modes.
The 48 notes are copies of the basic set of 12 notes between the tonic and octave of the seven types of musical scales:
256/243 9/8 32/27 81/64 4/3 1024/729 729/512 3/2 128/81 27/16 16/9 243/128
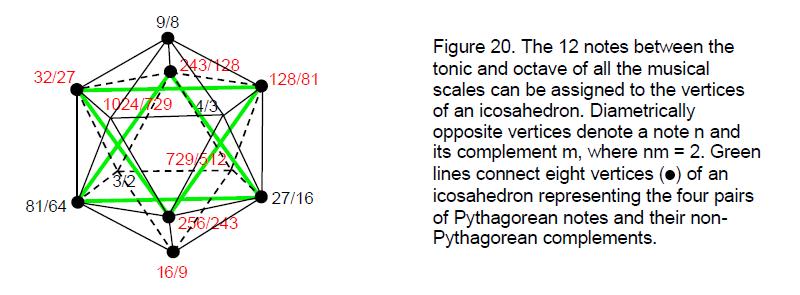
Eight notes comprise four pairs of Pythagorean notes and their non-Pythagorean complements. These four pairs can be assigned to eight of the 12 vertices of an icosahedron denoting these notes (Fig. 20). These are the 12 B vertices of the
16
disdyakis triacontahedron. The eight vertices are those of an octahedron.1
Including the tonic and the octave, the seven scales contain eight different Pythagorean notes and six different non-Pythagorean notes. The former cannot be assigned to an octahedron because they do not consist of four pairs of notes and their complements. This means that its vertices must denote four pairs of notes and their complements, where each pair is a Pythagorean note and a non-Pythagorean note. The four other notes comprise a pair of Pythagorean notes (perfect fourths & fifths) and a pair of non-Pythagorean notes:
Each diametrically opposite pair of B vertices denotes a note and its complement. The inversion symmetry of the icosahedron has its musical counterpart in the fact that the complement of any note in the seven different musical scales with tone ratio n is one with tone ratio 2/n that is also one of these notes. Notice that the four Pythagorean notes that can be assigned to four vertices of an octahedron: 9/8, 27/16, 81/64& 243/128, are each separated by a perfect fifth. Similarly for their respective complements 16/9, 32/27, 128/81 & 256/243. The four remaining B vertices of the icosahedron signify the pair of Pythagorean notes (4/3, 3/2) & the pair of non- Pythagorean notes (1024/729, 729/512) at the centre of the basic set of 12 different notes making up the seven different musical scales:
256/243 9/8 32/27 81/64 4/3 1024/729 729/512 3/2 128/81 27/16 16/9 243/128
The 30 Pythagorean notes of the eight D–D' scales between the tonic and the octave are assigned to the 30 A vertices of the disdyakis triacontahedron and its 18 non-Pythagorean notes, the tonic and the octave are assigned to the 20 C vertices of the dodecahedron.
The musical correspondence is summarised below:
________________________________
1It may be relevant that an octahedron with eight faces has 48 rotational and mirror symmetries.17
3. Comparison with the Tree of Life
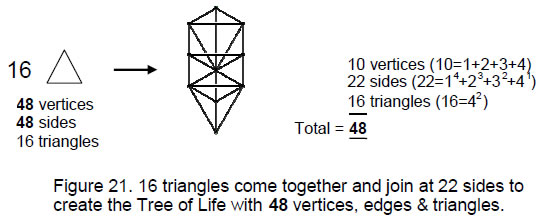
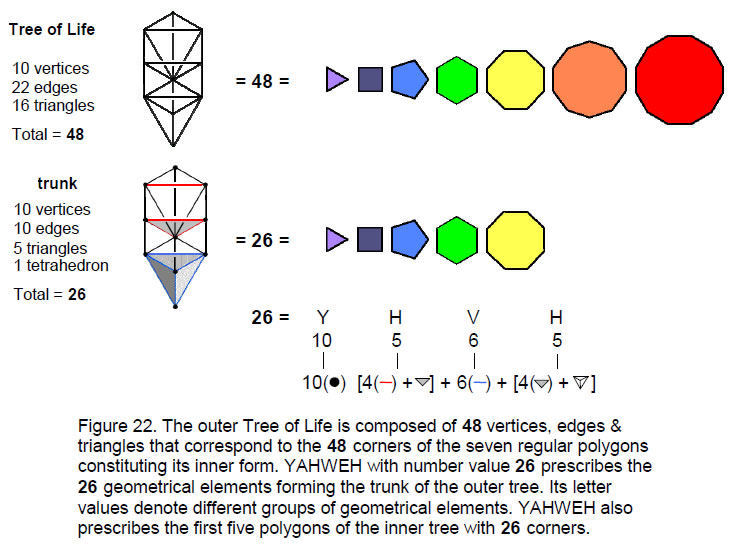
Given that previous articles have demonstrated that the disdyakis triacontahedron is the polyhedral form of the inner Tree of Life, it should come as no surprise that other aspects of this form should appear in the musical context, as now explained.16 separate triangles combine by joining 41 of their edges to create the outer form of the Tree of Life with 10 vertices of 16 triangles with 22 edges (Fig. 21). 64 geometrical elements (38 vertices, 26 edges) disappear in this union, where 64 = 43. It comprises 48 geometrical elements made up of 10 vertices, 22 edges and 16 triangles. As the geometrical representation of the integers 1, 2, 3 & 4, the ‘trunk’ of the Tree of Life consists of the point (Kether), line (Chokmah-Binah), triangle (Chesed-Geburah-Tiphareth) and tetrahedron (Netzach-Hod-Yesod-Malkuth). Fig. 22 shows that it is
18
19
made up of 26 geometrical elements. This trunk is prescribed by the Godname YAHWEH with number value 26, its letter values denoting different groups of elements. The counterpart of the 48 elements in the inner form of the Tree of Life is the 48 corners of the seven regular polygons. The counterpart of the trunk in the inner Tree of Life is the set of the first five polygons, which have 26 corners.
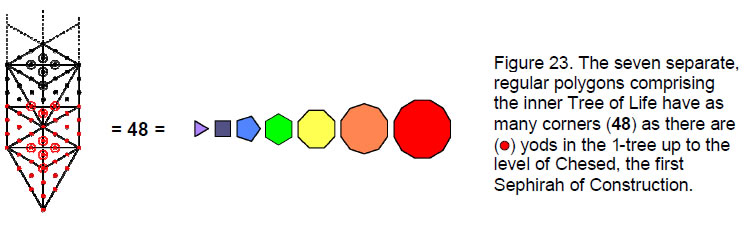
Transformed into tetractyses, the 19 triangles of the lowest Tree of Life of any set of overlapping Trees of Life contain 80 yods. There are 48 yods up to the level of the path joining Geburah to Chesed — the first Sephirah of Construction (Fig. 19). This further demonstrates that 48 fundamental degrees of freedom are needed to express just that part of the Tree of Life that contains the seven Sephiroth of Construction. This number is the basic structural parameter of the Tree of Life — whether geometrical elements in the case of its outer form or corners of polygons in the case of its inner form. It quantifies whatever holistic system is designed according to this blueprint. In the case of the eight Church musical modes, the number 48 is the number of notes between the tonic and octave. It should therefore come as no surprise that it figures so
prominently in the construction of the geometry of the disdyakis triacontahedron. We saw earlier that, if the 12 notes of the eight musical scales are assigned to the corners of the dodecagon, the extra 168 yods needed to construct it from 12 tetractyses symbolise the 168 intervals between their notes. Thus formed, its centre is surrounded by 12 vertices, 24 edges and 12 triangles, that is, 48 geometrical elements are needed to construct the dodecagon, starting from a point. Once again, the number 48 defines the minimal number of bits of information required to create a complete Tree of Life pattern.
When its faces are divided into three tetractyses, the simplest Platonic solid — the tetrahedron — has 48 hexagonal yods in its 12 tetractyses (Fig. 25). The basic building block of polyhedra is composed of 48 yods that symbolise the seven Sephiroth of Construction. Any system whose structure conforms to the universal blueprint of the Tree of Life must necessarily possess this characteristic number of degrees of freedom.
We found in Article 27 that, when its interior triangles and its faces are each divided into three triangles, the disdyakis triacontahedron comprises 2400 vertices, edges & triangles.16 As
492 – 1 = 3 + 5 + 7 + … + 97,
this number is the sum of the first 48 odd integers after 1. Yet again, the number 48 defines arithmetically the very geometrical composition of the disdyakis triacontahedron — the polyhedral manifestation of the inner Tree of Life.
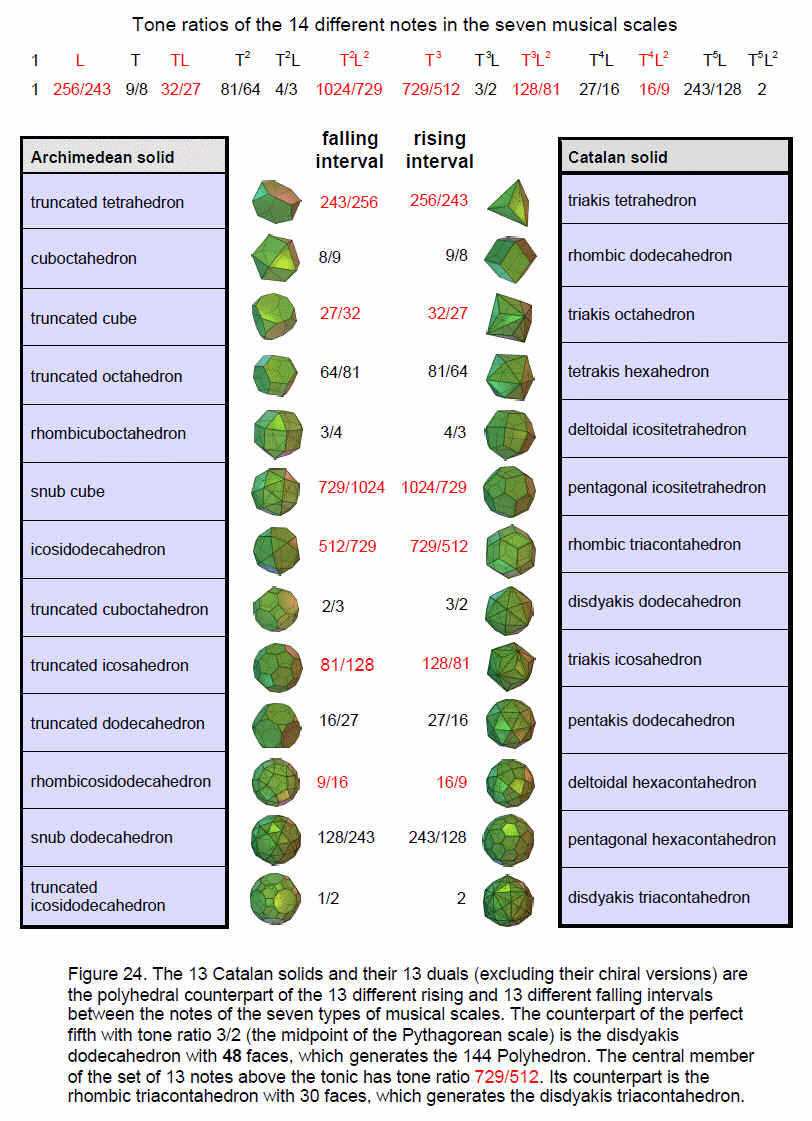
Just as the rhombic triacontahedron underlies the disdyakis triacontahedron, so the Catalan solid with the next larger number of faces — the disdyakis dodecahedron — is the foundation of the 144 Polyhedron, which is the result of adding tetrahedra to its 48 faces with 26 vertices. In fact, it may be seen as the ‘trunk’ of this polyhedron. Just as YAHWEH (YHVH) with number value 26 prescribes the trunk of the Tree of Life because the latter comprises 26 geometrical elements (Fig. 22) and the disdyakis dodecahedron because it has 26 vertices, so YAH (YH) with number value 15 marks out this member of the family of 26 Archimedean and Catalan solids. This is because,
20
starting from the simplest Catalan solid — the triakis tetrahedron — and counting back and forth between pairs of dual polyhedra, the disdyakis dodecahedron is the 15th polyhedron (see Fig. 24), whilst, starting from the simplest Archimedean solid, the 26th solid is the disdyakis triacontahedron, excluding chiral partners. The Godname YAHWEH therefore determines both polyhedra in the polyhedral Tree of Life whilst YAH prescribes the family of 15 Archimedean solids, the family of 15 Catalan solids and the disdyakis dodecahedron as the 15th in the two
families, including their chiral versions.
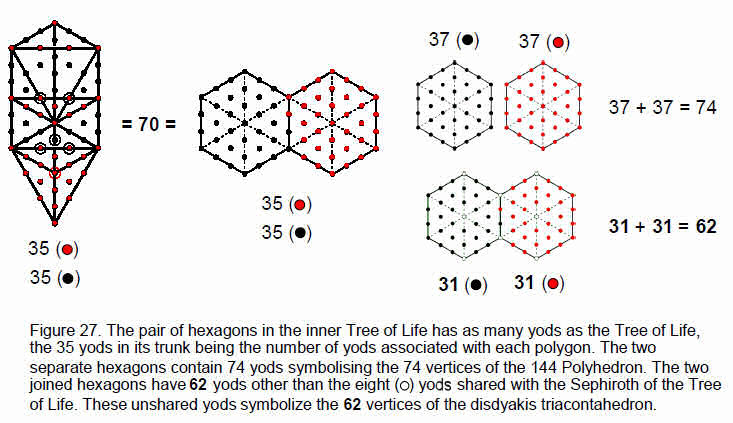
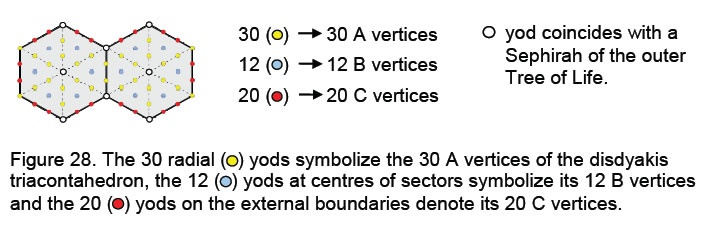
When the outer Tree of Life is projected onto the plane containing its inner form (Fig. 26), eight of the 70 corners of the two sets of enfolded polygons coincide with the projections of Sephiroth and Daath. The 62 unshared corners represent new degrees of freedom. They are the 62 vertices of the disdyakis triacontahedron. The hexagon is the fourth regular polygon. Constructed from tetractyses, a pair of separate hexagons is made up of 74 yods (Fig. 27). They symbolise the 74 vertices of the 144 Polyhedron.
Its 48 ‘new’ vertices correspond to the 48 yods on the boundaries of the pair of hexagons and at the centres of their sectors, whilst its 26 other vertices (vertices of the underlying disdyakis dodecahedron) correspond to the 26 radial yods. Joined together in the inner Tree of Life, the pair of hexagons has 62 yods other than those shared with the outer Tree of Life. They symbolise the 62 vertices of the disdyakis triacontahedron. The 12 yods at the centres of each sector of the hexagons denote its 12 B vertices, the 20 yods lying on their boundaries symbolise the 20 C vertices and the 30 radial yods symbolise its 30 A vertices.
The isomorphism between the pair of hexagons and the disdyakis triacontahedron provides a natural representation of the 12 different notes in the seven musical scales
21
because we found earlier that they correspond to the 12 B vertices of the icosahedron. The six yods at centres of sectors in one hexagon (Fig. 28) denote (in order of increasing tone ratios) the six notes 256/243, 9/8, 32/27, 81/64, 4/3 & 1024/729 and their mirror images in the other hexagon denote the complements of these notes. The 30 Pythagorean notes in the eight D–D' scales are symbolised by radial yods and the 20 notes consisting of the tonic, octave and 18 non-Pythagorean notes are represented by the 20 boundary yods.
That this parallelism between the pair of hexagons and the disdyakis triacontahedron is not merely due to coincidence is indicated by the fact that they require 168 more yods to construct their sectors from three tetractyses (Fig. 29). As discussed earlier (see Fig. 10), this is the number of rising and falling, repeated intervals between the notes between the tonic and the octave of the seven different types of musical scales.17 The 84 yods associated with one hexagon denote their 84 rising intervals and the 84 yods in the other hexagon denote their 84 falling intervals.
4. The holistic character of the number 33
The 62 vertices of the disdyakis triacontahedron are arranged in either seven sheets perpendicular to an A-A axis, 11 sheets perpendicular to a B-B axis or 15 sheets perpendicular to a C-C axis. The correspondence between this pattern and the note composition of the seven different musical scales was mapped out in Article 26.18 It was pointed out in Section 1 that they comprise 26 Pythagorean notes between the tonic and the octave and seven octaves, that is, 33 Pythagorean notes. The tonal composition of the former is:
The letter values of YAHWEH denote the numbers of notes of one or two types. Alternatively, the 26 Pythagorean notes between the tonic and the octave may be
22
divided up in terms of the seven musical scales/church modes listed in Table 1:
However the composition of the 26 Pythagorean notes is decided, the crucial point is that the 7:15:11 pattern of sheets of vertices is identical to the pattern of different notes in the seven different scales, the seven sheets of vertices corresponding to their seven octaves. The parallelism exists because both systems — one geometrical, one musical — are Tree of Life patterns that are prescribed by Divine Names such as YAH and YAHWEH. The number 33 is always a measure of a whole.
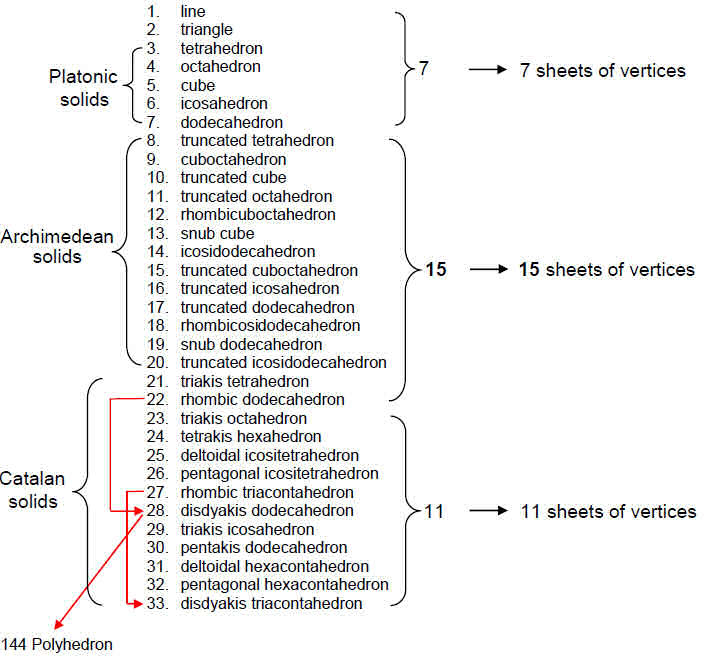
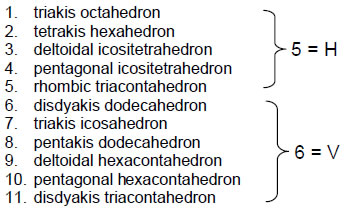
The same pattern can also be seen in the building up of the regular and semi-regular polyhedra. The first stage of creation of form is the straight line, the second stage is the triangle and the third stage is the tetrahedron, the simplest of the five regular polyhedra, or Platonic solids. The dodecahedron, the last of the Platonic solids, is formed at the seventh stage and the disdyakis triacontahedron, the last of the 26 semi-regular polyhedra, represents the 33rd stage:
23
Listed above are, firstly, the Archimedean solids and then the Catalan solids. Just as it exhibits 33 sheets of vertices, so the disdyakis triacontahedron is the 33rd stage in the generation of the semi-regular polyhedra. The 15th stage after the seventh generates the rhombic dodecahedron with 26 vertices & faces, 36 edges & faces and 50 vertices, edges & faces. With its geometry prescribed by four Godnames (YAH = 15, YAHWEH = 26, ELOHIM = 50 and ELOHA = 36), it should not be surprising that this polyhedron plays a fundamental role in the generation of the 144 Polyhedron. Sticking rhombic pyramids to its 12 faces creates the disdyakis dodecahedron with 48 faces and 26 vertices (shown above linked by a red arrow to the rhombic dodecahedron). It is this polyhedron that is fundamental to the generation of the 144 Polyhedron because it generates the latter in a way analogous to how the rhombic triacontahedron creates the disdyakis triacontahedron. Sticking tetrahedra to its 48 faces creates the 144 Polyhedron with (48+26=74) vertices and (3×48=144) faces, whilst adding pyramids to the faces of the rhombic triacontahedron generates the disdyakis triacontahedron.
It was shown in Article 2419 that the geometry of the Tree of Life generates the rhombic faces of the rhombic dodecahedron and the golden rhombic faces of the rhombic triacontahedron.
Confirmation that the rhombic dodecahedron is, as the 15th stage in the generation of the disdyakis triacontahedron, the polyhedral root of the polyhedral Tree of Life is provided by the letter values of YAHWEH. In the last 11 stages, the rhombic triacontahedron is the fifth stage and the disdyakis dodecahedron is the sixth stage and the first of the last five stages. The rhombic dodecahedron is picked out by the first two letters of YHVH and the two polyhedra that determine the two polyhedra in the polyhedral Tree of Life are selected by the number values of the last two letters H and V of YHVH:
Notice also that the disdyakis dodecahedron is 21st in the list of semi-regular polyhedra and so is prescribed by the EHYEH, Godname of Kether with number value 21. The 21st stage marks the triakis tetrahedron, the simplest of the Catalan solids. It was shown in Article 2920 that, if the holistic disdyakis triacontahedron is likened to the tetractys — the Pythagorean symbol of holistic systems — the triakis tetrahedron is its ‘yod.’ This is because the geometrical properties of the former are exactly ten times the corresponding one for the latter. The triakis tetrahedron is built from 137 vertices, edges & triangles, where 137 is the 33rd prime number and the number known to physicists to define the fine structure constant e2/ħc ≈ 1/137. The number 33 not only determines the stage of generation of the disdyakis triacontahedron — the last Catalan solid — but also the geometrical composition of the first Catalan solid, whose properties are multiplied tenfold in the latter!
The reason why 33 appears in the Pythagorean note composition of the seven musical scales and in the mathematical description of the disdyakis triacontahedron is that both
24
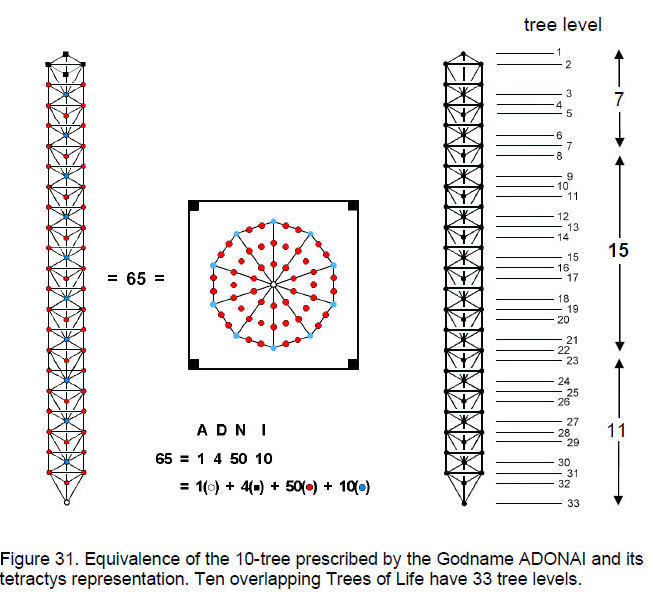
are holistic systems whose components are 33 in number. Or, better, that they are manifestations of a universal cycle that requires 33 stages to complete itself. This is demonstrated par excellence in the tree level structure of ten overlapping Trees of Life, each representing one of the ten Sephirah of the Tree of Life. Fig. 30 indicates that the latter has seven horizontal divisions marking the stages of emanation of Sephiroth of Construction. Although Daath is not a Sephirah, this point in the Tree of Life is Yesod of the next higher, overlapping tree and therefore counts as a division unless there is no higher tree. These divisions are called ‘tree levels.’ Fig. 31 shows that ten overlapping Trees of Life have 33 tree levels (in general, n trees have (3n+3) tree levels). They measure the complete cycle of emanation of 10 Sephiroth. In an abstract sense, the number 33 denotes the number of stages in the completion of a cycle of development of a system that culminates in an object that fully embodies the universal blueprint of the Tree of Life. The relationship between the 33 vertex sheets of the disdyakis triacontahedron and the 33 tree levels of 10 overlapping Trees of Life was analysed in Article 25.21
Also discussed there is what the 7:15:11 vertex sheet composition of the disdyakis triacontahedron means for superstring physics. The 10-dimensions of space-time that are predicted by superstring theory are mapped by 10 overlapping Trees of Life. The Godname ADONAI (ADNI)
25
26
assigned to Malkuth prescribes the lowest 10 trees because its number value 65 is the number of their Sephirothic emanations. Fig. 31 shows how the letter values of ADNI specify different types of emanations. The number 33 appears here because 65 is the 33rd odd integer after 1. Once again, it quantifies a holistic system, because each tree represents one of the Sephiroth.
Counting from the tonic of the first octave of the Pythagorean scale, the tone ratio 24 is the 33rd note and the perfect fifth of the fifth octave (Table 5). Counting from the latter, the 33rd note is 576 = 242 and still the perfect 5th of the new fifth octave. This is the 65th note from the tonic of the first octave. The Godname Adonai with number value 65 prescribes sequences of 33 notes in the Pythagorean scale whose last note has a tone ratio always 24 times that of the first note. This does not depend on which note is the starting point. Any sequence of 33 notes ends in one whose frequency is 24 higher than that of the first, thus demonstrating the cyclic character of this number.
Table 5. Every 33rd note in the Pythagorean scale increases in pitch by a factor of 24.
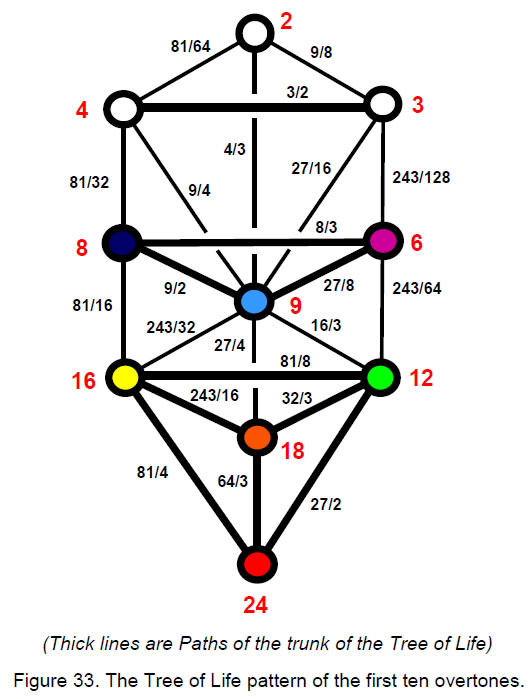
overtonesThe significance of the perfect 5th of the fifth octave is that it is the last of eight successive fifths (not all perfect fifths):
In general, every 33rd note is every eight successive fifth. Table 5 indicates that the 33rd note is the tenth overtone. 22 of the notes up to the perfect 5th of the fifth octave are fractional. They comprise 16 notes in the first three octaves (separated from the rest of the table by a thick line) and six notes in the fourth and fifth octaves up to the last fifth. This 6:16 division corresponds in the Tree of Life to the six Paths that are edges of the tetrahedron whose vertices are the four lowest Sephiroth and to the 16 Paths outside it (Fig. 33). The 32 fractional notes and overtones up to G5 conform to the geometrical pattern of the Tree of Life, the ten overtones corresponding to the ten
27
Sephiroth and the 22 fractional notes corresponding to the 22 Paths that connect them. The ordering of notes in Fig. 33 follows the traditional Kabbalistic numbering of Paths. As the tenth overtone, G5 with tone ratio 24 corresponds to Malkuth, the lowest Sephirah, signifying the physical manifestation of any holistic system conforming to the Tree of Life blueprint. The significance of this number to superstring theory is discussed in Article 12.22
The number of corners of the 7n regular polygons enfolded in n overlapping Trees of Life is
C(n) = 35n + 1,
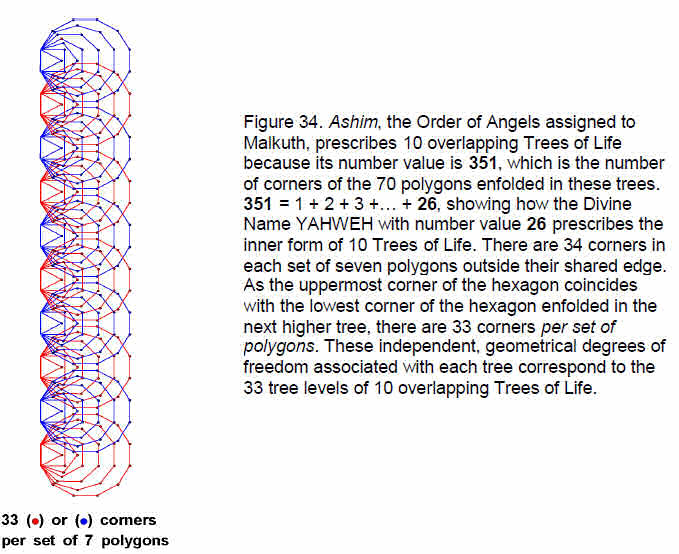
where “1” denotes the uppermost corner of the hexagon enfolded in the tenth tree (the hexagon is the only one of the seven regular polygons that shares a corner with polygons enfolded in adjacent trees. The shared corner is denoted by ‘1’ in the above formula). Therefore, C(10) = 351 = 1 + 2 + 3 + …. + 26. This shows how YAHWEH with number value 26 prescribes the inner form of 10 overlapping Trees of Life. 351 is the number value of Ashim (“Souls of Fire”), the Order of Angels assigned to Malkuth. The number of corners of the 7n polygons outside their n root edges = C'(n) – 2n = 33n + 1. C'(n+1) – C'(n) = 33. In other words, there are 33 corners per set of polygons outside
28
their root edge (Fig. 34). The emanation of successive Trees of Life generates 33 new geometrical degrees of freedom associated with their inner form. This again demonstrates the cyclic aspect of the number 33 in measuring the number of entities
(polyhedra, musical notes, etc) in a sequence that represents a holistic system conforming to the archetypal pattern of the Tree of Life.
When its triangles are turned into tetractyses, the number of yods in the lowest n overlapping Trees of Life is given by
Y(n) = 50n + 30.
Therefore, Y(33) = 1680. As discussed in many previous articles, this is the number of turns in each helical whorl of the UPA (Fig. 35), the indivisible unit of matter described by Annie Besant and C.W. Leadbeater 114 years ago with the aid of a yogic siddhi.
29
In other words, the lowest 33 Trees of Life are made up of as many yods as there are circularly polarized waves in a whorl. This is how the number 33 determines the structural parameter of superstrings inside atomic nuclei. Malkuth of the 33rd Tree of Life is the 65th emanation on the central Pillar of Equilibrium, showing how ADONAI, the Godname of Malkuth with number value 65, prescribes this number.
As pointed out in Article 22,23 there are seven steps leading to the generation of the disdyakis triacontahedron, starting with the tetrahedron. The first five are the Platonic solids and the sixth is the rhombic triacontahedron, the Catalan solid that is compounded from the dodecahedron and the icosahedron. When constructed from tetractyses, the numbers of hexagonal yods in their faces are listed below:
As discussed earlier, the disdyakis triacontahedron is the 33rd stage in the cycle of development of regular and semi-regular solids. Once again, the number 33 is associated with the superstring structural parameter 1680. The five Platonic solids and the two semi-regular solids in this list are the polyhedral counterpart of the five whole intervals and two leimmas in the Pythagorean musical scale:
T T L T T T T L
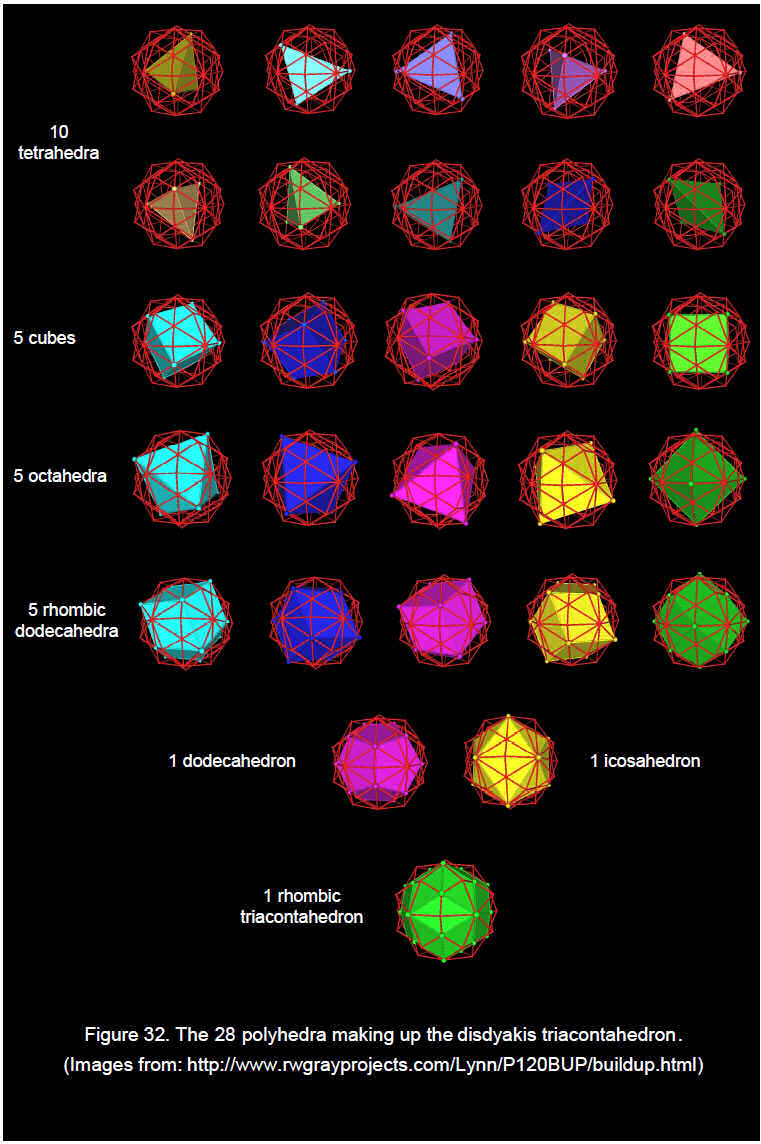
The 62 vertices of the disdyakis triacontahedron define the vertices of 28 regular (Platonic) and semi-regular (Catalan) solids: ten tetrahedra (two vertices at each C vertex), five cubes (two vertices at each C vertex), five octahedra (one vertex at each A vertex), one icosahedron (one vertex at each B vertex), one dodecahedron (one vertex at each C vertex), five rhombic dodecahedra (two vertices at each C vertex and one vertex at each A vertex) and one rhombic triacontahedron (vertices at B and C vertices). Constructed from tetractyses, the hexagonal yod populations of the faces of the 28 Platonic & Catalan solids definable within the disdyakis triacontahedron are:
There are 21 Platonic solids of the four types that the ancient Greeks believed were the shapes of particles of the elements Earth, Water, Air and Fire. Their hexagonal yod population is 1680 — the same as the number of hexagonal yods in the seven polyhedra listed above. This is remarkable evidence of beautiful, mathematical design. EHYEH, the Divine Name associated with Kether at the top of the Tree of Life has the number value 21. It prescribes this polyhedral embodiment of the superstring structural parameter 1680, its letter values specifying the numbers of polyhedra of each type:
30
The remaining three types of polyhedra also have 1680 hexagonal yods in their faces, giving a total number of 3360. This is astounding for two reasons:
1. Divine Unity symbolised by the Pythagorean Monad, or mathematical point ("0th-order tetractys"), differentiates, firstly, into the familiar tetractys ("1st-order tetractys") with 10 yods (three corners, seven hexagonal yods), secondly, into the “2nd-order tetractys” with 85 yods (15 corners, 70 hexagonal yods), and so on:
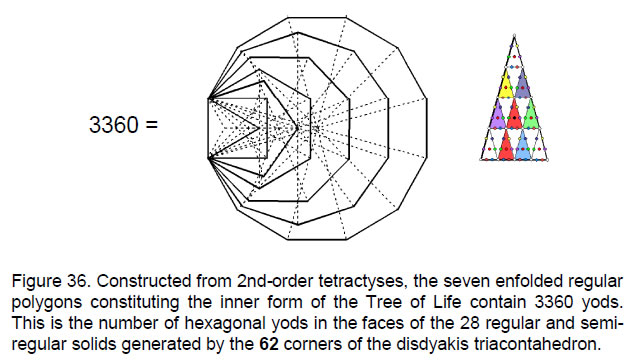
3360 is the number of yods in the seven enfolded, regular polygons constituting the inner form of the Tree of Life when their 47 sectors are each turned into 2nd-order tetractyses (Fig. 36).24
2. 3360 is the number of circularly polarised wave oscillations made during each of the five revolutions of the 10 whorls of the UPA (see Fig. 35). Each yod making up the seven enfolded polygons constructed from 2nd-order tetractyses symbolises one oscillation made in the 10 whorls during one complete revolution around the axis of the UPA. This is not coincidence but a demonstration of the equivalence between the 2-dimensional form of the inner Tree of Life — the seven enfolded polygons — and its
polyhedral form — the disdyakis triacontahedron.
Binah, the third Sephirah in the Tree of Life and the one embodying the cosmic feminine principle (Kabbalists call it Aima, the “Great Mother”), has a gematria number value of 67. The number of yods in n overlapping Trees of Life is
Y'(n) = 50n + 20.
31
Therefore, Y'(67) = 3370. There are 10 yods in the uppermost triangle whose base is the path joining Chokmah and Binah of the highest tree. Below Binah of the 67th tree are 3360 yods. Amazingly, the hexagonal yod population of the 28 polyhedra within the disdyakis triacontahedron is the number of yods below Binah of the very number of trees that equals the number value of Binah!
5. The musical counterpart of G2
The octonions form the fourth (and last) class of division algebras. An octonion has the form:N = a0e0 + a1e1 + a2e2 + …. + a7e7,
where the ai (i = 0–7) are real numbers, e0 is the identity element and the seven unit octonions ei (i = 1–7) are imaginary numbers: ei2 = –1. Their multiplication is anticommutative:
eiej = – ejei (i≠j)
non-associative:
ei(ejek) ≠(eiej)ek
and follows the rule
eiei+1 = ei+3.
Every unit imaginary octonion has an inverse, or conjugate, ei* = –ei, where eiei* = 1. Similarly, the conjugate of an octonion N is N*, where
N* = a0 – a1e1 – a2e2 – … – a7e7.
The norm of an octonion is ││N││= √N*N, where
││N││2 = a02 + a12 + a22 + … + a72.
The inverse of N is N–1 ≡ N*/││N││2, so that N–1N = NN–1 = 1. It was shown in Article 28 that there are 13 classes of real, linear combinations of two or more unit octonions. It means that there are 13 classes of octonions that are inverses to the former, so that YAHWEH with number value 26 prescribes the 26 classes of octonions and their inverses.
This pattern is analogous to the 13 Archimedean solids and their duals — the 13 Catalan solids. The counterpart of polyhedral duality in the world of octonions is the
32
relationship of an octonion N' = N–1 being the inverse of the octonion N, where N'N = 1. Its counterpart in music is the relationship between a note of tone ratio n and its complement of tone ratio m, where nm = 2. What is sufficiently remarkable in the analogy to take it seriously is that:
1. just as there are 13 classes of octonions and 13 classes of their inverses, so the seven musical scales are made up of 13 different notes above the tonic, that is, they have 13 rising intervals and 13 falling intervals;
2. just as the seven imaginary octonions have seven inverses ei* = –ei, so the 14 different notes of the seven scales are divided into seven notes and their complements:
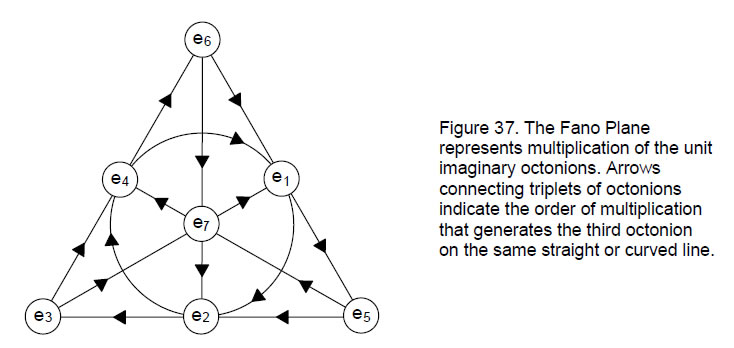
Moreover, just as the seven ei form seven ordered sets of three, or 3-tuples: (ei, ei+1, ei+3), where the product of two ordered members is the third in sequences represented by the circle and six lines of the Fano Plane shown in Fig. 37, so, too, the seven notes and their complements form seven different musical scales. The analogy between the imaginary octonions and the musical intervals is not perfect because multiplication of the former is non-commutative, whereas multiplication of the values of the latter is commutative. However, it is not the imaginary octonions per se that should be compared with musical intervals but, rather, the seven combinations of one, two and three octonions in each 3-tuple:
ei, ei+1, ei+3
eiei+1, ei+1ei+3, ei+3ei (6 permutations)
eiei+1ei+3 (6 permutations)Each 3-tuple has 12 permutations of two or three imaginary octonions. Similarly, as ei+3ei+1= – ei+1ei+3 = – ei = (–ei+3)(–ei+1) and ei-1 = –ei, then (ei+3)–1(ei+1)–1 = (ei)–1, that is, the inverses of each octonion in a 3-tuple also form a 3-tuple with 12 permutations of pairs or triplets. The seven octonions therefore have (7×12=84) permutations, as do
33
their seven inverses. Each permutation reduces to one of the octonions. The seven 3-tuples of octonions and the seven 3-tuples of their inverses display (84+84=168) distinct permutations of their members. Compare this with the fact25 that the seven musical scales have 84 rising intervals between their notes that are repetitions of the basic set of Pythagorean intervals, which means that they also have 84 falling intervals, that is, intervals between two notes falling in pitch. The number of rising intervals in each scale that are repetitions of the Pythagorean intervals varies from scale to scale:26
Total = 84.
Average = 84/7 = 12.This is unlike the number of permutations of pairs and triplets of imaginary octonions in each 3-tuple, which is the same (12) in each one. In terms of notes, the composition of the 84 Pythagorean intervals is
D E F G A 28 11 23 17 5 The interval 243/128 for note B and the interval 2 for the octave are absent because they are the only ones that never appear more than once in a scale (in the former case, the C, E, F & B scales).
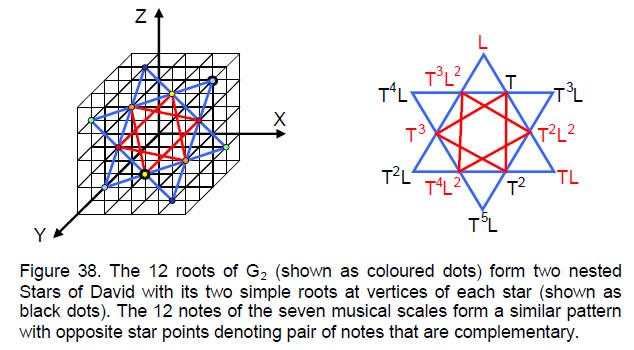
The smallest of the five exceptional groups, the rank-2 group G2 has 14 roots. It has two simple roots (0,1,–1) and (1,–2,1) denoted by black dots in Fig. 38 and 12 roots consisting of six pairs:
They form two nested Stars of David. The red star shown in Fig. 39 denotes the first triplet of roots and their inversions and the blue star denotes the second triplet of roots and their inversions.
Compare this with the seven pairs of intervals and their complements between notes in the seven musical scales:
The tonic and the octave play the role of the two simple roots and the six pairs of intervals and their complements correspond to the six pairs of roots of G2 and their inversions. This correspondence permits a nested Star of David representation of the 12 intervals (Fig. 38). Complementarity of intervals corresponds to spatial inversion of roots of G2. Diametrically opposite vertices of each star signify an interval and its
34
complement. Whatever the assignment of intervals to star points, the members of one triplet have tone ratios in the same relative proportions as those of the other triplet because the latter are their complements with tone ratios that, being reciprocally related, are in the same proportions, although reversed in order. The two red triplets (T, T2, T3) and (T2L2, T3L2, T4L2) have tone ratios in the relative proportions 1:T:T2, i.e., those of the perfect 4th, the perfect 5th and the major 6th of the C scale. What is non-trivial, however, is that the two blue triplets (L, LT, LT2) and (T3L, T4L, T5L) have tone ratios in the same proportion.
If M-theory is isomorphic to music even more than what previous articles have revealed, this appearance of the same relative proportions between intervals represented by different Stars of David may be telling us that subgroups of rank 3 such as SU(3) play a role that extends beyond that already known for it as the gauge symmetry group governing the colour force between quarks. Perhaps the analogy between the root structure of G2 and the 14 basic notes of the seven musical modes is indicating that there is
a fundamental representation of SU(7) with 48 gauge fields consisting of an SU(3) triplet, an SU(3) antitriplet and two SU(3) singlets?
The Klein Configuration is the {7,3} tiling in the hyperbolic plane of the 168 automorphisms of the Riemann surface of the famous ‘Klein Quartic’:
x3y + y3z + z3x = 0.
As a surface of genus 3, the Klein curve is a Hurwitz curve having the maximum number of automorphisms for a surface of genus 3. Figure 39 depicts these transformations as black hyperbolic triangles distributed over 14 sectors of the Klein Configuration, 12 per sector, to create 24 heptagons with 168 triangular sectors that cover a 3-torus (Fig. 40). As the 168 element PSL(2,7) of the Klein Configuration is isomorphic to the symmetry group SL(2,3) of the Fano Plane that describes octonion multiplication and as the 14-dimensional G2 is the group of automorphisms of the octonions, the 12 triangles in each of the sectors of the Klein Configuration represent each of the 14 elements of G2. These sectors correspond to the 14 notes of the seven musical scales and their 168 triangles correspond to the 168 repeated, rising and falling Pythagorean intervals between these notes (or, alternatively, to the 168 intervals between the notes above the tonic of the eight D–D' scales).
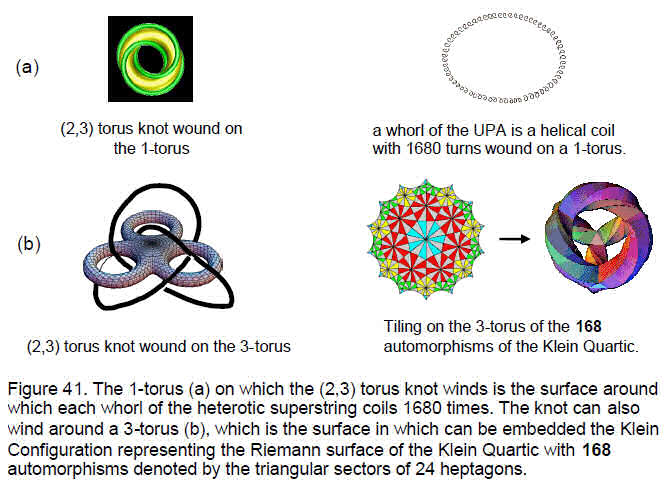
The (2,3) torus knot is a knot that winds twice around a 1-torus as it makes three
35
revolutions. It can wind on a 3-torus as well. (Fig. 41). The former is the surface around which each whorl of the UPA/heterotic superstring winds 1680 times. The latter is the surface in which the Klein Configuration can be embedded. As the octonions provide a natural basis for the Lie algebra of E8 and are connected through the Fano Plane to the Klein Quartic, the (2,3) torus knot determines both the toroidal form and the winding number 1680 of the E8×E8 heterotic superstring.
Because it is well-known to mathematicians that G2 is the automorphism group of the octonions, perhaps it should not come as a surprise that the pattern of basic intervals in the seven musical scales is similar to the root structure of G2, given that we have already demonstrated a correspondence between intervals and the properties of octonions that is too rich to be merely coincidental. Nevertheless, it is still remarkable that the same mathematical structure should appear in the 8-component
Table 6. Number values of the Sephiroth in the four Worlds.
Sephirah
Angels
ChakraKether Chokmah Binah Chesed Geburah Tiphareth Netzach Hod Yesod Malkuth 36
octonions and in the seven 8-note musical scales — even as far as the number of their repeated rising and falling intervals being the order of the symmetry group SL(3,2) for octonions! Moreover, the pattern of intervals of the musical scales is independent of the pitch of a particular octave, remaining true whether the pitch of the tonic is several hundred cycles per second or 1024 cycles per second — the frequency associated with subatomic processes, although such fast vibrations would no longer amount to the kind of sound that is detectable to the human ear, which is only sensitive to sounds spanning up to about ten octaves. The remarkable analogy between the musical scales and octonions strongly suggests that, far from being a now defunct musical scale that is of interest only to historians of science and music, the Pythagorean musical scale shares with octonions a vital role in the unified, holistic description of the real world. This is further strongly indicated by the analogous structures of the polyhedral Tree of Life and the ancient musical modes of the Roman Catholic Church. The universality of this system, whose 2-dimensional counterpart is the outer and inner forms of the Tree of Life, means that it has many different layers of interpretation. Music is one such layer, and it provides insight into the general meaning of the polyhedral Tree of Life.
References
1Phillips, Stephen M. Article 14: “Why the Greek Musical Modes Are Sacred,” (WEB, PDF), pp. 4–5.2 Chappell, W. The History of Music, vol. 1 (London, 1874), pp. 50–51.
4 Numbers in boldface are the number values of the Sephiroth, their Godnames, their Archangels and Mundane Chakras, shown in Table 6 above. They are calculated by means of the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers associated with its letters.
5 Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence with Octonion Algebra and Superstrings,” (WEB, PDF), pp. 9–12.
6 Phillips, Stephen M. Article 4: “The Godnames Prescribe the Inner Tree of Life,” (WEB, PDF), pp. 4–5.
8 Ibid. Compare Tables 3–9, pp. 9–11.
13 Phillips, Stephen M. Article 29: “The Triakis Tetrahedron and the Disdyakis Triacontahedron Embody the Fine-Structure Constant and the Structural Parameter of the Heterotic Superstring,” (WEB, PDF), pp. 4–5.
14 Phillips, Stephen M. Article 3: “The Sacred Geometry of the Platonic Solids,” (WEB, PDF), p. 10.
16 Phillips, Stephen M. Article 27: “How the Disdyakis Triacontahedron Embodies the Structural Parameter 1680 of the E8×E8 Heterotic Superstring,” (WEB, PDF), pp. 14–16.
18 Phillips, Stephen M. Article 26: “How the Seven Musical Scales Relate to the Disdyakis Triacontahedron,” (WEB, PDF), pp. 9–10.
37
19 Phillips, Stephen M. Article 24: “More Evidence for the Disdyakis Triacontahedron as the 3-dimensional Realisation of the Inner Tree of Life and its Manifestation in the E8×E8 Heterotic Superstring,” (WEB, PDF), pp. 6–7.
21 Phillips, Stephen M. Article 25: “The 33 Vertex Sheets of the Disdyakis Triacontahedron Signify the 33 Tree Levels of Ten Overlapping Trees of Life,” (WEB, PDF), pp. 13-15, 20.
22 Phillips, Stephen M. Article 12: “New Pythagorean Aspects of Music and Their Connection to Superstrings,” (WEB, PDF), pp. 24–32.
23 Phillips, Stephen M. Article 22: “The Disdyakis Triacontahedron as the 3-dimensional Counterpart of the Inner Tree of Life,” (WEB, PDF), p. 14.
24 For proof, see ref. 4 in ref. 5.
38