#34 How sacred geometries embody the heterotic superstring gauge symmetry groups E₈ & E₈×E₈

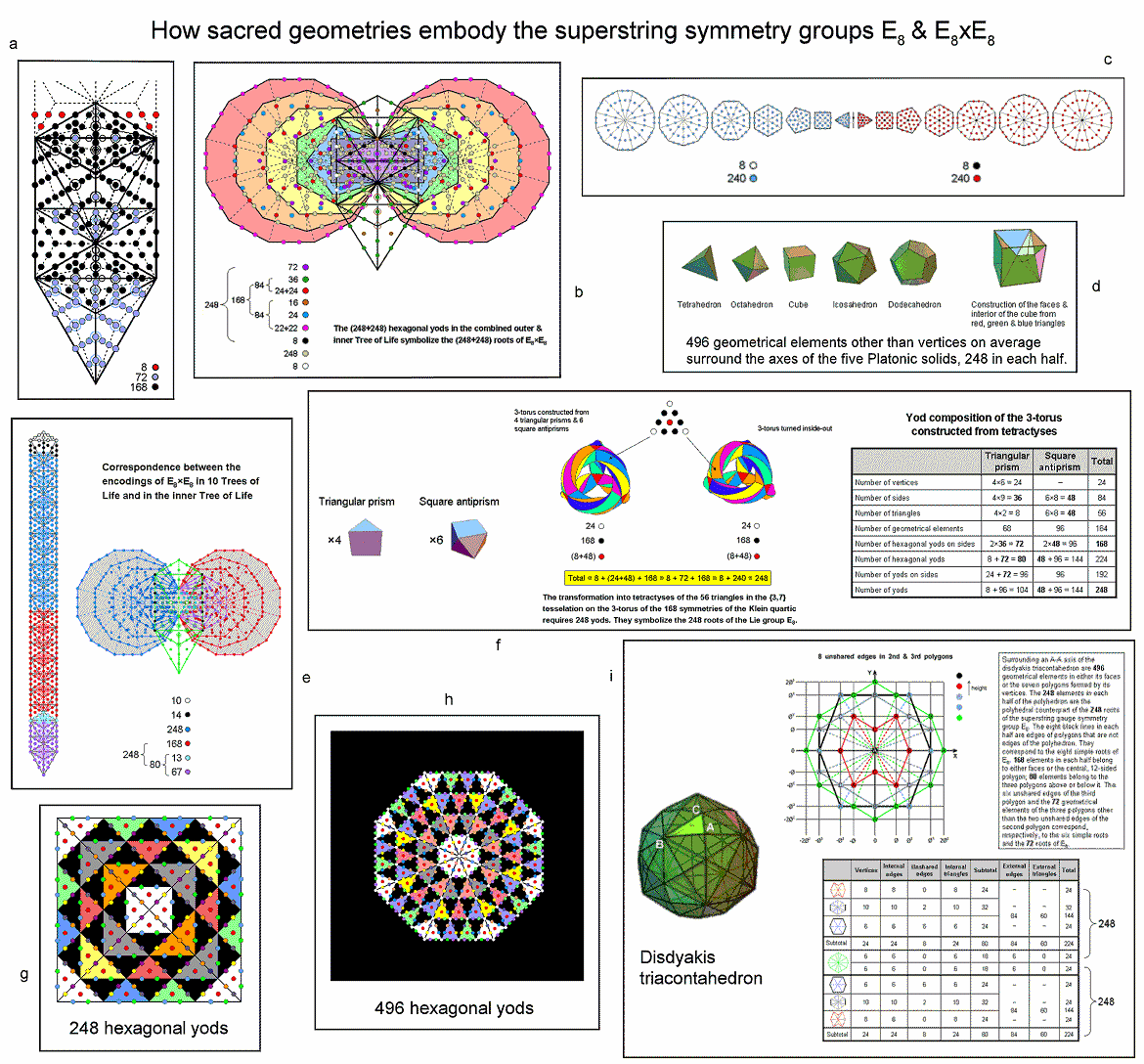
a) 1-tree
The 1-tree is the lowest Tree in any set of overlapping Trees of Life. When its 19 triangles are Type A, it has 251 yods (see #6). Eleven of these (not shown in the diagram) coincide with SLs of the 1-tree. As well as the 240 yods that are not SLs, there are four red yods below the apex of the 1-tree on either side of the central Pillar of Equilibrium. Below the top of the 1-tree are 248 yods, where 248 is both the number value of Raziel, the Archangel of Chokmah, and the dimension of E₈, the rank-8, exceptional Lie group. The eight yods outside the 1-tree and below its apex denote the eight simple roots of E₈ and the 240 yods that are not SLs denote its 240 roots.

The trunk of the Tree of Life is the sequence:

point (Kether)
line (Chokmah-Binah Path)
triangle (Chesed-Geburah-Tiphareth)
tetrahedron (Netzach-Hod-Yesod-Malkuth)

When all triangles are Type A, the trunk contains 80 yods, where 80 is the number of Yesod, i.e, 70 yods other than SLs. The "root" of the Tree of Life is the pair of hexagonal yods on the Path connecting Daath and Tiphareth whose projection onto the plane of the (7+7) enfolded polygons of the inner Tree of Life is their root edge. The root and trunk of the Tree of Life contain 72 blue yods. They denote the 72 roots of E₆, the rank-6 exceptional subgroup of E₈. The remainder of the 1-tree (its "branches") contains 168 black yods. They denote the remaining 168 roots of E₈. See further discussion here.

b) Outer & inner Trees of Life
The outer Tree of Life with its 16 triangles turned into tetractyses contains 70 yods. Of these, 10 yods coincide with SLs at the corners of these tetractyses, leaving 60 hexagonal yods. The inner Tree of Life with the 94 sectors of its (7+7) enfolded polygons turned into tetractyses contains 444 hexagonal yods. Two pairs of hexagonal yods lying on each side pillar coincide with hexagonal yods in the two hexagons when the outer Tree of Life is superimposed on its inner form. The number of hexagonal yods in the combined outer & inner Trees of Life = 60 − 4 − 4 + 444 = 496. This is the dimension of E₈×E₈, one of the two gauge symmetry groups that require a dimension of 496 in order to describe superstring forces that are free of quantum anomalies. Each hexagonal yod denotes a root of E₈×E₈, associated with which is a gauge boson that transmits the unified, E₈×E₈ heterotic superstring force. This embodiment of its 496 roots is discussed in detail here.

c) (7+7) separate polygons of the inner Tree of Life
With their sectors turned into tetractyses, the two sets of seven separate polygons contain 480 hexagonal yods surrounding their centres. Four yods lie on the separate root edge, so that two hexagonal yods are added to this straight line. Such transformation of the 14 polygons and a separate line denoting their root edge, therefore, requires (480+14+2=496) new yods. 248 such yods are associated with each set of seven polygons. They include the seven centres and one hexagonal yod in the separate root edge. These eight yods (either black or white) denote the eight simple roots of E₈. The 240 red or blue hexagonal yods added by the transformation of each set of polygons denote its 240 roots. The mirror symmetry of the distribution of yods in the root edge and the two sets of polygons is responsible for the direct product nature of E₈×E₈. This is how the inner Tree of Life in its expanded form encodes the root composition of one of the two possible symmetry groups describing superstring forces.

d) Five Platonic solids
When their 50 faces are divided into their 180 sectors, their face-centres and vertices are joined to their centres and the resulting internal triangles divided into their sectors, the five Platonic solids are composed (other than their vertices) of 2480 points, lines & triangles that surround axes drawn through their centres and two opposite vertices. On average, 496 geometrical elements other than vertices surround the axis of a Platonic solid, 248 elements making up each half. See here & here for detailed analysis.

e) Inner Tree of Life & 10 Trees of Life
Ten overlapping Trees of Life contain 520 yods when their triangles are tetractyses (see #24). This is the number of yods in the (7+7) enfolded polygons outside their root edge when their 94 sectors are tetractyses. There are 248 yods up to Chesed of the fifth Tree, which is the 31st SL, and 496 yods up to (but excluding) Chesed of the tenth Tree. The seven yods on each side pillar of the outer Tree of Life coincide with yods in each hexagon. Each set of seven polygons has five centres that are not also corners of polygons. The number of unshared yods outside the root edge that surround these10 independent centres = 520 − 7 − 7 − 5 − 5 = 496. Each set of seven polygons contains 248 unshared yods that surround their independent centres. They symbolize the 248 roots of E₈. The mirror symmetry of both the outer Tree and the two sets of polygons making up its inner form is responsible for the repetition of the Lie group E₈ in the direct product E₈×E₈ with dimension 496. See here for more discussion.

f) 3-torus & its inside-out version
The 3-torus can be constructed from four triangular prisms and six square antiprisms. When the 56 triangles making up their faces are tetractyses, the 3-torus contains 248 yods, as does its version turned inside-out. 496 yods are needed to construct the 3-torus and its inside-out version. It is discussed here.

g) Square with 2nd-order tetractyses as sectors
When its sectors are 2nd-order tetractyses, a square contains 248 coloured hexagonal yods. Each hexagonal yod symbolizes one of the 248 roots of E₈, the rank-8, exceptional Lie group. E₈×E₈ heterotic superstring theory predicts that 248 gauge bosons transmit the unified force between superstrings of ordinary matter. It is discussed here.

h) Octagon with 2nd-order tetractyses as sectors
When its sectors are 2nd-order tetractyses, an octagon contains 496 coloured hexagonal yods. Each yod symbolizes one of the 496 roots of either SO(32) or E₈×E₈ — the two symmetry groups governing anomaly-free interactions between superstrings. It is discussed here.

i) Disdyakis triacontahedron
The disdyakis triacontahedron has 62 vertices, 180 edges & 120 triangular faces. It has three types of vertices: A, B & C. The 60 vertices that surround an axis passing through two opposite A vertices lie in seven parallel sheets that are perpendicular to this axis. The vertices form the shapes of various n-gons. There are 496 points, straight lines & triangles surrounding the axis that make up either the faces of the disdyakis triacontahedron or the sectors of the seven internal polygons formed by its 60 vertices. The 248 geometrical elements making up each half of the polyhedron include eight sides of polygons that are not polyhedral edges. They are indicated in the diagram by black lines. These sides correspond to the eight simple roots of E₈. The correspondence between the root composition of E₈×E₈ and the geometrical composition of the disdyakis triacontahedron and its seven internal polygons is analyzed further here.

j) 2-d Sri Yantra

j

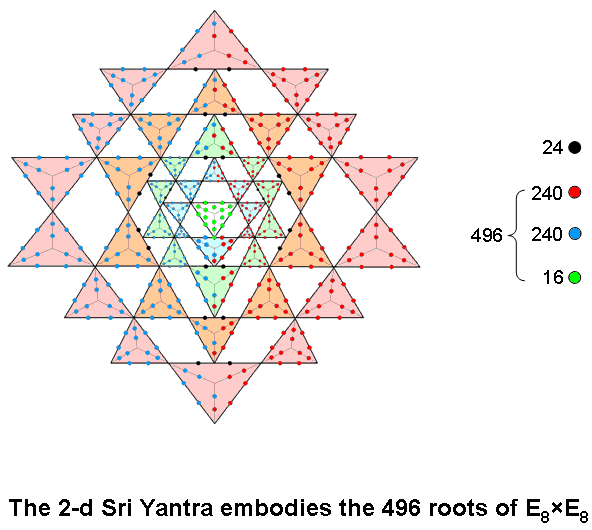
According to Table 8 in Article 35, when its 43 triangles are transformed into Type A triangles, the two-dimensional Sri Yantra contains 757 yods. 756 yods surround the bindu point at its centre. Of these, 16 green yods belong solely to the central triangle (its two upper corners are also corners of the innermost set of eight triangles, so that green yods denoting yods exclusive to the central triangle are not assigned to them). According to this table, 504 hexagonal yods line the 252 sides of the 126 tetractyses in the 42 triangles surrounding the central one. The tips of some of these triangles touch 12 of their sides. From a strict, mathematical point of view, these particular sides are not single, straight lines but pairs of lines joined at the tip of another triangle. This leaves (252–12=240) true sides (i.e., single, straight lines) with 480 hexagonal yods. These yods cannot be divided into two sets of 240 that are mirror images of one another, if the mirror is horizontal, because three of the four sides excluded from the layer of ten blue triangles in Figure 1 of Article 35 (or see here) belong solely to its upper half, creating an imbalance. However, a mirror symmetry persists after excluding the 12 sides if the mirror is vertical, because, then, 240 red hexagonal yods and 240 blue hexagonal yods lie either on or, respectively, to the right and left of the vertical axis passing through the centre of the central triangle, which is surrounded by (240+240=480) hexagonal yods on true sides of triangles and 16 yods intrinsic to the central triangle, i.e., 496 yods that symbolize the 496 roots of  E₈×E₈.The 24 hexagonal yods lining sides that are touched by other true triangles are coloured black. The two hexagonal yods in the side of the triangle touched by the lowest corner of the central triangle are not black because, although it has the appearance of a triangle, it is, mathematically speaking, not a true, triangular area, the bindu (a separate point) coinciding with its centre. In the 3-dimensional Sri Yantra, the central triangle really is a triangle in the pure, mathematical sense because the bindu hovers above it instead of being embedded in its surface. The 16 green yods in the central triangular perimeter that surround the bindu are intrinsic to it because none of them is shared with any of the 42 triangles distributed around it. They symbolize the 16 simple roots of E₈×E₈. The (240+240=480) hexagonal yods in the 240 single lines making up the true sides of these 42 triangles denote its (240+240=480) roots.

See also the discussion in The holistic pattern of the Sri Yantra under the heading "496 = 248 + 248".

<< Previous    1...   32  33  [34]  35  36  ...56    Next >>

Home