| << Previous 1... 31 32 [33] 34 35 ...56 Next >> |
#33 How sacred geometries embody the superstring structural parameter 1680

| Click here to see a high-resolution PDF version of this picture. |
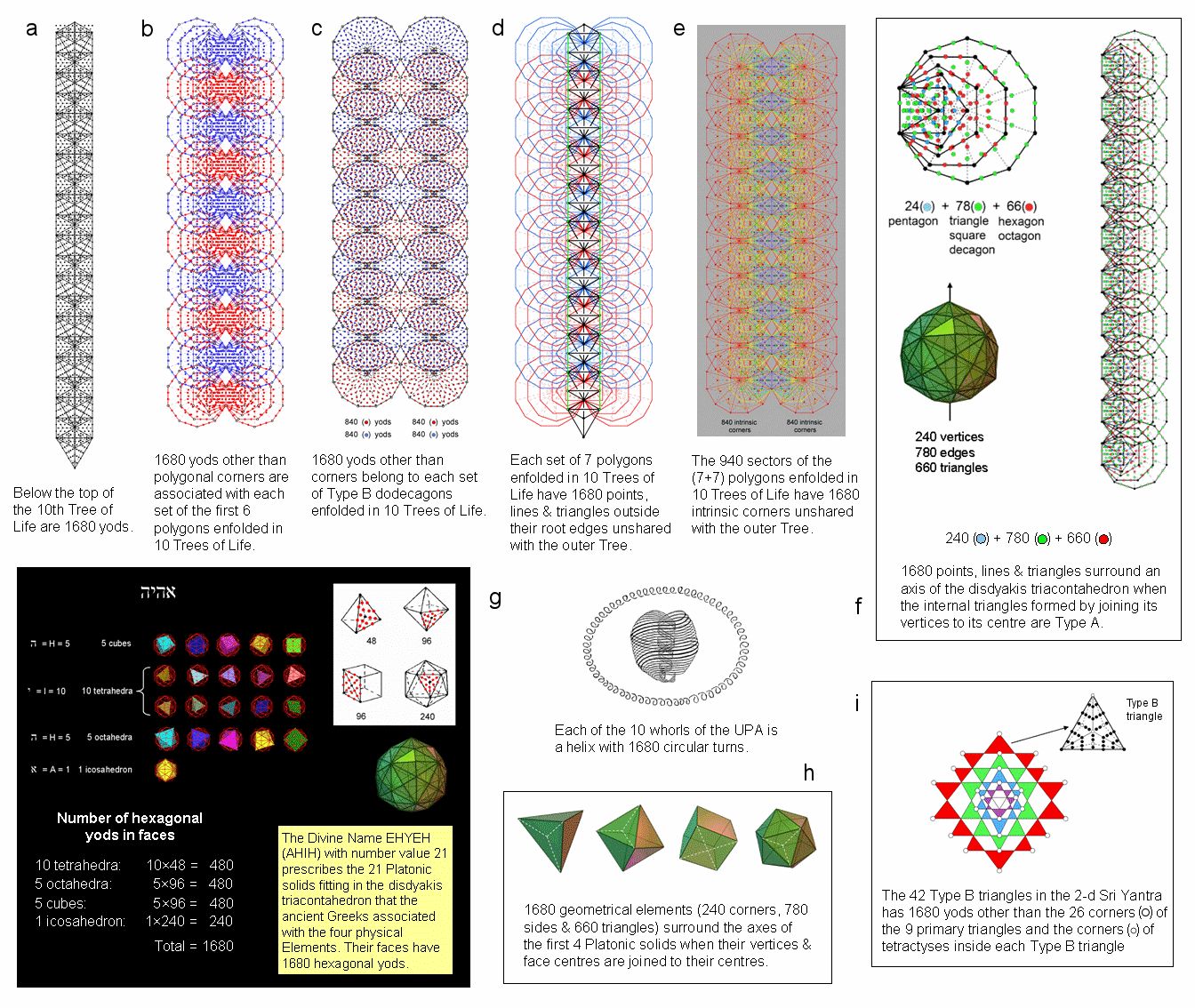
a) ADONAI, the Godname of Malkuth, prescribes the lowest 10 Trees mapping the 10 spatial dimensions of 11-dimensional space-time predicted by M-theory because its number value 65 is the number of SLs in the 10-tree. Below the 65th SL are 1680 yods when all the triangles are Type A. They symbolize the 1680 circular turns of each helical whorl of the UPA, the subquark state of the E8×E8 heterotic superstring remote-viewed by Annie Besant & C.W. Leadbeater (see Occult Chemistry). This Tree of Life representation of each whorl is discussed further in #2.
b) The two sets of the first six enfolded polygons of the inner Tree of Life constitute a holistic system, containing 384 yods unshared with polygons enfolded in the next higher Tree when their 70 sectors are tetractyses. They comprise 48 corners of the 12 polygons and 336 yods. 168 yods other than these corners are associated with each set of six polygons. Associated with each set of 60 polygons enfolded in the 10-tree are 240 corners and 1680 yods. Each yod denotes a turn of a helical whorl of the subquark superstring. This is discussed in #3.
c) The 12 sectors of a Type B dodecagon have 13 corners and 168 other yods. The two joined Type B dodecagons have 24 corners of sectors and 336 yods, 168 yods being associated with each one. Hence, 1680 yods other than such corners are associated with each set of Type B dodecagons enfolded in 10 Trees of Life. See #3 for further discussion.
d) The seven enfolded polygons of the inner Tree of Life comprise 176 corners (points), sides (lines) & triangles. Outside the root edge with two endpoints and a line there are three corners & two lines that coincide with either side pillar of the outer Tree of Life. Therefore, (176−2−1−3−2=168) geometrical elements in each set of seven enfolded polygons outside the root edge are intrinsic to the inner Tree of Life because they are unshared with the outer Tree. Outside the root edges of each set of 70 polygons enfolded in the 10-tree are 1680 intrinsic geometrical elements. This is discussed in #18.
e) The 94 sectors of the (7+7) enfolded polygons have 80 corners. When the polygons are Type B, 94 corners (centres of sectors) are added. Of the 174 corners of the 282 triangles in the (7+7) Type B polygons, six corners coincide with corners of triangles belonging to the outer Tree of Life. This leaves 168 unshared corners that are intrinsic to the inner Tree of Life. The 2820 triangles in the 940 sectors of the (70+70) polygons enfolded in the 10-tree have 1680 intrinsic corners. See also #26.
f) Surrounding an axis of the disdyakis triacontahedron with its edges as sides of internal Type A triangles are 1680 geometrical elements. They comprise 240 corners, 780 sides & 660 triangles. Compare this with the fact that associated with each set of the first six polygons enfolded in the 10-tree are 1680 yods other than their corners that comprise 240 yods in the pentagons, 780 yods in the triangles, squares & decagons and 660 yods in the hexagons & octagons. This is also discussed in #4.
g) 21 Platonic solids that are either tetrahedra, octahedra, cubes or icosahedra can be fitted in the vertices of the disdyakis triacontahedron. They have 1680 hexagonal yods in their faces when the latter are constructed from tetractyses. See further discussion in #5.
h) When their vertices and centres of faces are joined to their centres, the tetrahedron, octahedron, cube & icosahedron have 1680 geometrical elements surrounding axes passing through their centres and two opposite vertices (its centre and any two vertices in the case of the tetrahedron). Like the disdyakis triacontahedron, they, too, comprise 240 corners, 780 sides & 660 triangles. This is analyzed further in #20 & #31.
i) The 2-dimensional Sri Yantra is the result of the overlap of nine primary triangles (see here). 26 of their 27 corners belong to the 42 resulting triangles that surround the central one. When these triangles are Type B, they contain 1680 yods other than these 26 original corners (denoted in the diagram by white yods) and the 168 internal corners (also coloured white) of the 378 tetractyses in these triangles. See #6 discussed at Superstrings as sacred geometry/Sri Yantra.
| << Previous 1... 31 32 [33] 34 35 ...56 Next >> |