#36 A 7-pointed star representation of the superstring structural parameter 16800

It was shown in #13 that 1680 yods surround the centre of a 10-pointed star with a parallelogram as each point whose halves are 2nd-order tetractyses. Replacing each yod in a 2nd-order tetractys by a 1st-order tetractys generates the 3rd-order tetractys. It has 49 yods along each side, where 49 is the number value of EL ChAI, the Godname of Yesod. A parallelogram with 49 yods along each side has (49²=2401) yods. Hence, (7×2400=16800) yods surround the centre of a star whose points are such parallelograms. The side of each 3rd-order tetractys has 15 black gaps between adjacent, grey 1st-order tetractyses. The number of gaps in each 3rd-order tetractys = 1 + 2 + 3 + ... + 15 = 120. Each point contains 240 such gaps, so that the 7-pointed star has 1680 gaps. Each gap is actually a 1st-order tetractys containing seven coloured, hexagonal yods and three white yods at its corners. In the star are (7×1680) coloured, hexagonal yods. As it is composed of 16800 (=10×1680) yods, there remain (3×1680) yods. These are depicted in the diagram opposite as white yods, whether they are corners or hexagonal yods. (A high-resolution image of the 7-pointed star in PDF format is available here). Each yod denotes a circular turn of the 10 whorls of the UPA/subquark superstring. A coloured, hexagonal yod denotes a turn in the seven minor whorls, both the yod and the minor whorl expressing a Sephirah of Construction, whilst a white yod denotes a turn in the three major whorls, both expressing the Sephiroth of the Supernal Triad:

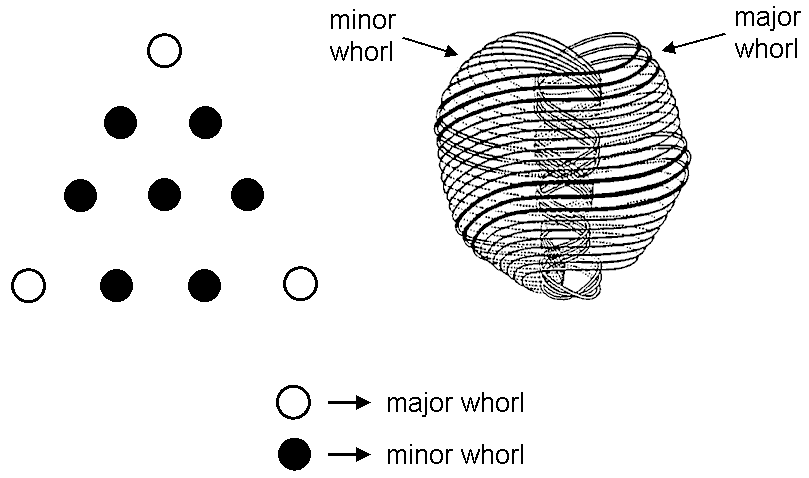
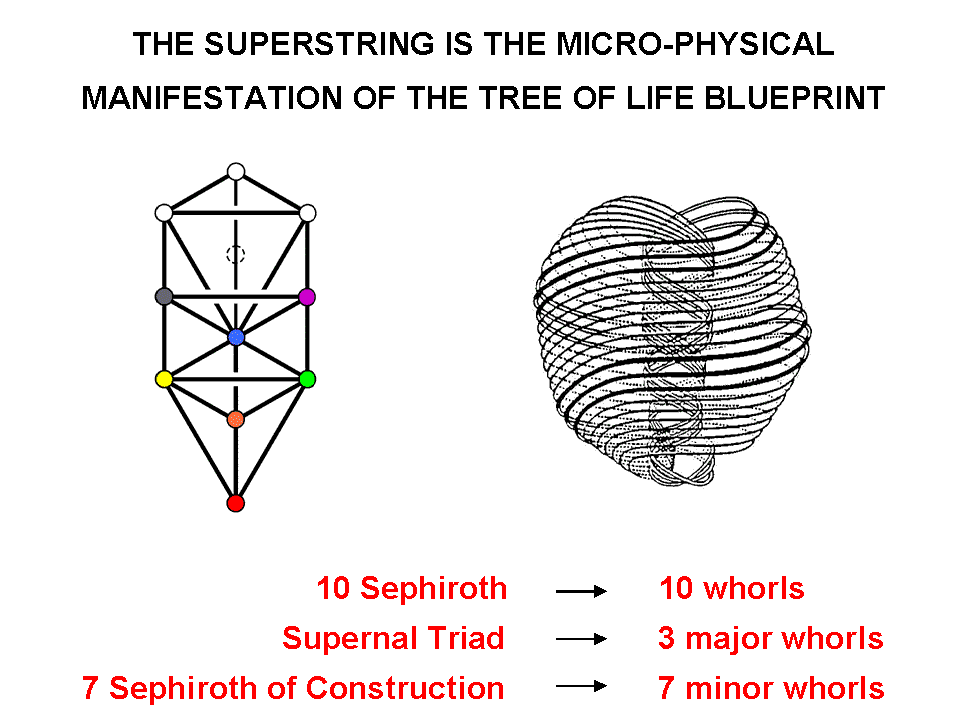
The significance of this representation of the number of 1st-order spirillae in the UPA is that the division of each tetractys into the three yods symbolizing the Supernal Triad and the seven hexagonal yods symbolizing the seven Sephiroth of Construction creates the numbers of spirillae in the major and minor whorls. The fact that the analogous property exists discredits the criticism that the representation is no more than an ad hoc construction because this property would then have to exist purely by chance, which is implausible.

The number of EL ChAI determines the spirilla population of the UPA in the following way: as 49² − 1 = 2400 = 1×2×3×4(1³+2³+3³+4³) and

49 = [1² + 2² + 3² + 4² +… + 24² (=1²×2²×3²×4²)] ⁄(1³+2³+3³+4³),

the number of nth-order spirillae in a minor whorl is

N(n) = 1680×7^n-1 = 240×7ⁿ

    = 49^n/2(49² − 1)/10.

In a universe with exact E₈ gauge symmetry which did not distinguish between the nine spatial dimensions of a superstring, the major and minor whorls of the latter would each contain the same number N(n) of nth-order spirillae, and the number of such spirillae in the UPA would be

10N(n) = 49^n/2(49² − 1)
  =1×2×3×4(1² + 2² + 3² + 4² +…+ 1²×2²×3²×4²)^n/2⁄(1+2+3+4)^n-2.

The number of "bubbles in koilon" (see here) constituting a subquark/superstring constituent of up and down quarks would be 

B ≡ 10N(8) = 1×2×3×4(1³ + 2³ + 3³ + 4³)(1² + 2² + 3² + 4² +… + 1²×2²×3²×4²)⁴⁄(1+2+3+4)⁴⁺⁴

                                                                                                                                               = 13,835,522,400

                 ≈ 10¹⁰ [= (1+2+3+4)^1+2+3+4],

i.e., approximately 10 billion (10¹⁰). This demonstrates the profound connection between the (1+2+3+4=10)-dimensional structure of superstrings and the Pythagorean integers 1, 2, 3 & 4. Notice that even the order of magnitude of B is defined solely by the Pythagorean Decad!

B can also be written as

B = 2400(1+2400)² = 2400×49⁴ = 49⁴(49² − 1) = 49⁶ − 49⁴,

where

is not only the number of space-time components of the 240 gauge fields corresponding to non-zero roots of E₈ but also the number of yods in the 48 Trees representing the cosmic physical plane above the lowest Tree/subplane, which has 80 yods, where 80 is the number of Yesod. In other words, we discover the truly remarkable fact that, if the fourth power of the number 49 of the Godname EL ChAI of Yesod is assigned to every one of the 2400 yods of the 49-tree above the lowest Tree representing its "foundation" (the meaning of Yesod), their sum is the number of bubbles in koilon constituting a superstring in the limit of exact E₈ gauge symmetry! 

 
The 4th-order tetractys shown above has 7³ coloured 1st-order tetractyses in 3rd-order tetractyses that correspond to the 7 Sephiroth of Construction. Each 1st-order tetractys has 7 hexagonal yods symbolizing these Sephiroth. There are (7⁴=49²=2401) hexagonal yods in lower-order tetractyses that symbolize Sephiroth of Construction. 2400 such yods surround the hexagonal yod at the centre of the 4th-order tetractys. This means that 2400 degrees of freedom expressing the six Sephiroth of Construction above Malkuth manifest physically in any holistic system. An example of this is the disdyakis triacontahedron, which has 2400 geometrical elements that surround its axis passing through two opposite vertices when its interior triangles and its faces are Type A triangles (see here). 

Since the number of hexagonal yods in the coloured 1st-order tetractyses in a 4th-order tetractys = 7⁴ = 49² (see diagram above), where 7 is the fourth odd integer, the number of such yods surrounding its centre (one of these hexagonal yods) =  49²  − 1 = 2400. We discover the amazing fact that the number of bubbles in koilon in a superstring in the limit of unbroken E₈ symmetry (that is, when all whorls are minor whorls) is the sum of the fourth power of 49 assigned to every one of the 2400 hexagonal yods that surround the centre of a 4th-order tetractys, where 49 is the square of the fourth odd integer. This demonstrates par excellence the potency of the Pythagorean Tetrad in defining fundamental parameters of nature.

As

49² − 1 = 2400 = 48×50 = 3 + 5 + 7 + ... + 97,

50 = (3+5+7+...+97) ⁄48,

i.e., the number value 50 of ELOHIM is the arithmetic mean of the first 48 odd integers after 1 that add up to 2400, which is both the number of yods in each point of the 7-pointed star discussed above that surround its centre and the number of hexagonal yods in coloured 1st-order tetractyses that surround the centre of a 4th-order tetractys. Therefore,

16800 = 7×2400 = 7(3+5+7+...+97) = 21 + 35 + 49 + ... + 679,

i.e., 16800 is the sum of 48 odd integers, spaced 14 units apart, starting with 21 (the number of EHYEH, the Godname of Kether) and ending with 679, where

679 = (1³+3³+5³+7³+9³+11³+13³)⁄7,

49 = 1 + 3 + 5 + 7 + 9 + 11 + 13

and 97 (the number value of Haniel, the Archangel of Netzach, and the 49th odd integer) is the sum of the Godname numbers of the Sephiroth of the Supernal Triad:

97 = 21 + 26 + 50

  = (1³+3³+5³+7³+9³+11³+13³)⁄(1+3+5+7+9+11+13).

It was pointed out in #1 that 2400 points, lines & triangles surround an axis of the disdyakis triacontahedron when its faces and interior triangles are Type A. This is the sum of the 48 odd integers after 1 up to 97, which is the 49th odd integer. EL ChAI prescribes the number 2400 both geometrically through the 4th-order tetractys and arithmetically through the relation: 49² − 1 = 2400.

Each of the 50 revolutions of the 10 whorls of the UPA comprises 336 circular turns. This number is prescribed by EL, the Godname of Chesed with number value 31, because

 

336 = (12+22+32+...+312) ⁄31.

 

 

This has the following geometrical meaning: the pentagram expresses EL (אל) because, with four yods lining the side of each point, there are 30 yods on its boundary, where 30 is the number value of L (lamed), the value 1 of E (alef) being denoted by the yod at the centre of the star. Assigning the integers 1–31 to these yods (the particular assignment does not matter) generates the number 496 of Malkuth as their sum:

1 + 2 + 3 + 4 +... + 31 = 496.

This is the dimension of SO(32) and E₈×E₈, the two Lie groups describing the unified force between the two types of heterotic superstrings. If, instead, the squares of the integers 1–31 are assigned to these 31 yods, they add up to the same number that assigning the number 336 to each yod would generate:

1² + 2² + 3² + 4² + ... + 31² = 31×336.

Not only can the pentagram be thought of as symbolizing the five revolutions of each whorl of the UPA/subquark superstring, its shape, when compounded from the squares of the first 31 integers, determines the number (336) of circular turns in each revolution of a whorl! This remarkable property demonstrates the connection between this ancient symbol and the form of the subquark superstring.

As 496 =16×31 = 1 + 2 + 3 + ... + 31 and 336 = 16×21, the number 16800 can be written as

16800 = 336×50 = 21×50×496 ⁄31 = 21×50×(1+2+3+4+...+31) ⁄31.

This relates the superstring structural parameter 16800 paranormally derived by the micro-psi observations of Besant & Leadbeater to the dimension 496 of the two symmetry groups SO(32) and E₈×E₈ that were found in 1984 to be free of quantum anomalies (see here). Also:

336×496 = 4²(1²+2²+3²+4²+...+31²) = 4² + 8² + 12² + ... + 124²,

so that

which relates the superstring structural parameter 168 and the dimension 248 of E₈ to the sum of the squares of the first 31 even integers. Here is a beautiful illustration of how the Godname numbers prescribe holistic parameters — in this case two numbers that measure the oscillatory form of superstrings and their forces other than gravity. It constitutes powerful evidence for their archetypal nature. The number 62 is the number value of Tzadkiel, the Archangel of Chesed. Here is a remarkable, chance-defying conjunction of the numbers of the Godname (31) and Archangelic name (62) of the same Sephirah! As 168×248 = 84×496, where 84 = 1² + 3² + 5² + 7² and 496 = 1³ + 3³ + 5³ + 7³, the following arithmetic identity is generated:

(1²+3²+5²+7²)(1³+3³+5³+7³) = 2² + 4² + 6² + ... + 62².

Notice also, using the equation highlighted above in pink, that

16800×248 = 20² + 40² + 60² + ... + 620²,

where 620 is the number of Kether (see its representation by a decagon here). This is related to the number 26 of YAHWEH through:

 6200 = 2² + 3² + 4² + ... + 26²,

  i.e.,

620 = (2²+3²+4²+...+26²) ⁄10.

 As 16800×248 = 168×24800 = 168×6200×2²,

168×6200 = 10² + 20² + 30² + ... + 310²,

so that the superstring structural parameter 168 is determined by the number 31 of EL and the number 26 of YAHWEH:

168 = (10²+20²+30²+...+310²) ⁄(2²+3²+4²+...+26²) = 10²(1²+2²+3²+...+31²) ⁄(2²+3²+4²+...+26²),

and

= (100²+200²+300²+...+3100²) ⁄(2²+3²+4²+...+26²).

This is the total number of circular turns in the 10 whorls of the UPA/subquark superstring. Its inner or outer half comprises 25 revolutions of these whorls with 8400 turns, where

In other words, this superstring structural parameter is prescribed by ADONAI MELEKH, the complete Godname of Malkuth with number value 155 because it is the arithmetic mean of the 31 squares that start with 5², are spaced five units apart and end with 155². The pentagram provides a representation of this Godname number as well as the number 31 of EL (see here). Notice that, as 496 = 16×31 = 1 + 2 + 3 + ... + 31, 16 = (1+2+3+...+31) ⁄31 and 80 = 5×16 = (5+10+15+...+155) ⁄31, i.e., the number 80 of Yesod is the arithmetic mean of the first 31 integers that start with 5, are spaced five units apart and end with 155.

840 = 29² − 1 = 3 + 5 + 7 + ... + 57, i.e., it is the sum of the first 28 odd integers after 1. Therefore, 8400 (=840×10) is the sum of (10×28=280) odd integers, thereby relating the number value 280 of Sandalphon, the Archangel of Malkuth, to the number value 155 of the Godname of this Sephirah. Also, 8400 = 30×280 and 16800 = 60×280. It means that assigning the number 280 to the 30 yods lining a pentagram and to the 30 internal yods surrounding its centre generates the superstring structural parameter 16800 established by C.W. Leadbeater (see here). The number 8400 assigned to its boundary and interior correspond, respectively, to the 8400 turns in the outer half and the 8400 turns in the inner half of the 10 whorls of the UPA:

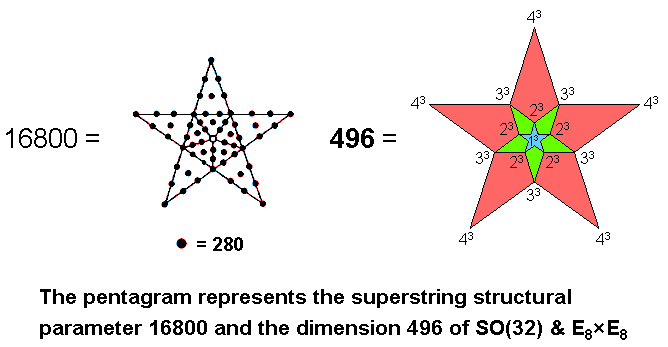
This is how the boundary of the pentagram corresponds to the outer half of the UPA and its interior corresponds to its inner half. Assigning the cubes of 1, 2, 3 & 4 to the centre and points of two pentagrams nested within a third one generates as their sum the dimension 496 of SO(32) and E₈×E₈, the two Lie groups describing superstring interactions that are free of quantum anomalies. We see here how the Godname and Archangel of Malkuth determine the numbers describing the form of the subquark state of the heterotic superstring — the Malkuth aspect of the microscopic Tree of Life.

<< Previous    1...   34  35  [36]  37  38  ...56    Next >>

Home