
| << Previous 1... 29 30 [31] 32 33 ...56 Next >> |
#31 The five Platonic solids embody the root composition of the five exceptional Lie groups G2, F4, E6, E7 & E8

Suppose that the 50 faces of the five Platonic solids are divided into their sectors and that their 50 vertices and 50 face-centres are joined to their centres. Sides of sectors are sides of triangles inside the polyhedra with vertices and their centres at their corners. For consistency with the division of all F polygonal faces of a Platonic solid with V vertices and E edges into their nF sectors (n = 3, 4 or 5), these internal triangles must be divided likewise into their three sectors, i.e., regarded as Type A triangles. Tabulated below are the numbers of non-vertex corners, sides & triangles in their faces and interiors that surround their axes, each axis consisting of two vertices and two sides of internal triangles:
| Corners | Sides | Triangles | Total | |
| Faces: | F | E + nF | nF | E + F + 2nF |
| Interior: | E + nF | V − 2 + F + 3E + 3nF = 4E + 3nF | 3E + 3nF | 8E + 7nF |
| Total: | E + F + nF | 5E + 4nF | 3E + 4nF | 9E + F + 9nF |
(Euler's formula for a polyhedron: V − E + F = 2 has been used to simplify expressions). Tabulated below are the numbers of:
The numbers of non-vertex corners, sides & triangles in the faces and interiors of the five Platonic solids that surround their axes.
| Platonic solid |
Faces |
Interior | |||||||||||
| C | S | T | Subtotal | c | s | t | Subtotal | c′ | s′ | t′ | Subtotal | Total | |
| Tetrahedron (n = 3) | 4 | 18 | 12 | 34 | 6 | 24 | 18 | 48 | 12 | 36 | 36 | 84 | 166 |
| Octahedron (n = 3) | 8 | 36 | 24 | 68 | 12 | 48 | 36 | 96 | 24 | 72 | 72 | 168 | 332 |
| Cube (n = 4) | 6 | 36 | 24 | 66 | 12 | 48 | 36 | 96 | 24 | 72 | 72 | 168 | 330 |
| Icosahedron (n = 3) | 20 | 90 | 60 | 170 | 30 | 120 | 90 | 240 | 60 | 180 | 180 | 420 | 830 |
| Subtotal = | 38 | 180 | 120 | 338 | 60 | 240 | 180 | 480 | 120 | 360 | 360 | 840 | 1658 |
| Dodecahedron (n = 5) | 12 | 90 | 60 | 162 | 30 | 120 | 90 | 240 | 60 | 180 | 180 | 420 | 822 |
| Total = | 50 | 270 | 180 | 500 | 90 | 360 | 270 | 720 | 180 | 540 | 540 | 1260 | 2480 |
ELOHIM, the Godname of Binah with number value 50, prescribes the 50 faces of the five Platonic solids because they are composed of 500 (=50×10) points, lines & triangles other than their 50 vertices. Including the latter, their faces consist of 550 geometrical elements, where 550 =10×(1+2+3+4+5+6+7+8+9+10), showing how the Decad determines the geometrical composition of the regular polyhedra. According to the table, 2480 points, lines & triangles are needed to construct the five Platonic solids, given their vertices. This is the number of geometrical elements that surround their axes, each of which contains three points and two lines. Amazingly, as the unified superstring force with E8 symmetry is transmitted by 248 vector gauge fields, each with 10 space-time components, these fields have 2480 vector components. To every such component, there is a corresponding geometrical element in the five Platonic solids that lies outside the axis and is not a vertex. 248 is the number value of Raziel, the Archangel of Chokmah. YAHWEH, the Godname of this Sephirah, prescribes the dimension of E8 because it is the arithmetic mean of the squares of the integers after 1 up to 26, which is the number value of YAHWEH:
248 = (22 + 32 + 42 + ... + 262)/25.
On average, 248 geometrical elements other than vertices in each half of a Platonic solid surround its axis. The following evidence indicates that this property of the five Platonic solids is not due to coincidence. The five exceptional groups are G2 (dimension = 12+2), F4 (dimension = 48+4), E6 (dimension = 72+6), E7 (dimension = 126+7) & E8 (dimension = 240+8), where "N+n" means that the group has N roots and n simple roots. As G2≤F4≤E6≤E7≤E8, the geometrical counterpart in the five Platonic solids of an exceptional group must contain all the geometrical elements corresponding to a smaller, exceptional subgroup. The table shows that inside the solids and surrounding their axes are 1260 geometrical elements other than vertices that belong to triangles having some sides that are sides of sectors of their faces. 1260 is the number value of Tarshishim, the Order of Angels assigned to Netzach. They include (180+540=720) points & lines. Of these, the table indicates that (120+360=480) points & lines belong to the first four Platonic solids, which contain 120 points. Compare the correspondence between the roots of the five exceptional groups and the numbers of elements in the Platonic solids:
G2: 12 roots ↔ 120 internal points in the first four Platonic solids;
F4: 48 roots ↔ 480 internal points & lines in the first four Platonic solids;
E6: 72 roots ↔ 720 internal points & lines in the five Platonic solids;
E7: 126 roots ↔ 1260 internal points, lines & triangles in the five Platonic solids;
E8: 248 roots ↔ 2480 points, lines & triangles in the five Platonic solids.
We see that not only do the five Platonic solids have 2480 geometrical elements other than vertices surrounding their axes but they also are composed of sets of elements that are ten times the numbers of roots in the four exceptional subgroups of E8. This cannot as well be the result of chance! Rather, the more sensible conclusion to be drawn is that — whatever the reason for this — an isomorphism exists between the geometrical composition of the five Platonic solids and the root composition of E8 and its exceptional subgroups. Given that these famous polyhedra have been shown in the pages of this website to constitute a holistic system with features analogous to other sacred geometries, it should not be surprising that the number 2480 manifests in their geometrical composition. This remarkable analogy serves to demonstrate that superstring theory is part of the holistic pattern embodied in these geometries.
The icosahedron is the fourth Platonic solid. It has (20+60=80) points & triangles in its faces. It also has 80 points in its faces and in internal triangles formed by sides of their sectors. Intuitively speaking, the latter seems the more likely counterpart of the eight simple roots of E8 because they are all points, whereas the former number mixes points with triangles, i.e., two categories of geometrical elements. It is easily verified by combining the various numbers in the table that no other Platonic solid has a combination of 80 geometrical elements of the same kind. The 60 corners of the internal triangles of the icosahedron formed by the sides of the 60 sectors in its 20 faces are the counterparts of the six simple roots of E6, whilst the 20 centres of its faces are the counterparts of the two extra simple roots of E8. The remaining 2400 geometrical elements consist of the following:
|
Faces |
Interior (due to edges) |
Interior (due to sides of sectors) |
||||||||||
| Corners | Sides | Triangles | Subtotal | Corners | Sides | Triangles | Subtotal | Corners | Sides | Triangles | Subtotal | Total |
| 30 | 270 | 180 | 480 | 90 | 360 | 270 | 720 | 120 | 540 | 540 | 1200 | 2400 |
As pointed out above, the 720 geometrical elements in the interior triangles generated by the edges correspond to the 72 roots of E6. The (480+1200=1680) geometrical elements in the faces and in the interior triangles generated by the sides of sectors of faces correspond to the remaining 168 roots of E8. This website has given many examples of the 72:168 division of the parameter 240 embodied in sacred geometries (see The holistic pattern and here). It re-appears naturally in the geometrical composition of the five Platonic solids as the 720 internal geometrical elements generated by edges that surround the axes of the five Platonic solids and as the remaining 1680 geometrical elements other than the 80 corners in either the faces of the icosahedron or the internal triangles formed by sides of their sectors. An alternative combination that generates the same division is the 720 triangles in either the faces or inside the polyhedra that are created by sides of sectors: 180 + 540 = 720, for this leaves 1680 geometrical elements as (540+360=900) internal sides and (30+270+90+270+120=780) corners, sides & triangles. In fact, this can be said to be the preferred choice because it generates (apart from the factor of 10) the gematria number values of Cholem and Yesodoth (see analysis below for how this happens in the case of the first four Platonic solids).
The embodiment of the dimension 248 of E8 by the five Platonic solids was discussed in #19. Each half of a Platonic solid on average has 248 geometrical elements other than vertices surrounding its axis. The 38 faces of the first four Platonic solids have 120 sectors with 68 corners and 180 sides, i.e., 248 corners & sides.
Including their 30 vertices, there are (30−8=22) vertices surrounding the axes of the first four Platonic solids. The table above shows that 1658 other geometrical elements surround their axes. The total number of such elements = 1658 + 22 = 1680 = 168×10. This is another fundamental parameter of superstring physics that is yet to be discovered by string theorists, being the number of circular turns that C.W. Leadbeater counted in each helical whorl of the UPA/subquark superstring (see #20 for its discussion in the context of the Platonic solids). Confirmation that this number does not appear by chance in the context of the first four Platonic solids is provided by their composition when their vertices are included:
| Corners | Sides | Triangles | Total |
| 22 + 38 + 60 + 120 = 240 | 180 + 240 + 360 = 780 | 120 + 180 + 360 = 660 | 1680 |
780 (=78×10) sides and (240+660=900=90×10) corners & triangles surround their axes. The number 168 is the gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. The number value of Cholem is 78 and the number value of Yesodoth is 90:
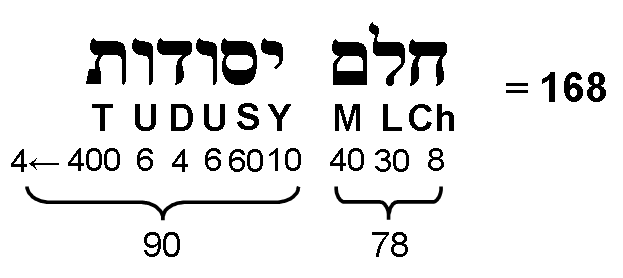
We see that the first four Platonic solids, thought by the ancient Greeks to be the shapes of the particles of the Elements Earth, Water, Air & Fire, not only embody the superstring structural parameter 1680 but also reproduce in their geometrical make-up the number values of the two Hebrew words in the Kabbalistic name of the Mundane Chakra of Malkuth! It is improbable in the extreme that both numbers, as well as their sum, should appear by chance in the geometry of these Platonic solids in such a natural way. Instead, we are witnessing the manifestation in a holistic, geometrical system of the mathematical archetypes embodied in the Kabbalistic system of Godnames, Archangelic Names, Orders of Angels and Mundane Chakras (see here). They determine the properties of all sacred geometries because the latter are isomorphic, so that they possess properties that are quantified by the same numbers — namely, the gematria number values of the Godnames, etc. This is simply illustrated by the fact that the average number of geometrical elements in each half of the first four Platonic solids that surround their axes = 1680/8 = 210 = 21×10, where 21 is the number value of EHYEH ("I am"), the Godname of Kether.
As 132 − 1 = 168 and 13 yods line each side of a parallelogram tiled with 32 tetractyses, the number 1680 is the number of yods surrounding the centre of a 10-pointed star whose "points" are such parallelograms:
.png)
The 320 tetractyses have 240 corners and 1440 hexagonal yods. They are the counterpart of the 240 corners and (780+660=1440) sides & triangles that surround the axes of the first four Platonic solids. Alternatively, the 900 yods in the inner halves of the 10 parallelograms (coloured blue in the diagram above) and the 780 yods in their outer, red halves correspond to the 900 corners & triangles and the 780 sides surrounding the axes. The 900 yods comprise 240 corners & centres of the 10 blue tetractyses and 660 other yods. They correspond to the 240 corners and 660 triangles that surround the axes of the first four Platonic solids. The 10-pointed star constructed from tetractyses is a representation of the geometrical composition of these solids.
#12 at Superstrings as sacred geometry/Disdyakis triacontahedron proves that, when the 180 internal triangles formed by joining the vertices of the disdyakis triacontahedron to its centre are divided into their sectors, there are 1680 corners, sides & triangles surrounding any axis that passes through two diametrically opposite vertices. They consist of 240 corners, 780 sides & 660 triangles. This is remarkable, for the table above indicates that the same numbers of corners, sides and triangles surround the axes of the first four Platonic solids! The reason for this is simple: both holistic systems are isomorphic representations of the same archetypal pattern.
The 1680 geometrical elements surrounding the axes of the first four Platonic solids consist (referring to the last table) of 240 points, (180+240+120+180=720) sides & triangles either in their faces or in their interiors formed by their edges and (360+360=720) internal sides & triangles formed by sides of sectors of their faces. This 240:720:720 division has its parallel in the 1-tree, which has 240 yods other than Sephiroth, and the two sets of seven separate Type B polygons making up the inner Tree of Life, each of which contains 720 yods surrounding their centres (see #20 and here). It also manifests in the 10-pointed star constructed from tetractyses as their 240 corners and as the 720 hexagonal yods in each half of the star. The following remarkable correspondences emerge:
| 240 | 720 | 1680 | |
| First four Platonic solids: | 240 corners of triangles surround axes. | 720 sides & triangles in each half surround axes. | 1680 corners, sides & triangles surround axes. |
| 1-tree & (7+7) separate Type B polygons: | 240 yods other than Sephiroth. | 720 yods surround centres of 7 separate Type B polygons. | 1680 yods in 1-tree & (7+7) separate Type B polygons. |
| Disdyakis triacontahedron: | 240 corners of triangles surround axis. | 720 sides & triangles surround axis in each half. | 1680 corners, sides & triangles surround axis. |
| 10-pointed star: | 240 corners of 320 tetractyses surround centre of star. | 720 hexagonal yods in each half of star. | 1680 yods surround centre of star. |
These correspondences between the first four Platonic solids, the 1-tree & (7+7) separate polygons and the disdyakis triacontahedron are also discussed here. Other correspondences in sacred geometries that embody the superstring structural parameter 1680 are discussed in #33. Notice that, when their 30 vertices are included, the first four Platonic solids have 240 corners of triangles surrounding their axes, which contain eight vertices, so that they have 248 corners. Here is how the first four Platonic solids embody not only the superstring structural parameter 1680 but also the very dimension 248 of the exceptional Lie group E8 involved in E8×E8 heterotic superstring theory. The eight vertices on their axes correspond to the eight simple roots of E8 and the 240 corners surrounding them correspond to its 240 roots. Any suggestion by a sceptic that the number 248 could turn up here by chance in conjunction with the number 1680 is implausible in the extreme — particularly so when it is one of four different sacred-geometrical systems that display the same 240:720:720 pattern in their embodiment of this number. Instead, this analogy with the 248 roots of E8 strikingly confirms the superstring nature of the basic constituent of matter paranormally described over a century ago by Annie Besant & C.W. Leadbeater.
| << Previous 1... 29 30 [31] 32 33 ...56 Next >> |