| << Previous 1... 23 24 [25] 26 27 ...81 Next >> |
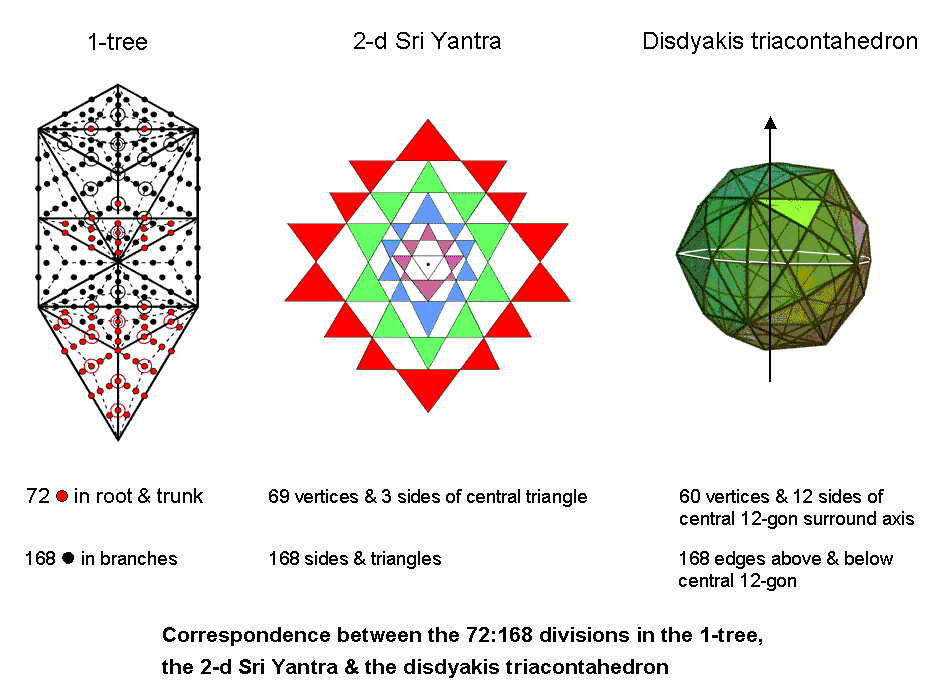
#25 Correspondence between the 72:168 divisions in the 1-tree, the 2-d Sri Yantra & the disdyakis triacontahedron

It was shown on page 34 of Superstrings as sacred geometry/Tree of Life that the 1-tree can be regarded as composed of a root, a trunk & branches. Its root is the Path connecting Daath and Tiphareth, its trunk is the mathematical sequence:
(as discussed in #6), and its branches are the remaining geometrical elements outside its trunk. In terms of the human skeleton, discussed in Article 33, the trunk of the 1-tree is the axial skeleton, the 80 bones in the latter corresponding to the 80 yods in the trunk (10 SLs, 70 yods). There is a pair of hexagonal yods in its root. So the root & trunk contain (70+2= 72) yods other than SLs (Daath is Yesod of the next higher Tree and therefore must be treated as an SL), whilst the branches contain 168 yods (check: 72 + 168 = 240, which is the number of yods in the 1-tree other than SLs).
Compare this with the geometrical composition of the 2-dimensional Sri Yantra. Surrounding its central point are 69 points, three lines of the central triangle, i.e., 72 points & lines, and 168 lines & triangles. Compare this also with the disdyakis triacontahedron. This polyhedron — the outer form of the Polyhedral Tree of Life — has 60 vertices and 180 edges surrounding an axis passing through two diametrically opposite vertices. When the latter are A vertices (the peaks of the 30 pyramids whose Golden Rhombic bases are the faces of a rhombic triacontahedron), the central plane of the disdyakis triacontahedron is a 12-gon with 12 corners and 12 sides. (180−12=168) edges on both sides of it and (60+12=72) vertices & sides surround the axis. The latter is the polyhedral counterpart of the 72 yods in the root and trunk of the 1-tree and the former corresponds to the 168 yods in its branches (see "1-tree" in #6). Intuitively, this makes sense because the vertices of a polyhedron are more fundamental than its edges. Like the literal branches of a tree, the edges of a polyhedron are what gives it its shape. Its vertices do not do this because they are just points in space that can be joined in different ways to create edges. They merely furnish various potential polyhedra, one of which is realized when they are joined together in a certain way. These instances of the number 168 in three sacred geometries illustrate its form-generating meaning as the number value of the Mundane Chakra of Malkuth, the Sephirah denoting the outer, physical form of whatever conforms to the Tree of Life.
| << Previous 1... 23 24 [25] 26 27 ...81 Next >> |