
Disdyakis triacontahedron
| << Previous 1... 19 20 [21] 22 23 ...56 Next >> |
#21 The disdyakis triacontahedron embodies the 5040 1st-order spirillae in the three major whorls of the UPA
Using Euler's formula to simplify the expressions in #20 for the numbers of corners, sides & triangles in a polyhedron with V vertices, E sides and n-gons as its F faces generates the following formulae for the numbers of corners, sides & triangles that surround its centre:
| Corners | Sides | Triangles | Total | |
| Faces: | 2 + E | E + nF | nF | 2 + 2E + 2nF |
| Interior: | E + nF | 2 + 4E + 3nF | 3E + 3nF | 2 + 8E + 7nF |
| Total = | 2 + 2E + nF | 2 + 5E + 4nF | 3E + 4nF | 4 + 10E + 9nF |
The number "2" denotes either the two opposite corners or the two sides shared by some internal triangles that make
up an axis passing through two diametrically opposite vertices and the centre of the polyhedron. The number "4"
denotes the pair of corners and the pair of sides that form this axis. For the disdyakis triacontahedron, E = 180,
F = 120 & n = 3. Its geometrical composition is shown below:
|
|
|
Disdyakis triacontahedron |
Geometrical composition of the disdyakis triacontahedron
| Corners | Sides | Triangles | Total | |
| Faces: | 2 + 180 | 540 | 360 | 2 + 1080 |
| Interior: | 540 | 2 + 1800 | 1620 | 2 + 3960 |
| Total = | 2 + 720 | 2 + 2340 | 1980 | 4 + 5040 |
720 (=72×10) corners surround its axis, where 72 is the number of Chesed. 360 (=36×10) corners in each half surround its axis, where 36 is the number value of ELOHA, the Godname of Geburah. This Godname also prescribes the 360 triangles in its faces. 361 corners in each half surround its centre, where 361 = 192. As 19 is the tenth odd integer, the Decad determines the number of these corners.
According to the table, the disdyakis triacontahedron has 1080 geometrical elements in its 120 faces that surround its axis. This means that, given a point in space as any vertex, another 1081 geometrical elements are needed to construct its faces from triangles. This is the number value of Tiphareth, the central Sephirah of the Tree of Life, of which the disdyakis triacontahedron is the polyhedral counterpart! The meaning of Tiphareth is "beauty," which aptly characterizes the mathematically beautiful properties one would expect to see in such an archetypal object as the outer form of the Polyhedral Tree of Life. As 192 = 361 and 1081 = 1 + 3×360,
3(192 – 1) + 1 = 1081.
192 = 1 + 3 + 5 + 7 +... + 37.
Therefore,
1081 = 1 + 3(3 + 5 + 7 +... + 37),
i.e., 1081 is the sum of (1 + 3×18 = 55) odd integers, where
1
2 3
55 = 4 5 6
7 8 9 10 .
55 is both the tenth triangular number and the tenth member of the well-known sequence of Fibonacci numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ....
Of the 720 corners surrounding the axis, 60 are vertices of the polyhedron, leaving 660 (=66×10) corners. As 66 is the 65th integer after 1, ADONAI, the Godname of Malkuth with number value 65, determines the integer that measures the number of new points in space needed to construct the disdyakis triacontahedron.
990 triangles are in each half of the polyhedron, where
990 = 10(102 – 1) = 10(3 + 5 + 7 +... + 19),
showing once again how the Decad determines its properties.
(720+2340=3060) corners & sides surround the axis of the disdyakis triacontahedron. Each half has 1530 (=153×10) corners & sides. ELOHIM SABAOTH, the Godname of Hod with number value 153, prescribes the polyhedron. Of the 3060 corners & sides, 60 corners are vertices of the polyhedron and 180 sides are its edges. (3060 – 60 – 180 = 2820 = 282×10) corners & sides are generated. 282 is the number value of Aralim, the Order of Angels assigned to Binah.
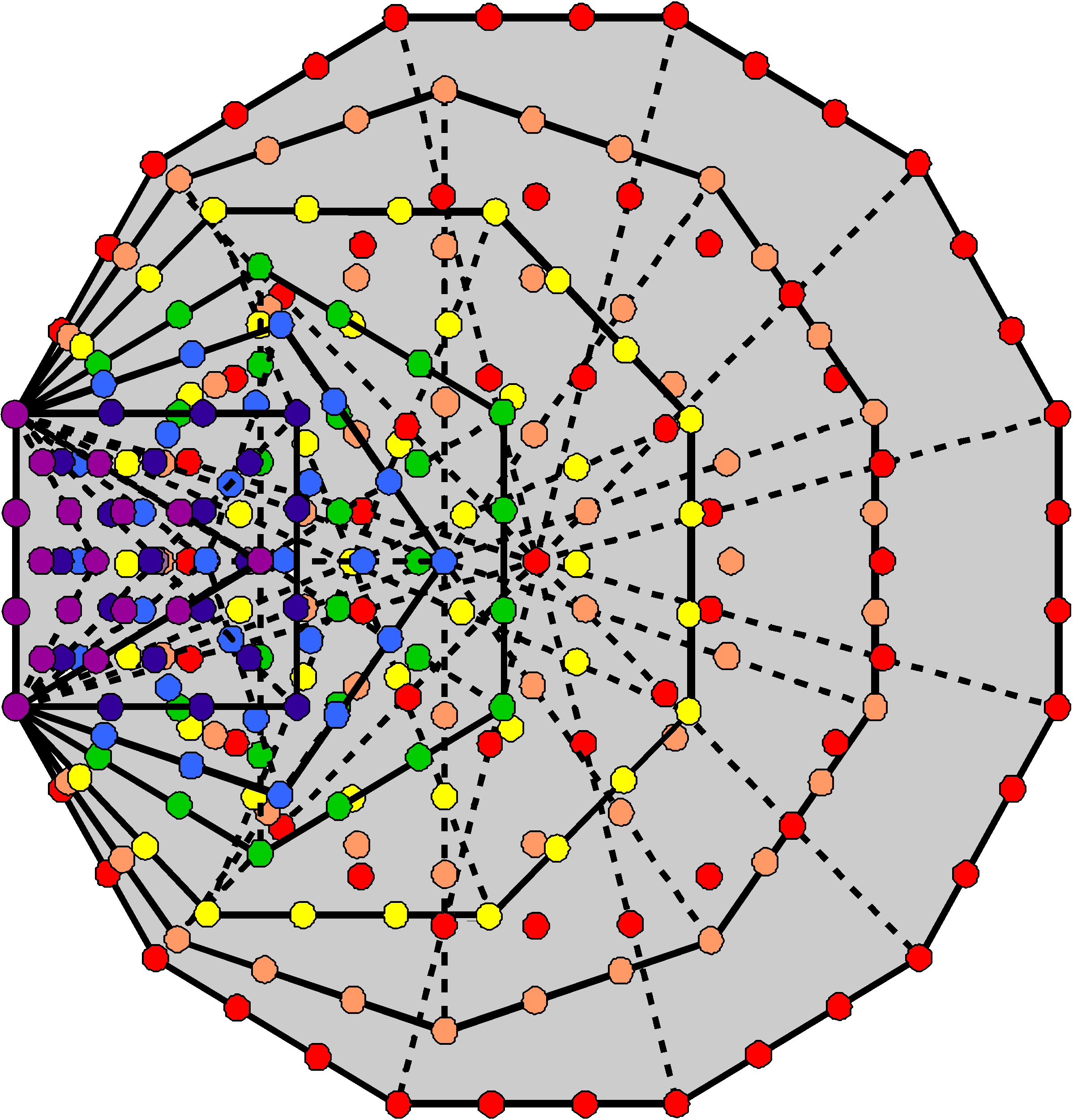
(720+1980=2700) corners & triangles surround the axis. Of these, 60 are vertices, leaving 2640 (=264×10) generated corners & triangles. 264 is a defining parameter of the inner form of the Tree of Life, being the number of yods in its seven enfolded polygons when their 47 sectors are tetractyses:
The 120 faces in the disdyakis triacontahedron comprise 540 (=54×10) sides and 360 (=36×10)
triangles, i.e., 900 (=90×10) sides & triangles. This demonstrates the archetypal 36:54
pattern of the Lambda Tetractys (see here). It is further evidence for the unique status of this polyhedron as the
outer form of the Polyhedral Tree of Life.
The disdyakis triacontahedron has 4320 sides & triangles surrounding its axis. Each half of the polyhedron contains 2160 (=216×10) sides & triangles, where 216 is the number of Geburah. The gematria numbers of both the name and Godname of this Sephirah determine the geometrical composition of the disdyakis triacontahedron. This is true, of course, for every Sephirah, as the numbers of the Sephiroth in the four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah & Assiyah constitute a complete, mathematical description of a holistic system.
There are 5040 corners, sides & triangles surrounding the axis of the disdyakis triacontahedron. As pointed out in the discussion of the first four Platonic solids in #20, this is the number of 1st-order spirillae in the three major whorls of the UPA/heterotic superstring. It comprises the 1680 geometrical elements when just its vertices are joined to its centre and the 2×1680 elements added when the centres of its 120 triangular faces divided into 360 sectors are joined to its centre. The arithmetic property:
712 – 1 = 5040 = 3 + 5 + 7 +... + 141
indicates that the number 5040 is the sum of the first 70 odd integers after 1. As
412 – 1 = 1680 = 3 + 5 + 7 +... + 81,
2×1680 = 5040 – 1680 = 712 – 412 = 112×30 = 83 + 85 + 87 +... + 141.
1680 is the sum of the first 40 odd integers after 1 and 2×1680 is the sum of the last 30 odd integers up to 141. As discussed in #15, these relations lead to a natural correspondence between integers and the sacred geometry of the Tree of Life that is revealed by the tetractys. Moreover, as the number of yods in an n-gon with 2nd-order tetractyses as its n sectors = 72n + 1, where "1" denotes its centre, we see that a 70-gon has (70×72 =5040) yods surrounding its centre. Remarkably, not only the first 70 odd integers after 1 add up to 5040 but a 70-gon has this number of yods surrounding its centre when its sectors are 2nd-order tetractyses! The value n = 70 is the only value of n for which 72n = (n+1)2 − 1 =(n+2)n. It shows the uniqueness of the number 5040 as the complete measure of the geometrical composition of the Polyhedral Tree of Life. Shown below is a heptagon (regular 7-gon) with 504 yods surrounding its centre:
We found in #20 that 2520 geometrical elements surround the axes of the five Platonic solids. This is what each half of the disdyakis triacontahedron has surrounding its axis. Its display of the holistic parameter 252 demonstrates its identity as the outer form of the Polyhedral Tree of Life. As each helical whorl of the UPA consists of 840 turns in its outer 2½ revolutions around its spin axis and 840 turns in its inner 2½ revolutions, the three major whorls comprise (840×3 = 2520) turns in their outer and inner halves. The disdyakis triacontahedron is the complete, polyhedral manifestation of this structure, only partially realized in the five Platonic solids in the sense that their 2520 geometrical elements are analogous only to the 2520 turns in either the outer or inner halves of the three major whorls.
If one or more other polyhedra possessed the same property of having 5040 geometrical elements surrounding its axis, this would undermine the claim that it is evidence of the holistic nature of the disdyakis triacontahedron. Let us examine the issue in the context of the 13 Archimedean solids and their duals — the Catalan solids (the two extra enantiomorphs in each class can be ignored as they have the same numbers of edges and faces as their chiral partners, so that they must be composed of the same number of geometrical elements as their partners). The formula (10E+9nF) for the number of geometrical elements surrounding the axis of a regular polyhedron needs to be modified in the case of polyhedra having several polygons as their faces. This is done by replacing the term "nF" by "∑niFi, where ni is the number of sectors of Fi similar faces and the summation is over all types of faces, the sectors of a regular or irregular polygon being determined by joining its corners to its centroid. It is not immediately obvious from inspection of the modified formula whether another polyhedron can have as many geometrical elements as the disdyakis triacontahedron because, although it has the most edges, another polyhedron might exist that has faces with a larger, total number of sectors. The table below lists the numbers of geometrical elements for the Archimedean and Catalan solids. Each row contains an Archimedean solid and its dual, and they are listed in order of increasing number of faces of Catalan solids so as to leave the disdyakis triacontahedron at the bottom of the list for convenience of inspection.
Number of geometrical elements surrounding the axes of the Archimedean & Catalan solids.
|
Archimedean solid |
Faces |
Edges E | 10E + 9∑nF |
Catalan solid |
Faces |
Edges E |
10E + 9∑nF | ||
| truncated tetrahedron | 8 | 4 triangles 4 hexagons |
18 | 504 | triakis tetrahedron | 12 | 12 isosceles triangles | 18 | 504 |
| cuboctahedron | 14 | 8 triangles 6 squares |
24 | 672 | rhombic dodecahedron | 12 | 12 rhombi | 24 | 672 |
| truncated cube | 14 | 8 triangles 6 octagons |
36 | 1008 | triakis octahedron | 24 | 24 isosceles triangles | 36 | 1008 |
| truncated octahedron | 14 | 6 squares 8 hexagons |
36 | 1008 | tetrakis hexahedron | 24 | 24 isosceles triangles | 36 | 1008 |
| rhombicuboctahedron | 26 | 8 triangles 18 squares |
48 | 1344 | deltoidal icositetrahedron | 24 | 24 kites | 48 | 1344 |
| snub cube | 38 | 32 triangles 6 squares |
60 | 1680 | pentagonal icositetrahedron | 24 | 24 irregular pentagons | 60 | 1680 |
| icosidodecahedron | 32 | 20 triangles 12 pentagons |
60 | 1680 | rhombic triacontahedron | 30 | 30 rhombi | 60 | 1680 |
| truncated cuboctahedron | 26 | 12 squares 8 hexagons 6 octagons |
72 | 2016 | disdyakis dodecahedron | 48 | 48 scalene triangles | 72 | 2016 |
| truncated icosahedron | 32 | 12 pentagons 20 hexagons |
90 | 2520 | triakis icosahedron | 60 | 60 isosceles triangles | 90 | 2520 |
| truncated dodecahedron | 32 | 20 triangles 12 decagons |
90 | 2520 | pentakis dodecahedron | 60 | 60 isosceles triangles | 90 | 2520 |
| rhombicosidodecahedron | 62 | 20 triangles 30 squares 12 pentagons |
120 | 3360 | deltoidal hexacontahedron | 60 | 60 kites | 120 | 3360 |
| snub dodecahedron | 92 | 80 triangles 12 pentagons |
150 | 4200 | pentagonal hexacontahedron | 60 | 60 irregular pentagons | 150 | 4200 |
| truncated icosidodecahedron | 62 | 30 squares 20 hexagons 12 decagons |
180 | 5040 | disdyakis triacontahedron | 120 | 120 scalene triangles | 180 | 5040 |
We notice that an Archimedean solid has the same number of geometrical elements as its dual and that the disdyakis triacontahedron is, indeed, the only Catalan solid with 5040 geometrical elements. Although this is the same as its dual, the truncated icosidodecahedron, it does not mean that we are forced to attribute some holistic status to this Archimedean solid as well, for the possession of a single parameter that characterizes true sacred geometry is a necessary, but not a sufficient, condition for having this status. Notice that the pentagonal icositetrahedron and its dual — the snub cube —have 1680 geometrical elements surrounding their axes. Now, this is the number of turns in each helical whorl of the UPA/subquark superstring, and elsewhere on this website we show how sacred geometries, identified as such for other reasons, embody this structural parameter of the heterotic superstring. But embodying this number does not mean per se that the snub cube possesses sacred geometry. "One swallow does not make a summer," and other properties measured by holistic parameters need to be considered before this status can be conferred upon a polyhedron. True sacred geometry is measured by many holistic parameters, not just one, so that, if only one or two such parameters appear in objects, it will be merely coincidental and they will not possess sacred geometry. This means that, for the purpose of distinguishing sacred geometry from non-sacred geometry, an object must display other holistic parameters — enough of them to eliminate the possibility that their appearance is due to chance. For example, the number 120 is also a holistic parameter, e.g., it is the number of yods on the boundary of the seven enfolded polygons of the inner Tree of Life when their sectors are tetractyses. But the number does not characterize the geometry of the truncated icosidodecahedron, whilst polyhedra that do possess this number, such as the rhombicosidodecahedron and the deltoidal hexacontahedron, do not display another holistic parameter, namely, the number 180. Only the disdyakis triacontahedron exhibits all these numbers (and others, of course), and it is this that makes it unique amongst the Archimedean and Catalan solid in possessing sacred geometry. The sceptic may wish to question the status of these numbers as genuine signatures of sacred geometry, but his doubt is easily expelled by pointing out the chance-defying frequency of their occurrence in examples of sacred geometry which are already historically recognized as such. As pointed out in The holistic pattern, they manifest certain patterns of numbers in a manner that excludes chance as a plausible explanation for their presence. It enables certain numbers to be identified as parameters of holistic systems and to be used as criteria for judging what is —and what is not — an object of sacred geometry. Obviously, one can construct any geometrical object that could possess a given holistic parameter. However, this, alone, does not make the artefact an example of sacred geometry! That special property is bestowed on an object that possesses many such parameters forming well-established patterns of the kind discussed in The holistic pattern. These restrictions eliminate as candidates for sacred geometry all those in which one or two holistic parameters appear by chance that do not fit these patterns.
| << Previous 1... 19 20 [21] 22 23 ...56 Next >> |