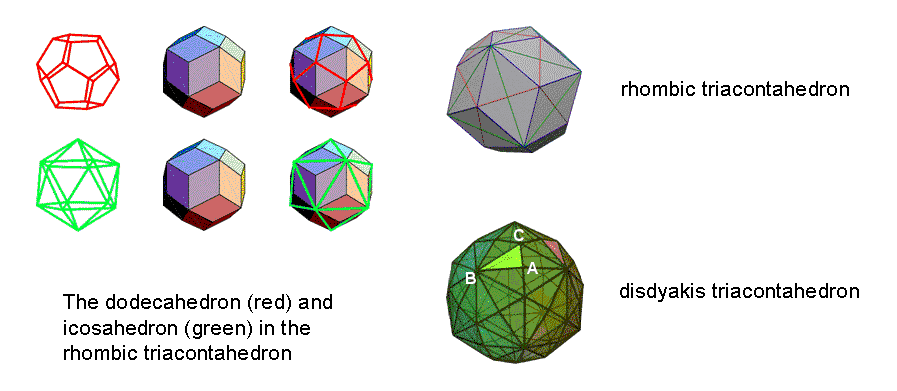
| << Previous 1... 14 15 [16] 17 18 Next >> |
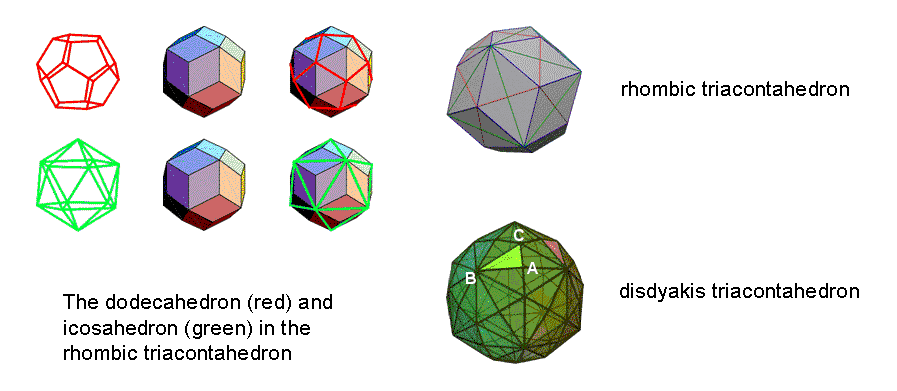
As the outer form of the so-called "Polyhedral Tree of Life" (see here and Article 23), the disdyakis triacontahedron is a polyhedron with 62 vertices, 180 edges & 120 triangular faces. The vertices comprise 30 A vertices, 12 B vertices & 20 C vertices. The 180 edges consist of 60 AB, 60 BC & 60 AC. When its axis is a straight line passing through two diametrically opposite A vertices, there are four B vertices in the central 12-gon (see diagram on previous page) and four B vertices in each half. Hence, there are three sets of four B vertices. The diagram shown opposite indicates that the 12 B vertices are those of an icosahedron with green edges, whilst the 20 C vertices are those of a dodecahedron with red edges, the 32 vertices forming a rhombic triacontahedron with 30 Golden Rhombic faces. Three red edges (AC) of the dodecahedron are associated with each of the 20 triangular, icosahedral faces with three green sides. Hence, the 60 AC edges are composed of three sets of 20 AC edges. Adding them to the three sets of B vertices generates three sets of 24 geometrical elements (four B vertices & 20 AC edges).
Associated with each of the 12 faces of the underlying dodecahedron are five AB edges and five BC edges (see the rhombic triacontahedron). Hence, there are 12 sets of five AB edges and 12 sets of five BC edges. This may be seen as five sets of 12 AB edges and five sets of 12 BC edges, i.e., as five sets of 24 edges (12 AB, 12 BC).
The 20 C vertices consist of ten C vertices in one half of the polyhedron and ten C vertices in its other half. The 28 A vertices surrounding the axis passing through two opposite A vertices comprise 14 A vertices in each half. Hence, (10+14=24) A & C vertices surround the axis in each half.
Surrounding the axis are (60+180=240) vertices & edges. They consist of 72 B vertices & AC edges grouped into three sets of 24 and 168 vertices & edges grouped into seven sets of 24 (two sets of 24 vertices and five sets of edges). In other words, the 240 vertices & edges form ten sets of 24 that divide into groups of 72 and 168. This is the same pattern as that found in Article 53 for the inner Tree of Life, the two Type A dodecagons, the two Type A decagons, the first three Platonic solids and the 2-dimensional Sri Yantra (see also here). The 72:168 division of the holistic parameter 240 is intrinsic to all sacred geometries (see The holistic pattern) because they embody the root composition of the superstring gauge symmetry group E8 and its subgroups, in particular, E6. This tenfold division manifests in the subquark state of the E8×E8 heterotic superstring as the ten whorls of the UPA, along each of which are spread 24 gauge charges of E8. The symmetry breakdown from E8 to E6 appears in the difference between its major and minor whorls, which carry, respectively, the 72 gauge charges of E6 and the 168 remaining gauge charges of E8.
Another way in which the geometrical composition of the disdyakis triacontahedron displays a 10-fold division is analyzed here. How the 1-tree exhibits an analogous 10-fold pattern is discussed here.