In the discussion in Superstrings as sacred geometry of the Tree of Life basis of superstrings, it was shown that the 240 yods lining the sides of the two separate sets of seven enfolded polygons comprise 72 corners and 168 hexagonal yods (see here). This 72:168 division is reproduced in the first three Platonic solids as the 72 hexagonal yods in half of the tetrahedron and half of the octahedron and as the 168 hexagonal yods in their other halves and in the cube (see here). It will be now be shown how this division is embodied in the disdyakis triacontahedron.

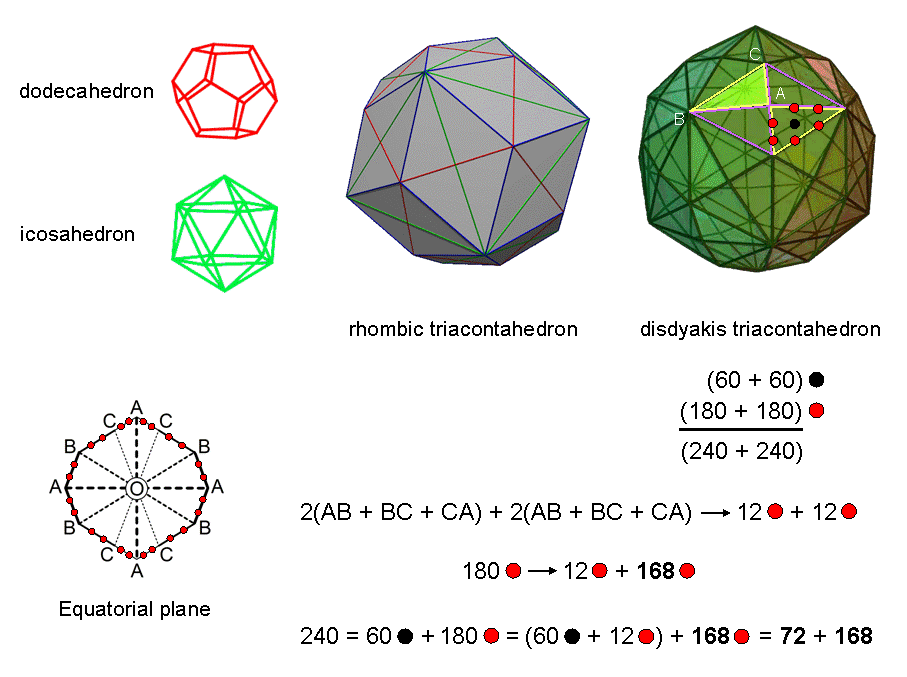
The red and green diagonals of the rhombic triacontahedron are the edges of, respectively, a dodecahedron and an icosahedron. Their lengths are in the proportion of the Golden Ratio Φ = 1.618... . Sticking pyramids on each of the 30 Golden Rhombic bases of the rhombic triacontahedron generates the disdyakis triacontahedron with 62 vertices, 120 triangular faces & 180 edges. When these faces are turned into tetractyses, (180×2=360) red hexagonal yods line their sides and 120 black hexagonal yods are at their centres. Hence, their faces have (120+360=480) hexagonal yods. The 240 hexagonal yods in each half of the polyhedron consist of 60 black hexagonal yods at centres of tetractyses and 180 red hexagonal yods on their 90 sides. The equatorial plane perpendicular to an axis passing through two diametrically opposite A vertices is bounded by a 12-gon with four A, four B & four C vertices and with four AB sides, four BC sides & four CA sides. Each half of the 12-gon has two AB, two BC & two CA sides with 12 red hexagonal yods on them. Therefore, there are (180−12=168) red hexagonal yods on the 84 edges above the equatorial plane and 168 red hexagonal yods on the 84 edges below it. In each half of the polyhedron are (60+12=72) hexagonal yods either lining half of the central 12-gon or at centres of 60 tetractyses. We see that there are (72+168) hexagonal yods in the 60 faces in each half of the disdyakis triacontahedron. This 72:168 division is the single, polyhedral counterpart of the similar division found earlier in the two separate sets of seven enfolded polygons and in the first three Platonic solids. It confirms the archetypal character of this polyhedron as the single, polyhedral version of the universal pattern embodied in holistic systems. The 240 hexagonal yods in each half symbolize the 240 roots of E₈, so that the disdyakis triacontahedron embodies the root composition of E₈×E₈. This is further confirmation of the identification of the UPA as the subquark state of the E₈×E₈ heterotic superstring because, just as each whorl has 1680 circularly polarized oscillations, so, too, the disdyakis triacontahedron has 1680 geometrical elements surrounding any one of its 31 possible axes (see here). The 72 hexagonal yods in each half of the polyhedron denote the 72 roots of E₆, the rank-6 exceptional subgroup of E₈, and the 168 hexagonal yods on edges in each half above or below its equatorial plane denote its remaining roots. The two halves, one the mirror image of the other, correspond to the two similar groups E₈ in the direct product E₈×E₈.

Each of the 30 pyramids in the disdyakis triacontahedron with a Golden Rhombus as its base has four inclined faces that consist of two similar ones outlined in yellow and two similar ones outlined in violet (see picture). The latter are the mirror image of the former. The 60 faces in each half of this polyhedron comprise two sets of 30 triangles. The 60 black hexagonal yods at their centres divide into two sets of 30. The 12 red hexagonal yods on the six sides of each half of the 12-gon consist of two sets of six hexagonal yods because the six sides comprise three different sides that are repeated. Therefore, the 72 hexagonal yods naturally divide into two sets of 36. This is analogous to the 36 corners in each of the two separate sets of seven enfolded polygons making up the inner Tree of Life (see here). The 168 red hexagonal yods on the 84 edges either both or below the equator of the disdyakis triacontahedron are arranged as 84 pairs. This corresponds to the 84 hexagonal yods in each set of seven enfolded polygons. The (36+84=120) yods lining the 42 sides in each set have their counterpart in the disdyakis triacontahedron as the (36+84=120) hexagonal yods in each half of the polyhedron that get duplicated in the second set of 30 faces and in the second set of edges in half the 12-gon.

<< Previous    1...   13  14  [15]  16  17  ...18    Next >>

Home