ARTICLE 53
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
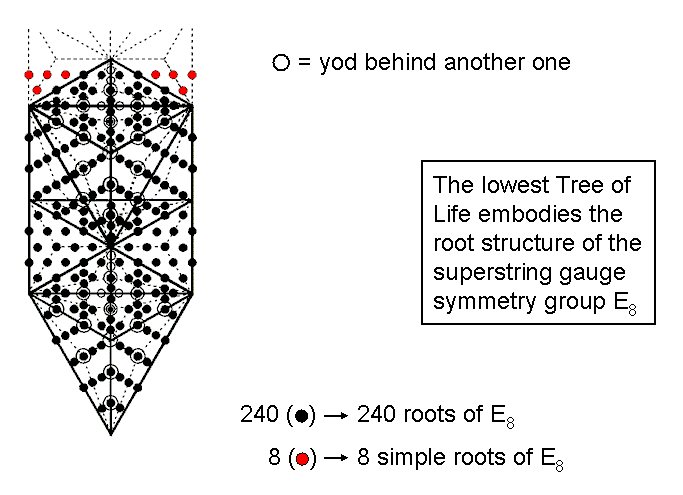
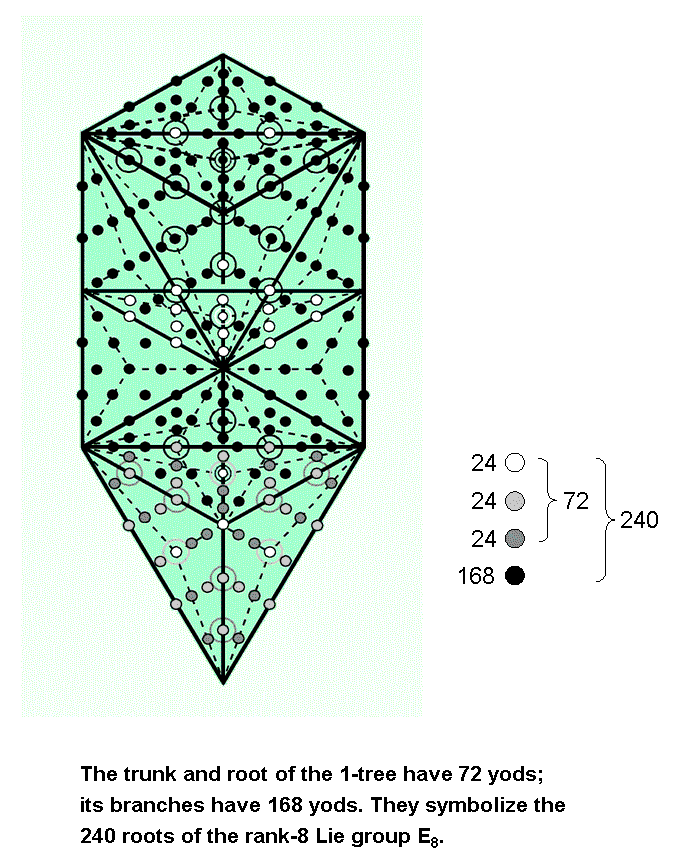
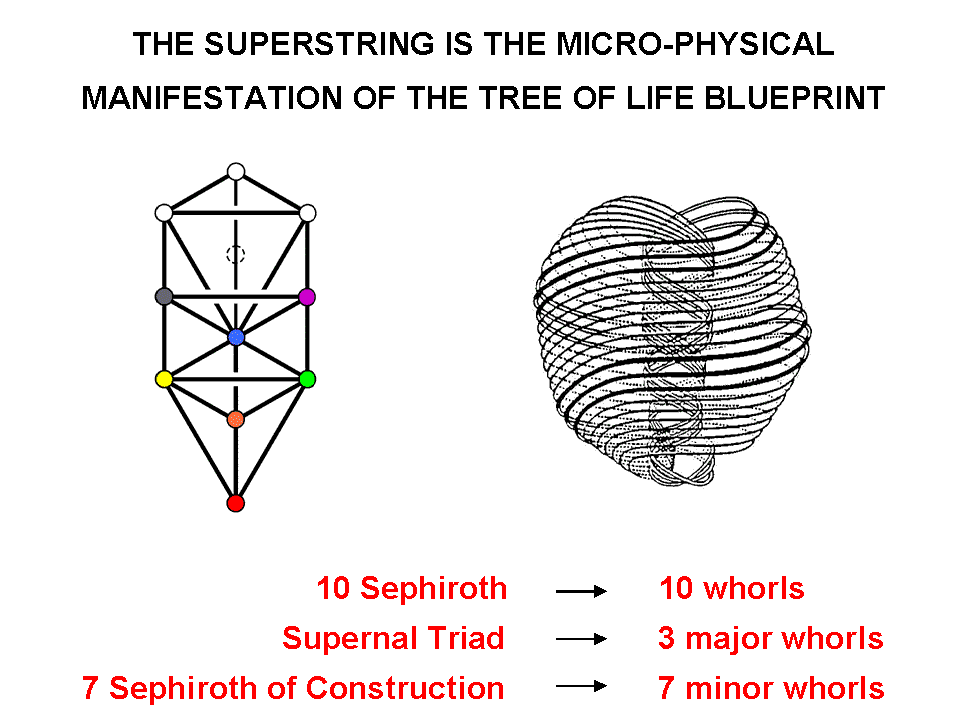
Five sacred geometries , — the inner form of the Tree of Life, the first three Platonic solids, the 2-dimensional Sri Yantra, the disdyakis triacontahedron and the 1-tree — are shown to possess 240 structural components or geometrical elements. They correspond to the 240 roots of the rank-8 Lie group E8 because in each case they divide into 72 components or elements of one kind and 168 of another kind, in analogy to the 72 roots of E6, the rank-6 exceptional subgroup of E8, and to the remaining 168 roots of E8. Furthermore, the 72 components are proved to form three sets of 24 and the 168 components are shown to form seven sets of 24, so that all 240 components form ten sets of 24. Each sacred geometry therefore has a ten-fold division, indicating a similar division in the holistic systems that they represent. The best-known example of this is the Kabbalistic Tree of Life with ten Sephiroth that comprise the Supernal Triad and the seven Sephiroth of Construction. A less well-known example is the "ultimate physical atom," or UPA, the basic unit of matter paranormally described over a century ago by the Theosophists Annie Besant and C.W. Leadbeater. This has been identified by the author as the E8×E8 heterotic superstring constituent of up and down quarks. Its ten whorls (three major, seven minor) correspond to the ten sets of structural components making up each sacred geometry. The analogy suggests that 24 E8 gauge charges are spread along each whorl as the counterpart of each set of 24 components. The ten-fold composition of the E8×E8 heterotic superstring predicted by this analogy with sacred geometries is a consequence of the ten-fold nature of God, which is most explicitly represented in the Tree of Life.
1
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
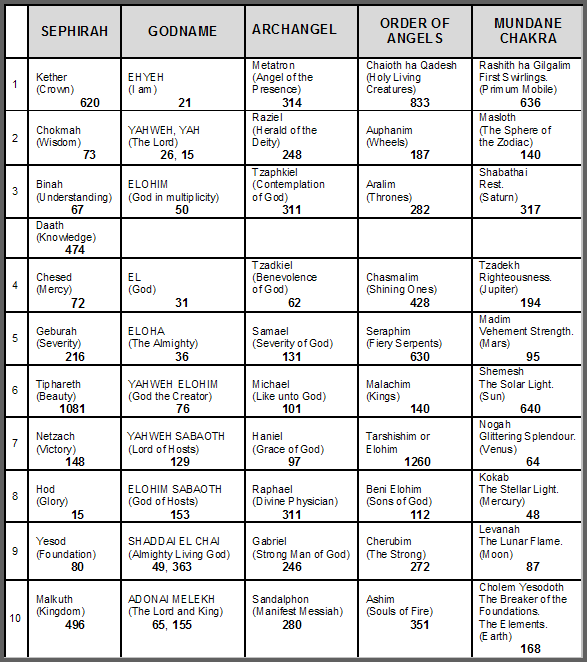
(Numbers in this table referred to in the article will be written in boldface).
2
1. The inner Tree of Life
The 10-fold UPA/superstring as the 10-fold division of the (7+7) polygonsThe 240 roots of the Lie group E8 can be regarded as consisting of the 72 roots that are also roots of its exceptional subgroup E6 and 168 other roots (Fig. 1). When their 47 sectors are tetractyses, the seven enfolded polygons of the inner Tree of Life have 120 yods on their 42 sides, where
120 = 22 + 42 + 62 + 82.
They comprise 36 (= 62) black yods at the corners of polygons and 84 (= 22 + 42 + 82) red hexagonal yods. The two separate sets of seven enfolded polygons have (2×36=72) black yods at their corners and (2×84=168) red hexagonal yods. The distinction between corners and hexagonal yods corresponds to E6

Figure 1. The 72 corners and 168 hexagonal yods on the sides of the two sets of seven enfolded polygons symbolize the 72 roots of E6 and the 168 extra roots of E8.
being a subgroup of E8. This is the sacred geometrical counterpart of the symmetry-breakdown of E8 into E6 that has been considered by superstring theorists in order to reproduce the physics of the Standard Model. Each yod on the boundaries of the polygons symbolizes a root of E8 to which corresponds a gauge charge and its associated gauge boson that mediates the unified force between superstrings.
The group E6 contains the exceptional subgroup F4 with dimension 52. It has four simple roots and 48 roots. As the first six enfolded polygons have 24 corners outside their shared root edge, the counterpart of these 48 roots are the (24+24=48) black yods at the corners of the two sets of the first (6+6) enfolded polygons that are outside their root edges. The two separate dodecagons have (12+12=24) corners. We see that the 72 corners divide naturally into three groups of 24 corners. Do the 168 red hexagonal yods also split up naturally into seven groups of 24? Indeed, they do! Below are shown the numbers of hexagonal yods on the sides of one set of seven enfolded polygons:
triangle square pentagon hexagon octagon decagon dodecagon
4 6 8 10 14 18 24
(the root edge must be associated with the dodecagon because this then generates its 24 hexagonal yods). The 18 hexagonal yods on the sides of the decagon can only be grouped with the six hexagonal yods of the square in order to form a set of 24, the 14 hexagonal yods of the octagon can only be grouped with the ten hexagonal yods of the hexagon and the eight hexagonal yods of the pentagon can only be grouped with the four hexagonal yods of the remaining triangle to generate 24 hexagonal yods in both pairs. Hence, there are two sets of 24 (dodecagons), two sets of 24 (decagon & square), two sets of 24 (octagon & hexagon) and one set of 24 (triangle & pentagon). No other combinations are possible. Amazingly, both the 72 corners and the 168 hexagonal yods group naturally into ten sets of 24 yods. The significance of this for superstrings is as follows: in some of
Figure 2.
3
his research articles on his website, the author identified the UPA described by Besant & Leadbeater as the subquark state of the E8×E8 heterotic superstring. Its ten whorls "carry" the 240 gauge charges of E8 corresponding to the 240 roots of this group. In the spirit of heterotic string theory, 24 gauge charges are regarded as spread out along each whorl. The three major whorls carry 72 gauge charges and the seven minor whorls carry 168 gauge charges. This 72:168 division is precisely what we see in the distinction between the 72 corners and the 168 hexagonal yods on the sides of the two sets of seven enfolded polygons! The corners of a tetractys are analogous to the three major whorls, which are the micro-physical manifestation of the three Sephiroth of the Supernal Triad, and its hexagonal yods correspond to the seven minor whorls, which are the micro-physical manifestation of the seven Sephiroth of Construction (Fig. 2). Remarkably, this analogy extends even to individual whorls, for the ten sets of 24 gauge charges of E8 carried by the ten whorls correspond to the ten sets of corners and hexagonal yods.
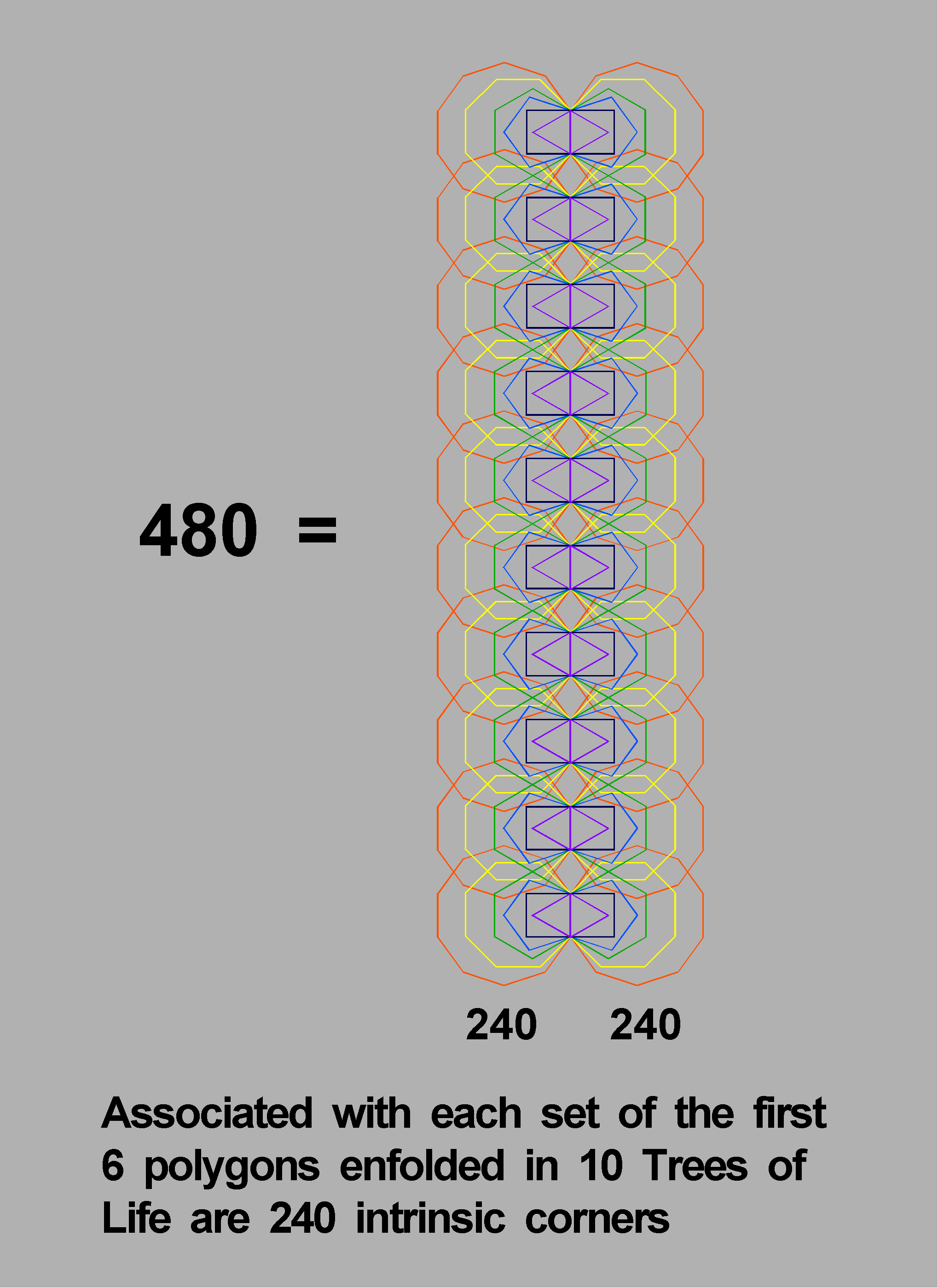
The counterpart in the first six enfolded polygons (which constitute a holistic set in themselves) of each set of 24 gauge charges are the 24 intrinsic corners associated [1] with them. The 60 polygons enfolded in ten overlapping Trees of Life, each mapping a whorl, have 240 associated corners that correspond to the 240 roots of E8 and their associated gauge charges (Fig. 3). The (240+240) intrinsic corners associated with both sets of 60 polygons enfolded in ten overlapping Trees of Life denote the (240+240=480) roots of E8×E8, i.e., the mirror symmetry of the inner Tree of Life is responsible for the direct product nature of the
Figure 3. The (240+240) intrinsic corners of the first (6+6) polygons enfolded in 10 overlapping Trees of Life denote the (240+240) roots of E8×E8.
Each Tree represents one of the 10 whorls of the subquark state of the E8×E8 heterotic superstring.
anomaly-free gauge symmetry group of the unified force between E8×E8 heterotic superstrings.
[1] The two endpoints of the root edge are shared by both sets of seven polygons. One can be associated with one set and one with the other set. The topmost corner of each hexagon coincides with the lowest corner of a hexagon enfolded in the next higher Tree. Both sets of the first six polygons have 50 corners. 25 of them are associated with each set, but only 24 belong exclusively to each one in the sense of being unshared with polygons enfolded in the next higher Tree. In other words, only 24 corners are intrinsic to a set.
4
As
3
5 7 112 − 1 = 120 =
9
11
13
15 17 19 21, i.e., as 120 is the sum of the first ten odd integers after 1, the number 240 is the sum of the ten even integers that start with 6 and are four units apart:
6
10 14
240 = 18 22 26
30 34 38 42 .
In terms of the numbers 1, 2, 3 & 4 symbolized by the four rows of dots in the tetractys, the factorization of 240 as 10×24 is expressed as (1+2+3+4)×1×2×3×4.
As 52 − 1 = 24 = 3 + 5 + 7 + 9, the number 240 is the sum of the tetractys arrays of the first four odd integers after 1:
3 5 7 9
3 3 5 5 7 7 9 9
240 = 3 3 3 + 5 5 5 + 7 7 7 + 9 9 9
3 3 3 3 5 5 5 5 7 7 7 7 9 9 9 9 .
The sum of the 12 odd integers at the corners of these tetractys is 72 and the sum of the remaining 28 odd integers is 168. This is the arithmetic counterpart of the 72 corners and 168 hexagonal yods that line the two sets of the seven enfolded polygons. A beautiful harmony always exists between number and geometry when the latter is sacred. At the end of this article, it is proved that the number 16800 — the number of 1st-order spirillae in the UPA/superstring — is the sum of 240 odd integers.
The 10-fold UPA/superstring as the 10-fold division of the two Type A dodecagons
As 168 extra yods are needed to construct the Type A dodecagon from tetractyses, i.e., it embodies the very number that determines the structure of the UPA/heterotic superstring, it should come as no surprise that the geometry of the dodecagon also embodies the 10-fold pattern of this particle, as now proved.
The pair of Type A dodecagons (Fig. 4) has 24 corners, 24 red sides & 24 blue sides of its sectors, i.e., three sets of 24 geometrical elements. Each sector is divided into three triangles with three green sides and one internal corner (apart from the shared centre of the dodecagon). Hence, the 24 sectors are, additionally, composed of 24 internal corners, three sets of 24 green sides and three sets of 24 triangles, i.e., seven sets of 24 geometrical elements. The two Type A dodecagons, therefore, naturally comprise ten sets of 24 geometrical elements.
These sets are the counterpart of the ten whorls of the UPA/heterotic superstring, each of which carries 24 gauge charges of the superstring gauge symmetry group E8. The three sets of 24 corners & sides that create the 24 sectors of the two dodecagons correspond to the three major whorls of the UPA, each carrying 24 E8 gauge charges. The seven extra sets of 24 geometrical elements needed to turn the dodecagon into a Type A dodecagon correspond to the seven minor whorls, each carrying 24 E8 gauge charges. We saw previously that the 120 yods lining the 42 sides of the seven enfolded polygons divide into ten sets of 12, further divided into three sets (36 corners) and seven sets (168 hexagonal yods). Each yod corresponds to one of the geometrical elements making up the Type A dodecagon.
Figure 4. The two Type A dodecagons.
The 10-fold UPA/superstring as the 10-fold division in the yods on edges of tetractyses in the pair of Type A decagons
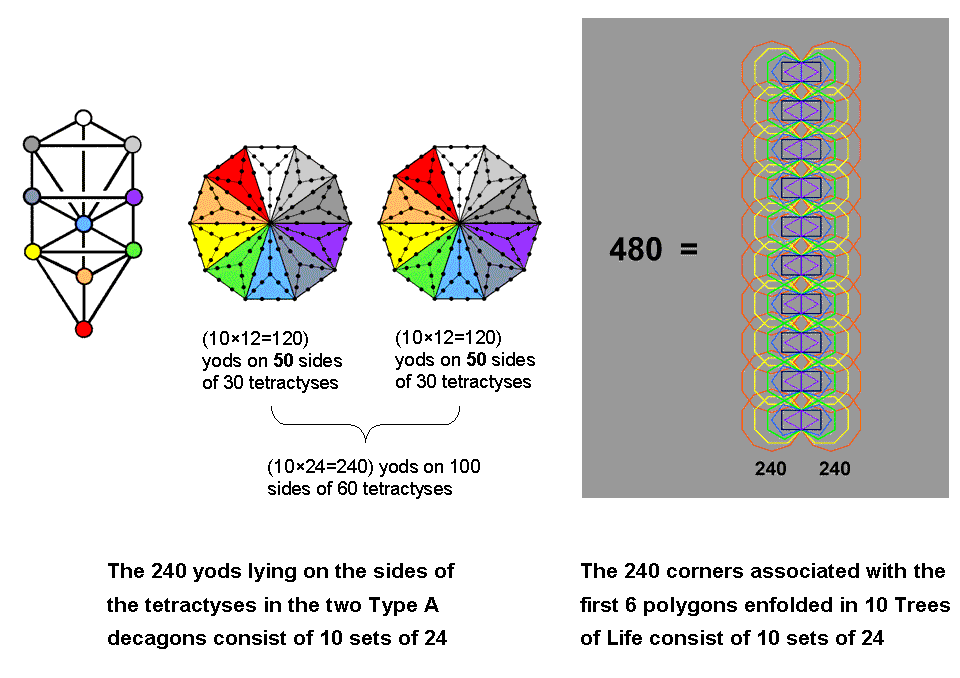
The sixth regular polygon in the inner form of the Tree of Life is the decagon. Constructed from tetractyses, it is the polygonal representation of ten overlapping Trees of Life because its 61 yods correspond to the 61 SLs up to Chesed of the tenth Tree. Each sector is the counterpart of a Tree, the six yods per sector being the counterparts of the six SLs per Tree. The centre of the Type A decagon is surrounded by 120 yods that line the 50 sides of its 30 tetractyses. There are 12 boundary yods per5
Figure 5. The 240 yods on sides of tetractyses in the two Type A decagons correspond to the 240 corners associated with the first six polygons enfolded in ten Trees of Life.
sector. The two Type A decagons have (120+120=240) yods surrounding their centres that line the 100 sides of their 60 tetractyses (Fig. 5). They comprise (12+12=24) boundary yods per pair of sectors. Therefore, the 240 boundary yods consist of ten sets of 24 yods. Three pairs of sectors (coloured white, grey & dark grey) have (3×24=72) boundary yods. The remaining seven pairs of sectors (coloured the seven colours of a rainbow) have (7×24=168) boundary yods. Starting from a point (the centre of a decagon), 240 yods are needed to delineate the tetractyses that make up two Type A decagons, 24 per pair of sectors. This 72:168 pattern is analogous to what was discussed earlier. Instead of ten geometrical elements, each repeated (12+12) times, we now have (12+12) yods that are repeated ten times.
The first six enfolded polygons up to the decagon have 26 corners. One of the corners is an endpoint of the root edge shared not only amongst the six polygons but also with the second set of six polygons — the mirror image of the first set. When sets of polygons enfolded in overlapping Trees of Life are considered, the topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree. This means that 25 corners of a set of six enfolded polygons are intrinsic to them. One corner (an endpoint of the root edge) can be associated with the set and one (the other endpoint) can be associated with the second set. Hence, 24 corners are associated with and intrinsic to the set of six polygons enfolded in each Tree. The 60 polygons of the first six types enfolded in ten overlapping Trees of Life have (10×24=240) corners, that is, 24 corners repeated ten times. This is the inner Tree of Life basis of the 24 E8 gauge charges spread along each whorl of a UPA/subquark.
The Decad defines both the decagon with ten sides and the tenth polygon — the dodecagon. The pair of either polygon embodies ten sets of 24 geometrical elements or yods. Their subatomic counterparts are the 24 E8 gauge charges carried by each of the ten whorls of a UPA, which is the subquark state of an E8×E8 heterotic superstring. Here is yet more evidence provided by sacred geometry of the ten-fold nature of the basic unit of matter paranormally described by Annie Besant & C.W. Leadbeater.
The 10-fold UPA/superstring as the 10-fold division in the 240 hexagonal yods in the seven separate polygons of the inner Tree of Life
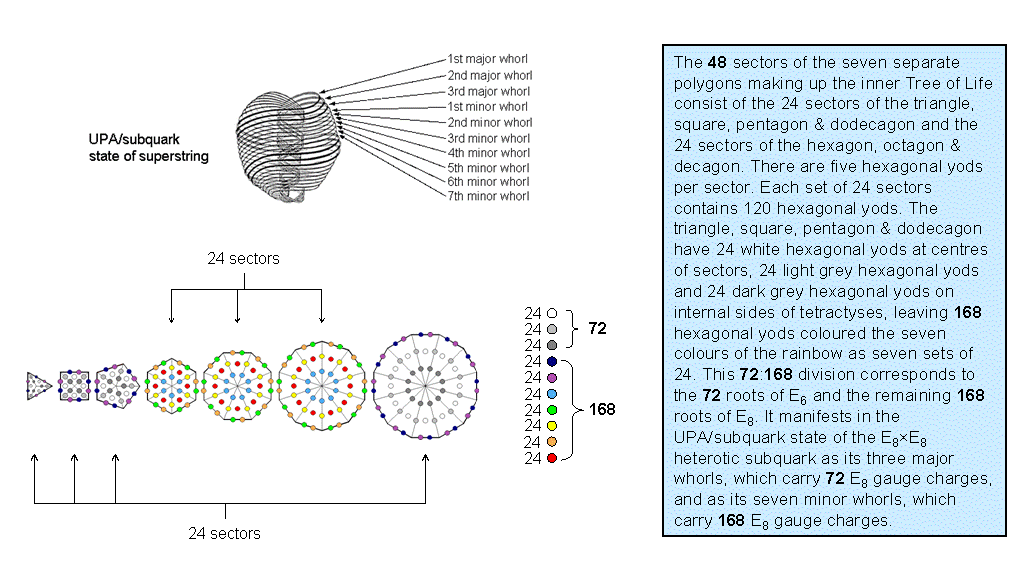
The seven separate polygons of the inner Tree of Life have 48 sectors, where 48 is the number value of Kokab, the Mundane Chakra of Hod (see Table 1). As tetractyses, they contain 240 hexagonal yods that naturally group into ten sets of 24, as now explained.
6
Figure 6. The 24:24 division of the sectors of the seven separate polygons corresponds to the major/minor distinction in the ten whorls of the UPA/subquark state of the E8×E8 heterotic superstring.
As a parameter of holistic systems, the number 48 displays a 24:24 division that always characterizes them. For the seven separate polygons, the triangle, square, pentagon & dodecagon have 24 sectors and the hexagon, octagon & decagon have 24 sectors (Fig. 6). The only other possible combinations of polygons with 24 sectors are firstly, the triangle, pentagon, hexagon & decagon, and secondly, the square, octagon & dodecagon (the two possibilities arise because the triangle and pentagon have the same number of sectors as the octagon). Just as the seven Sephiroth of Construction comprise two triads: Chesed-Geburah-Tiphareth and Netzach-Hod-Yesod, and Malkuth, so research by the author has confirmed that this 3:3:1 pattern is shown by the seven polygons of the inner Tree of Life, i.e., they group into triangle-square-pentagon, hexagon-octagon-decagon & dodecagon. Only the former combinations of polygons respect this grouping because the latter combinations are each taken from both sets of three polygons. Although, arithmetically speaking, either pair of combinations is possible because each combination has 24 corners, the former will be favoured here because it preserves the analogy between the outer and inner Trees of Life. There are five hexagonal yods per sector. Therefore, the 240 hexagonal yods comprise 24 sets of five in the triangle, square, pentagon & dodecagon and 24 sets of five in the hexagon, octagon & decagon. Alternatively, they may be regarded as five sets of 24 and another five sets of 24, i.e., as ten sets of 24. This 5:5 differentiation reflects the division of the Tree of Life into the so-called "Upper Face" spanned by the highest five Sephiroth and the "Lower Face" spanned by the lowest five Sephiroth. It arises here from the primary division of the 48 sectors into two sets of 24.
Figure 6 displays the ten sets of 24 hexagonal yods, the yods in each set having the same colour. Each colour corresponds to one of the ten Sephirah. The white, light grey & dark grey yods correspond to the Supernal Triad, which, being part of the Upper Face, means that these yods belong to the triangle, square, pentagon & dodecagon. The question is: which of the five hexagonal yods in each sector should be coloured white, light grey & dark grey? For overlapping Trees of Life, Kether, Chokmah & Binah of a given Tree become Tiphareth, Netzach & Hod of the next higher Tree, whilst Tiphareth is Malkuth of the next higher Tree, the Sephirah that is symbolized by the hexagonal yod at the centre of a tetractys. These Sephiroth of Construction belong to different triads. Hence, the white, light grey and dark grey hexagonal yods must be, respectively, the central hexagonal yod and the two hexagonal yods either on a side of a polygon or on an internal side of a tetractys. The latter possibility has been chosen here.
The ten sets of 24 hexagonal yods symbolize the ten whorls of the UPA/subquark state of the E8×E8 heterotic superstring. The white hexagonal yods at the centres of the 24 sectors in the triangle, square, pentagon & dodecagon denote the 24 E8 gauge charges carried by the first major whorl, the 24 light grey hexagonal yods denote the 24 E8 gauge charges carried by the second major whorl, the 24 dark grey hexagonal yods denote the 24 E8 gauge charges carried by the third major whorl, etc. The ten-fold pattern of the distribution of hexagonal yods arises from the simple facts that there are five such yods per sector and that the 48 sectors of the seven polygons divide into two sets of 24.
7
2. The Platonic solids
Constructed from tetractyses, the Platonic solids have three types of hexagonal yods: 1. hexagonal yods at centres of tetractyses; 2. hexagonal yods on edges of solids, and 3. hexagonal yods on sides of tetractyses inside the boundaries of faces. Their numbers are calculated and tabulated below:Table 2. Hexagonal yod populations in the faces of the five Platonic solids.
(the numbers of yods are further divided into their two halves in order to indicate the numbers of hexagonal yods in each half of the polyhedron). The first three Platonic solids have 240 hexagonal yods comprising 120 hexagonal yods either at centres of tetractyses or on edges and 120 hexagonal yods on interior sides (Fig. 7). This 120:120 division in the 240 hexagonal yods in the 18 faces of the first three Platonic solids re-occurs in both the icosahedron and the dodecahedron because each half-polyhedron has 120 hexagonal yods. As we saw in Section 1, each of the two separate sets of seven enfolded polygons has 120
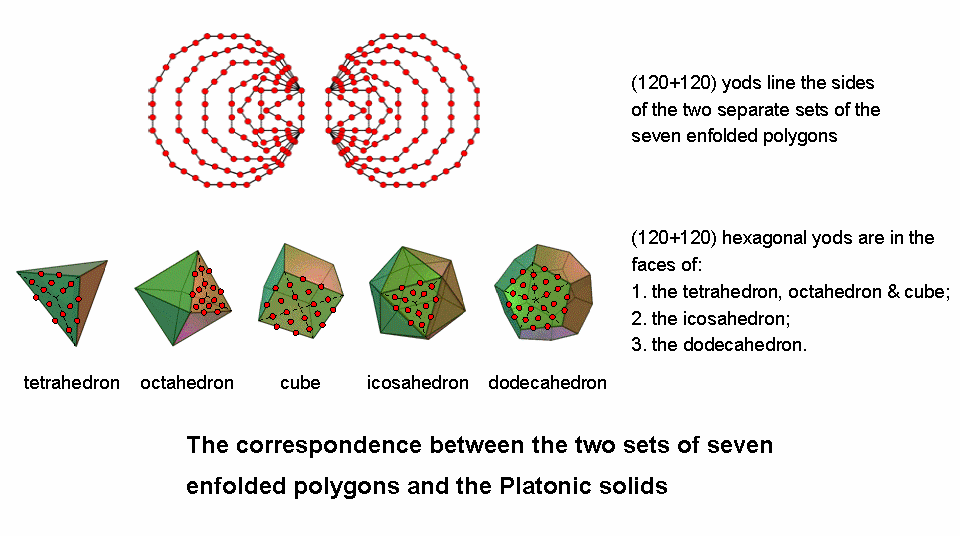
Figure 7
yods on their boundaries. Both sets have 240 yods on their boundaries that comprise 72 corners and 168 hexagonal yods. We saw there that these 240 boundary yods symbolize the 240 roots of the superstring gauge symmetry group E8, the 72 corners denoting the 72 roots of its exceptional subgroup E6, leaving 168 roots represented by the 168 hexagonal yods. The table indicates that their counterparts in the first three Platonic solids are the 72 hexagonal yods in one half of the tetrahedron and the octahedron and the 168 hexagonal yods in their other half and in the cube. The 72:168 division in the holistic parameter 240 manifests in the first three Platonic solids. Moreover, just as the 72 corners were found to be composed of three sets of 24 corners of a unique combination of polygons, so the 72 hexagonal yods consist of 24 hexagonal yods in one half of the tetrahedron, 24 hexagonal yods that either line edges of the octahedron or are centres of tetractyses and 24 hexagonal yods on sides of tetractyses inside the faces of the octahedron. Finally, just as the 168 hexagonal yods on the sides of the two sets of polygons were found earlier to be distributed amongst the polygons in a way that naturally generates seven sets of 24, so, too, Table 2 shows that the 168 hexagonal yods in the other half of the tetrahedron & octahedron and in the cube group naturally into seven sets of 24:
8
1. 24 (6+6+12) hexagonal yods that are in that half of the tetrahedron;
2. 24 (12+12) hexagonal yods that are either centres of tetractyses or line edges of the other half of the octahedron;
3. 24 hexagonal yods that are sides of tetractyses in that half;
4. 24 (12+12) hexagonal yods at centres of tetractyses in the cube;
5. 24 (12+12) hexagonal yods that line its edges;
6. 24 hexagonal yods lining sides of tetractyses in one half of the cube, and
7. 24 hexagonal that line sides in the other half of the cube.(the red numbers are those that appear as such in the table). The mathematical analogy between the two systems of sacred geometries exists because one encodes in the yods shaping the two-dimensional, regular polygons the same pattern as that what exists in the faces of the three-dimensional, regular polyhedra. As with the two sets of seven enfolded polygons, the 240 hexagonal yods in the 18 faces of the tetrahedron, octahedron & cube can be grouped into ten sets of 24. Here, therefore, are two sacred geometries that encode in analogous ways the 10-fold structure of the UPA as ten whorls, each carrying 24 gauge charges of E8. The importance of this discovery for the future development of M-theory cannot be emphasized too strongly. This as yet undiscovered 10-fold composition of the superstring is the manifestation in the subatomic world of the 10-fold nature of God, as represented by both the Tree of Life and Pythagoras' tetractys. Predicting this 10-foldness will be an authentic sign of the validity of any future candidate for the much sought M-theory that unifies the five superstring theories with General Relativity.
The 240 hexagonal yods repeated in the fourth Platonic solid symbolize the 240 roots of the second, similar Lie group E8′ that is part of the gauge symmetry group E8×E8′ governing the unified force between one of the two types of heterotic superstrings. The first four Platonic solids embody not only the dimension 248 of E8 as the 248 corners & sides of the sectors of its faces (see p. 12, Article 3) but also the numbers of roots of E8 and E8×E8′. It has been proved on page 5 at Superstrings as sacred geometry/Platonic solids that 1680 geometrical elements surround their axes when their faces are divided into their sectors and the face centres are joined to the centres of the solids. Here is irrefutable evidence that the UPA paranormally described by Besant & Leadbeater is an E8×E8′ heterotic superstring (actually, an E8'-singlet state), for both the basic structural parameter of the UPA and the root composition of this symmetry group are embodied in the first four Platonic solids symbolising the physical Elements Earth, Air, Fire & Water — a remarkable property that is too implausible to attribute to chance.
It was pointed out in Section 1 that the 48 corners outside the root edge of the two separate sets of the first (6+6) enfolded polygons denote the 48 roots of F4, the rank-4 exceptional subgroup of E6 whose 72 roots are denoted by the 72 corners of the two separate sets of the (7+7) enfolded polygons. What is their counterpart in the first three Platonic solids? Table 2 above indicates that the 72 hexagonal yods in the six faces making up half the tetrahedron and half the octahedron are:
Hexagonal yods Hexagonal yods Hexagonal yods Total
at centres on edges on interior sides
Tetrahedron: 6 6 12 24
Octahedron: 12 12 24 48The 48 hexagonal yods in the four faces in a half of the octahedron denote the 48 roots of F4.
In Section 4, we shall discuss the properties of the disdyakis triacontahedron, the 120-face Cartan solid which was shown in Article 23 to be the outer form of the polyhedral version of the Tree of Life. We shall find that it embodies both these properties in the same way that the first four Platonic solids do, namely, 1680 geometrical elements surround an axis of the disdyakis triacontahedron, whilst 240 hexagonal yods are in the 60 faces making up each half of it when they are turned into tetractyses. Like these Platonic solids, the disdyakis triacontahedron also embodies the number 248 (see Article 44). The re-appearance of the paranormally-obtained structural parameter of the superstring in a polyhedron that Article 23 identified as the outer form of the "Polyhedral Tree of Life" cannot be a coincidence. Instead, it confirms the archetypal nature of this number whose significance awaits discovery by theoretical physicists.
3. The 2-dimensional Sri YantraThe geometrical make-up of the 2-dimensional Sri Yantra (Fig. 8) is tabulated below:
Table 3. Geometrical composition of the 2-dimensional Sri Yantra.
Number of vertices Number of sides Number of triangles Total Central 'triangle' 1 3 0 4 1st group of triangles 4 + 8 = 12 8×3 = 24 8 44 2nd group of triangles 6 + 10 = 16 10×3 = 30 10 56 3rd group of triangles 2 + 10 = 12 10×3 = 30 10 52 4th group of triangles 28 14×3 = 42 14 84 Total 69 129
42 240
9

Mathematically speaking, the central, downward-pointing, white triangle does not count as a true, triangular area (hence the two inverted commas enclosing the word ‘triangle’ in the first row of the table) because the bindu at the centre of the 2-dimensional Sri Yantra is a point that lies in its plane, so that this triangle does not enclose an area of space but is really only three lines and three points, the upper two of which coincide with corners of violet triangles belonging to the first group. The 42 triangles surrounding the centre have 126 sides, i.e., they comprise 168 lines & triangles. Including the lowest corner of the central ‘triangle,’ 69 points surround the centre of the 2-dimensional Sri Yantra. Three straight lines create the shape of the innermost 'triangle.' Hence, the 240 points, lines & triangles that surround its centre comprise (69+3=72) points & lines and 168 lines & triangles. This is the counterpart of the similar 72:168 division manifested by the two separate sets of seven enfolded polygons making up the inner Tree of Life and by the first three Platonic solids. We shall see in the next section that it also appears in the disdyakis triacontahedron — the outer form of the polyhedral Tree of Life. It is the counterpart of the 72 roots of E6 and the remaining 168 roots of E8. Notice that the 168 lines & triangles comprise the 42 lines in the fourth (red) group of triangles and 42 triangles, i.e., 84 lines & triangles, as well as 84 lines in the first three groups. Alternatively, the four groups of triangles in each half of the Sri Yantra comprise 63 sides and 21 triangles, i.e., 84 sides & triangles. This 84:84 division is characteristic of sacred geometries, e.g., in the case of the two sets of seven enfolded polygons discussed in Section 1, there are 84 hexagonal yods on the sides of the polygons in each set.
The first (violet) & third (green) groups of triangles have (12+12=24) vertices. The central ‘triangle’ comprises one unshared vertex and three straight lines. They group into two sets: one that is made up of this vertex and the straight line opposite it and one that comprises the two lines that meet at this point. The second (blue) & fourth (red) groups of triangles have (16+28=44) vertices, i.e., 22 vertices in each half of the Sri Yantra, making two sets of 22 vertices. Combining them with the set of point & line and with the set of two lines creates two sets of 24 vertices & sides. Hence, the 72 points & lines discussed in the previous paragraph divide into three sets of 24:
1. 1st & 3rd groups have 24 vertices;
2. Central ‘triangle,’ 2nd & 4th groups have 23 vertices & one side;
3. Central ‘triangle,’ 2nd & 4th groups have 22 vertices & two sides.
Figure 8. The Sri Yantra.
The third group of triangles has ten sets of three sides and the fourth group has 14 sets of three sides. Together, they form three sets of (10+14=24) sides and one set of (10+14=24) triangles. The first and second groups in the Sri Yantra have (8+10=18) triangles, i.e., nine in each half. The second group has 15 sides in each half. There are therefore (9+15=24) sides & triangles in each half of the first and second groups, as well as a set of 24 sides in the former group. The 168 sides & triangles in the four groups of triangles divide into seven sets of 24:
1. 3rd & 4th groups have set of 24 sides;
2. 1st & 2nd groups have 24 sides & triangles in one half of Sri Yantra;
3. 1st & 2nd groups have 24 sides & triangles in other half of Sri Yantra;
4. 3rd & 4th groups have set of 24 sides;
5. 3rd & 4th groups have set of 24 sides;
6. 3rd & 4th groups have set of 24 sides;
10
7. 3rd & 4th groups have set of 24 triangles;
In conclusion, the 240 geometrical elements surrounding the central bindu in the 2-dimensional Sri Yantra consist of ten sets of 24 elements that divide into three sets of vertices & lines and into seven sets of sides & triangles. They are the counterpart of the three major whorls and seven minor whorls of the UPA/subquark.
4. The disdyakis triacontahedron
As the outer form of the Polyhedral Tree of Life (see Article 23), the disdyakis triacontahedron is a Catalan solid [1] with 62 vertices, 180 edges & 120 triangular faces. The vertices comprise 30 A vertices, 12 B vertices & 20 C vertices (Fig. 9). The 180 edges consist of 60 AB, 60 BC & 60 AC edges. When its axis is a straight line passing through two diametrically opposite A vertices, its central 12-gon is formed by four A, four B & four C vertices. Four B vertices are above this plane and four B vertices are below it. Hence, there are three sets of four B vertices. Figure 8 shows that the 12 B vertices are those of an icosahedron
Figure 9. The rhombic triacontahedron & the disdyakis triacontahedron.
with 30 green edges, whilst the 20 C vertices are those of a dodecahedron with 30 red edges. The 32 B & C vertices forming a rhombic triacontahedron with 30 Golden Rhombic faces. Three AC edges (raised, red half-edges of the dodecahedron) are associated with each of the 20 icosahedral triangular faces with three green sides. Hence, the 60 AC edges are composed of three sets of 20 AC edges. Adding them to the three sets of B vertices generates three sets of 24 geometrical elements (four B vertices & 20 AC edges):
1. 4 B vertices in upper half & AC edge associated with 20 icosahedral faces;
2. 4 B vertices in central 12-gon & AC edge associated with 20 icosahedral faces;
3. 4 B vertices in lower half & AC edge associated with 20 icosahedral faces.
Associated with each of the 12 faces of the underlying red dodecahedron are five green half-edges, which become raised into five AB edges, and five blue edges, which are BC edges (see the rhombic triacontahedron). Hence, there are 12 sets of five AB edges and 12 sets of five BC edges. This may be seen as five sets of 12 AB edges and five sets of 12 BC edges, i.e., as five sets of 24 edges (12 AB & 12 BC).
The 20 C vertices consist of 10 C vertices in one half of the polyhedron and 10 C vertices in its other half. The 28 A vertices surrounding the axis passing through two opposite A vertices comprise 14 A vertices in each half. Hence, (10+14=24) A & C vertices surround the axis in each half, i.e., there are two sets of 24 A & C vertices.
There are therefore seven more sets of 24 geometrical elements: two sets of 24 A & C vertices and five sets of 12 AB & 12 BC edges.
Surrounding the A-A axis of the disdyakis triacontahedron are (60+180=240) vertices & edges. They consist of 72 B vertices & AC edges grouped into three sets of 24 and 168 vertices & edges grouped into seven sets of 24 (two sets of 24 vertices and five sets of edges). In other words, the 240 vertices & edges form ten sets of 24 that divide into groups of 72 and 168. This is the same pattern as found earlier for the inner Tree of Life, the two Type A dodecagons, the two Type decagons, the first three Platonic solids and the 2-dimensional Sri Yantra. It is intrinsic to all sacred geometries because they embody the root
[1] Catalan solids are the duals of the 13 different Archimedean solids created by replacing their vertices with faces and vice versa.
11
composition of the superstring gauge symmetry group E8 and its subgroups, in particular E6. This fundamental 10-fold division manifests in the subquark state of the E8×E8 heterotic superstring as the ten whorls of the UPA described by Besant & Leadbeater. The symmetry breakdown from E8 to E6 appears in the difference that Leadbeater reported between the major and minor whorls, which carry, respectively, the 72 E8 gauge charges of E6 and the remaining 168 gauge charges of E8. The major whorls are made thicker by the inclusion of an extra (n+1)th-order spirilla in every 25 nth spirillae, so that, instead of the latter being composed of 175 (n+1)th-order spirillae (as in the minor whorls), in a major whorl they contain 176 (n+1)th-order spirillae, where n = 1-6).
10-fold geometrical composition of the disdyakis triacontahedronArticle 27 showed that, when both the internal triangles and the faces of the disdyakis triacontahedron are Type A triangles, 2400 corners, sides & triangles surround any axis passing through two diametrically opposite vertices (see Table 1, p. 4). It will now be proved that the 10-fold division of vertices & edges found above for this polyhedron extends to its total geometrical composition. In other words, the 2400 geometrical elements divide naturally into ten sets of 240 elements that divide further into three sets of 240 and seven sets of 240. The meaning of this 10-fold division is that, associated with the 240 roots of E8 are 240 gauge fields, each with ten components, so that 240 components of these fields are defined by each of the 10 dimensions of superstring space-time. Each geometrical element making up the disdyakis triacontahedron that surrounds its axis therefore bears a formal correspondence to a component of the 240 gauge fields of E8.
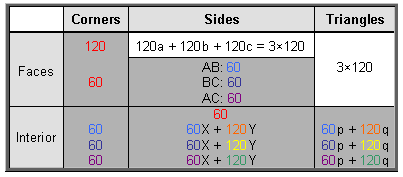
Figure 10 shows one of the 120 faces with centre O. a, b & c are the internal sides of its three sectors that terminate, respectively, on A, B & C vertices. It also depicts an internal triangle with polyhedral vertices at two corners and the centre of the polyhedron at its third corner. The three sides meeting at O′ are of two types: one (X) that terminates on a vertex and one (Y) that ends at the centre. The three sectors of an internal triangle are of two types: one (p) that has a polyhedral edge as one side and two (q) that do not have an edge as a side. The edges are of three types: AB, BC & AC. As the disdyakis triacontahedron has 180 edges, there are 60 edges of each type, each one generating in an internal triangle two X sides & one Y side, one triangle of class p & two triangles of class q, as well as a centre O′. Table 4 shows the numbers of geometrical elements in the faces and interior of the polyhedron that surround its axis:
Table 4. Geometrical composition of the disdyakis triacontahedron.
In the faces are three sets of 120 sides and three sets of 120 triangles, i.e., three sets of 240 sides & triangles, or 720 (=72×10) geometrical elements. There are also 120 corners that are centres of faces and 60 vertices, as well as 60 sides joining the latter to the centre of the polyhedron. These form a set of 240 corners & sides. There are three sets of 120 Y sides & 120 q triangles (indicated in orange, yellow & green), i.e., three sets of 240 geometrical elements, and there are three sets of 60 edges, 60 internal corners, 60 internal sides & 60 internal triangles (indicated in blue, indigo & violet), i.e., three sets of 240 elements. Hence, there are seven more sets of 240 geometrical elements.
We see that the 2400 geometrical elements comprise ten sets of 240 that are made up of three sets in the faces and seven sets that comprise two triplets of sets and a single set. This 3:3:3:1 pattern reproduces the pattern of Sephiroth of the Tree of Life:
12
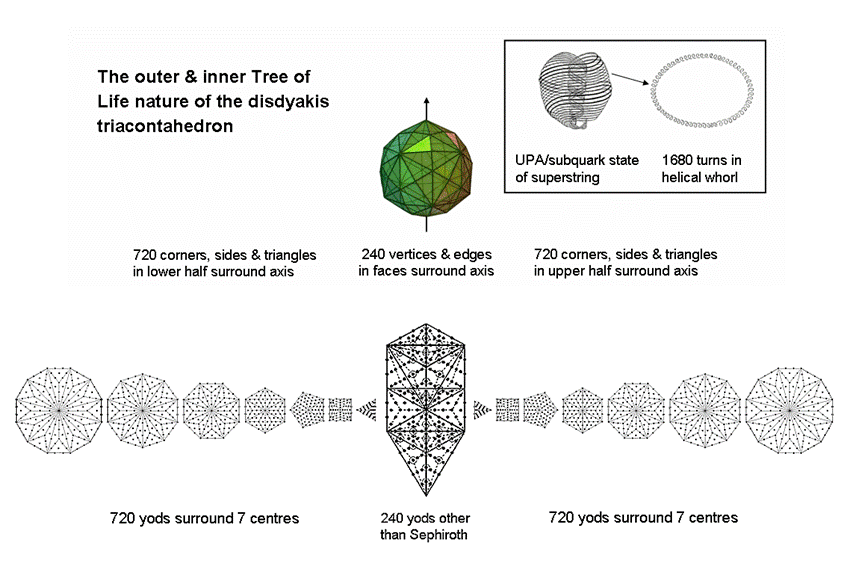
Figure 11. The 720:240:720 pattern of yods in the two sets of seven polygons and the 1-tree corresponds to the pattern of distribution of the 1680 geometrical elements that surround an axis of the disdyakis triacontahedron.
13
Kether-Chokmah-Binah
Chesed-Geburah-Tiphareth
Netzach-Hod-Yesod
MalkuthThere are 720 elements in the faces that are unshared with the remaining 1680 elements. This pattern is the counterpart of the 72 roots of E6 and the 168 other roots of E8. The 1680 elements comprise 60 vertices & 180 edges, i.e., 240 elements in the faces, leaving 1440 elements in the interior, 720 elements being in each half of the disdyakis triacontahedron. The division:
1680 = 720 + 240 + 720
Is embodied in the 240 yods other than SLs in the 1-tree and the 720 yods that surround the centres of the two sets of seven Type B polygons of the inner Tree of Life (Fig. 11). Every yod or geometrical element corresponds to a circular turn of each helical whorl of the UPA/subquark superstring.
5. The 1-tree
The 10-fold UPA/superstring as the 10-fold division in the 1-tree
When its 19 triangles are turned into Type A triangles, i.e., when each triangle is divided into its three sectors which are then changed into tetractyses, the 1-tree contains 251 yods (Fig. 12). Their 11 corners are “Sephirothic levels” (SLs), as Daath is Yesod of the next higher Tree. Hence, the transformation generates (251−11=240) yods that belong to (19×3=57) tetractyses. The 19 triangles have 25 sides. Inside them are (19×3=57) sides of tetractyses. (251−57=194) yods are on the (25+57=82) sides of these tetractyses, where 194 is the number value of Tzadekh, the Mundane Chakra of Chesed (see Table 1). The
Figure 12. The 251 yods in the 1-tree generated when its 19 triangles are Type A. (Circles denote yods that are directly behind other yods).
194 yods comprise (2×82=164) hexagonal yods and (11+19=30) corners. The 1-tree contains (251−30=221) hexagonal yods.
Figure 13. The 1-tree embodies the 248 roots of E8.
The 1-tree is the lowest Tree of a set of overlapping Trees of Life. Below its apex (Kether) and outside the 1-tree on each side are four red hexagonal yods (Fig. 13). One is at the centre of a tetractys, two are on a side of this tetractys and another is on the vertical side of another tetractys. These eight hexagonal yods belonging to the next higher Tree of Life consist of two that are at centres of two tetractyses and six that are on four sides of four tetractyses. Below the apex of the 1-tree are therefore eight red, hexagonal yods that belong to the second Tree and 240 black yods other than Sephiroth that belong to the lowest14
Tree, that is, 248 yods other than Sephiroth, where 248 is the number value of Raziel, the Archangel of Chokmah. The eight red hexagonal yods outside the 1-tree symbolize the eight simple roots of E8, the rank-8, exceptional Lie group with dimension 248; the 240 black yods denote its 240 roots. As the latter include 221 hexagonal yods in the 1-tree, there are (8+221=229) hexagonal yods in the 248 yods that are below the top of the 1‑tree. 229 is the 50th prime number, showing how ELOHIM, the Godname of Binah with number value 50, prescribes the number of hexagonal yods below the top of the lowest Tree of Life. As the eight hexagonal yods outside it belong to four tetractyses, the 248 yods belong to (57+4=61) tetractyses, where 61 is the 31st odd integer and 31 is the number value of EL, the Godname of Chesed. They comprise 19 corners, (57+2=59) hexagonal yods at centres of 61 tetractyses & (164+6=170) hexagonal yods on their (82+4=86) sides.
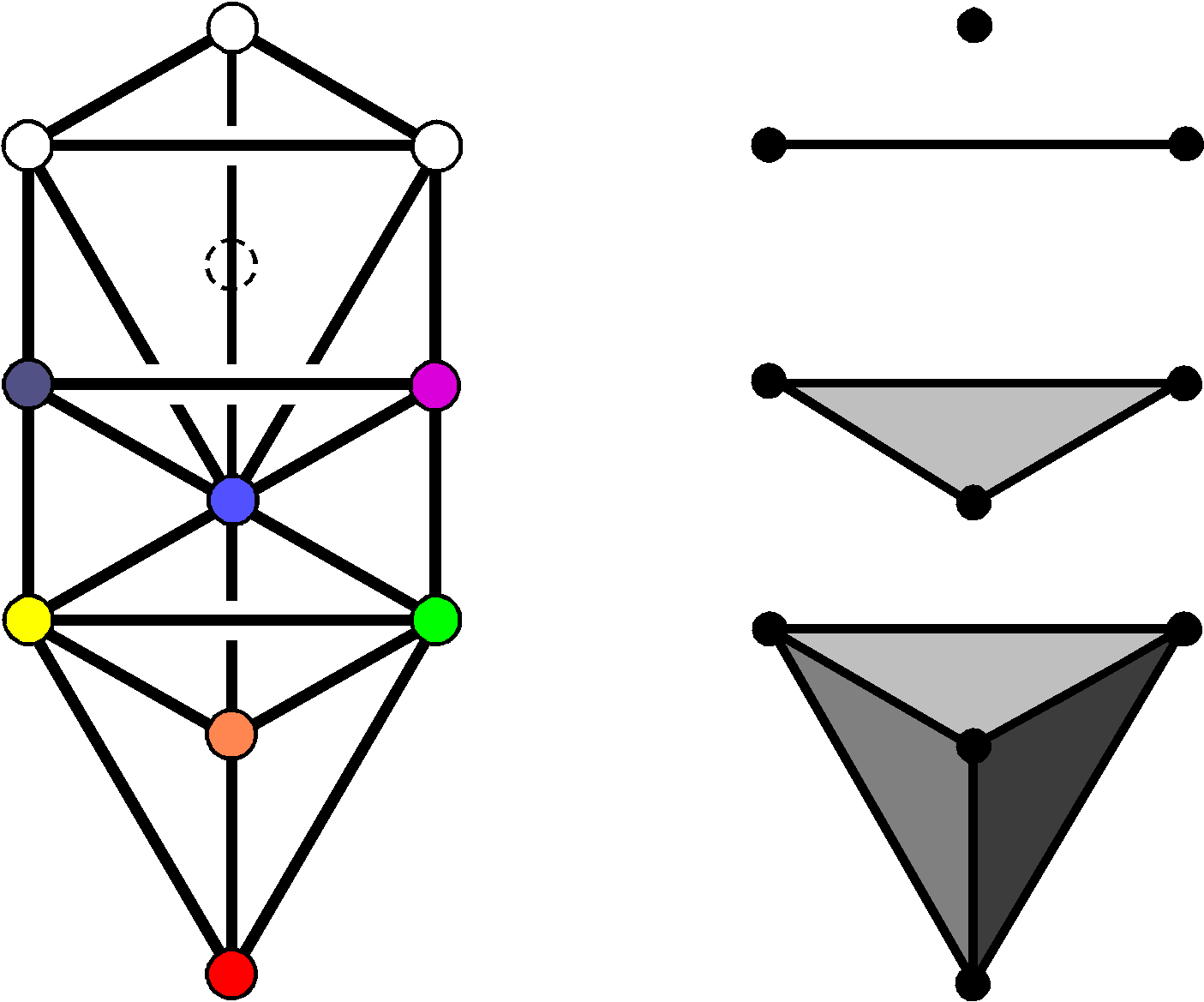
Figure 14. The Tree of Life & its trunk.
The trunk of the Tree of Life (Fig. 14) consists of the mathematical sequence of the point (Kether), straight line (Chokmah-Binah Path), triangle (corners at Chesed, Geburah & Tiphareth) & tetrahedron (vertices at Netzach, Hod, Yesod & Malkuth). It expresses the emergence of basic, 3-dimensional form from the dimensionless point. The ten points in space needed to achieve this represent the integers 1, 2, 3 & 4, which are also symbolized by the four rows of the Pythagorean tetractys. The trunk is composed of 26 geometrical elements (ten points, ten lines, five triangles & one tetrahedron), where 26 is the number value of YAHWEH, the Godname of Chokmah (see Table 1). When these triangles are Type A triangles, the trunk has 15 corners of 15 triangular sectors with 25 sides, i.e., 55 geometrical elements, where 55 is the tenth triangular number:
55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
and the tenth Fibonacci number. This demonstrates how the Decad (10) arithmetically determines the geometrical composition of the trunk of the Tree of Life that represents this number. Table 5 lists the numbers of yods in the trunk other than those coinciding with Sephiroth:
Table 5. The non-Sephirothic yod population of the trunk of the Tree of Life.
Corners Hexagonal yods
at centreHexagonal yods
on sidesTotal Point 0 0 0 0 Line 0 0 2 2 Triangle 1 3 12 4 + 12 Tetrahedron 4 12 12 + 24 = 36 4 + (12+12) + 24 Total 5 15 50 (2+4+4=10) + 12 + 24 + 24 = 70
ADONAI, the Godname of Malkuth with number value 65, prescribes the trunk because its 15 tetractyses have 65 hexagonal yods. ELOHIM, the Godname of Binah with number value 50, shapes the trunk because 50 hexagonal yods line its 25 sides. The branches of the 1-tree are all those parts of it other than its trunk. They have (240−70=170) yods. As the 240 yods comprise 19 corners of 57 tetractyses & 221 hexagonal yods, the branches contain (19−5=14) corners & (221−65=156) hexagonal yods in (57−15=42) tetractyses, i.e., (14+156=170) yods. The distinction between the trunk & branches of the 1-tree therefore generates the division: 240 = 70 + 170, where 70 = 5 corners + 65 hexagonal yods and 170 = 14 corners + 156 hexagonal yods. The 240 yods include (19+57=76) corners & centres of tetractyses, where 76 is the number value of YAHWEH ELOHIM, the Godname of Tiphareth.
According to Table 5, the numbers of yods in the trunk are:
70 = 10 + 12 + 24 + 24.
Suppose that we add the two hexagonal yods on the Path joining Daath and Tiphareth. The projection of this line onto the plane of the (7+7) enfolded polygons making up the inner Tree of Life is the side that they all share — what we have called the "root edge." This Path is its counterpart in the outer Tree of Life. It is what may be called the "root" of the Tree of Life. Its trunk and root constitute a set of 72 yods, where
72 = (10+2) + 12 + 24 + 24 = (12+12) + 24 + 24 = 24 + 24 + 24.
The 72 yods consist of three sets of 24 yods (Fig. 15). This leaves (170−2=168) yods in the branches made up of 14 corners and 154 hexagonal yods in 14 Type A triangles with two hexagonal yods on each of their 14 sides (there are actually 15 sides but one is the line between Daath & Tiphareth,
15
Figure 15. The 1-tree embodies the 240 roots of the superstring gauge symmetry E8. Circles represent yods that are behind other yods.
the two hexagonal yods on which have been added to the 70 yods in the trunk). There are nine hexagonal yods inside each Type A triangle, so that the 168 yods comprise 14 corners, 14 sets of nine hexagonal yods and 14 pairs of hexagonal yods, i.e., 14 sets of 12 yods, or seven sets of 24 yods. Each set of 24 yods comprises two centres of triangles of the 1-tree, four hexagonal yods on two Paths & 18 hexagonal yods inside two triangles. The latter consist of six hexagonal yods at centres of six tetractyses & 12 hexagonal yods on six sides of them, so that the 24 yods comprise two corners of tetractyses, six hexagonal yods at their centres and (4+12=16) hexagonal yods on their sides. This 2:6:16 pattern is identical to what is found for the 24 transverse dimensions of bosonic strings, for they comprise two large-scale dimensions, six dimensions of the compactified space of superstrings and 16 higher dimensions. The following correspondences exist:
This is not coincidental, because the 240 yods symbolize the 240 roots of E8, whose associated gauge charges are spread along the ten whorls of the E8×E8 heterotic superstring, ten to a whorl, and each gauge charge is the result of an oscillation along each of the 24 transverse dimensions of space. Nevertheless, this analogy between the hidden yod composition of the 1-tree and the pattern of dimensions of space predicted by the theories of bosonic strings and superstrings is remarkable.
Notice that the 72 yods, which symbolize the 72 roots of E6, the rank-6, exceptional subgroup of E8, have
16
Figure 16. The (7+7) triangles making up the branches of the 1-tree.
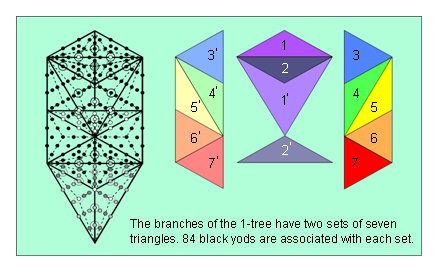
been compounded from a set of 70 yods making up the trunk of the 1-tree and the two hexagonal yods on the Daath-Tiphareth Path that constitutes its root. Figure 1 indicates that the 72 roots also consist of a set of 70 roots and two roots represented by the 8-tuples (½, ½, ½, ½, ½, ½, ½, ½) and (-½, -½, -½, -½, -½, -½, -½, -½). So the group-theoretical composition of the roots of E6 is paralleled by the yod composition of the trunk and the root of the Tree of Life.The 240 yods needed to construct the 1-tree from Type A triangles divide into ten sets of 24 yods, which divide further into three sets of 24 and seven sets of 24. This 3:7 division is the Tree of Life counterpart of the three major whorls and seven minor whorls of the UPA/subquark state of the E8×E8 heterotic superstring (see Fig. 2). The three major whorls are the manifestation of the root and trunk of the 1-tree and the seven minor whorls are the manifestation of its branches. The factorization: 168 = 7×24 is made possible by the facts that: 1. the branches of the 1-tree contain 14 triangles, and 2. each side of the 1-tree is the mirror image of the other. Five triangles (coloured dark or light shades of red, orange, yellow, green & blue) are on each side of the central Pillar of Equilibrium, which is straddled by four triangles coloured light & dark shades of indigo and violet (Fig. 16). The dark shades of these two colours can be associated with one side of the 1-tree and the light shades can be associated with the other side. Therefore, the factor of seven in the factorization arises simply from the fact that seven triangles can be associated with the left-hand side of the 1-tree and seven triangles can be associated with its right-hand side. There are two hexagonal yods on a side shared by two triangles. One hexagonal yod is associated with one triangle and the second one should be regarded as associated with the other triangle. This allows 12 yods to be associated with each triangle. Each set of 24 yods consists of 12 yods associated with a triangle in each side of the 1-tree, so that the 168 yods divide into two sets of 84 yods associated with each half of it. This 84:84 division was encountered in earlier analyses of sacred geometries in this article and has been discussed in previous articles in many different contexts. It manifests in the subquark as the outer and inner halves of each helical whorl of the UPA, each having 840 circular turns that make 2½ revolutions around its axis of spin, that is, 168 turns make a half-revolution and 84 turns make a quarter-revolution. Figure 1 indicates that the 168 roots of E8 that are not roots of E6 consist of three sets of 28 (i.e., 84 roots), a set of 56 & another set of 28 (i.e., 84 roots). So these 168 roots divide naturally into two sets of 84 roots. Their counterparts in the branches of the 1-tree are the 84 yods that belong to the seven triangles associated with its left-hand or right-hand half.
Four corners of tetractyses, four hexagonal yods at their centres & eight hexagonal yods on their sides (i.e., 16 yods) are aligned with the central Pillar of Equilibrium straddled by the four triangles. Hence, (168−16=152) yods belong to the branches in both halves of the 1-tree. 76 yods in the branches belong to each half, where 76 is the number value of YAHWEH ELOHIM, the Godname of Tiphareth. The eight hexagonal yods symbolizing the eight simple roots of E8 consist of four yods outside the 1-tree on either side of the Pillar of Equilibrium (see Fig. 13). Outside the trunk are (76+4=80) yods on either side, where 80 is the number value of Yesod. This is also the number of yods in the trunk when the (10+1) Sephirothic corners of the 19 triangles are included.
The 1-tree consists of 30 corners of 57 triangles with 82 sides, i.e., 112 corners & sides, where 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod, and 87 corners & triangles, where 87 is the number value of Levanah, the Mundane Chakra of Yesod. The 1-tree consists of 169 points, lines & triangles. In other words, below its apex are 168 geometrical elements. The number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, is the number of geometrical elements needed to construct the 1-tree, starting from the mathematical point represented by its apex. Here is yet more, truly amazing evidence that the gematria number values of the Hebrew names of the Sephiroth, their Godnames, etc have a geometrical basis.
In conclusion, the natural, ten-fold splitting into ten sets of 24 geometrical elements of the number 240 embodied in five sacred geometries has its realization in the microscopic world as the ten whorls of the E8×E8 heterotic superstring, each carrying 24 gauge charges of E8, as described over a century ago by Annie Besant & C.W. Leadbeater in the particle that they claimed is the basic unit of matter.
Endnotes
Proof that 16800 is the sum of 240 odd integersUsing the identity:
17
168 = 132 – 1,
16800 = 168×102 = (132– 1)102 = 1302 – 102 = (2×65)2 – (2×5)2 = 4(652 − 52).
As652 = 1 + 3 + 5 +... + 129
and
52 = 1 + 3 + 5 + 7 + 9,
therefore,
16800 = 4(11 + 13 + 15 +... + 129),
i.e., 16800 is the sum of [4×(65–5) = 4×60 = 240] odd integers, the largest of which is 129. This is the number of YAHWEH SABAOTH, the Godname of Netzach, which is the fourth Sephirah of Construction, counting from Malkuth (see Table 1).
18

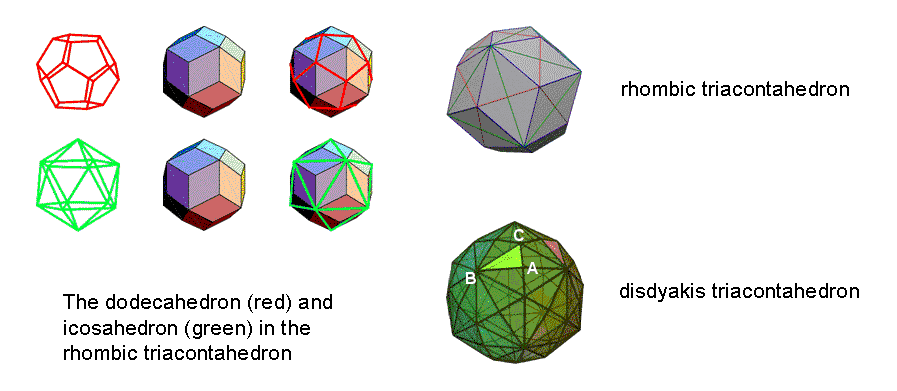

.png)